全国卷新课标高考中档大题专项训练立体几何与空间向量
2024年9-10月新高考数学名校模拟大题汇编:立体几何(解析版)

2024年9-10月新高考数学名校大题汇编:立体几何大题必备基础知识梳理【知识点一:空间向量及其加减运算】(1)空间向量在空间,我们把具有大小和方向的量叫做空间向量,向量的大小叫做向量的长度或模.空间向量也可用有向线段表示,有向线段的长度表示向量的模,若向量a 的起点是A ,终点是B ,则向量a也可以记作AB ,其模记为a或AB .(2)零向量与单位向量规定长度为0的向量叫做零向量,记作0.当有向线段的起点A 与终点B 重合时,AB=0.模为1的向量称为单位向量.(3)相等向量与相反向量方向相同且模相等的向量称为相等向量.在空间,同向且等长的有向线段表示同一向量或相等向量.空间任意两个向量都可以平移到同一个平面,成为同一平面内的两个向量.与向量a 长度相等而方向相反的向量,称为a 的相反向量,记为-a .(4)空间向量的加法和减法运算①OC=OA+OB=a +b ,BA=OA-OB=a -b.如图所示.②空间向量的加法运算满足交换律及结合律a +b =b +a ,a +b +c =a +b +c【知识点二:空间向量的数乘运算】(1)数乘运算实数λ与空间向量a 的乘积λa 称为向量的数乘运算.当λ>0时,λa 与向量a方向相同;当λ<0时,向量λa 与向量a 方向相反.λa 的长度是a的长度的λ 倍.(2)空间向量的数乘运算满足分配律及结合律λa +b =λa +λb ,λμa =λμ a .(3)共线向量与平行向量如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量,a 平行于b ,记作a ⎳b.(4)共线向量定理对空间中任意两个向量a ,b b ≠0,a ⎳b的充要条件是存在实数λ,使a =λb.(5)直线的方向向量如图8-153所示,l 为经过已知点A 且平行于已知非零向量a 的直线.对空间任意一点O ,点P 在直线l 上的充要条件是存在实数t ,使OP =OA +ta ①,其中向量a 叫做直线l 的方向向量,在l 上取AB =a ,则式①可化为OP =OA +tAB =OA +t OB -OA =1-t OA +tOB ②①和②都称为空间直线的向量表达式,当t =12,即点P 是线段AB 的中点时,OP =12OA +OB ,此式叫做线段AB 的中点公式.(6)共面向量如图8-154所示,已知平面α与向量a ,作OA=a,如果直线OA 平行于平面α或在平面α内,则说明向量a 平行于平面α.平行于同一平面的向量,叫做共面向量.(7)共面向量定理如果两个向量a ,b不共线,那么向量p 与向量a,b共面的充要条件是存在唯一的有序实数对x ,y ,使p =xa +yb.推论:①空间一点P 位于平面ABC 内的充要条件是存在有序实数对x ,y ,使AP =xAB +yAC;或对空间任意一点O ,有OP-OA=xAB+yAC,该式称为空间平面ABC 的向量表达式.②已知空间任意一点O 和不共线的三点A ,B ,C ,满足向量关系式OP =xOA +yOB +zOC (其中x +y +z =1)的点P 与点A ,B ,C 共面;反之也成立.【知识点三:空间向量的数量积运算】(1)两向量夹角已知两个非零向量a ,b ,在空间任取一点O ,作OA =a ,OB =b ,则∠AOB 叫做向量a ,b 的夹角,记作a ,b ,通常规定0≤a ,b ≤π,如果a ,b =π2,那么向量a ,b 互相垂直,记作a ⊥b .(2)数量积定义已知两个非零向量a ,b ,则a b cos a ,b 叫做a ,b 的数量积,记作a ⋅b ,即a ⋅b =a b cos a,b.零向量与任何向量的数量积为0,特别地,a ⋅a =a 2.(3)空间向量的数量积满足的运算律:λa ⋅b =λa ⋅b ,a ⋅b =b ⋅a (交换律);a ⋅b +c =a ⋅b +a ⋅c(分配律).【知识点四:空间向量的坐标运算及应用】(1)设a =a 1,a 2,a 3 ,b=b 1,b 2,b 3 ,则a +b=a 1+b 1,a 2+b 2,a 3+b 3 ;a -b=a 1-b 1,a 2-b 2,a 3-b 3 ;λa=λa 1,λa 2,λa 3 ;a ⋅b=a 1b 1+a 2b 2+a 3b 3;a ⎳b b ≠0⇒a 1=λb 1,a 2=λb 2,a 3=λb 3;a ⊥b⇒a 1b 1+a 2b 2+a 3b 3=0.(2)设A x 1,y 1,z 1 ,B x 2,y 2,z 2 ,则AB =OB -OA=x 2-x 1,y 2-y 1,z 2-z 1 .这就是说,一个向量在直角坐标系中的坐标等于表示该向量的有向线段的终点的坐标减起点的坐标.(3)两个向量的夹角及两点间的距离公式.①已知a =a 1,a 2,a 3 ,b =b 1,b 2,b 3 ,则a =a 2=a 12+a 22+a 32;b =b2=b 12+b 22+b 32;a ⋅b=a 1b 1+a 2b 2+a 3b 3;cos a ,b =a 1b 1+a 2b 2+a 3b 3a 12+a 22+a 32b 12+b 22+b 32;②已知A x 1,y 1,z 1 ,B x 2,y 2,z 2 ,则AB=x 1-x 22+y 1-y 2 2+z 1-z 2 2,或者d A ,B =AB.其中d A ,B 表示A 与B 两点间的距离,这就是空间两点的距离公式.(4)向量a 在向量b 上的投影为a cos a ,b=a ⋅b b.【知识点五:法向量的求解与简单应用】(1)平面的法向量:如果表示向量n 的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作n ⊥α,如果n⊥α,那么向量n叫做平面α的法向量.几点注意:①法向量一定是非零向量;②一个平面的所有法向量都互相平行;③向量n 是平面的法向量,向量m 是与平面平行或在平面内,则有m ⋅n =0.第一步:写出平面内两个不平行的向a=x 1,y 1,z 1 ,b=x 2,y 2,z 2 ;第二步:那么平面法向量n=x , y , z ,满足n ⋅a=0n ⋅b =0⇒xx 1+yy 1+zz 1=0xx 2+yy 2+zz 2=0.(2)判定直线、平面间的位置关系①直线与直线的位置关系:不重合的两条直线a ,b 的方向向量分别为a ,b.若a ∥b,即a =λb,则a ∥b ;若a ⊥b,即a ⋅b=0,则a ⊥b .②直线与平面的位置关系:直线l 的方向向量为a ,平面α的法向量为n ,且l ⊥α.若a ∥n ,即a =λn ,则l ⊥α;若a ⊥n ,即a ⋅n =0,则a ∥α.(3)平面与平面的位置关系平面α的法向量为n 1,平面β的法向量为n 2.若n 1∥n 2,即n 1=λn 2,则α∥β;若n 1⊥n 2,即n 1⋅n 2=0,则α⊥β.【知识点六:空间角公式】(1)异面直线所成角公式:设a ,b分别为异面直线l 1,l 2上的方向向量,θ为异面直线所成角的大小,则cos θ=cos a,b =a ⋅b a b.(2)线面角公式:设l 为平面α的斜线,a 为l 的方向向量,n为平面α的法向量,θ为l 与α所成角的大小,则sin θ=cos a ,n=a ⋅na n.(3)二面角公式:设n 1,n 2分别为平面α,β的法向量,二面角的大小为θ,则θ=n 1 ,n 2 或π-n 1 ,n 2(需要根据具体情况判断相等或互补),其中cos θ =n 1 ⋅n 2n 1 n 2.【知识点七:空间中的距离】求解空间中的距离(1)异面直线间的距离:两条异面直线间的距离也不必寻找公垂线段,只需利用向量的正射影性质直接计算.如图,设两条异面直线a ,b 的公垂线的方向向量为n ,这时分别在a ,b 上任取A ,B 两点,则向量在n上的正射影长就是两条异面直线a ,b 的距离.则d =AB ⋅n |n |=|AB ⋅n ||n|即两异面直线间的距离,等于两异面直线上分别任取两点的向量和公垂线方向向量的数量积的绝对值与公垂线的方向向量模的比值.(2)点到平面的距离A 为平面α外一点(如图),n为平面α的法向量,过A 作平面α的斜线AB 及垂线AH .|AH |=|AB |⋅sin θ=|AB |⋅|cos <AB ,n >|=|AB ||AB ⋅n |AB ⋅n =|AB ⋅n|nd =|AB ⋅n||n|【必考题型汇编】1.(湖南省长沙市2025届高三六校九月大联考解析第16题)如图,四边形ABCD 与四边形ADEF 均为等腰梯形,BC ⎳AD ,EF ⎳AD ,AD =4,AB =2,BC =EF =2,AF =11,FB ⊥平面ABCD ,M 为AD 上一点,且FM ⊥AD ,连接BD 、BE 、BM .(1)证明:BC ⊥平面BFM ;(2)求平面ABF 与平面DBE 的夹角的余弦值.方法提供与解析:(1)解析:因为FB ⊥平面ABCD ,又AD ⊂平面ABCD ,所以FB ⊥AD .又FM ⊥AD ,且FB ∩FM =F ,所以AD ⊥平面BFM .因为BC ⎳AD ,所以BC ⊥平面BFM .(2)解析:作EN ⊥AD ,垂足为N ,则FM ⎳EN .又EF ⎳AD ,所以四边形FMNE 是平行四边形,又EN ⊥AD ,所以四边形FMNE 是矩形,又四边形ADEF 为等腰梯形,且AD =4,EF =2,所以AM =1.由(1)知AD ⊥平面BFM ,所以BM ⊥AD .又AB =2,所以BM =1.在Rt △AFM 中,FM =AF 2-AM 2=10.在Rt △FMB 中,∴FB =FM 2-BM 2=3.由上可知,能以BM 、BC 、BF 所在的直线分别为x 轴、y 轴、z 轴建立如图所示空间直角坐标系.则A -1,-1,0 ,B 0,0,0 ,F 0,0,3 ,D -1,3,0 ,E 0,2,3 ,所以,AB =1,1,0 ,BF =0,0,3 ,BD =-1,3,0 ,BE=0,2,3 ,设平面ABF 的法向量为m=x 1,y 1,z 1 ,由m ⋅AB=0m ⋅BF =0,得x 1+y 1=0z 1=0 ,可取m =1,-1,0 ;设平面BDE 的法向量为n=x 2,y 2,z 2 ,由n ⋅BD=0n ⋅BE =0,得-x 2+3y 2=0-2y 2+3z 2=0 ,可取n=9,3,2 .因此,cos ‹m ,n›=m ⋅n m ⋅n=9-31+1⋅81+9+4=34747.依题意可知,平面ABF 与平面DBE 的夹角的余弦值为34747.2.(辽宁省沈阳市郊联体2024年高三上学期开学联考解析第17题)如图,已知斜三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C ⊥侧面AA 1B 1B ,侧面BB 1C 1C 是矩形,侧面AA 1B 1B 是菱形,∠BAA 1=60°,AB =2BC =2,点E ,F ,G 分别为棱AA 1,A 1C ,BB 1的中点.(1)证明:FG ⎳平面ABC ;(2)求二面角A 1-B 1C -E 的余弦值.方法提供与解析:解析:(1)证明:因为点E ,F ,G 分别为棱AA 1,A 1C ,BB 1的中点,连接EF ,EG ,则EF ⎳AC ,EG ⎳AB ,又因为EF ⊄平面ABC ,AC ⊂平面ABC ,所以EF ⎳平面ABC ,同理可得EG ⎳平面ABC ,因为EF ∩EG =E ,EF ⊂平面EFG ,EG ⊂平面EFG ,所以平面EFG ⎳平面ABC ,因为FG ⊂平面EFG ,所以FG ⎳平面ABC .(2)解:侧面BB 1C 1C 是矩形,所以BC ⊥BB 1,又因为平面BB 1C 1C ⊥平面AA 1B 1B ,平面BB 1C 1C ∩平面AA 1B 1B =BB 1,所以BC ⊥平面AA 1B 1B ,又BE ⊂平面AA 1B 1B ,因此BC ⊥BE .在菱形AA 1B 1B 中,∠BAA 1=60°,因此△AA 1B 是等边三角形,又E 是AA 1的中点,所以BE ⊥AA 1,从而得BE ⊥BB 1.如图,以B 为坐标原点,BE ,BB 1,BC 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.因为AB =2BC =2,所以BE =AB sin60°=3,因此B 10,2,0 ,A 13,1,0 ,E 3,0,0 ,C 0,0,1 ,所以B 1C =0,-2,1 ,B 1E =3,-2,0 ,B 1A 1=3,-1,0 ,设平面EB 1C 的法向量为m=x 1,y 1,z 1 ,由m⊥B 1C,得-2y 1+z 1=0 ,令y 1=1,得m =23,1,2设平面A 1B 1C 的法向量为n=x 2,y 2,z 2 ,由n ⊥B 1Cn ⊥B 1A 1,得-2y 2+z 2=03x 2-y 2=0 ,令y 2=1,得n =33,1,2 ,cos ‹m ,n ›=m ⋅n m ⋅n =23+1+4193⋅163=171976,即二面角A 1-B 1C -E 的余弦值为171976.3.如图,在四棱柱ABCD -A 1B 1C 1D 1中,AA 1⊥平面ABCD ,底面ABCD 为梯形,AD ⎳BC ,BC =4,AB =AD =DC =AA 1=2,Q 为AD 的中点.(1)在A 1D 1上是否存在点P ,使直线CQ ⎳平面AC 1P ,若存在,请确定点P 的位置并给出证明,若不存在,请说明理由;(2)若(1)中点P 存在,求平面AC 1P 与平面ABB 1A 1所成的锐二面角的余弦值.方法提供与解析:(1)解析:(几何法)存在,证明如下:在四棱柱ABCD -A 1B 1C 1D 1中,因为平面ABCD ⎳平面A 1B 1C 1D 1,所以可在平面A 1B 1C 1D 1内作C 1P ⎳CQ ,由平面几何知识可证△C 1D 1P ≅△CDQ ,所以D 1P =DQ ,可知P 是A 1D 1中点,因为C 1P ⊂平面AC 1P ,所以CQ ⎳平面AC 1P .即存在线段A 1D 1的中点,满足题设条件.满足条件的点只有一个,证明如下:当CQ ⎳平面AC 1P 时,因为CQ ⎳平面A 1B 1C 1D 1,所以过C 1作平行于CQ 的直线既在平面A 1C 1P 内,也在平面A 1B 1C 1D 1内,而在平面A 1B 1C 1D 1内过C 1只能作一条直线C 1P ⎳CQ ,故满足条件的点P 只有唯一一个.所以,有且只有A 1D 1的中点为满足条件的点P ,使直线CQ ⎳平面AC 1P .(2)解析:(坐标法)过点D 作DF ⊥BC ,垂足为F ,又因为DD 1⊥平面ABCD ,以D 为坐标原点,分别以DA ,DF ,DD 1所在直线为x 轴,y 轴,z 轴建立如图的空间直角坐标系D -xyz ,则A 2,0,0 ,P 1,0,2 ,C 1-1,3,2 ,A 12,0,2 ,B 3,3,0 ,P A =1,0,-2 ,PC 1 =-2,3,0 ,AB =1,3,0 ,AA 1=0,0,2设平面P AC 1的法向量为n=x ,y ,z ,则有n ⋅P A=0,n ⋅PC 1 =0,即x -2z =0,-2x +3y =0. 令x =23,得y =4,z =3,所以n=23,4,3 .设平面ABB 1A 1的法向量为m=x ,y ,z .则有AB ⋅m =0,AA 1 ⋅m =0,即x +3y =0,2z =0. 令x =3,得y =-1,z =0,所以m=3,-1,0 .所以cos n ,m =n ⋅m n m=6-4+0231=3131.故平面AC 1P 与平面ABB 1A 1所成的锐二面角的余弦值为3131.4.(福建泉州市2025届高中毕业班模拟检测(一)解析第16题)4:如图,在四棱锥P -ABCD 中,PD =PC =CB =BA =12AD =2,AD ⎳CB ,∠CPD =∠ABC =90°,平面PCD ⊥平面ABCD ,E 为PD 中点.(1)求证:PD ⊥平面PCA ;(2)点Q 在棱P A 上,CQ 与平面PDC 所成角的正弦值为63,求平面PCD 与平面CDQ 夹角的余弦值.方法提供与解析:(1)解析:由题意:BC =AB =2,∠ABC =90°,AC =AB 2+BC 2=22同理CD =22,又AD =4,CD 2+AC 2=AD 2,CD ⊥AC .而CD =22=PD 2+PC 2,即PC ⊥PD ,又平面PCD ⊥平面ABCD ,平面PCD ∩平面ABCD =CD ,AC ⊂平面ABCD ,AC ⊥平面PCD ,PD ⊂平面PCD ,PD ⊥AC ,又PC ⊥PD ,且PC ⊂面PCA ,AC ⊂面PCA ,PC ∩AC =C ,PD ⊥平面PCA .(2)解析:以C 为原点,建立如图所示的空间直角坐标系,则C 0,0,0 ,A 0,22,0 ,D 22,0,0 ,P 2,0,2 ,所以CD =22,0,0 ,CP =2,0,2 ,P A=-2,22,-2 ,设PQ =λP A 0<λ<1 ,有CQ =CP +λP A=21-λ ,22λ,21-λ ,取面PCD 的一个法向量m =0,1,0 ,则cos CQ ,m =22λ41-λ 2+8λ2=63,λ=12,故CQ =22,2,22.令n=x ,y ,z 是平面CDQ 的一个法向量,则n ⋅CD =0n ⋅CQ =0,即22x =022x +2y +22z =0,令y =1,有n =0,1,-2 ,则cos ‹n ,m › =n ⋅m n m=55,故平面PCD 与平面CDQ 夹角的余弦值为55.5.(长沙市雅礼中学2025届高三上学期(9月)综合自主测试解析第17题)5:如图(1),在△ABC 中,CD ⊥AB ,BD =2CD =2AD =4,点E 为AC 的中点.将△ACD 沿CD 折起到△PCD 的位置,使DE ⊥BC ,如图(2).图(1)图(2)(1)求证:PB ⊥PC ;(2)在线段BC 上是否存在点F ,使得CP ⊥DF ?若存在,求二面角P -DF -E 的余弦值;若不存在,说明理由。
专题九 立体几何与空间向量(教师版)--2020-2023高考真题数学专题分类汇编

专题九立体几何与空间向量--2020-2023高考真题数学专题分类汇编真题卷题号考点考向2023新课标1卷12基本的立体图形正方体、球体、四面体、圆柱体的结构特征14简单几何体的表面积与体积求四棱台的体积18空间直线、平面的垂直、二面角线线平行的判定、已知二面角确定动点位置2023新课标2卷9基本的立体图形、二面角圆锥的结构特征、圆锥的表面积与体积、二面角的定义14简单几何体的表面积与体积求四棱台的体积20空间直线、平面的垂直、二面角异面垂直的判定、求二面角2022新高考1卷4简单几何体的表面积与体积求棱台的体积8简单几何体的表面积与体积、外接球求棱锥的体积、球的切接问题9空间角求异面直线成角、线面角19空间中的距离、空间角求点到平面的距离、求二面角2022新高考2卷7简单几何体的表面积与体积求外接球的表面积11简单几何体的表面积与体积求三棱锥的体积20空间直线、平面的平行、空间角线面平行的判定、求二面角2021新高考1卷3基本的立体图形求圆锥的母线长12基本的立体图形几何体中的动点问题(动点轨迹、三棱锥的体积、线线垂直的判定、线面垂直的判定)20空间直线、平面的垂直、简单几何体的表面积与体积线线垂直的判定、求三棱锥的体积4简单几何体的表面积与体积求球的表面积2021新高考2卷5简单几何体的表面积与体积求正四棱台的体积10空间直线、平面的垂直线线垂直的判定19空间直线、平面的垂直、空间角面面垂直的判定、求二面角2020新高考1卷4空间角求线面角16基本的立体图形球的截面问题20空间直线、平面的垂直、空间角线面垂直的判定、求线面角正弦值的最值2020新高考2卷13简单几何体的表面积与体积求三棱锥的体积20空间直线、平面的垂直、空间角线面垂直的判定、求线面角【2023年真题】1.(2023·新课标I 卷第12题)(多选)下列物体中,能够被整体放入棱长为1(单位:)m 的正方体容器(容器壁厚度忽略不计)内的有()A.直径为0.99m 的球体B.所有棱长均为1.4m 的四面体C.底面直径为0.01m ,高为1.8m 的圆柱体D.底面直径为1.2m ,高为0.01m 的圆柱体【答案】ABD 【解析】【分析】本题考查正方体内接其它几何体的问题,属于综合题.由正方体、球体、四面体、圆柱体的结构特征和棱长、直径的大小关系,逐个分析选项可得解.【解答】解:选项A ,正方体的内切球直径为10.99>,故A 正确;选项B ,连接正方体的六个面对角线,可以得到一个正四面体, 1.4>,故B 正确;对于C ,D ,假设放入最大的圆柱AB ,A ,B 分别为圆柱下、上底面的圆心,设圆柱底面半径为r ,正方体体对角线为CD ,||3CD =263AC ∴=,当r 取定时,圆柱的高 max 36.h r =对于C ,当0.005r =时, max 360.005 1.72 1.8h =≈<,故C 错.对于D ,当0.6r =时, max 30.660.260.01h =->,故D 正确.故选:.ABD 2.(2023·新课标II 卷第9题)(多选)已知圆锥的顶点为P ,底面圆心为O ,AB 为底面直径,120,2APB PA ︒∠==,点C 在底面圆周上,且二面角P AC O --为45︒,则()A.该圆锥的体积为πB.该圆锥的侧面积为43πC.22AC =D.PAC ∆3【答案】AC 【解析】【分析】本题考查求圆锥的体积与侧面积,及圆锥中的其他量,属于基础题.A ,B 选项,通过解PAB ∆,求出圆锥的高PO 与底面直径AB ,从而求出体积与侧面积;C ,D 选项,利用PDO ∠为二面角P AC O --的平面角,解三角形求出,PD AC 的长,进一步求出PAC ∆的面积.【解答】解:对于A :在PAB ∆中,2,120PA PB APB ︒==∠=,则1PO =,23AB =故圆锥的体积2111333V PO OA πππ=⋅⋅⋅=⋅⋅⋅=,故A 正确;对于B :圆锥的侧面展开图为扇形,扇形的半径为2,弧长为,故圆锥的侧面积为122S =⋅⋅=,故B 错误;对于C :取AC 中点D ,连接,PD OD ,则,PD AC OD AC ⊥⊥,则PDO ∠为二面角P AC O --的平面角,即45PDO ︒∠=,在Rt PDO ∆中,1PO =,故1,DO PD ==,在Rt ODA ∆中,AD ===,故AC =C 正确;对于D :11222PAC S PD AC ∆=⋅⋅==,故D 正确.故选.AC 3.(2023·新课标I 卷第14题)在正四棱台1111ABCD A B C D -中,2AB =,111A B =,1AA =,则该棱台的体积为__________【答案】【解析】【分析】本题考查正四棱台的体积,属于中档题.可将正四棱台补成正四棱锥,然后分析求解即可.【解答】解:如图,将正四棱台1111ABCD A B C D -补成正四棱锥,则 2AO =,22SA =,162OO =,故 12121(3V S S S S h =++,2222166(2121).326V =⨯++⨯⨯4.(2023·新课标II 卷第14题)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为__________【答案】28【解析】【分析】本题主要考查棱台的体积,属于基础题.根据题意正四棱锥被截后剩余部分为正四棱台,直接计算即可求解.【解答】解:由题意可得四棱台的高为3,上底面面积为224⨯=,下底面面积为4416⨯=,故正四棱台的体积 1(416416)328.3V =⨯+⨯⨯=所得棱台的体积为28.5.(2023·新课标I 卷第18题)如图,在正四棱柱1111ABCD A B C D -中,2AB =,1 4.AA =点2A ,2B ,2C ,2D ,分别在棱1AA ,1BB ,1CC ,1DD 上,21AA =,222BB DD ==,2 3.CC =(1)证明:2222//B C A D ;(2)点P 在棱1BB 上,当二面角222P A C D --为150 时,求2.B P【答案】证明:(1)如图,作21A E BB ⊥于点E ,21D F CC ⊥于点F ,则有22//A E D F ,22A E D F =,即四边形22A EFD 是平行四边形,从而22//A D EF ,又22//B E C F ,221B E C F ==,即四边形22B EFC 是平行四边形,从而22//B C EF ,从而2222//B C A D ,得证.(2)如图,以点B 为原点,以BC 、BA 、1BB 分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系.设(0,0,)P t ,2(2,0,3)C ,2(0,2,1)A ,2(2,2,2)D ,22(2,0,1)A D = ,22(2,-2,2)A C = ,2(0,-2,1)A P t =-,设平面222A C D 的一个法向量为,则,即,令12z =-,则11x =,11y =-,故(1,1,2)m =--设平面22PA C 的一个法向量为,则,即,令22z =,则23x t =-,21y t =-,故(3,1,2)n t t =--二面角222P A C D --的平面角为150 ,,解得1t =或3,则2 1.B P =【解析】本题考查了立体几何中线线平行的判定、二面角等知识,属于中档题.(1)作21A E BB ⊥于点E ,21D F CC ⊥于点F ,构造两个平行四边形,根据平行于同一直线的两直线平行,即可证明2222//.B C A D (2)适当建立空间直角坐标系,设点(0,0,)P t ,分别求出平面222A C D 与平面22PA C 的一个法向量,m n,由二面角222P A C D --为150 ,可知,解出t 的值,进而求得2 1.B P =6.(2023·新课标II 卷第20题)如图三棱锥A BCD -中,DA DB DC ==,BD CD ⊥,60ADB ADC ︒∠=∠=,E 为BC 的中点.(1)证明:;BC DA ⊥(2)点F 满足EF DA =,求二面角D AB F --的正弦值.【答案】解:(1)连接AE ,DE ,DB DC = ,DE BC ∴⊥,又DA DB DC == ,60ADB ADC ︒∠=∠=,ACD ∴ 与ABD 均为等边三角形,AC AB ∴=,AE BC ∴⊥,AE DE E ⋂=,BC ∴⊥平面ADE ,.BC DA ∴⊥(2)设2DA DB DC ===,BC ∴=DE AE ∴==,2AD =,2224AE DE AD ∴+==,AE DE ∴⊥,又AE BC ⊥ ,DE BC E ⋂=,AE ∴⊥平面BCD ,如图建立空间直角坐标系,D ∴,A,B ,(0,0,0)E,(EF DA F =⇒,(DA ∴=,AB =,(AF =,设平面DAB 与平面ABF 的一个法向量分别为1111(,,)n x y z = ,2222(,,)n x y z =,设二面角D AB F --平面角为θ,,1212|||cos |3||||n n n n θ⋅∴=== ,3sin 3θ∴=【解析】本题考查了线面垂直的性质、二面角的求解,是中档题.(1)先判定线面垂直,再结合线面垂直的性质定理得结论;(2)建立空间直角坐标系,得出平面DAB 的法向量和平面ABF 的法向量,由空间向量求解可得结论.【2022年真题】7.(2022·新高考I 卷第4题)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5m 时,相应水面的面积为2140.0;km 水位为海拔157.5m 时,相应水面的面积为2180.0.km 将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m 上升到157.5m时,增加的水量约为 2.65)≈()A.931.010m ⨯B.931.210m ⨯ C.931.410m ⨯ D.931.610m ⨯【答案】C 【解析】【分析】本题考查了棱台的体积公式的应用,属于基础题.读懂题意,结合棱台的体积公式即可求解.【解答】解:依据棱台的体积公式1(3V S S h =⋅+'+⋅1(14000000018000000093=⋅+⨯931.410.m ≈⨯8.(2022·新高考I 卷第8题)已知正四棱锥的侧棱长为l ,其各顶点都在同一个球面上,若该球的体积为36π,且3l ,则该正四棱锥体积的取值范围是()A.81[18,4B.2781[,]44C.2764[,]43D.[18,27]【答案】C 【解析】【分析】本题考查了球的切接问题,涉及棱锥的体积、球的体积、导数等知识,属较难题.有正四棱锥的外接球的性质,可得2212(6)33V a h h h h ==-,利用求导求最值,即可解答.【解答】解:方法(1):设正四棱锥P ABCD -的高为1PO h =,底面边长为a ,球心为O ,由已知易得球半径为3R =,所以22222222)(3)9622(6))2a h h l a h h a h l ⎧+-=⎪⎧=⎪⇒⎨⎨=-⎩⎪+=⎪⎩,因为393962722l h h ⇒⇒,故所以2212(6)33V a h h h h ==-,求导2(4)V h h '=-,所以22(6)3V h h =-在3[,4]2上单调递增,在9[4,2上单调递减,所以max 64(4)3V V ==,min 39327min{(),(()2224V V V V ===,故该正四棱锥体积的取值范围是2764[,].43方法(2):由方法(1)中知22(6)3V h h =-,3922h ,求导2(4)V h h '=-,所以22(6)3V h h =-在3[,4]2上单调递增,在9[4,2上单调递减,所以max 64(4)3V V ==,min 39327min{(),(()2224V V V V ===,故该正四棱锥体积的取值范围是2764[,].439.(2022·新高考II 卷第7题)已知正三棱台的高为1,上下底面的边长分别为同一球面上,则该球的表面积为()A.100π B.128πC.144πD.192π【答案】A 【解析】【分析】本题主要考查了正三棱台和外接球的关系应用,球体表面积公式的应用.【解答】解:由题意易得上底面所在平面截球面所得圆的半径为3,下底面所在平面截球面所得圆的半径为4,设该球的半径为R ,当正三棱台的上、下底面在球心异侧时,1=,无解;所以正三棱台的上、下底面在球心同侧,所以1=,解得225R =,因此该球的表面积为24100.S R ππ==10.(2022·新高考I 卷第9题)(多选)已知正方体1111ABCD A B C D -,则()A.直线1BC 与1DA 所成的角为90︒B.直线1BC 与1CA 所成的角为90︒C.直线1BC 与平面11BB D D 所成的角为45︒D.直线1BC 与平面ABCD 所成的角为45︒【答案】ABD 【解析】【分析】本题主要考查直线与直线所成角及直线与平面所成角,属于中档题.根据正方体的结构特征对各个选项逐一判断分析,即可得解.【解答】解:如图,因为11BC B C ⊥,11//B C DA ,所以11BC DA ⊥,故A 正确;对于选项:B 因为11A B ⊥平面11BB C C ,1BC ⊂平面11BB C C ,所以111BC A B ⊥,又11BC B C ⊥,且1111A B B C B ⋂=,11A B ,1B C ⊂平面11CDA B ,所以1BC ⊥平面11CDA B ,且1CA ⊂平面11CDA B ,所以直线11BC CA ⊥,故B 正确;对于选项:C 连接11AC 与11B D 交于点1O ,因为1B B ⊥平面1111A B C D ,11AC ⊂平面1111A B C D ,所以111B B A C ⊥,又1111A C B D ⊥,且1111B D B B B ⋂=,11B D ,1B B ⊂平面11BB D D ,所以11A C ⊥平面11BB D D ,则11O BC ∠即为直线1BC 与平面11BB D D 所成的角,111111sin 2O C O BC BC ∠==,所以1130O BC ∠=︒,故C 错误;对于选项:D 直线1BC 与平面ABCD 所成的角即为145C BC ∠=︒,所以D 正确.11.(2022·新高考II 卷第11题)(多选)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,//FB ED ,2AB ED FB ==,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为1V ,2V ,3V ,则()A.322V V =B.312V V =C.312V V V =+D.3123V V =【答案】CD 【解析】【分析】本题主要考查三棱锥的体积,属于基础题.【解答】解:设22AB ED FB ===,则1142233V =⨯⨯=,21221.33V =⨯⨯=连结BD 交AC 于M ,连结EM 、FM ,则FM =,EM =3EF =,故13222EMF S ==,3123EMF V S AC =⨯= ,312V V V =+,3123.V V =12.(2022·新高考I 卷第19题)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C --的正弦值.【答案】解:(1)设A 到平面1A BC 的距离为d ,因为直三棱柱111ABC A B C -的体积为4,即可得14ABC S AA ⋅= ,故111433A ABC ABC V S AA -=⋅= ,又111114333A ABC A A BC A BC V V S d d --==⋅=⨯= ,解得d =,所以A 到平面1A BC 的距离为;(2)连接1AB ,因为直三棱柱111ABC A B C -中,1AA AB =,故四边形11AA B B 为正方形,即11AB A B ⊥,又平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =,1AB ⊂平面11ABB A ,故1AB ⊥平面1A BC ,因为BC ⊂平面1A BC ,所以1AB BC ⊥,又因为1AA BC ⊥,11,AB AA ⊂平面11ABB A ,且11AB AA A ⋂=,故BC ⊥平面11ABB A ,因为AB ⊂平面11ABB A ,则BC AB ⊥,所以1,,BB AB BC 三条直线两两垂直,故如图可以以B为原点建立空间直角坐标系,设1AA AB a ==,BC b =,则1A B =,由条件可得,解得,则(0,0,0)B ,(2,0,0)C ,(0,2,0)A ,1(0,2,2)A ,1AC 的中点(1,1,1)D ,所以(0,2,0)BA = ,(1,1,1)BD = ,(2,0,0)BC =,设平面ABD 的一个法向量为1(,,)n x y z =,,取1(1,0,1)n =-,同理可求得平面BCD 的一个法向量为2(0,1,1)n =-,所以1212121|cos ,|2n n n n n n ⋅<>==,所以二面角A BD C --的正弦值为2【解析】本题考查了平面与平面所成角的空间向量求法、点到面的距离的几何求法、几何体的体积公式,考查了空间中的垂直关系的证明与应用,属于中档题.(1)利用等体积法以及三棱锥的体积公式即可求解.(2)根据题干首先证明1,,BB AB BC 三条直线两两垂直,且12AA AB BC ===,建立直角坐标系,求出平面ABD 的一个法向量和平面BCD 的一个法向量,利用向量法即可求出二面角A BD C --的正弦值.13.(2022·新高考II 卷题20题)如图,PO 是三棱锥P ABC -的高,PA PB =,AB AC ⊥,E 是PB 的中点.(1)证明://OE 平面;PAC (2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B --正弦值.【答案】解:(1)法一:连接OA 、OB ,因为PO 是三棱锥P ABC -的高,所以PO ⊥平面ABC ,所以PO OA ⊥,PO OB ⊥,所以90POA POB ∠=∠=︒,又PA PB =,PO PO =,所以POA ≌POB ,所以OA OB =,作AB 中点D ,连接OD 、DE ,则有OD AB ⊥,又AB AC ⊥,所以//OD AC ,又因为OD ⊂/平面PAC ,AC ⊂平面PAC ,所以//OD 平面PAC ,又D 、E 分别为AB 、PB 的中点,所以,在BPA 中,//DE PA 又因为DE ⊂/平面PAC ,PA ⊂平面PAC ,所以//DE 平面PAC ,又OD 、DE ⊂平面ODE ,OD DE D ⋂=,所以平面//ODE 平面PAC ,又OE ⊂平面ODE ,所以//OE 平面;PAC 法二:(1)连接OA 、OB ,因为PO 是三棱锥P ABC -的高,所以PO ⊥平面ABC ,所以PO OA ⊥,PO OB ⊥,所以90POA POB ∠=∠=︒,又PA PB =,PO PO =,所以POA ≌POB ,所以OA OB =,又AB AC ⊥,在Rt ABF ,O 为BF 中点,延长BO ,交AC 于F ,连接PF ,所以在PBF 中,O 、E 分别为BF 、PB 的中点,所以//EO PF ,因为EO ⊂/平面PAC ,PF ⊂平面PAC ,所以//EO 平面;PAC(2)法一:过点D 作//DF OP ,以DB 为x 轴,DO 为y 轴,DF 为z 轴.建立如图所示的空间直角坐标系.因为3PO =,5PA =,由(1)4OA OB ==,又30ABO CBO ∠=∠=︒,所以2OD =,23DB =,所以(0,2,3)P ,(23,0,0)B ,(23,0,0)A -,3(3,1,)2E ,设AC a =,则(23,,0)C a -,平面AEB 的法向量设为1111(,,)n x y z = ,直线AB 的方向向量可设为(1,0,0)a =,直线DP ⊂平面AEB ,直线DP 的方向向量为(0,2,3)b =,所以,所以10x =,设13y =,则12z =-,所以1(0,3,2);n =-平面AEC 的法向量设为2222(,,)n x y z = ,(0,,0)AC a = ,3(33,1,)2AE = ,所以,所以20y =,设23x =,则26z =-,所以3,0,6);n =-所以1cos n < ,1221212124313||||1339133n n n n n ⋅>====⋅⨯,二面角C AE B --的平面角为θ,则211sin 1cos 13θθ=-=,所以二面角C AE B --的正弦值为1113法二:(2)过点A 作//AF OP ,以AB 为x 轴,AC 为y 轴,AF 为z 轴建立所示的空间直角坐标系.因为3PO =,5PA =,由(1)4OA OB ==,又30ABO CBO ︒∠=∠=,所以,43AB =,所以(23,2,3)P ,(43,0,0)B ,(0,0,0)A ,3(33,1,)2E ,设AC a =,则(0,,0)C a ,平面AEB 的法向量设为1111(,,)n x y z = ,(43,0,0)AB = ,3(33,1,)2AE = ,所以,所以10x =设12z =-,则13y =,所以1(0,3,2);n =-平面AEC 的法向量设为2(,,)n x y z = ,(0,,0)AC a = ,3(33,1,)2AE = ,所以,所以20y =,设23x =,则26z =-,所以2(3,0,6);n =-所以1cos n < ,1221212124313||||1339133n n n n n ⋅>====⋅⨯二面角C AE B --的平面角为θ,则211sin 1cos 13θθ=-=,所以二面角C AE B --的正弦值为11.13【解析】本题考查线面平行与二面角的求解,考查学生的空间想象与计算能力,有一定的难度.【2021年真题】14.(2021·新高考I 卷第3题)已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2B.22C.4D.42【答案】B 【解析】【分析】本题考查圆锥的侧面展开图,属于基础题.设圆锥母线长为l ,求出圆锥的底面周长,即为展开图半圆的弧长,计算可得答案.【解答】解:设圆锥的母线长为l ,所以底面圆周长为,由展开图可知半圆的弧长为,所以l π=,得l =,故选:.B 15.(2021·新高考II 卷第4题)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36000km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为6400km 的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )(S r πα=-单位:2km ),则S 占地球表面积的百分比约为()A.26% B.34%C.42%D.50%【答案】C 【解析】【分析】本题考查球的表面积,考查直线与平面所成的角,属于中档题.由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.【解答】解:如图所示:由题意可得,S 占地球表面积的百分比约为:222(1cos )1cos 42r r πααπ--=640016400360000.4242%.2-+=≈=故选.C 16.(2021·新高考II 卷第5题)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为()A.20+B. C.563D.2823【答案】D 【解析】【分析】本题考查了棱台的结构特征与体积的求法.由正四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.【解答】解:作出图形,连接该正四棱台上下底面的中心,如图所示,因为该正四棱台上下底面边长分别为2,4,侧棱长为2,所以该棱台的高h ==下底面面积116S =,上底面面积24S =,所以该棱台的体积121(3V h S S =+1(16433=+=故选:.D 17.(2021·新高考I 卷第12题)(多选)在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中[0,1]λ∈,[0,1]μ∈,则()A.当1λ=时,1AB P 的周长为定值B.当1μ=时,三棱锥1P A BC -的体积为定值C.当12λ=时,有且仅有一个点P ,使得1A P BP ⊥D.当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P【答案】BD 【解析】【分析】本题考查了动点轨迹,线面平行与线面垂直的判定,锥体的体积问题等,综合性强,考查了逻辑推理能力与空间想象能力,属于拔高题.判断当1λ=时,点P 在线段1CC 上,分别计算点P 为两个特殊点时的周长,即可判断选项A ;当1μ=时,点P 在线段11B C 上,利用线面平行的性质以及锥体的体积公式,即可判断选项B ;当12λ=时,取线段BC ,11B C 的中点分别为M ,1M ,连结1M M ,则点P 在线段1M M 上,分别取点P 在1M ,M 处,得到均满足1A P BP ⊥,即可判断选项C ;当12μ=时,取1CC 的中点1D ,1BB 的中点D ,则点P 在线的1DD 上,证明当点P 在点1D 处时,1A B ⊥平面11AB D ,利用过定点A 与定直线1A B 垂直的平面有且只有一个,即可判断选项.D 【解答】解:对于A ,当1λ=时,1BP BC BB μ=+ ,即1CP BB μ=,所以1//CP BB ,故点P 在线段1CC 上,此时1AB P 的周长为11AB B P AP ++,当点P 为1CC 的中点时,1AB P 的周长为+,当点P 在点1C 处时,1AB P 的周长为1+,故周长不为定值,故选项A 错误;对于B ,当1μ=时,1BP BC BB λ=+ ,即1B P BC λ= ,所以1//B P BC ,故点P 在线段11B C 上,因为11//B C 平面1A BC ,所以直线11B C 上的点到平面1A BC 的距离相等,又1A BC 的面积为定值,所以三棱锥1P A BC -的体积为定值,故选项B 正确;对于C ,当12λ=时,取线段BC ,11B C 的中点分别为M ,1M ,连接1M M ,因为112BP BC BB μ=+ ,即1MP BB μ= ,所以1//MP BB ,则点P 在线段1M M 上,当点P 在1M 处时,1111A M B C ⊥,111A M B B ⊥,又1111B C B B B ⋂=,所以11A M ⊥平面11BB C C ,又1BM ⊂平面11BB C C ,所以111A M BM ⊥,即1A P BP ⊥,同理,当点P 在M 处,1A P BP ⊥,故选项C 错误;对于D ,当12μ=时,取1CC 的中点1D ,1BB 的中点D ,因为112BP BC BB λ=+ ,即DP BC λ= ,所以//DP BC ,则点P 在线的1DD 上,当点P 在点1D 处时,取AC 的中点E ,连接1A E ,BE ,因为BE ⊥平面11ACC A ,又1AD ⊂平面11ACC A ,所以1AD BE ⊥,在正方形11ACC A 中,11AD A E ⊥,又1BE A E E ⋂=,BE ,1A E ⊂平面1A BE ,故1AD ⊥平面1A BE ,又1A B ⊂平面1A BE ,所以11A B AD ⊥,在正方体形11ABB A 中,11A B AB ⊥,又11AD AB A ⋂=,1AD ,1AB ⊂平面11AB D ,所以1A B ⊥平面11AB D ,因为过定点A 与定直线1A B 垂直的平面有且只有一个,故有且仅有一个点P ,使得1A B ⊥平面1AB P ,故选项D 正确.故选:.BD 18.(2021·新高考II 卷第10题)(多选)如图,在正方体中,O 为底面的中心,P 为所在棱的中点,M ,N 为正方体的顶点,则满足MN OP ⊥的是()A. B.C. D.【答案】BC【解析】【分析】本题考查了空间中两直线的位置关系以及垂直的判定,考查了数形结合思想和直观想象能力,属于中档题.根据线面垂直的判定定理可得BC 的正误,平移直线MN 构造所考虑的线线角后可判断AD 的正误.【解答】解:设正方体的棱长为2,对于A ,如图(1)所示,连接AC ,易知//MN AC ,且MN 、AC 、OP 在同一平面内,由图可知直线OP 与AC 相交且不垂直,故MN OP ⊥不成立,故A 错误.对于B ,如图(2)所示,取MT 的中点为Q ,连接PQ ,OQ ,则OQ MT ⊥,PQ MN ⊥,由正方体SBCN MADT -可得SM ⊥平面MADT ,而OQ ⊂平面MADT ,故SM OQ ⊥,而SM MT M ⋂=,SM ,MT ⊂平面SNTM ,故OQ ⊥平面SNTM ,又MN ⊂平面SNTM ,所以OQ MN ⊥,而OQ PQ Q ⋂=,,OQ PQ OPQ ⊂平面,所以MN ⊥平面OPQ ,而PO ⊂平面OPQ ,故MN OP ⊥,故B 正确.对于C ,如图(3),连接BD ,则//BD MN ,由B 的判断可得OP BD ⊥,故OP MN ⊥,故C 正确.对于D ,如图(4),取AM '的中点G ,连接PG ,OG ,M N '',则//MN M N '',PG =,OG =PO =,则222PO PG OG =+,可得PG OG ⊥,根据三角形的性质可知PO 与PG 不垂直,故PO 与MN 不垂直,故D 错误.故选.BC19.(2021·新高考I 卷第20题)如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:;OA CD ⊥(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.【答案】(1)证明:AB AD = ,ABD ∴ 是以BD 为底的等腰三角形,又O 为BD 的中点,OA BD ∴⊥,平面ABD ⊥平面BCD ,且平面ABD ⋂平面BCD BD =,OA ⊂平面ABD ,OA ∴⊥平面BCD ,CD ⊂ 平面BCD ,.OA CD ∴⊥(2)解:以O 为坐标原点,OD 为y 轴,OA 为z 轴,垂直OD 且过O 的直线为x 轴,建立空间直角坐标系.OCD 是边长为1的等边三角形,,,,不妨设, 点E 在棱AD 上,2DE EA =,12(0,,)33x E ∴,,,设向量为平面BCE 的法向量,设3a =,则1b =-,2c x=,即显然是平面BCD 的法向量, 二面角E BC D --的大小为45︒,,即,解得1(x =舍去1)-,11133OA 21.33226A BCD BCD V S -∴=⋅=⨯⨯⨯⨯= 【解析】本题考查立体几何的面面垂直的性质,二面角余弦值的求法,三棱锥的体积.(1)先证明OA ⊥平面BCD ,利用线面垂直的性质即可证明.(2)先建系,利用已知二面角的角度求出三棱锥的高度,即可求解体积.20.(2021·新高考II 卷第19题)在四棱锥Q ABCD -中,底面ABCD 是正方形,若2,5, 3.AD QD QA QC ====(1)证明:平面QAD ⊥平面ABCD ;(2)求二面角B QD A --的平面角的余弦值.【答案】解:(1)证明:取AD 的中点为O ,连接,.QO CO因为QA QD =,OA OD =,则QO AD ⊥,而2,AD QA ==1AO DO ==, 2.QO ==在正方形ABCD 中,2AD CD ==,1DO =,故CO =,因为3QC =,故222QC QO OC =+,故QOC 为直角三角形且QO OC ⊥,因为OC AD O = ,OC 、AD ⊂平面ABCD ,故QO ⊥平面ABCD ,因为QO ⊂平面QAD ,故平面QAD ⊥平面.ABCD (2)在平面ABCD 内,过O 作//OT CD ,交BC 于T ,则OT AD ⊥,因为(1)中的QO ⊥平面ABCD ,OT ⊂平面ABCD ,QO OT ⊥,故可以OT 为x 轴,以OD 为y 轴,以OQ 为z 轴,建如图所示的空间直角坐标系.则,故(2,1,2),(2,2,0).BQ BD =-=- 设平面QBD 的一个法向量(,,)n x y z = ,则00n BQ n BD ⎧⋅=⎪⎨⋅=⎪⎩ 即,取1x =,则11,2y z ==,故1(1,1,).2n = 而平面QAD 的法向量为(1,0,0)m = ,故cos ⟨,m n ⟩12.3312==⨯又二面角B QD A --的平面角为锐角,故其余弦值为2.3【解析】本题考查了面面垂直的判定和运用空间向量求解二面角的问题,注意数形结合思想的运用.(1)取AD 的中点为O ,连接,QO CO ,可证QO ⊥平面ABCD ,从而得到平面QAD ⊥平面.ABCD(2)在平面ABCD内,过O作//⊥,以OT为x轴,以OD为y轴,以OQOT CD,交BC于T,则OT AD为z轴,建立空间直角坐标系,求出平面QAD、平面BQD的法向量后可求二面角的余弦值.【2020年真题】21.(2020·新高考I卷第4题、II卷第4题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的O,地球上一点A的纬度是指OA与地晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为)球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40︒,则晷针与点A处的水平面所成角为()A.20︒B.40︒C.50︒D.90︒【答案】B【解析】【分析】本题是立体几何在生活中的运用,考查空间线面角的定义和求法,属于中档题.由纬度的定义和线面角的定义,结合直角三角形的性质,可得晷针与点A处的水平面所成角.【解答】解:可设A所在的纬线圈的圆心为O',OO'垂直于纬线所在的圆面,由图可得OHA ∠为晷针与点A 处的水平面所成角,又40OAO ︒∠'=且OA AH ⊥,在Rt OHA 中,O A OH '⊥,40OHA OAO ︒∴∠=∠'=,故选:.B 22.(2020·新高考I 卷题16题)已知直四棱柱1111ABCD A BCD -的棱长均为2,60.BAD ︒∠=以1D 为5为半径的球面与侧面11BCC B 的交线长为________.【答案】22π【解析】【分析】本题考查空间中球与平面的交线问题,注意球心到面的距离和形成的交线位置与所对应的圆弧和圆心角,属于难题.由已知得点1D 到面11BB C C 的距离即为点1D 到11B C 的距离,3,则根据勾股定理可得截面的圆半径为532r =-=,球与侧面11BB C C 所形成的交线为一段圆弧,其圆心角为2π,则根据弧长公式即可得解.【解答】解:直四棱柱棱长为2,底面是边长为2的菱形,侧面是边长为2的正方形,又60BAD ︒∠=,可得111D C B =60∠︒,点1D 到面11BB C C 的距离即为点1D 到11B C 的距离,即为3则根据勾股定理可得截面的圆半径为r ==,11112B C >=,且2<,则球与侧面11BB C C 所形成的交线为一段圆弧,其圆心角为2π,故形成的交线长为222l ππ==.故答案为2.223.(2020·新高考II 卷题13题)已知正方体1111ABCD A B C D -的棱长为2,M 、N 分别为1BB 、AB 的中点,则三棱锥1A NMD -的体积为__________.【答案】13【解析】【分析】本题考查利用等体积法求多面体的体积,是基础的计算题.由题意画出图形,再由等体积法求三棱锥1A NMD -的体积.【解答】解:如图,正方体1111ABCD A B C D -的棱长为2,M 、N 分别为1BB 、AB 的中点,111122ANM S ∴=⨯⨯= ,111112.323A NMD D AMN V V --∴==⨯⨯=故答案为:1.324.(2020·新高考I 卷题20题)如图,四棱锥P ABCD -的底面为正方形,PD ⊥底面.ABCD 设平面PAD 与平面PBC 的交线为.l (1)证明:l ⊥平面;PDC (2)已知1PD AD ==,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值.【答案】解:(1)PD ⊥ 底面ABCD ,且AD ⊂平面ABCD ,PD AD ∴⊥,ABCD 为正方形,AD DC ∴⊥,又PD DC D ⋂= ,且PD 、DC 在平面PDC 内,AD ∴⊥平面PDC ,//AD BC ,且BC ⊂平面PBC ,AD ⊂/平面PBC ,//AD ∴平面PBC ,又 平面PAD 与平面PBC 的交线为l ,且AD ⊂平面PAD ,//AD l ∴,l ∴⊥平面PDC ;(2)以D 为原点,以DA 、DC 、DP 分别为x 、y 、z 轴,建立空间直角坐标系如图所示:由1PD AD ==,得(0,0,1)P ,(1,1,0)B ,(0,1,0)C ,(0,0,0)D ,则(1,1,1)PB =- ,(0,1,0)DC = ,设点Q 的坐标为(,0,1)t ,平面QCD 的法向量为000(,,)n x y z =,则(,0,1)DQ t = ,即有,即,取01x =,得(1,0,)n t =-,又设PB 与n夹角为α,PB 与平面QCD 所成角为θ,则cos ||||PB n PB n α⋅=== ,于是sin θ==,当0t =时,3sin 3θ=,当0t <时,sin θ==,又1[()]2(()t t -+---当且仅当t 1=-时,取等号),即得30sin 3θ<,当0t >时,sin θ==,又12(t t +当且仅当t 1=时,取等号),即得36sin 33θ<,综上可知,PB 与平面QCD 所成角的正弦值的最大值为63【解析】本题考查了线面角的求解及线面垂直的判定定理、线面平行的判定定理和性质定理,属于拔高题.(1)本题先证明AD ⊥平面PDC ,再证明//AD 平面PBC ,再利用线面平行性质定理证得//AD l ,从而证得l ⊥平面PDC ;(2)本题可以建立空间直角坐标系,设出Q 点坐标,求出PB 和平面QDC 的法向量,再利用向量夹角公式求解,再结合基本不等式可求出PB 与平面QCD 所成角的正弦值最大值.25.(2020·新高考II 卷第20题)如图,四棱锥P ABCD -的底面为正方形,PD ⊥底面.ABCD 设平面PAD 与平面PBC 的交线为.l (1)证明:l ⊥平面PDC ;(2)已知1PD AD ==,Q 为l 上的点,QB =,求PB 与平面QCD 所成角的正弦值.【答案】解:(1)证明:过P 在平面PAD 内作直线//l AD ,由//AD BC ,可得//l BC ,即l 为平面PAD 和平面PBC 的交线,PD ⊥ 平面ABCD ,BC ⊂平面ABCD ,PD BC ∴⊥,又BC CD ⊥,CD PD D ⋂=,CD ,PD ⊂平面PCDBC ∴⊥平面PCD ,//l BC ,l ∴⊥平面PCD ;(2)如图,以D 为坐标原点,直线DA ,DC ,DP 所在的直线为x ,y ,z 轴,建立空间直角坐标系D xyz -,1PD AD == ,Q 为l 上的点,QB =,PB ∴=,1QP =,则(0,0,0)D ,(1,0,0)A ,(0,1,0)C ,(0,0,1)P ,(1,1,0)B ,设(1,0,1)Q ,则(1,0,1)DQ = ,(1,1,1)PB =- ,(0,1,0)DC = ,设平面QCD 的法向量为(,,)n a b c =,则,,取1c =,可得(1,0,1)n =- ,cos n ∴< ,63||||32n PB PB n PB ⋅>===⋅ PB ∴与平面QCD 所成角的正弦值为6.3【解析】本题考查空间线面垂直的判定,以及线面角的求法,考查转化思想和向量法的运用,考查运算能力和推理能力,属于中档题.(1)过P 在平面PAD 内作直线//l AD ,推得l 为平面PAD 和平面PBC 的交线,由线面垂直的判定和性质,即可得证;(2)以D 为坐标原点,直线DA ,DC ,DP 所在的直线为x ,y ,z 轴,建立空间直角坐标系D xyz -,求出(0,1,1)Q ,运用向量法,求得平面QCD 的法向量,结合向量的夹角公式求解即可.。
第七章 必刷大题14 空间向量与立体几何

1.(2022·新高考全国Ⅰ改编)如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为2 2.(1)求A到平面A1BC的距离;(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求平面ABD与平面BCD夹角的正弦值.2. 如图,四棱锥P-ABCD的底面为正方形,P A⊥平面ABCD,M是PC的中点,P A=AB.(1)求证:AM⊥平面PBD;(2)设直线AM与平面PBD交于O,求证:AO=2OM.3. 如图,在四棱锥P-ABCD中,P A⊥平面ABCD,AB∥CD,P A=AB=2CD=2,∠ADC=90°,E,F分别为PB,AB的中点.(1)求证:CE∥平面P AD;(2)求点B到平面PCF的距离.4. (2022·全国乙卷)如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC 的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD 所成的角的正弦值.5.(2023·青岛模拟)如图①,在梯形ABCD中,AB∥DC,AD=BC=CD=2,AB=4,E为AB的中点,以DE为折痕把△ADE折起,连接AB,AC,得到如图②的几何体,在图②的几何体中解答下列问题.(1)证明:AC⊥DE;(2)请从以下两个条件中选择一个作为已知条件,求平面DAE与平面AEC夹角的余弦值.①四棱锥A-BCDE的体积为2;②直线AC与EB所成角的余弦值为6 4.6. (2022·连云港模拟)如图,在三棱锥A-BCD中,△ABC是正三角形,平面ABC⊥平面BCD,BD⊥CD,点E,F分别是BC,DC的中点.(1)证明:平面ACD⊥平面AEF;(2)若∠BCD=60°,点G是线段BD上的动点,问:点G运动到何处时,平面AEG与平面ACD的夹角最小.。
全国卷新课标高考中档大题专项训练立体几何与空间向量

高考中档大题专项训练-立体几何与空间向量1.如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF =错误!,EF交BD于点H.将△DEF沿EF折到△D′EF的位置,OD′=错误!.1证明:D′H⊥平面ABCD;2求二面角B-D′A-C的正弦值.1证明由已知得AC⊥BD,AD=CD.又由AE=CF得错误!=错误!,故AC∥EF.因此EF⊥HD,从而EF⊥D′H.由AB=5,AC=6得DO=BO=错误!=4.由EF∥AC得错误!=错误!=错误!.所以OH=1,D′H=DH=3.于是D′H2+OH2=32+12=10=D′O2,故D′H⊥OH.又D′H⊥EF,而OH∩EF=H,所以D′H⊥平面ABCD.2解如图,以H为坐标原点,错误!的方向为x轴正方向,错误!的方向为y轴正方向,错误!的方向为z轴正方向,建立空间直角坐标系,则H0,0,0,A-3,-1,0,B0,-5,0,C3,-1,0,D′0,0,3,错误!=3,-4,0,错误!=6,0,0,错误!=3,1,3.设m=x1,y1,z1是平面ABD′的法向量,则错误!即错误!所以可取m=4,3,-5.设n=x2,y2,z2是平面ACD′的法向量,则错误!即错误!所以可取n=0,-3,1.于是cos〈m,n〉=错误!=错误!=-错误!. sin〈m,n〉=错误!.因此二面角B-D′A-C的正弦值是错误!.2.在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.1已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;2已知EF=FB=错误!AC=2错误!,AB=BC,求二面角F-BC-A的余弦值.1证明设FC中点为I,连接GI,HI.在△CEF中,因为点G,I分别是CE,CF的中点,所以GI∥EF.又EF∥OB,所以GI∥OB.在△CFB中,因为H是FB的中点,所以HI∥BC.又HI∩GI=I,BC∩OB=B,所以平面GHI∥平面ABC.因为GH平面GHI,所以GH∥平面ABC.2解连接OO′,则OO′⊥平面ABC.又AB=BC,且AC是圆O的直径,所以BO⊥AC.以O为坐标原点,建立如图所示的空间直角坐标系.由题意得B0,2错误!,0,C-2错误!,0,0.过点F作FM⊥OB于点M,所以FM=错误!=3,可得F0,错误!,3.故错误!=-2错误!,-2错误!,0,错误!=0,-错误!,3.设m=x,y,z是平面BCF的法向量.由错误!可得错误!可得平面BCF的一个法向量m=错误!,因为平面ABC的一个法向量n=0,0,1,所以cos〈m,n〉=错误!=错误!.所以二面角F-BC-A的余弦值为错误!.3.将边长为1的正方形AA1O1O 及其内部绕OO1旋转一周形成圆柱,如图,AC 长为错误!π,11A B 长为错误!,其中B1与C 在平面AA1O1O 的同侧.1求三棱锥C —O1A1B1的体积;2求异面直线B1C 与AA1所成的角的大小.解 1连接O 1B 1,则11A B =∠A 1O 1B 1=错误!,∴△O 1A 1B 1为正三角形,∴111O A B S =错误!,∴111—C O A B V=错误!OO 1·111O A B S =错误!.2设点B 1在下底面圆周的射影为B ,连接BB 1,则BB 1∥AA 1,∴∠BB 1C 为直线B 1C 与AA 1所成角或补角,BB 1=AA 1=1.连接BC ,BO ,OC ,AB =11A B =错误!,AC =错误!,∴BC =错误!,∴∠BOC =错误!,∴△BOC 为正三角形,∴BC =BO =1,∴tan∠BB 1C =错误!=1,∴∠BB 1C =45°,∴直线B 1C 与AA 1所成的角的大小为45°.4.如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=错误!为棱AD的中点,异面直线PA与CD所成的角为90°.1在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;2若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.解1在梯形ABCD中,AB与CD不平行.延长AB,DC,相交于点MM∈平面PAB,点M即为所求的一个点.理由如下:由已知,BC∥ED,且BC=ED.所以四边形BCDE是平行四边形.从而CM∥EB.又EB平面PBE,CM平面PBE.所以CM∥平面PBE.说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点2方法一由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.从而CD⊥PD.所以∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.设BC=1,则在Rt△PAD中,PA=AD=2.过点A作AH⊥CE,交CE的延长线于点H,连接PH.易知PA⊥平面ABCD,从而PA⊥CE.且PA∩AH=A,于是CE⊥平面PAH.又CE平面PCE,所以平面PCE⊥平面PAH.过A作AQ⊥PH于Q,则AQ⊥平面PCE.所以∠APH是PA与平面PCE所成的角.在Rt△AEH中,∠AEH=45°,AE=1,所以AH=错误!.在Rt△PAH中,PH=错误!=错误!.所以sin∠APH=错误!=错误!.方法二由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.于是CD⊥PD.从而∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.由∠PAB=90°,且PA与CD所成的角为90°,可得PA⊥平面ABCD.设BC=1,则在Rt△PAD中,PA=AD=2.作Ay⊥AD,以A为原点,以错误!,错误!的方向分别为x轴,z轴的正方向,建立如图所示的空间直角坐标系,则A0,0,0,P0,0,2,C2,1,0,E1,0,0.所以错误!=1,0,-2,错误!=1,1,0,错误!=0,0,2.设平面PCE的法向量为n=x,y,z.由错误!得错误!设x=2,解得n=2,-2,1.设直线PA与平面PCE所成的角为α,则sin α=错误!=错误!=错误!.所以直线PA与平面PCE所成角的正弦值为错误!.5.如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC =CD=错误!.1求证:PD⊥平面PAB;2求直线PB与平面PCD所成角的正弦值;3在棱PA上是否存在点M,使得BM∥平面PCD若存在,求错误!的值;若不存在,说明理由.1证明∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又AB⊥AD,AB平面ABCD,∴AB⊥平面PAD.∵PD平面PAD,∴AB⊥PD,又PA⊥PD,PA∩AB=A,∴PD⊥平面PAB.2解取AD中点O,连接CO,PO.∵PA=PD,∴PO⊥AD.又∵PO平面PAD,平面PAD⊥平面ABCD,∴PO⊥平面ABCD,∵CO平面ABCD,∴PO⊥CO,∵AC=CD,∴CO⊥AD.以O为原点建立如图所示空间直角坐标系.易知P0,0,1,B1,1,0,D0,-1,0,C2,0,0.则错误!=1,1,-1,错误!=0,-1,-1,错误!=2,0,-1.设n=x0,y0,1为平面PDC的一个法向量.由错误!得错误!解得错误!即n=错误!.设PB与平面PCD的夹角为θ.则sin θ=|cos〈n,错误!〉|=错误!=错误!=错误!.3解设在棱PA上存在点M,使得BM∥平面PCD,则存在λ∈0,1使得错误!=λ错误!,因此点M0,1-λ,λ,错误!=-1,-λ,λ.∵BM平面PCD,∴BM∥平面PCD,当且仅当错误!·n=0,即-1,-λ,λ·错误!=0,解得λ=错误!,∴在棱PA上存在点M使得BM∥平面PCD,此时错误!=错误!.。
高考数学复习重难点03 空间向量与立体几何(解析版)-2021年高考数学专练(新高考)

重难点 03 空间向量与立体几何【高考考试趋势】立体几何不管新旧高考中都是一个必考知识点,一直在高中数学中占有很大的分值,未来的高考中立体几何也会持续成为高考的一个热点。
新高考中不分文理,主要考查简单几何体的体积,表面积以及外接圆问题,有关角的问题;另外选择部分主要考查在点线面位置关系,简单几何体三视图有所弱化;选择题主要还是以几何体的基本性质为主,解答题部分主要考查平行,垂直关系以及二面角问题。
前面的热点专题已经对立体几何进行了一系列详细的说明,本专题继续加强对新高考中立体几何出现的习题以及对应的题目类型进行必要的加强。
本专题包含了高考中几乎所有题型,学完本专题以后,对以后所有的立体几何你将有一个更加清晰的认识。
【知识点分析及满分技巧】基础知识点考查:一般来说遵循三短一长选最长。
要学会抽象问题具体会,将题目中的直线转化成显示中的具体事务,例如立体坐标系可以看做是一个教室的墙角。
有关外接圆问题:一般图形可以采用补形法,将几何体补成正方体或者是长方体,再利用不在同一个平面的四点确定一个立体平面原理,从而去求。
内切圆问题:转化成正方体的内切圆去求。
求点到平面的距离问题:采用等体积法。
求几何体的表面积体积问题:应注意巧妙选取底面积与高。
对于二面角问题应采用建立立体坐标系去求,但是坐标系要注意采用左手系务必要标记准确对应点以及法向量对应的坐标。
【限时检测】(建议用时:90分钟)一、单选题1.(2020·辽宁葫芦岛市·高三月考)已知,是两条不重合的直线,是一个平面且,则“a b βb β⊂”是“”的( )a β⊥ab ⊥r rA .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【分析】由线面垂直的判定和性质分别判断充分性和必要性即可.【详解】充分性:因为,,由线面垂直的性质可得,故充分性成立;a β⊥b β⊂a b ⊥r r 必要性:若,,则直线与平面可能相交、平行或在平面内,故必要性不成立.a b ⊥r rb β⊂a β所以“”是“”的充分不必要条件.a β⊥ab ⊥r r故选:A.2.(2020·全国福建省漳州市教师进修学校高三二模(文))已知正方体的棱长为1111ABCD A B C D -1,点E 是底面ABCD 上的动点,则的最大值为( )()111CE CA D B -⋅ AB .1CD【答案】B【分析】建立空间直角坐标系,由向量的数量积运算,计算可得选项.【详解】以点D 为原点,为轴建立空间直角坐标系,则1,,DA DC DD ,,x y z 111(0,0,1),(1,1,1),(1,0,1),D B A 设,其中,则,(,,0)E x y [],0,1x y ∈()()11111,,1,1,1,0CE CA A E x y D B -==--=所以,等号成立的条件是,故其最大值为1,111()11CE CA D B x y -⋅=+-≤ (1,1,0)E 故选:B .3.(2020·上海长宁区·高三一模)设、为两条直线,、为两个平面,则下列命题中假命题是( m n αβ)A .若,,,则m n ⊥m α⊥n β⊥αβ⊥B .若,,,则//m n m α⊥//n βαβ⊥C .若,,,则m n ⊥//m α//n β//αβD .若,,,则//m n m α⊥n β⊥//αβ【答案】C【分析】根据面面垂直与平行的判定定理判断.【详解】A .若,,,相当于两平面的法向量垂直,两个平面垂直,A 正确;m n ⊥m α⊥n β⊥B .若,,则,又,则平面内存在直线,所以,所以,B//m n m α⊥n α⊥//n ββ//c n c α⊥αβ⊥正确;C .若,,,则可能相交,可能平行,C 错;m n ⊥//m α//n β,αβD .若,,,则的法向量平行,所以,D 正确.//m n m α⊥n β⊥,αβ//αβ故选:C .【点睛】关键点点睛:本题考查两平面平行与垂直的判断,掌握两平面平行与垂直的和性质定理是解题关键.另外从空间向量角度出发,利用平面的法向量之间的关系判断两平面平行与垂直也是一种行之有效用较简单的方法.4.(2020·云南高三其他模拟(文))在正四面体中,是棱的中点,则异面直线与ABCD M BD AB 所成角的余弦值为( )CM ABCD【答案】A【分析】取的中点为,可得,即为所求(或其补角),在中利用余弦定理求解AD N //MN AB CMN ∠CMN △即可.【详解】设正四面体的棱长为2,ABCD 取的中点为,因为是棱的中点,所以,AD N M BD //MN AB 所以即为所求(或其补角).CMN ∠在中,,CMN △112MN AB ==CM CN ==所以.222cos 2MN CM CN CMN MN MC +-∠===⋅故选:A.5.(2020·河南郑州市·高三月考(文))三棱柱中,侧面与底面垂直,底面是边长为111ABC A B C -2的等边三角形,若直线与平面所成角为,则棱柱的高为( )1AB 11ACC A 45 A .B .2CD .1【答案】C【分析】本题首先可绘出三棱柱,取中点并连接、、,然后通过题意以及线面111ABC A B C -11A C D 1B D AD 1AB 角的定义得出即直线与平面所成角,,最后根据1B AD Ð1AB 11ACC A 145B AD ∠= 即可得出结果.1A A 【详解】如图,绘出三棱柱,111ABC A B C -取中点,连接、、,11A C D 1B D AD 1AB 因为三棱柱侧面与底面垂直,底面是边长为的等边三角形,111ABC A B C -2所以,平面,,,111B D A C ^1B D ⊥11ACC A 11A D =1B D =由线面角的定义即可得出即直线与平面所成角,1B AD Ð1AB 11ACC A则,,145B AD ∠= 1AD B D ==1A A =故选:C.【点睛】关键点点睛:本题考查线面角的应用,过不平行于平面的直线上一点作平面的垂线,这条直线与平面交点与原直线与平面的交点的连线与原直线构成的角即线面所成角,考查计算能力,考查数形结合思想,是中档题.6.(2020·四川泸州市·高三一模(理))已知三棱锥中,平面平面,且A BCD -ABD ⊥BCD 和都是边长为2的等边三角形,则该三棱锥的外接球表面积为( )ABD △BCD △A .B .C .D .4π163π8π203π【答案】D由题意画出图形分别取与的外心,过分别作两面的垂线,相交于,结合已知ABD △BCD △,E F ,E F O 由,求出三棱锥外接球的半径,则外接球的表面积可求.R OC ==【详解】如图,由已知可得,与均为等边三角形,ABD △BCD △取中点,连接,,则,BD G AG CG AG BD ⊥∵平面平面,则平面,ABD ⊥BCD AG ⊥BCD 分别取与的外心,过分别作两面的垂线,相交于,ABD △BCD △,E F ,E F O 则为三棱锥的外接球的球心,O A BCD -由与均为边长为的等边三角形,ABD △BCD △2可得,11233OE OF CG ===⨯=,223CE ∴==,R OC ∴====∴三棱锥A −BCD 的外接球的表面积为.2220443R πππ⨯=⨯=7.(2020·上海高三专题练习)如图,正四棱锥的底面边长和高均为2,M 是侧棱PC 的中P ABCD -点,若过AM 作该正四棱锥的截面,分别交棱PB 、PD 于点E 、F (可与端点重合),则四棱锥的体P AEMF -积的取值范围是()A .B .C .D .1,12⎡⎤⎢⎥⎣⎦14,23⎡⎤⎢⎥⎣⎦41,3⎡⎤⎢⎥⎣⎦8,19⎡⎤⎢⎥⎣⎦【答案】D【分析】设,则,然后利用等体积法由,PE PF x y PB PD ==,PE xPB PF yPD ==P AEMFP AEF P EMF V V V ---=+,得到,再消元得到,令()223P AFM P AEM V V xy x y --=+==+331y x y =-223331P AEMF y V y -=⋅-31y t -=,利用对勾函数的性质求解.【详解】设,则,PE PF x y PB PD ==,PE xPB PF yPD==所以,412,323P AEF P ABD P MEF P BCD V xy V xy V xyV xy ----=⋅=== ,1212,2323P AFM P ACD P AEM P ABC V y V y V x V x ----=⋅==⋅=,()223P AEMF P AEF P EMF P AFM P AEM V V V V V xy x y -----=+=+==+所以,则,3x y xy +=331y x y =-令,因为,31y t -=1,12y ⎡⎤∈⎢⎥⎣⎦所以,1,22t ⎡⎤∈⎢⎥⎣⎦所以,()221311412,319992t y t y t t +⎛⎫⎡⎤==++∈ ⎪⎢⎥-⎝⎭⎣⎦所以,2238,13319P AEMFy V y -⎡⎤=⋅∈⎢⎥-⎣⎦故选:D【点睛】方法点睛:求解棱锥的体积时,等体积转化是常用的方法,转化原则是其高易求,底面放在已知几何体的某一面上.求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体以便于求解.8.(2020·全国高三其他模拟)如图,正方体,的棱长为6,点是棱的中点,1111ABCD A B C D -F 1AA 与的交点为,点在棱上,且,动点(不同于点)在四边形内AC BD O M BC 2BM MC =T M ABCD 部及其边界上运动,且,则直线与所成角的余弦值为()TM OF ⊥1B F TMABCD .79【答案】B【分析】在棱上取一点,且,连接,取棱的中点,连接,,则可得的DC N 2DN NC =NM 1CC H DH BH T 轨迹为线段,则异面直线与所成的角,利用余弦定理即可求出.MN HDB ∠1B F TM 【详解】易知.因为平面,所以,BD AC ⊥AF ⊥ABCD AF BD ⊥所以平面,又平面,所以,BD ⊥AFO OF ⊂AFO BD OF ⊥在棱上取一点,且,连接,则,DC N 2DN NC =NM //NM BD 所以,所以动点的轨迹为线段(不包含).NM OF ⊥T MN M 取棱的中点,连接,易知,1CC H DH 1//DH FB 则异面直线与所成的角.连接,HDB ∠1B F TM BH 因为,,DH ==BD =BH =所以.222cos 2DH BD BH HDB DH BD +-∠==⨯故选:B.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;(2)认定:证明作出的角就是所求异面直线所成的角;(3)计算:求该角的值,常利用解三角形;(4)取舍:由异面直线所成的角的取值范围是,当所作的角为钝角时,应取它的补角作为两条异0,2π⎛⎤⎥⎝⎦面直线所成的角.二、多选题9.(2020·湖北武汉市·高二期中)已知直线m ,n ,平面α,β,给出下列命题正确的是( )A .若m ⊥α,n ⊥β,且m ⊥n ,则α⊥βB .若m // α,n // β,且m // n ,则α // βC .若m ⊥α,n // β,且m ⊥n ,则α⊥βD .若m ⊥α,n // β,且m // n ,则α⊥β【答案】AD 【分析】根据直线与平面平行,垂直的性质定理,判断定理,灵活判断,可以正确推导,也可以举反例说明.【详解】解:对于A :若,,且可以判断是正确的,因为可以设两个平面的法向量为m α⊥n β⊥m n ⊥αβ⊥,,可得数量积为零,即,所以可判断是正确的,故 正确,1n u r 2n u u r 12n n ⊥αβ⊥A 对于B :若,,且,则.不正确,如两个面相交,两个相交的墙面,直线,//m α//n β//m n //αβm 都平行于交线,也满足,,,所以不正确;n //m α//n βB 对于C :若,,且,则有可能,不一定,所以不正确;m α⊥//n βm n ⊥//αβαβ⊥C 对于D :若,,且,,,,故正确; m α⊥//n β//m n n α∴⊥//n βαβ∴⊥D 故选:AD .【点睛】本题考察了直线与平面的位置关系,熟练掌握好平行,垂直的定理即可判断,属于中档题.10.(2020·全国高三其他模拟)已知三棱锥的四个顶点都在球上,,P ABC -O 1AB BC AC ===,平面平面,则( )6APC π∠=PAC ⊥ABCA .直线与直线垂直B .到平面OA BC P ABC C .球的表面积为D .三棱锥的体积为O 133πO ABC -18【答案】ACD 【分析】设外接圆的圆心为,根据外接球的性质以及线面垂直的判定定理与性质得到,从而ABC A 1O OA BC ⊥判断选项A 的对错;利用正弦定理求得外接圆的半径,根据临界情况判断选项B 的对错;借助PAC △2r球半径、截面圆半径、球心到截面的距离之间的关系,求出球半径,即可求出球的表面积,从而判断选项C 的对错;利用三角形的面积公式求得的面积,即可利用锥体的体积公式求出三棱锥的ABC A O ABC -体积,进而判断选项D 的对错.【详解】设外接圆的圆心为,连接,,因为为外接球的球心,所以平面,所以ABC A 1O 1OO 1O A O 1OO ⊥ABC .因为,所以,所以平面,所以,故A1OO BC ⊥1AB BC AC ===1O A BC ⊥BC ⊥1OO A OA BC ⊥正确.设外接圆的圆心为,的中点为,连接,由于,,所以圆的PAC △2O AC D 2O D 1AC =6APC π∠=2O 半径,则易知,所以点到的距离的最大值为,,21112sin 6r π=⨯=2O D =PAC 1+P 2O 三点共线),故B 错误.D 由于,所以圆的半径.连接,则,且1AB BC AC ===1O 1112sin 3r π=⨯=1O D 1O D =,由于平面平面,平面平面,所以平面.连接1OD AC ⊥PAC ⊥ABC PAC ABC AC =1O D ⊥PAC ,则平面,所以四边形是矩形,于是,在直角2OO 2OO ⊥PAC 12OO DO 21OO O D ==2O A 三角形中,,故球的表面积,故C 正2OO A 222222213112OA OO O A =+=+=O 13134123S ππ=⨯=确.由于平面,且,所以三棱锥的体积为1OO ⊥ABC 12OO O D ==ABC S !O ABC -113OO ⨯⨯,所以D 正确.1138ABC S ==△【点睛】关键点点睛:求解本题的关键:(1)根据正弦定理求出的外接圆半径;(2)利用球半径、截面PAC △圆半径、球心到截面的距离之间的关系求三棱锥的外接球半径.三、填空题11.(2020·上海高三专题练习)圆锥底面半径为,母线长为,则其侧面展开图扇形的圆心角1cm 2cm ___________.θ=【答案】;π【分析】根据圆的周长公式易得圆锥底面周长,也就是圆锥侧面展开图的弧长,利用弧长公式可得圆锥侧面展开图扇形的圆心角的大小.【详解】因为圆锥底面半径为,所以圆锥的底面周长为,1cm 2cm π则其侧面展开图扇形的圆心角,22πθπ==故答案为:.π【点睛】思路点睛:该题考查的是有关圆锥侧面展开图的问题,解题思路如下:(1)首先根据底面半径求得底面圆的周长;(2)根据圆锥侧面展开图扇形的弧长就是底面圆的周长,结合母线长,利用弧长公式求得圆心角的大小.12.(2020·四川泸州市·高三一模(理))如图,棱长为1的正方体中,为线段1111ABCD A B C D -P 上的动点(不含端点),给出下列结论:1A B①平面平面;11A D P ⊥1A AP ②多面体的体积为定值;1CDPD ③直线与所成的角可能为;1D P BC 3π④可能是钝角三角形.1APD △其中正确结论的序号是______(填上所有正确结论的序号).【答案】①②④【分析】根据面面垂直的判定定理可判断①的正误;根据正方体的性质及椎体的体积公式,可判断②的正误;根据题意当P 运动到B 的位置时,最大即为,根据正弦函数的定义即可求得的最11A D P∠11A D B∠11sin A D B大值,即可判断③的正误;如图建系,利用向量的夹角公式,即可求得的表达式,根据1cos ,AP D P <>范围,即可判断④的正误,即可得答案.λ【详解】对于①:因为正方体,所以平面,1111ABCD A B C D -11A D ⊥11ABB A 又为线段上的动点,所以平面,P 1A B 11A D ⊥1A AP 又平面,所以平面平面,故①正确;11A D ⊂11A D P 11A D P ⊥1A AP对于②:因为正方体,所以,1111ABCD A B C D -1111122CDD S =⨯⨯=A 又为线段上,所以P 到平面的距离恒等于1,P 1A B 1CDD 所以多面体的体积,为定值,故②正确;1CDPD 1111=1=326P CDD V -⨯⨯对于③:因为,所以与所成的角,即为与所成的角,即即为所11BC A D A 1D P BC 1D P 11A D 11A D P ∠求,由图可得,当P 运动到B 的位置时,最大即为,11A D P ∠11A D B ∠此时1111=1A D A B D P ==,在中,,11Rt D A B A 1111sin sin 3A B A D B D P π===<=所以,所以当P 运动时,不可能为,故③错误;113A D B π∠<11A D P ∠3π对于④:分别以DA 、DC 、为x ,y ,z 轴正方向建系,如图所示:1DD 所以,所以,11(1,0,0),(1,1,0),(1,0,1),(0,0,1)A B A D 1=(0,1-1)A B,因为为线段上运动,设,,,所以,P 1A B 11A P A B λ=[0,1]λ∈(1,,)P y z 1(0,,1)A P y z =- 所以,所以,1y z λλ=⎧⎨-=-⎩(1,,1)P λλ-所以,1(0,,1),(1,,)AP D P λλλλ=-=-所以111cos ,AP D P AP D P AP D P ⋅<>===因为,所以当时,,[0,1]λ∈1(0,2λ∈1cos ,0AP D P <>=<即此时为钝角,所以可能是钝角三角形,故④正确.1APD ∠1APD △故答案为:①②④【点睛】解题的关键是熟悉正方体的性质及面面垂直的判定定理、体积公式等知识,在判断是否为钝角三1APD △角形时,可建系,利用向量求夹角公式求解.考查分析理解,计算化简的能力,属中档题.13.(2020·四川泸州市·高三一模(文))已知直四棱柱,的所有棱长均为4,且1111ABCD A B C D -,点是棱的中点,则过点且与垂直的平面截该四棱柱所得截面的面积为120ABC ∠=︒E BC E 1BD ______.【分析】取的中点,在取点,使得,分别连接,且与交于点,连AB F 1BB M 1BM =,,EF ME MF BD EF N 接,根据线面位置关系,平面,得到截面为等腰三角形,再结合三角形的面积公MN 1BD ⊥MEF MEF A 式,即可求解.【详解】由题意,取的中点,在取点,使得,AB F 1BB M 1BM =分别连接,且与交于点,连接,,,EF ME MF BD EF N MN 因为底面为菱形,可得,ABCD AC BD ⊥又由是的中点,可得,所以,,E F ,BC AB //EF AC EF BD ⊥因为直四棱柱,可得,所以平面,1111ABCD A B C D -1EF BB ⊥EF ⊥11BDD B 又由平面,可得,1BD ⊂11BDD B 1EF BD ⊥在正方形中,可得,因为,可得,11BDD B 11BD B D ⊥1//MN B D 1MN BD ⊥从而得到平面,此时为等腰三角形,1BD ⊥MEF MEF A 在直角中,,可得BME A 2,1BE BM ==ME =又由,111244EN EF AC ===⨯=在直角中,可得,MNE A MN==所以截面的面积为1122S EFMN =⋅=⨯=.【点睛】解答空间中点、线、面位置关系的确定截面问题常见解题策略:1、根据空间平行关系的转化找出几何体的截面,其中有时对于平行关系条件理解不透导致错误;对面面平行判定定理的条件“面内两相交直线”认识不清导致错解;2、根据空间中的垂直关系找几何体的截面,对于空间中的垂直关系中确定线面垂直是关键,结合线线垂直则需借助线面垂直的性质,垂直关系的判定定理和性质定理合理转化是证明垂直关系的基本思想.14.(2020·全国高一)在三棱锥中,平面,,,D ABC -AD ⊥ABC 3AC=BC =,若三棱锥,则此三棱锥的外接球的表面积为______1cos 3BAC ∠=D ABC -【答案】20π【分析】设出外接球的半径、球心,的外心、半径 r , 连接,过作的平行线交于R O ABC A 1O 1AO O OE AD ,连接,,如图所示,在中,运用正弦定理求得 的外接圆的半径r ,再利用E OA OD ABC A ABC A 的关系求得外接球的半径,运用球的表面积公式可得答案.1,,R r OO 【详解】设三棱锥外接球的半径为、球心为,的外心为、外接圆的半径为,连接,R O ABC A 1O r 1AO过作平行线交于,连接,,如图所示,则,,,O OE AD E OA OD OA OD R ==1O A r =OE AD ⊥所以为的中点.E AD 在中,由正弦定理得,解得.ABCA 2sin BC r BAC ==∠r =在中,由余弦定理,可得,ABC A 2222cos BC AB AC AB AC BAC =+-⋅⋅∠2117963AB AB =+-⋅⋅得.4AB =所以11sin 3422ABC S AB AC BAC =⋅⋅∠=⨯⨯=△因为,所以.连接,又,所以1133D ABC ABC V S AD AD -=⋅⋅=⨯⨯=△AD =1OO 1//OO AD 四边形为平行四边形,1EAO O ,所以.112EA OO AD ===R ===所以该三棱锥的外接球的表面积.224π4π20πS R ===故答案为:.20π【点睛】本题考查三棱锥的外接球,及球的表面积计算公式,解决问题的关键在于利用线面关系求得外接球的球心和球半径,属于中档题.四、解答题15.(2020·四川成都市·高三其他模拟(理))如图,在直四棱柱(侧棱垂直于底面的棱柱).中,底面是菱形,且是凌的中点,1111ABCD A B C D -ABCD 111,2AB AA E ==1AA EC =(1)求证:平面;1D E ⊥EDC (2)求二面角的大小.D EC B --【答案】(1)证明见解析;(2).3π【分析】(1)由勾股定理可得,得出平面,再通过和即可得证;DE CD ⊥CD ⊥11ADD A 1CD ED ⊥1D E ED ⊥(2)以点为坐标原点,以所在直线分别为轴建立空间直角坐标系,利用向量法可D 1,,DA DC DD ,,x y z 求出.【详解】解:(1)因为点是的中点,所以,E 1AA 1AE =又,故在中,1AD =Rt EAD A DE =由题可知,,则,1EC DC ==222DC DE EC +=所以.DE CD ⊥因为四棱柱是直四棱柱,1111ABCD A B C D -故平面,平面,CD ⊥11ADD A 1ED ⊂Q 11ADD A 故,1CD ED ⊥因为,所以.112ED ED DD ===1D E ED ⊥又,所以平面;CD ED D = 1D E ⊥ECD (2)由(1)可知,两两相垂直,1,,DA DC DD 故以点为坐标原点,以所在直线分别为轴建立空间直角坐标系,D 1,,DA DC DD ,,x y z.()()()()110,0,2,1,0,1,,0,1,01,1,2D E C B 所以,()()()111,0,1,1,1,1,0,1,1ED EC EB =-=--=设平面的法向量为,1D EC (),,n n y z = 则10000x z n ED x y z n EC ⎧-+=⎧⋅=⇒⎨⎨-+-=⋅=⎩⎩令则1,x =()1,2,1n = 设平面的法向量为,1B EC (),,m a b c = 则,10000b c m EB a b c m EC ⎧+=⎧⋅=⇒⎨⎨-+-=⋅=⎩⎩令,则,1b =()2,1,1m =- 则,1cos ,2m n m n m n ⋅<>== 因为二面角为锐角,则二面角的大小为.3π【点睛】利用法向量求解空间角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.16.(2020·贵州安顺市·高三其他模拟(理))如图,底边是边长为3的正方形,平面ABCD 平面,.ADEF ⊥ABCD //,,AF DE AD DE AF DE ⊥==(1)求证:平面平面;ACE ⊥BED (2)在线段上是否存在点,使得二面角的大小为60°?若存在,求出的值;AF M M BE D --AMAF 若不存在,请说明理由.【答案】(1)证明见解析;(2)存在;.14AM AF =【分析】(1)利用面面垂直的性质和线面垂直的判定定理,可证明;(2)以为坐标原点,建立空间直角坐标系D .设,求出二面角夹角的余弦值,构造的等式,求解即可求出比例关系.D xyz -()3,0,M t M BE D --t t 【详解】解:(1)因为平面平面,平面平面,平面,ADEF ⊥ABCD ADEF ABCD AD =DE ⊂ADEF ,DE AD ⊥所以平面,DE ⊥ABCD 因为平面,所以,AC ⊂ABCD DE AC ⊥又四边形是正方形,所以,ABCD AC BD ⊥因为,平面,平面,DE BD D ⋂=DE ⊂BED BD ⊂BED 所以平面.AC ⊥BED又平面,AC ⊂ACE 所以平面平面;ACE ⊥BED (2)因为两两垂直,所以以为坐标原点,建立如图所示的空间直角坐标系.,,DA DC DE D D xyz-则,,假设在线段上存在符合条件的点()((3,0,0,3,0,,A F E ()()3,3,0,0,3,0B C AF ,设,,则,M ()3,0,Mt 0t ≤≤()(()0,3,,3,,3,3,0BM t BF CA =-=--=- 设平面的法向量为,MBE (),,m x y z = 则,·30·330m BM y tz m BE x y ⎧=-+=⎪⎨=--+=⎪⎩ 令,得,y t=(),,3m t t = 由(1)知平面,所以是平面的一个法向量,CA ⊥BED CABED ,·1cos ,cos 602m CA m CA m CA ︒====整理得,解得(舍去),22150t -+=t =t =故在线段上存在点,使得二面角的大小为60°,此时.AF M M BE D --14AM AF=本题考查面面垂直的性质和证明面面垂直,考查已知二面角的大小求参数,属于中档题.方法点睛:(1)由面面垂直的性质可得到线面垂直;(2)由线面垂直,得出线线垂直;(3)再找一组线线垂直,即可得到线面垂直;(4)由线在面内,可得到面面垂直.17.(2020·全国高三其他模拟)如图,在四棱锥中,底面为矩形,为等腰直角S ABCD -ABCD SAD A三角形,,,是的中点,二面角的大小等于120°.SA SD ==2AB =F BC S AD B --(1)在上是否存在点,使得平面平面,若存在,求出点的位置;若不存在,请AD E SEF ⊥ABCD E 说明理由.(2)求直线与平面所成角的正弦值.SA SBC【答案】(1)在线段上存在点满足题意,为的中点;(2.E E AD 【分析】(1)取中点,可证,得线面垂直后可得面面垂直;AD E ,AD EF AD SD ⊥⊥(2)由(1)知就是二面角的平面角,得,建立空间直角坐标系SEF ∠S AD B --120SEF ∠=︒,用空间向量法求线面角.E xyz -解:(1)在线段上存在点满足题意,且为的中点.E E AD 如图,连接,,,EF SE SF ∵四边形是矩形,∴.ABCD AB AD ⊥又,分别是,的中点,E F AD BC ∴,.//EF AB AD EF ⊥∵为等腰直角三角形,,为的中点,SAD A SA SD =E AD ∴.SE AD ⊥∵,平面,平面,SE EF E = SE ⊂SEF EF ⊂SEF ∴平面.AD ⊥SEF 又平面,AD ⊂ABCD ∴平面平面.SEF ⊥ABCD 故上存在中点,使得平面平面.AD E SEF ⊥ABCD(2)解:由(1)可知就是二面角的平面角,SEF ∠S AD B --∴.120SEF ∠=︒以为坐标原点,,的方向分别为,轴正方向,建立如图所示的空间直角坐标系,E EA EFx y E xyz -由为等腰直角三角形,,得,SADA SA SD ==4AD ===.2SE ==可得,,,,(0,S -()2,0,0A ()2,2,0B()2,2,0C -∴,,,(2,1,SA =(2,3,SB = (2,3,SC =- 设是平面的法向量,(),,n x y z = SBC 则即0,0,n SB n SC ⎧⋅=⎨⋅=⎩230,230,x y x y ⎧+=⎪⎨-+=⎪⎩可取.(n = 设直线与平面所成的角为,SA SBC θ则,sin cos ,SA θ=∴直线与平面.SA SBC 【点睛】方法点睛:求解线段上点的位置的探索性问题,一般是先根据条件猜测点的位置,再给出证明,所求点多为中点或三等分点中某一个,也可以根据相似知识找点,求解时注意中位线的性质及三点共线条件的应用.18.(2020·全国高三其他模拟)如图,四边形中,是等腰直角三角形,,MABC ABC A 90ACB ∠=︒是边长为2的正三角形,以为折痕,将向上折叠到的位置,使点在平面MAC △AC MAC △DAC △D 内的射影在上,再将向下折叠到的位置,使平面平面,形成几何ABC AB MAC △EAC A EAC ⊥ABC 体.DABCE (1)点在上,若平面,求点的位置;F BC //DF EAC F (2)求二面角的余弦值.D BCE --【答案】(1)为的中点;(2.F BC 【分析】(1)设点在平面内的射影为,连接,,取的中点,易得平面.取D ABC O OD OC BC F //OF EAC 的中点,连接,由平面平面,得到平面,又平面,则AC H EH EAC ⊥ABC EH ⊥ABC DO ⊥ABC ,则平面,然后由面面平行的判定定理证明.//DO EH //DO EAC (2)连接,以为坐标原点,,,所在直线分别为,,轴,建立空间直角坐标OH O OF OH OD x y z 系,分别求得平面的一个法向量为和平面的一个法向量为,由BDC (),,m x y z = EBC (),,n a b c = 求解.cos ,m n m n m n ⋅=⋅ 【详解】(1)如图,设点在平面内的射影为,连接,,D ABC O OD OC ∵,AD CD =∴,OA OC =∴在中,为的中点.Rt ABC △O AB 取的中点,连接,,BC F OF DF 则,又平面,平面,//OF AC OF ⊄EAC AC ⊂EAC ∴平面.//OF EAC 取的中点,连接,AC H EH 则易知,又平面平面,平面平面,EH AC ⊥EAC ⊥ABC EAC ABC AC =∴平面,EH ⊥ABC 又平面,DO ⊥ABC ∴,又平面,平面,//DO EH DO ⊄EAC EH ⊂EAC ∴平面.//DO EAC 又,DO OF O ⋂=∴平面平面.//DOF EAC 又平面,DF ⊂DOF∴平面,此时为的中点.//DF EAC F BC (2)连接,由(1)可知,,两两垂直,以为坐标原点,,,所在直线OH OF OH OD O OF OH OD 分别为,,轴,建立如图所示的空间直角坐标系,x yz 则,,,,()1,1,0B-(D (0,1,E ()1,1,0C 从而,,.()0,2,0BC =u u ur (BD =-(1,2,BE =- 设平面的一个法向量为,BDC (),,m x y z = 则即0,0,BC n BD m ⎧⋅=⎨⋅=⎩20,0,y x y =⎧⎪⎨-++=⎪⎩得,取,则,.0y=x =1z=)m = 设平面的一个法向量为,EBC (),,n a b c = 则即0,0,BC n BE n ⎧⋅=⎨⋅=⎩20,20,b a b =⎧⎪⎨-+=⎪⎩得,取,,0b =a =1c =-)1n =-r 从而.cos ,m n m n m n⋅===⋅ 易知二面角为钝二面角,D BCE --所以二面角.D BCE --【点睛】关键点点睛:(1)在求解与图形的翻折有关的问题时,关键是弄清翻折前后哪些量变了,哪些量没变,哪些位置关系变了,哪些位置关系没变;(2)利用向量法求二面角的关键是建立合适的空间直角坐标系及准确求出相关平面的法向量.19.(2020·全国高三专题练习(理))如图,在四棱柱中,底面是边长为21111ABCD A B C D -ABCD 的菱形,,,点分别为棱,的中点.60BAD ∠=︒1AD DD ⊥,M N 1DD BC(1)求证:平面;//CM 1AD N(2)若,二面角与平面所成角的正弦值.1AC BD ⊥D MC B --AM BCM【答案】(1)证明见解析;(2.【分析】(1)取的中点,连接,得四边形为平行四边形,得,再由线面平行的1AD E ,EM EN EMCN CM //NE 判定定理即可证明平面;//CM 1AD N (2)先证平面,然后建立空间直角坐标系,写出相关点的坐标,求出平面和平面1DD ⊥ABCD DMC的一个法向量,再由二面角的长,得与平面的一个BCM D MC B --DM MA BCM 法向量,最后利用向量的夹角公式即可求得直线与平面所成角的正弦值.AM BCM 【详解】(1)如图,取的中点,连接.因为为棱的中点,所以且.1AD E ,EM EN M 1DD //ME AD 12ME AD =因为四边形是菱形,为的中点,所以且,ABCD N BC //CN AD 12CN AD =所以且,所以四边形为平行四边形,所以,//C ME N ME CN =EMCN CM //NE 又平面,平面,所以平面.CM ⊄1AD N NE ⊂1AD N //CM 1AD N (2)连接,因为底面是菱形,所以,又,,,所以BD ABCD AC BD ⊥1AC BD ⊥1=BD BD B ⋂平面,所以,又,,所以平面.取AC ⊥1DBD 1AC DD ⊥1AD DD ⊥AC AD A = 1DD ⊥ABCD AB 的中点,连接,则,以为坐标原点,,所在直线分别为轴建立F DF DF DC ⊥D ,,DF DC DD ,,x y z 如图所示的空间直角坐标系.设,则,,,,,()120DD a a =>()0,0,0D ()0,0,M a ()0,2,0C )B )1,0A -所以.())0,2,,1,0MC a CB =-=- 设平面的法向量为,则,即,取,得BCM (),,m x y z = 00m MC m CB ⎧⋅=⎨⋅=⎩200y az y -=⎧⎪-=1x =.m ⎛= ⎝ 易知平面的一个法向量为DMC ()1,0,0n =r 由题意得,.cos ,m n =〈〉=a =所以,.1,MA =- (m =u r 设直线与平面所成的角为,AM BCM θ则sin cos ,||||m MA m MA m MA θ⋅=〈〉===⋅所以直线与平面.AM BCM【点睛】方法点睛:直线和平面所成的角的求法方法一:(几何法)找作(定义法)证(定义)指求(解三角形),其关键是找到直线在平→→→→面内的射影作出直线和平面所成的角和解三角形.方法二:(向量法),其中是直线的方向向量,是平面的法向量,是直线和平面sin AB n AB n α= A AB l n α所成的角.。
(高中段)大题考法立体几何第二课时空间向量与空间角3
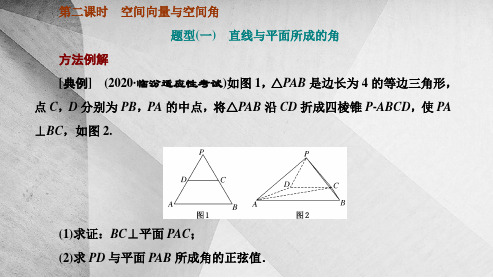
[解] (1)证明:在△ABC 中,BC=2,AB=4,∠ABC=60°,所以 AC2= BC2+AB2-2BC·AB·cos B=12,
则有 AC2+BC2=AB2,即 AC⊥BC. 又因为 PA⊥BC,PA∩AC=A,PA⊂平面 PAC,AC⊂平面 PAC,所以 BC ⊥平面 PAC. (2)由(1)知 AC⊥BC,以点 C 为坐标原点,CA,CB 所在 直线分别为 x,y 轴建立如图所示的坐标系 C-xyz. 则 C(0,0,0),A(2 3,0,0),B(0,2,0),D( 3,-1,0), 易知 P 在底面的射影为 AC 与 BD 的交点, 所以 P233,0,236,―PD→= 33,-1,-2 36,
由(1)知―A→P =0,1, 22是平面 PCB 的一个法向量,
记 n =―A→P ,则
n ,m
n ·m =
|n |·|m
|=2 5
5 .
所以二面角
B-PC-E
的余弦值为2 5
5 .
融通方法 利用空间向量求二面角的解题模型
应用体验 (2020·河北“五个一”名校联考)在四棱锥 P-ABCD 中,AD ∥BC,AB=BC=CD=12AD,G 是 PB 的中点,△PAD 是 等边三角形,平面 PAD⊥平面 ABCD. (1)求证:CD⊥平面 GAC; (2)求二面角 P-AG-C 大小的正弦值.
设平面 AEF 的一个法向量为 n =(x1,y1,z1),
n ·―AE→=0,
则 n
·―AF→=0,
即x21x+1+z1λ=y1=0,0.
令 y1=2,则zx11==λ-. λ, ∴n =(-λ,2,λ).
设平面 PCD 的一个法向量为 m =(x2,y2,z2),
立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
高考大题专项(四) 立体几何

| || |
所以异面直线 PC 与 BQ
=
2
,
3
2
所成角的余弦值为 3 .
解题心得用向量法求异面直线所成角的一般步骤
(1)选择三条两两垂直的直线建立空间直角坐标系.
(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量.
(3)利用向量的夹角公式求出向量夹角的余弦值.
(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.
高考大题专项(四) 立体几何
【考情分析】
从近五年的高考试题来看,立体几何是历年高考的重点,约占整个试卷的
15%,通常以一大两小的模式命题,以中、低档难度为主.简单几何体的表面
积与体积、点、线、面位置关系的判定与证明以及空间角的计算是考查
的重点内容,前者多以客观题的形式命题,后者主要以解答题的形式命题考
【例题】 (2020安徽高三三模)如图,边长为2的等边三角形ABC所在平面与
菱形A1ACC1所在平面互相垂直,且BC∥B1C1,BC=2B1C1,A1C=
(1)求证:A1B1∥平面ABC;
(2)求多面体ABC-A1B1C1的体积.
3 1.
AC
(1)证明∵四边形A1ACC1是菱形,
∴AC∥A1C1.
对点训练2(2020辽宁高三三模)如图,在直棱柱ABCDA1B1C1D1中,底面ABCD为菱形,AB=BD=2,BB1=2,BD
与AC相交于点E,A1D与AD1相交于点O.
(1)求证:AC⊥平面BB1D1D;
(2)求直线OB与平面OB1D1所成的角的正弦值.
(1)证明∵底面ABCD为菱形,∴AC⊥BD.
查.着重考查推理论证能力和空间想象能力,而且对数学运算的要求有加强
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考中档大题专项训练-立体几何与空间向量1.如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置,OD ′=10.(1)证明:D ′H ⊥平面ABCD ; (2)求二面角B -D ′A -C 的正弦值. (1)证明 由已知得AC ⊥BD ,AD =CD . 又由AE =CF 得AE AD =CF CD,故AC ∥EF . 因此EF ⊥HD ,从而EF ⊥D ′H .由AB =5,AC =6得DO =BO =AB 2-AO 2=4. 由EF ∥AC 得OH DO =AE AD =14.所以OH =1,D ′H =DH =3.于是D ′H 2+OH 2=32+12=10=D ′O 2,故D ′H ⊥OH . 又D ′H ⊥EF ,而OH ∩EF =H , 所以D ′H ⊥平面ABCD . (2)解 如图,以H 为坐标原点,HF →的方向为x 轴正方向,HD →的方向为y 轴正方向,HD ′—→的方向为z 轴正方向,建立空间直角坐标系,则H (0,0,0),A (-3,-1,0),B (0,-5,0),C (3,-1,0),D ′(0,0,3),AB →=(3,-4,0),AC →=(6,0,0),AD ′→=(3,1,3).设m =(x 1,y 1,z 1)是平面ABD ′的法向量,则 ⎩⎪⎨⎪⎧m ·AB →=0,m ·AD ′→=0,即⎩⎪⎨⎪⎧3x 1-4y 1=0,3x 1+y 1+3z 1=0,所以可取m =(4,3,-5).设n =(x 2,y 2,z 2)是平面ACD ′的法向量,则 ⎩⎪⎨⎪⎧n ·AC →=0,n ·AD ′→=0,即⎩⎪⎨⎪⎧6x 2=0,3x 2+y 2+3z 2=0,所以可取n =(0,-3,1).于是cos 〈m ,n 〉=m ·n |m ||n |=-1450×10=-7525.sin 〈m ,n 〉=29525.因此二面角B -D ′A -C 的正弦值是29525.2.在如图所示的圆台中,AC 是下底面圆O 的直径,EF 是上底面圆O′的直径,FB 是圆台的一条母线.(1)已知G ,H 分别为EC ,FB 的中点,求证:GH∥平面ABC ;(2)已知EF =FB =12AC =23,AB =BC ,求二面角F -BC -A 的余弦值.(1)证明 设FC 中点为I ,连接GI ,HI .在△CEF 中,因为点G ,I 分别是CE ,CF 的中点, 所以GI ∥EF .又EF ∥OB ,所以GI ∥OB .在△CFB 中,因为H 是FB 的中点,所以HI ∥BC .又HI ∩GI =I ,BC ∩OB =B , 所以平面GHI ∥平面ABC .因为GH 平面GHI ,所以GH ∥平面ABC .(2)解 连接OO ′,则OO ′⊥平面ABC .又AB =BC ,且AC 是圆O 的直径,所以BO ⊥AC . 以O 为坐标原点,建立如图所示的空间直角坐标系.由题意得B (0,23,0),C (-23,0,0). 过点F 作FM ⊥OB 于点M ,所以FM =FB 2-BM 2=3,可得F (0,3,3). 故BC →=(-23,-23,0),BF →=(0,-3,3). 设m =(x ,y ,z )是平面BCF 的法向量. 由⎩⎪⎨⎪⎧m ·BC →=0,m ·BF →=0,可得⎩⎨⎧-23x -23y =0,-3y +3z =0.可得平面BCF 的一个法向量m =⎝⎛⎭⎪⎫-1,1,33,因为平面ABC 的一个法向量n =(0,0,1),所以cos 〈m ,n 〉=m ·n |m ||n |=77.所以二面角F -BC -A 的余弦值为77.3.将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,AC 长为23π,11A B 长为π3,其中B1与C 在平面AA1O1O 的同侧.(1)求三棱锥C —O1A1B1的体积;(2)求异面直线B1C 与AA1所成的角的大小. 解 (1)连接O 1B 1,则11A B =∠A 1O 1B 1=π3,∴△O 1A 1B 1为正三角形, ∴111O A B S=34, ∴111—C O A B V =13OO 1·111O A B S =312. (2)设点B 1在下底面圆周的射影为B , 连接BB 1,则BB 1∥AA 1,∴∠BB 1C 为直线B 1C 与AA 1所成角(或补角),BB 1=AA 1=1.连接BC ,BO ,OC ,AB =11A B =π3,AC =2π3, ∴BC =π3,∴∠BOC =π3,∴△BOC 为正三角形,∴BC =BO =1,∴tan∠BB 1C =BCBB 1=1, ∴∠BB 1C =45°,∴直线B 1C 与AA 1所成的角的大小为45°.4.如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=12为棱AD的中点,异面直线PA与CD所成的角为90°.(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;(2)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.解(1)在梯形ABCD中,AB与CD不平行.延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.理由如下:由已知,BC∥ED,且BC=ED.所以四边形BCDE是平行四边形.从而CM∥EB.又EB平面PBE,CM平面PBE.所以CM∥平面PBE.(说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点) (2)方法一由已知,CD⊥PA,CD⊥AD,PA∩AD=A,所以CD⊥平面PAD.从而CD⊥PD.所以∠PDA是二面角P-CD-A的平面角.所以∠PDA=45°.设BC=1,则在Rt△PAD中,PA=AD=2.过点A作AH⊥CE,交CE的延长线于点H,连接PH.易知PA⊥平面ABCD,从而PA⊥CE.且PA∩AH=A,于是CE⊥平面PAH.又CE平面PCE,所以平面PCE⊥平面PAH.过A作AQ⊥PH于Q,则AQ⊥平面PCE.所以∠APH是PA与平面PCE所成的角.在Rt△AEH中,∠AEH=45°,AE=1,所以AH =22. 在Rt△PAH 中,PH = PA 2+AH 2=322. 所以sin∠APH =AH PH =13.方法二 由已知,CD ⊥PA ,CD ⊥AD ,PA ∩AD =A , 所以CD ⊥平面PAD . 于是CD ⊥PD .从而∠PDA 是二面角P -CD -A 的平面角.所以∠PDA =45°. 由∠PAB =90°,且PA 与CD 所成的角为90°,可得PA ⊥平面ABCD . 设BC =1,则在Rt△PAD 中,PA =AD =2.作Ay ⊥AD ,以A 为原点,以AD →,AP →的方向分别为x 轴,z 轴的正方向,建立如图所示的空间直角坐标系,则A (0,0,0),P (0,0,2),C (2,1,0),E (1,0,0). 所以PE →=(1,0,-2),EC →=(1,1,0),AP →=(0,0,2). 设平面PCE 的法向量为n =(x ,y ,z ). 由⎩⎪⎨⎪⎧n ·PE →=0,n ·EC →=0.得⎩⎪⎨⎪⎧x -2z =0,x +y =0.设x =2,解得n =(2,-2,1).设直线PA 与平面PCE 所成的角为α, 则sin α=|n ·AP →||n |·|AP →|=22×22+-22+12=13. 所以直线PA 与平面PCE 所成角的正弦值为13.5.如图,在四棱锥P -ABCD 中,平面PAD⊥平面ABCD ,PA⊥PD,PA =PD ,AB⊥AD,AB =1,AD =2,AC =CD = 5.(1)求证:PD⊥平面PAB ;(2)求直线PB 与平面PCD 所成角的正弦值;(3)在棱PA 上是否存在点M ,使得BM∥平面PCD 若存在,求AMAP的值;若不存在,说明理由. (1)证明 ∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,又AB ⊥AD ,AB 平面ABCD , ∴AB ⊥平面PAD .∵PD 平面PAD ,∴AB ⊥PD ,又PA ⊥PD ,PA ∩AB =A ,∴PD ⊥平面PAB .(2)解 取AD 中点O ,连接CO ,PO .∵PA =PD ,∴PO ⊥AD . 又∵PO 平面PAD ,平面PAD ⊥平面ABCD , ∴PO ⊥平面ABCD ,∵CO 平面ABCD ,∴PO ⊥CO , ∵AC =CD ,∴CO ⊥AD .以O 为原点建立如图所示空间直角坐标系.易知P (0,0,1),B (1,1,0),D (0,-1,0),C (2,0,0). 则PB →=(1,1,-1),PD →=(0,-1,-1),PC →=(2,0,-1). 设n =(x 0,y 0,1)为平面PDC 的一个法向量. 由⎩⎪⎨⎪⎧n ·PD →=0,n ·PC →=0得⎩⎪⎨⎪⎧-y 0-1=0,2x 0-1=0,解得⎩⎪⎨⎪⎧y 0=-1,x 0=12.即n =⎝ ⎛⎭⎪⎫12,-1,1.设PB 与平面PCD 的夹角为θ.则sin θ=|cos 〈n ,PB →〉|=⎪⎪⎪⎪⎪⎪⎪⎪n ·PB →|n ||PB →|=⎪⎪⎪⎪⎪⎪⎪⎪12-1-114+1+1×3=33.(3)解 设在棱PA 上存在点M ,使得BM ∥平面PCD ,则存在λ∈[0,1]使得AM →=λAP →,因此点M (0,1-λ,λ),BM →=(-1,-λ,λ). ∵BM 平面PCD ,∴BM ∥平面PCD ,当且仅当BM →·n =0,即(-1,-λ,λ)·⎝ ⎛⎭⎪⎫12,-1,1=0,解得λ=14,∴在棱PA 上存在点M 使得BM ∥平面PCD ,此时AM AP =14.。
