力法对称结构
合集下载
结构力学-力法中对称性的利用

对弯矩X1,一对轴力X2和对剪力X3。X1和X2是正
对称的,X3是反对称的。
X2 X1
X3 X1 X2
EI1
对 称
轴
EI2
EI2
(a)
图8-17
X3 (b)基本结构
绘出基本结构的各单位弯矩力(图解-18),可以看出 M1图和M2图是正对称的,而M3是反对称的。
X1=1
X2=1
X3=1
M1图
M2图
M3图
+ 1P=0 22Y2+ 2P=0
当对称结构承爱一般非对称荷载时,我们还可以将荷
载分解为正,反对称的两组,将它们分别作用于结构上求 解,然后将计算叠加(图8-24)。显然,若取对称的基本 结构计算,则在正对称荷载作用下只有正对称的多余未知 力,反对称荷载作用下只有反对称的多余未知力。
P
q
P/2 q/2 P/2
P/2
+ q/2
q/2 P/2
图8-24
转到下一节
是这样的例子。为了使副系数为零,可以采取未知力分组
的方法。
AP
BP
(a)
X1
X2 X1
(b) 基本体系
(c)
(d)
X2
这就是将原有在对称们置上的两个多个未知力X1和X2分 解为新的两组未知力:一组为两个成正对称的未知力Y1, 另一驵为两个成反对称 的未知力Y2(图8-23a)。新的未 知力与原未知力之间具有如下关系:
可知副系数 13 =31=0, 23 =32 =0 于是方程可以简
化为
11X1 12 X 2 1P 0
21X1 22 X 2 2P 0
33 X 3 3P 0
力法

=
P
P X1
P
△1X1 X1
=
X1
+
△1P
变形协调方程: △1X1+ △1P=0 △1X1 = δ11X1 一次超静定结构力法的基本方程为:
δ11
δ11X1+△1P=0
X1=1
二次超静定结构力法的基本方程为:
11 X 1 12 X 2 1P 0 21 X 1 22 X 2 2 P 0
二、基本结构 去掉超静定结构的多余约束所得的静定结构为力法的基本结构 基本结构一定是无多余约束的几何不变体系。同一个超静定结 构,由于去掉的多余约束不同,所得的基本结构也不同,因此力法 解题的基本结构不是唯一的,可有多种选择。 【例8-2】力法解图 (a)所示超静定刚架,试选择基本结构。 P2
B
P1
基本未知量: X1=RB
(2)去掉固定端A的转动约束,得基本结构如图 (2)所示; 基本未知量: X1= mA
【例8-2】力法解图 (a)所示超静定刚架,试选择基本结构。 P2 P2 P2
B
B B
P1
RB
A
P1
A
P1 (3) X1=YA XA
A
XA
YA
(a) mA
(4)
(3)去掉固定端A的竖向约束,得基本结构如图 (3)所示; 基本未知量: X1= YA
对称轴 对称轴
2EI
P 对称轴
P
P
P 对称轴
P
P EI
2EI
2EI
对称结构、对称荷载 P 对称轴 P
等代结构 P
对称结构、反对称荷载 P 对称轴 P
等代结构 P
对称结构、对称荷载
等代结构
结构力学 (1)

X1 3EI 3 l
基本结构已 为何为 0 无支座位移
5. 内力计算(静定结构)
M M1 X1 M P
内力全部由多余未知力引 起
31
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
M M 1 X 1 (
3EI ) x; 0 x l 3 l
3EI 3EI ) 3 2 l l
对于支座位移
A B
1. 超静定结构支座移动、温度改变使结构产生变形,同时产生内力。
C
C
A
B
C’
FyC
静定结构 无内力和支座反力
超静定结构 有内力和支座反力
23
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
对于温度变化
A
t t
B
C
A
t t
B
C
C’
FyC
静定结构 无内力和支座反力
X2
X3
X1
a 0 11 X 1 12 X 2 13 X 3 1C 0 2 C b 0 21 X 1 22 X 2 23 X 3 0 X X X 0 3C 31 1 32 2 33 3 0
1 P 1C 0 11 X 1 12 X 2 13 X 3 P 基本结构由支座 2P X X X 0 位移引起的 21 1 22 2 23 3 22 CP X X X 0 3P i 方向位移 3 P 31 1 32 2 33 3 3 C
29
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
基本结构(II)
基本结构已 为何为 0 无支座位移
5. 内力计算(静定结构)
M M1 X1 M P
内力全部由多余未知力引 起
31
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
M M 1 X 1 (
3EI ) x; 0 x l 3 l
3EI 3EI ) 3 2 l l
对于支座位移
A B
1. 超静定结构支座移动、温度改变使结构产生变形,同时产生内力。
C
C
A
B
C’
FyC
静定结构 无内力和支座反力
超静定结构 有内力和支座反力
23
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
对于温度变化
A
t t
B
C
A
t t
B
C
C’
FyC
静定结构 无内力和支座反力
X2
X3
X1
a 0 11 X 1 12 X 2 13 X 3 1C 0 2 C b 0 21 X 1 22 X 2 23 X 3 0 X X X 0 3C 31 1 32 2 33 3 0
1 P 1C 0 11 X 1 12 X 2 13 X 3 P 基本结构由支座 2P X X X 0 位移引起的 21 1 22 2 23 3 22 CP X X X 0 3P i 方向位移 3 P 31 1 32 2 33 3 3 C
29
§6.6 支座位移、温度变化等作用下时的超静定结构的计算
基本结构(II)
结构力学-力法-对称性应用-去一半计算

例8-5 试计算如图示圆环的内力。EI=常数。 P
R
o
取1/4
基本体系
P 解:这是一个三次超静定。有两个对称轴,故取四分之一结构,
则为一次超静定。
M1 =1,
Mp=-PRsin/2
X1=1
P
R
o M1图
R
PR/2
o
Mp图
PR(-2)/2
PR/
P M图
如图示,则系数和自由项为:
11=M12ds/EI=1/EI0/2Rd=R/2EI 1P=M1Mpds/EI=1/EI/2(-PRsin)rd=-PR2/2EI
转到下一节
M图(a)
1
C
K
B
a/4
A
MK图(d)
若取(d)的基本结构则有:
Ky=-1/EI1(a/2a/4)1/23pa/88=-3pa3/1408EI1 综上所述,计算超静定结构的步骤是:
(1) 解算超静定结构,求出最后内力,此为实际状态。 (2) 任选一种基本结构,加上单位力求出虚拟状态的内力。 (3) 按位移计算公式或图乘法计算所求位移。
Ky
1 EI1
1 2
a 2
a 2
5 3 Pa 6 88
1 2EI1
1 2
3 88
Pa
15 Paa 88
a 2
1 2
Pa a 4
a 2
3Pa3 1408EI1
3pa/88
B
C I1
p
15pa/88
2I1
A
于是得:
X1=- 1P/11=PR/
最后弯矩为:M=M1X1+MP=PR/-Prsin=PR(1/-sin/2)
第六章-力法(二) ,同济大学结构力学课件,朱慈勉版教材,吕凤悟老师课件
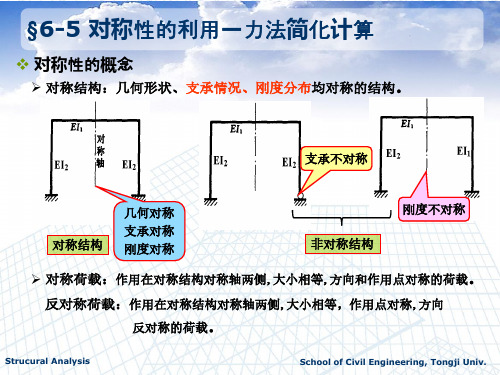
根据对称结构的受力特征,在对称或反对称荷载作用下,可以取半结构 计算,另外半结构的内力可通过对称或反对称镜像得到。
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种:
根据对称轴上的杆件和截面的变形(或位移)特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
对称性的概念
对称结构:几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种:
根据对称轴上的杆件和截面的变形(或位移)特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
对称性的概念
对称结构:几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
整理力法对称结构剖析
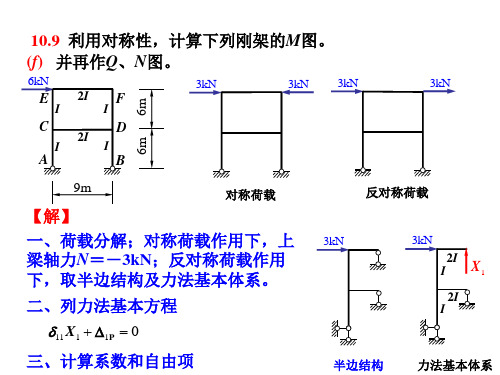
三、计算系数和自由项
反对称荷载
3kN
3kN
2I
I X1
2I I
半边结构
力法基本体系
4.5 4.5
4.5 X1 1
18 18 36
M1 (m)
MP (kN·m)
10.8 10.8
10.8
10.8
2.4
25.2
7.2 18
18 3 7.2
25.2
5.6
M (kNm)
2.4
3
8
11
1 2EI
1 2
4.5 4.5 4.5
l
M1
P Pl Pl 2Pl
MP
11
1 EI
1 2
ll
l
22 3
l
l
l
5l 3 3 EI
1P
1 EI
(
1 2
l
Pl) l
1 ( 2
l
l)(2Pl
2 3
)
7 Pl 3
6EI
四、解方程
5l 3
7 Pl 3
3EI X1 6EI 0
得 X1 7P /10
五、作M 图
M M1X1 MP
7 Pl 10
10
13 Pl
10 A
M
(c) 2F
F
F
l l l
l l
A
B
l
l
F
F
正对称荷载, A 不产生弯矩 B
l
l
A 反对称荷载 B
2P C
D
P
P
P
P
l
E
F
l
A
B
2l
【解】
对称荷载
反对称荷载
3kN
3kN
2I
I X1
2I I
半边结构
力法基本体系
4.5 4.5
4.5 X1 1
18 18 36
M1 (m)
MP (kN·m)
10.8 10.8
10.8
10.8
2.4
25.2
7.2 18
18 3 7.2
25.2
5.6
M (kNm)
2.4
3
8
11
1 2EI
1 2
4.5 4.5 4.5
l
M1
P Pl Pl 2Pl
MP
11
1 EI
1 2
ll
l
22 3
l
l
l
5l 3 3 EI
1P
1 EI
(
1 2
l
Pl) l
1 ( 2
l
l)(2Pl
2 3
)
7 Pl 3
6EI
四、解方程
5l 3
7 Pl 3
3EI X1 6EI 0
得 X1 7P /10
五、作M 图
M M1X1 MP
7 Pl 10
10
13 Pl
10 A
M
(c) 2F
F
F
l l l
l l
A
B
l
l
F
F
正对称荷载, A 不产生弯矩 B
l
l
A 反对称荷载 B
2P C
D
P
P
P
P
l
E
F
l
A
B
2l
【解】
对称荷载
力法

33 x 3 3 p 0
二: 取半边结构进行计算
1 正对称荷载作用下 (1)奇数跨正对称结构
C 截面有轴力、弯矩,无剪力;有竖直位移,无水平位 移和转角;简化为定向支座
(2)偶数跨正对称结构
C C
C截面 有轴力、弯矩,无剪力;无竖直位移,无水平位移 和转角;简化为固定端
2 反对称荷载作用下 (1)奇数跨正对称结构
FP 2
C截面 有剪力,无轴力和弯矩;有水平位移和转角,无竖直 位移;简化为滑动支座
(2)偶数跨正对称结构
FP
FP
FP
FP
FP
F P FQC
FQC
FP
C截面只有剪力,无轴力和弯矩;无竖直位 移,有水平位移和转角;简化为刚接点
这对剪力只使两柱 分别产生等值反向 轴力,而不使其它 杆件产生内力;又 因原结构中间柱的 内力等于该两柱内 力之代数和,故该 剪力对原结构的内 力无影响,可略去
图A
图B
(3)作单位弯矩图和荷载弯矩图
M
计算:
1
M
p
11
1 66 26 1 1 22 22 224 2 2 3 2 EI 2 3 3 EI EI 2 EI
1 2 EI 6 216 3 6 3 4 1 2 24 3 2 984 1 2 EI 3 4 EI EI
A B l 基本结构(一)
X1
11 x 1 A
原结构
A L 1 基本结构(二) B X1
11 x 1 1 C 0
单位荷载法与力法的联系
(1)核心思想:变形体虚功原理
we
=
wi
单位荷载法是应用变形体虚功原理求未 知位移,力法是应用变形体虚功原理求 未知力
对称及反对称性质的利用
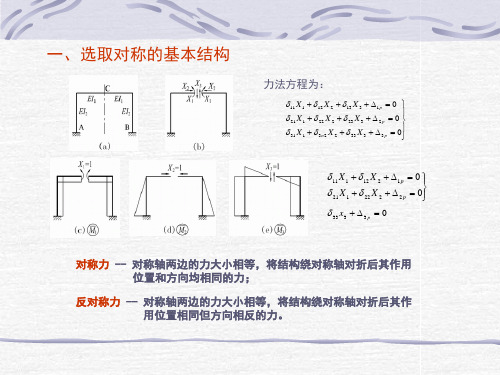
31 X 1 3n2 X 2 33 X 3 3 p 0
11 X1 12 X 2 1p 0 21 X1 22 X 2 2 p 0 33 x3 3 p 0
3p 0
X3=0
对称荷载在对称结构中只引起 对称的反力、内力和变形。
力法方程为:
11 X 1 12 X 2 13 X 3 1p 0
一、选取对称的基本结构
力法方程为:
11 X 1 12 X 2 13 X 3 1p 0
21 X 1 22 X 2 23 X 3 2 p 0
31 X 1 3n2 X 2 33 X 3 3 p 0
11 X1 12 X 2 1p 0 21 X1 22 X 2 2 p 0 33 x3 3 p 0
X1=0 和 X2=0
反对称荷载在对称结构中只引起
反对称的反力、内力和变形。
•当对称结构上作用任意荷载时
例 利用对称性计算图示刚架,并绘弯矩图。
解:1)选取对称的基本结构
2)力法方程
11X1 1p 0
3)计算系数和自由项
绘单位弯矩图和荷载弯矩图
11
2 EI
(1 22 2
22 3
2 4 2)
1 EI
(1 2
l 2
l 2
2 3
l 2
l 2
l
l) 2
7l 3 24 EI
1 p
1 EI
(1 2
pl 2
l
l) 2
Pl 3 8EI
将系数和自由项代入力法方程,得
Pl3
X1
1Hale Waihona Puke p 118EI 7l 33P 7
24EI 绘内力图。
对称力 -- 对称轴两边的力大小相等,将结构绕对称轴对折后其作用 位置和方向均相同的力;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 3
2
1 4.564.5 151.875
EI
EI
1P
1 2EI
1 4.54.536 2
2 3
1 4.5618 1 364.5
EI
2 EI
四、解方程
3
Q (kN)
161.875 364.5 EI X1 EI 0
2.4
得 X1 2.4kN
五、作M 图
8 N (kN) MM1X1MP 六、作Q、N 图
1P
1 EI
(12l
Pl)l
(1ll)(2Pl 2
23)
7Pl3
6EI
四、解方程
5l3 3EI
X1
7Pl3 6EI
0
得 X1 7P/10
五、作M 图
MM1X1MP
7 Pl 10 7 Pl 10 3 Pl Pl 10 13 Pl
10 A
M
(c) 2F
F
F
l l l
l l
A
B
l
l
F
F
正对称荷载, A 不产生弯矩 B
反对称荷载
3kN
3kN
2I
I X1
2I I
半边结构
力法基本体系
4.5 4.5
4.5 X 1 1
18 18 36
M 1 (m)
M P (kN·m)
10.8 10.8
10.8
10.8
2.4
25.2
7.2 18
18 3 7.225.25源自6M (kNm)2.4
3
8
11
1 2EI
1 2
4.54.54.5
2P C
D
P
P
P
P
l
E
F
l
A
B
2l
【解】
对称荷载
一、荷载分解;对称荷载作用下 ,上梁轴力N=-P;反对称荷载 P 作用下,取半边结构及力法基本 体系。
二、列力法基本方程
11X11P0
三、计算系数和自由项
半边结构
反对称荷载
P X1
力法基本体系
l
l l
X1 1
l
M1
P
Pl Pl 2Pl
MP
11E 1I1 2lll2 32lll35E l3I
7 Pl 10 7 Pl 10 3 Pl Pl 10 13 Pl
10 A
M
例 试用力法计算图示刚架,画出弯矩图。EI =常数。
6kN/m
解: 一、取半边结构及力法基本体系
C
二、列力法基本方程
4m
11X11P0
A
B
三、计算系数和自由项
4m 6kN/m
4m 6kN/m
C
C X1
A
半边结构
A
力法基本体系
1
1
C
X1=1 D
A
M1
B
C 18
18 (4.5) 13.5
A
MP
18
D
(4.5) 13.5
B
C 18
18 (4.5) 13.5
A
M
C
3
6A
Q
C
3
A
N
18
D
(4.5) 13.5
B
五、作M图 M M 1X1M PM P 六、作Q图和N图 七、讨论
D
B6 D
3
B
该对称结构在反对称荷载 作用下,取半边结构,是静定 结构。
4A
48
48
A
X1 1
C
M 1 (m)
C
M P (kN/m)
48
48
C
A 24
M
24 B
(kN/m)
11E 1I4 2424 336E 4I
1PE 1I4 24483E 8I4
四、解方程
64
384
3EI X1 EI 0
得 X1 18
五、作M图 MM1X1MP
【例】用等代结构计算图示结构,绘弯矩图,EI为常数。
三、计算系数11和自由项1P
11E 1I( 1 2lll3 22lll) 34E l3I
1PE 1I(1 2lFl)l2 F E l3 I
四、解方程
4l3
Fl3
3EI X1 2EI 0
3F l 8
得 X1 3F/8
五、作M 图
B
MM1X1MP
【例】用力法计算图示结构,并绘出M图 。EI=常数。
1P
1 1l EI 2
Pl 4
l Pl3
2 16EI
四、解方程
7l3
Pl3
24EI
X1
16EI
0
得 X13P/14
五、作M 图
MM1X1MP
【例】用半边等代结构计算图示结构,绘弯矩图,EI为常数。
l
C
P
E
D
P
P
F
P X1
l
A
B
2l
【解】
半边结构
一、取半边结构及力法基本体系
二、列力法基本方程
11X11P0
P/4
P/2 P/4
荷载左右对称上下反 对称,取1/4结构。
l/2
l/2
l/2
X1 1 M 1
M P Pl / 4
3Pl 28
3Pl
2A8
3Pl 28
P
4Pl 28
4Pl 28
M
3Pl 28
3Pl
B2 8
3Pl 28
二、列力法基本方程
11X11P 0
三、计算系数和自由项
11E 1I1 22 l2 l2 l3 2l2 l2 l 27 4lE 3I
l
l
A 反对称荷载 B
l
l
F
F
【解】 一、荷载分解为正对称荷 载和反对称荷载;正对称 荷载,不产生弯矩;反对 称荷载作用下取半边结构 及力法基本体系。
X 1 二、列力法基本方程
A 半边结构
l
A力法基本体系
l
11X11P0
l l
X 1=1
M1
Fl
2F
3F l 8
MP
3F l 8
5Fl A
8
M
5F l 8
【10.3】 用力法解下列刚架,并作M、Q、N图。
1kN/m
C
I2 4I1
1kN/m
D
【解】 一、取力法基本体系
6m
I1
I1
二、列力法基本方程
A
6m
B
6m
11X1+1P=0 三、计算系数11和自由项1P
1kN/m
C
1kN/m
X1
D
1P
M1MP dx0 EI
四、解方程
A 力法基本体系 B
11X100 得 X1 0
三、计算系数和自由项
力法基本体系
l
l l
X1 1
l
M1
P
Pl Pl 2Pl
MP
11E 1I1 2lll2 32lll35E l3I
1P
1 EI
(12l
Pl)l
(1ll)(2Pl 2
23)
7Pl3
6EI
四、解方程
5l3 3EI
X1
7Pl3 6EI
0
得 X1 7P/10
五、作M 图
MM1X1MP
M 1 (m)
D
11E 2I1 26662 31E 4I4
1P
M1MP dx 1 1636063
EI
EI 3
4
B6
3240 EI
C
D
M P (kN·m)
A
B
四、解方程
144 3240 EI X1 EI 0
得
X122.5kN
C
22.5
AM
D
(kN·m)
B
135
五、作M图 MM1X1MP
10.10 试作图示刚架的M图。提示:支座反力是静定的,可视支 座反力为荷载作用在结构上。
1kN/m
C I2 4I1 I1
A
6m
6m
10.5 用力法计算下列排架,作M图。
(a)
20kN/m EA
C
D
I
I
A
B
6m
6m
6m
【解】 一、取力法基本体系 二、列力法基本方程
11X11P 0
三、计算系数11和自由项1P
20kN/m
X1
C
D
A
B
力法基本体系
6
360 (90) 225
X1 1 C
A
q
q
a /2
q X2
X1
EA= o o
q a
a /2
1/4结构
1/15
7/120 1/30
力法基本体系
1/15
1/30
7/120
1/15
1/15
M图(×qa2)
10.9 利用对称性,计算下列刚架的M图。
(f) 并再作Q、N图。
6kN
3kN
3kN
3kN
3kN
E 2I F
I
I
6m 6m
C
D
2I
I
I
A
B
9m
【解】
对称荷载
一、荷载分解;对称荷载作用下,上 梁轴力N=-3kN;反对称荷载作用 下,取半边结构及力法基本体系。
二、列力法基本方程
11X11P0
三、计算系数和自由项
P
P
