2016年第十六届中环杯决赛
第十六届“中环杯”中小学生思维能力训练活动三年级决赛试题答案

第16 届中环杯三年级决赛
一、填空题A (本大题共8 小题,每题6 分,共48 分):
1. 计算:45⨯21+17 ⨯63 =。
【答案】2016
2. 一个三位数abc 满足a ⨯b⨯c 仍然是一个三位数。
满足条件的最小abc 为。
【答案】269
3. D 老师手里有60 颗红色玻璃珠和50 颗黑色玻璃珠。
一个神奇的机器被使用一次后会
将4 颗红色玻璃珠变成1 颗黑色玻璃珠,或者将5 颗黑色玻璃珠变成2 颗红色玻璃珠。
D 老师使用了30 次这个机器后,红色玻璃珠就全没有了。
这时,黑色玻璃珠有
颗。
【答案】20
4. 下图是一个乘法数字谜,最后的乘积为。
【答案】56500
5. 一个五位数abcde ,从五个数码中任意取出两个数码,构成一个两位数(保持数码在
原先五位数中的前后顺序),这样的两位数有10 个:33、37、37、37、38、73、77、
78、83、87,则abcde =。
【答案】37837
6. 有四头奶牛,每头奶牛要么是正常的,要么是变异的。
一头正常的奶牛有4 条腿,并
且永远说假话;一头变异的奶牛要么有3条腿、要么有5 条腿,并且永远说真话。
2006年上海市中环杯数学竞赛闵行区入围决赛名单
闵行区六年级组
网络编号
准考证号码
姓名
年级
所在学校
指导教师
备
8769
张中意
六
闵行区上宝中学
曹雁华
9030
骆钇澐
六
闵行区上宝中学
曹雁华
8979
张溯
六
闵行区上宝中学
曹雁华
8887
胡莹婕
六
闵行区上宝中学
曹雁华
8920
具鑫兰
六
闵行区上宝中学
余漫江
8927
季成易
六
闵行区上宝中学
茅卫星
8921
李家浩
七
闵行区上宝中学
茅卫星
9712
方文侃
七
闵行区上宝中学
茅卫星
9668
肖琨
七
闵行区上宝中学
邓安美
15892
夏天坤
七
闵行区文绮中学
许晓刚
11053
楼仕杰
七
闵行区文绮中学
许晓刚
11376
瞿屹晖
七
闵行区莘松中学
杨效荣
10888
褚子吟
七
闵行区莘松中学
陈宏声
11825
龚一轮
七
闵行区莘松中学
9910
章进明
八
闵行区上宝中学
曹燕华
15527
陈诗哲
八
闵行区上宝中学
王嫄
12628
孙旭东
八
闵行区上宝中学
曹燕华
14758
郁桑
八
闵行区上宝中学
马志刚
14423
张翌恒
2016年第十六届四年级中环杯决赛试题详解

2016年第十六届四年级中环杯决赛试题(详解)1、 计算:0.2×63+1.9×126+196×9=【解析】(计算:积不变原则;提取公因数;)原式=0.2×7×9+1.9×9×14+14×14×9=1.4×9+14×9×1.9+14×9×14=1.4×9+1.4×9×19+1.4×9×140=1.4×9×(1+19+140)=1.4×9×160=14×9×16=20162、 一个质数a 比一个完全平方数b 小10,则a 的最小值是 。
(说明:完全平⽅数是指能表示为⼀个整数的平⽅的数,比如4=22,9=32,所以4、9都是完全平⽅数)【解析】(数论:质数和完全平方数的基本性质)因为质数a 与完全平方数b 相差10,所以a 和b 的末尾相同完全平方数的末尾只能是0、1、4、5、6、9除了2、5以外其余质数的末尾只能是1、3、7、9当a=5时,b=15,15不是完全平方数。
所以a 的末尾一定是1或者9当b 的末尾是1时,符合的完全平方数有81、121、441、……对应的a 就是71、120、431、……这时最小的a 是71当b 的末尾是9时,符合的完全平方数有49、169、289、……对应的a 就是39、159、279、……综上,质数a 的最小值就是713、 如图,C 、E 、B 三点共线,CB ⊥AB ,AE ∥DC ,AB=8,CE=5,则△AED 的面积是 .【解析】(几何:平行线间的等积变形和三角形面积计算公式)联结AC ,因为AE ∥DC ,所以△AED 的面积等于△ACE 的面积,△ACE 的面积等于5×8÷2=20,所以△AED 的面积也是204、 三支蜡烛分别能燃烧30、40、50分钟(但是不是同时点燃的),已知这三支蜡烛同时处于燃烧状态的时间有10分钟,只有一只蜡烛处于燃烧状态的时间有20分钟,那么正好有两只蜡烛同时处于燃烧状态的时间有 分钟。
国内外大型网球赛事

国内外大型网球赛事一、网球四大公开赛 (2)1. 澳洲公开赛(USTRALIAN OPEN) (2)2. 法国公开赛(FRENCH OPEN) (3)3. 温布敦公开赛(WIMBLEDON TENNIS CHAMPIONSHIPS) (4)4. 美国公开赛(U.S. OPEN) (7)二、三大网球团体赛 (8)1、台维斯杯网球赛简介(Davis Cup) (8)2、霍普曼杯(Hopman Cup)简介 (9)3、联合会杯(Fed Cup)网球赛 (10)三、ATP大师杯赛 (10)四、大师系列赛 (11)五、国内大型网球赛事 (13)中国网球公开赛( China Open) (13)CTA全国网球俱乐部联赛 (15)中国网球大奖赛 (16)2006国际女子网球系列赛 (17)2006年DUNLOP&《网球》杂志杯业余网球赛 (19)雪佛兰业余网球大赛 (19)上海网球123推广计划 (20)中国业余网球公开赛 (21)中国大学生网球联赛 (22)年终业余网球大师杯 (22)国际男子"永丰杯"网球巡回赛 (23)"水井坊杯"中国大城市业余网球团体赛(简称CTC) (23)2006中网网球擂台争霸战 (24)六、地区网球赛事 (25)PTA北京大学网球联赛 (25)Wilson杯罗兰时尚网球赛 (25)2005 Wilson杯内蒙古业余网球公开赛 (25)2005红人杯业余网球赛 (27)2005“新民晚报”杯上海市大学生网球联赛 (27)2006 “威能杯”百家社区网球公开赛 (28)首届省港澳"新年鸿杯"网球团体赛 (29)“新年鸿杯”2006广东城际网球邀请赛 (29)“鹰牌花旗参杯”上海精英网球公开赛 (30)"李宁"打造北京青少年网球品牌赛事 (31)一、网球四大公开赛四大公开赛,又称为大满贯赛,是所有的职业正式网球比赛中奖金最多、积分最多、地位最高的比赛,也是所有网球选手最想拿到的冠军。
第16届WMO全国总决赛4年级复赛
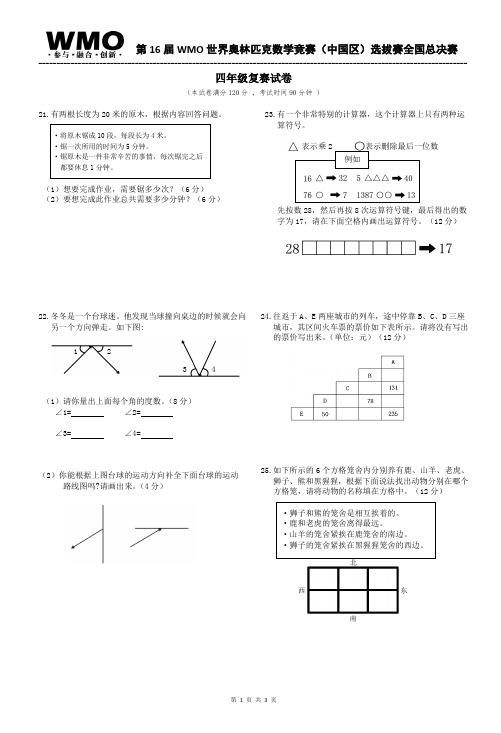
四年级复赛试卷(本试卷满分120分 ,考试时间90分钟 )21.有两根长度为20米的原木,根据内容回答问题。
·将原木锯成10段,每段长为4米。
·锯一次所用的时间为5分钟。
·锯原木是一件非常辛苦的事情,每次锯完之后 都要休息1分钟。
(1)想要完成作业,需要锯多少次?(6分) (2)要想完成此作业总共需要多少分钟?(6分)22.冬冬是一个台球迷。
他发现当球撞向桌边的时候就会向 另一个方向弹走。
如下图:(1)请你量出上面每个角的度数。
(8分)∠1= ∠2=∠3= ∠4=(2)你能根据上图台球的运动方向补全下面台球的运动 路线图吗?请画出来。
(4分)23.有一个非常特别的计算器,这个计算器上只有两种运 算符号。
表示乘2 表示删除最后一位数先按数28,然后再按8次运算符号键,最后得出的数 字为17,请在下面空格内画出运算符号。
(12分)24.往返于A 、E 两座城市的列车,途中停靠B 、C 、D 三座 城市,其区间火车票的票价如下表所示。
请将没有写出 的票价写出来。
(单位:元)(12分)25.如下所示的6个方格笼舍内分别养有鹿、山羊、老虎、 狮子、熊和黑猩猩,根据下面说法找出动物分别在哪个 方格笼,请将动物的名称填在方格中。
(12分) ·狮子和熊的笼舍是相互挨着的。
·鹿和老虎的笼舍离得最远。
·山羊的笼舍紧挨在鹿笼舍的南边。
·狮子的笼舍紧挨在黑猩猩笼舍的西边。
1 234北南 西 东 例如26.某跳水运动员的8次跳水平均成绩是8分,如果把其中一次成绩改为8分后,8次跳水的平均成绩变成了7分,那么被改动的跳水成绩原来是多少分?(12分)27.右图是按照条件给方格涂颜色的例子,按照同样的条件给下面的方格涂颜色。
(12分)28.每年农历的8月15日,中国把这一天称之为“中秋节”,韩国把这一天称之为“秋夕节”,泰国把这一天称之为“祈月节”。
这一天,智雅的妈妈买了一些松饼和月饼。
上海市第九届“中环杯”中小学生思维能力训练活动决赛浦东新区汇总表
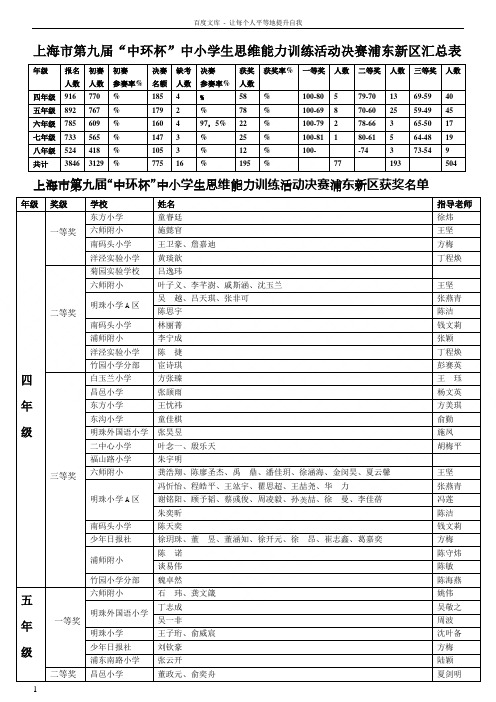
上海市第九届“中环杯”中小学生思维能力训练活动决赛浦东新区汇总表年级报名人数初赛人数初赛参赛率%决赛名额缺考人数决赛参赛率%获奖人数获奖率% 一等奖人数二等奖人数三等奖人数四年级916 770 % 185 4 %58 % 100-80 5 79-70 13 69-59 40 五年级892 767 % 179 2 % 78 % 100-69 8 70-60 25 59-49 45 六年级785 609 % 160 4 97,5% 22 % 100-79 2 78-66 3 65-50 17 七年级733 565 % 147 3 % 25 % 100-81 1 80-61 5 64-48 19 八年级524 418 % 105 3 % 12 % 100- -74 3 73-54 9 共计3846 3129 % 775 16 % 195 % 77 193 504 上海市第九届“中环杯”中小学生思维能力训练活动决赛浦东新区获奖名单年级奖级学校姓名指导老师四年级一等奖东方小学童睿廷徐炜六师附小施懿窅王坚南码头小学王卫豪、詹嘉迪方梅洋泾实验小学黄琰歆丁程焕二等奖菊园实验学校吕逸玮六师附小叶子义、李芊澍、戚斯涵、沈玉兰王坚明珠小学A区吴越、吕天琪、张非可张燕青陈思宇陈洁南码头小学林丽菁钱文莉浦师附小李宁成张颖洋泾实验小学陈捷丁程焕竹园小学分部宦诗琪彭赛英三等奖白玉兰小学方张臻王珏昌邑小学张颉雨杨文英东方小学王忱祎方美琪东沟小学童佳棋俞勤明珠外国语小学张昊昱施凤二中心小学叶念一、殷乐天胡梅平福山路小学朱宇明六师附小龚浩翔、陈廖圣杰、禹鼎、潘佳玥、徐涵海、金闵昊、夏云馨王坚明珠小学A区冯忻怡、程皓平、王竑宇、瞿思超、王喆尧、华力张燕青谢铭阳、顾予韬、蔡彧俊、周凌毅、孙喆、徐曼、李佳蓓冯莲朱奕昕陈洁南码头小学陈天奕钱文莉少年日报社徐玥珠、董昱、董涵知、徐开元、徐昂、崔志鑫、葛嘉奕方梅浦师附小陈诺陈守炜谈易伟陈敏竹园小学分部魏卓然陈海燕五年级一等奖六师附小石玮、龚文箴姚伟明珠外国语小学丁志成吴敬之吴一非周波明珠小学王子珩、俞威宸沈叶备少年日报社刘钦豪方梅浦东南路小学张云开陆颖二等奖昌邑小学董政元、俞奕舟夏剑明五年级二等奖东方小学陈卓余黄唯真二中心小学刘昀霖彭雪晶福山路小学罗天宇赵瑾六师附小潘哲成、杨英哲、施歆予姚伟明珠小学张晶磊、魏依琳顾舫刘子衡、朱瑞宸、朱珺仪、黄彦文、陈音喆沈叶备少年日报社屠杰、封帆、薛梦王莹、康健、罗文豪、顾舒凌、王嘉俊方梅洋泾实验小学李钧诚丁程焕竹园小学高继扬叶荭婷王轶乔王轶娜三等奖白玉兰小学高思承蔡俊磊昌邑小学朱辰宇、朱旻昊夏剑明二中心小学葛嘉文、陈书锴彭雪晶福山路小学施嘉捷赵瑾六师二附小朱逸玮张诚六师附小金琳、闫昶宇、王清怡冯铭朱翔宇、潘易凡、陈昱邦、王逸伦、张悦嘉姚伟明珠外国语小学钱宁周波朱邦晟、赵雅珺、马凯文吴敬之明珠小学沈偲阳、邱杨、王佳萱、徐梓熠、谢润中、刘博宁、夏晨聪、顾寅超、杨晔、施舒洋、王天沈叶备明珠小学金尚丰、许宇轩顾舫南码头小学叶智霖豆晓莲少年日报社吴祺尧、季金捷、刘思嘉、谈妍霏、张圣民、方梅浦东南路小学杨宇昊陆颖郭奉岐严勤栖霞小学穆青李国正上海实验东校吴明轩康逸红外高桥实验小学王子晗黄琼洋泾实验小学秦文雍丁程焕竹园小学分部刘天琦钱红君六年级一等奖上海市实验学校张天奇徐大玮张江集团学校董天诚周红霞二等奖上海市实验学校章开泰唐惠康徐晓骏、刘继媛徐大玮三等奖建平实验中学蒋正高忠超浦东模范中学谢棋泽董悦浦东外国语学校陆家晟赵瑾上海实验东校陈泽宇卫美华上海市实验学校王崇安、顾正扬、陈聿铭、周子陶、蔡万鑫、刘轶炜徐大玮郭祺、蔡亭亭、耿萌哲唐惠康张江集团学校严夏、周嘉琛、郑翰天周红霞竹园中学贾盛杰王书伟七年级一等奖上海市实验学校张嘉彦王海生二等奖上海市实验学校曹君旸、陈力路红英阮张宇、杨舒涵王海生张江集团学校喻望李磊七年级三等奖三等奖建平实验中学布依宁秦莉建平西校曹翔宇、马赫德张雷坤胡义嘉刘鹏邵方洲李景华上海实验东校李嘉吴其胜上海市实验学校李江南、华恺元、孙帆、倪馨仪、易涵坤、张建逸、徐亦飞王海生张广浩、顾济尘路红英张江集团学校石一玮李磊致远中学王楷文汪莹竹园中学何奇、蔡泽昆王书伟八年级二等奖张江集团学校娄国奕、王逸然、王诗圣胡文备三等奖建平西校李劲王晓慧戴镇高培芳张江集团学校邵昱东、王塬夫、刘圣鹏、李岳泽、华凌昊胡文备竹园中学楼家祺、蔡景薇沈茂宏上海市第九届“中环杯”中小学生思维能力训练活动决赛浦东新区获奖名单年级奖级学校姓名指导老师四年级一等奖六师二附小张江山二等奖福山外国语学校杨程凯、新世纪孙云扬上海市实验学校戚岚罡、王睿哲建平实验小学姚江逸三等奖福山外国语学校张健瑞、张羽阳、杨肇远、支鑫奕、秦世新、岳海音、罗致理、廖健行、王舜莹、王太阳、陈佳琪、石月张江高科实验小学王苍上海市实验小学黄明德、单志健、张今、李逸斐明珠小学王慧欣海桐小学陈祖杰上南五村小学邬梦莹五年级一等奖浦东建平实验小学翟润天新世纪顾浩钦南码头小学刘钦豪二等奖明珠小学黄彦文上海实验学校翟淦、沈岑楷浦东建平实验小学廖倩南码头小学屠杰、康健、罗文豪、王嘉俊、薛梦王莹、顾舒凌、封帆福山外国语学校杨天颖、徐尧新世纪小学瞿欣浦东昌邑小学张天扬三等奖三等奖福山外国语学校董圣岚、尹秋阳、任靓婕、周汤昊、赵李洋、李子聿、凌子阳、胡强波、虞晶帆、宋一凡、胡怡慧、许樱瀚海桐小学徐铮浦东建平实验小学杨添屹南码头小学刘思嘉、张圣民、吴祺尧、谈妍霏、季金捷上海市实验小学徐思泽、黄宇洁、徐晟、蒋知耘梅园小学沈卓珺、齐晨辰、胡砺寒上南二村小学常辰浦东明珠小学徐江俊杰二中心小学周莹鋆浦东华高小学金雪怡预备三等奖建平实验小学张敬庭。
2016第十六届中环杯五年级决赛详解

第十六届“中环杯”小学生思维能力训练活动 五年级决赛
城隍喵
【第 3 题】 一个超过 20 的自然数 N ,在14 进制与 20 进制中都可以表示为回文数(回文数就是指正读与倒读都一样的 数,比如12321、3443 都是回文数,而12331不是回文数)。N 的最小值为 ________(答案用10 进制表示)。 【分析与解】 数论,进制与位值。 因为 N 20 ; 所以 N 在14 进制与 20 进制中都不是一位数;
我们希望 N 要尽可能小,故设 N aa bb ;
14
20
即 N a 14 a b 20 b ; N 15a 21b ;
则 N 既是15 的倍数又是 21 的倍数;
故 N 是 15, 21 3 5 7 105 的倍数;
而 105 77 55 ,符合题意;
10
14
20
这个父亲的财产有1000 80000 81000 元;
老大分得1000 81000 1000 1 9000 元;
10 即每个孩子都分到了 9000 元; 这位父亲一共有 81000 9000 9 个孩子。 (方法三)
设这位父亲一共有 n 个孩子;
则倒数第二个孩子分得1000n 1 元以及剩余的 1 ;
第十六届“中环杯”中小学生思维能力训练活动 五年级决赛
2016 年 3 月 5 日 12 : 30 ~ 14 : 00 考试时间: 90 分钟 满分:100 分
一、填空题 A :(本大题共 8 小题,每题 6 分,共 48 分)
【第 1 题】
第16届中环杯决赛试卷与答案六年级(外地)

⎝ ⎭ 第 16 届中环杯六年级决赛(非上海卷)一、填空题 A (本大题共 8 小题,每题 6 分,共 48 分): 1. 计算: 2016 ⨯ ⎛ 1 + 4 + 8 + 19+29 ⎫ = .2 ⨯3 3 ⨯ 7 7 ⨯15 15 ⨯ 34 34 ⨯ 63 ⎪【答案】9762. 有些三位数具有下面的性质:(1)去掉百位数字后,剩下的两位数是一个完全平方数;(2)去掉个位数字后,剩下的两位数也是一个完全平方数;所有满足这些性质的三位数之和为 .【答案】19933. 一件物品的原价是一个有限小数,提价4% 之后变为n 元( n 为正整数),那么n 的最小值为 .【答案】134. 将八个1⨯1⨯1的小立方体堆叠成一个2 ⨯ 2 ⨯ 2 的大立方体,所有的小立方体要么是白色的,要么是黑色的。
最后,大立方体中的黑色小立方体与白色小立方体是间隔放置的 (如下图)将这个大立方体展开,可以得到下面的图 .【答案】 E5.环环、杯杯两人同时从A 地出发到B 地。
2 小时后,环环先到B 地,杯杯还需要1 小时才能到达B 地。
当环环到达B 地时,环环、杯杯共行了15 千米。
整个过程中,两人的速度都保持不变,则A 、B 两地相距千米【答案】96.如图,阴影部分是一个对称的四角星形,其中四个顶点构成一个正方形,另外四个顶点在一个圆周上。
正方形的边长为10 厘米,阴影部分面积是正方形面积的 1 ,那么圆3的半径为厘米【答案】537.125n 3的运算结果中至少有一个数码为9,满足条件的最小正整数n 为.【答案】728.下图是A 城市的地铁线路,一共有六条线:p, q, r, s,t,u 。
两条直线的交点表示换乘站,乘客可以从一条线路转换到另一条线路。
小明从X 站出发,目的地是Y 站。
小明一旦离开X 站后,就不会再回到X 站;一旦到达Y 站后就不会再次离开Y 站;小明每条线路最多乘一次。
那么,一共有多少条不同的路线可以让小明顺利到达Y 站u【答案】81二、填空题 B (本大题共 4 小题,每题 8 分,共 32 分):9.已知a 、b 、c 是互不相同的正整数,它们都不是完全平方数,但是ab 、bc 、ca 都是完全平方数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15.一共 99 人参加了某个数学竞赛,比赛分为三场,分别考察参赛者几何、数论、组合的能 力。小明在数论考试中得了第 16 名,在组合考试中得了第 30 名,在几何考试中得了第 23 名,并且小明在三场考试中没有与任何人并列(每门考试的满分不一定是 100 分)。最后的总 名次是将三次考试的分数相加,从高到低排列后得到的。如果我们用第 A 名表示小明可能 得到的最好总名次(A 越小表示总名次越好),用第 B 名表示小明可能得到的最差总名次,则 100 A B ( )。
1 2
3 4
13.一个骰子 6 个面上分别写着数字 1、2、3、4、5、6,每次投掷骰子后都会将面朝上的数 字记录下来。 任意一个数字一旦出现三次, 整个投掷过程就结束了。 小明一共投掷了 12 次, 他的投掷过程就结束了,所有记录下的数之和为 47.那么他最后 我们考察可以表示为 10 n 1 的数,其中 n 为一个正整数,比如: 11 10 1 1 , 331 10 33 1 。 如果这样的数不能表示为两个较小的形如 10 n 1 的数的乘积(这两个较小 的数可以相等),我们就将这个数称为“中环数”。比如 341=11×31,它可以表示为两个形如 10 n 1 的数的乘积,所以它不是 “ 中环数 ”。又比如 11,它无法表示为更小的两个形如 10 n 1 的数的乘积,所以它是“中环数”。那么在 11、21、31、…、991 中,“中环数”有 ( )个。
6.小胖在编一本书的页码时,一共用了 1101 个数字。已知页码是从 1 开始的连续自然数。 这本书一共有( )页。
7.如图是用棋子摆成的“巨”字。按以下规律继续摆下去,一共摆了 16 个“巨”字。那么共需 要( )枚棋子。
8.春天到了,学校组织学生春游。但是由于某种原因,春游分为室内活动与室外活动。参加 室外活动的人比参加室内活动的人多 480 人。现在把室内活动的 50 人改为室外活动,这样 室外活动的人数正好是室内活动人数的 5 倍。 则参加室内、 室外活动的共有( )人。
14.大正方形内有两个小正方形,这两个小正方形可以在大正方形内任意移动(小正方形的任 何部分都不能移出大正方形,小正方形的边必须与大正方形的边平行)。如果这两个小正方 形的重叠面积最小为 9,最大为 25,并且三个正方形(一个大正方形和两个小正方形)的边长 之和为 23,则三个正方形的面积之和为( )。
9.如图,5×5 的方格中有三个小方格已经染黑。现在要将一个 1×3 的白长方形(不能选已经 染黑的方格)染黑,要求其不能与已经染黑的方格产生公共边或者公共点。有( )种 选法。
10.一次数学竞赛有 5 道题目,每道题目的分值都是一个不同的自然数。题号越小的题目所 占的分值越少(比如第 1 题的分值小于第 2 题的分值)。小明做对了所有的题目,他前 2 题的 总得分为 10 分,后 2 题的总得分为 18 分。那么小明总共得了( )分。
17.右面的两幅图表示两个箭头画在不同的 4 厘米×4 厘米方格内的情况。现在将这两个箭头 画在同一副 4 厘米×4 厘米的方格内,则这两个箭头的重叠部分的面积为( )平方厘 米。
18.有 A、B、C 三类人共 25 人。A 类人永远说真话,B 类人永远说假话,C 类人永远间隔 着说真话和假话(比如某个 C 类人这次说真话了,那么他说的下一句话肯定为假话,再下一 句话又是真话)。 牧师问每个人:“你是不是 A 类人?”17 个人回答“是”。 牧师又问每个人:“你是不是 C 类人?”12 个人回答“是”。 牧师又问每个人:“你是不是 B 类人?”8 个人回答“是”。 这 25 人中,有( )人是 C 类人。
19.小明希望 1~12 这 12 个数字排在一个圆周上, 使得任意相邻的两个数字之差(大减小)为 2 或 3.那么不同的排法有( )种(旋转后相同的排法算同一种)。
20.如图,将 1、2、…、25 填入表中,每个小方格内填入一个数字,所有数字能且只能被使 用一次,其中一些数已被填入。要求,每个小方格内的数都等于与其相邻(有公共边或者公 共定点的就称为相邻)的两个小方格内数之和(除 1、 2 的小方格)。 比如: 与 4 相邻的有 1、 3, 符合题意。则“?”处所填数字为( )。
第十六届“中环杯”三年级(初赛)试题
1. 计算: 2015 2015 2014 2013 ( ). 2. 在下面算式的方框中填入适当的符号(只能填加、减、乘、除这四种符号),使得算式成 立。 (6 2) (3 4) (6 2) 25 3. 用 1~9 这九个数字组成三个三位数 a,b,c(每个数字能且只能使用一次), 则 a b c 的最大 ). 值为(
11.如果一个正整数 x 满足:3x 的位数比 x 的位数多(比如 343 的位数为 3,3×343=1029 的位 数为 4),那么这样的 x 称为“中环数”。将所有的“中环数”从小到大排成一排,其中第 50 个 “中环数”是( )。 12.将 1~9 填入右表,每个数字使用一次,每个小方格填入一个数,其中 1、2、3、4 已经填 好了。如果两个小方格有一条公共边,我们就称这两个小方格相邻。如果与填 9 的小方格 相 邻 的 小 方 格 内 的 数 之 和 为 15 , 那 么 与 填 8 的 小 方 格 相 邻 的 小 方 格 内 的 数 之 和 为 ( )。
4.甲有一张 40 厘米×30 厘米的长方形纸片,他从上面剪下来 10 张 5 厘米×5 厘米的小纸片, 得到右图。这 10 张小纸片的边与长方形的对应边互相平行,而且它们之间不会互相重叠。 那么,剩下图形的周长为( )厘米。
5.小明在右图中的黑色小方格内,每次走动,小明都进入相邻的小方格(如果两个小方格有 公共边,就称它们是相邻的),每个小方格都可以重复进入多次。经过四次走动后,小明所 在的不同小方格有( )种。
21 6 23 7 9 25 24 5 4 1 8 3 2 22 ?
