LINGO软件的使用
LINGO使用说明比较简单
LINGO使用说明比较简单
第九步，分析和优化结果。
优化模型求解完成后，你可以通过结果显
示区中的结果表格和图表来分析和优化结果。
LINGO还提供了一些分析工具，如灵敏度分析和场景分析，帮助你深入理解模型的行为和性能。
第十步，保存和导出结果。
在 LINGO 中，你可以保存整个优化模型
及其求解结果，以供将来使用。
通过点击菜单栏中的“文件”选项，选择“保存”或“导出”，就可以将模型和结果保存为不同的文件格式，如LINGO模型文件（.lng）、Excel 文件（.xls）或文本文件（.txt）。
通过上述十个步骤，你可以使用LINGO软件完成一个优化模型的建立、求解和分析。
当然，LINGO还具备其他高级功能和应用，如混合整数规划、随机规划和非线性规划等，可以根据你的具体需求进行进一步学习和应用。
LINGO使用手册和官方网站上有更多详细的说明和案例，可以帮助你更好
地使用和理解LINGO软件。
LINGO软件的使用方法
2
2
答案
model: max=98*x1+277*x2-x1^2 -0.3*x1*x2-2*x2^2; x1+x2<100; x1<2*x2; @gin(x1); @gin(x2); end ※@gin()是调用的整数函数
第三节 在LINGO中使用集合
• 例题：某公司要决定下四个季度帆船生 产量。下四个季度需求量分别是40条， 60条，75条，25条。每季度生产能力40 条，生产费用400美元/条，如果加班生产 费用450美元/条，每季度库存费20美元/ 条。假定生产提前期为0，初始库存10条， 问如何安排生产总费用最小？
显式列举法 元素列表 隐式列举法
第四节 运算符及其优先级
• 算术运算符：＋，－，*，/，^ • 逻辑运算符： #AND#,#OR#.#NOT#,#EQ#,#NE#,#GT#,# GE#,#LT#,#LE#,TRUE,FALSE • 关系运算符：<(即<=),=,>(即>=)
优先级
优先级 表： 最高 运算符 #NOT#,-(负号） ^ *,/ +,-(减号） #EQ#,#NE#,#GT#,#GE#, #LT#,#LE# #AND#,#OR# <,=,>
集合循环函数
• 用法：@function(setname:expression_list); • 具体如下：@for @sum @max @min
变量界定函数
• • • • @BND(L,X,U)-限制L<=X<=U @BIN(X)-限制X为0或1 @FREE(X)-取消对X的符号限制 @GIN(X)-限制X为整数
• • • • • • • • • 以model:开始，以end结束。 不区分大小写。 目标函数为max=。 语句以；结束。 数与变量之间的乘号不能省。 约束S.t.省略不写。 <与<=,>与>=是等价的。 非负约束可以不输入。 说明语句以！开头。
LINGO应用教程
第十章 LINGOLingo 软件是求解线性规划、非线性规划的数学软件，也可用于一些线性和非线性方程组的求解等。
Lingo 实际上也是最优化问题的一种建模语言，包括许多常用的数学函数供使用者建立优化模型时调用，并可以接受与其他数据文件交换数据。
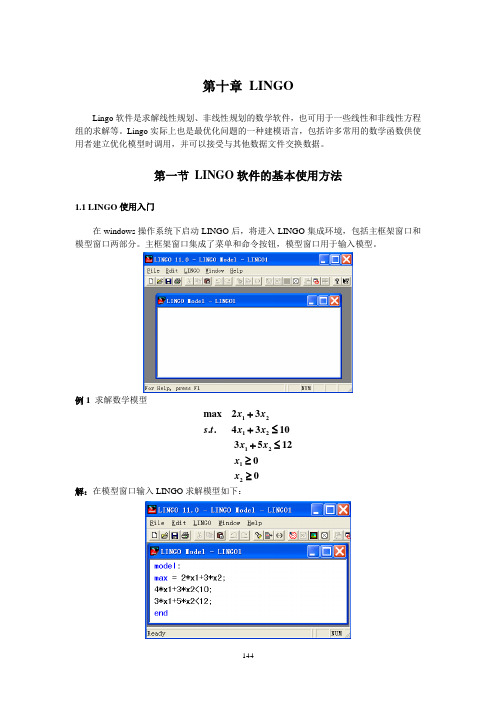
第一节 LINGO 软件的基本使用方法1.1 LINGO 使用入门在windows 操作系统下启动LINGO 后，将进入LINGO 集成环境，包括主框架窗口和模型窗口两部分。
主框架窗口集成了菜单和命令按钮，模型窗口用于输入模型。
例1 求解数学模型12121212max 23..4310351200x x s t x x x x x x ++≤+≤≥≥解：在模型窗口输入LINGO 求解模型如下：输入模型后选择菜单LINGO|Solve 或者按工具栏的，LINGO开始编译模型，如有语法错误将返回一个错误的消息并指明错误出现的位置；如果通过编译，LINGO将激活Solver运算器寻求模型的最优解，首先出现Solver Status状态窗口显示模型求解的运算状态信息：状态窗口显示的信息含义如下：“Global optimal solution found”表示得到全局最优解。
“Objective value: 7.454545”表示最优目标值为7.454545。
“Total solver iterations：2” 表示迭代2次得到结果。
“V alue”给出最优解中各变量的值：x1=1.272727，x2=1.636364。
Reduced Cost 值列出最优单纯形表中判别数所在行的变量的系数，表示当变量有微小变动时，目标函数的变化率。
其中基变量的reduced cost值应为0，对于非基变量xj，相应的reduced cost值表示当某个变量xj 增加一个单位时目标函数减少的量( max型问题)。
本例中此值均为0。
SLACK OR SURPLUS值给出约束条件的松驰变量或剩余变量的值。
怎样使用LINGO软件
会丢失；
• ·后缀“ldt”表示LINGO数据 文件；
• ·后缀“ltf”表示LINGO命令 脚本文件；
LINDO格式的模型文
•
·后缀“lgr”Biblioteka 示LINGO报告 文件；件
• ·后缀“mps”表示MPS（数
学规划系统）格式的模型文
件；
• ·“*.*”表示所有文件。
2 用Lingo求解 二次规划（ QP）模型
之和不可能超过100件，且产品甲的产量不可能超过乙的产 量的两倍。写成数学表达式，就是
x1＋x2≤100, x1≤2x2
综上所述
max ｚ＝98 x1＋277 x2－x12－0.3
x1 x2－2x22
（1.1）
s．t．
x1＋x2≤100 x1≤2x2 x1，x2≥０
（1.2） （1.3）
（1.4）
修改运行时的 内存限制
激活敏感 性分析
例3.1 一奶制品加工厂用牛奶生产A1，A2两种奶制品，1 桶牛奶可以在甲车间用12h加工成3kgA1，或者在乙车间 用8h加工成4kg A2。根据市场需求，生产出的A1，A2全部 能售出，且每千克A1获利24元，每千克A2获利16元。现 在加工厂每天能得到50桶牛奶的供应，每天正式工人总的 劳动时间为480h，并且甲车间的设备每天至多能加工 100kg A1，乙车间的设备的加工能力可以认为没有上限限 制（即加工能力足够大）。试为该厂制定一个生产计划， 使每天获利最大，并进一步讨论以下3个附加问题：
• 用“LINGO | Solve （Ctrl +S）”命令来运 行这个程序。
• （如果想要了解运行状 态窗口中各项的含义， 可先点击工具栏上的图 标 ，再点击运行状态 窗口，屏幕上自动弹出 运行状态窗口的帮助信 息。）
Lingo 数学软件的使用方法
仓库 10 6 7 17 4 12 4 19 4 13 16
客 11 客 12 客 13 客 14 客 15 客 16 客 17 客 18 客 19 客 20
3 6 4 10 12 19 8 7 10 4
2 17 18 19 15 18 16 9 8 8
4 8 16 2 15 11 8 8 3 14
Lingo 数学软件的使用方法
一、Lingo 使用介绍
LINGO 是用来求解线性和非线性优化问题的简易工具。LINGO 内置了一种建立最优化模型 的语言，可以简便地表达大规模问题，利用 LINGO 高效的求解器可快速求解并分析结果。 功能：可以求解非线性规划。也可以做线性规划、整数规划。 特点：运算速度快，允许使用集合来描述大规模的优化问题；
（2） 某仓库供应某客户全部需求量时的运费（单位：万元） 仓库 1 客1 客2 客3 客4 客5 客6 客7 客8 客9 客 10 9 14 6 15 6 19 11 19 4 5 仓库 2 10 16 9 12 8 14 4 20 9 13 仓库 3 2 10 2 18 4 19 8 13 15 9 仓库 4 6 4 1 9 3 3 5 15 6 10 仓库 5 7 10 20 17 7 9 13 16 9 15 仓库 6 15 18 14 18 11 4 20 20 13 1 仓库 7 仓库 8 15 14 20 12 6 15 20 3 1 16 1 1 5 2 2 5 16 8 7 7 仓库 9 18 16 20 18 5 20 8 6 17 20
@SMAX(x1,x2,x3,…,xn)
@FLOOR(x) 最接近 x 的整数 5． 变量定界函数 @BND(L,x,U) @BIN(x) @FREE(x) @GIN(x) 限制 x 的范围 L<=x<=U x为0或1 取消对 x 的限制 x 为整数
2.Lingo优化软件的使用方法
然后再在求解的基础上，在菜单上选择lingo/range(ctr+R), 计算机会自动对每个变量和资源用有量进行范围分析：保 持最优基不变的情况下，变量或约束行的右端允许增加和 减少的量。注意：对整数规划和0-1规划灵敏度分析意义不 大。
Ranges in which the basis is unchanged:
数学模型如下：
max z [ t (i) r (i)]x (i) s(i) y(i)
i 1 i 1
3
3
s.t.
3 c ijx i b( j) j 1,2,3 i 1 x (i) My(i) i 1,2,3 ___ x (i) 0, x Z y(i) 0,1 i 1,2,3
产品1
资源A 资源B 资源C 2 2 1
产品2 产品3
4 3 2 8 4 3
资源量
500 300
单件可变费 固定费用 单件售价
4 100 8
5 150 10
6 200 12
分析问题和设置变量 x(i)表示第i种产品的产量；i=1,2,3 c(i,j)表示第i种产品对第j种资源的消耗量；i=1,23,j=1,23 b(j)表示第j种资源的拥有量； r(i)表示第i种产品的单件可变费用; s(i)表示第i种产品的固定费用； t(i)表示第i种产品的单位售价。 总收益=销售收入-固定费用-可变费用，由于不知道第i种产品 生产与否，所以，必须给定第i种产品的选择变量 y(i)表示第I种产品的生产选择，y(i)=0,表示不生产第i种产品， y(i)=1表示生产第i种产品。
#LT#(小于) #LE#(小于等于) 逻辑运算的结果只有“真”（TRUE)和“假”（FALES)， Llingo用1表示True,其它的都是False。
LINGO基本用法
LINGO基本用法1、概况 (1)2、LINGO的基本用法 (1)3、用LINGO编程语言建立模型 (2)4、建立LINGO/LINDO优化模型需要注意的几个基本问题 (3)5、对求解结果的分析 (3)LINGO基本用法LINGO是专门用来求解各种规划问题的软件包，其功能十分强大，是求解优化模型的最佳选择。
1、概况LINGO是美国LINDO系统公司开发的求解数学规划系列软件中的一个，它的主要功能是求解大型线性、非线性和整数规划问题，LINGO分为Demo、Solve Suite、Super、Hyper、Industrial、Extended等六种不同版本。
只有Demo版是免费的。
LINGO的不同版本对模型的变量总数，非线性变量的数目，整形变量数目和约束条件的数量作出了不同的限制。
LINGO的主要功能：(1) 既能求解线性规划问题，也有较强的求解非线性规划问题的能力；(2) 输入模型简练直观(3) 运行速度快，计算能力强(4) 内置建模语言，提供几十个内部函数，从而能以较少语句，较直观的方式描述较大规模的优化模型(5) 将集合的概念引入编程语言，很容易将实际问题转换为LINGO模型(6) 能方便地与Excel，数据库等其他软件交换数据2、LINGO的基本用法通常一个优化模型由下列三部分所组成：(1) 目标函数：一般表示成求某个数学表达式的最大值或最小值。
(2) 决策变量：目标函数值取决于哪些变量(3) 约束条件：对变量附加一些条件限制（通常用等式或不等式表示）注：LINGO默认所有决策变量都非负，因而变量非负条件可以不必输入。
LINGO的语法规定：(1) 求目标函数的最大值或最小值分别用MAX=…或MIN=…来表示；(2) 每个语句必须以分号";"结束，每行可以有多个语句，语句可以跨行；(3) 变量名称必须以字母(A~Z)开头，由字母，数字(0~9)和下划线所组成，长度不超过32个字符，不区分大小写；(4) 可以给语句加上标号，例如[OBJ] MAX= 20*X1+300*X2;(5) 以！开头，以；号结束的语句是注释语句；(6) 如果对变量的取值范围没有作特殊说明，则默认所有决策变量都非负；(7) LINGO模型以语句“MODEL:”开头，以“END”结束，对于比较简单的模型，这两个语句可以省略。
LINGO使用说明(比较简单)
Lingo介绍Lingo是美国LINDO系统公司（Lindo Symtem Inc）开发的求解数学规划系列软件中的一个（其他软件为LINGDO,GINO,What’s Best等），它的主要功能是求解大型线性、非线性和整数规划问题，目前的版本是lingo11.0。
lingo分为Demo、solve suite、hyper、industrial、extended等六类不同版本，只有Demo版本是免费的，其他版本需要向LINDO系统公司（在中国的代理商）购买，Lingo的不同版本对模型的变量总数、非线性变量个数、整型变量个数和约束条件的数量做出不同的限制（其中extended版本无限制）。
Lingo的主要功能特色为：（1）既能求解线性规划，也有较强的求解非线性规划的能力；（2）输入模型简练直观；（3）运行速度快、计算能力强；（4）内置建模语言，提供几十种内部函数，从而能以较少语句，较直观的方式描述较大规模的优化模型；（5）将集合的概念引入编程语言，很容易将实际问题转换为Lingo语言；（6）能方便地与excel、数据库等其他软件交换数据。
学校图书馆40本《lingo和excel在数学建模中的应用》，袁新生、邵大宏、郁时炼主编，科学出版社Lingo程序设计简要说明在数学建模中会遇到如规划类的题型，在这种模型中总存在着一个目标，并希望这个目标的取值尽可能的大或小，同时与这个目标有关的一系列变量之间存在一些约束。
在构造出目标函数和约束条件的表达式后，我们需要对求出这个最值和各变量的取值。
一般我们用LINGO来对模型进行求解，本文将通过举一个简单的例子，围绕这个例子逐步学习LINGO 的使用。
LINGO只是一个求解工具，我们主要的任务还是模型的建立！当你在windows下开始运行LINGO系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model –LINGO1的窗口是LINGO的默认模型窗口，建立的模型都都要在该窗口内编码实现。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十八章LINGO软件的使用18.1 LINGO入门18.1.1 LINGO软件的安装过程点击LINGO9.0 for Windows安装文件，出现点击“Next”按钮，出现此时需要接受安装协议。
系统安装时默认的目录是C:\LINGO9。
安装完成前，会出现下图所示的对话框：这个对话框询问你希望采用的默认的建模（即编程）语言，系统推荐的是采用LINGO语法，也就是选项“LINGO（recommended）”；你也可以选择“LINDO”将LINDO语法作为默认的设置。
当然，安装后你也可以通过“LINGO｜Options｜File Format命令来修改默认的建模（即编程）语言。
在上图中按下“OK”按钮，系统就会完成LINGO的安装过程。
18.1.2 LINGO基础知识LINGO有两种命令格式：一种是常用的Windows模式，通过下拉式菜单命令驱动LINGO 运行，界面是图形式的，使用起来也比较方便；另一种是命令行（Command-Line）模式，仅在命令窗口（Command Window）下操作，通过输入行命令驱动LINGO运行。
由于其使用字符方式输入，初学者往往不太容易掌握。
在这里，我们主要介绍在菜单驱动模式下LINGO的使用方法。
LINGO 9.0软件比以前的版本有了很大的改进，功能大大增强，性能更加稳定，计算的结果更加可靠。
LINGO软件不仅可用于求解非线性规划问题，还可以用以求解非线性整数规划问题；LINGO包含了内置的建模语言，模型中所需的数据可以以一定格式保存在独立的文件中；LINGO允许以简练、直观的方式描述较大规模的优化问题。
注：LIGDO公司目前已将LINDO软件从其产品中删除了。
事实上，LINDO软件的所有功能（包括LINDO语法格式）都在LINGO中得到了支持。
当你在windows下开始运行LINGO系统时，会得到类似下面的一个窗口：外层是主框架窗口，包含了所有菜单命令和工具条，其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口，建立的模型都都要在该窗口内编码实现。
状态行最左边显示的是“Ready”表示“准备就绪”；右下角显示的是当前时间，时间前面是当前光标的位置“Ln1,Col1”（即1行1列）。
将来，用户可以用选项命令（LINGO｜Options菜单命令）决定是否需要显示工具栏和状态行。
在LINGO 模型窗口中，选择菜单命令“File｜Open(F3)”，可以看到下图所示的标准的“打开文件”对话框，我们看到有各种不同的“文件类型”：● 后缀“lg4”表示LINGO 格式的模型文件，是一种特殊的二进制格式文件，保存了我们在模型窗口中所能够看到的所有文本和其他对象及其格式信息，只有LINGO 能读出它，用其他系统打开这种文件时会出现乱码；● 后缀“lng ”表示文本格式的模型文件，并且以这个格式保存模型时LINGO 将给出警告，因为模型中的格式信息（如字体、颜色、嵌入对象等）将会丢失；● 后缀“ldt ”表示LINGO 数据文件；● 后缀“ltf ”表示LINGO 命令脚本文件；● 后缀“lgr ”表示LINGO 报告文件；● 后缀“ltx ”表示LINGO 格式的模型文件；● 后缀“mps ”表示MPS(数学规划系统)格式的模型文件；● “*.*”表示所有文件除“lg4”文件外，这里的另外几种格式的文件其实都是普通的文本文件，可以用任何文本编辑器打开和编辑。
18.1.3二个简单的LINGO 程序下面举两个例子说明如何在LINGO 中如何进行规划问题求解。
例1.1求解如下的LP （线性规划）问题：12min 23x x +..s t12350x x +≥1100x ≥122600x x +≤12,0x x ≥在模型窗口中输入如下代码：min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;如下图所示：注：（1）LINGO中不区分大小写字母，变量（和行名）可以使用不超过32个字符表示，且必须以字母开头。
（2）LINGO中模型以“MODEL:”开始，以“END”结束。
对简单的模型，这两个语句也可以省略。
（3）LINGO中的语句的顺序是不重要的，因为LINGO总是根据“MAX=”或“MIN=”语句寻找目标函数，而其它语句都是约束条件（当然注释语句和TITLE除外）。
（4）LINGO模型是由一系列语句组成，每个语句以分号“;”结束。
（5）LINGO中以感叹号“!”开始的是说明语句（说明语句也需要以分号“;”结束）。
（6）LINGO中解优化模型时假定所有变量非负（除非用限定变量取值范围的函数@free或@sub或slb另行说明）。
然后点击工具条上的按钮得到：下面对上图的各个部分进行说明。
Solution Report（LINGO的结果报告窗口）Global optimal solution found 表示全局最优解找到.Objective value: 800.0000 表示最优目标值为800.0000.Total solver iterations: 2 表示用单纯行法进行了两次迭代.Variable 表示变量, 此问题中有两个变量X1, X2.Value 给出最优解中各变量(Variable)的值: X1=250.0000, X2=100.0000.Reduced Cost 给出最优的单纯形表中目标函数行中变量对应的系数. 其中基变量的Reduced Cost值一定为0;对于非基变量(非基变量本身的取值一定为0)和max问题,相应的Reduced Cost值表示当该非基变量增加一个单位(其它非基变量保持不变)时目标函数的减少的量.在这个例子中最优解中两个变量都是基向量, 因此对应的ReducedCost的值都为0.Slack or Surplus (松弛或剩余)给出约束对应的松弛变量的值:第2和第4行松弛变量均为0,说明对于最优解来讲,两个约束(第2和4行)均取等号,即都是紧约束.Dual Price 给出对偶价格(也称影子价格)的值.例1.2某家具公司制造书桌、餐桌和椅子，所用的资源有三种：木料、木工和漆工。
生产数据如下表所示：若要求桌子的生产量不超过5件，如何安排三种产品的生产可使利润最大？用DESKS、TABLES和CHAIRS分别表示三种产品的生产量，建立LP模型。
max=60*desks+30*tables+20*chairs;8*desks+6*tables+chairs<=48;4*desks+2*tables+1.5*chairs<=20;2*desks+1.5*tables+.5*chairs<=8;tables<=5;求解这个模型，查看报告窗口（Reports Window）,如下图:可以看到如下结果。
Global optimal solution found at iteration: 3Objective value: 280.0000Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0.0000003 0.000000 10.000004 0.000000 10.000005 5.000000 0.000000“Global optimal solution found at iteration: 3”表示3次迭代后得到全局最优解。
“Objective value:280.0000”表示最优目标值为280。
“Value”给出最优解中各变量的值：造2个书桌（desks）, 0个餐桌（tables）, 8个椅子（chairs）。
所以desks、chairs是基变量（非0），tables是非基变量（0）。
“Slack or Surplus”给出松驰变量的值：第1行松驰变量 =280（模型第一行表示目标函数，所以第二行对应第一个约束）第2行松驰变量 =24第3行松驰变量 =0第4行松驰变量 =0第5行松驰变量 =5“Reduced Cost”列出最优单纯形表中判别数所在行的变量的系数，表示当变量有微小变动时, 目标函数的变化率。
其中基变量的reduced cost值应为0，对于非基变量 X j, 相应的 reduced cost值表示当某个变量X j 增加一个单位时目标函数减少的量( max型问题)。
本例中：变量tables对应的reduced cost值为5，表示当非基变量tables的值从0变为 1时（此时假定其他非基变量保持不变,但为了满足约束条件，基变量显然会发生变化），最优的目标函数值 = 280 - 5 = 275。
“DUAL PRICE”（对偶价格）表示当对应约束有微小变动时, 目标函数的变化率。
输出结果中对应于每一个约束有一个对偶价格。
若其数值为p，表示对应约束中不等式右端项若增加1 个单位，目标函数将增加p个单位（max型问题）。
显然，如果在最优解处约束正好取等号（也就是“紧约束”，也称为有效约束或起作用约束），对偶价格值才可能不是0。
本例中：第3、4行是紧约束，对应的对偶价格值为10，表示当紧约束3) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 20变为 3) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 21时，目标函数值 = 280 +10 = 290。
对第4行也类似。
对于非紧约束（如本例中第2、5行是非紧约束），DUAL PRICE 的值为0, 表示对应约束中不等式右端项的微小扰动不影响目标函数。
有时, 通过分析DUAL PRICE, 也可对产生不可行问题的原因有所了解。
18.2 集的使用LINGO允许把相联系的对象聚合成集（sets）。
一旦把对象聚合成集，就可以利用集来最大限度的发挥LINGO语言的优势。
集是LINGO建模语言的基础，是程序设计最强有力的基本构件。
借助于集，能够用一个单一的、长的、简明的复合公式表示一系列相似的约束，从而可以快速方便地表达规模较大的模型。
一个集可能是一系列食品、汽车等。
每个集成员可能有一个或多个与之有关联的特征，我们把这些特征称为属性。
属性值可以预先给定，也可以是未知的，有待于LINGO求解。
例如，食品集中的每个产品可以有一个价格属性；汽车集中的每辆车可以有一个货车或客车属性, 也可以有一个动力属性。