材料力学-弯矩剪力图共54页
合集下载
剪力图和弯矩图(最全面)-剪刀图弯矩图特征 PPT

P q
Pa 2
qa2 2
A
BM
x x
+ P
=
=+
A
B M1
Pa 2
+
+
q
qa 2
A
B M2
2 +
x
三、对称性与反对称性的应用: 对称结构在对称载荷作用下,Q图反对称,M图对称;对称
结构在反对称载荷作用下,Q图对称,M图反对称。
[例8] 作下列图示梁的内力图。
P
PL
Q
x
0L 0.5P L 0.5P L
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
qa2/2
解:求支反力 RAq2a; RDq2a
左端点A:
Q qa; M 0 2
x
B点左: Qqa;M1qa2
2
2
B点右: Q qa;M1qa2
2
2
C点左: Qqa;M1qa2
M
– N图
P1a
M图 P1a+ P2 l
二、曲杆:轴线为曲线的杆件。 内力情况及绘制方法与平面刚架相同。
[例11] 已知:如图所示,P及R 。试绘制Q、M、N 图。
解:建立极坐标,O为极点,OB
R
P
极轴,q表示截面m–m的位置。
A
q
B
O
x
q q qq M ( ) P P ( R x R c ) o P ( 1 c s R ) ( o 0 s )
q q q Q () P 1 P si( n 0)
材料力学,弯矩剪力图-知识归纳整理

千里之行,始于足下。 第 45 页/共 53 页
求知若饥,虚心若愚。 第 46 页/共 53 页
千里之行,始于足下。 第 47 页/共 53 页
求知若饥,虚心若愚。 第 48 页/共 53 页
千里之行,始于足下。 第 49 页/共 53 页
求知若饥,虚心若愚。 第 50 页/共 53 页
求知若饥,虚心若愚。 第 8 页/共 53 页
千里之行,始于足下。 第 9 页/共 53 页
求知若饥,虚心若愚。 第 10 页/共 53 页
千里之行,始于足下。 第 11 页/共 53 页
求知若饥,虚心若愚。 第 12 页/共 53 页
千里之行,始于足下。 第 13 页/共 53 页
求知若饥,虚心若愚。 第 14 页/共 53 页
千里之行,始于足下。 第 27 页/共 53 页
求知若饥,虚心若愚。 第 28 页/共 53 页
千里之行,始于足下。 第 29 页/共 53 页
求知若饥,虚心若愚。 第 30 页/共 53 页
千里之行,始于足下。 第 31 页/共 53 页
求知若饥,虚心若愚。 第 32 页/共 53 页
千里之行,始于足下。 第 39 页/共 53 页
求知若饥,虚心若愚。 第 40 页/共 53 页
千里之行,始于足下。 第 41 页/共 53 页
求知若饥,虚心若愚。 第 42 页/共 53 页
千里之行,始于足下。 第 43 页/共 53 页
求知若饥,虚心若愚。 第 44 页/共 53 页
千里之行,始于足下。 第 33 页/共 53 页
求知若饥,虚心若愚。 第 34 页/共 53 页
千里之行,始于足下。 第 35 页/共 53 页
材料力学4-弯矩图剪力图 PPT课件
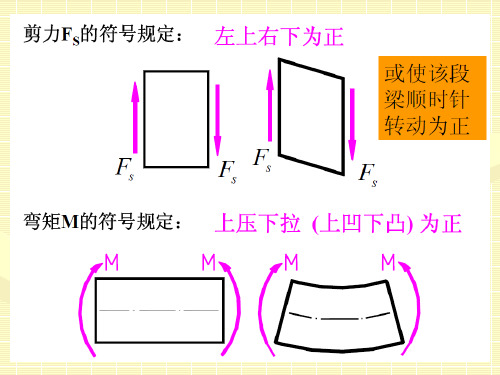
梁上最大弯矩可能发生在Fs(x) = 0 的截面上或梁段边界 的截面上。最大剪力发生在全梁或梁段的界面。
在集中力作用处剪力图有突变,其突变值等于集中力的 值。弯矩图的相应处形成尖角。
在集中力偶作用处弯矩图有突变,其突变值等于集中力 偶的值,但剪力图无变化。
矩就等于梁在各项荷载单独作用下同一 横截面上弯矩的代数和。
叠加原理:由几个外力共同作用时所引起的某一参数 (内力、应力、位移),就等于每个外力单独作用时 所引起的该参数值的代数和。
• 5.4 内力与分布荷载间的关系及其应用
剪力图上某点处的切线斜率 等于该点处荷载集度的大小
弯矩图上某点处的切线斜率 等于该点处剪力的大小。
q(x)、Fs (x)图、M(x)图三者间的关系
梁上有向下的均布荷载,即 q(x) < 0 Fs (x)图为一向右下方倾斜的 直线 M(x)图为一向下凸的二次抛 物线
• 5.3 剪力方程与弯矩方程 剪力图与弯矩图
一、剪力和弯矩方程: 剪力和弯矩沿梁长度方向的表达式,表示的是剪力和
弯矩沿轴线长度方向的分布情况
二、剪力图和弯矩图 以X轴表示横截面位置,以纵坐标表示相应截面
上的剪力Fs 、弯矩M,称为剪力图、弯矩图。 剪力图为正值画在x 轴上侧,负值画在x 轴下侧 弯矩图为正值画在x 轴下侧,负值画在x 轴上侧
作剪力图和弯矩图的几条规律
梁上集中力作用处左、右两侧横截面上,剪 力值(图)有突变,其突变值等于集中力的 数值。在此处弯矩图则形成一个尖角。
梁上集中力偶作用处左、右两侧横截面上 的弯矩值(图)也有突变,其突变值等于 集中力偶矩的数值。但在此处剪力图没有 变化。
作剪力图和弯矩图的几条规律
梁上的最大剪力发生在全梁或各梁段的边界 截面处;梁上的最大弯矩发生在全梁或各梁 段的边界截面,或Fs = 0的截面处。
[数学]材料力学_弯矩剪力图PPT资料54页
![[数学]材料力学_弯矩剪力图PPT资料54页](https://img.taocdn.com/s3/m/1d47a890c281e53a5802ffa1.png)
aF
b
A
x
C
FA
l
B
FA
Fb l
FB
FB
Fa l
AC段 A
M(x)
FSxFl b0xa
FA
x
FS(x)
MxFxb0xa
l
F Sx F BF l a axlM(x)
MxFB(lx)
Falx
l
FS(x)
axl
CB段 B FB
3、作剪力图和弯矩图
aF
b
A
x
C
FA
l
Fb
FS
l
Fb l
M
FS1x
Fb l
B
a
Me
b
A
B
C
FA
l
FB
解: 1、求支反力
MA0
FA
Me l
M eF A l0
FB
Me l
2、 列剪力方程和弯矩方程
a
b
FA
Me l
A
x
C
FA
l
B
FB
FB
Me l
剪力方程无需分段: M(x)
F SxMF A (x ) M le0xl
A
FA
x
FS(x)
B FS(x) FB
弯CABC矩段段方::程—M M —x 两x 段F F :A Ax x M M lee xM le 0 l x xa a xl
x
Mxqlxqx2
22
FS,max
ql 2
ql 2 ql2 8
M
l/2
Mmax
ql2 8
* 载荷对称、结构对称则剪力图反对称,弯矩图对称
材料力学剪力图与弯矩图

dFQ q 0 FQ const.=C 平行于x轴的直线
dx
dM dx
FQ
C,
M
Cx D
第45页/共103页
斜直线
第5章 剪力图与弯矩图
载荷集度、剪力、弯矩之间的微分关系
FQ
FQ const.=C
q=0
dFQ q 0 dx
dM dx
FQ =const.
x
x
M Cx D
M
第46页/共103页
第34页/共103页
第5章 剪力图与弯矩图
剪力方程与弯矩方程
第35页/共103页
第5章 剪力图与弯矩图
剪力方程与弯矩方程
例题 2
q
A
B
l
一端为固定铰链支座、另一端为辊轴支座的梁,称为简支梁(simple supported beam)。梁上承受集度为q的均布载荷作用,梁的长度为l。
试写出:该梁的剪力方程和弯矩方程。
C
l
B
M=0
l
MO=2FPl FQ= FP FP
A
C
l
B
M=-FPl
l
第33页/共103页
第5章 剪力图与弯矩图
应用力系简化方法确定梁的剪力和弯矩
MA=0 MO=2FPl
FP
A
FA= FP
C l
B l
M=0 MO=2FPl
FP
A
FQ= FP
C l
B l
MO=2FPl
FP
M=FPl
B
A
C
l
l
FQ= FP
梁的力学模型与工程中梁的模型
梁的力学模型
外伸端 固定铰支座
C
剪力图和弯矩图(史上最全面)ppt课件

1.25 1
q=2kN/m
+
x
_
1
26
§4–5 按叠加原理作弯矩图
一、叠加原理: 多个载荷同时作用于结构而引起的内力等于每个载荷单独
作用于结构而引起的内力的代数和。
Q(P1P2 Pn) Q1(P1) Q2(P2) Qn(Pn)
M (P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
分区点A: Q qa; M qa2
M 的驻点: Q 0 ; M 3 qa2 2
x
右端点: Q 0; M 3 qa2 2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
1
第四章 弯曲内力
§4–1 平面弯曲的概念及梁的计算简图 §4–2 梁的剪力和弯矩 §4–3 剪力方程和弯矩方程 ·剪力图和弯矩图 §4–4 剪力、弯矩与分布荷载集度间的关系及应用 §4–5 按叠加原理作弯矩图 §4–6 平面刚架和曲杆的内力图
弯曲内力习题课
2
§4–1 平面弯曲的概念及梁的计算简图
求支反力qa2qa2qa2241练习直接画内力图p12944dj对称载荷m反对称载荷同时可以提前讲内力图的对称关系2改错见下页ppt3由q图作m图和载荷图p135416b由m图作q图和载荷图p135417a4讲解组合梁的内力图p13046aqa4qa43qa47qa4qa323qa已知q图求外载及m图梁上无集中力偶
qL 1
2q
解:截面法求内力。 1--1截面处截取的分离体
材料力学-课件4-2梁的剪力和弯矩.剪力图和弯矩图
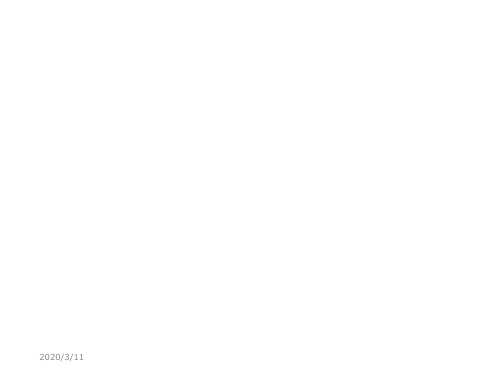
a2
qa 2
qa
2
a2
qa 2
8
qa 2 8
F
F
A
B
F
F2
F2
a aa a
F2 F2
F2
F2
Fa 2
Fa 2
结构对称,载荷对称,则FS图反对称, M图对称
2020/3/11
符 号
Fs>0
Fs<0
规
定
:
M>0
M<0
使微段梁有顺时针转动趋势的剪力为正,反之为 负;使微段梁产生向下凸变形的弯矩为正,反之为 负。
4.1
例题
FA
A
MA FA
A
MA
试确定截面C及截面D上的剪力和弯矩
2Fl
lC
l
FCs
l
C MC
2Fl
FCs
MC
C
l
F
B D
FCs F
MC Fl
X1 A 1m 35kN
15
20
kN
20
10kN m
4m
2.5
FSx12k0N
X2
B
0 x1 1
25kN
M x12x0 1
0x1 1
F Sx2 2 5 1x2 0
25
Mx225x021x2 04x222
0x2 4
20 31.25
kNm
2020/3/11
l2 l2
1 Fl 4
-
+ 1 Fl 8
l2 l2
+
1 Fl 4
A C
m 1 Fl 4 C
l
1 Fl
-4
例题 4.15
6k N
剪力图和弯矩图(史上最全面)

0
M2
1 2
q(x2
a)2
qLx2
qL 1
q 2
1a
2b
y x
图(a)
qL B
M2
x2
Q2
图(c)
15
§4–3 剪力方程和弯矩方程 ·剪力图和弯矩 图
1. 内力方程:内力与截面位置坐标(x)间的函数关系式。
Q Q(x) M M (x)
剪力方程 弯矩方程
2. 剪力图和弯矩图: 剪力图 弯矩图
Q Q(x) 的图线表示 M M (x) 的图线表示
与 M1
x
m
反
M
M2
M1 M2 40m
[例1] 绘制下列图示梁的弯矩图。
(1)
2P
M
a
a
P
Pa + x
=
=
2P
M1
–
x
2Pa
+
+
M2
2Pa
+
P
41 x
(2)
a
q
M
–
x
=
a q
qa2 M1
=+
M
qa2/4
+
q
B
RA
qa 4
; RB
7qa 4
x
7qa/4
x
25
[例9] 已知Q图,求外载及M图(梁上无集中力偶)。
Q(kN)
2 +
–
3
1m
2m
5kN
1
+
x
1m 1kN
M(kN·m)
1.25 1
q=2kN/m
+
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
Me
b
A
B
C
FA
l
FB
解: 1、求支反力
MA0
FA
Me l
M eF A l0
FB
Me l
2、 列剪力方程和弯矩方程
a
b
FA
Me l
A
x
C
FA
l
B
FB
FB
Me l
剪力方程无需分段: M(x)
F SxMF A (x ) M le0xl
A
FA
x
FS(x)
B FS(x) FB
弯CABC矩段段方::程—M M —x 两x 段F F :A Ax x M M lee xM le 0 l x xa a xl
q
剪力方程 弯矩方程
FSFS(x) MM (x)
反映梁的横截面上的剪力和弯 矩随截面位置变化的函数式
显示剪力和弯矩随截面位移的 变化规律的图形则分别称为剪力 图和弯矩图。
注意: 不能用一个函数表 达的要分段,分段点为:集中力 作用点、集中力偶作用点、分布 力的起点、终点。
A
B
x
L
Fs(x)qx, (0xl)
构件 Component, Structural member 杆 bar 梁 beam
拉压杆:承受轴向拉、压力
扭 杆:承受扭矩 墙
桥板 梁:承受横向力
楼板
为什么梁特别重要? 地球引力场方向 + 人类需要空间
§5-1 平面弯曲的概念及工程实例
一、弯曲实例 工厂厂房的天车大梁:
火车的轮轴:
F
F
F
F
楼房的横梁:
阳台的挑梁:
屋顶大梁上的孔为什么开在中间?上、下两 边各开一个半圆孔可以吗?
工程中的弯曲构件
梁为什么做成变截面的? 梁为什么可以开孔? 孔开在哪里最合理?
二、弯曲的概念:
受力特点——作用于杆件上的外力都垂直于杆的轴线。 变形特点——杆轴线由直线变为一条平面的曲线。
主要产生弯曲变形的杆--- 梁。
FS2x
Fa l
FB
Байду номын сангаас
M1x
Fbx l
M2(x)Fl alx
x
Fab x
l
aF
b
A
x
C
l
Fb
FS
l
* 在 集中力F 作用 处,剪力图有突变, 突变值为集中力的 大小;弯矩图有转 折
Fb
x
l
Fab x
M
l
abl/2时, MmaxF4l为极大值。
例 图示简支梁在C点受矩为Me 的集中力偶作用。试 作梁的剪力图和弯矩图。
M FN
FAy
FS
M FN
FS
3
Fx 0 FN 0
Fy 0 FSFAyF1
FMc0 M F Ax yF 1(xa)
FS剪力,平行于
横截面的内力合力
M 弯矩,垂直于
横截面的内力系的 FBy 合力偶矩
§5-2 剪力和弯矩及其方程
M FN
M FN
FAy
FS
FS
FBy
截面上的剪力对梁上任意一点的矩为顺时针 转向时,剪力为正;反之为负。
FAy 2. 用截面法研究内力
FSE
FAy
求图示简支梁E 截面的内力
解:1. 确定支反力
Fy 0 FAyFBy2F
MA0
FBy FBy 3aF a2Fa
F FBy 3
FAy
5F 3
Fy 0
5F 2FFSE 3
FSE
F 3
ME
ME 0 2Fa2ME53F32a
ME
3Fa 2
§5-2 剪力和弯矩及其方程
x
Mxqlxqx2
22
FS,max
ql 2
ql 2 ql2 8
M
l/2
Mmax
ql2 8
* 载荷对称、结构对称则剪力图反对称,弯矩图对称
* 剪力为零的截面弯矩有极值。
例 图示简支梁受集中荷载F作用。试作梁的剪力图 和弯矩图。
aF
b
A
B
x
C
FA
l
FB
解:1、求支反力
FA
Fb l
FB
Fa l
2、列剪力方程和弯矩方程 ——需分两段列出
P
q
M
RA
NB
常见弯曲构件截面
目录
平面弯曲
•具有纵向对称面 •外力都作用在此面内 •弯曲变形后轴线变成对称面内的平面曲线
目录
静定梁的分类(三种基本形式)
q(x)— 分布力 1、悬臂梁:
2、简支梁:
L M — 集中力偶
3、外伸梁:
L q — 均布力
F — 集中力
L
L
(L称为梁的跨长)
§5-2 剪力和弯矩及其方程
Fs(+)
Fs(–) Fs(+) 左上右下为正;反之为负
Fs(–)
§5-2 剪力和弯矩及其方程
M FN
M FN
FAy
FS
FS
FBy
截面上的弯矩使得梁呈凹形为正;反之为负。
M(+)
M(+)
M(–)
左顺右逆为正;反之为负
M(–)
内力方向规定
FQ FN
FN
FQ
§5-2 剪力和弯矩及其方程 例题5-1
任 意 截 面 的 剪 力 一 侧 横 向 力 代 数 值
横向力:载荷和约束反力 分布力和集中力
方向:左上右下为正, 反之为负
任 意 截 面 的 弯 矩
一 侧 外 力 对 截 面 形 心 之 矩 代 数 值
外力:载荷和约束反力
方向:左顺右逆为正,
分布力、集中力和集中力偶
反之为负
三、剪力方程、弯矩方程:
aF
b
A
x
C
FA
l
B
FA
Fb l
FB
FB
Fa l
AC段 A
M(x)
FSxFl b0xa
FA
x
FS(x)
MxFxb0xa
l
F Sx F BF l a axlM(x)
MxFB(lx)
Falx
l
FS(x)
axl
CB段 B FB
3、作剪力图和弯矩图
aF
b
A
x
C
FA
l
Fb
FS
l
Fb l
M
FS1x
Fb l
B
M(x)1qx2, (0xl)
Fs
2
x
(-)
ql
0.5ql 2
x
M
FAY
MA
L
A
x
F(x)
FL
M(x)
[例] 列出梁内力方程并画出内力图。
F B
解:①求支反力
FAY F; M AFL
②写出内力方程
Fs(x)FAYF (0xl)
F
M(x)FAYxMA
F(xL) (0xl)
x
③根据方程画内力图
注意:弯矩图中正的弯矩值
x
绘在x轴的下方(即弯矩值绘
在弯曲时梁的受拉侧)。
例 图示简支梁受集度为q的满布荷载作用。试作梁的剪力图
和弯矩图。
q
A
B
l
FA
x
解:1、求支反力
FA
FB
ql 2
FB
2、列剪力方程和弯矩方程
FSxFAqxq2lqx
M xFAxq x2 xq2lxq22x
3、作剪力图和弯矩图
q A
l
FS
B
FS
x
qlq 2
FSE
FSE
5F 3
2F F 3
左上右下为正;反之为负
§5-2 剪力和弯矩及其方程
FBy
F 3
FAy
5F 3
FAy
FBy
截面上的弯矩等于截面任
ME
一侧外力对截面形心力矩的代
FAy
2F
数和。
ME
ME
5F 3a 32
2F
a 2
3 Fa 2
左顺右逆为正;反之为负
法则 计算任意截面的剪力和弯矩
FSE O
FAy
ME
O
FSE
ME FBy
FBy
F 3
FAy
5F 3
分析右段得到: FBy
Fy 0 FSEFBy0
FSEFByF3
Mo 0
3a ME FBy 2 Fa
3Fa ME 2
§5-2 剪力和弯矩及其方程
FBy
F 3
FAy
5F 3
FAy
FBy
FSE
FAy
2F
截面上的剪力等于截 面任一侧外力的代数和。
