安德森《商务与经济统计》(第10版)(上册)课后习题详解(离散型概率分布)
商务与经济统计作业(仅供参考)
第一章数据与统计资料P 1825. 表1-8是一个由25只影子股票组成的数据集,(表略)a 数据集中有几个变量?答:数据集中有5个变量。
b哪些变量是数量变量?哪些变量是品质变量?答:市场价值、市盈率和毛利率属于数量变量;交易所和股票代码是品质变量。
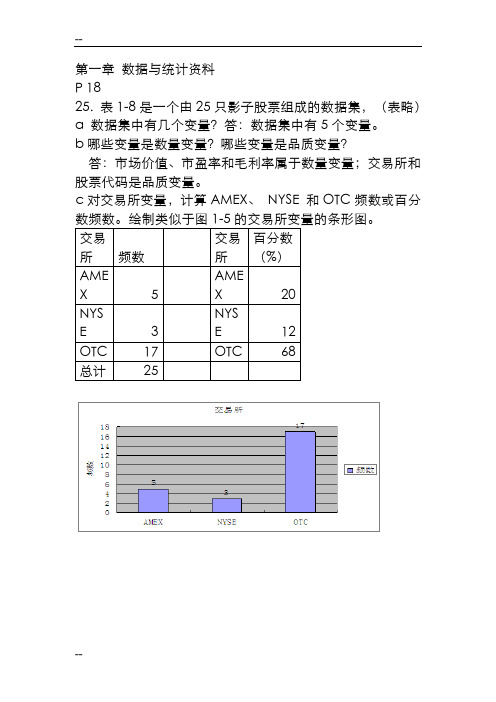
c对交易所变量,计算AMEX、NYSE 和OTC频数或百分数频数。
绘制类似于图1-5的交易所变量的条形图。
e 平均市盈率是多少?答:利用EXCEL的求平均值功能得出平均市盈率是20.2第二章表格法和图形法P 235按字母顺序,美国最常见的6个姓氏为:布朗、戴维斯、约翰逊、琼斯、史密斯和威廉姆斯。
假设根据一个由50个人组成的样本,得到如下的姓氏数据(图略)a相对频数分布和百分数频数分布。
mstotal 50 b构建条形图c 构建饼形图d根据这些数据,最常见的3个姓氏是哪些?答:最常见的3个姓氏分别是史密斯、约翰逊和威廉姆斯。
P5051 表2-17 给出了50家《财富》500强公司的所有者权益、市场价值和利润数据。
(图略)a.构建所有者权益和利润变量的交叉分组表。
对利润数据以0-200,200-400,…,1000-1200分组,对所有者权益数据以0-1200,1200-2400,…,4800-6000分组。
b. 计算(a)中交叉分组表的行百分数。
P 5153. 参考表2-17中的数据集a. 绘出显示利润和所有者权益变量之间关系的散点图。
b. 评价这两个变量之间的关系。
答:二者呈正相关的关系,即所有者权益增加,利润也增加。
但因为所有点并不在一条直线上,所以这种关系不是完全的。
案例2-1 Pelican 商店1. 主要变量的百分数频数分布2. 条形图或饼形图,以显示因促销活动而使顾客购买的百分数。
3. 顾客类型(常规性或奖励性)与销售额的交叉分组表,并评价其相似性与差异性。
动取得了显著成效。
使用折扣赠券购买的奖励性顾客占全体顾客总数的70%,分布于各个销售额区域,尤其在销售额100内的范围里做出了突出贡献,尽管未使用折扣赠券的常规性顾客也主要集中在该销售额区域,但比重明显低于奖励性顾客,且在200以上的销售额区域则无常规性顾客,奖励性顾客的消费金额也扩大到300。
商务统计课后习题答案

Expected Price(Yi) 15 14 15 17 11 19 13 14 10 13 141
Totals
(Xi-X)2 Xi-X Yi-Y (Xi-X)(Yi-Y) -1.805 0.9 3.258025 -1.6245 2.195 -0.1 4.818025 -0.2195 0.011025 -0.105 0.9 -0.0945 3.783025 1.945 2.9 5.6405 -3.805 -3.1 14.47803 11.7955 6.795 4.9 46.172025 33.2955 -2.205 -1.1 4.862025 2.4255 -0.105 -0.1 0.011025 0.0105 -3.805 -4.1 14.478025 15.6005 0.895 -0.9 0.801025 -0.8055 92.67225 66.024
^
y = 0.275 + 0.95x
Texas Instruments has a higher risk. 53. a.
Satisfaction Rating(%) 100 80 60 Satisfaction Rating(%) 40 20 0 0 20 40 60 80
b. The relationship is positive. c. =43.92307692 y=65.92307692
b1=∑(Xi-X)(Yi-Y)/ ∑(Xi-X)2 =-170/1150 =-0.148 b0=y-b1 =17+.148*35=22.18
^
y=22.18-0.148x
b. SSR=25.1896 SSE=8.8696 MSR=SSR/Regression degrees of freedom=25.1896 MSE=SSE/n-2= 8.8696/4=2.2174 F=MSR/MSE=25.1896/2.2174=11.36 Fa=7.71<F
《商务统计学》题集

《商务统计学》题集一、选择题(每题2分,共10分)1.下列哪项不属于商务统计学的应用范围?A. 市场调查B. 质量控制C. 财务分析D. 天气预测2.在统计学中,总体是指什么?A. 研究的全部对象B. 研究中的一部分对象C. 某个具体的样本D. 某一特定数据3.下列哪种抽样方法是随机抽样?A. 方便抽样B. 系统抽样C. 配额抽样D. 判断抽样4.如果一组数据的均值是20,中位数是22,那么这组数据的分布可能是?A. 正偏态B. 负偏态C. 对称分布D. 无法确定5.在回归分析中,解释变量和被解释变量分别是什么?A. 因变量和自变量B. 自变量和因变量C. 都是自变量D. 都是因变量二、填空题(每空1分,共10分)1.在统计学中,用来衡量数据分布集中趋势的指标有______、______和______。
2.若一组数据的四分位数Q1=10,Q2=20,Q3=30,则该组数据的中位数为______。
3.在假设检验中,如果P值小于显著性水平α,则我们______原假设。
4.统计表中,频数和频率分别表示数据的______和______。
5.在回归分析中,回归系数的经济意义是解释变量每增加一个单位,被解释变量平均增加______单位。
三、判断题(每题1分,共10分)1.统计学的目的是收集、整理、分析和解释数据,从而帮助人们做出决策。
( )2.在正态分布中,均值、中位数和众数三者相等。
( )3.标准差是衡量数据波动大小的一个重要指标,标准差越大,说明数据的波动越大。
( )4.在假设检验中,如果P值大于显著性水平α,则我们有足够的证据拒绝原假设。
( )5.相关系数r的取值范围是[-1, 1],r=1表示完全正相关,r=-1表示完全负相关。
( )6.如果一组数据的偏度系数大于0,则说明这组数据是正偏态分布。
( )7.在抽样调查中,样本容量越大,抽样误差就越小。
( )8.统计推断是通过样本数据来推断总体的特征。
( )9.移动平均法是一种常用的时间序列预测方法。
安德森《商务与经济统计》(第10版)(上册)课后习题详解(连续型概率分布)

圣才电子书
d.计算 E(x)。
十万种考研考证电子书、题库视频学习平台
e.计算Var (x)。
解:a.绘制概率密度函数图,如图 6-2 所示。
图 6-2 概率密度函数图 b.P(x<15)=0.10×(15-10)=0.50 c.P(12≤x≤18)=0.10×(18-12)=0.60 d. E(x) 10 20 15
a.一瓶清洁剂的重量在 12 和 12.05 盎司之间的概率是多少?
5 / 35
圣才电子书 十万种考研考证电子书、题库视频学习平台
d.P(
x
)= 1 ×(305-290)=0.5790
25.9
e.由于 P(x
)= 1 ×(310.6-290)=0.7954,所以这 100 名高尔夫运动员 25.9
中击球距离至少为 290 码的人数为:100×0.7954=80(名)。
6.液体清洁剂瓶上的标签表明每瓶装有 12 盎司。清洁剂的重量服从如下概率密度函 数
e.这些运动员中有多少人击球距离至少为 290 码?
解:a.区间长度=310.6-284.7=25.9(码),所以击球距离的概率密度函数为:
1
f
(
x)
25.9
0
284.7 x 310.6 其他
b.P(x<290)= 1 ×(290-284.7)=0.2046
25.9
c.P(x
)= 1 ×(310.6-300)=0.4092 25.9
2 e.Var(x) (20 10)2 8.33
12
3.德尔塔(Delta)航空公司宣称其从辛辛那提到坦帕的航班的飞行时间为 125 分钟。 假定我们认为实际飞行时间服从区间 120 到 140 分钟上的均匀分布。
《商务统计学》概率

从图中可以看出全集S中的样本点要么在 A中,要么在 中,即一个事件与其互补 事件之和为全部样本空间。在概率计算 问题中可以表示为:
20
例4-4 某位销售经理看过销售报告后声 称, 新的客户合同最终没有实现销售的 概率为75%。如果用A表示销售这一事件
, 表示没有销售, 则该经理是在说明 , 于是我们可以得到
3
4.1.2 事件和样本空间
假设一枚硬币被掷出, 记录朝上的一面 。我们看见和记录的结果称为一个观测 , 或者一次测量。获得一个观测的过程 称为试验。试验(test)是一个会产生 若干可能结果的过程, 试验的结果是一 些观测值或测度值。
4
从一副52张的扑克牌中抽取一张就是一 个试验, 它的一个可能结果就是方片Q 被抽中。每一种可能的试验结果称为一 个基本事件(fundamental event)或 基础结果。
25
例4-6 某大型的计算机软件公司的人事
部经理进行了一项研究。发现在近两年
内离开公司的员工中,有30%的人离开
的主要原因是对所拿的薪水不满意,
20%的人是对分配给他们的工作不满意
,12%的人既对所拿薪水不满意,又对分
配给他们的工作不满意。若有一位员工
在最近两年离开了公司,他离开的原因
是对所拿薪水不满意或对分配给他的工
53
解: 设 A=“抽出一件产品为废品”,
B=“抽出的产品属于第i )条生
(产线”, 根据题意可知
,
且
为互不相容事件,所以
由全概率公式可得:
即随机抽取的产品是废品的概率为0.038
54
4.7 贝叶斯定理
贝叶斯定理(Bayes’ theorem)是条件 概率的推广, 强调的是序列事件, 尤其 是用从第二个事件获得的信息对第一个 已经发生的事件的概率进行修正。
商务与经济统计课后答案

商务与经济统计课后答案【篇一:商务经济统计学复习题】.简答题1.简要谈谈你对统计与统计学的初步认识。
2.谈谈你对统计的三种含义的理解,并举出现实经济生活中你所了解到的运用统计学的一个例子3.试就统计数据的四种类型给出统计整理与显示的方法(统计图要求划出示意图)。
4.概述数据的离散程度的常用的测度方法(异众比率标准差离散系数)。
5.什么是个体指数? 什么是总指数?它们的作用分别是什么?6.试简要说明总量指标、平均指标和相对指标的在统计学中的作用。
7.只能用统计条形图和饼图来展示的是哪种类型的数据?画出这两种图形的示意图。
8.自己用一个实例画出统计条形图和饼图的示意图,它们通常可以用来展示哪种类型的数据? 9.某高校毕业生就业指导中心想对2007届本校大学本科毕业生的毕业去向做一网上调查,请你为此设计一份半开放式(即:既含有封闭式问题又含有开放式问题)调查问卷。
(要求涉及学生的性别、专业、意向中的毕业去向:如出国、考研、自主创业、自主择业,以及意向中的就业领域、工薪待遇、单位性质、工作地区等等信息)。
二.填空题1.将下列指标按要求分类(只填写标号即可)(1)我国高等院校2006届本科毕业生就业率;(2)某贺岁片在国内上演第一周的票房收入;(3) 2006年第3季度一汽大众销售的某品牌小汽车台数占其全部小汽车销售量的比率;,(5)进藏铁路开通后第一周,每天乘火车前往西藏的旅客的累计人数;(6)第3季度某商场的月平均销售额。
哪些是时点时标;哪些是时期指标;哪些是平均指标;哪些是相对指标。
2.统计调查方式除了重点调查,典型调查之外,另三种主要方式是 3.加权调和平均公式为4.异众比率公式是其含义是5.一组数据中非众数组所占的比率叫做,它可测度分类数据的趋势;离散系数测度的是总体的平均离散程度,它的计算公式是v?=。
6.将下列指标分类:(1)2005年我国人均占有粮食产量(2)我国第五次人口普查总人口数(3)股价指数(4)销售量指数(5)单位产品成本(6)某商店全年销售额(7)某企业在岗职工人数和下岗职工人数的比例 (8)我国高等院校“十五”期间年平均招生人数哪些是时期指标哪些是时点指标;哪些是一般平均数, 哪些是序时平均数;哪些是相对指标 7.个体指数是反映项目或变量变动的相对数;反映多种项目或变量变动的相对数是。
高考数学一轮复习第10章计数原理概率随机变量及其分布10.7离散型随机变量及其分布列习题课件理
X3
4
5
P 0.1 0.3 0.6
第十七页,共42页。
13.已知甲盒内有大小相同的 1 个红球和 3 个黑球,乙 盒内有大小相同的 2 个红球和 4 个黑球,现从甲、乙两个盒 内各任取 2 个球.设 ξ 为取出的 4 个球中红球的个数,则
3 P(ξ=2)=___1_0____.
第十八页,共42页。
∴q=1- 22,故选 C.
第六页,共42页。
5.已知某一随机变量 X 的概率分布如下,且 E(X)=6.9, 则 a 的值为( )
X4 a 9 P m 0.2 0.5 A.5 B.6 C.7 D.8
解析 因为在分布列中,各变量的概率之和为 1,所以 m= 1- (0.2+ 0.5)= 0.3,由数 学期望 的计 算公式, 可得 4×0.3+a×0.2+9×0.5=6.9,a=6,故选 B.
第十五页,共42页。
12.(2018·临汾联考)口袋中有 5 只球,编号为 1,2,3,4,5, 从中任意取 3 只球,以 X 表示取出的球的最大号码,则 X
X3
4
5
P 0.1 0.3 0.6 的分布列为_____________________________.
第十六页,共42页。
解析 X 的取值为 3,4,5.又 P(X=3)=C135=110, P(X=4)=CC2335=130,P(X=5)=CC2435=35. ∴随机变量 X 的分布列为
第二十二页,共42页。
B级 三、解答题 15.(2018·太原模拟)根据某电子商务平台的调查统计显 示,参与调查的 1000 位上网购物者的年龄情况如图所示.
第二十三页,共42页。
(1)已知[30,40),[40,50),[50,60)三个年龄段的上网购物 者人数成等差数列,求 a,b 的值;
商务统计试题4参考答案及评分标准
《商务统计》试题4参考答案及评分标准一、判断题(每题1分,共10分)三、填空题(每题3四、计算题(每题15分,共45分)1.(1)令μ1、μ2分别表示塔吉特、沃尔玛两家零售商的顾客总体,则原假设为H 0:μ1−μ2=0(2分),备择假设为 H a :μ1−μ2≠0(1分)。
(2)应该应用标准正态分布的z 统计量(1分)。
因为两家零售商顾客满意度服从正态分布,且两家零售商顾客满意度的方差σ12、σ22已知。
则x̅1−x̅2服从均值为μ1−μ2,标准差为σx̅1−x̅2=√σ1/n 12+σ2/2212√σ1/n 1+σ2/2(2分)。
检验统计量z =12√σ1/n 1+σ2/2=√122/25+122/30=2.46(2分)。
(3)显著性水平是α=0.05,则拒绝域的临界值z 0.025=1.96, 拒绝原假设的决策准则为:z ≥1.96或者z ≤−1.96时,拒绝原假设H 0(2分)。
2.46>1.96,因此拒绝原假设。
塔吉特、沃尔玛两家零售商的顾客满意度存在显著差异(1分)。
(4)两家零售商顾客满意度的差μ1−μ2的的置信区间为(x̅1−x̅2)±z α2√σ12n 1+σ22n 2(2分)。
在1−α=95%的置信水平下,置信区间(x̅1−x̅2)±z α2√σ12n 1+σ22n 2=(79−71)±1.96√12225+12230=8±6.37(2分)。
2.(1)总的平均值x̿=133+139+136+1444=138(2分)。
(2)组间平方和:SSTR =∑n j (x̅j −x̿)2k j=1=330(2分)。
组间均方:MSTR =SSTR k−1=3303=110(1分)。
(3)误差平方和:SSE =∑(n j −1)s j 2k j=1=764(2分)。
均方误差:MSE =SSEnT−k=76416=47.75(1分)。
(4)(每空0.5分,共5分)。
概率论与数理统计第二章课后习题及参考答案.
概率论与数理统计第二章课后习题及参考答案1.离散型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=≤=.4,1,42,7.0,21,2.0,1,0)()(x x x x x X P x F 求X 的分布律.解:)0()()(000--==x F x F x X P ,∴2.002.0)01()1()1(=-=----=-=F F X P ,5.02.07.0)02()2()2(=-=--==F F X P ,3.07.01)04()4()4(=-=--==F F X P ,∴X 的分布律为2.设k a k X P 32()(==, ,2,1=k ,问a 取何值时才能成为随机变量X 的分布律.解:由规范性,a a a n n k k 2321]32(1[32lim)32(11=--=⋅=+∞→∞+=∑,∴21=a ,此时,k k X P 32(21)(⋅==, ,2,1=k .3.设离散型随机变量X 的分布律为求:(1)X 的分布函数;(2)21(>X P ;(3))31(≤≤-X P .解:(1)1-<x 时,0)()(=≤=x X P x F ,11<≤-x 时,2.0)1()()(=-==≤=X P x X P x F ,21<≤x 时,7.0)1()1()()(==+-==≤=X P X P x X P x F ,2≥x 时,1)2()1()1()()(==+=+-==≤=X P X P X P x X P x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=.2,1,21,7.0,11,2.0,1,0)(x x x x x F .(2)方法1:8.0)2()1()21(==+==>X P X P X P .方法2:8.02.01)21(121(1)21(=-=-=≤-=>F X P X P .(3)方法1:1)2()1()1()31(==+=+-==≤≤-X P X P X P X P .方法2:101)01()3()31(=-=---=≤≤-F F X P .4.一制药厂分别独立地组织两组技术人员试制不同类型的新药.若每组成功的概率都是0.4,而当第一组成功时,每年的销售额可达40000元;当第二组成功时,每年的销售额可达60000元,若失败则分文全无.以X 记这两种新药的年销售额,求X 的分布律.解:设=i A {第i 组取得成功},2,1=i ,由题可知,1A ,2A 相互独立,且4.0)()(21==A P A P .两组技术人员试制不同类型的新药,共有四种可能的情况:21A A ,21A A ,21A A ,21A A ,相对应的X 的值为100000、40000、60000、0,则16.0)()()()100000(2121====A P A P A A P X P ,24.0)()()()40000(2121====A P A P A A P X P ,24.0)()()()60000(2121====A P A P A A P X P ,36.0)()()()0(2121====A P A P A A P X P ,∴X 的分布律为5.对某目标进行独立射击,每次射中的概率为p ,直到射中为止,求:(1)射击次数X 的分布律;(2)脱靶次数Y 的分布律.解:(1)由题设,X 所有可能的取值为1,2,…,k ,…,设=k A {射击时在第k 次命中目标},则k k A A A A k X 121}{-== ,于是1)1()(--==k p p k X P ,所以X 的分布律为1)1()(--==k p p k X P , ,2,1=k .(2)Y 的所有可能取值为0,1,2,…,k ,…,于是Y 的分布律为1)1()(--==k p p k Y P , ,2,1,0=k .6.抛掷一枚不均匀的硬币,正面出现的概率为p ,10<<p ,以X 表示直至两个面都出现时的试验次数,求X 的分布律.解:X 所有可能的取值为2,3,…,设=A {k 次试验中出现1-k 次正面,1次反面},=B {k 次试验中出现1-k 次反面,1次正面},由题知,B A k X ==}{,=AB ∅,则)1()(1p p A P k -=-,p p B P k 1)1()(--=,p p p p B P A P B A P k X P k k 11)1()1()()()()(---+-=+=== ,于是,X 的分布律为p p p p k X P k k 11)1()1()(---+-==, ,3,2=k .7.随机变量X 服从泊松分布,且)2()1(===X P X P ,求)4(=X P 及)1(>X P .X 100000060000400000P0.160.240.240.36解: )2()1(===X P X P ,∴2e e2λλλλ--=,∴2=λ或0=λ(舍去),∴224e 32e !42)4(--===X P .)1()0(1)1(1)1(=-=-=≤-=>X P X P X P X P 222e 31e 2e 1----=--=.8.设随机变量X 的分布函数为⎩⎨⎧<≥+-=-.0,0,0,e )1(1)(x x x x F x 求:(1)X 的概率密度;(2))2(≤X P .解:(1)⎩⎨⎧<≥='=-.0,0,0,e )()(x x x x F x f x ;(2)2e 31)2()2(--==≤F X P .9.设随机变量X 的概率密度为xx Ax f e e )(+=-,求:(1)常数A ;(2))3ln 210(<<X P ;(3)分布函数)(x F .解:(1)⎰⎰+∞∞--+∞∞-+==xAx x f xx d e e d )(1A A x A x x x 2|e arctan d e 21e 2π==+=∞+∞-∞+∞-⎰,∴π2=A .(2)61|e arctan 2d e e 12)3ln 210(3ln 2103ln 210==+=<<⎰-x xx x X P ππ.(3)x xx x xx t t f x F e arctan 2d e e 12d )()(ππ=+==⎰⎰∞--∞-.10.设连续型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧>≤<-+-≤=.a x a x a a x B A a x x F ,1,,arctan ,,0)(其中0>a ,试求:(1)常数A ,B ;(2)概率密度)(x f .解:(1) 2arcsin (lim )0()(0)(π⋅-=+=+-=-=+-→B A a x B A a F a F a x ,1)(lim )0()(2==+==⋅++→x F a F a F B A a x π,∴21=A ,π1=B .(2)⎪⎩⎪⎨⎧≥<-='=.a x a x x a x F x f ,0,,1)()(22π.11.设随机变量X 的概率密度曲线如图所示,其中0>a .(1)写出密度函数的表达式,求出h ;(2)求分布函数)(x F ;(3)求)2(a X aP ≤<.解:(1)由题设知⎪⎩⎪⎨⎧≤≤-=其他.,0,0,)(a x x ah h x f 2d )(d )(10ahx x a h h x x f a=-==⎰⎰+∞∞-,∴ah 2=,从而⎪⎩⎪⎨⎧≤≤-=其他.,0,0,22)(2a x x a a x f .y hO a x(2)0<x 时,0d 0d )()(===⎰⎰∞-∞-xxt t t f x F ,a x <≤0时,220202d )22(d 0d )()(a x a x t t a a t t t f x F xx-=-+==⎰⎰⎰∞-∞-,a x ≥时,1)(=x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.a x a x axa x x x F ,1,0,2,0,0)(22.(3)41411(1)2()()2(=--=-=≤<a F a F a X a P .12.设随机变量X 在]6,2[上服从均匀分布,现对X 进行三次独立观察,试求至少有两次观测值大于3的概率.解:由题意知⎪⎩⎪⎨⎧≤≤=其他.,0,62,41)(x x f ,记3}{>=X A ,则43d 41)3()(63==>=⎰x X P A P ,设Y 为对X 进行三次独立观测事件}3{>X 出现的次数,则Y ~43,3(B ,所求概率为)3()2()2(=+==≥Y P Y P Y P )(()(333223A P C A P A P C +=3227)43(41)43(333223=+⋅=C C .13.设随机变量X 的概率密度为⎩⎨⎧<<=其他.,0,10,3)(2x x x f 以Y 表示对X 的三次独立重复观察中事件}21{≤X 出现的次数,求:(1)}21{≤X 至少出现一次的概率;(2)}21{≤X 恰好出现两次的概率.解:由题意知Y ~),3(p B ,其中81d 321(2102==≤=⎰x x X P p ,(1)}21{≤X 至少出现一次的概率为512169)811(1)1(1)0(1)1(33=--=--==-=≥p Y P Y P .(2)}21{≤X 恰好出现两次的概率为51221811(81()1()2(223223=-=-==C p p C Y P .14.在区间],0[a 上任意投掷一个质点,以X 表示这个质点的坐标.设这个质点落在],0[a 中任意小区间内的概率与这个小区间的长度成正比例.试求X 的分布函数.解:0<x 时,事件}{x X ≤表示X 落在区间],0[a 之外,是不可能事件,此时0)()(=≤=x X P x F ;a x ≤≤0时,事件}{x X ≤发生的概率等于X 落在区间],0[x 内的概率,它与],0[x 的长度x 成正比,即x k x X P x F =≤=)()(,a x =时,1)(=≤x X P ,所以a k 1=,则此时axx F =)(;a x ≥时,事件}{x X ≤是必然事件,有1)(=x F ,综上,⎪⎪⎩⎪⎪⎨⎧≥<≤<=,a x a x a x x x F ,1,0,,0,0)(.15.设X ~),2(2σN ,又3.0)42(=<<X P ,求)0(>X P .解:)24222()42(σσσ-<-<-=<<X P X P 3.0)0(2(=Φ-Φ=σ,∴8.03.0)0()2(=+Φ=Φσ,∴8.0)2()2(1)0(1)0(=Φ=-Φ-=≤-=>σσX P X P .16.设X ~)4,10(N ,求a ,使得9.0)10(=<-a X P .解:)10()10(a X a P a X P <-<-=<-)22102(a X a P <-<-=)2()2(a a -Φ-Φ=9.01)2(2=-Φ=a,∴95.0)2(=Φa,查标准正态分布表知645.12=a,∴290.3=a .17.设X ~)9,60(N ,求分点1x ,2x ,使得X 分别落在),(1x -∞,),(21x x ,),(2∞x 的概率之比为3:4:5.解:由题知5:4:3)(:)(:)(2211=><<<x X P x X x P x X P ,又1)()()(2211=>+<<+<x X P x X x P x X P ,∴25.041)(1==<x X P ,33.031)(21==<<x X x P ,125)(2=>x X P ,则5833.0127)(1)(22==>-=≤x X P x X P .25.0)360()360360()(111=-Φ=-<-=<x x X P x X P ,查标准正态分布表知03601<-x ,∴03601>--x ,则75.0)360(1)360(11=-Φ-=--Φx x 查标准正态分布表,有7486.0)67.0(=Φ,7517.0)68.0(=Φ,75.02)68.0()67.0(=Φ+Φ,∴675.0268.067.03601=+=--x ,即975.571=x .5833.0360()360360()(222=-Φ=-≤-=≤x x X P x X P ,查标准正态分布表知5833.0)21.0(=Φ,∴21.03602=-x ,即63.602=x .18.某高校入学考试的数学成绩近似服从正态分布)100,65(N ,如果85分以上为“优秀”,问数学成绩为“优秀”的考生大致占总人数的百分之几?解:设X 为考生的数学成绩,则X ~)100,65(N ,于是)85(1)85(≤-=>X P X P )1065851065(1-≤--=X P 0228.09772.01)2(1=-=Φ-=,即数学成绩为“优秀”的考生大致占总人数的2.28%.19.设随机变量X 的分布律为求2X Y =的分布律.解:Y 所有可能的取值为0,1,4,9,则51)0()0(====X P Y P ,307)1()1()1(==+-===X P X P Y P ,51)2()4(=-===X P Y P ,3011)3()9(====X P Y P ,∴Y 的分布律为20.设随机变量X 在)1,0(上服从均匀分布,求:(1)X Y e =的概率密度;(2)X Y ln 2-=的概率密度.解:由题设可知⎩⎨⎧<<=其他.,0,10,1)(x x f ,(1)当0≤y 时,=≤}{y Y ∅,X 2-1-013P5161511513011X 0149P51307513011∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;e 0<<y 时,)e ()()(y P y Y P y F X Y ≤=≤=)(ln )ln (y F y X P X =≤=,此时,yy f y y y F y F y f X XY X 1)(ln 1)(ln )(ln )()(=='⋅'='=;e ≥y 时,1)()(=≤=y Y P y F Y ,0)(=y f Y ;∴⎪⎩⎪⎨⎧<<=其他.,0,e 0,1)(y y y f Y .(2)当0≤y 时,=≤}{y Y ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;当0>y 时,)e ()ln 2()()(2y Y X P y X P y Y P y F -≥=≤-=≤=)e (1)e (122y X y F X P ---=<-=,此时,222e 21)e ()e ()()(yy y X Y X F y F y f ---='⋅'-='=;∴⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY .21.设X ~)1,0(N ,求:(1)X Y e =的概率密度;(2)122+=X Y 的概率密度;(3)X Y =的概率密度.解:由题知22e 21)(x X xf -=π,+∞<<∞-x ,(1)0≤y 时,=≤=}e {y Y X ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;0>y 时,)(ln )ln ()e ()()(y F y X P y P y Y P y F X X Y =≤=≤=≤=,此时,2)(ln 2e 21)(ln 1)(ln )(ln )()(y X XY X y f yy y F y F y f -=='⋅'='=π;综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2)(ln 2y y y f y Y π.(2)1<y 时,=≤+=}12{2y X Y ∅,∴0)()(=≤=y Y P y F Y ;1≥y 时,21()12()()(22-≤=≤+=≤=y X P y X P y Y P y F Y )2121(-≤≤--=y X y P 当1=y 时,0)(=y F Y ,故1≤y 时,0)(=y F Y ,0)(=y f Y ;当1>y 时⎰⎰------==210221212d e22d e21)(22y x y y x Y x x y F ππ,此时,41e)1(21)()(---='=y Y Y y y F y f π,综上,⎪⎩⎪⎨⎧≤>-=--.1,0,1,e )1(21)(41y y y y f y Y π.(3)0<y 时,=≤=}{y X Y ∅,∴0)()()(=≤=≤=y X P y Y P y F Y ,0≥y 时,)()()()(y X y P y X P y Y P y F Y ≤≤-=≤=≤=)()(y F y F X X --=,0=y 时,0)(=y F Y ,∴0≤y 时,有0)(=y F Y ,0)(=y f Y ;0>y 时,22e 22)()()()()(y X X Y Y Y yf y f y F y F y f -=-+=-'+'=π,综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 22)(22y y y f yY π.22.(1)设随机变量X 的概率密度为)(x f ,+∞<<∞-x ,求3X Y =的概率密度.(2)设随机变量X 的概率密度为⎩⎨⎧>=-其他.,00,e )(x x f x 求2X Y =的概率密度.解:(1)0=y 时,0)()(=≤=y Y P y F Y ,0)(=y f Y ;0≠y 时,)()()()()(333y F y X P y X P y Y P y F X Y =≤=≤=≤=,3233331())(()()(-⋅=''='=y y f y y F y F y f XY Y ;∴⎪⎩⎪⎨⎧=≠=-.0,0,0),(31)(332y y y f y y f Y .(2)由于02≥=X Y ,故当0<y 时,}{y Y ≤是不可能事件,有0)()(=≤=y Y P y F Y ;当0≥y 时,有)()(()()()(2y F y F y X y P y X P y Y P y F X X Y --=≤≤-=≤=≤=;因为当0=y 时,0)0()0()(=--=X X Y F F y F ,所以当0≤y 时,0)(=y F Y .将)(y F Y 关于y 求导数,即得Y 的概率密度为⎪⎩⎪⎨⎧≤>-+=.,;,000)](([21)(y y y f y f y y f X X Y ,⎪⎩⎪⎨⎧≤>+=-.0,0,0),e e (21y y yyy .23.设随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其他.,0,0,2)(2ππx xx f 求X Y sin =的概率密度.解:由于X 在),0(π内取值,所以X Y sin =的可能取值区间为)1,0(,在Y 的可能取值区间之外,0)(=y f Y ;当10<<y 时,使}{y Y ≤的x 取值范围是),arcsin []arcsin ,0(ππy y - ,于是}arcsin {}arcsin 0{}{ππ<≤-≤<=≤X y y X y Y .故)arcsin ()arcsin 0()()(ππ<≤-+≤<=≤=X y P y X P y Y P y F Y ⎰⎰-+=ππyX y X x x f x x f arcsin arcsin 0d )(d )(⎰⎰-+=ππππyy x xx xarcsin 2arcsin 02d 2d 2,上式两边对y 求导,得22222121)arcsin (21arcsin 2)(yyy yyy f Y -=--+-=ππππ;综上,⎪⎩⎪⎨⎧<<-=其他.,0,10,12)(2y y y f Y π.。
商务与经济统计04-概率论 PPT
本章主要内容
试验,计数法则,概率的分配 事件及其概率 几种基本的概率关系 条件概率 Bayes定理
概率
概率是对一个事件发生的可能性的数值描述. 概率总是在0和1之间 概率接近于0表示事件几乎不会发生 该率接近于1表示概率几乎一定发生
试验与样本空间
试验是指已知其所有可能的结果的任何过程 试验的样本空间指所有可能的试验结果的集合 样本点指某一个特定的试验结果
CnN
N n
N! n!(Nn)!
其中:
N! = N(N - 1)(N - 2) . . . (2)(1) n! = n(n - 1)( n - 2) . . . (2)(1) 0! = 1
概率分配方法
古典概率方法 相对频数方法 主观方法
大家应该也有点累了,稍作休息
大家有疑问的,可以询问和交流
古典概率方法
先验概率
新信息
应用 Bayes 定理
后验概率
举例: 海珠保险公司
海珠保险公司的调查人员发现平均每一千份索赔 中会有一份欺诈
A1 = 正常索赔 A2 = 欺诈索赔 先验概率 P(A1) = .999, P(A2) = .001
新信息
调查人员还发现欺诈索赔中无业人员占40%,正常索 赔中无业人员占10%。用事件B表示索赔人员是无业人 员
48概率的几种基本关系?事件的补集?事件的并集?事件的交集?互斥事件事件的补集?事件a的补集由不属于事件a的所有样本点组成?事件a的补集用ac表示事件aac样本空间s?事件a和b的并集包括所有属于事件a或事件b的样本点?事件a和b的并集用a??b表示?样本空间s事件a事件b事件的并集?事件的并集事件mm股票盈利事件cc股票盈利m??cm股票盈利或c股票盈利m??c108102585208208pm??cp108p102p58p52p08p208
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a.所有的试验结果为:(H,H),(H,T),(T,H),(T,T)。
b.令 x=两次抛掷中出现正面的次数
c.随机变量 x 的取值如表 5-1 所示。
表 5-1
结果
x
(H,H)
2
(H,T)
1
(T,H取值,分别为 0,1,2。所以是离散的。
2.考虑工人组装产品的试验,记录工人组装产品所需的时间。
表 5-4
3 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:a.回答正确的问题数的取值为:0,1,2,….,20。所以随机变量是离散的。 b.到达收费站的汽车数的取值为:0,1,2,….。所以随机变量是离散的。 c.出现错误的报告数的取值为:0,1,2,….,50。所以随机变量是离散的。
表 5-2 试(Y,Y,Y)(Y,Y,N)(Y,N,Y)(Y,N,N)(N,Y,Y)(N,Y,N)(N,N,Y)(N,N,N) 验 结 果
2 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
N3
2
2
1
2
1
1
0
4.已知佛罗里达州的 12 个租借机构的房屋抵押率。令随机变量表示这些租借机构中 提供 30 年固定利率为 8.5%或更少的机构的个数。试问,这个随机变量可以取什么值?
4 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
d.当 x>30 时,f(35)=0.40,即 x>30 的概率是 0.40。
8.以下是坦帕总医院(Tampa General Hospital)20 天内手术室的使用情况:有 3 天只使用 1 间,有 5 天使用 2 间,有 8 天使用 3 间,有 4 天医院的 4 问手术室都被使用。
a.根据相对频数法对任一天中手术室的使用数目建立概率分布。 b.画出概率分布图。 c.证实这个概率分布确实满足离散型概率分布的条件。 解:a.根据相对频数法对任一天中手术室的使用数目建立概率分布如表 5-6 所示。
x 1 2 3 4 总计 b.概率分布图如图 5-1 所示。
表 5-6 f(x)
3/20=0.15 5/20=0.25 8/20=0.40 4/20=0.20
d.在 8 小时工作日中非生产性的小时数的取值为:0 x 8 。所以随机变量是连续的。
e.磅数的取值为 x>0。所以随机变量是连续的。
7.随机变量 x 的概率分布如表 5-5 所示。 表 5-5
a.这是一个概率分布吗?为什么? b.x=30 的概率是多少? c.x 小于或等于 25 的概率是多少? d.x 大于 30 的概率是多少?
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 5 章 离散型概率分布
1.考虑一个抛两次硬币的试验。
a.列出所有的试验结果。
b.定义一个表示两次抛掷中出现正面的次数的随机变量。
c.对每一种可能的试验结果,给出随机变量的取值。
d.这个随机变量是离散的还是连续的?
解:设 H=正面,T=反面。
答:这个随机变量可以取 0,1,2,…,12。
5.为进行一种血液分析,试验员需要两道程序:第一道程序可能需要经过 l 步或 2 步
来完成;第二道程序可能需要经过 1 步、2 步或 3 步来完成。
a.列出进行一次分析产生的所有试验结果。
b.如果令随机变量表示完成一次分析所需步骤数,列出与每一试验结果相对应的随机
1 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
a.定义一个随机变量表示组装产品所需的时间(以分钟计)。 b.随机变量可取什么值? c.随机变量是离散的还是连续的? 解:a.令 x=组装产品所需的时间(以分钟计) b.它可以取任何正值,即 x>0。 c.随机变量是连续的。
解:a.由于对任意的 x,均有 f(x)≥0,并且 f (x) 0.20 0.15 0.25 0.40 1 ,
所以是一个概率分布。 b.当 x=30,f(30)=0.25,即概率为 0.25。 c.当 x≥25,f(20)+f(25)=0.20+0.15=0.35,即 x 小于或等于 25 的概率是 0.35。
变量的值。
解:a.S={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)}。
b.与每一试验结果相对应的随机变量的值如表 5-3 所示。
表 5-3
试验结果
(1,1) (1,2) (1,3) (2,1) (2,2) (2,3)
完成一次分析所需步骤数 2
3
4
3
4
5
6.表 5-4 是一系列试验及相关的随机变量。为每一例子确定随机变量的可取值及判断 随机变量是离散的还是连续的。
1.00
5 / 51
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-1 c.对于 x=1,2,3,4,均有 f(x)≥0;并且∑f(x)=0.15+0.25+0.40+0.20=1。 9.在美国,有 38%的四年级儿童不能阅读适龄读物。孩子是否有阅读问题需要经过专 门的教育机构来鉴定。对那些有阅读问题的孩子,这些机构还提供专门的方法帮助他们提高 阅读能力。有阅读问题的孩子中的绝大部分应该在三年级之前得以发现和纠正。但是,联邦 法律规定,除非孩子的学习能力落后于同龄儿童大约两年以上,否则禁止这些特殊教育机构 向他们提供帮助。这意味着,他们的问题至少是在三年级以后才能被发现和纠正。表 5-7 是各年龄段中出现阅读问题的孩子的人数(USA Today,2001.9.6)。
3.3 个学生为暑假在 Brookwood 学院工作而被安排进行面试。试验的结果为被录用 或不被录用。定义试验结果为 3 人面试的结果。
a.列出所有的试验结果。 b.定义一个随机变量,描述面试的录取人数。此随机变量是离散的还是连续的? c.列出与每一试验结果相对应的随机变量的值。 解:令 Y=被录用,N=不被录用。 a.S={(Y,Y,Y),(Y,Y,N),(Y,N,Y),(Y,N,N),(N,Y,Y),(N,Y, N),(N,N,Y),(N,N,N)}。 b.令 N=面试的录取人数,N 是离散型随机变量。 c.每一试验结果相对应的随机变量的值如表 5-2 所示。
