期权定价的二叉树模型
期权的二叉树定价模型

17
利用风险中性定价法计算上面例题
• 已知股票现价为$20,三个月末股票价格可能上涨到$22或下降到 $18。本例中所考虑的期权是一份执行价格为$21,有效期为三个 月的欧式看涨期权,无风险利率是年率12%。 • 在风险中性假设条件下,股票价格上升变化的概率是p。在这样的 世界中,股票的预期收益率一定等于无风险利率12%。这意味着一 定满足: 22p +18(1 –p)= 20e0.12*0.25 p=0.6523。 • 在三个月末尾,看涨期权价值具有$1价值的概率为0.6523,价值 为零的概率为0.3477。因此,看涨期权的期望值为: 0.6523 1 + 0.3477 0 = $0.6523 • 利用无风险利率进行贴现,可以得到该期权的价值为: 0.6523e-0.12*0.25=0.633 • 这一计算结果与前面所得结果相同,这说明利用无套利理论和风 险中性定价方法计算的结论相同。
f
u
f
d
Su Sd
(1)
11
当组合中股票的△取值为 f
u
Su Sd
f 时
d
• 所构造的组合一定是无风险组合,根据无套利假设条件, 组合的收益一定为无风险利率。 rT ( Su f ) e • 我们用r表示无风险利率,则该组合的现值为: u • • 而该组合的初始价值为S △ -f ,因此
19
6
在无套利假设条件下,无风险证券组合 的收益率一定为无风险利率。
• 假设无风险利率为年率 12% 。我们可以计算该组 合的现在价值一定是$4.5,即: • 我们用 f 表示期权的价格。已知股票现在价格为 $20,因此该组合现在的价值为: • 20*0.25 – f = 5 – f • 于是 5 – f = 4.367 • 求解可得 f = 0.633 • 在无套利假设条件下,期权的价值一定为 $0.633 。
第五讲期权定价理论I二叉树模型

记每步时长为Δt,那么单步二叉树模型下的期权价格 为:
f=e-rΔt[pfu +(1-p)fd] 其中,p=(erΔt-d)/(u-d)。由此可以计算出期初和第一步
到期时各个节点的期权价值:
fu=e-rΔt[pfuu+(1-p)fud] fd=e-rΔt[pfud+(1-p)fdd]
f=e-rΔt[pfu+(1-p)fd] 把fu和fd代入f可得:
f=e-2rΔt[ p2 fuu+2p(1-p)fud+(1-p)2 fdd] 因此,期权的价格为期权预期收益以无风险利率进行
贴现的现值。 想象一下,三步二叉树模型下期权的定价问题。
16
(四)看跌期权的情形
例5:考虑如下图11.7两年期的欧式看跌股票期 权,执行价格为52元,股票的当期价格为50元, 假设时期分为两步,每步期长为1年,且每步 股票价格要么上涨20%,要么下跌20%,无风 险利率为5%。
23
(七)Δ
回忆:Δ是什么? Δ=(fu–fd)/(S0u-S0d) 什么意思? Δ为期权价格变化与标的股票价格的变化之比; Δ为我们针对每个期权空头而持有的股票数量,
目的是构建一个无风险资产组合。 Δ对冲(delta hedging)通常是指构建一个无风险
对冲。看涨期权的Δ为正,看跌期权的Δ为负。 计算图11.1和11.7中的Δ。
26
4. 期货期权的定价 在风险中性世界里,期货的价格增长率为0。假设期货
的为期F0,初因价此格,为F0,时间长度为Δt的期货的期望价格也 E(FT)=pF0u+(1-p)F0d=F0 p=(1-d)/(u-d) 例10:一个期货的当前价格为31,波动率为30%,无风
期权定价的二叉树模型(ppt 39页)

第7章 期权定价的二叉树模型
2022/3/23
22
ftrf S S f1 22S2 S 2f2rf f
c St N d1 X erf Tt N d2
St erf Tt N d1 X N d2 erf Tt
EST Nd1 X N d2 erf Tt EST Nd1 X N d2 erf Tt
2022/3/23
21
风险中性定理表达了资本市场中的这样的 一个结论:即在市场不存在任何套利可能性的 条件下,如果衍生证券的价格依然依赖于可交 易的基础证券,那么这个衍生证券的价格是与 投资者的风险态度无关的。
这个结论在数学量,尤其是期望收益率。
公平的入局费=2000×50%+0×50%= 1000元
第7章 期权定价的二叉树模型
2022/3/23
13
愿意支付的入局费 风险类型 数量 入局费<1000元 风险厌恶者 众多 入局费=1000元 风险中性者 入局费>1000元 风险喜好者 极少
如果有人愿意无条件地参加公平的赌博, 则这样的人被认为是风险中性。风险中性者对 风险采取无所谓的态度。
考虑以下组合:
①买入1份股票看涨期权 ②卖空Δ股股票
显然,适当调整Δ可以使得上述组合为无风 险组合。
第7章 期权定价的二叉树模型
2022/3/23
3
如果这个组合是无风险组合,则其价值与 状态无关,所以,以下数学表达式成立:
22118
解得,
0.25
也就是说,1份看涨期权多头加上0.25股股 票空头构成的组合是无风险组合。
这就是风险中性定价的基本思想。
第7章 期权定价的二叉树模型
2022/3/23
18
我们回到之前的示例中,在那里,我们可 以把股票价格上升的概率定义为p,于是在到 期日T时刻,股票价格的期望值为:
期权定价公式的二叉树推导与分析

期权定价公式的二叉树推导与分析期权作为金融衍生品的重要组成部分,对于投资者和风险管理师来说具有重要意义。
期权的价值取决于多种因素,包括标的资产的价格、行权价格、剩余到期时间、无风险利率、波动率等。
期权的定价是金融领域的一个重要问题,准确的期权定价可以帮助投资者更好地进行投资决策和风险管理。
本文将介绍期权的定价公式,并通过二叉树的方法推导期权的价格,最后对各种情况下期权定价的计算方法与特点进行分析。
期权的定价公式是由费雪·布莱克、迈伦·斯科尔斯和罗伯特·默顿提出的布莱克-斯科尔斯模型。
该模型基于一些假设,例如无摩擦市场、无套利机会等,通过 Black-Scholes方程求解期权的定价。
具体公式如下:C = SₐN(d1) - XₐN(d2)其中, C为期权的公允价值; Sₐ为标的资产当前的价格; Xₐ为期权的行权价格; N(d1)和 N(d2)分别为正态分布变量的累积分布函数;d1和 d2分别为: d1 = (ln(Sₐ/Xₐ) + (r + σ²/2)T) / (σ√T) d2 = d1 - σ√T T为期权的剩余到期时间,以年为单位; r为无风险利率;σ为标的资产的年波动率。
二叉树方法是一种常用的期权定价模型,它可以用来推导期权的预期价格。
二叉树方法的思路是将期权的到期时间划分为若干个时间段,并假设标的资产在每个时间段内只有两种可能的价格,即上涨或下跌。
基于这个假设,我们可以构建一个二叉树来描述标的资产的价格变动情况。
假设初始时刻为 t0,标的资产的价格为 S0,行权价格为 X。
在每个时间段Δt内,标的资产的价格有两种可能的变化:上涨到 Su = S0 × u,或者下跌到 Sd = S0 × d,其中 u > 1,d < 1,u和 d分别为标的资产的上涨和下跌因子。
假设该期权的剩余到期时间为 T,共分为 n个时间段。
那么在 t0时,该期权的预期价格为:C0 = ∑CN(d1, d2, u, d) × (u × S0 - X)^+ ×Δt其中, N(d1, d2, u, d)为风险中性概率; (u × S0 - X)^+表示当标的资产价格上涨时,取 u × S0 - X,否则取 0;Δt为每个时间段的时间长度。
二叉树期权定价模型

二叉树期权定价模型
二叉树期权定价模型是指基于二叉树构建的期权定价模型,该模型结合了终值定理(Binomial Option Pricing Model;BOPM)和二叉树的理论。
该模型的精确性比一般的期权定价模型(即欧式期权定价模型)要高,为投资者提供了更多的信息和选择。
二叉树期权定价模型以股票价格移动变量来构建定价模型,而欧式期权定价模型只考虑股票价格固定。
该模型使用二叉树,其中每个分支都对应一定的定价模型,以确定期权价格。
该方法有三个基本步骤:1)构建二叉树;2)确定期权执行价值;3)通过使用backward卷积,利用当前价格和当前的期权价值,来决定每个分支的期权价格。
二叉树期权定价模型具有不同的算法变种,它们能够捕获市场(股价)的单向和双向变化,以及波动性。
它比欧式期权模型更精确,也更灵活,可以捕获一系列特殊事件,比如空头期权,复合期权,多元期权,多档次期权。
此外,二叉树期权定价模型还能够用来估算期权的损失或收益,并对复杂的期权进行定价。
总的来说,二叉树期权定价模型是一种简单的,有效的,能够捕获市场变化的定价模型,为投资者提供了更多的信息和选择。
该模型比较早出现于二十世纪九十年代,自此后逐渐普及,并得到广泛应用。
二叉树期权定价模型

二叉树期权定价模型(一)单期二叉树定价模型(1)一定数量的股票多头头寸(2)该股票的看涨期权的空头头寸股票的数量要使头寸足以抵御资产价格在到期日的波动风险,即该组合能实现完全套期保值,产生无风险利率。
C0=1+r-d Cu u-1-r Cdu—d 1+r u—d 1+r最初,投资于0.5股股票,需要投资25元;收取6.62元的期权费,尚需借入18.38元。
半年后,股价如果股价涨到66.66元,0.5股股票收入33.33元,借款本息18.75(18.35*1.02)看期权的持有人会执行期权,期权出售人补足价差14.58(66.66-50),投资人的净损益=0股价如果跌到37.5元,0.5股股票收入18.75元,支付借款本息18.75元,投资人的净损益为0因此该看涨期权的公平价值就是6.62元。
(二)两期二叉树模型把6个月的时间分为两期,每期3个月。
现在股价50元,看涨期权的执行价格52.08元。
每期股价有两种可能:上升22.56%或下降18.4%;无风险利率为每3个月1%。
股价:计算Cu的价值:有两种办法:1.复制组合定价H=(23.02-0)÷(75.10-50)=0.91713借款=(50×0.91713)÷1.01=45.40元3个月后股票上行的价格是61.28元Cu=投资成本=购买股票支出-借款=61.28×0.91713-45.40=10.8元2.风险中性定价期望报酬率=1%=上行概率×22.56%+下行概率×(-18.4%)[22.56%=(74.10-61.28)/61.28 18.4%=(50-61.28)/61.28上行概率=0.47363期权价值6个月后的期望值=0.47363*23.02+(1-0.47363)*0=10.9030元Cu=10.9030÷1.01=10.8元根据Cu和Cd计算C0的价值:1.复制组合定价H=(10.8-0)/(61.28-40.80)=0.5273借款=(40.80×0.5273)÷1.01=21.3008元C0=投资成本=购买股票支出-借款=50×0.5273-21.3008=5.062.风险中性原理C0=0.47363×10.8÷1.01=5.06元(三)多期二叉树模型u =1+上升百分比=d =1-下降百分比=1 / ue =自然常数,约等于2.7183σ=标的资产连续复利收益率的标准差t =以年表示的时段长度。
期权二叉树定价模型

期权二叉树定价模型期权二叉树定价模型是一种常用的金融衍生品定价模型,用于计算期权合约的公平价格。
该模型基于二叉树的数据结构,将时间分为离散的步长,在每个步长上模拟期权的价格变化。
在期权二叉树定价模型中,二叉树的每个节点表示期权的一个可能价格,树的每一层表示时间的一个步长。
从根节点开始,根据期权的流动性和到期前可执行的次数,构建二叉树模型。
在每个节点上,计算期权的价值,以确定其合理价格。
在构建二叉树模型时,需要考虑期权的标的价格、波动率、到期时间和无风险利率等因素。
这些因素将被用来计算每个节点上的期权价格。
在每个步长上,通过向上或向下移动树的节点,模拟标的价格的波动,从而更新节点上的期权价格。
在二叉树的叶子节点上,期权的价值是已知的,可以直接计算。
在其他节点上,通过对未来价格的概率分布进行加权,计算期权的合理价格。
树的最后一层即为到期时间,即期权到期时的状态。
根据到期状态计算出期权的现值,并通过向根节点回溯,确定期权的公平价格。
期权二叉树定价模型的优点在于能够在离散时间步长上快速确定期权的价格,并且可以灵活地应用于不同类型的期权合约。
此外,该模型对于包含多个期权合约的复杂结构,如欧洲期权、美式期权和亚洲期权等,也具有较高的适用性。
然而,期权二叉树定价模型也存在一些局限性。
首先,该模型假设标的价格的波动服从几何布朗运动,这在实际市场中并不成立,因此模型的有效性有一定的限制。
其次,通过选择适当的步长数和树的深度来平衡精确度和计算效率是一个挑战。
总的来说,期权二叉树定价模型是一个常用且有效的金融工具,可以用于估计期权合约的公平价格。
该模型基于二叉树的数据结构,通过离散时间步长模拟期权的价格变化,并通过回溯计算确定期权的公平价格。
虽然该模型存在一定的局限性,但在实际应用中仍被广泛应用。
期权二叉树定价模型是一种基于离散时间步长和二叉树结构的金融衍生品定价模型。
它是Black-Scholes模型的一种改进方法,通过模拟期权价格的变化来计算期权的公平价格。
期权定价的二叉树模型
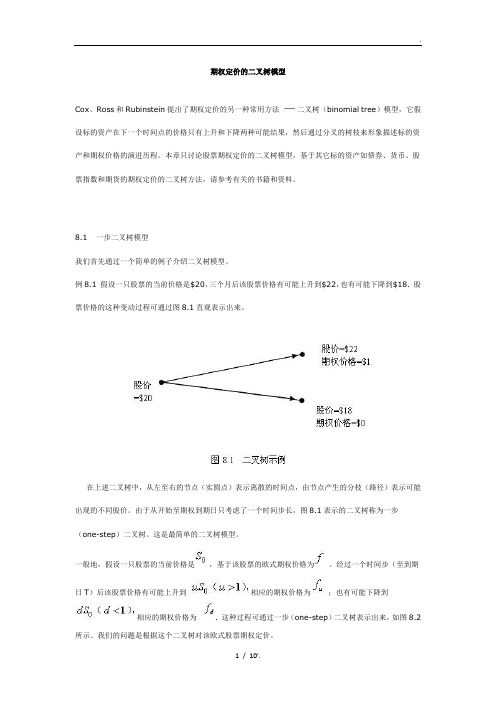
期权定价的二叉树模型Cox、Ross和Rubinstein提出了期权定价的另一种常用方法二叉树(binomial tree)模型,它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果,然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。
本章只讨论股票期权定价的二叉树模型,基于其它标的资产如债券、货币、股票指数和期货的期权定价的二叉树方法,请参考有关的书籍和资料。
8.1 一步二叉树模型我们首先通过一个简单的例子介绍二叉树模型。
例8.1 假设一只股票的当前价格是$20,三个月后该股票价格有可能上升到$22,也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。
在上述二叉树中,从左至右的节点(实圆点)表示离散的时间点,由节点产生的分枝(路径)表示可能出现的不同股价。
由于从开始至期权到期日只考虑了一个时间步长,图8.1表示的二叉树称为一步(one-step)二叉树。
这是最简单的二叉树模型。
一般地,假设一只股票的当前价格是,基于该股票的欧式期权价格为。
经过一个时间步(至到期日T)后该股票价格有可能上升到相应的期权价格为;也有可能下降到相应的期权价格为. 这种过程可通过一步(one-step)二叉树表示出来,如图8.2所示。
我们的问题是根据这个二叉树对该欧式股票期权定价。
为了对该欧式股票期权定价,我们采用无套利(no arbitrage)假设,即市场上无套利机会存在。
构造一个该股票和期权的组合(portfolio),组合中有股的多头股票和1股空头期权。
如果该股票价格上升到,则该组合在期权到期日的价值为;如果该股票价格下降到,则该组合在期权到期日的价值为。
根据无套利假设,该组合在股票上升和下降两种状态下的价值应该相等,即有由此可得(8.1)上式意味着是两个节点之间的期权价格增量与股价增量之比率。
在这种情况下,该组合是无风险的。
以表示无风险利率,则该组合的现值(the present value)为,又注意到该组合的当前价值是,故有即将(8.1)代入上式,可得基于一步二叉树模型的期权定价公式为(8.2)(8.3)需要指出的是,由于我们是在无套利(no arbitrage)假设下讨论欧式股票期权的定价,因此无风险利率应该满足: .现在回到前面的例子中,假设相应的期权是一个敲定价为$21,到期日为三个月的欧式看涨权,无风险的年利率为12%,求该期权的当前价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u1
u2
u2
u1
u2
u1
风险回避型效用函数 风险爱好型效用函数 风险中立型效用函数
U=f(财富)→U=g(E(R) ) U=h(风险)→U=q(σR) R=φ(σR)
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
风险中性的投资者对风险不要求回报,他 们投资于任何资产所要求的收益率等于无风险 收益率。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
5.00-C0元
3个月
4.50元
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
⒉ 单步二叉树模型的推广
无风险组合:Δ股股票多头+1份期权空头
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
金融学
财富的效用
凹性效用函数
风险厌恶者 风险中性者
风险喜好者
线性效用函数 凸性效用函数
愿意支付的
W0
Wh
风险金
不同风险类型者的财富效用曲线
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
投资学
⒉ 风险中性定价理论
风险中性理论又称风险中性定价方法( Risk Neutral Pricing Theory ),是考克斯(Cox J.C.)和 斯蒂芬·罗斯(Stephen A. Ross)于1976年推导期 权定价公式时建立的。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
2020/4/8
第7章 期权定价的二叉树模型
单步二叉树模型至少给我们两点启示: ⑴期权价格与股票价格变化的真实概率无 关(这与我们的直觉不一致) ⑵期权价格在定价形式上可以看成到期日 价值期望值的贴现值(按无风险利率贴现)
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
所谓风险中性假设就是: 如果对一个问题的分析过程和投资者的风险 偏好无关,则可以将问题放到一个假设的风险中 性的世界里进行分析,所得的结果在真实的世界 里也应成立。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
Hale Waihona Puke 第7章 期权定价的二叉树模型
这就是风险中性定价的基本思想。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
我们回到之前的示例中,在那里,我们可 以把股票价格上升的概率定义为p,于是在到 期日T时刻,股票价格的期望值为:
代入p值,得
在我们的假设下,从概率角度讲,股票价格 以无风险利率增长(也就是说股票的期望收益率 等于无风险利率)。
公平的入局费=2000×50%+0×50%= 1000元
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
愿意支付的入局费 风险类型 数量 入局费<1000元 风险厌恶者 众多 入局费=1000元 风险中性者 入局费>1000元 风险喜好者 极少
如果有人愿意无条件地参加公平的赌博, 则这样的人被认为是风险中性。风险中性者对 风险采取无所谓的态度。
期权定价的二叉树模型
路漫漫其修远兮, 吾将上下而求索
2020年4月8日星期三
一、单步二叉树模型 ⒈ 一个示例
3个月
执行价格为21 元的看涨期权 。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
股票和股票期权所面临的系统风险相关,适 当配置两种资产可以消除系统风险,组建无风险 组合。
风险中性定理表达了资本市场中的这样的 一个结论:即在市场不存在任何套利可能性的 条件下,如果衍生证券的价格依然依赖于可交 易的基础证券,那么这个衍生证券的价格是与 投资者的风险态度无关的。
这个结论在数学上表现为衍生证券定价的 微分方程中并不包含有受投资者风险态度的变 量,尤其是期望收益率。
路漫漫其修远兮, 吾将上下而求索
二、风险中性定价
⒈ 风险中性假设
公平赌博是指赌博结果的预期只应当和入局 前所持有的资金量相等,即赌博的结果从概率平 均的意义上来讲应当是“不输不赢”。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
有一个掷硬币的赌局(假定硬币是完全对称 的),正面朝上可以赢得2000元,反面朝上 则无钱收回。试问你愿意以多少钱作为入局费 参加这样的赌博?
考虑以下组合 :①买入1份股票看涨期权 ②卖空Δ股股票
显然,适当调整Δ可以使得上述组合为无风 险组合。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
如果这个组合是无风险组合,则其价值与 状态无关,所以,以下数学表达式成立:
解得,
也就是说,1份看涨期权多头加上0.25股股 票空头构成的组合是无风险组合。
投资回报率=无风险利率+风险溢价
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
在一个假想的风险中性的世界(RiskNeutral World )里,所有的市场参与者都是风 险中性的,那么,所有的资产不管其风险的大 小或是否有风险,预期收益率都相同,都等于 无风险收益率,因此,所有资产现在的市场均 衡价格都应等于其未来价值的预期值,加上考 虑到货币的时间价值,就都是未来预期价值按 无风险收益率贴现的价值(即现值)。
2020/4/8
第7章 期权定价的二叉树模型
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
利用风险中性假设的分析方法进行金融 产品的定价,其核心环节是构造出风险中性 的概率。
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
将Δ代入f,得
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
路漫漫其修远兮, 吾将上下而求索
2020/4/8
第7章 期权定价的二叉树模型
在之前的示例中 ,
我们得到:
结果与之前一致。
路漫漫其修远兮, 吾将上下而求索
