基本不等式及其应用(二)【自主学习】
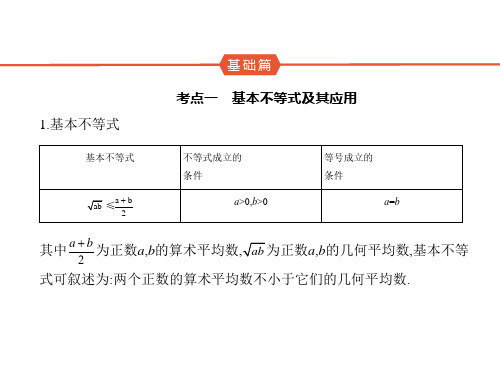
2.基本不等式

则x y 的最大值是
。
解决最大(小)值问题
结论:利用
求最值时要注意下面三条:
(1)一正:各项均为正数
(2)二定:两个正数积为定值,和有最小值。 积定,和最小 两个正数和为定值,积有最大值。 和定,积最大
(3)三相等Βιβλιοθήκη 求最值时一定要考虑不等式是否能取 “=”。
题型三:构造积为定值,利用基本不等式求最值
ab叫做a,b的 几何平均数
这样,基本不等式可以表述为: 两个正数的算术平均数不小于它们的几何平均数。
注意:
重要不等式与基本不等式有什么区别与联系?
题型一:利用基本不等式判断代数式的大小关系
例1:设a>0,b>0,给出下列不等式
(1)a 1 2 (2)(a 1 )(b 1) 4
1.利用基本不等式求最值需注意的问题 (1)各数(或式)均为正; (2)和或积其中之一为定值; (3)等号能否成立,
即“一正二定三相等”,这三个条件缺一不可.
注意:要特别注意不等式成立的条件及等号成 立的条件.
创设应用基本不等式的条件 合理拆分项或配凑因式是常用的技巧,而 拆与凑的目标在于使等号成立,且每项为正 必 要时需出现积为定值或和为定值.
第一讲 不等式和绝对值不等式 2、基本不等式及其应用
一、重要不等式(定理一):
一般地,对于任意实数a,b,我们有
a2+b2≥2ab
(当且仅当a=b时,取“=”号)
文字语言:两个数的平方和不小于它们积的2倍
二、基本不等式(定理二)
如果a, b>0, 那么
当且仅当a=b时,等号成立。
如果a,b都是正数,我们就称 a b为a,b的 算术平均数 2
基本不等式及实际应用

最小值 2 P .
(2)如果和x+y是定值S,那么当 x=y时积xy有最 大值
1 2 S 4
. 即“一正、二定、三相等”,这三
个条件缺一不可.
思维活动:
4 1函数y x 4 x 0的值域 ______
(2)已知 x 0, y 0,且 x 5 y 20, 求 2
情境二:运输
兴 趣 是 最 好 的 老 师
进货结束后装车运回。所购大米需装6辆 卡车,途径一座长为100米的大桥,假设 卡车均以v(m/s)的速度匀速前进,并出 于安全考虑规定每两辆卡车的间距不得小 v 于 5 m(卡车长忽略不计),则全部卡车 安全过桥最快需多少时间?
2
解:设卡车全部安全过桥共需t 秒,
该厂每天需要饲料200千克,每千克饲料的价格 为1.8元,饲料的保管与其他费用为平均每千克 每天0.03元,购买饲料每次支付运费300元. (1)求该厂多少天购买一次饲料才能使平均每
天支付的总费用最少?
(2)若提供饲料的公司规定,当一次购买饲料 不少于5吨时其价格可享受八五折优惠(即为原
价的85%).问该厂是否可以考虑利用此优惠条
例2:一段长为36米的篱笆围成一个矩形 菜园,问这个矩形的长、宽各为多少时, 菜园的面积最大,最大面积是多少?
例2:一段长为36米的篱笆围成一个矩形 菜园,问这个矩形的长、宽各为多少时, 菜园的面积最大,最大面积是多少?
解:(1)设矩形的长、宽各为 x , ym,由题意可得
2 x y 36且 x 0, y 0 。矩形的面积为 xym
答:当底面的长与宽均 为4米时,用纸最少
例4、李老师花10万元购买了一辆家用汽车,如果每年使用的保险费,养
第2章不等式基本不等式及其应用

基本不等式及其应用1.基本不等式:ab ≤a +b2(1)基本不等式成立的条件:a >0,b >0.(2)等号成立的条件:当且仅当a =b 时取等号. 2.几个重要的不等式 (1)a 2+b 2≥2ab (a ,b ∈R ). (2)b a +ab ≥2(a ,b 同号). (3)ab ≤⎝⎛⎭⎫a +b 22(a ,b ∈R ).(4)a 2+b 22≥⎝⎛⎭⎫a +b 22 (a ,b ∈R ). 以上不等式等号成立的条件均为a =b . 3.算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为a +b 2,几何平均数为ab ,基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数. 4.利用基本不等式求最值问题 已知x >0,y >0,则(1)如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值2p .(简记:积定和最小) (2)如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值p 24.(简记:和定积最大)概念方法微思考1.若两个正数的和为定值,则这两个正数的积一定有最大值吗?提示 不一定.若这两个正数能相等,则这两个数的积一定有最大值;若这两个正数不相等,则这两个正数的积无最大值.2.函数y =x +1x的最小值是2吗?提示 不是.因为函数y =x +1x 的定义域是{x |x ≠0},当x <0时,y <0,所以函数y =x +1x 无最小值.1.(2020•上海)下列等式恒成立的是( ) A .222a b ab + B .222a b ab +-C .2||a b ab +D .222a b ab +-【答案】B【解析】A .显然当0a <,0b >时,不等式222a b ab +不成立,故A 错误;B .2()0a b +,2220a b ab ∴++,222a b ab ∴+-,故B 正确;C .显然当0a <,0b <时,不等式2||a b ab +不成立,故C 错误;D .显然当0a >,0b >时,不等式222a b ab +-不成立,故D 错误.故选B .2.(2020•海南)已知0a >,0b >,且1a b +=,则( ) A .2212a b + B .122a b ->C .22log log 2a b +-D 2【答案】ABD【解析】①已知0a >,0b >,且1a b +=,所以222()22a b a b ++,则2212a b +,故A 正确. ②利用分析法:要证122a b ->,只需证明1a b ->-即可,即1a b >-,由于0a >,0b >,且1a b +=,所以:0a >,10b -<,故B 正确.③22222log log log log ()22a b a b ab ++==-,故C 错误. ④由于0a >,0b >,且1a b +=,利用分析法:要证2成立,只需对关系式进行平方,整理得2a b ++,即1,故122a b +=,当且仅当12a b ==时,等号成立.故D 正确. 故选ABD .3.(2020•天津)已知0a >,0b >,且1ab =,则11822a b a b+++的最小值为_________. 【答案】4【解析】0a >,0b >,且1ab =, 则118882422222a b a b a b a b a b ab a b a b a b+++++=+=+=++++,当且仅当82a b a b+=+,即2a =+,2b =2a =,2b =取等号, 故答案为:4.4.(2020•江苏)已知22451(,)x y y x y R +=∈,则22x y +的最小值是_________. 【答案】45【解析】方法一、由22451x y y +=,可得42215y x y -=,由20x ,可得2(0y ∈,1],则44222222211411(4)555y y x y y y y y y-++=+==+221142455y y =,当且仅当212y =,2310x =, 可得22x y +的最小值为45; 方法二、222222222254254(5)4()()24x y y x y y x y ++=+=+,故2245x y +, 当且仅当222542x y y +==,即212y =,2310x =时取得等号,可得22x y +的最小值为45. 故答案为:45. 5.(2019•上海)若x ,y R +∈,且123y x +=,则yx的最大值为_________. 【答案】98【解析】113222y y x x =+,∴29()822y x =; 故答案为:98.6.(2019•天津)设0x >,0y >,24x y +=,则(1)(21)x y xy++的最小值为_________.【答案】92【解析】0x >,0y >,24x y +=, 则(1)(21)2212552x y xy x y xy xy xy xy xy++++++===+; 0x >,0y >,24x y +=,由基本不等式有:4222x y xy =+, 02xy ∴<, 552xy, 故:5592222xy ++=; (当且仅当22x y ==时,即:2x =,1y =时,等号成立), 故(1)(21)x y xy ++的最小值为92;故答案为:92. 7.(2019•天津)设0x >,0y >,25x y +=的最小值为_________.【答案】【解析】0x >,0y >,25x y +=,==;由基本不等式有:6224xyxy=;当且仅当时,即:3xy =,25x y +=时,即:31x y =⎧⎨=⎩或232x y =⎧⎪⎨=⎪⎩时;等号成立,;故答案为:8.(2018•上海)已知实数1x 、2x 、1y 、2y 满足:22111x y +=,22221x y +=,121212x x y y +=,的最大值为_________. +【解析】设1(A x ,1)y ,2(B x ,2)y , 1(OA x =,1)y ,2(OB x =,2)y ,由22111x y +=,22221x y +=,121212x x y y +=, 可得A ,B 两点在圆221x y +=上, 且111cos 2OA OB AOB =⨯⨯∠=, 即有60AOB ∠=︒,即三角形OAB 为等边三角形,1AB =,A ,B 两点 到直线10x y +-=的距离1d 与2d 之和,要求之和的最大值,显然A ,B 在第三象限,AB 所在直线与直线1x y +=平行, 可设:0AB x y t ++=,(0)t >,由圆心O到直线AB的距离d=,可得1=,解得t=,1+=,9.(2018•天津)已知a,b R∈,且360a b-+=,则128ab+的最小值为_________.【答案】14【解析】a,b R∈,且360a b-+=,可得:36b a=+,则66611111222228222224a a a ab a a a++=+=+=,当且仅当6122aa+=.即3a=-时取等号.函数的最小值为:14.故答案为:14.1.(2020•衡阳三模)已知a,b R+∈,22a b+=,则1ab a+的最小值为() A.32B1C.52D.【答案】B【解析】由a,b R+∈,22a b+=,∴1211222a a ab a bb a b ab a++=+=+++,(当且仅当b=即2a=2b=时取等号),故则1ab a+1+,故选B.2.(2020•道里区校级四模)若正实数a,b满足112a b+=ab的最小值为()A B.C.4 D.8【答案】A【解析】正实数a,b满足111222a b ab+,解可得,2ab ,当且仅当112a b=时取等号, 则ab故选A .3.(2020•道里区校级四模)若实数a ,b 满足122()lg lga lgb a b+=+,则ab 的最小值为( )AB.C .32lg D .2lg【答案】B【解析】因为122()lg lga lgb a b+=+,所以1222a b ab +=,当且仅当12a b=时取等号, 解可得,22ab . 故选B .4.(2020•衡阳三模)已知a ,(0,)b ∈+∞,22a b +=,则1a b a+的取值范围是( ) A .(0,)+∞ B .1,)+∞C .5[,)2+∞D .)+∞【答案】B【解析】已知a ,(0,)b ∈+∞,22a b +=,∴12121122ba a a ab a b b a ba b a b a++=+=+++=, 当且仅当2a bb a=,即2a =2b =时,取=号, 故选B .5.(2020•贵阳模拟)已知a ,b 均为正数,函数2()log f x a x b =+的图象过点(4,1),则2a bab+的最小值为( ) A .6 B .7C .8D .9【答案】D【解析】由题意可得,2log 41a b +=即21a b +=,0a >,0b >, 则2121222()(2)59a b a b a b ab b a b a b a +=+=++=++,当且仅当22a bb a=且21ab +=即13a b ==时取等号, 故选D .6.(2020•镇海区校级模拟)若0a >,0b >,且11a b+22a b +的最小值为( ) A .2B .C .4D .【解析】0a >,0b >,且11a b+∴112a b,可得2ab .当且仅当a b =时取等号.2224a b ab ∴+,当且仅当a b =时取等号.则22a b +的最小值为4, 故选C .7.(2020•辽宁三模)若441x y +=,则x y +的取值范围是( ) A .(-∞,1]- B .[1-,)-∞ C .(-∞,1] D .[1,)-∞【答案】A【解析】由基本不等式可得,若441x y +=, 有14424424x y x y x =+=, 即11444x y+-=, 根据指数函数4x y =是单调递增函数可得, 1x y +-,故x y +的取值范围是(-∞,1]-, 故选A .8.(2020•潮州二模)若直线220(0,0)ax by a b -+=>>过圆222410x y x y ++-+=的圆心,则91a b+的最小值是( ) A .16 B .10 C .12D .14【答案】A【解析】由题意可得圆222410x y x y ++-+=的圆心(1,2)-, 故2220a b --+=即1a b +=,(0,0)a b >>, 则919199()()1010216b a a b a b a b a b a b+=++=+++=, 当且仅当9b a a b =且1a b +=即14b =,34a =时取等号.故选A .9.(2020•石家庄模拟)a ,b 是两个互不相等的正数,则下列三个代数式中,最大的一个是( ) ①11()()a b b a ++,②22a b a b +++,③22()2a b ab ab a b+++A .必定是①B .必定是②C .必定是③D .不能确定【解析】因为0a >,0b >,所以①1111()()11224a b ab ab b a ab ab ++=++++=,(当且仅当1ab ab=时,取等号), ②222222a b a b a b +++=+,(当且仅当22a b a b +=+时,取等号), ③222()(2)422a b ab a b ab a b ab a b +++=++,(当且仅当22a b abab a b+=+时,取等号), 综上可知,①>②,③>②,但①和③不能确定大小. 故选D .10.(2020•葫芦岛模拟)若圆22(2)(1)5x y -+-=关于直线10(0,0)ax by a b +-=>>对称,则21a b+的最小值为( )A .4B .C .9D .【答案】C【解析】由题意可知,圆心(2,1)在直线10ax by +-=, 则21a b +=, 又因为0a >,0b >, 所以212122()(2)5549b a a b a b a b a b+=++=+++=, 当且仅当22b a a b =且21a b +=即13a =,13b =时取等号,此时取得最小值9. 故选C .11.(2020•韶关二模)已知0x >,0y >,且121x y+=,则2x y +的最小值是( ) A .7 B .8C .9D .10【答案】C【解析】根据题意,若0x >,0y >,且121x y+=, 则122222(2)()552549y x x y x y x y x y +=++=+++⨯=+=, 当且仅当3x y ==时,等号成立, 故2x y +的最小值是9; 故选C .12.(2020•诸暨市模拟)已知22log (4)2log a b +=,则a b +的最小值是( )A .2B 1C .94D .52【答案】C【解析】222log (4)2log log (4)a b ab +==, 44a b ab ∴+=,且0a >,0b >,∴144b a+=, 则11414149()()(5)(25)4444a b a a b a b b a b a b a +=++=+++=;当且仅当244a b a b ab =⎧⎨+=⎩即3234a b ⎧=⎪⎪⎨⎪=⎪⎩时取=,则a b +的最小值是94, 故选C .13.(2020•湘潭四模)直线220(0,0)ax by a b +-=>>过函数1()11f x x x =++-图象的对称中心,则41a b +的最小值为( ) A .9 B .4C .8D .10【答案】A【解析】函数1()11f x x x =++-图象的对称中心为(1,2),所以1a b +=, 41414()()415249b a a b a b a b a b +=++=++++=,当且仅当223a b ==时等号成立; 故选A .14.(2020•重庆模拟)已知a ,0b >,22a b +=,则1b a b+的取值范围是( ) A .(0,)+∞ B .[2,)+∞ C .1,)+∞ D.)+∞【答案】C【解析】a ,0b >,22a b +=,∴21211222b a bb a b a a b a b a b++=+++=, 当且仅当2b aa b=,即2a =,2b =时等号成立, 故选C .15.(2020•滨海新区模拟)已知正实数a ,b 满足1a b +=,则2241a b a b+++的最小值为( ) A .13 B .11C .10D .9【答案】C【解析】由224141411a b a b a b a b a b+++=+++=++ 1a b +=,∴414144()()5259b a b a a b a b a b a b a b +=++=++⨯=,当且仅当13b =,23a =时取等号. ∴2241a b a b+++的最小值为9110+= 故选C .16.(2020•河东区一模)已知实数a 、b ,0ab >,则22224aba b a b +++的最大值为( )A .16B .14C .17D .6【答案】A【解析】由于2220a b ab +>, 所以222222424ababa b a b ab a b +++++,故:22114246222ab ab a b ab ababab==+++++,(当且仅当a b =时,等号成立). 故选A .17.(2020•辽阳二模)已知0a >,0b >,32a b ab +=,则23a b +的最小值为( ) A .20 B .24 C .25 D .28【答案】C【解析】因为0a >,0b >,32a b ab +=,所以321b a+=,则32666623()(23)1321325a b a a b a b b a b a b +=++=++⨯=,当且仅当5a b ==时,等号成立. 故选C .18.(2020•大连一模)已知0a >,0b >,111a b+=,则a b +的最小值为( ) A .14B .12C .2D .4【答案】D 【解析】111a b+=, 11()()112214b aa b a b a b a b∴+=+⨯+=++++=,当且仅当b aa b=时等号成立, a b ∴+的最小值为4.故选D .19.(2020•浙江模拟)对于0c >,当非零实数a ,b 满足224240a ab b c -+-=,且使|2|a b +最大时,345a b c-+的最小值为( )A .12-B .12C .2-D .2【答案】C【解析】224240a ab b c -+-=, ∴2215()4416c b a b =-+,由柯西不等式得,22222215[()][2][2()]|2|416415b ba b a b a b -++-+=+ 故当|2|a b +最大时,有4462b a -=, 32a b ∴=,210c b =, ∴22234534511211()(2)2310222a b c b b b b bb -+=-+=-=--, 12b =时,取得最小值为2-. 故选C .20.(2020•吉林模拟)若24loglog 1x y +=,则2x y +的最小值为( )A .2B .C .4D .【答案】C【解析】因为2224444log log log log log ()1x y x y x y +=+==, 24(0,0)x y x y ∴=>>,则2224x y x y +=,当且仅当22x y ==时等号成立,则2x y +的最小值为4.故选C .21.(2020•天津二模)已知0x >,0y >,23x y +=,则2x y xy +的最小值为__________.【解析】因为0x >,0y >,23x y +=,则21211212333333xy x x x y x y x xy y x y x y x yx ++=+=+⨯=+++=,当且仅当23x y y x ==x =y =时取等号,。
基本不等式及应用

基本不等式及应用的实际应用情况背景介绍基本不等式是数学中常见的一类不等式,它们可以帮助我们描述和解决各种实际问题,从而在许多领域中发挥着重要作用。
基本不等式包括线性不等式、二次函数不等式和绝对值不等式等。
在实际应用中,我们经常需要根据给定的条件和目标,通过建立和求解基本不等式来得到满足特定条件的解集。
应用过程下面将分别介绍线性不等式、二次函数不等式和绝对值不等式的应用过程及效果。
1. 线性不等式线性不等式是形如ax + b > 0或ax + b < 0的一次方程组,其中a、b为已知系数,x为未知数。
线性不等式在实际应用中广泛存在,例如:a. 生产问题假设某工厂生产两种产品A和B,并且单位时间内生产A产品所需的材料成本为10元,生产B产品所需的材料成本为20元。
如果工厂每天最多能使用500元购买原材料,而单位时间内生产A产品利润为5元,生产B产品利润为8元。
我们需要确定每种产品的最大生产量,以最大化利润。
设A产品的生产量为x,B产品的生产量为y。
根据题目中的条件,我们可以列出以下不等式:10x + 20y ≤ 500 (材料成本限制)5x + 8y ≥ 0 (利润要求)通过求解这个线性不等式组,我们可以得到A和B产品的最大生产量,从而实现最大化利润。
b. 资金问题假设某人有两个银行账户A和B,在一段时间内账户A每天存款增加10元,账户B 每天存款增加15元。
如果初始时两个账户的余额分别为1000元和2000元,并且他希望在一定时间后至少有6000元的总余额。
我们需要确定这个时间段内至少需要存款多少天。
设经过x天后,账户A和B的余额分别为a和b。
根据题目中的条件,我们可以列出以下不等式:a = 1000 + 10xb = 2000 + 15x a + b ≥ 6000通过求解这个线性不等式组,我们可以得到至少需要存款多少天才能达到目标总余额。
2. 二次函数不等式二次函数不等式是形如ax^2 + bx + c > 0或ax^2 + bx + c < 0的二次方程,其中a、b、c为已知系数,x为未知数。
2024年高考数学----基本不等式及不等式的应用
成立仅用来验证最值是否能取到,不能用来求值.
3.一个重要的不等式链条:
1
2
1
≤
ab ≤ a b ≤
2
a2 b2
(a>0,b>0)
2
ab
上述链条中的任意两个中有将“和式”转化为“积式”或将“积式”
转化为“和式”的放缩功能,并且有很多不同的变形,如:a2+b2≥2ab, a b
2
≤
a2
2
b2
2)a+b≥2 ab (a>0,b>0),当且仅当a=b时取等号.
3)ab≤
a
2
b
2
(a,b∈R),当且仅当a=b时取等号.
4)a+ 1 ≥2(a>0),当且仅当a=1时取等号;a+ 1 ≤-2(a<0),当且仅当a=-1时取
a
a
等号.
注意:运用基本不等式及其变形时,一定要验证等号是否成立.另外,等号
4
注意:1.求最值时要注意三点:“一正”“二定”“三相等”.所谓“一 正”是指两数均为正数,“二定”是指应用基本不等式求最值时,和或积 为定值,“三相等”是指必须满足等号成立的条件. 2.连续使用基本不等式时,等号要同时成立.
综合篇
考法 不等式的恒成立、能成立、恰成立等问题的解题策略 1.恒成立问题:若f(x)在区间D上存在最小值,则不等式f(x)>A在区间D上恒 成立⇔f(x)min>A(x∈D); 若f(x)在区间D上存在最大值,则不等式f(x)<B在区间D上恒成立⇔f(x)max< B(x∈D). 2.能成立问题:若f(x)在区间D上存在最大值,则在区间D上存在实数x使不 等式f(x)>A成立⇔f(x)max>A(x∈D); 若f(x)在区间D上存在最小值,则在区间D上存在实数x使不等式f(x)<B成 立⇔f(x)min<B(x∈D). 3.恰成立问题:不等式f(x)>A恰在区间D上成立⇔f(x)>A的解集为D;不等式 f(x)<B恰在区间D上成立⇔f(x)<B的解集为D.
不等式讲基本不等式及其应用课件pptx

在实数域上,柯西-施瓦茨不等式是一个基本的不等式, 它在线性代数和数学分析中都有重要的应用。
范德蒙公式
范德蒙公式是柯西不等式的推广,它在线性代数和概率论 中都有重要的应用。
排序不等式的推广
排序不等式是一种重要的组合不等式,它在线性代数、概 率论和统计学中都有广泛的应用。对排序不等式进行扩展 和推广,可以得到更为广泛和深刻的不等式。
排序不等式的证明
通过构造一个满足排序不等式的数组 ,利用数学归纳法和排序不等式的性 质得出。
排序不等式的应用
在优化、经济、计算机科学等领域有 广泛应用。
03
基本不等式的应用
最大值与最小值的求法
代数法
利用基本不等式,结合代数变形技巧,求出函数 的最值。
三角法
利用基本不等式,结合三角函数性质,求出函数 的最值。
在最大利润问题中,常常需要利用基本不等式来建立数学模型,通过优化资源配 置或制定合理价格策略来达到最大利润。例如,在投资组合理论中,利用基本不 等式可以确定最优投资组合比例,使得投资组合的期望收益最大。
资源分配问题
总结词
通过基本不等式,合理分配资源,实现整体效益最大化。
详细描述
在资源分配问题中,常常需要利用基本不等式来确定资源的 分配比例,以实现整体效益最大化。例如,在电力系统规划 中,可以利用基本不等式来确定各地区的电力分配比例,以 保证整个系统的稳定性和可靠性。
基本不等式的形式
算术平均数与几何平均数
算术平均数:一组数的和除以这组数的个数。 算术平均数不总是大于或等于几何平均数。
几何平均数:两个正数的乘积的平方根。 当且仅当两数相等时,算术平均数等于几何平均数。
柯西不等式
柯西不等式
基本不等式及其应用(优秀经典专题及答案详解)

(1)基本不等式成立的条件:a >0,b >0.(2)等号成立的条件:当且仅当a =b .知识点二几个重要的不等式(1)a 2+b 2≥2ab (a ,b ∈R);(2)b a +a b ≥2(a ,b 同号);(3)ab ≤⎝⎛⎭⎫a +b 22(a ,b ∈R);(4)⎝⎛⎭⎫a +b 22≤a 2+b 22(a ,b ∈R);(5)2ab a +b ≤ab ≤a +b 2≤ a 2+b 22(a >0,b >0).知识点三算术平均数与几何平均数设a >0,b >0,则a ,b 的算术平均数为a +b 2,几何平均数为ab ,基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数.知识点四利用基本不等式求最值问题已知x >0,y >0,则(1)如果xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2p (简记:积定和最小).(2)如果x +y 是定值q ,那么当且仅当x =y 时,xy 有最大值是q 24(简记:和定积最大).【特别提醒】1.此结论应用的前提是“一正”“二定”“三相等”.“一正”指正数,“二定”指求最值时和或积为定值,“三相等”指等号成立.2.连续使用基本不等式时,牢记等号要同时成立. 考点一利用基本不等式求最值【典例1】(江西临川一中2019届模拟)已知x <54,则f (x )=4x -2+14x -5的最大值为_______ 【答案】1【解析】因为x <54,所以5-4x >0, 则f (x )=4x -2+14x -5=-⎝⎛⎭⎫5-4x +15-4x +3≤-2+3=1.当且仅当5-4x =15-4x ,即x =1时,取等号. 故f (x )=4x -2+14x -5的最大值为1. 【方法技巧】【方法技巧】1.通过拼凑法利用基本不等式求最值的实质及关键点通过拼凑法利用基本不等式求最值的实质及关键点拼凑法就是将相关代数式进行适当的变形,通过添项、拆项等方法凑成和为定值或积为定值的形式,然后利用基本不等式求解最值的方法.拼凑法的实质是代数式的灵活变形,拼系数、凑常数是关键.2.通过常数代换法利用基本不等式求解最值的基本步骤通过常数代换法利用基本不等式求解最值的基本步骤(1)根据已知条件或其变形确定定值(常数);(2)把确定的定值(常数)变形为1;(3)把“1”的表达式与所求最值的表达式相乘或相除,进而构造和或积为定值的形式;的表达式与所求最值的表达式相乘或相除,进而构造和或积为定值的形式;(4)利用基本不等式求解最值.利用基本不等式求解最值.【变式1】(山东潍坊一中2019届模拟)已知x >0,y >0,x +3y +xy =9,则x +3y 的最小值为________.【答案】6【解析】由已知得x +3y =9-xy ,因为x >0,y >0,所以x +3y ≥23xy ,所以3xy ≤⎝⎛⎭⎫x +3y 22,当且仅当x =3y ,即x =3,y =1时取等号,即(x +3y )2+12(x +3y )-108≥0. 令x +3y =t ,则t >0且t 2+12t -108≥0,得t ≥6,即x +3y 的最小值为6.【方法技巧】通过消元法利用基本不等式求最值的策略【方法技巧】通过消元法利用基本不等式求最值的策略当所求最值的代数式中的变量比较多时,通常是考虑利用已知条件消去部分变量后,凑出“和为常数”或“积为常数”,最后利用基本不等式求最值.,最后利用基本不等式求最值.考点二 利用基本不等式解决实际问题【典例2】【2019年高考北京卷理数】年高考北京卷理数】李明自主创业,李明自主创业,李明自主创业,在网上经营一家水果店,在网上经营一家水果店,在网上经营一家水果店,销售的水果中有草莓、销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x 元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.①当x =10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;元;②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x 的最大值为__________.【答案】①130 ;②15.【解析】(1)x=10,顾客一次购买草莓和西瓜各一盒,需要支付60+80-10=130元.(2)设顾客一次购买水果的促销前总价为y 元,120y <元时,李明得到的金额为80%y ⨯,符合要求.120y ≥元时,有()80%70%y x y -⨯≥⨯恒成立,即()87,8yy x y x -≥≤,即min 158y x ⎛⎫≤= ⎪⎝⎭元,所以x 的最大值为15。
基本不等式和其应用

由题意,先局部运用基本不等式,再利用不等式的性质即可得证. 证明 ∵x>0,y>0,z>0,
∴xy+xz≥2 xyz>0,xy+yz≥2 yxz>0,
xz+yz≥2 zxy>0,
∴xy+xz xy+yzxz+yz≥8
yz· xz· xyz
xy=8.
当且仅当 x=y=z 时等号成立.
主页
利用基本不等式证明不等式是综合法证明不等式的一种情况,证 明思路是从已证不等式和问题的已知条件出发,借助不等式的性 质和有关定理,经过逐步的逻辑推理最后转化为需证问题.
(1)依题意,得(x+1)(2y+1)=9, ∴(x+1)+(2y+1)≥2 x+12y+1=6, 即 x+2y≥4.
当且仅当xx+ +12= y+22y+xy=1,8, 即xy==12, 时等号成立. ∴x+2y 的最小值是 4. (2)∵a>b>0,∴b(a-b)≤b+2a-b2=a42, 当且仅当 a=2b 时等号成立.
以上三个小题都不具备应用基本不等式求最值的三个条件,可将 负数转化为正数,通过添项、拆项或变系数,使其积(或和)转化 为定值.
主页
解 (1)∵x<0,∴-x>0, ∴f(x)=2+4x+x=2--4x+-x.
∵-4x+(-x)≥2 4=4, 当且仅当-x=-4x,即 x=-2 时等号成立. ∴f(x)=2--4x+-x≤2-4=-2, ∴f(x)的最大值为-2. (2)∵x>1,∴x-1>0, ∴f(x)=x+x-1 1=x-1+x-1 1+1 ≥2 x-1·x-1 1+1=2+1=3.
主页
代入①式得,a=160,从而 b=180, 即当 a=160,b=180 时,S 取得最大值. ∴铝合金窗的宽为 160 cm,高为 180 cm 时,可使透光部分的面 积最大.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第48课基本不等式及其应用(二)
(本课对应学生用书第104-105页)
自主学习回归教材
1. 基本不等式的应用
(1) 研究函数的性质;
(2) 求解最值问题;
(3) 确定参数的取值范围;
(4) 解决实际问题.
2. 基本不等式的综合应用
三角函数、数列、立体几何、解析几何中的最值问题.
3. 解不等式的问题的一般步骤
(1) 分析题意;
(2) 建立数学模型;
(3) 解决数学问题;
(4) 检验作答.
1. (必修5P91习题3改编)函数y=x+4
x(x≠0)的值域为.
[答案](-∞,-4]∪[4,+∞)
[解析]分x>0与x<0两种情况讨论,再结合基本不等式求解.
2. (必修5P91习题4改编)已知函数y=tan θ+cos
sin
θ
θ,θ∈
,
2
π
π
⎛⎫
⎪
⎝⎭,那么函数y的最大值
为. [答案]-2
[解析]因为θ∈
,
2
π
π
⎛⎫
⎪
⎝⎭,所以sin θ>0,cos θ<0,
sin
cos
θ
θ<0,y=tan θ
+cos
sin
θ
θ=-
--
sin cos
cos sin
θθ
θθ
⎛⎫
⎪
⎝⎭≤-2,当且仅当sin θ=-cos θ,即θ=
3
4
π
时取等号.
3. (必修5P90例3改编)过定点P(1,2)的直线在x轴与y轴的正半轴上的截距分别为a,b,则ab的最小值为.
[答案]8
[解析]设直线方程为x
a+
y
b=1,则
1
a+
2
b=1≥
,所以ab≥8,所以ab的最小值为8,当
且仅当1
a=
2
b,即a=2,b=4时取等号.
4. (必修5P91习题3改编)函数
2
的最小值为.
[答案]5 2
[解析]
2
,设
(t≥2),易知y=t+
1
t在[2,+∞)上单
调递增,所以当t=2,
=2,x=0时,y
min
=
5
2.
5. (必修5P90练习1改编)已知(m-2)(n-1)=4,且m>2,n>1,那么m+n的最小值是.
[答案]7
[解析]由(m-2)(n-1)=4,得m=4-1n +2,所以m+n=4-1n +2+n=4
-1n +(n-1)+3≥+3=7(当且仅当n=3时取等号),故m+n 的最小值为7.。
