气体在多孔气体中的扩散
一、孔扩散

Reaction Engineering)
西南科技大学
§6-3 气体在多孔介质中的扩散 一、孔扩散
当0.01< <10时,为过渡区扩散,扩散系数为: 1 DA , 扩散系数D DA 1 by A 1 Dk A DAB
个方面进行修正,一方面实际的扩散距离远大于扩散的表观距离; 另一方面颗粒除了孔隙还有骨架,骨架部分没有扩散。
p Di Dei m
τm--曲析因子,一般由实验测定,在3-5之间; εp—孔隙所占的分率(如果颗粒内各相同性的话)。
化学反应工程(Chemical
Reaction Engineering)
其中, NA,NB--气体A,B的扩散通量, yA为A的摩尔分率。
当NA= -NB 时(等分子扩散)
化学反应工程(Chemical
Reaction Engineering)
西南科技大学
§6-3 气体在多孔介质中的扩散
二、颗粒内的扩散
di N i Dei dZ
Dei为组分I的有效扩散系数。与孔扩散系数相比,需要对两
西南科技大学
§6-3 气体在多孔介质中的扩散 一、孔扩散
当
≤0.01时,属于正常的扩散--孔内扩散于气体的自由
扩散差别不大,与孔直径无关,扩散系数同DAB(分子扩散系 数,查手册、估 算或通过实验得到) 当 ≥10时,称为努森扩散--气体与孔壁碰撞的机会
远远大于分子之间的碰撞机会。此时的扩散系数为努森扩 散系数,可以表示
chapterⅥ 多相系统中的化学反应与传递模型
第三节 气体在多孔介质中的扩散 一、孔扩散
当孔内外无压差时,没有层流流动问题。当 有浓度差存在时,有组分的扩散存在。使用费克
多孔材料的载气效应与传质性能

多孔材料的载气效应与传质性能多孔材料是一类由许多微小孔隙组成的材料,其表面积较大,孔隙结构丰富。
这些孔隙可以用于吸附和储量气体,因此多孔材料在各种领域中都得到了广泛应用。
在多孔材料中,载气效应是一个重要的性能指标。
载气效应是指材料中吸附和储气的能力。
多孔材料的载气效应受到许多因素的影响,包括孔隙大小、孔隙结构、材料表面性质等。
孔隙大小会影响气体分子在材料中的扩散速率,较小的孔隙会增加气体分子与材料表面接触的机会,从而提高吸附和储气能力。
孔隙结构则决定了气体分子在材料中的运动路径,复杂的孔隙结构可以提供更多的吸附位点,增加载气量。
材料表面性质是影响吸附和储气的关键因素之一,较大的比表面积可以提供更多的吸附位点,从而增加载气量。
多孔材料的传质性能与其载气效应密切相关。
传质性能是指物质在材料中的扩散速率。
多孔材料的孔隙结构决定了物质在材料中的扩散路径和速率。
较小的孔隙可以提供更长的扩散距离,从而减缓物质的扩散速率。
另外,孔隙结构的连通性也会影响物质的传质性能。
如果孔隙之间存在良好的连通性,物质可以通过孔隙网络进行扩散,传质速率将会更快。
多孔材料的载气效应和传质性能也与其应用领域密切相关。
例如,在储氢材料领域中,多孔材料的载气效应和传质性能对储氢系统的性能至关重要。
高载气效应可以增加储氢量,提高储氢系统的能力。
同时,良好的传质性能可以提高氢气的释放速率,从而提高储氢系统的效率。
在吸附材料领域,多孔材料的载气效应和传质性能对分离和纯化过程的效率和能耗有着重要影响。
较高的载气效应可以增加吸附材料对目标物质的吸附和储存能力,从而提高分离纯化过程的效率。
良好的传质性能可以减少物质在吸附材料中的滞留时间,降低能耗。
综上所述,多孔材料的载气效应和传质性能是影响其应用性能的重要指标。
孔隙大小、孔隙结构和材料表面性质是影响载气效应的关键因素,而孔隙结构和连通性是影响传质性能的重要因素。
多孔材料的载气效应和传质性能对储氢、吸附分离等领域的应用具有重要意义。
多孔材料中的微介孔结构对气体分子扩散的影响研究

多孔材料中的微介孔结构对气体分子扩散的影响研究多孔材料是一类具有高度孔径可调制和内外表面可调性能的复杂材料,其应用领域广泛,比如吸附、催化、分离、储能等。
在上述应用领域中,多孔材料的孔道结构是决定其性能的重要因素之一。
而在气体分子扩散这一方面,多孔材料中的微介孔结构更是对气体分子扩散起到了决定性的影响。
在多孔材料中,孔道的大小、形状、布局以及连通性都会影响气体分子传输的性质。
通常来说,孔径越小,对小分子的拦截就越彻底;孔径越大,对大分子的影响就越大。
而形状不同的孔道也会对分子传输的过程有所影响。
比如在一些分类酸或碱的多孔材料中,它们中心的多面体孔道能在大分子和小分子之间形成一个有效的分离通道,这意味着在孔道内,有选择性地分离不同大小的分子。
“柿子井”就是一种典型的多面体孔道结构,可以利用其通道的形状和大小,对不同大小的气体分子进行选择性的传输。
此外,多孔材料中微介孔的连通性也将会影响气体分子的扩散。
当多孔材料中随机分布的孔道连接在一起,且整个材料中形成一个大的孔结构网络时,气体分子的扩散速率就会显著提高。
因此,在多孔材料中,微介孔的孔径大小和孔道布局的优化是尤为重要的工作,有助于提高材料的气体传输性能。
最后,值得一提的是,多孔材料中微介孔的孔隙率也会对材料的气体传输性能发挥重要作用。
在微介孔结构的孔隙率较低时,沉积在孔道内的分子将会形成一种表面吸附状态,从而降低传输速率。
这时候,合适的孔隙率设计可以使异相反应在孔结构内得到更好的加速和控制。
总的来说,多孔材料中微介孔结构对气体分子扩散的影响非常重要,而多孔结构的微介孔大小、形状、布局、连通性和孔隙率设计则是优化材料气体传输性能的重要途径。
同时,这也展示了在材料设计和预测材料性能时,研究孔道结构的重要性和实用性。
多尺度分形多孔介质气体有效扩散系数的数学模型

多尺度分形多孔介质气体有效扩散系数的数学模型牟新竹;陈振乾【摘要】基于毛细管束假设和分形理论,建立了一种计算多孔介质中气体有效扩散系数的数学模型.利用分形几何理论,引入孔隙面积分形维数、孔道迂曲度分形维数以及孔隙连通性等参数定量表征多孔介质中真实的内部结构,构建出多孔介质、多尺度孔隙结构的分形模型,系统地研究了多孔介质中不同尺度孔隙下的气体扩散过程,推导出了分形多孔介质气体有效扩散系数模型,并分析讨论了多孔介质微结构参数对气体有效扩散系数的影响.研究结果表明,气体有效扩散系数随着平面孔隙度的增大而近似呈线性增加,孔隙面积分形维数与气体有效扩散系数呈正相关,而孔道迂曲度分形维数与气体有效扩散系数呈负相关;不同孔隙度情况下,气体有效扩散系数随着孔隙最小/最大直径比的变化趋势不同,孔隙连通性越强的多孔介质,气体有效扩散系数越大.【期刊名称】《东南大学学报(自然科学版)》【年(卷),期】2019(049)003【总页数】7页(P520-526)【关键词】多孔介质;分形;气体扩散;多尺度【作者】牟新竹;陈振乾【作者单位】东南大学能源与环境学院,南京210096;东南大学能源与环境学院,南京210096【正文语种】中文【中图分类】TK121多孔介质中的气体扩散是许多学科和工程领域的一个基本问题,其有效扩散系数的大小对多孔介质中热质传递过程至关重要.气体有效扩散系数模型通常包含经验和拟合常数,但模型中很少提供详细的多孔介质结构信息[1].稳态条件下,气体扩散遵循Fick扩散规律[2].气体在多孔介质孔隙中的扩散过程,主要受其内部孔隙形态学特征的影响.孔隙形态的复杂多变导致了不同的传输机制下的扩散过程,在同一多孔介质内部的质量传递过程中,气体扩散主要包括容积扩散、努森扩散和过渡区扩散[3-4].因此,在研究多孔介质中气体的质量扩散时,需充分考虑到其形态学特征,从常规尺度到微纳米尺度,将各种尺度下的气体扩散过程细化分析,从而得到气体的有效扩散系数.大多数随机和无序的多孔介质都具有分形特征,这些介质通常被称为分形多孔介质,利用分形几何理论描述多孔介质被认为是一种可靠有效的方法[5-8].Zhang[9]基于分形理论构建了包含宏观及微观结构的多孔介质气体输运模型,同时考虑了泊肃叶流和努森流2种机制,并根据达西定律计算了有效渗透率;Cao等[2]对分形多孔介质中气体扩散进行了一系列数值研究,并通过数据拟合的方式提出了一种气体扩散系数的表达式;Zheng等[1]基于分形毛细管束模型,利用前人总结的各种机制下的扩散系数模型,分析了分子扩散和努森扩散2种机制共存下的气体扩散,推导了一种新的气体有效扩散系数模型;熊建银等[10]基于压汞实验数据,通过对建材的微观结构进行提炼,提出了预测建材中VOC扩散系数的宏观-介观两尺度模型;Shou等[11]考虑了气体在分子扩散区、努森扩散区以及过渡区的气体输运机制,提出了气体通过微纳米级纤维多孔材料的气体扩散分形模型;基于分形理论,Xiao等[12]推导出了多孔纳米纤维中气体扩散系数的解析模型.Xu等[13]提出了燃料电池中多孔介质气体扩散的多尺度分形模型,其中微尺度和纳米尺度的孔隙中存在分子扩散和努森扩散2种机制.综上所述,尽管目前有一些修正模型能够描述多尺度下的多孔介质中气体扩散过程,但是通常存在包含经验常数、微观扩散机理考虑不完全等问题.由于多孔介质内部结构的异质性和随机性,因此,本文根据多孔介质微观孔隙结构特征,利用分形理论,构建出多孔介质多尺度孔隙结构的分形模型,研究了多孔介质中不同尺度孔隙下的气体扩散过程,推导出了分形多孔介质气体有效扩散系数模型,并分析了多孔介质微结构参数对气体有效扩散系数的影响.1 多孔介质孔隙结构特性1.1 孔隙大小分布的分形特性本文假设多孔介质是由一束弯曲且平行的、同时存在一定连通性的毛细管组成,圆形毛细管横截面积变化沿气体扩散方向平滑过渡,如图1所示.在同一横截面内,多孔介质中的孔隙分布具有分形特性[14-15],在多孔介质中,所有毛细管/孔隙的入口和出口分别位于同一平面.图1 多孔介质结构示意图多孔介质中毛细管/孔隙的大小分布遵循分形标度规律,孔隙的累计数目N与孔隙直径λ服从如下标度关系[16]:(1)式中,λmax为孔隙最大直径,m;Df为孔隙面积分形维数.孔隙直径在(λ,λ+dλ)范围内的孔隙数目dN可表示为(2)式中,-dN>0表示孔隙数目随着孔径的减小而增大.由于截面上的孔隙可以看成是不同直径λ的圆,因此可以通过式(2)利用微元法得到多孔介质截面上的总孔隙面积Ap,即Ap(3)式中,λmin为孔隙最小直径.同时,可以得到多孔介质截面总面积A为(4)式中,ε为平面孔隙度.1.2 孔隙的连通性在多孔介质中,不同的孔隙之间是相互连通的,孔隙的连通性是多孔介质孔隙空间形态的重要形态学特征.多孔介质中的传质过程受孔隙的连通性影响很大,相同孔隙率、相同孔隙分布的多孔介质其扩散系数差异也可能很大,多孔介质连通性越好,扩散系数越大.在本文中,孔隙的连通性分布假设遵循Gaussian(正态)分布[17],孔隙连通性概率密度公式为(5)式中,∂c为分布的相对比例常数;c为连通数,定义为在同一孔道上与其他孔道连通的数目,c>2;cm为孔隙的平均连通数;σc为连通数的标准差.如图2所示,连通数的变化会引起孔隙连通性的变化,进而影响组分的扩散,但并不会引起分形维数的变化.(a) c=3 (b) c=4 (c) c=5图2 不同孔隙连通数示意图1.3 孔道迂曲度的分形特性在分形多孔介质中,采用横截面积平滑变化的弯曲毛细管来模拟气体通道,弯曲毛细管的长度L(λ)与直径λ服从如下分形关系[16]:(6)式中,L0为毛细管沿扩散方向的特征长度;Dt为孔道迂曲度分形维数,在二维空间内,1<Dt<2.Dt=1表示一根直毛细管;Dt越大,毛细管越弯曲;Dt=2对应一根非常曲折的毛细管充满整个二维平面.孔隙通道的迂曲度定义为τ=L(λ)/L0,将之代入式(6),孔道迂曲度可以写成(7)式中,τ>1.迂曲度描述了多孔介质内部流动所通过路径的弯曲程度.2 气体有效扩散系数的数学模型目前对多孔介质中气体扩散的研究大部分只涉及一种扩散类型.对于分形多孔介质中的气体扩散问题,应以多孔介质内部复杂的孔隙结构为重点,根据孔隙结构的不同尺度,对气体扩散机理进行分类研究.多孔介质中气体扩散主要有容积扩散、努森扩散和过渡区扩散3种.在不同孔隙结构中可以通过努森数Kn的大小来判断主导机制,Kn定义为空间特征长度与气体分子自由行程之间的比值,即(8)式中,l为气体分子自由行程,其中,kB为玻尔兹曼常数,kB=1.380 6×10-23J/K;T为温度,K;p为压力,Pa;d为气体分子直径,m.当Kn<0.1时,即孔隙直径λ大于气体分子自由行程l,气体扩散完全是由不受壁面作用的分子无规则运动引起的,气体分子之间的碰撞为主要过程,此时黏滞流占主导地位,在这种扩散机制的作用下,气体扩散属于容积扩散.流体通过单个孔的流量qp可以通过Hagen-Poiseulle公式表示为(9)式中,Δp为气体在毛细管中的压力差,Pa;μ为气体黏性系数,Pa·s.当Kn>10时,即孔隙直径λ小于气体分子自由行程l,气体分子与孔壁之间的碰撞为主要过程,因而努森扩散为主导机制.单个孔内的气体流量qk可表示为(10)式中,M为气体的分子质量,kg/mol;R为气体常数,R=8.314 J/(mol·K);pm 为平均扩散压力,Pa.当0.1<Kn<10时,多孔介质的孔隙直径与气体分子自由行程较为接近,气体扩散机制较为复杂,不再受单一的扩散机制主导控制,而是同时存在2种扩散流动,气体扩散属于过渡区扩散,通过单个孔的气体流量qpk可表示为(11)从多孔介质的形态学特征分析中可以看出,分形多孔介质中各种尺寸大小的孔隙均存在,因此以上3种扩散情形会同时发生,气体以扩散形式通过多孔介质横截面的总流量Q为(12)式中,λk=0.1l,λp=10l分别为努森扩散和容积扩散机制条件下的临界直径.联立式(9)~(12),可得(13)根据Fick定律,气体通过多孔介质的总流量为(14)式中,Deff为有效扩散系数,m2/s;ΔC为孔道两端的浓度差,ΔC=Δp/(RT).联立式(13)和(14),可得分形多孔介质中气体有效扩散系数Deff为(15)式(15)是基于多尺度多孔介质的分形标度特征以及毛细管束假设,根据孔隙大小分布分形特性、孔隙连通性、孔道迂曲度分形特性求出了不同努森数范围内的气体有效扩散系数计算模型.模型中的每一个参数都具有清晰的物理意义,适用于研究各向同性均质多孔介质中的单相气体输运过程.气体有效扩散系数模型(15)是孔隙面积分形维数、孔道连通数、孔道迂曲度分形维数、孔隙度、孔隙最小/最大直径比、温度以及临界孔隙直径大小的函数.该数学模型可以揭示在多尺度分形多孔介质中黏滞流和努森扩散主导下的气体扩散的详细机理.3 结果与分析3.1 模型验证在利用式(15)计算气体有效扩散系数的过程中,孔隙面积分形维数Df通过下式计算[18]:(16)式中,DE为欧氏维数,二维空间DE=2,三维空间DE=3,本文主要研究气体在二维平面内的质量扩散,因此取DE=2;ε为平面孔隙度;λmin/λmax为多孔介质中孔隙直径最小值与最大值的比值.多孔介质中孔隙通道迂曲度分形维数可由下式计算[19]:(17)式中,为平均迂曲度;为平均孔隙直径;L0为毛细管沿扩散方向的特征长度.根据文献为体积孔隙率;不同的多孔介质材料具有不同的孔隙尺寸分布,由文献[20]可知,λmin/λmax的平均值约为0.001.因此,在本文的模型预测值计算中,λmin/λmax取0.001.将提出的多尺度分形多孔介质气体有效扩散率模型的预测值与现有的不同多孔介质样本实验数据[21]进行比较.以室温下多孔介质中氢气的有效扩散率的实验数据为基础,Kn数值在0.01~10范围内变化,即气体扩散涉及到努森扩散和容积扩散.样本参数如表1所示.表1 样本参数参数取值λmax/μm90μ/(μPa·s)8.8×10-6p/kPa101.325T/K293d/nm0.274将表1中样本参数代入到式(15)~(17)中,可以计算出气体有效扩散系数Deff.图3为本文建立的气体有效扩散系数模型预测值与Currie[21]的实验数据的对比.从图中可以看出,预测值与实验数据吻合较好,同时可以发现有效扩散系数随着平面孔隙度的增大近似呈线性增加,这是由于孔隙度的增大,气体扩散的有效路径和区域均会增多.从图3中也可以发现,在高孔隙度(>0.65)范围内,分形模型预测值明显小于实验数据,这是因为不同多孔介质样本孔隙尺寸分布差距较大,当孔隙率较高时,本文在模型预测时λmax仍然按照表1取固定值,因此导致了模型预测值与实验数据有所偏差.同时,Df、Dt通过半解析解的形式取值,解析式中的参数通过实验统计得来,存在一定的测量和统计误差.孔隙度、孔隙最小/最大直径比λmin/λmax、孔隙连通性等参数需要大量的实验数据分析得到,也会导致模型预测值存在一定的偏差.图3 模型预测值与实验数据[21]对比3.2 影响因素分析分析多孔介质微观孔隙结构特征参数(孔隙面积分形维数、孔道迂曲度分形维数、孔隙最小/最大直径比、孔隙连通性等)对所建立的气体有效扩散系数模型的影响.图4为孔隙度0.4时气体有效扩散系数Deff随孔隙面积分形维数Df的变化曲线.可以发现,气体有效扩散系数Deff随着孔隙面积分形维数Df的增大而增加.当Df<1.55时,Deff趋于0,这是由于Df较小的情况下,多孔介质的孔隙度非常小,气体扩散阻力相当大使扩散系数非常小;当1.55<Df<1.85时,Deff随着Df的增大而迅速增大;而当Df>1.85时,随着Df的增大,Deff基本保持不变,趋于稳定,这表明当Df增大到一定程度后,Deff达到该环境条件下气体扩散系数的最大值.从图4中还可以看出,孔道迂曲度分形维数越大,气体有效扩散系数越小,这与实际情况是一致的,因为Dt越大,孔道越弯曲复杂,气流在毛细管中的扩散阻力就越大.图4 孔隙面积分形维数Df对气体有效扩散系数Deff的影响图5给出了体有效扩散系数Deff随孔道迂曲度分形维数 Dt的变化情况.从图中可以看出, Deff图5 孔道迂曲度分形维数Dt对气体有效扩散系数Deff的影响随着Dt的增大而单调递减.同时也可以印证,在相同的Dt条件下,孔隙度越大,Deff越大.图6给出了在不同孔隙度条件下(Dt取值为1.1),气体有效扩散系数Deff随着孔隙最小/最大直径比λmin/λmax的变化情况.按照表1,假设λmax=90 μm,通过改变λmin值来调整λmin/λmax的大小.可以发现,不同的孔隙度情况下,Deff的变化趋势不同,当孔隙度ε<0.5时,随着λmin/λmax的增加,Deff先迅速增大,当λmin/λmax>0.01时,Deff逐渐减小;而当孔隙度ε>0.5时,随着λmin/λmax的增加,Deff一直增大,但λmin/λmax>0.01时,增速明显减缓.造成这种现象的原因可能是,在较小孔隙度的情况下,随着λmin/λmax的增大,根据式(16)可知,Df逐渐减小,但Df减小的幅度先慢后快,前期Df减小的幅度对Deff的影响较小,而随着λmin/λmax的增大,多孔介质中孔隙平均直径增大导致Deff短暂的增加,而当λmin/λmax持续增大后,Df减小幅度变快,Deff随着Df的急剧减小而降低.因此在实际应用中,不能盲目地通过增大多孔介质孔隙最小/最大直径比的方法来增强其内部的气体扩散.图6 孔隙最小/最大直径比λmin/λmax对气体有效扩散系数Deff的影响图7(a)给出了不同孔隙连通性的情况下,气体有效扩散系数Deff随孔隙度ε的变化情况.通过将模型中孔隙连通性概率密度函数的相对比例常数取不同值,可以定量分析孔隙连通性对Deff的影响.由图7可得,孔隙连通性强的多孔介质,气体有效扩散系数Deff越大,随着孔隙度ε的增大,连通性对Deff的影响越明显,但随着孔道迂曲度分形维数的增大,孔隙连通性的强弱反而对Deff的影响不再显著.这与实际情况是相符的,孔隙度较大时,孔隙连通性越强,气体扩散的阻力会越小,Deff增大的幅度越大;而孔道越弯曲复杂时,尽管孔隙连通性增强了,但气体扩散的阻力仍很大,对于Deff影响微乎其微.(a) 孔隙度ε变化(b) 孔道迂曲度分形维数Dt变化图7 连通性对气体有效扩散系数Deff的影响由上述分析可以看出,本文在毛细管假设的基础上,所建立的多尺度分形多孔介质中气体有效扩散系数模型比传统模型能更好地揭示内部气体扩散的机理.这就意味着如果一种多孔介质可以用分形理论来描述并满足毛细管假设,在研究各向同性均质多孔介质中的单相气体输运过程时,本文所建立的模型可以较为准确地预测其内部的气体有效扩散系数.4 结论1) 气体有效扩散系数Deff随着平面孔隙度ε的增大而近似呈线性增加.同时,气体有效扩散系数Deff随着孔隙面积分形维数Df的增加而增大,随着孔道迂曲度分形维数Dt的增加而减少.2) 不同的孔隙度ε情况下,Deff随着孔隙最小/最大直径比λmin/λmax的变化趋势不同,当孔隙度ε<0.5时,随着λmin/λmax的增加,Deff先迅速增大,当λmin/λmax>0.01时,Deff逐渐减小;而当孔隙度ε>0.5时,随着λmin/λmax的增加,Deff一直增大,但当λmin/λmax>0.01时,增速明显减缓.3) 孔隙连通性强的多孔介质,气体有效扩散系数Deff越大.随着孔隙度ε的增大,连通性对Deff的影响越明显,随着孔道迂曲度分形维数Dt的增大,孔隙连通性的强弱对Deff的影响不再显著.通过对模型的分析研究,可以掌握多孔介质中主导气体扩散强弱因素的影响规律,可应用于燃料电池、纳米多孔材料、化工纺织及生物组织干燥等领域中的气体输运过程,从常规尺度到微纳米尺度的孔隙范围内分析研究气体输运特性和机理.同时,可以帮助人们选取合适的多孔介质材料以达到工程实践目的.例如,可用于选取质子交换膜燃料电池的气体扩散层、设计多孔介质催化剂和催化剂载体.参考文献( References)【相关文献】[1]Zheng Q, Yu B M, Wang S F, et al. A diffusivity model for gas diffusion through fractal porous media[J].Chemical Engineering Science, 2012, 68(1): 650-655.DOI:10.1016/j.ces.2011.10.031.[2]Cao L Y, He R. Gas diffusion in fractal porous media[J]. Combustion Science and Technology, 2010, 182(7): 822-841. DOI:10.1080/00102200903341553.[3]MartíNez L, Florido-DíAz F J, Hernández A, et al. Characterisation of three hydrophobic porous membranes used in membrane distillation : Modelling and evaluation of their water vapour permeabilities[J]. Journal of Membrane Science, 2002, 203(1/2):15-27. [4]Moggridge G D . Diffusion-mass transfer in fluid systems[M]. Cambridge:Cambridge University Press, 1984:13-90.[5]Perfect E. Applications of fractals in soil and tillage research: A review[J]. Soil and Tillage Research, 1995, 36(1/2): 1-20. DOI:10.1016/0167-1987(96)81397-3.[6]Adler P M, Thovert J F. Real porous media: Local geometry and macroscopic properties[J]. Applied Mechanics Reviews, 1998, 51(9):537-585. DOI:10.1115/1.3099022. [7]Yu B M. Analysis of flow in fractal porous media[J]. Applied Mechanics Reviews, 2008, 61(5): 050801. DOI:10.1115/1.2955849.[8]Xu P. A discussion on fractal models for transport physics of porous media[J].Fractals, 2015, 23(3): 1530001. DOI:10.1142/s0218348x15300019.[9]Zhang L Z. A fractal model for gas permeation through porousmembranes[J].International Journal of Heat and Mass Transfer, 2008, 51(21/22): 5288-5295. DOI:10.1016/j.ijheatmasstransfer.2008.03.008.[10]熊建银, 张寅平, 王新轲,等. 多孔建材中VOC扩散系数的两尺度模型[J]. 工程热物理学报, 2008, 29(12):2091-2093.Xiong J Y, Zhang Y P, Wang X K, et al. Two scale model for predicting the VOC diffusion coefficient in porous building materials[J] Journal of Engineering Thermophysics. 2008, 29(12):2091-2093. DOI:10.3321/j.issn:0253-231X.2008.12.030.(in Chinese)[11]Shou D H, Fan J T, Mei M F, et al. An analytical model for gas diffusion though nanoscale and microscale fibrous media[J]. Microfluidics and Nanofluidics, 2014, 16(1/2): 381-389. DOI:10.1007/s10404-013-1215-8.[12]Xiao B Q, Yan H X, Xiao S X, et al. An analytical model for gas diffusion through fractal nanofibers in complex resources[J]. Journal of Natural Gas Science and Engineering, 2016, 33: 1324-1329. DOI:10.1016/j.jngse.2016.05.057.[13]Xu P, Qiu S X, Cai J C, et al. A novel analytical solution for gas diffusion in multi-scale fuel cell porous media[J]. Journal of Power Sources, 2017, 362: 73-79.DOI:10.1016/j.jpowsour.2017.07.015.[14]Yu B M, Lee L J, Cao H Q. Fractal characters of pore microstructures of textile fabrics[J]. Fractals, 2001, 9(2): 155-163. DOI:10.1142/s0218348x01000610.[15]Yu B M, Lee L J, Cao H Q. A fractal in-plane permeability model for fabrics[J]. Polymer Composites, 2002, 23(2): 201-221. DOI:10.1002/pc.10426.[16]Yu B M, Cheng P. A fractal permeability model for bi-dispersed porousmedia[J].International Journal of Heat and Mass Transfer, 2002, 45(14): 2983-2993. DOI:10.1016/s0017-9310(02)00014-5.[17]Segura L A, Toledo P G. Pore-level modeling of isothermal drying of pore networks : Effects of gravity and pore shape and size distributions on saturation and transport parameters[J]. Drying Technology, 2005, 111(2/3):237-252.[18]Yu B M, Li J H. Some fractal characters of porous media[J]. Fractals-complex Geometry Patterns & Scaling in Nature & Society, 2001, 9(3):365-372.[19]Yu B M. Fractal character for tortuous streamtubes in porous media[J]. Chinese Physics Letters, 2005, 22(1): 158-160. DOI:10.1088/0256-307x/22/1/045.[20]Feng Y J, Yu B M, Zou M Q, et al. A generalized model for the effective thermal conductivity of porous media based on self-similarity[J]. Journal of Physics D: Applied Physics, 2004, 37(21): 3030-3040. DOI:10.1088/0022-3727/37/21/014.[21]Currie J A. Gaseous diffusion in porous media. Part 2. Dry granular materials[J].British Journal of Applied Physics, 1960, 11(8): 318-324. DOI:10.1088/0508-3443/11/8/303.。
气体在多孔气体中的扩散
ta n h
6.4.4 内外扩散D都a 有 k影Gk aw响m 时的有效因子
对薄片催化剂
tanh
o
1
kw kG am
ta n h
o
tanh
tanh
1
Bim
传质的拜俄特数,表示外扩散与内扩 散阻力的相对大小
B im
LkG De
12
6.4.4 内外扩散都有影响时的有效因子
17
3、连串反应
A k1 P k2 D
对于一级反应(可推广 到任意正级数反应)
S′
P
rP
rA
k1cA k2cP k1cA
1
k1 k2
cP cA
cP cA
决定了选择性。但
cP cA
在颗粒内各处不同。
由于扩散的影响, cA随着深入颗粒的进程必 然下降,而 cP
比较复杂,可能正好相 反,也可能存在极值,但无论如何
A k1 P C B k2 S W
主反应 副反应
以一级反应为例:
rA k1cA rB k2cB
并且有 k1 > k2
14
6.5 内扩散与复合反应选择性的影响
无扩散影响时,瞬时选择性: 有扩散影响时,瞬时选择性:
SP
rA rB
k1cAS k2cBS
SP
RA RB
1k1cAS 2k2cBS
1tan1h331
8
6.4.2 内扩散有效因子
圆柱催化剂 Vp kp
a p De
d2cA dr2
1dcA r dr
kp De
cA
r Rp, cA cAS r 0, dcA dr0
cA I0
CO_2在多孔介质中扩散系数的测定

第22卷 第4期 石油化工高等学校学报 V ol.22 No.4 2009年12月 JO U RN A L OF PET RO CHEM ICA L U NI VERSIT IES Dec.2009文章编号:1006-396X(2009)04-0038-03CO2在多孔介质中扩散系数的测定郭 彪, 侯吉瑞, 于春磊, 李东东, 林 杨(中国石油大学(北京)教育部重点实验室提高采收率研究中心,北京102249)摘 要: 为了研究注CO2开采原油时CO2在地层中的扩散系数,采用一维扩散的数学模型,利用一维菲克第二定律和连续性方程推导出了CO2扩散系数的计算公式,设计了多孔介质采用露头砂填充,实验模型装置水平放置而消除了 对流扩散的影响,室内测定CO2扩散系数的双测压点的1m长的物理模拟装置,得出了在60!时不同压力下的扩散系数,实验条件更符合矿场实际,研究规律可用于矿场CO2驱过程中的参数优选。
关键词: CO2; 扩散系数; 模型; 一维扩散; 多孔介质; 测定中图分类号: T E357.11 文献标识码:A do i:10.3696/j.issn.1006-396X.2009.04.010Determination of Diffusion Coefficient for CarbonDioxide in the Porous M ediaGUO Biao,H OU Ji-rui,YU Chun-lei,LI Dong-do ng,LIN Yang(E nhanced O il Recover y Resear ch Center,MO E K ey L abor ator y of P etr oleum E ngineer ingin China Univ er sity of P etr oleum,Beij ing102249,P.R.China)Received8December2008;rev is ed5M arch2009;accep ted10S ep tember2009Abstract: T he diffusion co efficient of carbon diox ide in t he fo rmatio n for ex plo red o il by carbon diox ide injected w as researched.T he one-dimension diffusio n equat ion,combined t he second F ike s law and continuity equation w as deduced. T here w er e so me merits:the po ro us media w as stuffed w ith outcro pping sand;the device w as placed ho rizontally,w hich eliminated the convectiv e diffusio n;the simulator is1m,w hich could erase the boundary effect.T he derive the diffusion co efficient for diverse pressur es under the temperature at60!.T he physical simulato r w as packed the outcropping sand, which was much more ag reeable w ith the r ealit y.T he results can be used fo r par amet er o ptimizat ion in the field for CO2 floo ding.Key words: Car bo n dio xide;Diffusion coefficient;M odel;O ne-dimension diffusion;P oro us media;D et erminatioCo rr esponding author.T el.:+86-156********;fax:+86-10-89734612;e-mail:guobiao1982@y 测量气体扩散系数的方法一般说来分为两类:直接法和间接法[1-4]。
分形多孔介质中气体的非稳态扩散
p o r o u s me d i a wi t h d i f f e r e n t p o r e s t r u c t u r e s i s d i f f e r e n t .
Ke y wo r d s: p or o us me d i a; un s t e a d y s t a t e di f f u s i o n; f r a c t a l ;p or e s t r u c t ur e
Ts i n g h u a Un i v e r s i t y, Be i j i n g 1 O 0 0 8 4, C h i n a )
Abs t r a c t : An a v e r a g e mo d i f i e d c oe f f i c i e nt wa s u s e d t o mod i f y Fi c k’ S s e c o nd l a w a nd a t he or e t i c a l e q ua t i on wa s e s t a b l i s he d t o d e s c r i b e u ns t e a d y s t a t e ga s d i f f u s i o n i n f r a c t a l po r o us me di a .The e xp e r i me n t a l s y s t e m
M A Li a n g, HE Ron g
( Ke y La b o r a t o r y f o r T h e r ma l S c i e n c e a n d Po we r En g i n e e r i n g o f Mi n i s t r y o f Ed u c a t i o n,
分形多孔介质的孔隙特性对气体扩散的影响
扩 散 系 数 对 平 均 孔 径 的敏 感 度 ,其值 随 孔 隙 率 的增 大呈 线性 减 小 。
关 键 词 :分 形 ;多 孔 介 质 ;扩 散 ;孔 隙特 性
映 其 固 有 分 形 特 征 。在 此 模 型基 础上 ,根 据 经 典 分 子 动 理 论 建 立 扩 散 控 制 方 程 ,对 气 体 在 多 孑 介 质 中 的 扩 散 进 L 行 数 值 模 拟 。分 析 了 比表 面 积 、平 均 孔 径 、孔 隙 率 等 孔 隙 特 性 参 数 对 扩 散 的 影 响 , 获 得 了 分 形 多 孑 介 质 中气 体 L
第 6 2卷 第 l 期 1 21 0 1年 1 月 1
化
工
学
报
Vo. No 1 62 .11 No m b r 2 ve e O11
CI C J u n l ES o r a
分 形 多 孔 介 质 的 孔 隙 特 性 对 气 体 扩 散 的 影 响
陈永利 ,曹 立 勇 ,何 威 ,何 榕
DOI 0 3 6 /.s n 0 3 — 1 7 2 1 . 1 0 7 :1 . 9 9 j is . 4 8 1 5 . 0 1 1 . 0
中 图 分 类 号 :0 5 2 2 5 .
文 献 标 志 码 :A
文 章 编 号 :0 3 —1 5 ( 0 1 1 —3 2 一 O 48 17 21) 1 O4 6
ቤተ መጻሕፍቲ ባይዱ
( yL b r tr o h r l ce c n o rE g n e ig o i i r f E u ain, Ke a oa o y f rT ema i ea d P we n ie r f M ns y o d c t S n n t o
混合气体在典型多孔介质内扩散过程的数值模拟
b t e H4 ArH2d r g df s n i o o sme i ewenC / / u i i u i n p r u da n f o .Th eut s o h tte df s n o ers l h w t a h i u i f s f o
C Arwi ie t nice s ep r a is e malr h n0 5/ whl tedf H / lr ha raei t o erdu ni i s l a . a l s wi n nh wh t wel tf n mo e o su y t e efc fp r a iso h i u in p o e sa d t e it rc x l S e a d l t d h fe to o e rd u n t ed f so r c s n h n e a ~ - t f to e we n e c p ce fm u c m p n n u i gd fu ini o o sm e i.Th d 1 n h in b t e a h s e iso hio o e td rn i so p r u da f n emo e dt e a n m eia eh d a o t d h r ee v rf d b h x e i e tld t n l e a u e Th n t e u rc l t o d p e e e w r e i e y t e e p rm n a a a i i r t r . m i t e h
混合气体在典型多孔介质内扩散过程的数值模拟111a工况1的模拟结果b工况2的模拟结果三元混合气体在多孔介质内扩散过程的模拟结果a不同时刻ch4的压力分布b不同时刻ch4的摩尔通量分布d不同时刻ar的摩尔通量分布c不同时刻ar的压力分布e不同时刻h2的压力分布f不同时刻h2的摩尔通量分布工况1各组分在不同时刻的压力和摩尔通量分布httpwwwjdxbcnhttp112明显低于两侧这是由于入口区域的ch4首先受到边界条件的影响而向外部扩散并将该区域的部分ar带到外部500s以从而引起该处ar局部压力下降而在10于小分子h2相对ch4扩散较快率先进入孔内拖带未受ch4从而引起内部ar的压力局部升高
气体扩散代理模型
气体扩散代理模型
气体扩散代理模型是一种描述气体在多孔介质中扩散过程的物理模型。
它基于Fick第一定律,即扩散通量与浓度梯度成正比。
在多孔介质中,气体的浓度在不同区域之间存在差异,这种浓度梯度驱动气体从高浓度区域向低浓度区域扩散。
扩散系数是描述气体在多孔介质中扩散能力的重要参数,它与气体的物理性质、多孔介质的特性以及温度等因素有关。
气体扩散代理模型的数学表达通常采用偏微分方程,描述了气体浓度随时间和空间的变化。
在稳态条件下,扩散方程为:$\nabla·(D(x)·∇C(x))=0$,其中,$D(x)$是扩散系数,$C(x)$是气体浓度,$\nabla$表示梯度算子。
这个方程描述了气体浓度在多孔介质中变化的规律,通过求解该方程可以获得不同时刻、不同位置的气体浓度分布。
气体扩散代理模型在许多领域都有应用,例如石油、天然气、环境科学等。
在石油和天然气开采过程中,它可以用于描述天然气从储层到井筒的运移规律,指导开采策略的制定。
在环境科学中,它可以用于描述污染气体在土壤和地下水中的扩散过程,为污染治理提供依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内外扩散都有影响时的有效因子
内外扩散都有影响的 内外扩散均有影响时的 反应速率 o 有效因子 扩散无影响时的反应速 率
A kGam cAG cAS kwcAS okwcAG
c AS c AG k 1 w k G am
A kwcAS
r R p , c A c AS dcA r 0, 0 dr
比较薄片催化剂
L
kp De
R p sinh 3r R p cA c AS r sinh3
1 1 1 tanh3 3
6.4.2
内扩散有效因子
d 2c A dr 2 1 dcA k p cA r dr De
圆柱催化剂
Vp ap
kp De
r R p , c A c AS dcA r 0, 0 dr
I 0 2 r R p cA c AS I 0 2
I1 2 I 0 2
特别注意:
< 0.4, 1 > 3.0,
1
6.4.4
2、平行反应
P A
k1
S A
k2
主反应 副反应
n 1 AS
n rA 1 k1cA m rA 2 k2cB
无内扩散影响时,催化剂内浓度就是表面浓度 :
S′
P
kc 1 n m k1cAS k2 cAS 1 k2 c m n AS k1
6.5 内扩散与复合反应选择性的影响 1、两个独立并行的反应
k1 A P C k2 B S W
主反应 副反应
k1 > k2
以一级反应为例:
rA k1cA rB k2cB
ቤተ መጻሕፍቲ ባይዱ
并且有
6.5 内扩散与复合反应选择性的影响
无扩散影响时,瞬时选择性: 有扩散影响时,瞬时选择性:
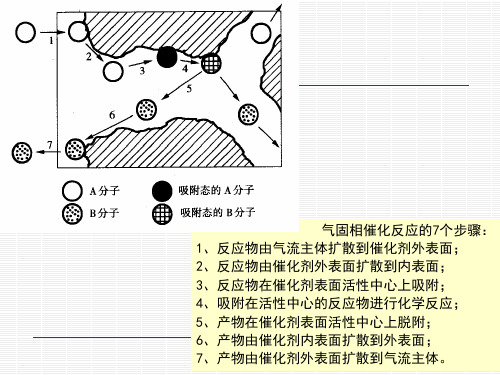
气固相催化反应的7个步骤: 1、反应物由气流主体扩散到催化剂外表面; 2、反应物由催化剂外表面扩散到内表面; 3、反应物在催化剂表面活性中心上吸附; 4、吸附在活性中心的反应物进行化学反应; 5、产物在催化剂表面活性中心上脱附; 6、产物由催化剂内表面扩散到外表面; 7、产物由催化剂外表面扩散到气流主体。
o
tanh 1 Bi m
LkG Bim De
tanh
传质的拜俄特数,表示外扩散与内扩 散阻力的相对大小
6.4.4
内外扩散都有影响时的有效因子
Bim 时,外扩散阻力可不计: tanh 0 tanh kw Bim 0 时,内扩散阻力可不计: Da am tanh k G kw 1 Da tanh am o kG kw k Da 11 w 1 tanh o k a x G mk a kw G m 1 Da 1 tanh k a G m o kw 1 tanh k a
梯尔模数
6.4.2
内扩散有效因子
内扩散有效 内扩散有影响时颗粒外 表面处的反应速率 rA 内扩散无影响时颗粒外 表面处的反应速率 r 因子
对一级不可 可逆反应
rA
1 k p c A dZ L
0
L
d 2 d 2
cA c AS
2 薄片催化剂
rA
k p cAS tanh( )
比较复杂,可能正好相 反,也可能存在极值, 但无论如何
cP c 将上升,也就是选择性 下降。 A
也就是说,对连串反应,内扩散导致选择性下降。 对内扩散阻力大(η<0.2),且有效扩散系数相等 的情况下,可以推导得:
RP k1 k 2 c PS SP = = - k 2 k1 c AS -R A 1+ k1 k 2
r k p c AS
cosh(Z ) L cosh
tanh( )
cAG
6.4.2
内扩散有效因子
cAG
R
r
dr
cAG
球形催化剂
cAG
2 dcA dcA 2 De 4 r dr De 4r 4r drk p c A dr r dr dr r
2
d dcA dcA dcA dr dr r dr dr r dr dr
6.4.2
内扩散有效因子
整理,并忽略dr2项,得,
d 2c A dr 2 2 dcA k p cA r dr De
球形催化剂
Vp ap kp De
6.3 气体在多孔气体中的扩散
1. 孔扩散(正常扩散)
2. 努森扩散
2ra
102
1.013 / p cm
2ra
10
DK 9.7 103 ra T / M
3.复合扩散
1 Da 1/( DK ) A (1 by A ) / DAB
b 1 NB / N A
2、平行反应
仍由式 有内扩散影响时,在催 化剂内部任意点上,
k﹙ 1 1 cA﹚ 表示瞬时选择性, SP n m k﹙ cA﹚ 1 k2 c m n ﹙ ﹚ k2 1 cA ﹙ A﹚ k1 < cAS , 瞬时选择性的变化取决于反应级数: 但,此时 ﹙cA ﹚ m n m> n m< n SP 不变 SP 增加 SP 下降
6.3 气体在多孔气体中的扩散
等摩尔二组分逆向扩散
1 DA 1 /( DK ) A 1 / D AB
dyi dci P Ni Dei Dei RT dZ dZ
多孔介质中的扩散
有效扩散系数
Dei P Di / m
扩散距离和扩散面积的校正
6.4.1
多孔催化剂内反应组分的浓度分布
n
3、连串反应
k1 k2 A P D
对于一级反应(可推广 到任意正级数反应)
S′
P
k1 cP rP k1cA k2cP 1 c rA k1cA k 2 A
cP cP c 决定了选择性。但 c 在颗粒内各处不同。 A A 由于扩散的影响, cA随着深入颗粒的进程必 然下降,而 cP
dcA dcA De a( ) z dZ De a( ) z k p c A adZ cA - dcA cA dZ dZ d 2c A k p a:扩散面积 c A 2 kp: 按催化剂体积计 D dZ e d 2 2 Z dZ 2 d 2L Z ) k cA Z cosh ( 2 2 p cA L , , L c AS L De c AS cosh
rA k1cAS SP rB k2cBS
当内扩散影响严重时,1 1
RA 1k1cAS SP RB 2 k2cBS
jS1
, 2 1
jS2
RA SP RB
k1 cAS k2 cBS
由于k 1 > k 2,选择性下降了。
薄片催化剂 基本假设: 催化剂颗粒等温; A
A
孔隙结构均匀,各向同性;
厚度远比长度和宽度小,即反应 物A从颗粒外表面向内表面的扩散 可按一维扩散问题处理。
cA - dcA
cA
Z dZ 2L
6.4.1
多孔催化剂内反应组分的浓度分布
A
单位时间扩散进入A量 – 单位时间扩散出的A A 量 = 单位时间反应的A量
kwcAG
kw 1 kG am
o 1 Da
k wc AG 1 D a
tanh
6.4.4
kw Da 内外扩散都有影响时的有效因子 kG am
对薄片催化剂
o
tanh
kw 1 tanh kG am
