全等三角形证明中的基本模型
初中数学全等三角形中的基本模型及常用辅助线

03
常用辅助线方法
中线法
中线倍长法
通过延长中线至等长,构造全等 三角形,常用于证明线段相等或 角相等。
中线性质应用
利用中线将三角形面积平分,或 将三角形划分为两个面积相等的 小三角形。
角平分线法
角平分线性质
角平分线上的点到角两边的距离相等 ,利用此性质可以构造全等三角形。
角平分线与平行线组合
通过作角平分线的平行线,构造相似 三角形,进而证明线段成比例或求线 段长度。
填空题答题技巧
准确理解题意
01
认真阅读题目,明确题目所考察的知识点和要求。
灵活运用知识
02
根据题目所给的条件和要求,灵活运用所学的知识点进行解答
。
注意答案的完整性和准确性
03
在填写答案时,要注意答案的完整性和准确性,避免漏填或错
填。
解答题答题思路展示
分析题意
认真阅读题目,理解题意,明确题目所考 察的知识点和要求。
基本模型与常用辅助 线
掌握在解决全等问题 时常用的辅助线作法 ,如倍长中线、截长 补短等。
熟悉几种常见的全等 三角形基本模型,如 角平分线模型、中线 模型等。
课堂检测题目设置及评价
题目设置
设置涵盖全等三角形定义、性质、判定方法以及基本模型和常用辅助线 的题目。
题目难度适中,既考查学生对基础知识的掌握,又考查其灵活运用能力 。
对应角相等
全等三角形的对应角相等。
周长相等
全等三角形的周长相等。
面积相等
全等三角形的面积相等。
典型例题解析
例1
解析
已知△ABC和△DEF中,AB = DE,BC = EF ,∠B = ∠E,求证:△ABC ≌ △DEF。
12.2 三角形全等的判定 初中数学模型

B1
A
E
D
C
7
知识点三:”旋转“ 模型
典例分析
AAS
例3:如图,∠A=∠B, AE= BE, 点D在AC边上 ,∠1=∠2,AE,BD
交于点O.求证:∆AEC≌∆BED.
证明:∵ ∠ADE3;∠C
又∵ ∠ ADE= ∠ 1+∠BDE
且∠ 1= ∠ 2
∴ ∠C= ∠BDE 在∆AEC和∆BED中,
△ABD,若∠ABC=25°,∠ADB=110°,
A3
1B
则∠DAC的度数是 90 ° .
D
2、将矩形ABCD沿AE折叠,得到如图所示
E
的图形.已知∠CEB'=60°,则
B
C
∠AEB′= 60 °.
B′
A
D
6
知识点二:”翻折对称“ 模型
学以致用
对顶角模型
3、如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC的度数 为 60 °.
∵ AD⊥CD AE⊥BE ∴ ∠AEB= ∠ADC=90 ° ∠BAE= ∠CAD (已证) 在△ABE和△ACD中, ∠AEB= ∠ADC (已证)
AB=AC(已知)
∴△ABE≌△ACD(AAS)
12
AAS
5
知识点二:”翻折对称“ 模型
学以致用
公共边模型
C
1、如图,△ABC沿直线AB向下翻折得到
“平移”模型
A
D
求证:AB∥DE.
证明:∵BE=CF ∴BE+EC=CF+EC(等式性质) B ∴BC=EF
AB=DE(已知)
在△ABC和△DEF中, AC=DF(已知)
(完整版)全等三角形经典模型总结
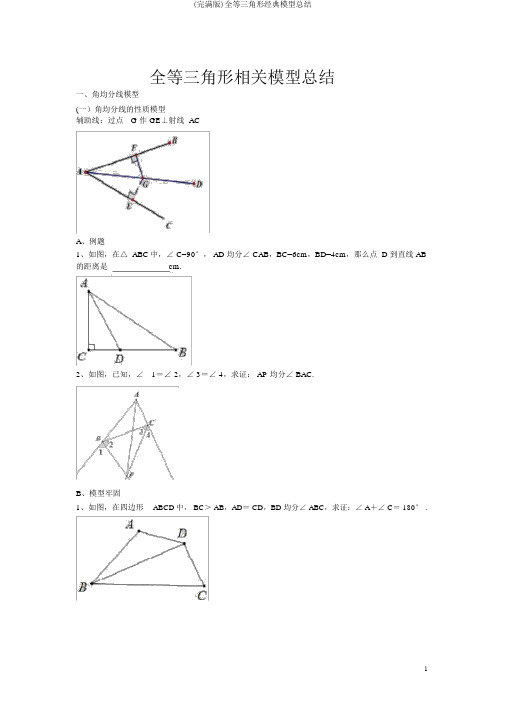
全等三角形相关模型总结一、角均分线模型(一)角均分线的性质模型辅助线:过点G 作 GE⊥射线 ACA、例题1、如图,在△ ABC中,∠ C=90°, AD 均分∠ CAB,BC=6cm,BD=4cm,那么点 D 到直线 AB 的距离是cm.2、如图,已知,∠1=∠ 2,∠ 3=∠ 4,求证: AP 均分∠ BAC.B、模型牢固1、如图,在四边形ABCD中, BC> AB,AD= CD,BD 均分∠ ABC,求证:∠ A+∠ C= 180° .(二)角均分线+垂线,等腰三角形必表现A、例题辅助线:延长ED 交射线 OB 于 F辅助线:过点 E 作 EF∥射线 OB例 1、如图,在△ABC中,∠ ABC= 3∠ C, AD 是∠ BAC的均分线, BE⊥ AD 于 F .1求证: BE( AC AB) .例 2、如图,在△ ABC中,∠ BAC的角均分线 AD 交 BC 于点 D,且 AB= AD,作 CM⊥ AD 交1AD 的延长线于M. 求证:AM( AB AC) .2(三)角分线,分两边,对称全等要记全两个图形飞辅助线都是在射线ON 上取点 B,使 OB= OA,从而使△ OAC≌△ OBC .A、例题1、如图,在△ ABC 中,∠ BAC=60°,∠ C=40°, AP 均分∠ BAC交 BC 于 P, BQ 均分∠ ABC 交AC 于 Q,求证: AB+ BP= BQ+ AQ .2、如图,在△ ABC 中, AD 是∠ BAC的外角均分线, P 是 AD 上异于点 A 的任意一点,试比较PB+ PC与 AB+ AC的大小,并说明原由 .B、模型牢固1、在△ ABC中, AB> AC, AD 是∠ BAC的均分线, P 是线段 AD 上任意一点(不与 A 重合) . 求证: AB-AC> PB- PC .2、如图,△ ABC中, AB= AC,∠ A= 100°,∠ B 的均分线交 AC 于 D,求证: AD+BD=BC .3、如图,△ ABC中, BC=AC,∠ C= 90°,∠ A 的均分线交 BC 于 D,求证: AC+ CD= AB .二、等腰直角三角形模型(一)旋转中心为直角极点,在斜边上任取一点的旋转全等:操作过程:(1)将△ ABD 逆时针旋转 90°,得△ ACM ≌ △ ABD,从而推出△ ADM 为等腰直角三角形 .(2)辅助线作法:过点 C 作 MC⊥ BC,使 CM= BD,连接 AM.(二)旋转中心为斜边中点,动点在两直角边上转动的旋转全等:操作过程:连接AD.(1)使 BF=AE(或 AF= CE),导出△ BDF ≌ △ADE.(2)使∠ EDF+∠ BAC= 180°,导出△ BDF ≌ △ ADE.A、例题1、如图,在等腰直角△ ABC中,∠BAC= 90°,点 M 、N 在斜边 BC上滑动,且∠ MAN =45°,试试究 BM、 MN 、 CN 之间的数量关系 .2、两个全等的含有 30°, 60°角的直角三角板 ADE 和 ABC,按以以下图放置, E、A、 C 三点在一条直线上,连接 BD,取 BD 的中点 M ,连接 ME、 MC.试判断△ EMC 的形状,并证明你的结论.B、模型牢固1、已知,以以下图,Rt△ABC中, AB= AC,∠ BAC=90°, O 为 BC中点,若 M 、N 分别在线段 AC、 AB 上搬动,且在搬动中保持AN= CM.(1)试判断△ OMN 的形状,并证明你的结论.(2)当 M、 N 分别在线段AC、 AB 上搬动时,四边形AMON 的面积如何变化?2、在正方形ABCD中, BE= 3,EF= 5, DF=4,求∠ BAE+∠ DCF为多少度 .(三)构造等腰直角三角形(1)利用以上(一)和(二)都可以构造等腰直角三角形(略);(2)利用平移、对称和弦图也可以构造等腰直角三角形.(四)将等腰直角三角形补全为正方形,以以下图:A、例题应用1、如图,在等腰直角△ABC 中, AC= BC,∠ ACB= 90°, P 为三角形ABC内部一点,满足 PB= PC, AP= AC,求证:∠ BCP= 15° .三、三垂直模型(弦图模型)A、例题已知:以以下图,在△ ABC中, AB= AC,∠ BAC= 90°, D 为 AC 中点, AF⊥ BD 于点 E,交 BC 于 F,连接 DF .求证:∠ ADB=∠ CDF .变式 1、已知:以以下图,在△ABC中, AB= AC,AM = CN, AF⊥ BM 于 E,交 BC 于 F,连接NF .求证:( 1)∠ AMB=∠ CNF;(2) BM= AF+ FN .变式 2、在变式 1 的基础上,其他条件不变,可是将BM 和 FN 分别延长交于点P,求证:( 1) PM= PN;( 2) PB= PF+ AF .四、手拉手模型1、△ ABE和△ ACF均为等边三角形结论:( 1)△ ABF≌△ AEC .(2)∠ BOE=∠ BAE=60° .(3) OA 均分∠ EOF .(四点共圆证)拓展:△ ABC和△ CDE均为等边三角形结论:( 1) AD= BE;(2)∠ ACB=∠ AOB;(3)△ PCQ为等边三角形;(4) PQ∥ AE;(5) AP=BQ;(6) CO均分∠ AOE;(四点共圆证)(7) OA= OB+OC;(8) OE=OC+ OD .((7),( 8)需构造等边三角形证明)例、如图①,点 M为锐角三角形 ABC内任意一点,连接 AM、BM、 CM.以 AB为一边向外作等边三角形△ ABE,将 BM绕点 B 逆时针旋转 60°获取 BN,连接 EN.(1)求证:△ AMB≌△ ENB;(2)若 AM+BM+CM的值最小,则称点 M为△ ABC的费尔马点.若点 M为△ ABC的费尔马点,试求此时∠ AMB、∠ BMC、∠ CMA的度数;(3)小翔受以上启示,获取一个作锐角三角形费尔马点的简略方法:如图②,分别以△ABC 的 AB、 AC 为一边向外作等边△ABE和等边△ ACF,连接CE、BF,设交点为M,则点M 即为△ ABC的费尔马点.试说明这种作法的依据.2、△ ABD 和△ ACE均为等腰直角三角形结论:( 1) BE= CD;(2) BE⊥ CD .3、四边形ABEF和四边形ACHD均为正方形结论:( 1) BD= CF;( 2)BD⊥ CF .变式 1、四边形 ABEF和四边形 ACHD均为正方形, AS⊥ BC 交 FD 于 T,求证:( 1) T 为 FD 中点;( 2)SV ABC SV ADF .变式 2、四边形 ABEF和四边形 ACHD均为正方形, T 为 FD 中点, TA 交 BC于 S,求证: AS⊥ BC .360 4、如图,以△ ABC的边 AB、 AC为边构造正多边形时,总有:1 2 180n五、半角模型条件: 1 , 且 + =180 ,两边相等.2思路: 1、旋转辅助线:①延长CD到 E,使 ED=BM,连 AE 或延长 CB到 F,使 FB=DN,连 AF②将△ ADN绕点 A 顺时针旋转 90°得△ ABF,注意:旋转需证F、 B、 M三点共线结论:( 1) MN = BM+ DN;(2)CV CMN=2 AB;(3) AM、 AN 分别均分∠ BMN 、∠ MND .2、翻折(对称)辅助线:①作AP⊥ MN 交 MN 于点 P②将△ ADN、△ ABM分别沿 AN、 AM翻折,但必然要证明M、P、 N 三点共线 .A、例题例1、在正方形 ABCD中,若 M、 N 分别在边 BC、 CD 上搬动,且满足 MN = BM+DN,求证:( 1)∠ MAN = 45°;(2)CV CMN=2 AB;(3) AM、 AN 分别均分∠ BMN 和∠ DNM .变式:在正方形 ABCD中,已知∠ MAN =45°,若 M 、N 分别在边 CB、DC 的延长线上搬动,AH⊥MN ,垂足为 H,(1)试试究线段 MN 、BM、 DN 之间的数量关系;(2)求证: AB= AH例 2、在四边形 ABCD 中,∠ B +∠ D = 180°, AB = AD ,若 E 、 F 分别为边 BC 、 CD 上的点,且满足 EF =BE + DF ,求证: EAF 1BAD .2变式:在四边形 ABCD 中,∠ B = 90°,∠ D = 90°, AB = AD ,若 E 、 F 分别为边 BC 、CD 上的点,且 EAF1 BAD ,求证: EF = BE +DF .2。
专题02 全等三角形中的六种模型梳理

专题02 全等三角形中的六种模型梳理一、概述全等三角形是初中数学中一个重要且常见的概念,对于几何学的学习具有重要的意义。
在全等三角形的学习中,有六种基本模型,它们是解决全等三角形问题的重要工具。
本文将对全等三角形中的六种模型进行深入探讨和梳理,帮助读者更加全面地理解和掌握这一知识点。
二、模型一:SSS全等模型在全等三角形中,如果两个三角形的三条边分别相等,则可以确定它们是全等三角形,这就是SSS全等模型。
如果已知两个三角形的三边分别相等,那么这两个三角形一定是全等的。
模型二:SAS全等模型SAS全等模型是指如果两个三角形的一条边和夹角以及另一边的长度分别相等,则可以确定它们是全等三角形。
如果已知两个三角形的一个角和两边分别相等,那么可以确定这两个三角形是全等的。
模型三:ASA全等模型在全等三角形中,如果两个三角形的一个角和两个角边相等,则可以确定它们是全等三角形,这就是ASA全等模型。
如果已知两个三角形的一个角和两个角边分别相等,那么可以确认这两个三角形是全等的。
模型四:HL全等模型HL全等模型是指如果两个直角三角形的斜边和一个直角边的长度分别相等,则可以确定它们是全等三角形。
如果已知两个直角三角形的斜边和一个直角边的长度分别相等,那么可以确定这两个三角形是全等的。
模型五:LL全等模型LL全等模型是指如果两个三角形的两个角和一个边分别相等,则可以确定它们是全等三角形。
如果已知两个三角形的两个角和一个边分别相等,那么可以确定这两个三角形是全等的。
模型六:对顶全等模型对顶全等模型是指如果两个三角形的两个对顶角和一个边分别相等,则可以确定它们是全等三角形。
如果已知两个三角形的两个对顶角和一个边分别相等,那么可以确定这两个三角形是全等的。
三、总结与回顾通过上述对全等三角形中六种模型的梳理,我们可以发现几何学中的相似和全等的概念是非常重要的。
在实际问题中,我们可以通过判断形状的相似或全等,推断出一些未知的信息,帮助我们解决问题。
人教版八年级数学全等三角形的常见模型总结(精选

人教版八年级数学全等三角形的常见模型总结(精选.)人教版八年级数学全等三角形常见模型总结要点梳理:全等三角形的判定与性质:一般三角形:边角边(SAS)、判角边角(ASA)、定角角边(AAS)、边边边(SSS)。
直角三角形:斜边、直角边定理(HL)。
性质:对应边相等,对应角相等(其他对应元素也相等,如对应边上的垂高相等)。
备判定:三角形全等必须有一组对应边相等。
注类型一:角平分线模型应用1.角平分性质模型:利用角平分线的性质。
例题解析:例1:如图1,在△ABC中,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那么点D到直线AB的距离是多少?答案】作DE⊥XXX于点E,DE=3cm。
例2:如图2,已知,∠1=∠2,∠3=∠4,求证:AP平分∠BAC。
答案】如图2,由角平分线的性质可知,PM=PN,PN=PQ,故PM=PQ,又因为PA是角BAC的平分线,所以XXX平分∠BAC。
类型二:角平分线模型应用2.角平分线,分两边,对称全等(截长补短构造全等)。
例题解析:例1:在△ABC中,∠BAC=60°,∠C=40°,AP平分∠XXX于P,BQ平分∠XXX于Q,求证:AB+BP=BQ+AQ。
答案】如图1,过O作OD∥BC交AB于D,∠ADO=∠ABC=180°-60°-40°=80°,又∵∠AQO=∠C+∠QBC=80°,∴∠ADO=∠AQO,又∵∠DAO=∠QAO,OA=AO,∴△ADO≌△AQO,∴OD=OQ,AD=AQ,又因为OD∥BP,所以∠PBO=∠DOB,又∠PBO=∠DBO,∴∠DBO=∠DOB,∴BD=OD,又∵∠XXX∠C+∠PAC=70°,∠BOP=∠OBA+∠BAO=70°,∴∠BOP=∠BPO,∴BP=OB,∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。
如图,将△ADE逆时针旋转60°,使△ADE≌△ABC,从而得到△MDE≌△MAC,因为M为BD的中点,所以ME=MC,因此△EMC为等腰三角形,且∠MDE=∠MAC=30°,所以△EMC为等腰直角三角形。
中考数学专题《全等三角形中的六种模型梳理》解析
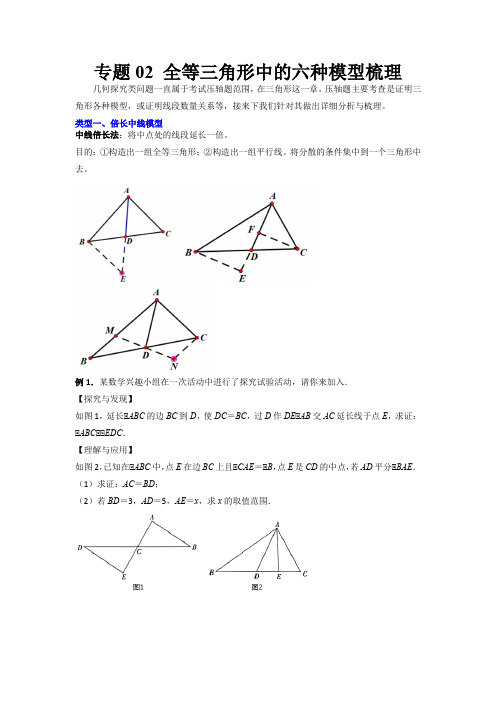
专题02 全等三角形中的六种模型梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型中线倍长法:将中点处的线段延长一倍。
目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中去。
例1.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】如图1,延长△ABC的边BC到D,使DC=BC,过D作DE△AB交AC延长线于点E,求证:△ABC△△EDC.【理解与应用】如图2,已知在△ABC中,点E在边BC上且△CAE=△B,点E是CD的中点,若AD平分△BAE.(1)求证:AC=BD;(2)若BD=3,AD=5,AE=x,求x的取值范围.【变式训练1】如图1,在ABC 中,CM 是AB 边的中线,BCN BCM ∠=∠交AB 延长线于点N ,2CM CN =.(1)求证AC BN =;(2)如图2,NP 平分ANC ∠交CM 于点P ,交BC 于点O ,若120AMC ∠=︒,CP kAC =,求CPCM的值.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>; (2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+; (3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【变式训练3】在ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,BM ⊥直线a 于点M .CN ⊥直线a 于点N ,连接PM ,PN .(1)如图1,若点B ,P 在直线a 的异侧,延长MP 交CN 于点E .求证:PM PE =.(2)若直线a 绕点A 旋转到图2的位置时,点B ,P 在直线a 的同侧,其它条件不变,此时7BMP CNP S S +=△△,1BM =,3CN =,求MN 的长度.(3)若过P 点作PG ⊥直线a 于点G .试探究线段PG 、BM 和CN 的关系.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)例.在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,P 为△ABC 外一点,且△MPN =60°,△BPC =120°,BP =CP .探究:当点M 、N 分别在直线AB 、AC 上移动时,BM ,NC ,MN 之间的数量关系.(1)如图①,当点M 、N 在边AB 、AC 上,且PM =PN 时,试说明MN =BM +CN . (2)如图②,当点M 、N 在边AB 、AC 上,且PM ≠PN 时,MN =BM +CN 还成立吗? 答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).(3)如图③,当点M 、N 分别在边AB 、CA 的延长线上时,请直接写出BM ,NC ,MN 之间的数量关系.【变式训练1】如图,在四边形ABCD 中,,180AB AD B ADC =∠+∠=︒,点E 、F 分别在直线BC 、CD 上,且12EAF BAD ∠=∠.(1)当点E 、F 分别在边BC 、CD 上时(如图1),请说明EF BE FD =+的理由.(2)当点E 、F 分别在边BC 、CD 延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF 、BE 、FD 之间的数量关系,并说明理由.【变式训练2】(1)阅读理解:问题:如图1,在四边形ABCD 中,对角线BD 平分ABC ∠,180A C ∠+∠=︒.求证:DA DC =.思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题; 方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题. 结合图1,在方法1和方法2中任选一种....,添加辅助线并完成证明. (2)问题解决:如图2,在(1)的条件下,连接AC ,当60DAC ∠=︒时,探究线段AB ,BC ,BD 之间的数量关系,并说明理由;(3)问题拓展:如图3,在四边形ABCD 中,180A C ∠+∠=︒,DA DC =,过点D 作DE BC ⊥,垂足为点E ,请直接写出线段AB 、CE 、BC 之间的数量关系.【变式训练3】在ABC 中,BE ,CD 为ABC 的角平分线,BE ,CD 交于点F . (1)求证:1902BFC A ∠=︒+∠;(2)已知60A ∠=︒.①如图1,若4BD =, 6.5BC =,求CE 的长; ②如图2,若BF AC =,求AEB ∠的大小.类型三、做平行线证明全等 例1.如图所示:ABC 是等边三角形,D 、E 分别是AB 及AC 延长线上的一点,且BD CE =,连接DE 交BC 于点M . 求让:MD ME =【变式训练1】 P 为等边△ABC 的边AB 上一点,Q 为BC 延长线上一点,且P A =CQ ,连PQ 交AC 边于D . (1)证明:PD =DQ .(2)如图2,过P 作PE △AC 于E ,若AB =6,求DE 的长.【变式训练2】已知在等腰△ABC 中,AB =AC ,在射线CA 上截取线段CE ,在射线AB 上截取线段BD ,连接DE ,DE 所在直线交直线BC 与点M .请探究:(1)如图(1),当点E 在线段AC 上,点D 在AB 延长线上时,若BD =CE ,请判断线段MD 和线段ME 的数量关系,并证明你的结论.(2)如图(2),当点E 在CA 的延长线上,点D 在AB 的延长线上时,若BD =CE ,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;类型四、旋转模型 例.如图1,AC BC =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点M ,连接CM .(1)求证:BE AD =,并用含α的式子表示AMB ∠的度数;(2)当90α=︒时,取AD ,BE 的中点分别为点P 、Q ,连接CP ,CQ ,PQ ,如图2,判断CPQ 的形状,并加以证明.【变式训练1】四边形ABCD 是由等边ABC ∆和顶角为120︒的等腰ABD ∆排成,将一个60︒角顶点放在D 处,将60︒角绕D 点旋转,该60︒交两边分别交直线BC 、AC 于M 、N ,交直线AB 于E 、F 两点.(1)当E 、F 都在线段AB 上时(如图1),请证明:BM AN MN +=;(2)当点E 在边BA 的延长线上时(如图2),请你写出线段MB ,AN 和MN 之间的数量关系,并证明你的结论;(3)在(1)的条件下,若7AC =, 2.1AE =,请直接写出MB 的长为 .【变式训练2】(1)问题发现:如图1,△ACB 和△DCE 均为等边三角形,当△DCE 旋转至点A ,D ,E 在同一直线上,连接BE .则:①△AEB 的度数为 °;②线段AD 、BE 之间的数量关系是 . (2)拓展研究:如图2,△ACB 和△DCE 均为等腰三角形,且△ACB =△DCE =90°,点 A 、D 、E 在同一直线上,若AD =a ,AE =b ,AB =c ,求a 、b 、c 之间的数量关系. (3)探究发现:图1中的△ACB 和△DCE ,在△DCE 旋转过程中,当点A ,D ,E 不在同一直线上时,设直线AD 与BE 相交于点O ,试在备用图中探索△AOE 的度数,直接写出结果,不必说明理由.【变式训练3】如图1,在Rt ABC 中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是______,位置关系是______. (2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN 的形状,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若4=AD ,10AB =,请直接写出PMN 面积的最大值.类型五、手拉手模型例.在等边ABC 中,点D 在AB 上,点E 在BC 上,将线段DE 绕点D 逆时针旋转60°得到线段DF ,连接CF .(1)如图(1),点D 是AB 的中点,点E 与点C 重合,连接AF .若6AB =,求AF 的长; (2)如图(2),点G 在AC 上且60AGD FCB ∠=︒+∠,求证:CF DG =;(3)如图(3),6AB =,2BD CE =,连接AF .过点F 作AF 的垂线交AC 于点P ,连接BP 、DP .将BDP △沿着BP 翻折得到BQP ,连接QC .当ADP △的周长最小时,直接写出CPQ 的面积.【变式训练1】△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形.(1)问题发现:如图1,若点A ,D ,E 在同一直线上,连接AE ,BE . ①求证:△ACD △△BCE ;②求△AEB 的度数.(2)类比探究:如图2,点B 、D 、E 在同一直线上,连接AE ,AD ,BE ,CM 为△DCE 中DE 边上的高,请求△ADB 的度数及线段DB ,AD ,DM 之间的数量关系,并说明理由. (3)拓展延伸:如图3,若设AD (或其延长线)与BE 的所夹锐角为α,则你认为α为多少度,并证明.【变式训练2】(1)如图1,锐角△ABC 中,分别以AB 、AC 为边向外作等腰直角△ABE 和等腰直角△ACD ,使AE =AB ,AD =AC ,∠BAE =∠CAD =90°,连接BD ,CE ,试猜想BD 与CE 的大小关系,不需要证明.【深入探究】(2)如图2,四边形ABCD 中,AB =5,BC =2,∠ABC =∠ACD =∠ADC =45°,求BD 2的值;甲同学受到第一问的启发构造了如图所示的一个和△ABD 全等的三角形,将BD 进行转化再计算,请你准确的叙述辅助线的作法,再计算;【变式思考】(3)如图3,四边形ABCD 中,AB =BC ,∠ABC =60°,∠ADC =30°,AD =6,BD =10,则CD = .【变式训练3】(1)问题发现:如图1,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 在同一条直线上,则AEB ∠的度数为__________,线段AD 、BE 之间的数量关系__________;(2)拓展探究:如图2,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由. (3)解决问题:如图3,ACB △和DCE 均为等腰三角形,ACB DCE α∠=∠=,则直线AD 和BE 的夹角为__________.(请用含α的式子表示)类型六、一线三角模型例.在ABC 中,90ACB ∠=︒,AC BC =,直线MN 经过点C 且AD MN ⊥于D ,BE MN ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①ADC △CEB △;②DE AD BE =+;(2)当直线MN 烧点C 旋转到图2的位置时,求证:DE AD BE =-;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.【变式训练1】【问题解决】(1)已知△ABC 中,AB =AC ,D ,A ,E 三点都在直线l 上,且有△BDA =△AEC =△BAC .如图①,当△BAC =90°时,线段DE ,BD ,CE 的数量关系为:______________;【类比探究】(2)如图②,在(1)的条件下,当0°<△BAC<180°时,线段DE,BD,CE的数量关系是否变化,若不变,请证明:若变化,写出它们的关系式;【拓展应用】(3)如图③,AC=BC,△ACB=90°,点C的坐标为(-2,0),点B的坐标为(1,2),请求出点A的坐标.【变式训练2】(1)如图1,在△ABC中,△BAC=90°,AB=AC,直线m经过点A,BD△直线m,CE△直线m,垂足分别为点D、E.求证:△ABD△△CAE;(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有△BDA=△AEC=△BAC=α,其中α为任意锐角或钝角.请问结论△ABD△△CAE是否成立?如成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图3,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为△BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若△BDA=△AEC=△BAC,求证:△DEF是等边三角形.【变式训练3】探究:(1)如图(1),已知:在△ABC中,△BAC=90°,AB=AC,直线m经过点A,BD△直线m,CE△直线m,垂足分别为点D、E.请直接写出线段BD,DE,CE之间的数量关系是.拓展:(2)如图(2),将探究中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有△BDA=△AEC=△BAC=α,其中α为任意锐角或钝角.请问探究中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.应用:(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为△BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若△BDA=△AEC=△BAC,请直接写出△DEF的形状是.。
全等三角形的七大模型全攻略 倍长中线模型(解析版)

倍长中线模型基本模型(1)如图,在△ABC 中,AD 为△ABC 的中线,延长AD 至点E ,使得DE =AD ,连接BE ,则△ADC ≌△EDB .(2)有三角形中线时,可过中点所在的边的两端点向中线作垂线,构造全等三角形,例:如图,AF 为△ABC 的中线,作BD ⊥AF 交AF 延长线于点D ,作CE ⊥AF 于点E ,则△BDN ≌△CEN .1(基本模型)如图,在ΔABC 中,D 是BC 上一点,连接AD ,已知CD =AB ,∠BAD =∠BDA ,AE 是ΔABD 的中线.求证:AC =2AE .(提示:延长AE 至F ,使EF =AE ,连接DF )【答案】见解析【详解】证明:如图,延长AE 至F ,使EF =AE ,连接DF .例题精讲∵AE 是ΔABD 的中线,∴BE =DE .在ΔABE 与ΔFDE 中,AE =EF∠AEB =∠FED BE =DE,∴ΔABE ≅ΔFDE .∴AB =FD ,∠B =∠EDF .∵CD =AB ,∴CD =FD .∵∠ADC =∠B +∠BAD ,∠ADB =∠BAD ,∠ADF =∠ADB +∠EDF =∠B +∠ADB ,∴∠ADC =∠ADF .在ΔADF 与ΔADC 中,AD =AD∠ADC =∠ADF CD =FD,∴ΔADF ≅ΔADC .∴AC =AF .∵AF =AE +EF =2AE ,∴AC =2AE .2(培优综合)(1)阅读理解:如图1,在△ABC 中,若AB =3,AC =5.求BC 边上的中线AD 的取值范围,小聪同学是这样思考的:延长AD 至E ,使DE =AD ,连接BE .利用全等将边AC 转化到BE ,在△BAE 中利用三角形三边关系即可求出中线AD 的取值范围,在这个过程中小聪同学证三角形全等用到的判定方法是,中线AD 的取值范围是;(2)问题解决:如图2,在△ABC 中,点D 是BC 的中点,DM ⊥DN .DM 交AB 于点M ,DN 交AC 于点N .求证:BM +CN >MN ;(3)问题拓展:如图3,在△ABC 中,点D 是BC 的中点,分别以AB ,AC 为直角边向△ABC 外作Rt △ABM 和Rt △ACN ,其中∠BAM =∠NAC =90°,AB =AM ,AC =AN ,连接MN ,请你探索AD 与MN 的数量与位置关系,并直接写出AD 与MN 的关系.【答案】(1)SAS ,1<AD <4;(2)见解析;(3)2AD =MN ,AD ⊥MN【详解】(1)解:如图1,延长AD 至E ,使DE =AD ,连接BE ,∵AD 为BC 边上的中线,∴BD =CD ,在△ADC和△EDB中,AD=ED∠ADC=∠EDB CD=BD,∴△ADC≌△EDB SAS,∴EB=AC=5,在△ABE中,根据三角形三边关系可得:BE-AB<AE<AB+BE,即2<AE<8,∵AE=2AD,∴2<2AD<8,∴1<AD<4,故答案为:SAS,1<AD<4;(2)证明:如图2中,延长ND至点F,使FD=ND,连接BF、MF,∵点D是BC的中点,∴BD=CD,在△BDF和△CDN中,ND=NF∠BDF=∠CDN CD=BD,∴△BFD≌△CND SAS,∴BF=CN,∵DM⊥DN,FD=ND,∴MF=MN,在△BFM中,由三角形的三边关系得:BM+BF>MF,∴BM+CN>MN;(3)解:结论:2AD=MN,AD⊥MN,如图3,延长AD于E,使得ED=AD,连接BE,延长DA交MN于F,∵点D是BC的中点,∴BD=CD,在△BDE和△CDA中,BD=CD∠BDE=∠CDA AD=ED,∴△CDA≌△BDE SAS,∴BE=AC,∠ACD=∠EBD,∵∠MAN+∠MAB+∠BAC+∠CAN=360°,∠BAM=∠NAC=90°,∴∠MAN+∠CAB=180°,∵∠BAC+∠ABC+∠ACB=180°,∴∠MAN=∠ABC+∠ACB=∠ABC+∠EBD=∠ABE,在△MAN和△ABE中,AM=AB∠MAN=∠ABE AN=BE,∴△ABE≌△MAN SAS,∴MN=AE=2AD,∠BAE=∠AMN,∵∠MAF+∠MAB+∠BAE=180°,∠MAB=90°,∴∠MAF+∠BAE=90°,∴∠MAF+∠AMN=90°,∴AF⊥MN,即AD⊥MN .3(分类讨论)在△ABC中,点P为BC边中点,直线a绕顶点A旋转,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)如图1,若点B,P在直线a的异侧,延长MP交CN于点E.求证:PM=PE.(2)若直线a绕点A旋转到图2的位置时,点B,P在直线a的同侧,其它条件不变,此时S△BMP+S△CNP= 7,BM=1,CN=3,求MN的长度.(3)若过P点作PG⊥直线a于点G.试探究线段PG、BM和CN的关系.【答案】(1)见解析;(2)MN=7;(3)线段PG、BM和CN的位置关系为BM⎳PG⎳CN,数量关系为2PG=CN-BM或2PG=BM-CN或2PG=CN+BM【详解】(1)证明:如图1,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMA=∠CNM=90°,∴BM⎳CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,在△BPM和△CPE中,∠BPM=∠CPE BP=CP∠MBP=∠ECP,∴△BPM ≌△CPE ASA ,∴PM =PE .(2)解:如图2,延长MP 与NC 的延长线相交于点E ,∵BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,∴∠BMN =∠CNM =90°,∴∠BMN +∠CNM =180°,∴BM⎳CN,∴∠MBP =∠ECP ,又∵P 为BC 中点,∴BP =CP ,又∵∠BPM =∠CPE ,∴在△BPM 和△CPE 中,∠BPM =∠CPEBP =CP ∠MBP =∠ECP,∴△BPM ≌△CPE ASA ,∴PM =PE ,BM =CE ,S △BPM =S △CPE ,∵BM =1,CN =3,∴NE =CN +CE =CN +BM =4,∵S △BMP +S △CNP =7,∴S △PNE =S △CPE +S △CNP =S △BMP +S △CNP =7,∴S △MNE =2S △PNE =14,∴12×MN ×4=14,∴MN =7.(3)位置关系:BM ⎳PG ⎳CN ,数量关系:分四种情况讨论∵BM ⊥直线a 于点M .CN ⊥直线a 于点N ,PG ⊥直线a 于点G ,∴BM ⎳PG ⎳CN ,①如图3,当直线a 与线段BP 交于一点时,由(1)可知PM =PE ,∴S △PMN =S △PEN =12S △MNE ,即12×12MN ⋅PG =12NE ⋅MN ,∴NE =2PG ,∵△BPM ≌△CPE ,∴BM =CE ,∵NE =CN -CE ,∴2PG =CN -BM .②当直线a 与线段CP 交于一点时,如图,延长MP 交CN 的延长线于点E .∵BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,∴∠BMN =∠CNM =90°,∴BM⎳CN ,∴∠MBP =∠ECP ,又∵P 为BC 边中点,∴BP =CP ,在△BPM 和△CPE 中,∠BPM =∠CPEBP =CP ∠MBP =∠ECP,∴△BPM ≌△CPE ASA ,∴PM =PE .∴S △PMN =S △PEN =12S △MNE,即12×12MN ⋅PG =12NE ⋅MN ,∴NE =2PG ,∵△BPM ≌△CPE ,∴BM =CE ,∵NE =CE -CN ,∴2PG =BM -CN .③如图4,当直线a 与线段CB 的延长线交于一点时.由(2)得:△BPM ≌△CPE ASA ,∴PM =PE ,S △BPM =S △CPE ,∴S 梯形BCNM =S △MNE =2S △MNP ,即12BM +CN ⋅MN =2×12MN ⋅PG ,∴2PG =CN +BM .④当直线a 与线段CB 的延长线交于一点时,如图,延长MP 交NC 的延长线于点E .∵BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,∴∠BMN =∠CNM =90°,∴∠BMN +∠CNM =180°,∴BM ⎳CN ,∴∠MBP =∠ECP ,又∵P 为BC 中点,∴BP =CP ,又∵∠BPM =∠CPE ,∴在△BPM 和△CPE 中,∠BPM =∠CPEBP =CP ∠MBP =∠ECP,∴△BPM ≌△CPE ASA ,∴PM =PE ,S △BPM =S △CPE ,∴S 梯形BCNM =S △MNE =2S △MNP ,即12BM +CN ⋅MN =2×12MN ⋅PG ,∴2PG =CN +BM .综上所述,线段PG 、BM 和CN 的位置关系为BM ⎳PG ⎳CN ,数量关系为2PG =CN -BM 或2PG =BM -CN 或2PG =CN +BM .1如图,在△ABC 中,AB =AC ,BE 是AC 的中线,点D 在AC 的延长线上,连接BD ,BC 平分∠EBD .(1)求证:∠ABE =∠D ;(2)求证:BD =2BE .【答案】(1)见详解(2)见详解【详解】(1)证明:∵AB =AC ,∴∠ABC =∠ACB ,∵BC 平分∠EBD ,∴∠EBC =∠DBC ,∵∠ACB =∠D +∠DBC ,∠ABC =∠ABE +∠EBC ,∴∠D +∠DBC =∠ABE +∠EBC ,∴∠ABE =∠D ;(2)证明:延长BE 到点F ,使得EF =EB ,连接CF ,如图所示:∵BE 是AC 的中线,∴AE =CE ,∵∠AEB =∠CEF ,∴△ABE ≌△CFE (SAS ),∴∠ABE =∠F ,∵∠ABE =∠D ,∴∠D =∠F ,∵∠FBC =∠DBC ,BC =BC ,∴△BCF ≌△BCD (AAS ),∴BD =BF ,∴BD =2BE .2某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】如图1,延长△ABC 的边BC 到D ,使DC =BC ,过D 作DE ∥AB 交AC 延长线于点E ,求证:△ABC ≌△EDC .【理解与应用】如图2,已知在△ABC 中,点E 在边BC 上且∠CAE =∠B ,点E 是CD 的中点,若AD 平分∠BAE .变式训练(1)求证:AC =BD ;(2)若BD =3,AD =5,AE =x ,求x的取值范围.【答案】[探究与发现]见解析;[理解与应用](1)见解析;(2)1<x <4【详解】解:[探究与发现]证明:∵DE ∥AB ,∴∠B =∠D ,又∵BC =DC ,∠ACB =∠ECD ,∴△ABC ≌△EDC (ASA );[理解与应用](1)证明:如图2中,延长AE 到F ,使EF =EA ,连接DF ,∵点E 是CD 的中点,∴ED =EC ,在△DEF 与△CEA 中,EF =EA∠DEF =∠CEA ED =EC,∴△DEF ≌△CEA (SAS ),∴AC =FD ,∴∠AFD =∠CAE ,∵∠CAE =∠B ,∴∠AFD =∠B ,∵AD 平分∠BAE ,∴∠BAD =∠FAD ,在△ABD 与△AFD 中,∠B =∠AFD∠BAD =∠FAD AD =AD,∴△ABD ≌△AFD (AAS ),∴BD =FD ,∴AC =BD ;(2)解:由(1)得:AF =2AE =2x ,△ABD ≌△AFD ,∴AB =AF =2x ,∵BD =3,AD =5,在△ABD 中,由三角形的三边关系得:AD -BD <AB <AD +BD ,即5-3<2x <5+3,解得:1<x <4,即x 的取值范围是1<x <4.3如图1,在△ABC 中,CM 是AB 边的中线,∠BCN =∠BCM 交AB 延长线于点N ,2CM =CN .(1)求证AC =BN ;(2)如图2,NP 平分∠ANC 交CM 于点P ,交BC 于点O ,若∠AMC =120°,CP =kAC ,求CP CM 的值.【答案】(1)见解析;(2)2k k +1【详解】(1)如图1所示,延长CM 至点D ,使CM =DM ,在△ACM 与△BDM 中,CM =DM∠AMC =∠BMD AM =BM,∴ΔACM ≅ΔBDM ,∴AC =BD ,∵2CM =CN ,∴CD =CN ,在△DCB 与△NCB 中,CD =CN∠DCB =∠NCB CB =CB,∴ΔDCB ≅ΔNCB ,∴BN =BD ,∴AC =BN ;(2)如图所示,∵∠AMC =120°,∴∠CMN =60°,∵NP 平分∠MNC ,∠BCN =∠BCM ,∠PNC +∠BCN =12∠AMC =60°,∴∠CON =120°,∠COP =60°,∴∠CMN +∠BOP =180°,作CQ =CP ,在△CPO与△CQO 中,CQ =CP∠QCO =∠PCO CO =CO,∴ΔCPO ≅ΔCQO ,∴∠1=∠2=∠3,∴∠4=∠5,在△NOB与△NOQ中,∠4=∠5∠BNO=∠QNO NO=NO,∴ΔNOB≅ΔNOQ,∴BN=NQ,∴CN=CP+NB,∴2CM=CP+AC,设AC=a,∴CP=ka,CM=a(k+1)2,∴CPCM=2kk+1.4(1)如图1,△ABC中,AD为中线,求证:AB+AC>2AD;(2)如图2,△ABC中,D为BC的中点,DE⊥DF交AB、AC于E、F.求证:BE+CF>EF.【答案】(1)证明见解析;(2)证明见解析.【详解】(1)如图,延长AD至点E,使ED=AD.∵AD为中线,∴BD=CD.∴在△ABD和△ECD中,BD=CD∠ADB=∠EDC AD=ED,∴△ABD≅△ECD(SAS),∴AB=EC.∵在△ACE中,AC+EC>AE,∴AC+AB>2AD.(2)如图,延长ED至点G,使DG=ED,连接CG,EG.∵AD为中线,∴BD=CD.∴在△BDE和△CDG中,BD=CD∠BDE=∠CDG ED=GD,∴△BDE≅△CDG(SAS),∴BE=CG.∵DE⊥DF,∴∠EDF=∠GDF=90°,∴在△EDF和△GDF中,ED=GD∠EDF=∠GDF=90°DF=DF,∴△EDF≅△GDF(SAS),∴EF=GF.∵在△CFG中,CG+CF>FG,∴BE+CF>EF .5如图,在△ABC中,AD为BC边的中线,E为AD上一点,连接BE并延长交AC于点F,若∠AEF=∠FAE,BE=4,EF=1.6,则CF的长为.【答案】2.4【详解】如解图,延长AD到点G,使DG=AD,∵AD为BC边的中线,∴BD=CD∵∠BDG=∠CDA,DG=AD∴△BDG≌△CDA SAS∴∠G=∠CAD,BG=AC∵∠AEF=∠FAE∴∠G=∠BEG∴BG=BE=AC=4∵∠AEF =∠FAE,EF=1.6∴AF=EF=1.6∴CF=AC-AF=2.4.故答案为:2.4.6在△ABC中,AB=AC,点D是△ABC内一点,点E是CD的中点,连接AE,作EF⊥AE,若点F在BD的垂直平分线上,∠BAC=α,则∠BFD=.(用α含的式子表示)课后训练【答案】180°-α.【详解】解:延长AE 至M ,使EM =AE ,连接AF ,FM ,DM ,∵点E 是CD 的中点,∴DE =CE ,在△AEC 与△MED 中,AE =EM∠AEC =∠DEM CE =DE,∴△AEC ≌△MED (SAS ),∴∠EAC =∠EMD ,AC =DM ,∵EF ⊥AE ,∴AF =FM ,∵点F 在BD 的垂直平分线上,∴FB =FD ,在△MDF 与△ABF 中,AB =DMBF =DF AF =FM,∴△MDF ≌△ABF (SSS ),∴∠AFB =∠MFD ,∠DMF =∠BAF ,∴∠BFD +∠DFA =∠DFA +∠AFM ,∴∠BFD =∠AFM=180°-2(∠DMF +∠EMD )=180°-(∠FAM +∠BAF +∠EAC )=180°-∠BAC=180°-α,故答案为:180°-α.7在通过构造全等三角形解决的问题中,有一种典型的方法是倍延中线.(1)如图1,AD 是ΔABC 的中线,AB =7,AC =5,求AD 的取值范围.我们可以延长AD到点M ,使DM =AD ,连接BM ,易证ΔADC ≅ΔMDB ,所以BM =AC .接下来,在ΔABM 中利用三角形的三边关系可求得AM 的取值范围,从而得到中线AD 的取值范围是;(2)如图2,AD是△ABC的中线,点E在边AC上,BE交AD于点F,且AE=EF,求证:AC=BF;(3)如图3,在四边形ABCD中,AD⎳BC,点E是AB的中点,连接CE,ED且CE⊥DE,试猜想线段BC,CD,AD之间满足的数量关系,并予以证明.【答案】(1)1<AD<6;(2)见解析;(3)CD=BC+AD,证明见解析【详解】(1)延长AD到点M,使DM=AD,连接BM,∵AD是ΔABC的中线,∴DC=DB,在ΔADC和ΔMDB中,AD=MD,∠ADC=∠MDB,DC=DB,∴ΔADC≅ΔMDB,∴BM=AC,在ΔABM中,AB-BM<AM<AB+BM,∴7-5<AM<7+5,即2<AM<12,∴1<AD<6;(2)证明:延长AD到点M,使DM=AD,连接BM,由(1)知△ADC≅△MDB,∴∠M=∠CAD,BM=AC,∵AE=EF,∴∠CAD=∠AFE,∵∠MFB=∠AFE,∴∠MFB=∠CAD,∴∠BMF=∠BFM,∴BM=BF,∴AC=BF,(3)CD=BC+AD,延长CE到F,使EF=EC,连接AF,∵AE=BE,∠AEF=∠BEC,∴ΔAEF≅ΔBEC,∴∠EAF=∠B,AF=BC,∵AD⎳BC,∴∠BAD+∠B=180°,∴∠EAF+∠BAD=180°,∴点F,A,D在一条直线上,∵CE⊥ED,∴∠DEF=∠DEC=90°,∴在Rt△DEF和Rt△DEC中,EF=EC,∠DEF=∠DEC,DE=DE,∴Rt△DEF≌Rt△DEC,∴FD=CD,∵FD=AD+AF=AD+BC,∴CD=BC+AD.8已知,在Rt△ABC中,∠BAC=90°,点D为边AB的中点,AE⊥CD分别交CD,BC于点F,E.(1)如图1,①若AB=AC,请直接写出∠EAC-∠BCD=;②连接DE,若AE=2DE,求证:∠DEB=∠AEC;(2)如图2,连接FB,若FB=AC,试探究线段CF和DF之间的数量关系,并说明理由.【答案】(1)①45°;②见解析;(2)CF=2DF,理由见解析【详解】(1)①∵∠EAC+∠ACD=90°,∠AEC+∠BCD=90°∴∠EAC-∠BCD=∠AEC-∠ACD∵∠EAC+∠BAE=90°∴∠ACD=∠BAE又∵∠AEC=∠B+∠BAE∴∠EAC-∠BCD=∠B+∠BAE-∠ACD∴∠EAC-∠BCD=∠B=45°故答案为45°.②如图,延长ED至点G,使得DG=DE,连接AG,∵点D为AB的中点,∴BD=AD,又∵∠ADG=∠BDE,∴△ADG≌△BDE,∴∠DGA=∠DEB,∴AG⎳BC,∴∠GAE=∠AEC,又∵AE=2DE,∴AE=EG,∴∠DGA=∠GAE,∴∠DEB=∠AEC.(2)CF=2DF.如图,延长CD至点H,使得DH=DF,连接BH,∵AD=BD,∠ADF=∠BDH,∴△HDB≌△FDA,∴BH=AF,∠H=∠AFD=∠AFC=90°,∵BF=AC.∴Rt△HBF≌Rt△FAC,∴CF=HF=2DF.9如图,在ABC中,∠ABC=45°,AD,BE分别为BC,AC边上的高,连接DE,过点D作DF⊥DE 与点F,G为BE中点,连接AF,DG.(1)如图1,若点F与点G重合,求证:AF⊥DF;(2)如图2,请写出AF与DG之间的关系并证明.【答案】(1)详见解析;(2)AF=2DG,且AF⊥DG,证明详见解析.【详解】解:(1)证明:设BE与AD交于点H..如图,∵AD,BE分别为BC,AC边上的高,∴∠BEA=∠ADB=90°.∵∠ABC=45°,∴△ABD是等腰直角三角形.∴AD=BD.∵∠AHE=∠BHD,∴∠DAC=∠DBH.∵∠ADB=∠FDE=90°,∴∠ADE=∠BDF.∴△DAE≌△DBF.∴BF=AE,DF=DE.∴△FDE是等腰直角三角形.∴∠DFE=45°.∵G为BE中点,∴BF=EF.∴AE=EF.∴△AEF是等腰直角三角形.∴∠AFE=45°.∴∠AFD=90°,即AF⊥DF.(2)AF=2DG,且AF⊥DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,∵点G为BE的中点,BG=GE.∵∠BGM∠EGD,∴△BGM≌△EGD.∴∠MBE=∠FED=45°,BM=DE.∴∠MBE=∠EFD,BM=DF.∵∠DAC=∠DBE,∴∠MBD=∠MBE+∠DBE=45°+∠DBE.∵∠EFD=45°=∠DBE+∠BDF,∴∠BDF=45°-∠DBE.∵∠ADE=∠BDF,∴∠ADF=90°-∠BDF=45°+∠DBE=∠MBD.∵BD=AD,∴△BDM≌△DAF.∴DM=AF=2DG,∠FAD=∠BDM.∵∠BDM+∠MDA=90°,∴∠MDA+∠FAD=90°.∴∠AHD=90°.∴AF⊥DG.∴AF=2DG,且AF⊥DG【点睛】本题考查三角形全等的判定和性质,关键在于灵活运用性质.10如图,△ABC中,AB=AC,∠BAC=90°,点D在CB上,连接AD,EA⊥AD,∠ACE=∠ABD.(1)求证:AD=AE;(2)若点F为CD中点,AF交BE于点G,求∠AGE的度数.【答案】(1)证明见解析;(2)90°.【详解】(1)证明:∵∠BAC=90°,EA⊥AD,∴∠BAC=∠DAE=90°,∴∠BAD=∠CAE,在△ABD和△ACE中,∠BAD=∠CAE AB=AC∠ABD=∠ACE,∴△ABD≌△ACE(ASA),∴AD=AE;(2)延长AF至M,使FM=AF,连接MC,在△ADF与△MCF中,DF=CF∠DAF=∠CFM AF=FM,∴△ADF≌△MCF(SAS),∴AD=CM,∠DAF=∠M,∴AD∥CM,∴∠ACM+∠DAC=180°,∵△ABD≌△ACE,∴AD=AE,∴AD=AE=CM,∵∠BAC+∠DAE=180°,∴∠BAC +∠DAC +∠CAE =180°,∴∠BAE +∠DAC =180°,∴∠BAE =∠ACM ,在△ABE 和△CAM 中,AB =AC∠BAE =∠ACM AE =CM,∴△ABE ≌△CAM (SAS ),∴∠ABG =∠CAF ,∵∠CAF +∠BAG =90°,∴∠ABG +∠BAG =90°,∴∠AGB =∠AGE =90°.11【观察发现】如图①,△ABC 中,AB =7,AC =5,点D 为BC 的中点,求AD 的取值范围.小明的解法如下:延长AD 到点E ,使DE =AD ,连接CE .在△ABD 与△ECD 中BD =DC∠ADB =∠EDCAD =DE∴△ABD ≅△ECD (SAS )∴AB =.又∵在△AEC 中EC -AC <AE <EC +AC ,而AB =EC =7,AC =5,∴<AE <.又∵AE =2AD .∴<AD <.【探索应用】如图②,AB ∥CD ,AB =25,CD =8,点E 为BC 的中点,∠DFE =∠BAE ,求DF 的长为.(直接写答案)【应用拓展】如图③,∠BAC =60°,∠CDE =120°,AB =AC ,DC =DE ,连接BE ,P 为BE 的中点,求证:AP ⊥DP .【答案】观察发现:EC ,2,12,1,6;探索应用:17;应用拓展:见解析【详解】观察发现解:如图①,延长AD 到点E ,使DE =AD ,连接CE ,在△ABD 与△ECD 中,BD =DC∠ADB =∠EDC AD =DE,∴△ABD ≌△ECD (SAS ),∴AB =EC ,在△AEC 中,EC -AC <AE <EC +AC ,而AB =EC =7,AC =5,∴2<AE<12.又∵AE=2AD,∴1<AD<6,故答案为:EC,2,12,1,6;探索应用解:如图2,延长AE,CD交于H,∵点E是BC的中点,∴BE=CE,∵CD∥AB,∴∠ABE=∠ECH,∠H=∠BAE,∴△ABE≌△HCE(AAS),∴AB=CH=25,∴DH=CH-CD=17,∵∠DFE=∠BAE,∴∠H=∠DFE,∴DF=DH=17,故答案为:17;应用拓展证明:如图2,延长AP到点F,使PF=AP,连接DF,EF,AD,在△BPA与△EPF中,PF=AP∠EPF=∠BPA PE=PB,∴△BPA≌△EPF(SAS),∴AB=FE,∠PBA=∠PEF,∵AC=BC,∴AC=FE,在四边形BADE中,∠BAD+∠ADE+∠DEB+∠EBA=360°,∵∠BAC=60°,∠CDE=120°,∴∠CAD+∠ADC+∠DEB+∠EBA=180°.∵∠CAD+∠ADC+∠ACD=180°,∴∠ACD=∠DEB+∠EBA,∴∠ACD=∠FED,在△ACD与△FED中,AC=FE∠ACD=∠FED CD=DE,∴△ACD≌△FED(SAS),∴AD=FD,∵AP=FP,∴AP⊥DP.12已知△ABC中,(1)如图1,点E为BC的中点,连AE并延长到点F,使FE=EA,则BF与AC的数量关系是.(2)如图2,若AB =AC ,点E 为边AC 一点,过点C 作BC 的垂线交BE 的延长线于点D ,连接AD ,若∠DAC =∠ABD ,求证:AE =EC .(3)如图3,点D 在△ABC 内部,且满足AD =BC ,∠BAD =∠DCB ,点M 在DC 的延长线上,连AM 交BD 的延长线于点N ,若点N 为AM 的中点,求证:DM =AB.【答案】(1)BF =AC ;(2)见解析;(3)见解析【详解】证明:(1)BF =AC由题意可得:BE =EC在△BEF 和△CEA 中BE =EC∠BEF =∠CEAEF =AE∴△BEF ≌△CEA (SAS )∴BF =AC(2)过点A 引AF ∥CD 交BE 于点F ,如下图:由题意可得:CD ⊥BC ,且∠EAF =∠ACD则AF ⊥BC又∵AB =AC∴AF 平分∠BAC ,∴∠BAF =∠EAF =∠ACD∴在△ABF 和△CAD 中,∠ABF =∠DACAB =AC∠BAF =∠ACD∴△ABF ≌△CAD ASA ∴AF =CD在△AFE 和△CDE 中,∠FAE =∠DCE∠AEF =∠CEDAF =CD∴△AFE ≌△CDE AAS ∴AE =EC(3)证明:过点M 作MT ∥AB 交BN 的延长线于点T ,MG ∥AD ,在MT 上取一点K ,使得MK =CD ,连接GK ,如下图:∵ABMT∴∠ABN =∠T∵∠ANB =∠MNT ,AN =MN∴△ANB ≌△MNT (AAS)∴BN=NT,AB=MT∵MG∥AD∴∠ADN=∠MGN∵∠AND=∠MNG,AN=NM∴△AND≌△MNG(AAS)∴AD=MG,DN=NG∴BD=GT∵∠BAN=∠AMT,∠DAN=∠GMN∴∠BAD=∠GMT∵∠BAD=∠BCD∴∠BCD=∠GMK∵AD=BC,AD=GM∴BC=GM又∵MK=CD∴△BCD≌△GMK(SAS)∴GK=BD,∠BDC=∠MKG∴GK=GT,∠MDT=∠GKT∴∠GKT=∠T∴DM=MT∵AB=MT∴DM=AB·21·。
专题13 全等三角形重难点模型(五大模型)(原卷版)

专题13全等三角形重难点模型(五大模型)模型一:一线三等角型模型二:手拉手模型模型三:半角模型模型四:对角互补模型模型五:平行+线段中点构造全等模型【典例分析】【模型一:一线三等角型】如图一,∠D=∠BCA=∠E=90°,BC=AC。
结论:Rt△BDC≌Rt△CEA模型二一线三等角全等模型如图二,∠D=∠BCA=∠E,BC=AC。
结论:△BEC≌△CDA图一图二应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
【典例1】如图,平面直角坐标系中有点A(﹣1,0)和y轴上一动点B(0,a),其中a>0,以B点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).(1)当a=2时,则C点的坐标为;(2)动点B在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.【变式1】点A的坐标为(4,0),点B为y轴负半轴上的一个动点,分别以OB、AB为直角边在第三象限和第四象限作等腰Rt△OBC和等腰Rt△ABD.(1)如图一,若点B坐标为(0,﹣3),连接AC、OD.①求证:AC=OD;②求D点坐标.(2)如图二,连接CD,与y轴交于点E,试求BE长度.【典例2】(1)猜想:如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试猜想DE、BD、CE有怎样的数量关系,请直接写出;(2)探究:如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α(其中α为任意锐角或钝角)如果成立,请你给出证明;若不成立,请说明理由;(3)解决问题:如图3,F是角平分线上的一点,且△ABF和△ACF均为等边三角形,D、E分别是直线m上A点左右两侧的动点,D、E、A互不重合,在运动过程中线段DE的长度始终为n,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.【变式2】已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE =9cm,∠BDA=∠AEC=∠BAC(1)如图①,若AB⊥AC,则BD与AE的数量关系为,CE与AD 的数量关系为;(2)如图②,判断并说明线段BD,CE与DE的数量关系;(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.【模型二:手拉手模型】应用:①利用手拉手模型证明三角形全等,便于解决对应的几何问题;②作辅助线构造手拉手模型,难度比较大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
把一个图形经过平移、翻折、旋转后,它们的位置虽然变化了,但是形状、大小都没有改变,即平移、翻折、旋转前后的图形全等. 我们把平移、翻折(轴对称)、旋转称为几何变换. 这一讲我们就来学习基本变换下的全等三角形. 常见平移模型【引例】如图,A E F B 、、、四点在一条直线上,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =.求证:CF DE =模块一 平移型全等知识导航知识互联网夯实基础全等中的基本模型FEDCBA【解析】 ∵AC CE ⊥,BD DF ⊥∴90ACE BDF ∠=∠=︒ 在Rt ACE △和Rt BDF △中 AC BDAE BF =⎧⎨=⎩∴()Rt Rt HL ACE BDF △≌△ ∴CE DF =,AEC BFD ∠=∠ ∴CEF DFE ∠=∠ 在CEF △和DFE △中 CE DF CEF DFE EF FE =⎧⎪∠=∠⎨⎪=⎩∴CEF DFE △≌△ ∴CF DE =【例1】 如图1,A 、B 、C 、D 在同一直线上,AB CD =,DE AF ∥,且.DE AF =求证:AFC DEB △≌△如果将BD 沿着AC 边的方向平行移动,图2,B 点与C 点重合时;图3,B 点在C 点右侧时,其余条件不变,结论是否成立,如果成立,请选择一种情况请予证明;如果不成立,请说明理由.图1F EDC BA图2FE D(C )B A图3FEDCB A常见轴对称模型知识导航模块二 对称型全等能力提升【例2】 ⑴如图,△ABC 中,AB =AC ,BD ⊥AC 于D ,CE ⊥AB 于E ,BD和CE 交于点O ,AO 的延长线交BC 于F ,则图中全等直角三角形的对数为( )A.3对B.4对C.5对D.6对⑵如图,ABE △和ADC △是ABC △分别沿着AB ,AC 翻折到同一平面内形成的.若1:2:315:2:1∠∠∠=,则4∠=________.【例3】 如图,AB AC =,D 、E 分别是AB 、AC 的中点,AM CD ⊥于M ,AN BE ⊥于N .求证:AM AN =.常见旋转模型:夯实基础能力提升知识导航模块三 旋转型全等E D N M C B A 4321EDCBA D O FE CBA【引例】如图,在ABC △中,::3:5:10A B ACB ∠∠∠=,若将ACB △绕点C 逆时针旋转,使旋转后的A B C ''△中的顶点B '在原三角形的边AC 的延长线上时,求BCA '∠的度数.【解析】 ∵::3:5:10A B ACB ∠∠∠=∴1018010018ACB ∠=︒⨯=︒∵由ACB △绕点C 旋转得到A'B'C △∴100A'CB'∠=︒∵180ACB A'CB'BCA'∠+∠-∠=︒ ∴100218020BCA'∠=︒⨯-︒=︒【教师铺垫】如图,点C 为线段AB 上一点,ACM △、CBN △是等边三角形.请你证明:⑴AN BM =; ⑵60MFA ∠=; ⑶DEC △为等边三角形; ⑷DE AB ∥. 【例4】 如图1,若△ABC 和△ADE 为等边三角形,M 、N 分别EB ,CD 的中点,易证:CD=BE ,△AMN 是等边三角形.⑴当把△ADE 绕A 点旋转到图2的位置时,CD=BE 是否仍然成立?若成立请证明,若不成立请说明理由;⑵当把△ADE 绕A 点旋转到图3的位置时,△AMN 是否还是等边三角形?若是,请给出证明;若不是,请说明理由.能力提升夯实基础A'B'CBAM D NEC BFA图2图3图1MNMN N MA BCDE ABC D E ABC ED【例5】 如图1,若四边形ABCD 、GFED 都是正方形,显然图中有AG =CE ,AG ⊥CE .⑴当正方形GFED 绕D 旋转到如图2的位置时,AG =CE 是否成立?若成立,请给出证明,若不成立,请说明理由;⑵当正方形GFED 绕D 旋转到B ,D ,G 在一条直线 (如图3)上时,连结CE ,设CE 分别交AG 、AD 于P 、H ,求证:AG ⊥CE .PHG GG图1图3图2FABCEF ABC DEABC DEF D辅助线:在几何学中用来帮助解答疑难几何图形问题,在原图基础之上另外所作的具有极大价值的直线或者线段.添辅助线的作用:凸显和集散1. 揭示图形中隐含的性质:当条件与结论间的逻辑关系不明朗时,通过添加适当的辅助线,将条件中隐含的有关图形的性质充分揭示出来,以便取得过渡性的推论,达到推导出结论的目的.2. 聚拢集中原则:通过添置适当的辅助线,将图形中分散、远离的元素,通过变换和转化,使他们相对集中,聚拢到有关图形上来,使题设条件与结论建立逻辑关系,从而推导出要求的结论.3. 化繁为简原则:对一类几何命题,其题设条件与结论之间在已知条件所给的图形中,其逻辑关系不明朗,通过添置适当辅助线,把复杂图形分解成简单图形,从而达到化繁为简、化难为易的目的.4. 发挥特殊点、线的作用:在题设条件所给的图形中,对尚未直接显现出来的各元素,通过添置知识导航模块四 辅助线添加初步适当辅助线,将那些特殊点、特殊线、特殊图形性质恰当揭示出来,并充分发挥这些特殊点、线的作用,达到化难为易、导出结论的目的.5. 构造图形的作用:对一类几何证明题,常须用到某种图形,这种图形在题设条件所给的图形中却没有发现,必须添置这些图形,才能导出结论,常用方法有构造出线段和角的和差倍分、新的三角形、直角三角形、等腰三角形等.【例6】 如图△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F .⑴说明BE =CF 的理由;⑵如果AB =a ,AC =b ,求AE 、BE 的长.【例7】 如图1,已知ABC △中,1AB BC ==,90ABC =︒∠,把一块含30︒角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF ),将直角三角板DEF 绕D 点按逆时针方向旋转.直线DE 交直线AB 于M ,直线DF 交直线BC 于N . ⑴ 在图1中, ①证明DM DN =;②在这一旋转过程中,直角三角板DEF 与ABC △的重叠部分为四边形DMBN ,请说明四边形DMBN 的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积; ⑵ 继续旋转至如图2的位置,DM DN =是否仍然成立?若成立,请给出证明;若不成立,请说明理由;⑶ 继续旋转至如图3的位置,DM DN =是否仍然成立?请写出结论,不用证明.能力提升GDABC EF图3图2图1FFFEEEDDDC CCBB BAAA【例8】 如图所示:AF CD =,BC EF =,AB DE =,A D ∠=∠.求证:BC EF ∥.训练1. 如图所示:AB AC =,AD AE =,CD 、BE 相交于点O .求证:AO 平分DAE ∠. 思维拓展训练(选讲)探索创新A BCD EFABCDEO NM训练2. 如图,BD CE 、分别是ABC △的边AC 和AB 边上的高,点P 在BD的延长线上,BP AC =,点Q 在CE 上,CQ AB =. 求证:⑴AP AQ =;⑵AP AQ ⊥.训练3. 在凸五边形中,B E ∠=∠,C D ∠=∠,BC DE =,M 为CD 中点.求证:AM CD ⊥.训练4. 如图,AB AE =,ABC AED ∠=∠,BC ED =,点F 是CD 的中点.求证:AF CD ⊥.F EDC BAQPEDCB AM EDC B A题型一 平移型全等 巩固练习【练习1】 ⑴ 如图⑴,若AB CD =,A E F C 、、、在一条直线上,AE CF =,过E F 、分别作DE AC ⊥,BF AC ⊥.求证:BD 平分EF .⑵ 若将DEC △的边EC 沿AC 方向移动到图⑵的位置时,其他条件不变,上述结论是否成立?请说明理由.(2)(1)ABCDE F GGFEDC BA题型二 对称型全等 巩固练习【练习2】 如图,已知Rt △ABC ≌Rt △ADE ,90ABC ADE ∠=∠=︒,BC 与DE 相交于点F ,连接CD 、EB .⑴图中还有几对全等三角形,请你一一列举; ⑵求证:CF=EF .题型三 旋转型全等 巩固练习【练习3】 如图,在Rt ABC △中,AB AC AD BC =⊥,,垂足为D .E F 、 实战演练F EDCBA F E D CB A分别是CD AD 、上的点,且CE AF =.如果62AED ∠=︒,那 么DBF ∠=__________.【练习4】 如图,已知ABD △和AEC △都是等边三角形,AF CD ⊥于F ,AH BE ⊥于H ,请问:AF 和AH 有何 关系?请说明理由.题型四 辅助线添加初步 巩固练习 【练习5】 如图①,一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转. ⑴ 如图②,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 满足的数量关系,并证明你的猜想;⑵ 若三角尺GEF 旋转到如图③所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与G 的延长线相交于点N ,此时,⑴中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.③②①OOCB DAFGENMEGFADBCCB(E)A(G)O H FE D C B A。
