2020最新湘教版九年级数学下册教学课件(所有课时)
合集下载
湘教版九年级下册数学精品教学课件 第1章 二次函数 不共线三点确定二次函数的表达式
一般式法求二次函数的表达式
探究归纳 问题1 （1）二次函数 y = ax2+bx+c ( a ≠ 0 )中有几个
待定系数？需要几个抛物线上的点的坐标才能求出来？
3个
3个
（2）下面是我们用描点法画二次函数的图象所列表
格的一部分，要求这个二次函数的表达式.
x -3 -2 -1 0 1 2
y 0 1 0 -3 -8 -15
A．8
B．14
C．8或14
D．-8 或 -14
7. 如图，抛物线 y＝x2＋bx＋c 过点A(－4，－3)，与 y 轴交于点 B，对称轴是 x＝－3，请解答下列问题：
(1) 求抛物线的表达式； 解：把点 A(－4，－3)代入 y＝x2＋bx＋c 得16－4b＋c ＝－3，c－4b＝－19. ∵对称轴是 x＝－3，∴ b ＝－3，
数的表达式. 解：设这个二次函数的表达式是 y = a(x - h)2 +k， 把顶点 (-2，1) 代入 y = a(x - h)2 +k 得 y = a(x + 2)2 +1， 再把点(1，-8) 代入上式得 a(1+2)2 + 1 = -8，解得 a = -1. ∴所求的二次函数的表达式是 y = -(x + 2)2 +1 或 y = -x2 - 4x -3.
再把点( 0，-3)代入上式得 所以 a( 0 + 3 )( 0 + 1 ) = -3， 解得 a = -1， 所以所求的二次函数的表达式是 y = -( x + 3)( x +1 )，即 y = -x2 - 4x -3.
归纳总结 交点法求二次函数解析式的方法 这种已知抛物线 x 轴的交点，求表达式的方法叫做交点法. 其步骤是：
2020版九年级数学下册第1章二次函数1.2二次函数的图象与性质(第3课时)课件湘教版
抛物线y= a(x-h)2+k
a>0
对称轴 x=_h_
顶点 坐标
_(_h_,_k_)_
开口 方向
_向__上__
a<0
x=_h_ _(_h_,_k_)_ _向__下__
在对称轴 的左边
y随x的增大 而__减__小__
y随x的增大 而__增__大__
在对称轴 的右边
y随x的增大 而__增__大___
y随x的增大 而__减__小__
C.y=(x-2)2-3
D.y=(x+2)2-3
★3.一抛物线和抛物线y=-2x2的形状、开口方向 完全相同,顶点坐标是(-1,3),则该抛物线的表达式 为___y_=_-_2_(_x_+_1_)_2+_3___.
★★4.已知二次函数图象的顶点是M(1,-9),且经过点 (-1,-5). 世纪金榜导学号 (1)求这个二次函数的表达式. (2)画出它的图象,并求出它的图象与x轴正半轴的交点 A的坐标,与y轴的交点B的坐标. (3)如果点O是原点,求四边形AOBM的面积.
【母题变式】 【变式一】已知二次函数的最小值为-1,当x>3时,y随x 的增大而增大,当x <3时,y随x的增大而减小,当x=4 时,y的值是1,求此二次函数的表达式.
解:∵当x>3时,y随x的增大而增大, 当x <3时,y随x的增大而减小, ∴该二次函数的图象关于直线x=3对称, 又∵二次函数的最小值为-1, ∴该二次函数的顶点为(3,-1),
1.2 二次函数的图象与性质 第3课时
【知识再现】 抛物线y=a(x-h)2的图象可由y=ax2经左右平移得到, 当h>0时,向右平移___h___个单位,当h<0时,向左平移 ___|_h_|___个单位.
1.2 第3课时 二次函数的图象与性质-2024-2025学年九年级数学下册课件(湘教版)
直线x=h
（h,k）
当x=h时，y最小值=k
当x＜h时，y随x的 增大而减小；x＞h 时，y随x的增大而 增大.
a＜0
向下 直线x=h
（h,k）
当x=h时，y最大值=k 当x＞h时，y随x的 增大而减小；x＜h 时，y随x的增大而 增大.
练一练
1点．坐标抛是物_线(_0_,-y_6_)_，12它x可2 以 看6 作的是开由口抛__向物__上线__，对y 称 轴12 是x2___y向_轴____下__，平顶
横坐标
a a
纵坐标
1 a-12
2
1 a-12 3
2
观察上表你 发现了什么？
从上表看出： 对于每一个相同的x 值， 函数
y
1 2
(
x
1)2
3的值都要比函数
y
1 2
(
x
1)2
的值大3，
y
8
y
1 2
(
x
1)2
3
76Leabharlann 5 4y1 2
(x
1)2
3
2
1
-4
-3
-2
y
1 2
(
x
1)2
-1
O1
2
3
4
5
6x
向上平移3个单位
y
1 2
(
x
1)2
3
探究三、 将二次函数
y
1 2
(x
1)2
的图象向下平移 7 个单位，
得到的是哪个函数的图象？
y
1 2
(
x
1)2
7
探究四、二次函数 y a( x h)2 与 y a(x h)2 k
（h,k）
当x=h时，y最小值=k
当x＜h时，y随x的 增大而减小；x＞h 时，y随x的增大而 增大.
a＜0
向下 直线x=h
（h,k）
当x=h时，y最大值=k 当x＞h时，y随x的 增大而减小；x＜h 时，y随x的增大而 增大.
练一练
1点．坐标抛是物_线(_0_,-y_6_)_，12它x可2 以 看6 作的是开由口抛__向物__上线__，对y 称 轴12 是x2___y向_轴____下__，平顶
横坐标
a a
纵坐标
1 a-12
2
1 a-12 3
2
观察上表你 发现了什么？
从上表看出： 对于每一个相同的x 值， 函数
y
1 2
(
x
1)2
3的值都要比函数
y
1 2
(
x
1)2
的值大3，
y
8
y
1 2
(
x
1)2
3
76Leabharlann 5 4y1 2
(x
1)2
3
2
1
-4
-3
-2
y
1 2
(
x
1)2
-1
O1
2
3
4
5
6x
向上平移3个单位
y
1 2
(
x
1)2
3
探究三、 将二次函数
y
1 2
(x
1)2
的图象向下平移 7 个单位，
得到的是哪个函数的图象？
y
1 2
(
x
1)2
7
探究四、二次函数 y a( x h)2 与 y a(x h)2 k
湘教版数学九年级下册1.2二次函数的图象与性质(第5课时)课件(共14张PPT)
3 开始取值 2
列表：自变量x从顶点的横坐标
x
3 7 y 2 x 2 2
2
3 2
2
3
5 2
3
－1
7 2
7 2
3 2
9 2
描点和连线：画出图象在对称轴右边的部分. 利用对称性，画出图象在对称轴左边的部分，这样就得到 函数 y 2x2 6x 1 的图象，如图
2
=-2(x -3x)-1
3 2 3 2 2 =-2 x 3 x ( ) ( ) 1 2 2
2
3 9 2( x ) 2 2 1 2 4
3 2 7 2( x ) 2 2
对称轴是直线
3 ，顶点坐标是 3 , 7 x 2 2 2
a 2 0 有最大值为5
3 1 x 2 4
2
顶点坐标为
3 1 , 2 4
2
y 2x 8x 3
2
3 2 x 2 4 x 2
3 2 2 x 4 x 4 4 2
2 x 2 5
2 （当a>0）：4ac b 4a
二次函数y=ax2+bx+c(a≠0)的图象和性质
１.顶点坐标与对称轴
２.位置与开口方向
３.增减性与最值 根据图形填表： 抛物线 顶点坐标 对称轴
y=ax2+bx+c(a>0) b 4ac b 2 2a , 4a b 直线x 2a
1 2 x 2 1 2
顶点坐标是（2，1），于是当x=2时，y达到最大值1.
2 一般地，对于二次函数 y ax bx c
列表：自变量x从顶点的横坐标
x
3 7 y 2 x 2 2
2
3 2
2
3
5 2
3
－1
7 2
7 2
3 2
9 2
描点和连线：画出图象在对称轴右边的部分. 利用对称性，画出图象在对称轴左边的部分，这样就得到 函数 y 2x2 6x 1 的图象，如图
2
=-2(x -3x)-1
3 2 3 2 2 =-2 x 3 x ( ) ( ) 1 2 2
2
3 9 2( x ) 2 2 1 2 4
3 2 7 2( x ) 2 2
对称轴是直线
3 ，顶点坐标是 3 , 7 x 2 2 2
a 2 0 有最大值为5
3 1 x 2 4
2
顶点坐标为
3 1 , 2 4
2
y 2x 8x 3
2
3 2 x 2 4 x 2
3 2 2 x 4 x 4 4 2
2 x 2 5
2 （当a>0）：4ac b 4a
二次函数y=ax2+bx+c(a≠0)的图象和性质
１.顶点坐标与对称轴
２.位置与开口方向
３.增减性与最值 根据图形填表： 抛物线 顶点坐标 对称轴
y=ax2+bx+c(a>0) b 4ac b 2 2a , 4a b 直线x 2a
1 2 x 2 1 2
顶点坐标是（2，1），于是当x=2时，y达到最大值1.
2 一般地，对于二次函数 y ax bx c
湘教版九年级下册数学精品教学课件 第2章 圆 第2课时 切线的性质
∴ ∠CAD = ∠CAO. 故 AC 平分∠DAB.
方法总结
利用切线的性质解题时，
常需连接辅助线，一般连接圆
心与切点，构造直角三角形， A
再利用直角三角形的相关性质
解题.
D C
O
B
例2 证明：经过直径两端点的切线互相平行.
已知：如图，AB 是圆 O 的直径，l1，l2 分别是经过
点 A，B 的切线. 求证：l1 // l2. 证明：∵AB 是圆 O 的直径，
在 △OAF 和 △OCF 中， OA ＝ OC，∠3 ＝ ∠2，OF ＝ OF， ∴△OAF ≌ △OCF（SAS）. ∴∠OAF = ∠OCF. ∵PC 是 ⊙O 的切线， ∴∠OCF = 90°， ∴∠OAF = 90°， ∴FA ⊥ OA. ∴AF 是 ⊙O 的切线.
（2）若 ⊙O 的半径为 4，AF = 3，求 AC 的长．
合作探究
切线的性质
问题1 如果直线 l 是 ⊙O 的切线，A 为切点，那么切
线 l 和半径 OA 垂直吗？
O
A
l
大家可以先用量角器 量量看.
两者成 90°角，也 就是说切线 l 与半
径 OA 垂直.
推导与验证 反证法证明这个结论
假设 l 与 OA 不垂直
则过点 O 作 OM ⊥ l，垂足为 M
4. 如图，PA 为 ⊙O 的切线，A 为切点．直线 PO 与
⊙O交于 B、C 两点，∠P ＝ 30°，连接 AO、AB、AC.
(1) 求证：△ACB ≌ △APO；
(1) 证明：∵PA 为 ⊙O 的切线，A 为切点， ∴∠OAP ＝ 90°. 又∵∠P ＝ 30°，∴∠AOB ＝ 60°， 又OA ＝ OB，∴△AOB 为等边三角形． ∴AB ＝ AO，∠ABO ＝ 60°.
1新湘教版九年级下册1.1二次函数教学课件(共12张PPT)
函数y ax2 bx c(其中a,b, c是常数)， 当a,b, c满足什么条件时
(1)它是二次函数? (2)它是一次函数？
(3)它是正比例函数？
第9页，共12页。
例：
一块矩形木板，长为120CM、宽为80CM，在木板4个角上 各截去边长为X（cm)的正方形，求余下面积S(cm)与X之
间的函数表达式。
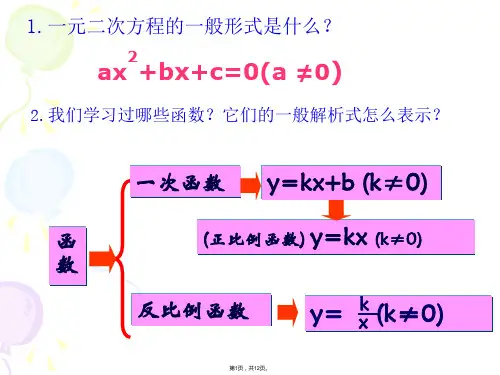
1.一元二次方程的一般形式是什么？
2
ax +bx+c=0(a
≠0)
2.我们学习过哪些函数？它们的一般解析式怎么表示？
一次函数 y=kx+b (k≠0)
函
(正比例函数) y=kx (k≠0)
数
反比例函数
y=
k x
(k≠0)
第1页，共12页。
1.1 二次函数的基本概念
第2页，共12页。
学校准备在校园里利用围墙的一段和篱笆墙围成一 个矩形植物园，已知篱笆墙的总长度为100m，设与 围墙相邻的一篱笆墙的长度都为x（m），求矩形植物
(7) y＝ x2 5x 6 (否) (8)y=mx²+nx+p (m,n,p为常数）
(否)
(否)
(9) y=3(x－1)²-3
(是)
(10)y=(x+3)²－x²
第6页，共12页。
(否)
y=ax2+bx+c (a、b、c为常数,a≠0)
(1)等号左边是函数y，右边是关于自变量x的 整式
(2) a,b,c为常数，且
a≠0.
(3)等式右边的最高次数为 ，可2以没有一次项和 常数项，但 不能没有二次项.
二次函数的特殊形式：
当b＝0时， y＝ax2＋c
当c＝0时， y＝ax2＋bx
(1)它是二次函数? (2)它是一次函数？
(3)它是正比例函数？
第9页，共12页。
例：
一块矩形木板，长为120CM、宽为80CM，在木板4个角上 各截去边长为X（cm)的正方形，求余下面积S(cm)与X之
间的函数表达式。
1.一元二次方程的一般形式是什么？
2
ax +bx+c=0(a
≠0)
2.我们学习过哪些函数？它们的一般解析式怎么表示？
一次函数 y=kx+b (k≠0)
函
(正比例函数) y=kx (k≠0)
数
反比例函数
y=
k x
(k≠0)
第1页，共12页。
1.1 二次函数的基本概念
第2页，共12页。
学校准备在校园里利用围墙的一段和篱笆墙围成一 个矩形植物园，已知篱笆墙的总长度为100m，设与 围墙相邻的一篱笆墙的长度都为x（m），求矩形植物
(7) y＝ x2 5x 6 (否) (8)y=mx²+nx+p (m,n,p为常数）
(否)
(否)
(9) y=3(x－1)²-3
(是)
(10)y=(x+3)²－x²
第6页，共12页。
(否)
y=ax2+bx+c (a、b、c为常数,a≠0)
(1)等号左边是函数y，右边是关于自变量x的 整式
(2) a,b,c为常数，且
a≠0.
(3)等式右边的最高次数为 ，可2以没有一次项和 常数项，但 不能没有二次项.
二次函数的特殊形式：
当b＝0时， y＝ax2＋c
当c＝0时， y＝ax2＋bx
湘教版九年级下册数学精品教学课件 第1章 二次函数 第1课时 抛物线形二次函数
实际 问题
建立二次 函数模型
利用二次函数的图象 和性质求解
实际问题的解
典例精析 例1 某公园要建造圆形喷水池，在水池中央 垂直于水面处安装一个柱子 OA，O 恰在水面中心， OA=1.25 m，由柱子顶端 A 处的喷头向外喷水，水流在各 个方向沿形状相同的抛物线落下，为使水流形状较为漂
亮，要求设计成水流在离 OA 距离为 1 m处达到距水面最 大高度 2.25 m.如果不计其它因素，那么水池的半径至少 要多少才能使喷出的水流不致落到池外？
探究 你能想出办法来吗？
建立函数模型
这是什么样的函数呢？ 拱桥的纵截面是抛物线， 所以应当是个二次函数
怎样建立直角坐标系比较简单呢？
以拱顶为原点，抛物线的对称轴为 y 轴，建立直角坐标系，如图．
从图看出，什么形式的二次函数图象是 这条抛物线呢？
由于顶点坐标是(0，0)， 因此这个二次函数的
形式为 y ax2 (a 0)
-2 -1 -2
-4
12
A
如何确定 a 是多少？ 已知水面宽 4 m 时，
-2 -1
12
拱顶离水面高 2 米，
-2
A
因此点 A( 2，-2)在抛物线上，
由此得出 2 a 22，解得 a 1 .
-4
因此，y 1 x2
2
，其中 ｜x｜是水面宽度的一半，y 是
2
拱顶离水面高度的相反数，这样我们就可以了解到水
设最多可安装 n 扇窗户， ∴1.5n + 0.8(n﹣1) + 0.8×2 ≤10.14， 解得 n ≤ 4.06．则最大的正整数为 4． 答：最多可安装 4 扇窗户.
5. 悬索桥两端主塔塔顶之间的主悬钢索，其形状可近似
2.5.3切线长定理课件(22张PPT)2023-2024学年湘教版数学九年级下册
B
课堂小结
切线长
切线长 定理
经过圆外一点作圆的切线，这点和切点 之间的线段的长.
内容
过圆外一点所画的圆的两条切线长 相等，圆心和这一点的连线平分两 条切线的夹角.
作用
提供了证线段和 角相等的新方法
辅助线
① 分别连接圆心和切点； ② 连接两切点； ③ 连接圆心和圆外一点.
A
∵PA和PB是⊙O的两条切线，
∴OA⊥AP，OB⊥BP.
O
P
又OA=OB,OP=OP.
∴Rt△AOP ≌ Rt△BOP.
B
∴PA=PB,∠APO=∠BPO.
归纳
由此得到切线长定理：
过圆外一点所画的圆的两条切线，它们的切线长相等.这一点和圆心的连
线平分两条切线的夹角.
A
几何语言:
PA = PB
O
P
B
OM
P
A
方பைடு நூலகம்总结
切线长问题辅助线的添加方法： （1）分别连接圆心和切点； （2）连接两切点； （3）连接圆心和圆外一点.
随堂练习
1. 如图, P 为☉O 外一点, PA , PB 分别切☉O 于点 A , B , CD 切☉O 于点 E 且分别交 PA , PB 于点 C , D ．若 PA ＝ 4 , 则△PCD 的周长 为（ C ）
归纳
切线长定义：
我们把圆的切线上某一点与切点之间的线段的
A
长叫做这点到圆的切线长.
O
P
如图，PA，PB为⊙O的两条切线，点A、B为
B
切点. 线段PA、PB的长就是点P到⊙O的切线长.
注意：切线是直线，不可度量； 切线长是切线上一点与切点之间的线段的长，可以度量.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020最新湘教版九年级数学下册 教学课件(所有课时)目录
0002页 0063页 0105页 0137页 0170页 0257页 0310页 0341页 0384页 0436页 0476页
第1章 二次函数 1.2 二次函数的图像与性质 1.4 二次函数与一元二次方程的联系 第2章 圆 2.2 圆心角、圆周角 2.4 过不共线三点作圆 2.6 弧长与扇形面积 第3章 投影与视图 3.3 三视图 4.1 随机事件与可能性 4.3 用频率估计概率
2020最新湘教版九年级数最新湘教版九年级数学下册教 学课件(所有课时)
1.1 二次函数
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.2 二次函数的图像与性质
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.3 不共线三点确定二次函数的 表达式
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.4 二次函数与一元二次方程的 联系
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.5 二次函数的应用
0002页 0063页 0105页 0137页 0170页 0257页 0310页 0341页 0384页 0436页 0476页
第1章 二次函数 1.2 二次函数的图像与性质 1.4 二次函数与一元二次方程的联系 第2章 圆 2.2 圆心角、圆周角 2.4 过不共线三点作圆 2.6 弧长与扇形面积 第3章 投影与视图 3.3 三视图 4.1 随机事件与可能性 4.3 用频率估计概率
2020最新湘教版九年级数最新湘教版九年级数学下册教 学课件(所有课时)
1.1 二次函数
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.2 二次函数的图像与性质
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.3 不共线三点确定二次函数的 表达式
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.4 二次函数与一元二次方程的 联系
2020最新湘教版九年级数学下册教 学课件(所有课时)
1.5 二次函数的应用