理论力学--动力学习题+答案
理论力学动力学部分试题及答案

1物体自地球表面以速度眄铅直上抛.试求该物体返回地面时的速度巧・假定空气阻力R=mkv2,其中k是比例常量,搜数值它等于单位质量在单位速度时所受的阻力。
m是物体质V 是物体速度,重力加速度认为不变.答:叮解:阻力方向在上升与下降阶段不同(其方向与速度y相反),故分段考虑(1)上升阶段:tn— - -tng一dt通过坐标变换有加V字二-刃护-加£ ,积分得axvdv(2)下落阶段:(1)g2.静止中心0以引力F=k2mr吸弓I质量是m的质点M,其中k是比例常量,r=OM是点M的矢径.运动开始时OMo=b,初速度时呵并与阪成夹角求质点M的运动方程。
x = b cos 处 + —cosasin ktky = —sinasin^k解:取坐标如图,质点M在任意位貳将fna = F 沿x、y轴投彫,得mx = 一F cos<p= -k2fnrcos (p= -Qmxfny = 一Fsin cp= -k2fnr sin (p= -k^my艮卩x+k2x = 0 , y+^2y = 0徽分方程得通解为:x = s coskt+c2 sin kt求导得x = -kc x sin kt + kc2 coskt , y = -kc3 sin kt + kc^ cos kt (2)已知初始条件f=0 z 妒b z /o=0,x0 = v0 sin a ,代入方程(1),(2)得点M的运动方程为v =—cosax = 2?cos Ar/ +—kcos ar sin kt -I sin asin kt y =c3 cos kt + c^ sin kt (1)九=v0 sin a3单摆M 的悬线长/,摆重G 支点B 具有水平向左的均加速度a.如将摆在&=0处静止 释啟,试确定悬线的张力T (表示成&的函数).解:质点的相对徴分方程为 ma r = mg+f +©投影到法线方向由式(2)得T = Gsin3 + —acos0 + — v 2g 0T = G 3 sin + 3 — cos — 2 —\ g S )答・ T - G(3sin3-cos^- 2-) g g投影到切线方向= T-Gsin^-0e cosB g !(2)由式(1)得 妙=gcos^-usin 0分离变量并积分|*V Xiv = \ f geos^10- [ asm Odd v 2 = 2"gsin &+ocos&-a 1(3)将式(3)代入上式代入式(2)得dt dt积分得4.水平面内弯成任意形状的细管以匀角速度G 绕点0转动.光滑小球M 在管內可自由 运动.设初瞬时小球在吆处,OMo=©相对初速^v o =0,求小球相对速度大小冬与极径r的关系。
理论力学课后答案-谢传峰、王琪-动力学第九章、第十章

1 2
2l m dx(
x sin )2 0 2l
2 ml 2
2 sin2 3
O C
系统的动能 T T1 T2 。 取 900 为势能零点,则系统的势能为:
V mgl cos
则拉格朗日函数:
L T V 2 ml2 (2
2 sin2 ) mgl cos 3
x
楔块 B 的速度 vB ,以及 B 相对于 A 的相对速度
满足如下的矢量关系(方向如图所示):
vB vA vBr
系统的动能为:
vBr vA
T
1 2
m
Av
A
2
1 2
mBvB 2
P1 2g
x 2
P2 2g
[(x
s cos)2
(ssin)2 ]
1 2g
(P1
P2 )x 2
度
转动。物体的质心 G 在垂直于 O1O2 的直线上,O3G l 。设 O1O2 和 O3G 是物体过 O3
点的惯量主轴,转动惯量为 J1 和 J 2 ,物体对另一过 O3 点的惯量主轴的转动惯量为 J 3 ,试
求物体的动能表达式并建立物体的运动微分方程。 解:
以该物体为研究对象,有一个自由度,取 O3G 和 OC 的夹角 为广义坐标。若以框架 O1O2OC 为动系,则物体的相对运动是以角速度 绕轴 O1O2 的定轴转动,牵连运动是以角 速度
垂直于 O1O2 的平面
z’
O3
θ G
y’
坐标系 O3 x y z 的三个坐标轴为过 O3 点的三个惯量主轴,则系统的动能为:
T
理论力学习题答案
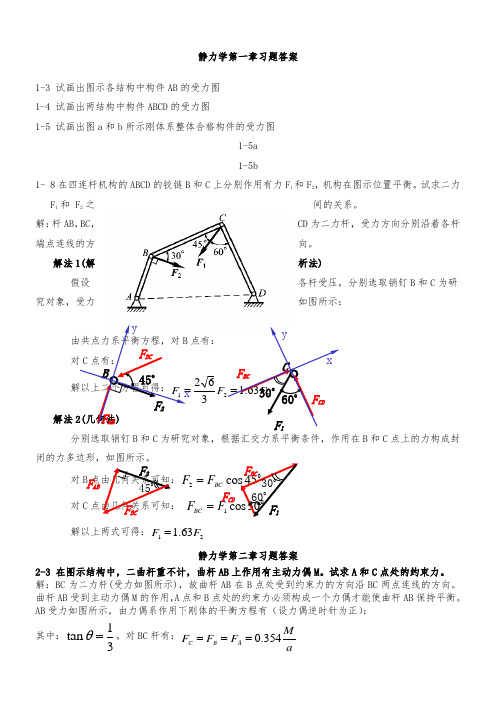
静力学第一章习题答案1-3 试画出图示各结构中构件AB 的受力图 1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a 1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:点有:362F 解法分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 2BC F F = 对C 1F F BC =解以上两式可得:2163.1F F =静力学第二章习题答案2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正): 其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== x F CD F ABA ,C 两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
对BC 杆有: 0=∑M030sin 20=-⋅⋅M C B F B对AB 杆有: A B F F = 对OA 杆有: 0=∑M01=⋅-A O F M A求解以上三式可得:m N M ⋅=31, N F F F C O AB 5===,方向如图所示。
《理论力学》动力学典型习题+答案
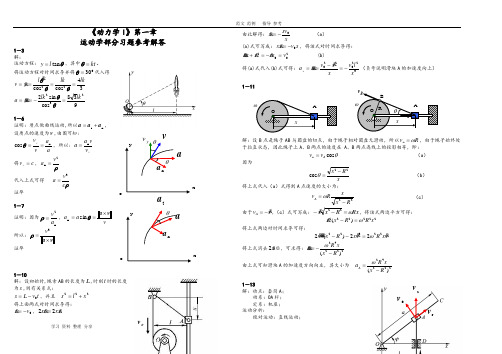
学习 资料 整理 分享《动力学I 》第一章 运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l y v ====θθθ 938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n v a =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得: 0v s-= ,x x s s 22= 由此解得:xsv x-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-==(负号说明滑块A 的加速度向上)1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为xR x 22cos -=θ (b ) 将上式代入(a )式得到A 点速度的大小为: 22Rx x Rv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222)(x R R x xω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后,可求得:22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左,其大小为 22242)(R xxR a A -=ω1-13解:动点:套筒A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动;o vo va ve vr vxovxot学习 资料 整理 分享 相对运动:直线运动; 牵连运动:定轴转动。
理论力学习题及解答1
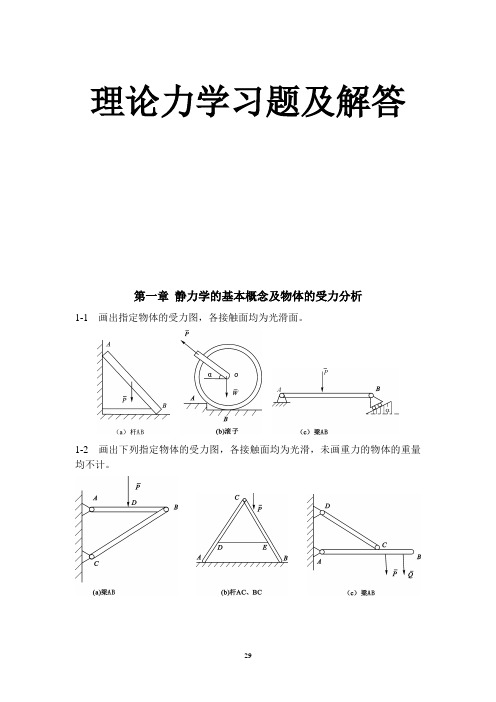
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
922144-理论力学之动力学-第二章d大纲习题

1.质点系的动量
n
p mivi
i 1
2.微分形式
dp
dt
n
Fi (e)
i 1
FR(e)
3.积分形式
pt2
pt1
n
I
(e) i
i 1
t2 t1
FR(e)dt
动量守恒
当:FRe 0
n
当: Fxei 0
i 1
则: p p0
则: px p0x
9
小结
一、动量定理
质点系相对定点与相对运动点动量矩的关系
Lo rA mvC rAC mvA LrA
Lo rC mvC LrC
质点系相对于动点的动量矩定理
dLrA
dt
n i1
M A(Fi(e) ) rAC
(maA)
质点系相对于质心的动量矩定理
dLrC
dt
n i1
MC (Fi(e) )
12
小结
三、动能定理
绳索AM的拉力与未剪断绳索 BM时相比,是增大了还是减
小了? =?绳索AM的拉力
不变。
剪断前: F mg
2 cos 剪断后: F mg cos
2
物块A、B放在半径为R处于静
止的水平圆盘的边缘,两者间的静
滑动摩擦因数为f,物块的质量分别
为mA > mB,将物块视为质点。圆盘
以角速度ω=αt 绕铅垂轴转动。
i1
Lo rC mv
Lz J z
2.相对于惯性参考系中定点的动量矩定理
dLo
dt
n
Mo (Fi(e))
i1 n
守恒情况: Mo (Fi(e)) 0 则:Lo (t) Lo (t0 )
动力学第一章习题解答(运动学部分)

《动力学I 》第一章 运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lk lk l yv ====θθθ938cos sin 2232lk lk ya =-==θθ1-6证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:aa v v y n cos ==θ,所以: yv v a a n =将c v y =,ρ2n va =代入上式可得 ρc va 3=证毕1-7证明:因为n2a v=ρ,va a v a ⨯==θsin n所以:va ⨯=3vρ证毕xoxoa1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s+=将上面两式对时间求导得:0v s-= ,x x s s 22= 由此解得:xsv x0-= (a )(a)式可写成:s v xx 0-= ,将该式对时间求导得: 2002v v s x x x=-=+ (b) 将(a)式代入(b)式可得:3220220xl v xxv xa x -=-== (负号说明滑块A 的加速度向上)1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为xR x 22cos -=θ (b )将上式代入(a )式得到A 点速度的大小为: 22Rx x Rv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222)(x R R x xω=- o vo v将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=-- 将上式消去x 2后,可求得:22242)(R x x R x--=ω由上式可知滑块A 的加速度方向向左,其大小为 22242)(R x x R a A -=ω1-13解:动点:套筒A ;动系:OA 杆; 定系:机座;运动分析:绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。
《理论力学》习题三答案

《理论力学》习题三答案一、单项选择题(本大题共30小题,每小题2分,共60分)1. 求解质点动力学问题时,质点的初始条件是用来( C )。
A 、分析力的变化规律; B 、建立质点运动微分方程; C 、确定积分常数; D 、分离积分变量。
2. 在图1所示圆锥摆中,球M 的质量为m ,绳长l ,若α角保持不变,则小球的法向加速度为( C )。
A 、αsin g ;B 、αcos g ;C 、αtan g ;D 、αtan gc 。
3. 已知某点的运动方程为2bt a S +=(S 以米计,t 以秒计,a 、b 为常数),则点的轨迹为( C )。
A 、是直线;B 、是曲线;C 、不能确定;D 、抛物线。
4. 如图2所示距地面H 的质点M ,具有水平初速度0v,则该质点落地时的水平距离l 与( B )成正比。
A 、H ; B、H ; C 、2H ;D 、3H 。
5. 一质量为m 的小球和地面碰撞,开始瞬时的速度为1v ,碰撞结束瞬时的速度为2v(如图3),若v v v ==21,则碰撞前后质点动量的变化值为( A )。
A 、mv ;B 、mv 2 ;C 、mv 3;D 、 0。
6. 一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量( B )。
A 、平行; B 、垂直; C 、夹角随时间变化; D 、不能确定。
7. 三棱柱重P ,放在光滑的水平面上,重Q 的匀质圆柱体静止释放后沿斜面作纯滚动,则系统在运动过程中( A )。
A 、沿水平方向动量守恒,机械能守恒;B 、动量守恒,机械能守恒;C 、沿水平方向动量守恒,机械能不守恒;D 、均不守恒。
图1图2图38. 动点M 沿其轨迹运动时,下列几种情况中,正确的应该是( A )。
A 、若始终有a v⊥,则必有v 的大小等于常量; B 、若始终有a v ⊥,则点M 必作匀速圆周运动;C 、若某瞬时有v ∥a,则点M 的轨迹必为直线;D 、若某瞬时有a 的大小为零,且点M 作曲线运动,则此时速度必等于零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P 2g
r aC
P g
2r aC
M
2Pr
;
aC
2(M 2P r) 5P r
g
当M >2Pr 时,aC 0 ,圆柱B的质心将上升。
理论力学电子教程
第八章 质点的运动微分方程
代入(3)、(4)并结合(2)式得:
A
B
2g 5r
aC
4 5
g
理论力学电子教程
第八章 质点的运动微分方程
(2)选圆柱A为研究对象
1 2
P g
r 2
A
M
Tr
(1)
选圆柱B为研究对象
1 2
P g
r
2
B
T
'
r
(2)
P g
aC
T 'P
(3)
运动学关系: aC ae ar r A r B (4)
3 4
mR2 2
T 1 mv2 1 mR2 2
2
4
理论力学电子教程
A
O
第八章 质点的运动微分方程
图示行星齿轮机构,已知系杆OA长为 2r,质量为m,行星齿轮可视为均质轮 ,质量为m,半径为r,系杆绕轴O转动
的角速度为。则该系统动量主矢的大
小为( 3mr ),对轴O的动量矩大小 为(13 mr2 ), 系统动3能为( 11 mr2 2 )。
由(1)~(4)式得:
B
4gM 2g 5 Pr2
Pr
A
6gM 5
2g Pr2
Pr
aC
2gM 4g 5Pr
Pr
2g(M 2Pr) 5Pr
当M >2Pr 时,aC 0 ,圆柱B的质心将上升。
理论力学电子教程
第八章 质点的运动微分方程
(2)也可以取整个系统为研究对象
LO
P 2g
0
xC1 xC 2
x
y
甲乙
m1g m2g
Mg
乙
首
x
甲
Mx m1(x 1.5) m2 (x 0.5) 0
x 0.5m2 1.5m1 30 75
m1 m2 M
260
x m2 g
Mg m1g
0.173m(实际应向左位移)
理论力学电子教程
第八章 质点的运动微分方程
点且垂直于盘平面的水平轴转动。设盘从最高位置无初速度地
开始绕O轴转动。求当圆盘中心C和轴O点的连线经过水平位置
时圆盘的角速度、角加速度及O处的反力。
y
【解】(1)用动能定理求角速度。
T1 0
T2
1 2
J 0 2
1 2
(1 2
mr 2
mr2 )2
3 4
mr 2 2
r C
W12 mgr
A、加速度大小不变、而方向在变化。 加速度始终为重 B、加速度大小在变化、而方向不变。 力加速度g。 C、加速度大小、方向都在变化。 D、加速度大小、方向都不变化。
2.判断题
(1)质点的运动方程和运动微分方程的物理意义相同.( × )
运动方程是位移与时间关系方程;运动微分方程是位移微分与力关系方程。
条件下圆柱B的质心将上升。
理论力学电子教程
第八章 质点的运动微分方程
解:(1)选圆柱A为研究对象
1 2
P g
r
2
A
Tr
(1)
选圆柱B为研究对象
1 2
P g
r
2
B
T
'
r
P g
aC
P
T
'
运动学关系:
(2) (3)
aC ae ar r A r B (4)
由(1)、(2)式得: A B
第八章 质点的运动微分方程
例11-3 图示的均质杆OA的质量为30kg,杆在铅垂位置时弹簧处
于自然状态。设弹簧常数k =3kN/m,为使杆能由铅直位置OA转
到水平位置OA',在铅直位置时的角速度至少应为多大?
解:研究OA杆
(1)OA杆所受外力的功:
W12
P 1.2
1k 2
(12
22)
309.81.2 1 3000[02 (2.4 1.2 2)2 ] 388.4(J)
【解】 细长杆作平面运动,欲求aB, 则必先求ac,
由基点法 aB aC aBC aC aBC aBnC ①
aBC
l
2
aBnC
l 2
2
0
应用平面运动微分方程 Mac
F,
aC
F M
②
JC
F
l 2
Fl 6F ③
2JC Ml
将②、③代入①中,得
J O
[ 1 12
mL2
m( L )2 ]
6
p mR
LO
J O
3 2
mR2
p mv
LC
JC
1 2
mR2
1 mL2
9
LO rC mvC LCr
LO
mv
R
JC
3 2
mR2
T
1 2
JO 2
1 mL2 2
18
T
1 2
JO 2
A
A
C• • C
B
B
理论力学电子教程
第八章 质点的运动微分方程
例10-4
已知:猴子A重=猴子B重,猴B抓住绳子由静止开始相 对绳以速度v上爬,猴A抓住绳子不动,问当猴B向上爬 时,猴A将如何运动?运动的速度多大?(轮重不计)
【解】
(e)
mO (F ) PA r PB r 0 ,
1 2
(1 2
mr 2
mr2 )2
3 4
mr 2 2
W12 mgr(1 cos )
由T2-T1=W12,得 3 mr22-0=mgr(1 cos )
4
(*) 4 g (1 cos ) 3r
两边对(*)式求导 (3)求O处约束反力
3 mr2 =mgr sin
2
(2)
OA杆的动能:T1
1 2
1 3
30 2.4202
28.802
T2 0
(3)对OA杆应用动能定理:
T2 T1 W12 0 28.802 388.4
0 3.67rad/s
理论力学电子教程
第八章 质点的运动微分方程
如图所示,均质杆AB质量为m,长为l,由图示位置( 450)无
【解】 Fx 0 且有AB杆初始静止,
因此,沿x轴方向质心位置应守恒,质心C始终在y轴上,A点 的坐标可表示为:
建立oxy:并令y轴通过质心,则
xA
CA cos
l 2
cos
yA BAsin l sin
消去 ,得:
4 x A2
y
2 A
l2
即A点的轨迹为椭圆。
由T2-T1=W12,得
3 mr22-0=mgr
4 g
C
O
x
4
3r
(a)
(2)当OC在同一水平位置时,由动量矩定理有:
JO
代入JO,有
d
dt
mgr
2g 3r
理论力学电子教程
第八章 质点的运动微分方程
法二:用动能定理求角速度及角加速度。
T1 0
T2
1 2
J 0 2
x 0.5m2 1.5m1 30 75
m1 m2 M
260
x
m1g m2g
Mg
乙
首
x
甲
0.173m(实际应向左位移)
x m2 g
Mg m1g
理论力学电子教程
第八章 质点的运动微分方程
例9-9 如图所示,均质杆AB长为l,铅垂地立在光滑水平面 上,求它从铅垂位置无初速度地倒下时,端点A的轨迹。
2
=2g sin
3r
作圆盘的受力分析和运动分析,有
aCn aC
r2 r r 2 g
3
4g 3r
4g 3
由质心运动定理,得
maCn
FOx
FOx
4 3
mg
maC
mg
FOy
FOy
1 mg 3
mg
C
aCn
aC
(b)
FOx FOy
理论力学电子教程
理论力学电子教程
第八章 质点的运动微分方程
【思考题】
1.选择题
(1)如图所示,质量为m的质点受力F作用,沿平
面曲线运动,速度为v。试问下列各式是否正确?
dv
dv
a.m dt F ,b.m dt F
( A)
v
M
F
A、a、b都正确; B、a、b都不正确。
C、a正确,b不正确;D、a不正确,b正确。
初速度地倒下,求该瞬时A端所受到地面的约束反力。
