判别分析 SPSS应用
判别分析实验报告 SPSS
一、实验目的及要求：1、目的用SPSS软件实现判别分析及其应用.2、内容及要求用SPSS对实验数据利用Fisher判别法和贝叶斯判别法，建立判别函数并判定宿州、广安等13个地级市分别属于哪个管理水平类型。
二、仪器用具：三、实验方法与步骤：准备工作：把实验所用数据从Word文档复制到Excel，并进一步导入到SPSS 数据文件中,同时，由于只有当被解释变量是属性变量而解释变量是度量变量时，判别分析才适用,所以将城市管理的7个效率指数变量的变量类型改为“数值（N)”,度量标准改为“度量（S）”，以备接下来的分析。
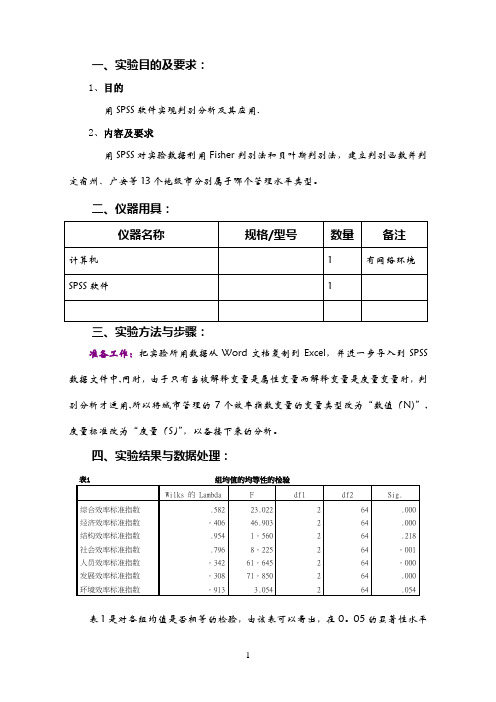
四、实验结果与数据处理：表1 组均值的均等性的检验Wilks 的 Lambda F df1 df2 Sig.综合效率标准指数.582 23.022 2 64 .000 经济效率标准指数。
406 46.903 2 64 .000 结构效率标准指数.954 1。
560 2 64 .218 社会效率标准指数.796 8。
225 2 64 。
001 人员效率标准指数。
342 61。
645 2 64 。
000 发展效率标准指数。
308 71。
850 2 64 .000 环境效率标准指数。
913 3.054 2 64 .054表1是对各组均值是否相等的检验，由该表可以看出，在0。
05的显著性水平上我们不能拒绝结构效率标准指数和环境效率标准指数在三组的均值相等的假设，即认为除了结构效率标准指数和环境效率标准指数外，其余五个标准指数在三组的均值是有显著差异的。
表2 对数行列式group 秩对数行列式1 6 —33.4102 6 -33.1773 6 —40。
584汇聚的组内 6 -32.308 打印的行列式的秩和自然对数是组协方差矩阵的秩和自然对数。
表3 检验结果箱的 M 140.196F 近似。
2。
498df1 42df2 1990.001Sig. .000 对相等总体协方差矩阵的零假设进行检验。
以上是对各组协方差矩阵是否相等的Box’M检验,表2反映协方差矩阵的秩和行列式的对数值。
EXCEL和SPSS在回归分析正交试验设计和判别分析中的应用
EXCEL和SPSS在回归分析正交试验设计和判别分析中的应用一、回归分析回归分析是一种统计方法，通过对自变量和因变量之间关系进行建模，预测因变量的值。
EXCEL和SPSS都可以进行回归分析，并提供了丰富的功能和工具。
在EXCEL中，可以使用内置的回归分析工具实现回归分析。
首先，需要将数据输入到工作表中，然后选择“数据”选项卡的“数据分析”，再选择“回归”选项。
接下来，填写变量范围和输出范围，并选择相关的统计信息和图表。
最后，点击“确定”即可得到回归分析的结果。
在SPSS中，进行回归分析的步骤稍有不同。
首先，需要导入数据文件，并选择“回归”选项。
然后，选择因变量和自变量，并设置统计选项。
最后，点击“运行”即可得到回归分析的结果。
二、正交试验设计正交试验设计是一种多因素实验设计方法，可以用于确定影响实验结果的因素及其相互作用关系。
使用正交试验设计可以减少实验次数，提高实验效率。
EXCEL和SPSS都提供了工具支持正交试验设计。
在EXCEL中，可以使用内置的“正交表生成器”来实现正交试验设计。
首先，选择“数据”选项卡的“数据分析”，再选择“正交设计表”。
接下来，填写因素数和水平数，并选择生成正交表的方式。
最后，点击“确定”即可生成正交试验设计的表格。
在SPSS中，进行正交试验设计的步骤稍有不同。
首先，需要定义因素和水平，并选择因素的类型和因素间交互作用。
然后，可以选择“生成”选项卡的“正交表”来生成正交试验设计的表格。
三、判别分析判别分析是一种统计方法，用于确定分类变量与一组预测变量之间的关系。
它可以用于预测一个事物属于哪个类别。
EXCEL和SPSS都可以进行判别分析，并提供了相应的功能和工具。
在EXCEL中，可以使用内置的“数据分析工具包”来实现判别分析。
首先，选择“数据”选项卡的“数据分析”，再选择“判别分析”。
接下来，填写变量范围和输出范围，并选择分类变量和预测变量。
最后，点击“确定”即可得到判别分析的结果。
【精品】多元统计分析--判别分析SPSS实验报告
【精品】多元统计分析--判别分析SPSS实验报告一、实验目的1．掌握判别分析的基本原理和应用方法；2．掌握SPSS软件进行判别分析的具体操作；3．通过一个实例，学习如何运用判别分析对指标进行判别。
二、实验内容三、实验原理1．判别分析基本原理：判别分析（Discriminant Analysis），是一种统计学中的分类技术，它是对变量进行归类的技术。
判别分析是用来确定一个对象或自变量集合属于哪一个预设类型或者组别的过程。
判别分析能够生成一个函数，将数据点映射到特定的类型上。
判别分析的应用领域非常广泛，主要应用于以下领域：（1）股票市场（预测股价的涨跌与时间、公司发展情况等因素的关系）；（2）医学（区分疾病、患者状态等）；（3）市场调查（确定客户类型、产品或服务喜好）；（4）产业分析（区分有助于产品销售的市场决策因素）；（5）经济学（预测月度或季度的经济指标）。
3．判别分析的主要应用步骤：（1）建立模型：首先选择和收集数据，将收集的数据分为训练集和测试集；（2）训练模型：使用训练数据建立模型；（3）评估模型：通过模型诊断来评估建立的模型的好坏；（4）应用模型：对新的数据建立模型并进行预测。
四、实验过程1. 上机操作：1）打开SPSS软件，加载数据文件；2）选择分类变量和连续变量；3）选择训练数据集；4）建立模型；5）预测实验数据集。
2. 操作步骤：SPSS分析的步骤如下：1）将数据输入SPSS软件，确保数据格式正确；2）选择Analyse- Classify- Discriminant；3）有两种不同的分类变量，单分类或多分类，如果你要解释一个特定的分类变量，选择单分类。
如果你不确定哪个分类变量最适合，请尝试不同的选项；4）选择两个或更个你认为与指定分类变量相关的连续变量；5）选择要用于判别分析的数据集；6）确定分类变量分类比率。
这可以在设置选项中完成；7）点击OK，开始进行分析；8）评估结果，包括汇总、判别函数、方差-方差贡献、判别矩阵；五、实验结果选取鸢尾花数据，经过训练，得到如下表所示的结果。
2024版SPSS判别分析方法案例分析
01 查看判别分析的结果输出，包括判别函数系数、 结构矩阵、分类结果等。
02 根据输出结果，解读判别分析的结果，如判别函 数的贡献、分类准确率等。
03 结合专业知识和实际背景，对结果进行合理解释 和讨论。
05
案例分析：某公司客户流失预测 模型构建
案例背景及问题描述
01
某大型电信公司面临客户流失问题，需要构建客户流失
04
SPSS判别分析操作过程
导入数据并建立数据集
1
打开SPSS软件，选择“文件”->“打开”>“数据”，导入需要分析的数据文件。
2
在数据视图中检查数据的完整性和准确性，确保 数据质量。
3
根据需要，对数据进行预处理，如缺失值处理、 异常值处理等。
选择合适的判别分析方法
根据研究目的和数据特点，选择合适 的判别分析方法，如线性判别分析、 二次判别分析等。
决策树与随机森林
基于贝叶斯定理和多元正态分 布假设，通过最大化类间差异 和最小化类内差异来建立线性 判别函数。适用于正态分布且 各类别协方差矩阵相等的情况。
放宽了LDA的假设条件，允许各 类别具有不同的协方差矩阵。 通过构建二次判别函数进行分 类。适用于更一般的数据分布 情况。
基于距离度量的方法，将新样 本分配给与其最近的K个已知样 本中最多的类别。适用于多类 别、非线性可分问题。
数据变换与标准化
数据变换
根据分析需求，对数据进行适当的变换，如对数变换、平 方根变换等，以改善数据的分布形态或满足分析要求。
数据标准化
对数据进行标准化处理，消除量纲和数量级的影响，使不 同变量具有可比性。常用的标准化方法包括Z分数标准化、 最小最大标准化等。
数据离散化
SPSS数据的判别分析
短期支付能力 1.09 1.51 1.01 1.45 1.56 .71 .22 1.31 2.15 1.19 1.88 1.99 1.51 1.68 1.26 1.14 1.27 2.49 2.01
5 zf
生产效率指标 .45 .16 .40 .26 .67 .28 .18 .25 .70 .66 .27 .38 .42 .95 .60 .17 .51 .54 .53
（2）各组变量的协方差矩阵相等。在此假设下，可以使用 很简单的公式计算判别函数和进行显著性检验。
（3）各判别变量之间具有多元正态分布，即每个变量对于 所有其他变量的固定值有正态分布。在此条件下，可精确计 算显著性检验值和分组归属的概率。
2023/5/3
11
zf
➢ 三、判别分析方法
距离判别 本专题将介绍的方法有费 贝歇 叶尔 斯判 判别 别
判别分析 (Discriminate Analysis)
知识要点：
1、什么是判别分析？ 2、理解距离判别、Bayes判别以及Fisher判别的基本思想 3、结合SPSS软件进行案例分析 4、判别分析的应用（※※）
zf
判别分析的应用
医学：
例1：在医学诊断中，一个病人肺部有阴影，医生要判断 他患的是肺结核、肺部良性肿瘤还是肺癌？ 肺结核病人、肺部良性肿瘤病人、肺癌病人组成三个总 体，病人来自其中一个总体，可通过病人的指标（阴影 大小、边缘是否光滑等）用判别分析判断他来自哪个总 体（即判断他患的什么病？）
逐步判别
2023/5/3
12
zf
距离判别
❖ 首先根据已知分类的数据，分别计算各类的重心即各组（类）的 均值，判别的准则是对任给样品，计算它到各类平均数的距离， 哪个距离最小就将它判归哪个类。
判别分析的一般步骤和SPSS实现
判别分析的一般步骤和SPSS实现判别分析是一种统计学方法，用于确定一组预测变量对于区分不同组别的目标变量的重要性。
它可以帮助我们理解和解释数据，以及预测未来的观察结果。
下面将介绍判别分析的一般步骤和如何使用SPSS软件来实现。
步骤一：数据收集和准备首先，收集需要的数据，并进行数据清洗和整理。
确保数据的完整性和准确性。
此外，还需要对数据进行标准化，以消除不同变量之间的度量单位差异。
步骤二：设定模型确定分析的目标变量和预测变量。
目标变量是我们想要预测或解释的变量，而预测变量则是用来预测目标变量的变量。
根据实际情况，选择适当的判别分析方法，如线性判别分析或二次判别分析。
步骤三：进行判别函数的计算计算出判别函数，用于将样本分成不同的组别。
判别函数是由预测变量的加权和组成的。
对于线性判别分析，判别函数的形式为：D = a1X1 + a2X2 + ... + anXn + c其中，D是判别分数，X是预测变量，a是权重，n是预测变量的数量，c是常数。
通过计算判别函数，可以根据判别分数将样本分到不同的组别。
步骤四：进行判别分析的检验判别分析的检验包括Wilks' Lambda检验和方差分析。
Wilks' Lambda检验用于检验判别函数是否统计显著，以判断预测变量的组合是否能够显著解释目标变量的变异性。
方差分析用于检验各个预测变量在不同组别之间的差异是否显著。
步骤五：解释和评估结果在判别分析的最后一步，需要对结果进行解释和评估。
根据判别分析的结果，可以判断哪些预测变量对于区分不同组别的目标变量最为重要。
此外，还可以对模型的准确性进行评估，比如使用十折交叉验证等方法。
使用SPSS软件进行判别分析的步骤如下：步骤一：导入数据首先，在SPSS软件中打开数据文件或导入数据。
确保数据的格式正确，包括变量类型、缺失值处理等。
步骤二：设定模型在SPSS中，选择"分析"菜单中的"分类"选项，然后选择"判别分析"。
判别分析的SPSS实现
判别分析的SPSS实现判别分析（Discriminant Analysis）是一种统计分析方法，用于识别和分类不同群体之间的差异。
它通过建立数学模型来寻找最佳判别函数，将样本划入事先定义好的不同类别中。
SPSS是一种流行的统计软件，可以用于进行多种数据分析，包括判别分析。
在SPSS中进行判别分析的步骤如下：1.导入数据：打开SPSS软件，并导入需要进行判别分析的数据集。
选择“文件”-“打开”-“数据”命令，找到数据文件并点击“打开”按钮。
2. 选择变量：从数据文件中选择需要用于判别的变量。
在数据视图中，点击变量名旁边的方框来选定变量。
可以按住Ctrl键并单击多个变量来进行选择。
3.运行判别分析：选择“分析”-“分类”-“判别分析”命令，打开判别分析对话框。
在对话框的“变量”选项卡中，将选择的变量移入“输入变量”框中。
如果有分类变量，可以选择将其移入“说明变量”框中。
4.设置判别函数模型：在对话框的“选项”选项卡中，可以设置判别分析的具体模型。
可以选择线性判别函数或二次判别函数，并设置解释变量和额外变量。
5.运行分析：点击对话框底部的“确定”按钮，运行判别分析。
SPSS将计算出最佳的判别函数，并用于分类和预测。
6.解释结果：判别分析完成后，可以查看结果并进行解释。
SPSS将输出各个变量的判别系数、判别函数结果、群体统计信息等。
可以根据这些结果来理解不同变量对分类的重要性。
7.进行预测：判别分析还可以用于对新样本进行分类和预测。
在对话框的“选项”选项卡中，选择“保存变量”选项，并指定一个新的变量名。
运行分析后，可以查看新变量的值，以得到新样本的分类结果。
8.检验结果：可以使用SPSS提供的各种统计方法来检验判别分析结果的显著性。
例如，可以进行方差分析来检验不同群体之间的差异性。
判别分析是一种有效的统计方法，可以用于各种不同的研究领域。
在SPSS中，通过简单的几个步骤就可以实现判别分析，并得到结果。
同时，SPSS还提供了丰富的数据可视化和结果解释功能，可以帮助用户更好地理解和解释判别分析的结果。
判别分析的SPSS操作
在“Method”选项组中选择进行逐步判别分析的方法，可供 选择的判别分析方法有5种：
1.Wilks’lambda Wilks’lambda方法。默认选项，每步 都是Wilk的概计量最小的进入判别函数。
2.Unexplained variance 不可解释方差方法。选择该项， 表示每步都是使各类不可解释的方差和最小变量进入判别函数。
对已知类别的样品判别分类
对已知类别的样品(通常称 为训练样品)用线性判别函 数进行判别归类，结果如 下表，全部判对。
(5)对判别效果作检验
判别分析是假设两组样品取自不同总体，如果两个总体的均值向量在统计上 差异不显著，作判别分析意义就不大：所谓判别效果的检验就是检验两个正态总体 的均值向量是否相等，取检验的统计量为：
1
《人类发展报告》中公布的。该报告建议，目前对人文发展的衡量应
当以人生的三大要素为重点，衡量人生三大要素的指示分别采用出生
时的预期寿命、成人识字率和实际人均GDP，将以上三个指示指标
的数值合成为一个复合指数，即为人文发展指数。资料来源UNDP
《人类发展报告》1995年。
2 今从1995年世界各国人文发展指数的排序中，选取高发展水平、中 等发展水平的国家各五个作为两组样品，另选四个国家作为待判样品 作判别分析。
单击添加副标题
判别分析的SPSS 操作
§1. 基本原理
§2.实例分析
§1. 基本原理
判别分析的目的是得到体现分类的函数关系式，即判别 函数。基本思想是在已知观测对象的分类和特征变量值的前 提下，从中筛选出能提供较多信息的变量，并建立判别函数； 目标是使得到的判别函数在对观测量进行判别其所属类别时 的错判率最小。
Fisher’s 选择该项，表示可以用于对新样本进行判别分 类的fisher系数，对每一类给出一组系数，并给出该组中判别分数 最大的观测量。
判别分析的SPSS实现
判别分析的SPSS实现判别分析是一种常用的统计方法，也是一种分类的机器学习方法。
它的目的是使用已知的分类信息来训练一个分类模型，然后根据这个模型来预测新的未知实例的分类。
SPSS是一种常用的统计软件，提供了方便易用的界面来进行判别分析。
下面将介绍如何在SPSS中进行判别分析。
首先，打开SPSS软件并加载要进行判别分析的数据。
可以通过"File"->"Open"来打开数据文件，或者直接将数据文件拖动到SPSS界面中。
然后，选择"Analyze"->"Classify"->"Discriminant"，进入判别分析的界面。
在界面中，需要选择要进行判别分析的变量，包括一个或多个预测变量和一个分类变量。
预测变量是判别分析模型的输入，而分类变量是判别分析模型的输出。
可以使用鼠标将变量从"Available"列表拖动到"Predictors"和"Target"列表中。
接下来，可以点击"Statistics"按钮来选择统计量。
在判别分析中，有几个常用的统计量可以选择。
例如，可以选择"Wilks' lambda"来衡量判别分析模型的预测准确率，或者选择"Group centroids"来了解不同分类的均值差异。
然后，点击"Options"按钮来设置其他选项。
在"Options"界面中，可以选择是否标准化变量，即将变量标准化为均值为0和标准差为1的形式。
标准化可以使得不同变量的尺度一致，有助于提高判别分析的性能。
此外，还可以选择输出判别函数的系数和判别函数值，以及设定分类概率的阈值等。
最后，点击"OK"按钮开始进行判别分析。
判别分析方法与SPSS
判别分析方法与SPSS判别分析（Discriminant Analysis）是一种常用的统计方法，用于分析两个或多个已知样本分类的特征，确定如何将新样本分配到已知分类中的方法。
该方法通常用于判别样本的所属类别或进行预测分类，并且可以应用于多个学科领域，如市场研究、医学、生物学等。
SPSS（Statistical Package for the Social Sciences）是一种常用的统计软件，广泛应用于社会科学领域的数据分析。
SPSS提供了丰富的统计方法和数据分析工具，包括描述统计、相关分析、回归分析等，同时也提供了判别分析方法。
在SPSS中，进行判别分析需要先导入数据集并选择“分类”方法。
在分类方法中，可以选择“线性鉴别法”或者“二次鉴别法”，通常选择线性鉴别法。
选择线性鉴别法后，可以选择“反向排序”和“选择必备输入变量”。
反向排序是指将判别函数的变量排序方式从最大向最小递减排序的方式转变为最小向最大递增排序。
选择必备输入变量是指程序会自动选择在判别分析中具有最大判别力的变量。
在SPSS中执行判别分析后，可以得到一些结果，其中最重要的是判别函数。
判别函数用于预测未知样本的类别，可以提供样本的判别得分，判别得分越高表示属于该类别的可能性越大。
判别分析的结果也包括统计指标，如Wilks' Lambda、标准化判别函数系数等。
Wilks' Lambda是判别分析的一个重要统计量，用于衡量所有判别函数的总效应，其值介于0和1之间，越接近0表示判别函数越有效。
标准化判别函数系数用于表示各个变量对判别函数的贡献，系数绝对值越大表示对判别函数的影响越大。
总之，判别分析是一种常用的统计方法，可用于分类和预测。
SPSS 是一种常用的统计软件，提供了判别分析方法和相关的数据分析工具，可以方便地进行判别分析并解释结果。
判别分析的一般步骤及SPSS实现
判别分析的一般步骤及SPSS实现判别分析是一种用于分类变量的统计方法，它可以用于确定一个或多个预测变量对于区分不同组之间差异的程度。
判别分析由一系列步骤组成，包括问题的定义、数据的准备、模型的建立、模型的评估和结果的解释。
以下是判别分析的一般步骤以及如何在SPSS中实现这些步骤的详细说明。
第一步：问题的定义在进行判别分析之前，需要明确研究的目的和问题。
例如，我们可能希望根据顾客的一些特征（如性别、年龄、收入等）来预测顾客是否购买一些产品。
这样的问题可以通过判别分析解决。
第二步：数据的准备在进行判别分析之前，需要确保数据满足分析的要求。
数据应包括一个或多个预测变量和一个分类变量。
如果数据中存在缺失值，需要进行缺失值的处理。
如果数据中存在异常值，可以选择忽略或进行适当的修正。
第三步：模型的建立在SPSS中，可以使用“分类函数”来建立判别分析模型。
选择“分析”菜单中的“分类”选项，然后选择“判别”子菜单。
在“判别”对话框中，选择一个或多个预测变量，并将分类变量指定为“因变量”。
此外，还可以选择是否进行卡方检验以及是否使用交叉验证等选项。
卡方检验可以用于评估预测变量与分类变量之间的关联性，而交叉验证可以用于评估模型对于不同样本的预测效果。
第四步：模型的评估在SPSS中，判别分析的模型评估结果可以在“判别”输出中找到。
主要关注以下几个指标：1.方差贡献表：可以查看每个预测变量对于判别函数的贡献程度，以及它们之间的相关性。
2.群组描述：可以查看不同组之间的平均值，以确定最能区分不同组的预测变量。
3.准确性表：可以查看模型的整体分类准确率以及每个组的分类准确率。
4.标准化系数表：可以查看每个预测变量对于判别函数的贡献程度，使用标准化系数来比较不同预测变量的影响。
第五步：结果的解释对于判别分析的结果进行解释是非常重要的，以帮助我们理解预测变量如何影响分类变量，并从中得出有用的结论。
可以通过参考判别函数的系数、标准化系数和方差贡献来解释结果。
判别分析实验报告 SPSS
判别分析实验报告 SPSS一、实验目的判别分析是一种用于分类和预测的统计方法。
本次实验旨在通过使用 SPSS 软件，掌握判别分析的基本原理和操作流程，能够运用判别分析方法对实际数据进行分类，并对分类结果进行评估和解释。
二、实验数据本次实验使用的数据集包含了两个类别（类别 A 和类别 B）的样本，每个样本具有若干个特征变量，如年龄、收入、教育程度等。
数据集共有 200 个样本，其中类别 A 有 100 个样本，类别 B 有 100 个样本。
三、实验步骤1、数据导入首先，打开 SPSS 软件，选择“文件”菜单中的“打开”选项，将实验数据文件导入到 SPSS 中。
2、变量定义在 SPSS 数据视图中，对各个变量进行定义，包括变量名称、变量类型、变量标签等。
3、判别分析操作选择“分析”菜单中的“分类”子菜单，然后点击“判别分析”选项。
在弹出的判别分析对话框中，将类别变量选入“分组变量”框中，将其他特征变量选入“自变量”框中。
4、选择判别方法SPSS 提供了多种判别方法，如费希尔判别法、贝叶斯判别法等。
本次实验选择费希尔判别法。
5、模型评估在判别分析结果中，查看判别函数的系数、判别函数的显著性检验、分类结果的准确性等指标，以评估模型的性能。
四、实验结果与分析1、判别函数系数判别函数的系数反映了各个自变量对判别函数的贡献程度。
通过查看系数的大小和符号，可以了解各个变量在区分不同类别中的重要性。
例如，年龄变量的系数为正，说明年龄越大，越有可能属于某个类别；而收入变量的系数为负，说明收入越低，越有可能属于另一个类别。
2、判别函数的显著性检验通过对判别函数的显著性检验，可以判断判别函数是否能够有效地区分不同的类别。
如果检验结果显著，说明判别函数具有统计学意义，可以用于分类。
3、分类结果SPSS 会给出每个样本的分类结果，以及分类的准确性。
通过比较实际类别和预测类别，可以评估模型的分类效果。
如果分类准确性较高，说明模型能够较好地对样本进行分类；如果分类准确性较低，则需要进一步分析原因，可能是数据质量问题、变量选择不当或者判别方法不合适等。
判别分析的一般步骤及SPSS实现
判别分析的SPSS实现
由此表可知,两个Fisher判别函数分别为： y 1 7 4 .9 9 1 .8 6 1 X 1 1 .6 5 6 X 2 0 .8 7 7 X 3 0 .7 9 8 X 4 0 .0 9 8 X 5 1 .5 7 9 X 6 y 2 2 9 .4 8 2 0 .8 6 7 X 1 1 .1 5 5 X 2 0 .3 5 6 X 3 0 .0 8 9 X 4 0 .0 5 4 X 5 0 .6 9 X 6
1
4
40.17 13.45 1.43 13.88 101.2 66.2
1
5
50.06 23.03 2.83 23.74 112.52 63.3
1
6
33.24 6.24 1.18 22.9 160.01 65.4
2
7
32.22 4.22 1.06 20.7 124.7 68.7
2
8
41.15 10.08 2.32 32.84 172.06 65.85
X 4 ： 55岁组死亡概率 X5 ： 80岁组死亡概率 X6 ： 平均预期寿命
表7.1 各地区死亡概率表
X1
X2
X3
X4
X5
X6
类别
1
34.16 7.44 1.12 7.87 95.19 69.3
1
2
33.06 6.34 1.08 6.77 94.08 69.7
1
3
36.26 9.24 1.04 8.97 97.3 68.8
比较三个值,可以看出第一个待判样品应该属于第三组.
判别分析的SPSS实现
表7.3 Bayes判别法的输出结果
Classification Fu nction Coe fficie n ts
判别分析的SPSS操作
判别分析的SPSS操作判别分析（Discriminant Analysis）是一种用于确定样本所属类别的统计分析方法。
它通过构建线性方程来将样本分类到不同的组中，该线性方程称为判别函数。
在进行判别分析之前，首先需要收集关于不同类别的样本数据，并且这些样本必须是可信的、有代表性的。
SPSS是一种常用的统计软件，可以进行判别分析。
下面将介绍使用SPSS进行判别分析的步骤。
一、数据准备在进行判别分析之前，需要针对每个样本收集一些特征变量的数据。
这些特征变量可以是连续变量或者分类变量。
同时，还需要收集样本的类别信息，类别信息必须是分类变量。
将这些数据输入到SPSS中的数据文件中。
二、进行判别分析1. 打开 SPSS 软件，在主界面点击 "Analyze"（分析），然后选择"Classify"（分类），再点击 "Discriminant"（判别）。
2. 在 "Discriminant Function"（判别函数）对话框中，选择"Variables"（变量）。
将所有的特征变量移动到 "Predictors"（预测变量）列表中，将类别信息移动到 "Grouping Variable"（分组变量）中。
3. 在 "Options"（选项）中，可以选择 "Statistics"（统计量）和"Save classification results"（保存分类结果）。
4.单击"OK"开始进行判别分析。
三、结果解读1. 判别分析将给出一些统计结果，其中最重要的是 "Canonical Discriminant Function Coefficients"（标准化判别系数）和"Structure Matrix"（结构矩阵）。
SPSS判别分析
SPSS判别分析SPSS（Statistical Package for the Social Sciences）是一款广泛使用的统计分析软件，也提供了强大的判别分析功能。
本文将介绍SPSS中判别分析的步骤、应用以及结果的解读。
一、判别分析的步骤1.数据准备：首先，将已知类别的样本数据录入SPSS中，每个样本对应一个实例，每个实例有一组预测变量和一个类别变量。
2.变量选择：选择要作为预测变量的特征或属性，并将其加入模型。
通常，只有连续型或分类型的自变量（预测变量）可以用于判别分析。
3.数据分割：将已知类别的样本数据分为训练集和测试集，一般按照70%的比例划分。
4.判别模型：使用SPSS中的判别分析功能建立判别模型。
在SPSS中，可以通过路径“分析-分类-判别”打开判别分析对话框。
5.模型评估：使用测试集来评估模型的准确性和性能。
可以查看分类结果的混淆矩阵，计算预测准确率、召回率、F1值等指标。
6.结果解读：根据模型的解读提示，分析各个预测变量对判别结果的重要性，找出主要影响判别的变量。
二、判别分析的应用领域判别分析广泛应用于各个领域，包括社会科学、医学、市场营销等。
以下是几个常见的应用案例：1.疾病诊断：通过患者的生物特征（如血液检测结果、基因表达谱等）来判断是否患有其中一种疾病。
2.风险评估：用于评估贷款申请者的信用风险，根据一些个人特征（如年龄、收入、居住地等）来预测违约概率。
3.市场细分：根据消费者的特征（如年龄、性别、购买行为等）将市场区分为不同的细分市场，以制定更精准的市场营销策略。
4.情感识别：通过分析文本数据（如社交媒体评论、产品评论等）来判断用户的情感倾向，以评估产品或服务的满意度。
三、结果解读判别分析的结果包括判别函数、判别系数和预测结果。
判别函数可以看作是一组线性加权的预测变量，用于将实例划分到不同的类别中。
判别系数表示了每个预测变量对判别结果的贡献程度，可以用于解释影响判断的主要变量。
SPSS中判别分析方法的正确使用
SPSS中判别分析方法的正确使用判别分析是一种经典的统计方法，用于将一组观测值分配到不同的已知类别中。
它被广泛应用于分类问题，如客户群体分类、药物分类等。
在SPSS中，判别分析方法可以通过以下步骤正确使用：第一步：准备数据首先，需要准备一个用于判别分析的数据集。
该数据集应包含预测变量（也称为自变量）和所属类别（也称为因变量）两部分。
预测变量是用来解释类别分布的变量，而所属类别是需要预测或分类的变量。
确保数据集中不含有缺失值或异常值。
第二步：设置分析方法在SPSS中，可以通过点击“分析”菜单，然后选择“分类”子菜单中的“判别”选项来设置判别分析。
在弹出的对话框中，将需预测的类别（也称为因变量）移动到“因变量”框中，将预测变量（也称为自变量）移动到“自变量”框中。
可以选择要使用的分析方法，如方差判别分析、线性判别分析等，然后点击“确定”开始分析。
第三步：解读输出结果SPSS将生成一个判别分析的结果报告，包括描述性统计、判别函数、马氏距离以及判别图等。
可以通过阅读输出结果了解到判别函数如何区分不同的类别，以及判别图如何表示不同的类别之间的差异。
此外，还可以观察描述性统计结果，比较不同类别之间的平均值、方差等指标，进一步理解类别分布的特征。
第四步：交叉验证为了验证判别分析的准确性和稳定性，可以使用交叉验证方法。
在SPSS中，可以选择在判别分析对话框的“交叉验证”选项中设置交叉验证方法。
交叉验证将数据集分为几个部分，然后使用其中一部分数据来估计判别函数，再使用剩余的数据来验证判别函数的准确性。
通过交叉验证可以得到判别分析的预测正确率，以及其它评估指标。
第五步：解读结果根据判别分析的结果报告和交叉验证的准确性评估，可以判断判别分析方法的准确性和稳定性。
如果预测正确率较高且稳定，那么可以认为判别分析是一个有效的分类方法。
此外，还可以利用判别函数的系数和贡献度等信息，评估不同预测变量对类别分布的贡献程度。
总结：判别分析是一种常用的分类方法，可用于解决各种分类问题。
SPSS数据的判别分析
SPSS数据的判别分析判别分析（Discriminant Analysis）是一种统计分析方法，用于确定一组变量如何能够最好地区分或判别不同的群体。
该方法可以用于解决分类问题，即将多个已知类别的观测对象分配到新的未知类别中。
SPSS是一种功能强大的统计软件，可以进行各种统计分析，包括判别分析。
在SPSS中，进行判别分析的步骤如下：1.打开SPSS软件并导入数据集。
2.选择“分析”菜单下的“判别分析”选项。
3.在弹出的对话框中，将要分类的变量（被解释变量）放入“因子”框中，用于判别的变量（解释变量）放入“变量”框中。
点击“分类图”按钮可以选择是否绘制分类图表。
4.点击“确定”按钮，进行判别分析。
判别分析的目标是找到一个线性组合，能够最好地将样本区分开来。
在SPSS的结果中，输出了多种统计量，包括判别系数，判别函数的系数，标准化判别函数系数等信息。
这些统计量可以帮助我们理解分类问题的解释力和判别函数的重要性。
判别函数是判别分析的核心输出，它可以根据变量的值来预测被解释变量的分类。
判别函数通常以线性函数的形式表示，例如：D = a1X1 + a2X2 + ... + anXn + b其中，D是判别函数的值，X1, X2, ..., Xn是解释变量的值，a1,a2, ..., an是判别函数的系数，b是常数项。
通过计算判别函数的值，就可以将新的观测对象分配到相应的分类中。
在SPSS中，可以使用“分类评估”功能来检验判别函数的准确性。
该功能可以计算被正确分类的对象的百分比，以及各个分类中的正确分类的百分比。
同时，SPSS还提供了一些可视化工具来帮助我们理解判别分析的结果。
例如，通过绘制分类图表，可以直观地了解不同分类之间的分隔情况。
此外，还可以通过散点图来展示解释变量和被解释变量之间的关系，以及如何影响判别函数的值。
判别分析在实际应用中具有广泛的应用。
例如，在医学领域，可以使用判别分析将患者分为不同的疾病分类，以便进行诊断和治疗。
用SPSS软件来实现判别分析
用SPSS软件来实现判别分析判别分析是一种统计模型和机器学习方法，可用于研究两个或更多群体之间的差异。
通过使用SPSS软件，我们可以对数据进行判别分析，并评估自变量的贡献程度，以及如何使用这些自变量来预测因变量。
要进行判别分析，首先需要准备数据。
在SPSS中，数据应该被整理为一个数据框，每一行代表一个样本，每一列代表一个特征或变量。
在判别分析中，我们需要明确选择一个因变量和若干个自变量。
在SPSS软件中，进行判别分析的步骤如下：步骤1:导入数据在SPSS中，首先需要导入我们的数据集。
点击“文件（File）”选项卡，选择“打开（Open）”，然后选择数据文件。
确保数据文件是一个包含正确数据格式的数据框。
如果数据集过大，可以选择只导入部分数据进行分析，可以通过“变量视图（Variable View）”进行选择。
步骤2:选择判别分析方法点击“分析（Analyze）”选项卡，选择“描述统计（Descriptive Statistics）”，选择“判别（Discriminant）”。
步骤3:设置因变量和自变量在弹出的“判别函数（Discriminant Function）”对话框中，将被解释的变量(因变量)从左边的“因变量（Dependent）”栏拖到右边的“因变量（Dependent）”栏。
然后，将讲自变量（特征）从左边的“自变量（Independent(s)）”栏拖到右边的“自变量（Independent(s)）”栏。
函数使用的哪些变量将取决于数据中可用的变量数。
步骤4:选择分类方法在“类型（Method）”选项中，选择判别分析的分类方法。
SPSS提供了两种方法：“协方差矩阵相等（Covariance matrices equal）”和“协方差矩阵不等（Covariance matrices not equal）”。
前者使用默认参数，即假设所有群体具有相同的协方差矩阵。
后者提供了更具灵活性的选项，可以允许不同群体拥有不同的协方差矩阵。
spss判别分析案例详解
spss判别分析案例详解SPSS判别分析案例详解。
在统计学中，判别分析是一种用于确定不同组别之间差异的统计方法。
它可以帮助我们理解不同变量之间的关系，以及这些变量在预测和分类方面的作用。
在本文中，我们将通过一个实际的案例来详细介绍如何使用SPSS进行判别分析。
案例背景：假设我们是一家电子商务公司的数据分析师，我们想要确定哪些因素对于用户购买高价值产品的决策具有影响力。
我们收集了一些用户的个人信息和他们的购买行为数据，希望通过判别分析找出影响用户购买高价值产品的关键因素。
数据准备：首先，我们需要将收集到的数据导入SPSS软件中。
在导入数据后，我们可以对数据进行初步的检查，确保数据的完整性和准确性。
接下来，我们需要选择判别分析作为我们的分析方法，并将购买高价值产品作为分类变量，个人信息和购买行为数据作为判别变量。
分析步骤：1. 设定判别分析的目的和假设，在进行判别分析之前，我们需要明确分析的目的是什么，以及我们的假设是什么。
在这个案例中，我们的目的是找出影响用户购买高价值产品的关键因素，我们的假设是个人信息和购买行为数据会对用户的购买决策产生影响。
2. 进行判别分析，在设定好目的和假设后，我们可以开始进行判别分析。
SPSS 会根据我们选择的分类变量和判别变量，自动进行变量选择和模型拟合，得出判别函数和判别系数。
通过判别函数和判别系数，我们可以了解每个判别变量对于不同组别的影响程度，以及它们对于用户购买高价值产品的预测能力。
3. 结果解释，在得出判别函数和判别系数后，我们需要对结果进行解释。
我们可以通过判别函数的系数来理解每个判别变量对于用户购买高价值产品的影响程度，以及它们之间的相互关系。
同时，我们还可以通过判别系数的大小来评估判别模型的预测能力和区分能力。
案例分析：通过对案例数据的判别分析，我们得出了以下结论：1. 个人收入、年龄和教育程度是影响用户购买高价值产品的重要因素，其中个人收入对用户购买高价值产品的影响最大，其次是年龄和教育程度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a. First 2 canonical discriminant functions were used in the analysis.
典则判别函数的特征值（即矩阵W-1B的特征 根 ）以及方差贡献。 典则相关系数（Canonical Correlation）。
判别分析结果输出（7）
Wilks' Lambda Test of Function(s) 1 through 2 2 Wilks' Lambda .025 .774 Chi-square 538.950 37.351 df 8 3 Sig. .000 .000
0 0 150
.0 .0 100.0
参与判别分析的观测量数据总结
判别分析结果输出（2）
Group Statistics
分类 刚毛鸢尾花
变色鸢尾花
佛吉尼亚鸢尾花
Total
花萼长 花萼宽 花瓣长 花瓣宽 花萼长 花萼宽 花瓣长 花瓣宽 花萼长 花萼宽 花瓣长 花瓣宽 花萼长 花萼宽 花瓣长 花瓣宽
花萼长 花萼宽 花瓣长 花瓣宽
单变量方差分析结果：进行假设检验，原假设不同类中 的同变量均值相等。 Wilk的 统计量。 F检验。
判别分析结果输出（4a）
a Covariance Matrices
分类 刚毛鸢尾花
花萼长 花萼长 花萼宽 花瓣长 花瓣宽 花萼长 花萼宽 花瓣长 花瓣宽 花萼长 花萼宽 花瓣长 花瓣宽 花萼长 花萼宽 花瓣长 花瓣宽
SPSS 判别分析和应用
观测量描述统计量 判别函数系数 标准化以及未标准化典则判别函数系数 类内相关矩阵和协方差矩阵 判别函数得分和据此划分的类别 判别函数的判别效果 交叉验证
点击菜单 Analysis→classify→discriminant
Discriminant功能界面－主对话框
变色鸢尾花ห้องสมุดไป่ตู้
佛吉尼亚鸢尾花
，
进一步分析 必要性，挑 选变量？
Total
a. The total covariance matrix has 149 degrees of freedom.
各类协方差矩阵和总协方差矩阵。 除刚毛鸢尾花外，另两种花的花瓣长和花萼长的协方差数 值较大。 总协方差阵中，花瓣长和花萼长的协方差数值较大。
分类统计结果：均值、方差、未加权的 权重和加权的权重。
判别分析结果输出（3）
Tests of Equality of Group Means Wilks' Lambda .397 .598 .059 .071 F 111.847 49.371 1179.052 960.007 df1 2 2 2 2 df2 147 147 147 147 Sig. .000 .000 .000 .000
对话框上部左侧的变量列表中选分析变量，点击钮使 之进入Independents框 对话框上部左侧的变量列表中选分组（类）变量，点击 钮使之进入Group Variable框 Enter independents togther 或 Use Stepwise method：所 选全部参与判别分析 还是 逐步方法挑选变量判别分析 5个功能按钮： 1) Select : 根据标识变量，选择部分数据参与分析 2) Statistics : 指定输出统计量 3) Method : 判别分析方法 4) Classify : 分类参数、图表输出、交叉验证 5) Save : 在数据文件之建立新变量显示输出结果
Tests null hypothesis of equal population covariance matrices.
各类协方差矩阵相等的假设检验：假设各类协方差矩 阵相等。 结果：置信水平为0.000，各类协方差矩阵不相等。
判别分析结果输出（6）
Eigenvalues Function 1 2 Eigenvalue % of Variance 30.419a 99.0 .293a 1.0 Cumulative % 99.0 100.0 Canonical Correlation .984 .476
Mean 50.06 34.28 14.62 2.46 59.36 27.66 42.60 13.26 66.38 29.82 55.60 20.26 58.60 30.59 37.61 11.99
Std. Deviation 3.52 3.79 1.74 1.05 5.16 3.15 4.70 1.98 7.13 3.22 5.54 2.75 8.63 4.36 17.68 7.62
分类使用的协方差阵 输出的统计图
各类先验概率相等； 根据各类样本量计算先验概率，各类先验概率与其样 本量成正比。
对每个观测量输出判别分数、实际类、预测类和后验概率等。 Limit cases to first：指定输出前n个观测量的分类结果。 输出分类小结，给出正确分类的观测量数，错分观测量数和 错分率。 交叉验证的判别分类结果，即所依据的判别函数是由除该观 测量以外的其它观测量导出的。
Valid N (listwise) Unweighted Weighted 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 50 50.000 150 150.000 150 150.000 150 150.000 150 150.000
费歇尔判别系数； 未标准化的判别方程系数。
合并类内相关矩阵； 合并类内协方差矩阵（各类协方差矩阵取平均计算）。 各类的协方差矩阵 总的协方差矩阵。
Classify对话框－分类参数和判别结果
Prior Probabilities：先验概率。 输出窗口中的有关分类结果 缺测值处理办法
Statistics 对话框－指定输出统计量
Descriptives：描述统计量 Function Coefficients：判别函数系数 Matrices：观测量的统计矩阵。
观测量均值； 单变量方差分析检验。原假设各类同一自变量均值相等。 各类协方差矩阵相等的检验。原假设各类协方差矩阵相等。
Wilk的Lambda 统计量：组内离差交叉乘积矩阵行列式与 总离差交叉乘积矩阵行列式比值。对判别函数的有效性 进行检验假设。 两判别函数自由度： (4－1＋1)(3－1)＝8；(4－2＋1)(3－ 2)＝3
该统计量服从自由度为(m-r+1)(G-r)的 χ2－分布. r 为第几个判别函数，m 为变量数，G 为类数。
判别分析应用实例1—— 全变量分析
数据集：鸢（yuan）尾花的花瓣和花萼 的长宽数据。 一共收集3种鸢（yuan）尾花，每种50个 样本，共150个样本。
判别分析结果输出（1）
Analysis Case Processing Summary Unweighted Cases Valid Excluded Missing or out-of-range group codes At least one missing discriminating variable Both missing or out-of-range group codes and at least one missing discriminating variable Total Total N 150 0 0 Percent 100.0 .0 .0
判别分析结果输出（4b）
a Pooled Within-Groups Matrices
花萼长
Covariance 花萼长
花萼宽
8.767 11.542 5.033 3.145 .471 1.000 .344 .452
花瓣长
16.129 5.033 18.597 4.287 .683 .344 1.000 .486
12.425 9.922 1.636 1.033 26.643 8.288 18.290 5.578 50.812 8.090 28.461 6.409 74.537 -4.683 130.036 53.507
花萼宽
9.922 14.369 1.170 .930 8.288 9.902 8.127 4.049 8.090 10.355 5.804 4.456 -4.683 19.036 -33.056 -12.083
Method对话框－ 选择变量的判别分析方法
Wilk’ lambda：每步使得Wilk的统计量最小的变量进入 判别函数（ 统计量－判别函数组内离差平方和与组间 离差平方和的比值）。 Unexplained variance：每步使得各类不可解释的方差之 和最小的变量进入判别函数； Mahalanobis’ distance：每步使得两类间最近的马氏距离 最大的变量进入函数； Smallest F ratio：每步使得两类间最小的F值最大的变量 进入函数； Rao’s V：每步使得Rao V统计量产生最大增量的变量进 入判别函数。
指定使用合并类内协方差矩阵进行分析。 指定使用各类协方差矩阵进行分析。
生成一个包括各类的散点图，根据前两个判别函数作图；如果只有一 个判别函数，则输出直方图。 对每类生成一个散点图，根据前两个判别函数作图。但如果只有一个 判别函数，则输出直方图。 生成区域图。即根据函数值把观测量分到各类中去的区域图，把一个 平面划分成与类数相同的区域，每类占据一个区，各类均值在各区中 用星号标注。
合并类内协方差矩阵和相关矩阵：阵中各元素是各类 协方差阵或相关阵中对应元素的均值。 花瓣长和花萼长的协方差值和相关系数值较大。
判别分析结果输出（5）
Test Results Box's M F Approx. df1 df2 Sig. 162.596 7.811 20 77566.75 .000