第11章 动态规划
动态规划.pdf

第三章:动态规划3.1 动态规划的基本概念一、动态决策问题:决策过程具有阶段性和时序性(与时间有关)的决策问题。
即决策过程可划分为明显的阶段。
二、什么叫动态规划(D.P.–Dynamic Program):多阶段决策问题最优化的一种方法。
广泛应用于工业技术、生产管理、企业管理、经济、军事等领域。
三、动态规划(D.P.)的起源:1951年,(美)数学家R.Bellman等提出最优化原理,从而建立动态规划,名著《动态规划》于1957年出版。
四、动态决策问题分类:1、按数据给出的形式分为:•离散型动态决策问题。
•连续型动态决策问题。
2、按决策过程演变的性质分为:•确定型动态决策问题。
•随机型动态决策问题。
五1、阶段(stage)n :作出决策的若干轮次。
n = 1、2、3、4、5。
2、状态(state)S n :每一阶段的出发位置。
构成状态集,记为S nS 1={A},S 2={B 1,B 2,B 3},S 3={C 1,C 2,C 3},S 4={D 1,D 2,D 3},S 5={E 1,E 2}。
阶段的起点。
3、决策(decision)X n :从一个阶段某状态演变到下一个阶段某状态的选择。
构成决策集,记为D n (S n )。
阶段的终点。
D 1(S 1)={X 1(A)}={B 1,B 2,B 3}= S 2,D 2(S 2)={X 2(B 1),X 2(B 2),X 2(B 3)}={C 1,C 2,C 3}=S 3,D 3(S 3)={X 3(C 1),X 3(C 2),X 3(C 3)}={D 1,D 2,D 3}=S 4,D 4(S 4)={X 4(D 1),X 4(D 2),X 4(D 3)}={E 1,E 2}=S 5D 5(S 5)={X 5(E 1),X 5(E 2)}={F;F}={F}。
4、策略(policy):全过程中各个阶段的决策Xn 组成的有序总体{Xn }。
如 A àB2àC1àD1àE2àF5、子策略(sub-policy):剩下的n个阶段构成n子过程,相应的决策系列叫n子策略。
优化问题的求解

11.5 最小二乘优化
一、线性最小二乘优化 线性最小二乘优化问题的一般数学描述为:
min 1 Cx d 2
2 2
Ax b (线性不等式约束) x s.t. Aeq x = beq (线性等式约束) lb x ub
MATLAB优化工具箱提供了函数lsqlin()来直接求解上述优化问题,该函 数的调用格式为: [x,resnorm,residual,exitflag,output,lambda]=lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0, options,p1,p2,...)
第11章 优化问题的求解
本章目标:求min(max)
xD
f ( x )或 min(max)
xD
F ( x)
11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8
线性规划 无约束优化 单目标约束优化 多目标约束优化 最小二乘优化 混合整数规划 动态规划 实例解析
11.1 线性规划
min max fi ( x ) Ax b Aeq x beq x s.t. lb x ub C ( x ) 0 (非线性不等式约束) Ceq ( x ) 0 (非线性等式约束)
MATLAB最优化工具箱中的fminimax()函数可以直接求解极小极大问题, 该函数的调用格式为 [x,fval,maxfval,exitflag,output,lambda]=fminimax(fun,x0,A,b,Aeq,beq,lb,ub, nonlcon,options,p1,p2,...) 另外,基于fminimax()函数,还可以求解相关的变形问题,如极小极小优 化问题:
哈工大现代控制理论基础第十一章 最优控制

11.1.1 最优控制问题的两个例子
[例1] 飞船的月球软着陆问题。 如图所示,飞船 靠其发动机产生一个与月球重力方向相反的推力 , 使得飞船到月球表面时速度为零, 即实现软着陆。 要求设计推力函数 ,使得发动机燃料消耗最少。
月球
[解]
设飞船的质量为 , 其高度和垂直速度分别为 和 ,月球的重力加速度为常数 ,飞船的自身 质量及所带燃料分别为 和 。
其中, 目标集 可表示为 性能指标 可表示为 其中 和 为连续可导的标量函数。
11.2 应用变分法求解无约束条件 的最优控制问题
11.2.1 泛函与变分
一. 泛函与泛函算子
所谓泛函,简单地说就是函数的函数,定义如下:
设
为给定的某类函数,如果对于这类函数中的
每一个函数,有某个数 与之相对应, 则称 为这类
哈工大现代控制理论基 础第十一章 最优控制
2020年4月24日星期五
11.1 最优控制问题的一般提法
最优控制研究的主要问题: 根据已建立的被控 对象的数学模型, 选择一个容许控制律, 使得被控 对象按照预定的规律运动,并使某一个性能指标达到 最大或最小。
从数学的观点来看, 最优控制问题是求解一类 带有约束条件的泛函极值问题, 属于变分学范畴。
经典的变分法只能解决控制无约束的问题, 即容许控制属于开集的一类最优控制问题。 然而, 工程中的控制常常是有约束的, 即容许控制是属于 闭集的。为了解决这个问题, 20世纪50年代,美国 学者贝尔曼和苏联科学院院士庞德里亚金分别独立 地拓展了经典变分法, 分别给出了动态规划方法和 极大值原理。 它们构成了最优控制的理论基础。
证明略
泛函变分的规则 泛函的变分是一种线性映射, 满足下列性质:
1 2 3 4
第10章 动态规划

管理运筹学
7
缺点
①没有统一的处理方法,求解时要根据问题的 性质,结合多种数学技巧。因此实践经验及 创造性思维将起重要的引导作用;
②“维数障碍”,当变量个数太多时,由于计 算机内存和速度的限制导致问题无法解决。 有些问题由于涉及的函数没有理想的性质使 问题只能用动态规划描述,而不能用动态规 划方法求解。
盈利 工厂 设备台数
0 1 2
3 4 5
甲厂
0 3 7 9 12 13
乙厂
0 5 10 11 11 11
管理运筹学
29
第一阶段:只有1个始点A,终点有B1,B2,B3,B4 。对始点和终 点进行分析和讨论分别求A到B1,B2,B3,B4的最短路径问题:
表10-4
本阶段始 点(状态)
A
阶段1 本阶段各终点(决策)
B1
B2
B3
B4
4+12=16 3+13=16 3+14=17 2+12=14
到E的最 本阶段最优终 短距离 点(最优决策)
第四阶段:两个始点D1和D2,终点只有一个;
表10-1
阶段4
本阶段始点 本阶段各终点(决策) 到E的最短距离
(状态)
E
D1
10
10
D2
6
6
分析得知:从D1和D2到E的最短路径唯一。
本阶段最优终点 (最优决策)
E E
管理运筹学
27
第三阶段:有三个始点C1,C2,C3,终点有D1,D2,对始点
和终点进行分析和讨论分别求C1,C2,C3到D1,D2 的最短路
运筹学第3版熊伟编著习题答案
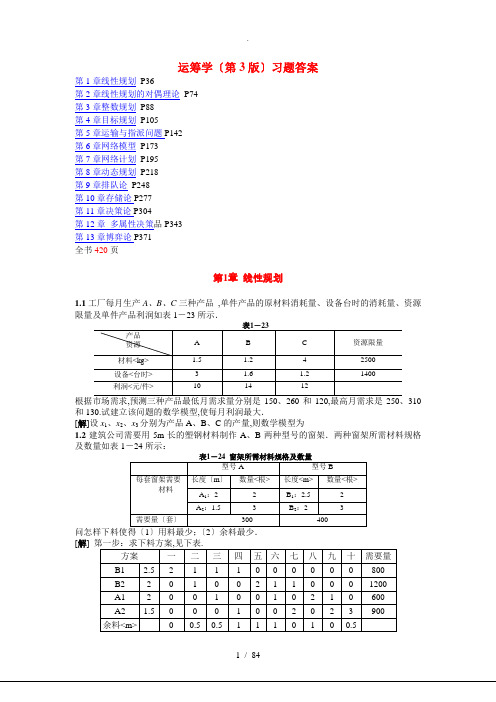
产品
资源
A
B
C
资源限量
材料<kg>
1.5
1.2
4
2500
设备<台时>
3
1.6
1.2
1400
利润<元/件>
10
14
12
根据市场需求,预测三种产品最低月需求量分别是150、260和120,最高月需求是250、310和130.试建立该问题的数学模型,使每月利润最大.
[解]设x1、x2、x3分别为产品A、B、C的产量,则数学模型为
-16
对应的顶点:
基可行解
可行域的顶点
X<1>=〔0,0,6,10,4〕、
X<2>=〔0,2.5,1,0,1.5,〕、
X<3>=〔2,2,0,0,0〕
X<4>=〔2,2,0,0,0〕
〔0,0〕
〔0,2.5〕
<2,2>
〔2,2〕
最优解:X=〔2,2,0,0,0〕;最优值Z=-16
该题是退化基本可行解,5个基本可行解对应4个极点.
第2章线性规划的对偶理论P74
第3章整数规划P88
第4章目标规划P105
第5章运输与指派问题P142
第6章网络模型P173
第7章网络计划P195
第8章动态规划P218
第9章排队论P248
第10章存储论P277
第11章决策论P304
第12章多属性决策品P343
第13章博弈论P371
全书420页
第
1.1工厂每月生产A、B、C三种产品,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.
《第11章 人员配备工作概述》

《第11章人员配备工作概述》第五章决策概述5.1决策的概念关于什么是决策的问题,众说纷纭,各有各的道理。
我们可将决策分为广义的和狭义的两类。
广义地说,把决策看作一个管理过程,是人们为了实现特定的目标,运用科学的理论与方法,系统地分析主客观条件,提出各种预选方案,从中选出最佳方案,并对最佳方案进行实施、监控的过程。
这一过程包括从设定目标,理解问题,确定备选方案,评估备选方案,到选择、实施的全过程。
狭义地说,决策就是为解决某种问题,从多种替代方案中选择一种行动方案的过程。
然而,无论我们如何表述决策的定义,在进行决策的过程中都必须遵守五项基本原则,即最优化原则、系统原则、信息准全原则、可行性原则和集团决策原则。
1.最优化原则决策作为一个管理过程的重要意义在于,在资源稀缺的约束条件下,任何做出的决策都应该有利于企业实现最大化的效益,有利于最大化地实现企业的价值。
也就是说,决策的制定应该以追求和实现企业价值最大化为目标。
2.系统原则任何决策的制定和实施、实现都存在于某一个决策环境中。
对于国民经济中的各种组织、实体来讲,他们的决策环境就是整个国民经济和整个世界经济;对于一个个体来讲,他的决策环境就是他所处的组织或实体。
不论是什么样的决策环境,都有作为一个系统的特性,也就是系统中的各种因素相互影响和相互作用的特性,同时系统中的各种因素都应协调地、平衡地变化发展。
因此,决策的制定必然要遵守系统的原则。
换一种说法,决策的制定应该以追求和实现最大化的系统的价值为目标。
3.信息准全原则各种先进、完备的决策技术的作用对象都是信息。
决策信息的准确和全面是取得高质量决策的前提条件。
在决策理论的发展过程中,有些决策理论所需要的决策信息由于很难收集到,使得这些决策理论的发展和实践都受到了很大的限制。
然而,信息技术的蓬勃发展给决策理论的发展注入了活力。
通过信息技术我们可以获得大量的我们所需要的以前没有办法获得的决策信息。
这一变化的出现,使得一些原来受制于决策信息收集困难的决策理论获得了新的发展的机会。
11第11章-MATLAB数据分析教程-由伟-清华大学出版社

lb =[0 0 0 0 ]; ub=[]; [x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
运行结果为: x = 0.5000
0.5000 0.0000 0.0000 fval = -0.3500
例2:求解 Min 5*x1+4*x2+7x3 s. t -2x1-7*x2+4x3>=2 -5*x2+2*x3>=-3 x1, x2, x3>=0
MATLAB程序为: f=[5
4 7]; A=[2 7 -4
0 5 -2];
b=[-2 3];
Aeq=[]; beq=[];
lb=[0 0 0]; ub=[]; [x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
所以,A、B、C、D的含量分别为0.50、0.50、 0.00、0.00时,材料的性能最好,能提高35%
例5:某公司要生产三种新材料:A 200公斤、B 160 公斤、C240公斤。需要用甲、乙两种添加剂,甲 现有30公斤,乙现有40公斤。每公斤A、B、C各 需要甲0.3、0.2、0.15公斤,需要乙0.25、0.18、 0.22公斤;每公斤A、B、C添加甲的成本分别为3、 2、1.5元,添加乙的成本分别为2.5、4、3元。设 计生产方案,使总成本最低
求解的MATLAB程序为: f=[5
2]; A=[-2 3
4 1]; b=[-1
3];
Aeq=[]; beq=[]; lb=[0
0]; ub=[]; [x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
运行结果为: x= 0.5000
《管理运筹学》第四版课后习题解析(下)

《管理运筹学》第四版课后习题解析(下)第9章目标规划1、解:设工厂生产A 产品1x 件,生产B 产品2x 件。
按照生产要求,建立如下目标规划模型。
112212121211122212min ()()s.t43452530555086100,,,0,1,2--+-+-+-++++-+=+-+==i i P d P d x x x x x x d d x x d d x x d d i ≤≤≥由管理运筹学软件求解得12121211.25,0,0,10, 6.25,0x x d d d d --++======由图解法或进一步计算可知,本题在求解结果未要求整数解的情况下,满意解有无穷多个,为线段(135/14,15/7)(1)(45/4,0),[0,1]ααα+-∈上的任一点。
2、解:设该公司生产A 型混凝土x 1吨,生产B 型混凝土x 2吨,按照要求建立如下的目标规划模型。
)5,,2,1(0,,0,014550.060.015550.040.030000100150100120275200.)()(min 2121215521442331222111215443322111Λ=≥≥≥≤+≤+=-++=-+=-+=-++=-++++++++-+-+-+-+-+----++-i d d x x x x x x d d x x d d x d d x d d x x d d x x ts d p d d p d p d d p i i 由管理运筹学软件求解得.0,0,20,0,0,0,0,35,40,0,120,120554433221121============+-+-+-+-+-d d d d d d d d d d x x3、解:设x 1,x 2分别表示购买两种基金的数量,按要求建立如下的目标规划模型。
,,01250543504.07.0100004525.min 2,122211121212211≥≥=-++=-++≤+++-+-+--+i i d d x x d d x x d d x x x x ts d p d p用管理运筹学软件求解得,0,0,0,818.206,091.159,636.113221121======+-+-d d d d x x所以,该人可以投资A 基金113.636份,投资B 基金159.091份。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章 动态规划一个随事件或阶段推移的系统叫做动态系统,动态规划是解决多阶段决策过程最优化的一种数学方法。
一个系统依据某种方式分为许多个不同的阶段,这些阶段不仅有着次序推移性,而且相互间有着依赖和影响。
这样,在多阶段决策过程中,每个阶段决策的选择,不仅要依据次序来考查某阶段的效果,而且要顾及此决策对以后各阶段决策的影响。
一般情况下,为得到整个系统的最优选择,必须放弃对某个阶段来说最佳的决策。
对各个阶段所做的决策形成确定整个系统的决策序列,称这样的决策序列为系统的一个策略。
对应某一确定的策略,整个系统依据某种数量指标衡量其决策的优劣。
多阶段决策过程就是在所有允许策略集合中。
确定一个达到最有指标的最优策略。
这种衡量系统的指标一般取最大值或最小值的策略。
因此,多阶段决策过程也是一个可以构成多个变量的最优化问题。
动态规划就是解决此类多阶段决策过程的最优化方法。
虽然动态规划主要解决多阶段决策的动态系统,但是可分阶段的静态系统问题也能作为特例用它有效地求解。
§11.1 动态规划的基本原理本章通过构造数学模型,形成具有特殊的动态系统过程,将基于某种方式把整个过程分成若干个互相联系的阶段,在其每个阶段都需要作出决策,从而使整个过程达到最佳效果。
同时,各个阶段决策的选择依赖于该阶段的状态以及前阶段或后阶段的变化。
各个阶段决策确定后,组成一个决策序列,从而形成了整个过程具有前后关联的链状结构的多阶段决策过程,称为序贯决策过程。
先用下面的最短路问题(问题可分成阶段性)来说明动态规划的基本思想。
例 1,最短路问题。
图11—1所示是一个路线网络图,连线上的数字表示两点之间的距离(或费用),要求寻找一条由A 到E 的路线,使距离最短(或费用最省)。
对于这样的一个比较简单的问题,可直接使用枚举法例举所有从A 到E 得路线,确定出所应走的路线是距离最短或费用最少,用动态规划的思想,如果已找到由A 到E 得最短路线是A —B 1—C2—D 2—E (记作L ),那么当寻求L 中的任何一点(如C 2)到E 得最短路时,它必然是L 子路线 C 2—D 2—E(记作L 1)。
否则,如D 2到E 的最短路是另一条路线L 2,则把A —B 1—C 2与L2连接起来,就会得到一条不同于L 的从A 到E 得最短路,根据最短路的这一特性,可以从最后一段开始,用逐步向前递推的方法,一次求出路段上各点到E 的最短路,最后得到A 到E 得最短路。
上述这种由系统的最后阶段逐段向初始阶段求最优的过程称为动态规划的解法。
该过程揭示了动态规划的基础思想,为便于对动态规划的思想和方法进行数学描述,下面先引入动态规划的基本概念并建立最优目标函数。
(1)分阶段:适当地依据具体情况将系统分成若干个相互联系的阶段,并将各个段按顺序或逆序加以编号(常用K ),描述阶段的变量称为阶段变量。
如例1可分为5个阶段,k=1,2,3,4,5.(2)状态:状态表示系统在某一阶段所处的位置。
描述过程状态的变量称为状态变量,第k 阶段的状态变量常用s k 表示,状态变量的集合用S k 表示。
如在例1中,第一阶段有一个状态就是初始位置A ,第三阶段有3个状态,即集合S3=}{1,2,3C C C .(3)决策:当系统处于某一阶段的某个状态时,可以作出不同的决定(或选择),从而确定下一阶段的状态,这种决定称为决策。
如在例1第二阶段中,从状态B2出发,其允许决策集合为D2(B2)=(4)策略:由系统各阶段确定的决策所形成的决策序列称为策略。
从初始状态s1出发,由系统的所有n 个阶段的决策所形成的策略成为全过程策略,从允许策略集合中找出达到最有效果的策略称为最优策略。
(5)状态转移方程:状态转移方程是确定过程有一个状态到另一个状态的演变过程。
若给定第k 阶段状态的演变过程,并且若该阶段的决策变量dk 一经确定,第k+1阶段的状态变量sk+1也就完全确定。
如例1中,状态转移方程为s k+1=d k (s k ).(6)阶段收益:若确定某一阶段的系统状态,执行某一阶段决策所得的效益称为阶段效益,他是整个系统总收益的一部分。
阶段效益是阶段状态和决策变量的函数。
如在例1中阶段效益为走完一段路程所走过的距离。
(7)指标函数和最优值函数:系统执行某策略所产生效果的优劣可用数学指标来衡量,它是各个阶段状态和决策的函数,称为指数函数。
(8)边值条件:在系统决策的状态推移进程中最初的条件称为边值条件。
由系统的最后阶段逐段向初始阶段求最优的过程称为速推解法,由系统的最前阶段逐段向终结阶段求最优的过程称为顺序推解法。
如例1显然有边值条件:f n+1(s n+1)=0.根据上述确定的阶段编号。
状态变量、决策变量、状态转移方程、边值条件及指标函数。
确定例1的最短路线,计算步骤如下:根据最短路线特性,寻找最短路线的方法,将从最后一段开始,用后向前逐步地推的方法,求出各点到点E 的最短路线,最后求得由点A 到点E 的最短线,所以,动态规划的方向是从各点逐段向始点方向寻找最短路线的一种方法,见图11—2.当k=4时,有D1到终点E 只有一条路线,故f 4(D1)=4,同理,f 4(D2)=3.当k=3时,出发点有C1,C2,C33个,若从C1出发,则有两个选择,一是至D1,一是至D2,则F 3(C1)=min 311431242(,)(1)(,)()r C D f D r C D f D +⎧⎫⎨⎬+⎭⎩ =min 3453+⎧⎫⎨⎬+⎩⎭=7. 其相应的决策为d 3(C 1)=D 1,表示由D 1,至终点E 的最短距离为7,其最短距离路线是C1—D1—E.同理,从C 2和C 3出发,则有f 3(C 2)=321415224244(,)()min 633(,)()r C D f D r C D f D ⎧++⎫⎧⎫⎪==⎨⎬⎨⎬++⎪⎭⎩⎭⎩。
其相应的决策为d 3(C 2)=D 2。
f3(C 3)=min 3314133242(,)()64min 10,(,)()93r C D f D r C D f D ++⎧⎫⎧⎫==⎨⎬⎨⎬++⎭⎩⎭⎩ 且d 3(C 3)=D 3。
类似地。
可计算当k=2时,有f 2(B 1)=12, d 2(B 1)=C 2.f2(B2)=11, d2(B2)=C2,f2(B3)=9, d2(B3)=C3 当k=1时,出发点只有一个点A,则f1(A)=min121222323(,)()312(,)()min5111579(,)()r A B f Br A B f Br A B f B⎧++⎫⎧⎫⎪⎪⎪⎪+=+=⎨⎬⎨⎬⎪⎪⎪⎪++⎭⎩⎭⎩,且d1(A)=B1,于是获得从始点A至终点E的最短距离为15,为便于找出最短路线,在按计算的顺序推之,可求出最优决策函数序列{dk},即由d1(A)=B1,d2(B)=C2,d3(C2)=D2,d4(D2)=E组成一个最优策略。
那么最短路线为A—B1—C2—D2—E.§11.2 中学生数学知识应用竞赛题举例例2今年盛夏酷暑,能源紧张,某工厂从能源部门获得5个单位某种能源,该工厂有3个部门需要这种能源,由于各部门所使用设备条件不同,生产的产品也不同,这样导致是用能源所产生的收益情况也不同,所用的能源为整数单位,各部门具体产生的收益(万元)如表11—1所示,为能有效地利用这种能源,工厂将如何分配能源给各部门,使工厂受益最大?表11—1解设3个部门分配到的能源分别为x1,x2,x3单位,相应每个单位所产生的收益设为c1(x1),c2(x2),c3(x3),a那么模型为Max{c1(x1)+c2(x2)+c3(x3)};s.t. x1+x2+x3≤5x1,x2,x3≥0为整数。
使用递推方法来求解。
按k=1,2,3为3阶段,用f k(z)表示在第k阶段所用能源为z 单位时,获得最大收益,即有f3(5)=max{c1(x1)+c2(x2)+c3(x3)};s.t. x1+x2+x3≤ 5.x1,x2,x3≥0为整数。
于是f3(5)=max{f2(5-x3)+c3(x3)}(x3=1,1,2,3..5)=max{f2(5),f2(4)+3,f2(3)+4,f2(2)+5,f2(1)+5,f2(0)+6};f2(5)=max{f1(5-x2)+c2(x2)}(x2=0,1,2,….5)=max{f1(5),f1(4)+1,f1(3)+3,f1(2)+4,f1(1)+6,f2(0)+8}f2(4)=max{f1(4-x2)+c2(x2)} (x2=0,1,2,…4)=max{f1(4),f1(3)+1,f1(2)+3,f1(1)+4,f1(0)+6};f2(3)=max{f1(3-x2)+c2(x2)}(x2=0,1,3)max{f1(3),f1(2)+1,f1(1)+3,f1(0)+4};f2(2)=max{f1(2),f(1)+1,f1(0)+3};f2(1)=max{f1(1),f1(0)+1}.将f1(0)=0,f1(1)=2,f1(2)=4,f1(3)=5,f1(4)=5,f1(5)=6回代得f2(1)=2f 2(2)=max{4,2+1,3}=4,f 2(3)=max{5,4+1,2+3,4}=5,f 2(4)=max{5,5+1,4+3,2+4,6}=7,f 2(5)=max{6,5+2,5+3,4+4,2+6,8}=8.f 2(5)=max{8,7+3,5+4,4+5,2+5,6}=10于是解为x 3*=1,x 2*=2,x 1*=2,最大收益为10(万元),即分配给3个部门的分别为:部门1,部门2都为2单位,而部门3为1单位,最大收益为10万元。
.§11.3 复合系统工作可靠性问题若某种机器的工作系统有n 个部件串联组成,只要有一个部件失灵,整个系统就不能工作,为提高系统工作的可靠性,在每一个部件上均配有主要元件的备用件,并且设计了备用元件自动投入装置。
显然,备用元件越多,整个系统正常工作的可靠性越大,但备用元件多了,整个系统的成本、重量、体积均相应增大,工作精度也降低,因此,最优化问题是在考虑上述限制条件下,应如何选择个部件的备用元件数,使整个系统的工作可靠性最大。
设部件i (i=1,2,…..n )上装有u i 个备用件时,它正常工作的概率为p i (u i )。
例 3 某个厂设计一种电子设备,由3种元件D 1,D 2,D 3组成,已知这3中元件的价格和可靠性如11—2所示。
要求在设计中所使用元件的费用不超过105元,试问:应如何设计室设备的可靠性达到最大(不考虑重量的限制)?解 按元件种类划分为3各阶段,设状态变量s k 表示能容许用在D k 元件至D 3元件的总费用;决策变量x k 表示在D k 元件上的并联个数;P k 表示一个D k 元件正常工作的概率,则为x k 个D k 元件不正常工作的概率,另最优值函数f k (s k )表示由状态s k 开始从D k 元件至D 3元件组成的系统的最大可靠性,因而有f 3(s3)=[]3331/20max 1(0.5);x x s ≤≤⎡⎤-⎣⎦ f 2(s2)=[]{}2223221/15max1(0.2)(15);x x s f s x ≤≤⎡⎤--⎣⎦ f 1(s2)=[]{}1112111/30max 1(0.1)(30).x x s f s x ≤≤⎡⎤--⎣⎦ 由于s 1=105,故解此问题只要求出f 1(105)即可,而 f1(105)={}[]{}[]{}{}1321113222223212433333133max 1(0.1)(10530)max 0.9(75),0.99(45),0.999(15),f (75)max 1(0.2)(7515)max 0.8(60),0.96(45),0.992(30),0.998(15),f (60)=max 1(1.5)max 0.5,0.75,x x x x x f x f f f x f x f f f f ≤≤≤≤≤≤⎡⎤--⎣⎦==--=⎡⎤-=⎣⎦但且{}0.8730.875,= f3(30)=0.5,f3(15)=0,所以f2(75)=max{0.8×0.875,0.96×0.75,0.992 ×.5,0.9984×0}=max{0.7,0.72,0.496}=0.72.同理f2(45)=max{0.8f3(30),0.96f3(30)}=max{0.4,0}=0.4,f2(15)=0.故f2(105)=max{0.9 ×.72,0.99×0.4,0.999×0}=max{0.648,0.396}=0.648.从而求得x1*=1,x2*=2,x3*=2为最优方案,即D1元件用2个,D3元件用2个,其总费用为100元,可靠性为0.648。
