线性代数的应用论文
线性代数小论文
(学院杏林学院班级国贸102 姓名李霞学号1004123046 ）线性代数小论文-----用矩阵解决经济管理学中的问题一、提要：线性代数理论有着悠久的历史和丰富的内容。
随着科学的发展，特别是电子计算机使用的日益普遍，作为重要的数学工具之一，线性代数的应用已经深入到了自然科学、社会科学、工程技术、经济、管理等各个领域。
虽然我们在学习线性代数这门课，可不免有同学要问这门课究竟要应用于生活哪一方面？由于我们是属于经济管理类的专业，因此我们学线性代数是为日后学习运筹、管理以及经济类课程打基础。
本文将举出一个矩阵在经济管理中的应用例子来解释线性代数的应用。
二、提出问题：风险型决策方法例1、某企业打算生产某产品。
根据市场预测分析，产品销路有三种可能性：销路好、一般和差，这三种情况出现的概率分别为0、3,0、45,0、25. 生产该产品有三种方案：改进生产线、新建生产线、外包生产。
各种方案的收益值在表5-4给出。
项目（1）改进生产线（2）新建生产线（3）外包生产销路好180 240 100销路一般120 100 70销路差-40 -80 16表5-4 各生产方案在不同市场情况下的收益/万元1、专业课中如何解决的最大效用值收益准则：解决风险决策常用的一个目标是使期望收益最大化。
学过概率统计之后，不难求出三种方案对应的期望收益分别为：（1）180*0.3+120*0.45+（-40）*0.25=98（2）240*0.3+100*0.45+（-80）*0.25=97（3）100*0.3+70*0.45+16*0.25=65.5因为第一种方案对应的期望效用值最大，所以选择改进生产线的方案。
2、线代课中如何解决的矩阵M=(0.3 0.45 0.25)矩阵N=(180 240 100120 100 70-40 -80 16)则：最大效用收益组成的矩阵=M*N=（98 97 65.5）因为第一种方案对应的期望效用值最大，所以选择改进生产线的方案。
线性代数的应用论文
论文:线性代数的应用与心得体会班级：姓名：学号:指导老师:完成时间：2014年10月20日目录摘要 (2)关键词 (2)一、线性代数被广泛运用的原因 (2)二、线性代数在实际中的应用 (2)1. 用二阶行列式求平行四边形面积,用三阶行列式求平行六面面体 (2)2. 希尔密码 (2)3.在人们平常日常生活的应用——减肥配方的实现 (3)4、在城市人们出行的应用——交通流的分析 (4)5、马尔可夫链 (5)6、在人口迁移的应用人口迁徙模型 (5)三、心得与体会 (7)摘要我们对线性代数的了解大概是,线性代数理论有着悠久的历史和丰富的内容,还有其主要知识：矩阵、方程组和向量；我们也应该了解其在众多的科学技术领域和实际生活中的应用都十分广泛;下面就是看一些具体实例应用,和一些心得体会;关键词线性代数；实际生活；应用实例；心得体会；;一、线性代数被广泛运用的原因为什么线性代数得到广泛运用,也就是说,为什么在实际的科学研究中解线性方程组是经常的事,而并非解非线性方程组是经常的事呢原因之一,大自然的许多现象恰好是线性变化的,研究的是单个变量之间的关系;例如我们高中学过的物理学科中,物理可以分为机械运动、电运动、还有量子力学的运动;而比较重要的机械运动的基本方程是牛顿第二定律,即物体的加速度同它所受到的力成正比,其实这又恰恰符合基本的线性微分方程;再如电运动的基本方程是麦克思韦方程组,这个方程组表明电场强度与磁场的变化率成正比,而磁场的强度又与电场强度的变化率成正比,因此麦克思韦方程组也正好是线性方程组;原因之二,之后随着科学的发展,我们不仅要研究单个之间的关系,还要进一步研究多个变量之间的关系,因为各种实际问题在大多数情况下可以线性化,而且由于计算机的发展,了的问题又可以计算出来,所以,线性代数因这方面的成为了解决这些问题的有力工具而被广泛应用;原因之三,在数学中线性代数与几何和代数有着不可分割的联系;线性代数所体现的观念与代数方法之间的联系,从具体概念变为出来的,对于强化人们的,增强科学性是非常有用的;二、线性代数在实际中的应用1.用二阶行列式求平行四边形面积,用三阶行列式求平行六面面体2.希尔密码希尔密码Hill Password是运用基本矩阵论原理的替换密码,由Lester S. Hill在1929年发明;每个字母当作26进制数字：A=0, B=1, C=2... 一串字母当成n维向量,跟一个n×n的矩阵相乘,再将得出的结果模26;注意用作加密的矩阵即密匙在\mathbb_^n必须是可逆的,否则就不可能译码;只有矩阵的行列式和26互质,才是可逆的;例题、设明文为HPFRPAHTNECL,密钥矩阵为：3.在人们平常日常生活的应用——减肥配方的实现大学生在饮食方面存在很多问题,多数大学生不重视吃早餐,日常饮食也没有规律,为了身体的健康就需要注意日常饮食中的营养;大学生每天的配餐中需要摄入一定的蛋白质、脂肪和碳水化合物,下表给出了这三种食物提供的营养以及大学生的正常所需营养它们的质量以适当的单位计量;设三种食物每100克中蛋白质、碳水化合物和脂肪的含量如下表,表中还给出了80年代美国流行的剑桥大学医学院的简捷营养处方;现在的问题是：如果用这三种食物作为每天 营养 每100g 食物所含营养g减肥所要求的每日营养量脱脂牛奶 大豆面粉 乳清 蛋白质 36 51 13 33 碳水化合物 52 34 74 45 脂肪73123个单位100g,表中的三个营养成分列向量为：12136511352,34,74,07 1.1a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦则它们的组合所具有的营养为11223312336511352347407 1.1x a x a x a x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥++=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦使这个合成的营养与剑桥配方的要求相等,就可以得到以下的矩阵方程：123365113335234744507 1.13x x Ax b x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⇒=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦用MA TLAB 解这个问题非常方便,列出程序ag763如下： A=36,51,13;52,34,74;0,7, b=33;45;3 x=A\b程序执行的结果为：0.2772 0.3919 0.2332x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦即脱脂牛奶的用量为,大豆面粉的用量为,乳清的用量为,就能保证所需的综合营养量;4、在城市人们出行的应用——交通流的分析某城市有两组单行道,构成了一个包含四个节点A,B,C,D 的十字路口如图所示;在交通繁忙时段的汽车从外部进出此十字路口的流量每小时的车流数标于图上;现要求计算每两个节点之间路段上的交通流量x 1,x 2,x 3,x 4;解：在每个节点上,进入和离开的车数应该相等,这就决定了四个流通的方程： 节点A: x 1+450＝x 2+610 节点B: x 2+520＝x 3+480 节点C: x 3+390＝x 4+600 节点D: x 4+640＝x 2+310将这组方程进行整理,写成矩阵形式：12233414= 160 = - 40 - = 210= -330x x x x x x x x ---其系数增广矩阵为：11 160 11 - 40 [,]1121011 -330A b -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦ 用消元法求其行阶梯形式,或者直接调用U0=rrefA,b,可以得出其精简行阶梯形式为1 0 0 -1330 0 1 0 -1 170 U0= 0 0 1 -1 210 0 0 0 00⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦注意这个系数矩阵所代表的意义,它的左边四列从左至右依次为变量x 1,x 2,x 3,x 4的系数,第五列则是在等式右边的常数项;把第四列移到等式右边,可以按行列写恢复为方程,其结果为：x 1=x 4+330, x 2=x 4+170, x 3=x 4+210图3 单行线交通流图0＝0由于最后一行变为全零,这个精简行阶梯形式只有三行有效,也就是说四个方程中有一个是相依的,实际上只有三个有效方程;方程数比未知数的数目少,即没有给出足够的信息来唯一地确定x1,x2,x3,和x4;其原因也不难从物理上想象,题目给出的只是进入和离开这个十字路区的流量,如果有些车沿着这四方的单行道绕圈,那是不会影响总的输入输出流量的,但可以全面增加四条路上的流量;所以x4被称为自由变量,实际上它的取值也不能完全自由,因为规定了这些路段都是单行道,x1,x2,x3,和x4;都不能取负值;所以要准确了解这里的交通流情况,还应该在x1,x2,x3,和x4中,再检测一个变量;5、马尔可夫链马尔可夫链Markov Chain,描述了一种状态序列,其每个状态值取决于前面有限个状态;马尔可夫链是具有马尔可夫性质的随机变量的一个数列;这些变量的范围,即它们所有可能取值的集合,被称为“状态空间”,而的值则是在时间n的状态;如果对于过去状态的条件概率分布仅是的一个函数,则这里x为过程中的某个状态;上面这个恒等式可以被看作是马尔可夫性质;例题、6、在人口迁移的应用人口迁徙模型设在一个大城市中的总人口是固定的;人口的分布则因居民在市区和郊区之间迁徙而变化;每年有6%的市区居民搬到郊区去住,而有2%的郊区居民搬到市区;假如开始时有30%的居民住在市区,70%的居民住在郊区,问十年后市区和郊区的居民人口比例是多少30年、50年后又如何这个问题可以用矩阵乘法来描述;把人口变量用市区和郊区两个分量表示,即,ck k sk x x x ⎡⎤=⎢⎥⎣⎦其中x c 为市区人口所占比例,x s 为郊区人口所占比例,k 表示年份的次序;在k=0的初始状态：0000.30.7c s x x x ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦;一年以后,市区人口为x c1= x c0+,郊区人口x s1= + x s0,用矩阵乘法来描述,可写成：11010.940.020.3 0.29600.060.980.7 0.7040c s x x Ax x ⎡⎤⎡⎤⎡⎤⎡⎤==⋅==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ 此关系可以从初始时间到k 年,扩展为2120k k k k x Ax A x A x --====,用下列MATLAB 程序进行计算：A=,;, x0=; x1=Ax0, x10=A^10x0 x30=A^30x0 x50=A^50x0程序运行的结果为：1103050 0.2960 0.2717 0.2541 0.2508,,,, 0.7040 0.7283 0.7459 0.7492x x x x ⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦无限增加时间k,市区和郊区人口之比将趋向一组常数 ;为了弄清为什么这个过程趋向于一个稳态值,我们改变一下坐标系统;在这个坐标系统中可以更清楚地看到乘以矩阵A 的效果;选u 1为稳态向量,T 的任意一个倍数,令u 1=1,3T 和u 2=-1,1T ;可以看到,用A 乘以这两个向量的结果不过是改变向量的长度,不影响其相角方向：110.940.02110.060.9833Au u ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦220.940.0210.920.920.060.9810.92Au u --⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦初始向量x0可以写成这两个基向量u1和u2的线性组合；0120.30110.250.050.250.050.7031x u u -⎡⎤⎡⎤⎡⎤==⋅-⋅=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦因此0120.250.05(0.82)k k k x A x u u ==-式中的第二项会随着k 的增大趋向于零;如果只取小数点后两位,则只要k>27,这第二项就可以忽略不计而得到01270.250.250.75k kk x A x u >⎡⎤===⎢⎥⎣⎦适当选择基向量可以使矩阵乘法结果等价于一个简单的实数乘子,避免相角项出现,使得问题简单化;这也是方阵求特征值的基本思想;这个应用问题实际上是所谓马尔可夫过程的一个类型;所得到的向量序列x1,x2,...,x k称为马尔可夫链;马尔可夫过程的特点是k时刻的系统状态x k完全可由其前一个时刻的状态x k-1所决定,与k-1时刻之前的系统状态无关;三、心得与体会没上线性代数的时候,心中还有点忐忑,怕自己学不好;但是当真的学时,用心听老师讲的每节课,还是感觉很轻松的;然后每章结束后的习题,自己认真完成,不会的再翻翻以前学过的知识点和笔记,自己就会豁然开朗,而且死死地记住题型,考试的时候不会紧张而且游刃有余;可以总结一下,线性代数主要研究三种对象：矩阵、方程组和向量;这三种对象的理论是密切相关的,大部分问题在这三种理论中都有等价说法;因此,熟练地从一种理论的叙述转移到另一种中去,是学习线性代数时应养成的一种重要习惯和素质;如果说与实际计算结合最多的是矩阵的观点,那么向量的观点则着眼于从整体性和结构性考虑问题,因而可以更深刻、更透彻地揭示线性代数中各种问题的内在联系和本质属性;由此可见,只要掌握矩阵、方程组和向量的内在联系,遇到问题就能左右逢源,举一反三,化难为易;线性代数作为数学的一门,体现了数学的思想;数学上的方法是相通的;比如,考虑特殊情况这种思路;线性代数中行列式按行或列展开公式的证明就是从更简单的特殊情况开始证起；解线性方程组时先解对应的齐次方程组,这些都是先考虑特殊情况;高数上解二阶常系数线性微分方程时先解其对应的齐次方程,这用的也是这种思路;通过思想方法上的联系和内容上的关系,线性代数中的内容以及线性代数与高等数学甚至其它学科可以联系起来;只要建立了这种联系,线代就不会像原来那样琐碎了;在线性代数的学习中,注重知识点的衔接与转换,努力提高综合分析能力;线性代数从内容上看纵横交错,前后联系紧密,环环相扣,相互渗透,因此解题方法灵活多变,学习时应当常问自己做得对不对再问做得好不好只有不断地归纳总结,努力搞清内在联系,使所学知识融会贯通,接口与切入点多了,熟悉了,思路自然就开阔了;现在我们可以在线完成过程考核,在电脑上登录,然后有不同的题型,说是考核其实也是一种练手和复习,加强知识的巩固;每一题解答过后都会有详解,可以看到自己到底错在哪,哪里学的不好;我觉得这是一种很好的学习工具,我们一定要好好利用,来学习线性代数;了解每种题型很关键,当然都离开不了矩阵、方程组和向量,掌握它们是关键;线性代数有很多在现实生活中的应用,我们要会运用线性代数来解决现实生活中的一些事或麻烦;我们的生活中到处都存在着数学,所以用心它的魅力吧;。
线性代数小论文
摘要：分析了若矩阵A 经过行初等变换化为矩阵B ，则A 与B 的列向量组具有完全相同的线性关系，以及此性质在线性代数的主要应用。
关键词：初等变换；线性相关；线性无关；线性表示线性代数主要研究的是线性问题。
一般而言，凡是线性问题常可以用向量空间的观点和方法加以讨论，因此向量空间成了线性代数的基本概念和中心内容。
向量空间理论的核心问题是向量间的线性关系。
其基本概念有向量的线性表示、向量组线性相关与线性无关、向量组等价、向量组的极大无关组，以及向量空间的基与维数等。
这些问题通常转化为解线性方程组或解齐次线性方程组。
1 线性相关性证明设A =(α1,α2,··· ,αn )，αi ∈P m，若矩阵A 经过行初等变换化为矩阵B ，则A 与B 的列向量组具有完全相同的线性关系。
证明：设A m ×n ，A 经过行初等变换化为B ，将A ，B 分别按列分块为A =(α1,α2,…,αn )，B=(β1, β2,···,βn )。
由于对A 只进行有限次行初等变换，故可知有满秩矩阵P ，使PA =B ，即P(α1,α2, ···,αn )=(β1, β2, ···,βn )，于是有i 1βj = P αj (j=1,2,3, ···,n) （1） 设A 和B 对应的列向量组为αi 1,αi 2, ···,αi r 和βi 1, βi 2,···,βi r (1≤i 1＜i 2＜···＜i r ≤n)，由(1)式得βik = P αik (k=1,2,3, ···,r)因此，如果αi 1,αi 2, ···,αi r 有线性关系式k 1αi 1+k 2αi 2+ ···+k r αi r =0(k r 为实数)，则k 1,k 2…k r 也必使得k 1βi 1+k 2 βi 2+···+k r βi r =k 1(P αi 1)+ k 2(P αi 2)+ ···+ k r (P αi r )=P (k 1αi 1+k 2αi 2+ ···+k r αi r )=P 0=0 反之，如果βi 1, βi 2,···,βi r 有线性关系式，得λ1βi 1+λ2βi 2+ ···+λr βi r =0则由P 的满秩性可知αj =P -1βj (j=1,2,3, ···,n)，于是有λ1αi 1+λ2αi 2+ ···+λr αi r =λ1P -1βi 1 +λ2P -1βi 2 + ···+λr P -1βi r= P -1(λ1βi 1+λ2βi 2+ ···+λr βi r )= P -10=0这表明向量组αi 1,αi 2, ···,αi r 与向量组βi 1, βi 2,···,βi r 有相同的线性相关性，证毕。
线性代数的应用论文
线性代数的应用论文引言线性代数作为数学的一个重要分支，广泛应用于各个领域，如物理学、经济学、计算机科学等。
本论文将重点介绍线性代数在计算机科学领域的应用，包括机器学习、图像处理和网络分析等方面。
机器学习中的线性代数应用线性回归在机器学习中，线性回归是一个重要的模型。
线性回归模型可以通过最小二乘法来估计参数。
其基本原理是通过线性变换将输入数据映射到输出数据，然后通过最小化残差平方和来确定最佳拟合直线。
实质上，线性回归模型就是在求解一个方程组，而这正是线性代数的重点内容。
通过矩阵运算和求解线性方程组，可以方便地求解线性回归模型的参数。
主成分分析主成分分析 (PCA) 是一种常用的降维技术，在特征提取和数据压缩中起着重要作用。
通过线性代数的方法，可以将高维的数据变换到低维空间中，同时保留最重要的信息。
主成分分析的核心是求解数据协方差矩阵的特征向量和特征值，只保留最大的特征值对应的特征向量作为主成分。
线性代数提供了有效的算法和工具，可以快速求解特征值和特征向量，从而实现主成分分析。
图像处理中的线性代数应用图像压缩在图像处理中，图像压缩是一个重要的应用领域。
通过压缩图像，可以减少存储空间和传输带宽的消耗。
其中，离散余弦变换 (DCT) 是一种常用的压缩方法。
DCT 将图像分解为一组不同频率的正弦波信号，然后根据信号能量的大小进行量化和编码。
通过变换和编码过程，DCT 可以将图像信息进行高效地表示和存储。
而 DCT 的计算过程正是基于线性代数的矩阵运算和线性变换。
图像恢复在图像处理中，图像恢复是一个挑战性任务。
例如，在图像降噪和去模糊中，需要从受损图像中恢复原始图像。
这可以通过求解一个逆问题来实现，而逆问题通常可以表示为线性代数的形式。
例如，降噪问题可以通过求解一个线性方程组来实现，去模糊问题可以通过求解一个矩阵方程来实现。
线性代数提供了强大的工具和算法，可以有效地解决图像恢复问题。
网络分析中的线性代数应用网络表示学习网络表示学习是网络分析领域的一个重要任务。
数学与应用数学线性代数大学期末论文
数学与应用数学线性代数大学期末论文摘要：线性代数是数学的一个重要分支，广泛应用于各个领域。
本文将从矩阵运算、线性方程组和特征值与特征向量等角度，对线性代数的基本概念和应用进行探讨，并结合具体实例，展示线性代数在科学、工程和计算机等领域的重要性。
1. 矩阵运算矩阵是线性代数重要的基本工具，它由数个数构成的一个矩形阵列。
矩阵运算包括矩阵的加法、减法、乘法和转置等。
加法和减法是对应位置的元素进行运算，而矩阵乘法是对矩阵的行和列进行组合运算。
矩阵乘法特点之一是不满足交换律，即AB≠BA。
这一性质使得矩阵乘法在解决线性方程组方面具有独特的优势。
通过矩阵乘法，可以将线性方程组转化为矩阵形式，从而利用矩阵运算的特性来求解。
2. 线性方程组线性方程组是线性代数的重要应用之一，广泛应用于经济学、物理学等领域。
线性方程组的解可以通过矩阵运算得到，其中最常用的方法是高斯消元法和矩阵的逆。
高斯消元法通过不断变换线性方程组的形式，将其转化为简化的行阶梯形式，从而求解方程组的解。
而矩阵的逆则是通过对矩阵的行列式和伴随矩阵进行计算，得到矩阵的逆矩阵。
对于可逆矩阵，利用逆矩阵可以直接求解线性方程组，简化了计算过程。
3. 特征值与特征向量特征值与特征向量是线性代数中的重要概念，对矩阵的性质和变换具有深刻的影响。
特征值是矩阵的一个特征，用于描述矩阵在特定方向上的变换比例。
特征向量则是对应于特征值的向量。
通过求解特征值和特征向量，可以衡量矩阵的稳定性、变换性质以及与其他矩阵的关系。
在实际应用中，特征值与特征向量在图像处理、数据压缩等方面有着广泛的应用。
4. 应用案例线性代数作为一门工具性学科，有着广泛的应用。
本文将结合科学、工程和计算机等领域，展示线性代数在实际问题中的重要性。
以图像压缩为例，通过矩阵运算和特征值与特征向量的计算，可以将高维图像通过降维的方式减少数据量，并保持图像质量的基本特征。
该方法在数据存储和传输方面具有重要意义。
2023年线性代数与其应用期末结课论文
2023年线性代数与其应用期末结课论文摘要：本文旨在探讨线性代数在不同领域中的应用，并对未来的发展趋势进行展望。
首先介绍线性代数的基本概念和理论框架，然后分析其在机器学习、图像处理、通信技术和金融领域中的实际应用。
同时，重点讨论线性代数在人工智能和数据科学中的重要性，并预测未来线性代数在这些领域中的持续应用和发展。
1. 引言线性代数是一门研究向量空间和线性映射的数学学科，是现代数学的基础之一。
它不仅在数学领域中发挥着重要作用，还被广泛应用于计算机科学、物理学、工程学等多个领域。
本文将重点探讨线性代数在不同领域的应用，并对其未来发展进行展望。
2. 线性代数的基本概念和理论框架线性代数的基本概念包括向量、矩阵、线性方程组等。
向量是最基本的概念，它可以表示空间中的一个点、一个箭头或一组数值。
矩阵是由若干个数按一定的规律排列形成的矩形阵列，它在线性代数中有着重要的作用。
线性方程组是一组线性方程的集合，通过矩阵运算可以找到它们的解。
3. 线性代数在机器学习中的应用机器学习是人工智能的重要分支，它使用大量的数据和算法来使计算机具备学习和预测的能力。
线性代数在机器学习中扮演着至关重要的角色，例如在特征提取、分类、回归等方面的应用。
通过矩阵运算和向量空间的概念，可以对数据进行降维处理，提取出最具代表性的特征，从而实现对复杂问题的分类和预测。
4. 线性代数在图像处理中的应用图像处理是将数字图像进行分析、改变和重建的过程。
线性代数在图像处理中具有广泛的应用，例如图像的压缩、滤波、增强等。
矩阵运算和线性变换可以对图像进行变换和处理，从而实现图像的降噪、清晰化等效果。
5. 线性代数在通信技术中的应用通信技术是信息传输的重要手段，线性代数在通信技术中扮演着关键的角色。
信号通过信道传输时，经常会受到噪声和干扰的影响。
线性代数的方法可以对信号进行编码、解码和纠错，从而提高通信系统的可靠性和效率。
6. 线性代数在金融领域中的应用金融领域对数据的处理和分析需求非常高，线性代数在金融领域中发挥着重要的作用。
线性代数论文
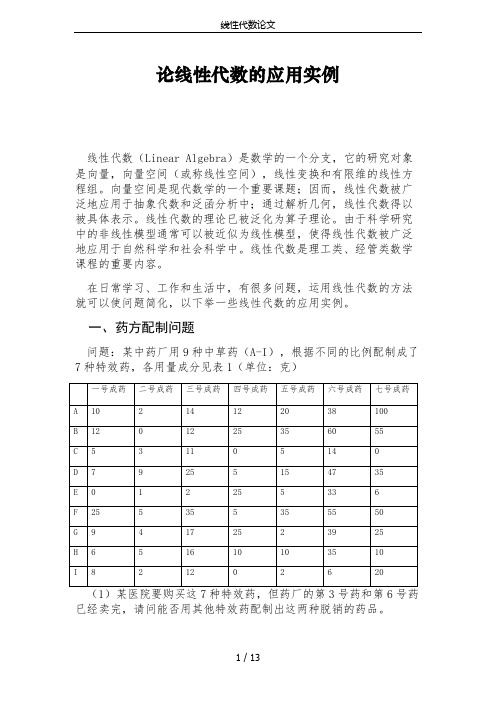
论线性代数的应用实例线性代数（Linear Algebra）是数学的一个分支，它的研究对象是向量，向量空间（或称线性空间），线性变换和有限维的线性方程组。
向量空间是现代数学的一个重要课题；因而，线性代数被广泛地应用于抽象代数和泛函分析中；通过解析几何，线性代数得以被具体表示。
线性代数的理论已被泛化为算子理论。
由于科学研究中的非线性模型通常可以被近似为线性模型，使得线性代数被广泛地应用于自然科学和社会科学中。
线性代数是理工类、经管类数学课程的重要内容。
在日常学习、工作和生活中，有很多问题，运用线性代数的方法就可以使问题简化，以下举一些线性代数的应用实例。
一、药方配制问题问题：某中药厂用9种中草药（A-I），根据不同的比例配制成了7种特效药，各用量成分见表1（单位：克）已经卖完，请问能否用其他特效药配制出这两种脱销的药品。
（2）现在该医院想用这7种草药配制三种新的特效药，表2给出了三种新的特效药的成分，请问能否配制？如何配制？解:(1)把每一种特效药看成一个九维列向量，分析7个列向量构成向量组的线性相关性。
若向量组线性无关，则无法配制脱销的特效药；若向量组线性相关，并且能找到不含3u，6u的一个最大线性无关组，则可以配制3号和6号药品。
可使用matlab软件进行运算：在Matlab窗口输入1 2 3 4 5 6 7[10;12;5;7;0;25;9;6;8];[2;0;3;9;1;5;4;5;2];[14;12;11;25;2;35;17;16;12]; [12;25;0;5;25;5;25;10;0]; [20;35;5;15;5;35;2;10;0]; [38;60;14;47;33;55;39;35;6]; [100;55;0;35;6;50;25;10;20];u u u u u u u =======1234567 [,,,,,,]u u u u u u u u =[0u ,r]=rref(u )计算结果为0u =10100000120030000101000001100000001⎛⎫⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭从矩阵中可以看出，有四个零行，r=1、2、4、5、7从最简行阶梯型0u 中可以看 出，R （u ）=5，向量组线性 相关，一个最大无关组为： 1u 2u 4u 5u 7u3u = 1u +22u 6u =32u +4u +5u故可以配制新药。
线性代数期末总结小论文
线性代数期末总结小论文在本学期的学习中，我系统地学习了线性代数的基本概念、基础理论和常见应用。
通过课堂的学习和教材的阅读，我对线性代数有了更深入的了解，掌握了一些基本的技巧和方法。
下面我将对我本学期所学的内容进行总结和回顾。
一、向量和矩阵向量是线性代数的基础概念之一，它是有方向和大小的量。
向量的加法、减法和数量乘法在几何上对应于向量的平移和伸缩。
我学习了向量的表示方法、向量的运算法则和向量方程的解法。
矩阵是一个二维数组，它是向量的推广。
矩阵的运算包括加法、减法、数量乘法和矩阵乘法等。
矩阵乘法的定义非常重要，它将两个矩阵的行与列进行乘积累加得到新的矩阵。
我还学习了矩阵的转置、逆矩阵、行列式等概念和计算方法。
二、线性变换和特征值特征向量线性变换是线性代数的核心概念之一，它是一个函数，将一个向量空间中的向量映射到另一个向量空间中的向量。
学习了线性变换的概念后，我学习了线性变换的表示方法和矩阵表示，矩阵表示能够简化线性变换的计算。
特征值和特征向量是线性变换非常重要的概念，它们描述了线性变换对应的一些特殊性质。
特征值是一个标量，特征向量是线性变换不变的非零向量。
我还学习了如何计算特征值和特征向量，以及它们在实际问题中的应用。
三、最小二乘法和奇异值分解通过学习最小二乘法，我了解到对于一组方程组，如果求解方程组的解是不可能的，或者解是存在但不唯一的，那么我们可以使用最小二乘法来求解一个最接近方程组的解。
最小二乘法在数据拟合、数据建模等领域有着广泛的应用。
奇异值分解是矩阵分解的一种方法，它将一个矩阵分解为三个矩阵的乘积，将原始矩阵转化为一个对角矩阵的形式，方便求解和分析。
奇异值分解在图像处理、数据压缩等领域有着重要的应用。
四、特征向量和特征值的应用特征向量和特征值在许多实际问题中都有广泛的应用。
在图像处理方面，特征向量和特征值可以用于图像的压缩和降噪；在自然语言处理中，特征向量和特征值可以用于文本的分类和聚类；在电路网络中，特征向量和特征值可以用于电路的分析和设计。
线性代数中矩阵的应用论文
线性代数中矩阵的应用论文线性代数中矩阵的应用论文线性代数中矩阵的应用论文【1】摘要：伴随着社会经济的快速发展，信息技术的进步，数学应用领域也得到了扩展，已从传统物理领域扩展至非物理领域，于当前现代化管理、高科技的发展以及生产力水平的提升中有着非常重要的作用。
下面笔者就线性代数中矩阵的应用进行研究，借助于关于矩阵应用的典型案例来分析，以加深人们对矩阵应用领域的认识。
关键词：代数应用线性矩阵线性代数作为数学分支之一，是一门重要的学科。
在线性代数的研究中，对矩阵所实施的研究最多，矩阵为一个数表，该数表能变换，形成为新数表，简而言之就是若抽象出某一种变化规律，可借助于代数理论知识来对所研究的这一数表实施变换，以此获得所需结论。
近年来，随着社会经济发展速度的加快，科学技术水平的提高，线形代数中矩阵的应用领域也变得更为广泛，本文就线性代数中矩阵的应用进行详细地阐述。
1 矩阵在量纲化分析法中的应用大部分物理量均有量纲，其主要分为两种，即基本量纲与导出量纲，其中基本量纲有社会长度L、时间T以及质量M，其他量均为导出量。
基于量纲一致这一原则，等号两端的各变量能构建一个相应的线性方程组，经矩阵变换来解决各量之间所存关系。
比如勾股定理证明，假设某RT△斜边长是c，两直角边长各为a和b，在此如果选△面积s，斜边c，两锐角a和β为需研究变量，则必定有以下关系，即，该公式中所存量纲有四个，其中有三个为基本量纲，则必然有一个量为无量纲，把上述量纲列成为矩阵，所获矩阵图形如，其中每一列表示一个变量量纲数据。
基于该矩阵，所获解线性方程为，综合上述方程可得解，即x11为2，x21为0，x31为0，因此，可得关系式，该公式中λ表示唯一需明确的无量纲量，从该公式可知RT△面积和斜边c平方之间成比例。
在此，于该三角形斜边做一高，把其划分为两个形似三角形，其面积各为s1与s2，此时，原RT△的边长a和b则是两个相似小三角形的斜边。
通过上述内容可知所获原理和结论相似，则有s1=λa2与s2=λb2，因s1+s2=s，对此，基于此，可证明勾股定理，即为。
关于线性代数的论文
《关于线性代数的论文》姓名：白月东学号：201212103030班级：2012级网络普高院系：计算机科学与技术学院指导教师：包志华分块矩阵的应用摘要：矩阵论是代数学中一个重要组成部分和主要研究对象，在线性代数中占有非常重要的地位。
分块矩阵可以用来降低较高级数的矩阵级数，使矩阵的结构更清晰明朗，从而使矩阵的相关计算简单化，而且还可以用于证明一些与矩阵有关的问题。
本文将分块矩阵运用于行列式运算、解线性方程组、求逆矩阵的问题以及特征值的问题的求解，还包括有关矩阵秩的证明和矩阵相似问题。
关键词：分块矩阵；行列式；矩阵的秩；逆矩阵；特征值.绪论：在已有的相关文献中，分块矩阵的一些应用如下：（1）从行列式的性质出发，推导出分块矩阵的若干性质，并举例说明这些性质在行列式计算和证明中的应用。
（2）借助分块矩阵的初等变换可以发现分块矩阵在计算行列式、求逆矩阵及矩阵的秩方面的应用。
（3）利用分块矩阵求高阶行列式。
如设A 、C 都是n 阶矩阵，其中0A ≠，并且AC CA =，则可求得A B AD BC CD=-。
（4）利用分块矩阵求解线性方程组。
分块矩阵有非常广泛的应用，本文将通过对分块矩阵性质的研究，比较系统的总结讨论分块矩阵在计算和证明方面的应用，从而确认分块矩阵为处理很多代数问题带来很大的便利。
1.分块矩阵的定义及相关运算性质1.1分块矩阵的定义矩阵分块,就是把一个大矩阵看成是由一些小矩阵组成的。
就如矩阵的元素(数) 一样,特别是在运算中,把这些小矩阵当作数一样来处理。
把矩阵分块运算有许多方便之处。
定义1 设A 是一个m n ⨯矩阵，若用若干横线条将它分成r 块，再用若干纵线条将他分成s 块，于是有rs 块的分块矩阵，1111...............s r rs A A A A A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，其中ij A 表示的是一个矩阵。
1.2分块矩阵的相关运算性质1.2.1加法设()ijm nA a ⨯=，()ijm nB b ⨯=，用同样的方法对B A,进行分块()ij r sA A ⨯=，()ijr sB B ⨯=，其中ij A ，ij B 的级数相同，则()ij ijr sA B A B ⨯+=+。
线性代数小论文
线性代数小论文在学习了线性代数两个多月后，也算是对它有了一些了解。
在此，我就从老师教学和我自身的学习方面谈谈我的体会，对教学改革提一些自己的意见。
首先，我想说明的是，大学里的学习是不能靠其他任何人的，只能靠自己，老师只是起到一个引导作用。
所以教材是我们最重要的学习资源，如果没有书本，就是天才也不可能学好。
我使用的线性代数教材是科学出版社出版李小刚主编的《线性代数及其应用》。
我比较了一下这本书和其他线代教材的区别，它有个很大的特点就是，别的教材第一章讲的是行列式，而它却直接通过介绍高斯消元法引入了矩阵的概念，在学习了矩阵后才介绍行列式的计算。
这是这本教材的优越之处，它包含了一个循序渐进的过程。
但是，它也有许多的不足之处，就个人在看这本教材时，觉得它举得实例太少了，并且例子不太全面，本来线性代数是一门比较抽象的学科，加上计算量大，学时少，所以要学好它，就只有靠自己在课余时间多加练习，慢慢领悟那些概念性的东西。
然后对于教材内容的侧重点，我觉得应该放在线性方程组这一块，因为它是其他问题的引出点，不管是矩阵，行列式，还是矩阵的秩和向量空间，都是为线性方程组服务的。
我们对向量组的线性相关性的讨论，还有对矩阵的秩，向量组的秩的计算，都是为了了解线性方程组的解的情况。
在线性方程组的求解过程中，我们运用了矩阵的行变换来求基础解系，当然这就相当于求极大无关组。
还有对线性相关和线性无关的讨论，这也关系到线性方程组的解。
所以在改革中，应该拿线性方程组为应用的实例，来一步一步的解剖概念和定理。
当然一些好的、典型的解题方法，也应该用具体的例子来讲解，这是一本教材必须具备的。
其次，老师在教学中，也应该以一些具体的实例入手来教学，就像开尔文说的，数学只不过是常识的升华而已，所以如果脱离了实际应用，只是讲抽象的概念和式子，是很难明白的，并且有实例的对照，可以加深记忆理论知识。
然后要注重易混淆概念的区别，必要时应该拿出来单独讲讲，比如矩阵和行列式的区别，矩阵只是为了计算线性方程而列的一个数据单而已，并无实际意义。
线性代数在工程中的应用3000字
线性代数在工程中的应用3000字
线性代数是工程学中不可或缺的重要一环，在互联网行业中，线性代数经常被用来处理复杂的数据结构问题，它是互联网界最基础的思维模型之一，被广泛用于网上应用、搜索引擎和机器学习系统等数字信息基础设施。
线性代数在互联网行业中最大的作用是网络建模。
以搜索引擎为例，搜索引擎内部会通过各种数学方法构建出一个复杂的网络模型，从而生成搜索结果排名更加合理，而这其中就牵扯到复杂数学方法，其中就包括了线性代数部分，而利用这些数学方法能够让搜索引擎更加清晰地定位搜索有关语义类别，寻找更准确的匹配结果。
线性代数在互联网行业也帮助实现各种机器学习的方案。
机器学习可以通过大量的例子自动学习模式，作为特征，每一个特征都可以用线性代数的方法表达，以此加以操作，可以使机器的学习能力更加强大。
如图像处理中的图像识别，就可以用线性代数表示出来，机器学习系统便可以与图像中的每一个像素进行处理，从而得出更加合理和更准确的判断结果。
此外，线性代数也可以用于数据分析、个性化推荐系统研究，当用户信息根据不同因素被划分为多个集群时，可以用线性代数的方法进行分析，从而解决个性化推荐系统的问题；在大数据领域，如果要对数据进行更有效的分析，线性代数会帮助我们更加快速准确地得出计算结果。
总的来说，线性代数在互联网行业的优势十分明显，它不仅拓展了互联网等技术领域，而且它的应用把数学内容从抽象上贴近到科学应用，帮助人们在实际生活中更加直接得到线性
代数有助于解决大量实际问题的益处，展现了线性代数对互联网行业广泛应用的巨大潜力。
线性代数论文(矩阵在自己专业中的应用及举例)
矩阵在自己专业中的应用及举例摘要：I、矩阵是线性代数的基本概念，它在线性代数与数学的许多分支中都有重要的应用，许多实际问题可以用矩阵表达并用相关的理论得到解决。
II、文中介绍了矩阵的概念、基本运算、可逆矩阵、矩阵的秩等内容。
III、矩阵在地理信息系统中也有许多的应用，比如文中重点体现的在计算机图形学中应用。
关键词：矩阵可逆矩阵图形学图形变换正文：第一部分引言在线性代数中，我们主要学习了关于行列式、矩阵、方程、向量等相关性比较强的内容，而这些内容在我们专业的其他一些学科中应用也是比较广泛的，是其它一些学科的很好的辅助学科之一。
因此，能够将我们所学的东西融会贯通是一件非常有意义的事，而且对我们的学习只会有更好的促进作用。
在计算机图形学中矩阵有一些最基本的应有，但是概念已经与线性代数中的有一些不同的意义。
在计算机图形学中，矩阵可以是一个新的额坐标系，也可以是对一些测量点的坐标变换，例如：平移、错切等等。
在后面的文章中，我通过查询一些相关的资料，对其中一些内容作了比较详细的介绍，希望对以后的学习能够有一定的指导作用。
在线性代数中，矩阵也占据着一定的重要地位，与行列式、方程、向量、二次型等内容有着密切的联系，在解决一些问题的思想上是相同的。
尤其他们在作为处理一些实际问题的工具上的时候。
图形变换是计算机图形学领域内的主要内容之一，为方便用户在图形交互式处理过程中度图形进行各种观察，需要对图形实施一系列的变换，计算机图形学主要有以下几种变换：几何变换、坐标变换和观察变换等。
这些变换有着不同的作用，却又紧密联系在一起。
第二部分 研究问题及成果1. 矩阵的概念定义：由n m ⨯个数排列成的m 行n 列的矩阵数表⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ann an an n a a a n a a a 212222111211 称为一个n m ⨯矩阵，其中an 表示位于数表中第i 行第j 列的数，i=1,2,3，…n ，又称为矩阵的元素。
线代论文
3. 个人总结· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·8 4. 参考文献· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·8 5.
2.1 行列式解法· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·5 2.2 克莱姆法则· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·6 2.3 具体实例· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·7
������������ ������������ ������
������������ ������������ ������������
线性代数结业论文优秀版(1)
线性代数结业论文优秀版(1)
线性代数结业论文优秀版
一、引言
线性代数作为数学基础课程中的重要组成部分，是理工科各类学科中
的必修课程之一。
本文旨在总结线性代数的基本概念和相关知识，结
合其在实际应用中的意义分析，以此体现线性代数的重要作用。
二、基本概念
线性代数的基本概念包括线性方程组、向量、矩阵、行列式等。
其中，线性方程组为线性代数的核心内容，其求解过程是通向后续知识的重
要桥梁。
向量在线性代数中具有举足轻重的地位，作为线性代数的基
本工具之一，可以使用向量进行模型建立、计算和求解。
矩阵则是上
述两者的应用，其具有高效性和便捷性，广泛应用于实际问题中。
行
列式则为线性代数的基础知识，是矩阵求逆和计算特征值等过程不可
或缺的工具。
三、实际应用
线性代数在实际应用中的意义十分重要。
例如，在图像处理领域中，
可以利用线性代数中矩阵的运算和变换理论实现图像的快速变换和处理；在机器学习和数据分析中，线性代数也有着广泛的应用，如求解
最小二乘问题和主成分分析等。
在物理学和工程学中，线性代数作为
嵌入高级数学和计算机科学的基础知识，被应用于矩阵力学和控制论
等领域。
四、总结
线性代数作为基础数学课程，它的应用涉及到各个领域，具有很高的
实际意义。
但同时，线性代数也是数学难度较高的课程之一，对于大
多数学生来说，需要付出极高的努力才能掌握其核心知识，在现代的数学研究中也仍是重要的一部分。
在今后的学习和工作过程中，我们也应该认真学习和应用线性代数的知识，提高自己的数学素质和综合能力。
浅谈线性代数在实际生活中的应用
浅谈线性代数在实际生活中的应用一、本文概述线性代数，作为数学的一个重要分支，其在理论研究和实际应用中都扮演着至关重要的角色。
本文将深入探讨线性代数在实际生活中的应用，旨在揭示其广泛的影响力和实用性。
我们将从线性代数的基本概念出发，逐步展开其在不同领域中的应用，包括计算机科学、物理学、经济学、工程学等。
通过具体案例和实例分析，我们将展示线性代数如何被用来解决现实问题，以及它在实际操作中的优势和效果。
本文旨在为读者提供一个全面了解线性代数应用的窗口，同时也希望激发读者对线性代数及其在实际生活中应用的兴趣和热情。
二、线性代数基础知识回顾线性代数作为数学的一个重要分支，它研究的对象是线性方程组、向量空间、线性变换和矩阵等。
在日常生活和实际应用中，线性代数的基础知识为我们提供了强大的工具和方法。
向量：向量是线性代数中的基本概念，可以看作是有方向和大小的量。
在实际生活中，我们可以将许多事物抽象为向量，如速度、力、位移等。
向量不仅可以表示单个量，还可以表示多个量之间的关系，如力的合成与分解等。
矩阵：矩阵是一个由数字组成的矩形阵列，是线性代数中另一个核心概念。
矩阵可以用来表示线性方程组，实现向量的线性变换，以及进行数据的组织和处理。
在实际应用中，矩阵被广泛应用于图像处理、数据分析和机器学习等领域。
线性方程组：线性方程组是由线性方程组成的方程组。
通过矩阵的方法，我们可以方便地求解线性方程组，找出满足所有方程的未知数的值。
这在解决实际问题中非常有用，如资源分配、经济预测等。
线性变换：线性变换是保持向量空间结构不变的变换，它可以通过矩阵来实现。
在实际生活中，许多现象都可以通过线性变换来描述，如弹性力学中的应力应变关系、电路分析中的电压电流关系等。
回顾这些基础知识，我们可以看到线性代数在实际生活中的应用非常广泛。
通过掌握和运用这些基础知识，我们可以更好地理解和解决实际问题。
三、线性代数在实际生活中的应用案例线性代数作为一种基础数学工具，在实际生活中的应用广泛而深入。
线性代数在中学数学中的应用 毕业论文
线性代数在中学数学中的应用毕业论文摘要：本文主要探讨了线性代数在中学数学中的应用。
我们首先介绍了线性代数的基本概念，如向量、矩阵、行列式等，然后讨论了这些概念在中学数学中的应用。
我们从三个方面进行了探讨：几何应用、代数应用和概率统计应用。
在几何应用方面，我们讨论了向量的坐标表示、向量的加减法和求模长、向量的点乘和叉乘等。
在代数应用方面，我们以解线性方程组为例，探讨了矩阵的应用。
在概率统计应用方面，我们以数据处理为例，介绍了矩阵在数据处理中的应用。
关键词：线性代数；中学数学；向量；矩阵；行列式Abstract:This paper discusses the application of linear algebra in high school mathematics. We first introduce the basic concepts of linear algebra, such as vectors, matrices, determinants, etc., and then discuss their applications in high schoolmathematics. We explore three aspects: geometric applications, algebraic applications, and probability and statistics applications. In terms of geometric applications, we discuss the coordinate representation of vectors, vector addition and subtraction, modulus length of vectors, and dot and cross products of vectors. In terms of algebraic applications, we use solving linear equations as an example to discuss the application of matrices. In terms of probability and statistics applications, we use data processing as an example to introduce the application of matrices in data processing.Keywords: linear algebra; high school mathematics; vectors; matrices; determinants1、引言线性代数是高等数学的一门基础课程，但它的应用不仅限于高等教育。
线性代数的应用论文
线性代数的应用论文引言线性代数是一门基础且重要的数学学科，它研究的是向量空间和线性变换。
线性代数在许多领域都有着广泛的应用，如物理学、工程学、计算机科学等。
本文将重点介绍线性代数在计算机科学中的应用。
矩阵在图形学中的应用图形学是计算机科学中的一个重要分支，它研究的是如何生成、操作和显示图形。
矩阵在图形学中起着关键作用，例如，矩阵可以用来表示变换矩阵，帮助我们实现图像的平移、旋转和缩放等操作。
此外，矩阵还可以用来表示图像的像素值，从而实现图像的处理和渲染。
线性方程组的求解线性方程组是线性代数的一个重要内容，它可以描述许多实际问题，如电路分析、机器学习等。
线性代数提供了求解线性方程组的方法，如高斯消元法、LU分解等。
这些方法可以有效地解决大规模线性方程组的求解问题，从而在实际应用中发挥着重要作用。
特征值与特征向量的应用特征值与特征向量是线性代数中的重要概念，它们可以帮助我们理解矩阵的性质和变换过程。
在图像处理中，特征值与特征向量可以用来实现图像的降噪和特征提取。
此外，在机器学习中，特征值与特征向量可以用来进行数据降维和特征选择，从而提高模型的性能和效果。
线性代数在机器学习中的应用机器学习是人工智能的一个重要领域，它研究的是如何使用数据和算法来构建模型并进行预测和决策。
线性代数在机器学习中起着关键作用，例如，线性回归模型和逻辑回归模型都是基于线性代数的理论和方法构建的。
此外，矩阵分解和特征值分解等线性代数的技术也被广泛应用于机器学习的算法中。
结论线性代数作为一门基础学科，其在计算机科学领域的应用非常重要。
本文简要介绍了线性代数在图形学、线性方程组求解、特征值与特征向量以及机器学习中的应用。
随着计算机科学的发展，线性代数的应用领域也将不断扩大，带来更多的创新和发展机会。
希望本文对读者了解线性代数在计算机科学中的应用有所帮助，并激发更多的兴趣和思考。
感谢阅读！参考文献•Strang, G. (2009). Introduction to Linear Algebra.Wellesley-Cambridge Press.•Lay, D.C., Lay, S.R., & McDonald, J.J. (2016). Linear Algebra and Its Applications. Pearson.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
论文:线性代数的应用与心得体会班级：姓名：学号:指导老师:完成时间：2014年10月20日目录【摘要】 (2)【关键词】 (2)一、线性代数被广泛运用的原因 (2)二、线性代数在实际中的应用 (2)1. 用二阶行列式求平行四边形面积，用三阶行列式求平行六面面体 (2)2. 希尔密码 (2)3.在人们平常日常生活的应用——减肥配方的实现 (3)4、在城市人们出行的应用——交通流的分析 (4)5、马尔可夫链 (5)6、在人口迁移的应用人口迁徙模型 (5)三、心得与体会 (7)【摘要】我们对线性代数的了解大概是，线性代数理论有着悠久的历史和丰富的内容，还有其主要知识：矩阵、方程组和向量；我们也应该了解其在众多的科学技术领域和实际生活中的应用都十分广泛。
下面就是看一些具体实例应用，和一些心得体会。
【关键词】线性代数；实际生活；应用实例；心得体会；。
一、线性代数被广泛运用的原因为什么线性代数得到广泛运用，也就是说，为什么在实际的科学研究中解线性方程组是经常的事，而并非解非线性方程组是经常的事呢？原因之一，大自然的许多现象恰好是线性变化的，研究的是单个变量之间的关系。
例如我们高中学过的物理学科中，物理可以分为机械运动、电运动、还有量子力学的运动。
而比较重要的机械运动的基本方程是牛顿第二定律，即物体的加速度同它所受到的力成正比，其实这又恰恰符合基本的线性微分方程。
再如电运动的基本方程是麦克思韦方程组，这个方程组表明电场强度与磁场的变化率成正比，而磁场的强度又与电场强度的变化率成正比，因此麦克思韦方程组也正好是线性方程组。
原因之二，之后随着科学的发展，我们不仅要研究单个变量之间的关系，还要进一步研究多个变量之间的关系，因为各种实际问题在大多数情况下可以线性化，而且由于计算机的发展，线性化了的问题又可以计算出来，所以，线性代数因这方面的成为了解决这些问题的有力工具而被广泛应用。
原因之三，在数学中线性代数与几何和代数有着不可分割的联系。
线性代数所体现的几何观念与代数方法之间的联系，从具体概念变为抽象出来的公理化方法，对于强化人们的数学训练，增强科学性是非常有用的。
二、线性代数在实际中的应用1.用二阶行列式求平行四边形面积，用三阶行列式求平行六面面体2.希尔密码希尔密码（Hill Password）是运用基本矩阵论原理的替换密码，由Lester S. Hill在1929年发明。
每个字母当作26进制数字：A=0, B=1, C=2... 一串字母当成n维向量，跟一个n×n 的矩阵相乘，再将得出的结果模26。
注意用作加密的矩阵（即密匙）在\mathbb_^n必须是可逆的，否则就不可能译码。
只有矩阵的行列式和26互质，才是可逆的。
例题、设明文为HPFRPAHTNECL,密钥矩阵为：3.在人们平常日常生活的应用——减肥配方的实现大学生在饮食方面存在很多问题，多数大学生不重视吃早餐，日常饮食也没有规律，为了身体的健康就需要注意日常饮食中的营养。
大学生每天的配餐中需要摄入一定的蛋白质、脂肪和碳水化合物，下表给出了这三种食物提供的营养以及大学生的正常所需营养（它们的质量以适当的单位计量）。
设三种食物每100克中蛋白质、碳水化合物和脂肪的含量如下表，表中还给出了80年代美国流行的剑桥大学医学院的简捷营养处方。
现在的问题是：如果用这三种食物作为每 营养 每100g 食物所含营养(g)减肥所要求的每日营养量脱脂牛奶 大豆面粉 乳清 蛋白质 36 51 13 33 碳水化合物 52 34 74 45 脂肪71.1312的用量为x 3个单位（100g ），表中的三个营养成分列向量为：12136511352,34,74,07 1.1a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦则它们的组合所具有的营养为11223312336511352347407 1.1x a x a x a x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥++=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦使这个合成的营养与剑桥配方的要求相等，就可以得到以下的矩阵方程：123365113335234744507 1.13x x Ax b x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⇒=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦用MA TLAB 解这个问题非常方便，列出程序ag763如下： A=[36,51,13;52,34,74;0,7,1.1] b=[33;45;3] x=A\b程序执行的结果为：0.2772 0.3919 0.2332x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦即脱脂牛奶的用量为27.7g ，大豆面粉的用量为39.2g ，乳清的用量为23.3g ，就能保证所需的综合营养量。
4、在城市人们出行的应用——交通流的分析某城市有两组单行道，构成了一个包含四个节点A,B,C,D 的十字路口如图6.5.2所示。
在交通繁忙时段的汽车从外部进出此十字路口的流量（每小时的车流数）标于图上。
现要求计算每两个节点之间路段上的交通流量x 1,x 2,x 3,x 4。
解：在每个节点上，进入和离开的车数应该相等，这就决定了四个流通的方程： 节点A: x 1+450＝x 2+610 节点B: x 2+520＝x 3+480 节点C: x 3+390＝x 4+600 节点D: x 4+640＝x 2+310将这组方程进行整理，写成矩阵形式：12233414= 160 = - 40 - = 210= -330x x x x x x x x ---其系数增广矩阵为：11 160 11 - 40 [,]1121011 -330A b -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦ 用消元法求其行阶梯形式，或者直接调用U0=rref([A,b]),可以得出其精简行阶梯形式为 1 0 0 -1330 0 1 0 -1170 U0= 0 0 1 -1 210 0 0 0 00⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦注意这个系数矩阵所代表的意义，它的左边四列从左至右依次为变量x 1,x 2,x 3,x 4的系数，第五列则是在等式右边的常数项。
把第四列移到等式右边，可以按行列写恢复为方程，其结果为：x 1=x 4+330, x 2=x 4+170,图3 单行线交通流图x3=x4+2100＝0由于最后一行变为全零，这个精简行阶梯形式只有三行有效，也就是说四个方程中有一个是相依的，实际上只有三个有效方程。
方程数比未知数的数目少，即没有给出足够的信息来唯一地确定x1,x2,x3,和x4。
其原因也不难从物理上想象，题目给出的只是进入和离开这个十字路区的流量，如果有些车沿着这四方的单行道绕圈，那是不会影响总的输入输出流量的，但可以全面增加四条路上的流量。
所以x4被称为自由变量，实际上它的取值也不能完全自由，因为规定了这些路段都是单行道，x1,x2,x3,和x4。
都不能取负值。
所以要准确了解这里的交通流情况，还应该在x1,x2,x3,和x4中，再检测一个变量。
5、马尔可夫链马尔可夫链（Markov Chain），描述了一种状态序列，其每个状态值取决于前面有限个状态。
马尔可夫链是具有马尔可夫性质的随机变量的一个数列。
这些变量的范围，即它们所有可能取值的集合，被称为“状态空间”，而的值则是在时间n的状态。
如果对于过去状态的条件概率分布仅是的一个函数，则这里x为过程中的某个状态。
上面这个恒等式可以被看作是马尔可夫性质。
例题、6、在人口迁移的应用人口迁徙模型设在一个大城市中的总人口是固定的。
人口的分布则因居民在市区和郊区之间迁徙而变化。
每年有6%的市区居民搬到郊区去住，而有2%的郊区居民搬到市区。
假如开始时有30%的居民住在市区，70%的居民住在郊区，问十年后市区和郊区的居民人口比例是多少？30年、50年后又如何？这个问题可以用矩阵乘法来描述。
把人口变量用市区和郊区两个分量表示，即,ck k sk x x x ⎡⎤=⎢⎥⎣⎦其中x c 为市区人口所占比例，x s 为郊区人口所占比例，k 表示年份的次序。
在k=0的初始状态：0000.30.7c s x x x ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦。
一年以后，市区人口为x c1= (1-0.02) x c0+0.06x s0，郊区人口x s1= 0.02x c0 + (1-0.06)x s0，用矩阵乘法来描述，可写成：11010.940.020.3 0.29600.060.980.7 0.7040c s x x Ax x ⎡⎤⎡⎤⎡⎤⎡⎤==⋅==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ 此关系可以从初始时间到k 年,扩展为2120k k k k x Ax A x A x --====,用下列MATLAB 程序进行计算：A=[0.94,0.02;0.06,0.98] x0=[0.3;0.7] x1=A*x0, x10=A^10*x0 x30=A^30*x0 x50=A^50*x0程序运行的结果为：1103050 0.2960 0.2717 0.2541 0.2508,,,, 0.7040 0.7283 0.7459 0.7492x x x x ⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦无限增加时间k ，市区和郊区人口之比将趋向一组常数 0.25/0.75。
为了弄清为什么这个过程趋向于一个稳态值，我们改变一下坐标系统。
在这个坐标系统中可以更清楚地看到乘以矩阵A 的效果。
选u 1为稳态向量[0.25,0.75]T 的任意一个倍数，令u 1=[1,3]T 和u 2=[-1,1]T 。
可以看到，用A 乘以这两个向量的结果不过是改变向量的长度，不影响其相角（方向）：110.940.02110.060.9833Au u ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦220.940.0210.920.920.060.9810.92Au u --⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦初始向量x0可以写成这两个基向量u1和u2的线性组合；0120.30110.250.050.250.050.7031x u u -⎡⎤⎡⎤⎡⎤==⋅-⋅=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦因此0120.250.05(0.82)k k k x A x u u ==-式中的第二项会随着k 的增大趋向于零。
如果只取小数点后两位，则只要k>27，这第二项就可以忽略不计而得到01270.250.250.75k kk x A x u >⎡⎤===⎢⎥⎣⎦适当选择基向量可以使矩阵乘法结果等价于一个简单的实数乘子，避免相角项出现，使得问题简单化。
这也是方阵求特征值的基本思想。
这个应用问题实际上是所谓马尔可夫过程的一个类型。
所得到的向量序列x 1,x 2,...,x k 称为马尔可夫链。
马尔可夫过程的特点是k 时刻的系统状态x k 完全可由其前一个时刻的状态x k-1所决定，与k-1时刻之前的系统状态无关。