苏教版数学高一《指数函数》精品导学案
苏教版数学高一《指数函数》精品学案

知识网络
学习目标
1.进一步掌握指数函数的图象、性质;
2.初步掌握函数图象之间最基本的初等变换。
【新课导学】
1.已知 , 与 的图象关于对称; 与 的图象关于对称.
2.已知 ,由 的图象
向左平移 个单位
得到 的图象;
向右平移 个单位
得到 的图象;
向上平移 个单位
得到 的图象;
【迁移应用】
1.(1)函数 恒过定点为________.
(2)已知函数 的图象不经过第二象限,则 的取值范围是__________.
2.怎样由 的图象,得到函数 的图象?
3.说出函数 与 图象之间的关系:
4已知 是定义在 上的奇函数,且 时, .
(1)求函数 的解析式;(2)画出函数 的图象;(3)写出函数 单调区间及值域;(4)求使 恒成立的实数 的取值范围.
【课堂小结】:
【课后反思】:
向下平移 个单位
得到 的图象.
【互动探究】
例1:说明下列函数的图象与指数函数 的图象的关系,并画出它们的示意图:
(1) ; (2)
例2:说明下列函数的图象与指数函数 的图象的关系,并画出它们的示意图:
(1) ;(2) .
例3:画出函数的图象并根据图象求它的单调区间:
(1) ;(2)
分析:先要对解析式化简.
苏教版数学高一《指数函数》精品教学设计 苏教

惯和品质;培养他们实事求是的科学态度,积极参与和勇于探索的精神。
教学重点:指数函数的概念和性质。
教学难点:指数函数的图象性质与底数a的关系。
教学方法:引导发现法;直观演示法;设疑诱导法;多媒体辅助教学所需设备:电脑多媒体辅助设备教师活动学生活动设计意图新课引入:设计一个游戏情境,学生分组,通过动手折纸,观察对折的次数与所得的层数之间的关系。
授课过程:一、1、创设情境,形成概念问题:庄子曰:一尺之棰,日取其半,万世不竭。
其含义是什么呢?能否给出表达式?学生分组,动手折纸,观察对折的次数与所得的层数之间的关系为学生分组讨论,先分析其含义,再转化为现代语言,建立数学模型,给出结论。
充分发挥学生的主体作用,发展学生的个性,培养学生自主学习的能力。
在学生动手操作的过程中激发学生学习热情和探索新知的欲望。
让学生动手操作,动脑思考,培养学生勇于探索的精神。
第一次第二次第三次第四次问题:某种细胞分裂时,由1个分裂成2个, 2个分裂成4个,4个分裂成8个,……如果分裂一次需要10min ,那么,一个细胞1h 后分裂成多少个细胞?教师给出指数函数的定义,即形如 (a>0且a≠1) 的函数称为指数函数,定义域为R 。
如:函数 y=2x y=(1/2)x y=10x 都是指数函数,它们的定义域都是实数集R ,提醒学生指数函数的定义是形式定义,如y=3×2x y=10x+5不是指数函数学生思考后回答并说明。
函数解析式是什么?)(2y N x x ∈=学生理解概念,并展开讨论,什么定义中规定a>0且a≠1呢? (1)若a<0, a x不一定有意义.如a=-2,当x=1/2,(2)若a=0,则当x>0时,a x=0; x ≤0时,a x 无意义. (3)若a=1,则对于任意x ∈R,a x=1为常量。
进一步探索问题,发现规律。
对a 的范围的具体分析,有利于学生对指数函数一般形式的掌握,同时为后面研究函数的图象和性质埋下了伏笔。
高中数学新苏教版精品学案《指数函数 》

指数函数【学习目标】1.理解指数函数的概念,并能正确作出其图象,掌握指数函数的性质;2.能运用指数函数的性质比较两个指数值的大小;3.培养学生发现问题和提出问题的能力。
善于独立思考的习惯,体会事物之间普遍联系的辩证观点。
【学习重难点】正确作出指数函数的图象,掌握指数函数的性质【课前导学】引例1 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……,1个这样的细胞分裂次后,得到的细胞个数与的函数关系是什么?分裂次数:1,2,3,4,…,细胞个数:2,4,8,16,…,由上面的对应关系可知,函数关系是=2。
引例2 某种商品的价格从今年起每年降低15%,设原来的价格为1,年后的价格为,则与的函数关系式为=。
在=2,=中指数是自变量,底数是一个大于0且不等于1的常量。
我们把这种自变量在指数位置上而底数是一个大于0且不等于1的常量的函数叫做指数函数,引入课题。
【课堂活动】一、建构数学:1.指数函数的定义函数=a(a>0且a≠1)叫做指数函数,其中是自变量,函数定义域是R。
探究1:为什么要规定a>0,且a≠1呢?①若a=0,则当>0时,a=0;当≤0时,a无意义。
②若a<0,则对于的某些数值,可使a无意义。
如=(-2),这时对于=错误!,=错误!,…等等,在实数范围内函数值不存在。
③若a=1,则对于任何∈R,a=1,是一个常量,没有研究的必要性。
为了避免上述各种情况,所以规定a>0且a≠1.在规定以后,对于任何∈R,a都有意义,且a >0 因此指数函数的定义域是R,值域是(0,∞)。
探究2:函数=2·3是指数函数吗?答案:不是,指数函数的解析式 =a 中,a 的系数是1.有些函数貌似指数函数,实际上却不是,如 =a (a >0且a ≠1,∈Z );有些函数看起来不像指数函数,实际上却是,如=a -(a >0,且a ≠1),因为它可以化为 =(a -1),其中a -1>0,且a -1≠1.思考 下列函数是为指数函数有 ② ③ ⑤ 。
高中数学新苏教版精品教案《苏教版高中数学必修1 3.1.2 指数函数》0

课题:指数函数教材:苏教版普通高中课程标准实验教科书必修1一、教学目标:知识目标:①知道指数函数的定义;②知道指数函数的图象和性质;感悟研究函数的规律和方法能力目标:①培养观察、联想、类比、猜测、归纳等思维能力;②体会数形结合思想、分类讨论思想,增强识图用图的能力情感目标:①通过自主探究,体验从特殊→一般→特殊的认知过程,了解指数函数的实际背景;②通过亲手实践,互动交流,激发学习兴趣,增强创新意识二、教学重点、难点:重点:指数函数的定义,图象和性质;难点:由指数函数图象探索并理解指数函数的性质三、教学工具:PPT、Ece、几何画板、实物投影仪教学方法:探究式教学法四、教学过程:亲爱的同学们,我们在前面的几节课中,系统的学习了函数的概念,研究了函数的图象与性质,今天我们将在前面学习的根底上继续学习并研究一类重要的函数,请同学们先看两个实际问题:一、情境导入情境一:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个……一个这样的细胞分裂次后,得到细胞分裂的个数为,请写出与之间的关系式与之间的关系式,可以表示为〔〕情境二:某放射性物质不断衰变为其他物质,每经过1年,这种物质剩留的质量是原来的50%,现有该物质质量为1,经过年的剩留量为,请写出与之间的关系式与之间的关系式,可以表示为〔〕二、新知探究〔一〕指数函数的定义问题组一:〔1〕请问函数和函数具有哪些相同的特征?〔2〕你能否写出类似结构的函数表达式?尝试一下〔3〕能否将上述几个具体的函数表达式统一写成一般的函数表达式呢?引导学生归纳:用字母代替其中的底数,将上述式子表示成的形式师:这里的是否有所限制呢?由上一节课?分数指数幂?所学知识可知,规定底数,指数的取值集合可以为全体实数但是假设底数,那么函数为,无论取何值,恒成立,归为常数函数故引出指数函数的定义:思考:函数是否为指数函数呢?同学们,我们了解了指数函数的定义以后,需要对指数函数的性质进行研究,以便帮助我们解决具体问题〔二〕指数函数的图象与性质问题组二:(1)我们在前面函数章节中研究了函数的哪些性质?(2)我们在前面函数章节中通过怎样的方法研究函数的性质?师:我们下面分三步走来实现通过函数图象研究函数性质的目的第一步:用列表描点的方法作出指数函数的图象利用实物投影来展示学生所作图象,结合实际情况对学生所作图象作出评价评价的主要方面有:曲线的延展性,平滑度,凹凸性,与轴的渐进关系等假设学生作图存在问题,可以结合指数函数的定义式想象图象的特征,运用数形结合的思想方法,由数想形,有形想数,来完善指数函数图象师:刚刚我们通过列表描出个别整数点的方式大致作出了指数函数的图象,那么对于指数函数更精确的图象究竟是什么样子的呢?下面我们以指数函数为例,利用计算机软件来作出它的精确图象第二步:用计算机软件Ece作出指数函数的图象引导学生结合图象指出指数函数的性质,完成指数函数的性质表格将探究得到的性质填入表格中:师:刚刚我们一起研究了具体的指数函数的图象与性质,但是指数函数作为一类函数,其性质是否可以按底数分成两大类呢?下面我们利用计算机软件——几何画板,通过改变底数的取值,来验证我们的猜测第三步:用计算机软件几何画板,演示底数取不同值时指数函数的图象的变化验证步骤二中总结出指数函数的性质,实现从特殊到一般地转化,总结出一类函数的性质,进一步完善表格师:经历了刚刚的“三部曲〞,我们终于探究得到了指数函数的性质,为了便于大家记忆图象与性质,老师送给大家一个“顺口溜〞,请看:性质概括:大1增,小1减,图象恒过〔0,1〕点;左右无限上冲天,永与横轴不沾边经过刚刚的一番探索,我们得到了指数函数的性质,运用指数函数的性质可以帮助我们解决那些数学问题呢?三、数学运用例1、比拟以下各组数中两个值的大小〔1〕,〔2〕,〔3〕,〔4〕,解:〔1〕可直接计算;〔2〕引起认知冲突,实现构造函数思想的自然引入;〔3〕略〔4〕构造两个指数函数和,由单调性易知:,利用“〞架设“桥梁〞解题反思:构造函数的思想,再运用指数函数的单调性解决问题练习:比拟以下各组数中两个值的大小:〔1〕;〔2〕例2、〔1〕,求实数的取值范围;〔2〕,求实数的取值范围解题反思:指数函数单调性的逆用练习:求满足以下条件的实数的取值范围:〔1〕;〔2〕四、归纳总结1、知识点上:掌握了研究具体函数的方法;掌握了指数函数的图象与性质2、思想方法上:〔1〕特殊→一般→特殊;〔2〕分类讨论;〔3〕构造函数;〔4〕数形结合五、课后稳固P54,习题2、3、4附:教学设计说明*教材的地位和作用:本节课是学生在已掌握了函数的一般性质和简单的指数运算的根底上,进一步研究指数函数,以及指数函数的图象与性质,它一方面可以进一步深化学生对函数概念的理解与认识,使学生得到较系统的函数知识和研究函数的方法,同时也为今后进一步熟悉函数的性质和作用,研究对数函数以及等比数列的性质打下坚实的根底因此,本节课的内容十分重要,它对知识起到了承上启下的作用此外,?指数函数?的知识与我们的日常生产、生活和科学研究有着紧密的联系,尤其表达在细胞分裂、贷款利率的计算和考古中的年代测算等方面,因此学习这局部知识还有着广泛的现实意义*学生的学情分析:本课时是学生在学习了分数指数幂的前提下,再进一步升华为指数函数的第一节课,它承上启下,对学生来说至关重要学生在前面已经学过了一般函数的性质和数形结合的思想,本节课就要学以致用高中数学应该表达以学生为主,让学生自主探索,领略数学的乐趣,教师应该在课堂上创立适当的情景让学生能在其中由浅入深的掌握知识点,教师是课堂的引领者而不是主宰者*教师的教法分析:本节课采用探究、比拟的教学方法通过教师在教学过程中的点拨,启发学生通过主动观察、主动思考、动手操作、自主探究来到达对知识的发现和接受*板书设计:。
高中数学新苏教版精品教案《苏教版高中数学必修1 3.1 指数函数》

课题 《指数函数》授课教师:扬中市第二高级中学 刘玉教材:苏教版《数学必修1》第2章 一、教学目标:知识与技能:1从实例中抽象出指数函数的模型,理解指数函数的概念2会画指数函数的图象,通过图象总结归纳出指数函数的性质 培养学生观察、分析、归纳等思维能力3理解指数函数的性质,并能运用性质解决比较指数式值大小的问题过程与方法:1通过自主操作和探索,让学生经历:“特殊→一般”的认知过程,完善认知结构 2体会函数思想、分类讨论思想、数形结合思想、从特殊到一般等数学思想方法 情感、态度与价值观:1让学生感受探索数学问题的过程,体会成功的乐趣和喜悦2让学生体会数学的抽象性、严谨性和统一性,培养他们实事求是的科学态度,积极参与和勇于探索的实践精神二、教学重点与难点:重点:指数函数的图象、性质及简单应用难点:探索归纳指数函数图象和性质突破方法:通过对具体函数的观察和归纳,学生间的合作交流,并加以多媒体动态演示,将具体化为抽象,并感受到对底数a 分类讨论的思维方式,从而达到重难点的突破三、教学方法:教法:多媒体辅助教学,采用启发式、引导发现的教学方法学法:自主探索、合作交流的学习方法四、学习过程:(一)复习:提问1:我们已经学习了哪几种函数?一次函数:)0(≠+=k b kx y ,二次函数)0(2≠++=a c bx ax y ,反比例函数:)0(≠=k x k y 提问2:研究一个函数,主要研究它的哪些方面?这些性质在图象上是如何表现的?函数的图象和性质,性质包括:定义域、值域、单调性、奇偶性等(板书)反应在图象上: 位置、 变化趋势、对称性提问3:研究函数性质的途径?图象,通过图象看函数的性质(看图说话)提问4:是不是一定要通过函数的图象才能得到函数的性质?以32+-=x y 为例,通过函数的解析式,我们也可以看出函数的性质。
总结: “数”——解析式;“形”——图象。
(板书)(二 )情境引入引例1:比较下列指数式的异同: 2213202153-22,2,2,2,2,2,22--,,能否把它们看成是函数值?若能,是什么函数的值? R x y x ∈=,2引例2: 《庄子·天下篇》中写道:“一尺之棰,日取其半,万世不竭”请你写出截取次x 后,木棰剩余量y 关于x 的关系式:12x y ⎛⎫= ⎪⎝⎭, *x N ∈ 这两个函数模型是我们以前学习的函数吗?不是,不满足以上三种函数的形式。
苏教版高中数学必修一第三章《3.1指数函数》教学设计

《指数函数》教学设计一、教材分析函数是数学学习的重点和难点,函数的思想贯穿整个数学学习。
本节课是学生在已掌握了函数的定义、性质和简单的指数运算的基础上,进一步研究指数的定义、图像和性质,一方面可以进一步深化学生对函数概念的理解和认识,使学生得到系统的函数知识和研究函数的方法;另一方面也为研究对数函数以及等比数列的性质打下基础。
本节课十分重要,它对知识起承上启下的作用。
二、学情分析在初中所学的基本初等函数的基础上,通过前几节课的对函数的定义的更详细了解,学生对函数有了一定的理解,已初步能用函数的观点分析问题、解决问题。
三、教学目标知识目标:熟悉指数函数的定义;掌握指数函数的图像和性质。
能力目标:通过教学培养学生观察、分析、归纳等思维能力,进一步巩固数形结合、分类讨论的数学思想,掌握从特殊到一般的学习数学的方法,增强识图用图的能力。
情感目标:通过探究学习,使学生学会认识事物的特殊性与一般性的关系,学会用函数的观点分析问题,并养成合作交流、独立思考、理论联系实际的习惯,激发学生学习数学的兴趣,树立学习数学的信心。
四、教学重点、难点重点是指数函数的图像和性质;难点是指数函数性质的应用。
教学方法:引导,观察,归纳,启发,探究,比较。
五、教学活动(一)温故知新(学生集体回答下列问题。
)1.指数式的形式2.指数的运算公式设计意图:通过多媒体演示,引导学生回忆指数的运算,培养学生温故知新的能力,为本节内容的学习做好准备。
(二)创设情境,导入新课(学生跟随教师动手折纸,在动态的操作中找到问题的答案)折纸是一门艺术,很受大家的青睐;折纸又是一个数学探究的过程,它溶于数学,所以以折纸为载体,出现了不少趣题,请同学们动手之后回答下面的问题:假设一张纸的厚度为1,对折x次,纸的厚度y是多少?答:对折1次,折纸厚度为21;对折2次,折纸厚度为22;对折3次,折纸厚度为23;对折4次,折纸厚度为24,……对折x次,折纸厚度y=2x 定义:一般地,形如y=ax,(a>0且a≠1)的函数叫做指数函数,其中x 是自变量,定义域为实数集R。
苏教版数学高一《指数函数》精品导学案
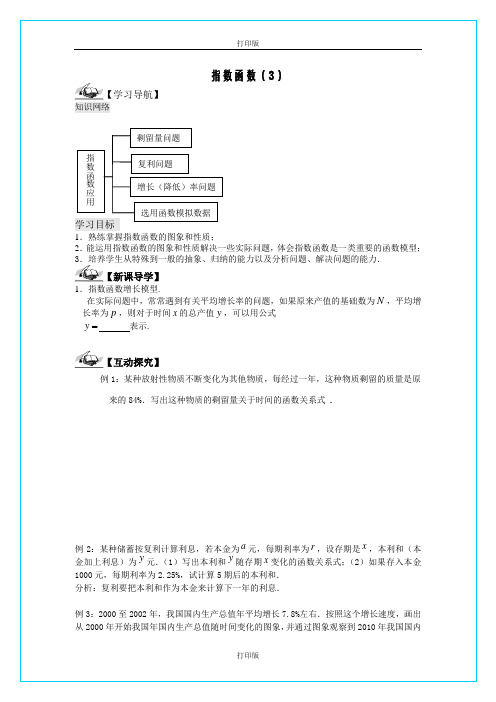
体积
…
…
(1)设想城市垃圾的体积每三年继续加倍,问 年信息,你估计 年前垃圾的体积是多少?
(3)如果 ,这时的 表示什么信息?
(4)写出 与 的函数关系式,并画出函数图象(横轴取 轴);
(5)曲线可能与横轴相交吗?为什么?
【课堂小结】:
【课后反思】:
【迁移应用】
1.(1)一电子元件厂去年生产某种规格的电子元件 个,计划从今年开始的 年内,每年生产此种规格电子元件的产量比上一年增长 ,则此种规格电子元件的年产量 随年数 变化的函数关系式为
_______________
(2)一电子元件厂去年生产某种规格的电子元件的成本是 元/个,计划从今年开始的 年内,每年生产此种规格电子元件的单件成本比上一年下降 ,则此种规格电子元件的单件成本 随年数 变化的函数关系式是
表示.
【互动探究】
例1:某种放射性物质不断变化为其他物质,每经过一年,这种物质剩留的质量是原来的84%.写出这种物质的剩留量关于时间的函数关系式.
例2:某种储蓄按复利计算利息,若本金为 元,每期利率为 ,设存期是 ,本利和(本金加上利息)为 元.(1)写出本利和 随存期 变化的函数关系式;(2)如果存入本金1000元,每期利率为2.25%,试计算5期后的本利和.
____________________________________.
2. 年 月 日,美国某城市的日报以醒目标题刊登了一条消息:”市政委员会今天宣布:本市垃圾的体积达到 ”,副标题是:”垃圾的体积每三年增加一倍”.如果把三年作为垃圾体积加倍的周期,请你完成下面关于垃圾体积 与垃圾体积的加倍的周期( 年)数 的关系的表格,并回答下列问题:
分析:复利要把本利和作为本金来计算下一年的利息.
指数函数学案

2.2.2指数函数(第一课时)(学案)教材:苏教版高中数学必修一一、教学目标1、了解指数函数模型的实际背景,认识学习指数函数的必要性。
2、理解指数函数的含义,能借助计算器或计算机画出指数函数的图像,探索并理解指数函数的性质;能运用指数函数的单调性,比较两个指数式值的大小。
3、引导学生观察、分析、抽象、概括,发展学生的思维能力。
二、教学重点、难点重点:指数函数图像、性质及简单运用难点:指数函数图像及性质的发现过程以及函数图像与底的关系。
三、教学过程1、模型准备(课前预习)阅读材料,回答问题:利息:是指一定资金在一定时期内的收益。
在现实生活中,银行计算利息的方法常见的有两种:单利与复利。
单利是指按照固定的本金计算利息;而复利是指对本金及其产生的利息一并计算,即把上一期的本利和作为下一期的本金( 俗称利滚利)。
若有本金1(万元),每期利率为%5,存x期,(1)若某银行储蓄按单利计算利息,请写出本利和y(万元)关于存期x变化的解析式。
(2)若某理财产品按复利计算利息,请写出本利和y(万元)关于存期x变化的解析式。
2、模型假设材料1:2011年中国某城市的日报用醒目标题刊登了“本市垃圾今年已达到1万立方米”,副标题是“垃圾的体积每年增加一倍”,请写出经过x年后,城市垃圾y(万立方米)关于x的函数关系式。
材料2:2010年6月环球在线消息:如果问澳大利亚人做过的最失策的一件事是什么?他们一定会说,那就是在1935年从昆士兰州引进了102只蔗蟾蜍。
如今,这些相貌奇丑、身带剧毒的蟾蜍已经成为这片大陆的梦魇,西澳大利亚州甚至向国防部求救,要求调集军队,背水一战。
此类蟾蜍繁殖力惊人,尽管人们采取多种措施来消灭蟾蜍,但效果都不理想。
澳大利亚境内的蟾蜍数量在“爆炸性增长”。
假设现有蟾蜍1(百万),数量每年增加两倍,请写出蟾蜍总数y(百万只)与年份x(年数)的函数关系式。
【思考】在现实生活中,你还能举出类似的增长模型吗?3、模型分析(1)画出)(R x y x ∈=2图像②描点、连线(2)根据图像,归纳x y 2=性质(3)再次阅读材料1,并回答:根据报纸所提供的信息,请写出x 年前,城市垃圾y (万立方米)关于x 的函数关系式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于前面指数函数的知识掌握要到位,理解函数是描述客观世界变化规律的基本数学模型,运用数学语言来描述客观事物。
【课前预习】
(一)知识回顾:
1.指数函数的概念:
2.指数函数图象及其性质:
(二)基础训练
1.已知 ,则a,b,c从小到大的顺序为。
2.函数y=ax(a>0且a≠1)的定义域是____,值域是___,函数图象所过的定点坐标为.若a>1,则当x>0时,y1;而当x<0时,y1.若0<a<1,则当x>0时,y1;而当x<0时,y1.
⑴ ;⑵ ;⑶ ;⑷ .
练习:
⑴将函数f (x)=3x的图象向右平移3个单位,再向下平移2个单位,可以得到函数的图象.
⑵将函数f (x)=3-x的图象向右平移2个单位,再向上平移3个单位,可以得到函数的图象.
⑶将函数 图象先向左平移2个单位,再向下平移1个单位所得函数的解析式是.
⑷对任意的a>0且a≠1,函数y=a2x1的图象恒过的定点的坐标是.函数y=a2x-1的图象恒过的定点的坐标是.
⑸如何利用函数f(x)=2x的图象,作y= 和y= 的图象?
⑹如何利用函数f(x)=2x的图象,作出函数y=|2x-1|的图象?
例3已知函数y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1-2x,试画出此函数的图象.
例4求函数 的最小值及取得最小值时的x值.
【课堂小结】1.指数函数的性质及应用;2.指数型函数的定点问题;3.指数型函数的草图及其变换规律.
【课堂探究】
一.情境问题
指数函数的性质除了比较大小,还有什么作用呢?我们知道对任意的a>0且a≠1,函数y=ax的图象恒过(0,1),那么对任意的a>0且a≠1,函数y=a2x-1的图象恒过哪一个定点呢?
二.数学建构
例1解不等式:(1) ;(2) ;
(3) ;(4) .
例2说明下列函数的图象与指数函数y=2x的图象的关系,并画出它们的示意图:
执笔人:祁正权审核人:姚东盐2011年10月*日
2.2.2指数函数第2课时
【教师活动】
【教学目标】
1.进一步理解指数函数的性质;
2.能较熟练地运用指数函数的性质解决指数函数的平移问题;
【教学重难点】
重点:指数函数的性质的应用;
难点:指数函数图象的平移变换.
【教学设想】(【教学准备】)
多媒体
【教学活动】(【教学流程】)
1.问题情境
2.建构数学概念
3.举例应用
4.课堂练习
5Hale Waihona Puke 小结作业【教学反思】小结:
小结:函数图象的对称变换规律.
小结:复合函数常常需要换元来求解其最值.
练习 课时训练补充
【学生活动】
【学习目标】
1.掌握指数函数的概念、图象和性质;
2.了解指数函数模型的实际案例,会用指数函数模型解决简单的实际问题。
【课时安排】1课时
【课后巩固】课本P556,8
【课后反思】
