勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理的证明方法
勾股定理的证明方法勾股定理是初等几何中的一个基本定理.这个定理有十分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴趣，因为这个定理太贴近人们的生活实际，以至于古往今来，下至平民百姓,上至帝王总统都愿意探讨和研究它的证明．下面结合几种图形来进行证明。
一、传说中毕达哥拉斯的证法（图1）左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、，斜边为的直角三角形拼成的.右边的正方形是由1个边长为的正方形和4个直角边分别为、,斜边为的直角三角形拼成的。
因为这两个正方形的面积相等（边长都是),所以可以列出等式，化简得。
在西方，人们认为是毕达哥拉斯最早发现并证明这一定理的,但遗憾的是，他的证明方法已经失传，这是传说中的证明方法，这种证明方法简单、直观、易懂.二、赵爽弦图的证法(图2）第一种方法:边长为的正方形可以看作是由4个直角边分别为、，斜边为的直角三角形围在外面形成的。
因为边长为的正方形面积加上4个直角三角形的面积等于外围正方形的面积，所以可以列出等式，化简得。
第二种方法：边长为的正方形可以看作是由4个直角边分别为、，斜边为的角三角形拼接形成的（虚线表示），不过中间缺出一个边长为的正方形“小洞”.因为边长为的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积，所以可以列出等式，化简得.这种证明方法很简明，很直观,它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神,是我们中华民族的骄傲。
三、美国第20任总统茄菲尔德的证法（图3）这个直角梯形是由2个直角边分别为、，斜边为的直角三角形和1个直角边为的等腰直角三角形拼成的。
因为3个直角三角形的面积之和等于梯形的面积，所以可以列出等式，化简得.这种证明方法由于用了梯形面积公式和三角形面积公式，从而使证明更加简洁，它在数学史上被传为佳话。
古希腊数学的伟大成就:1、使数学成为抽象性的一门科学；2、建立了演绎证明体系，希腊成为论证数学发祥地;3、创立了几何学、三角学，奠定了数论基础等；4、萌芽了一些高等数学，如数论、极限等;5、希腊人发现定理及证明，逻辑结构严密,论证认真细致，为后世树立了样板等；不足：如，重几何轻代数,认为几何方法是数学证明唯一方法，畏于无理数的存在，而不将算术应用于几何；几何作图严格限制规尺.古希腊的数学方法论泰勒斯最先提出数学方法论,数学命题要加以演绎证明，在数学中要建立一般的原理好人规则，数学命题的证明就是要借助一些公理或真实性已经确定的命题来论证某一命题真实性的思想过程.演绎证明的方法即演绎推理的方法，指从一般到特殊的推理方法,其核心是三段论法，即有两个已知判断,推出第三个判断，例如，平行四边形的对角线互相平分(第一个已知一般判断成为大前提），矩形是平行四边形（另一个已知较特殊的判断，成为小前提）,则矩形的对角线互相平分(推出新判断，即结论).用演绎法证明命题使几何由实验阶段,过渡到一门抽象的理论科学，使人类对自然的认识由感性(或经验)认识上升到理性认识，因此这是一个划时代的贡献。
毕达哥拉斯勾股定理证明
毕达哥拉斯勾股定理证明毕达哥拉斯勾股定理证明引言毕达哥拉斯勾股定理是数学史上一项重要的发现，它被广泛应用于几何学和物理学中。
本文将深入探讨毕达哥拉斯勾股定理的证明过程，并对其原理和应用进行全面评估。
让我们从简单的几何形状开始，逐步推导出这个定理的深刻意义。
1. 直角三角形的定义我们从直角三角形开始，这是研究毕达哥拉斯勾股定理的基础。
直角三角形是一种具有一个内角为90度的三角形。
我们将其三个边分别称为斜边、邻边和对边。
2. 毕达哥拉斯勾股定理的表述毕达哥拉斯勾股定理可以一句话概括为：直角三角形的斜边的平方等于邻边的平方与对边的平方之和。
用数学表达式来表示就是：a² + b² = c²，其中a和b是直角三角形的两条直角边，c是直角三角形的斜边。
3. 毕达哥拉斯勾股定理的第一个证明：几何方法我们以一个简单的正方形开始推导。
正方形的对角线可以作为两个直角边，那么根据勾股定理，对角线的平方等于两条直角边的平方和。
我们将正方形划分为四个直角三角形，每个直角三角形的两条直角边与两个直角边合并时构成一个直角边。
我们可以得出结论：正方形的对角线的平方等于四个直角三角形的两条直角边的平方和。
进一步，我们可以推广到其他几何形状，如长方形和正三角形。
这个证明方法是以简单的形状为基础，逐步推导出毕达哥拉斯勾股定理的普遍性。
4. 毕达哥拉斯勾股定理的第二个证明：代数方法我们还可以使用代数方法证明毕达哥拉斯勾股定理。
我们令直角三角形的直角边分别为a和b，斜边为c。
根据勾股定理，我们有a² + b² = c²。
接下来，我们将三条边的长度进行变换，假设每条边的长度为一个未知数x。
根据勾股定理，我们有x² + x² = c²，即2x² = c²。
我们可以将c²表示为2x²，并继续化简等式。
我们得到c² = 4(x²/2)，即c² = 4(x²/2)。
勾股定理简介与证明(3篇)
第1篇一、勾股定理简介勾股定理，又称为毕达哥拉斯定理，是数学中一个重要的几何定理。
它指出，在直角三角形中，直角边的平方和等于斜边的平方。
这个定理不仅在我国古代数学著作《周髀算经》中有记载，而且在古希腊、印度、埃及等地的数学文献中也有所体现。
勾股定理是解决直角三角形问题的基础，也是许多数学领域的重要工具。
二、勾股定理的证明1. 证明方法一：几何证明如图所示，设直角三角形ABC中，∠C为直角，AC、BC分别为直角边，AB为斜边。
作辅助线CD，使得CD⊥AB于点D。
（1）证明AC²+BC²=AB²由于CD⊥AB，∠ACD和∠BCD都是直角。
因此，三角形ACD和三角形BCD都是直角三角形。
根据直角三角形的性质，有：AC² = AD² + CD²BC² = BD² + CD²将上述两个等式相加，得到：AC² + BC² = (AD² + CD²) + (BD² + CD²)AC² + BC² = AD² + BD² + 2CD²由于AD+BD=AB，将AD+BD替换为AB，得到：AC² + BC² = AB² + 2CD²由于CD是AB的一半，即CD=AB/2，代入上式，得到：AC²+ BC² = AB² + 2(AB/2)²AC² + BC² = AB² + AB²AC² + BC² = 2AB²由于2AB²=AB²，因此：AC² + BC² = AB²（2）证明结论根据上述证明，得出勾股定理：在直角三角形中，直角边的平方和等于斜边的平方。
勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理（毕达哥拉斯定理） 是一个，是人类早期发现并证明的重要数学定理之一，用思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。
是的一个特例。
约有400种证明方法，是数学定理中证明方法最多的之一。
“”是勾股定理最基本的公式。
勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。
(3,4,5)就是。
也就是说，设直角三角形两直角边为a 和b ，斜边为c ，那么a 2+b 2=c 2，即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1如果的两条直角边长分别为a ，b ，斜边长为c ，那么。
勾股定理的逆定理命题2如果的三边长a ，b ，c 满足，那么这个三角形是直角三角形。
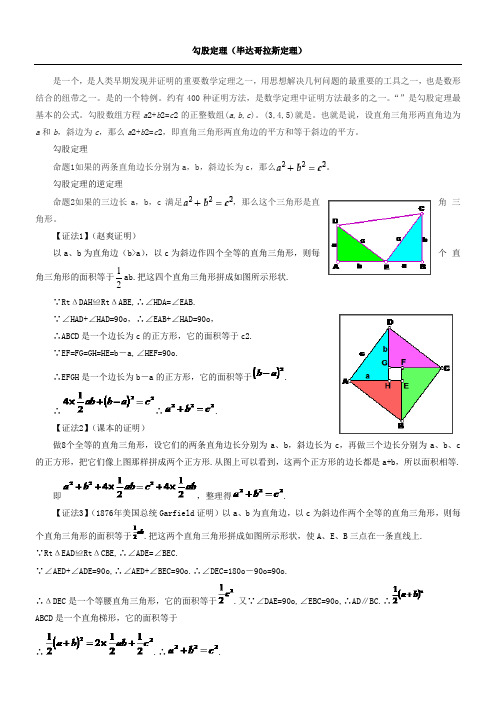
【证法1】（赵爽证明）以a 、b 为直角边（b>a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于21ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90o，∴∠EAB+∠HAD=90o，∴ABCD 是一个边长为c 的正方形，它的面积等于c2.∵EF=FG=GH=HE=b―a,∠HEF=90o.∴EFGH 是一个边长为b―a 的正方形，它的面积等于.∴∴.【证法2】（课本的证明） 做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a+b ，所以面积相等.即，整理得.【证法3】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC.∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o.∴ΔDEC 是一个等腰直角三角形，它的面积等于.又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ABCD 是一个直角梯形，它的面积等于 ∴.∴.【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。
数学勾股定理公式大全勾股定理的证明方法
数学勾股定理公式大全勾股定理的证明方法数学勾股定理公式是asup2;+bsup2;=csup2;。
勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。
数学勾股定理公式大全数学勾股定理公式是asup2;+bsup2;=csup2;。
勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。
勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。
在中国，周朝时期的商高提出了勾三股四弦五的勾股定理的特例。
在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
勾股定理的证明方法做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们拼成两个正方形。
可以看到，这两个正方形的边长都是a+b，所以面积相等.即a的平方加b的平方，加4乘以二分之一ab等于c的平方，加4乘以二分之一ab，整理得a的平方加b的平方等于c的平方。
勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。
勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。
证明勾股定理的方法
证明勾股定理的方法勾股定理，也被称为毕达哥拉斯定理，是数学中的一条基本定理，它描述了直角三角形中直角边与斜边之间的关系。
证明勾股定理的方法有很多种，下面将介绍其中几种常见的方法。
方法一：几何证明法几何证明法是最常见的证明勾股定理的方法之一。
它通过构造几何图形，利用几何性质来证明定理的正确性。
下面以一种简单的几何证明法为例进行说明。
设直角三角形的两条直角边分别为a和b，斜边为c。
我们可以构造一个正方形，边长为a+b，如图所示。
[图1]根据正方形的性质，它的对角线相等，即对角线AC的长度等于对角线BD的长度。
又因为AC的长度等于a+b，BD的长度等于c，所以a+b=c。
这就证明了勾股定理。
方法二：代数证明法代数证明法是另一种常见的证明勾股定理的方法。
它通过代数运算和方程推导来证明定理的正确性。
下面以一种代数证明法为例进行说明。
设直角三角形的两条直角边分别为a和b，斜边为c。
根据勾股定理，我们有a²+b²=c²。
我们可以将这个方程转化为等价的形式进行证明。
首先，我们将c²展开，得到c²=a²+b²。
然后，我们将a²和b²分别展开，得到a²=(c-b)(c+b)和b²=(c-a)(c+a)。
将这两个等式代入c²=a²+b²中，得到c²=(c-b)(c+b)+(c-a)(c+a)。
我们可以进行简化运算，得到c²=2ac+2bc-2ab。
继续简化运算，得到c²+2ab=2ac+2bc。
再将等式两边同时除以2，得到(c²+2ab)/2=(2ac+2bc)/2。
化简得到c²+ab=ac+bc。
根据等式两边的相等性，我们可以得到a(c-b)=b(c-a)。
再将等式两边同时除以c-a，得到a=b。
同样的方法，我们可以得到b=a。
挑战思维极限 勾股定理的365种证明
挑战思维极限勾股定理的365种证明挑战思维极限：勾股定理的365种证明导语：挑战思维极限，是人类一直以来的追求。
人们通过不断突破自己的认知边界，探索未知的领域。
勾股定理作为数学领域里最基础、最经典的定理之一，几乎是每个学生在数学课堂上必须掌握的内容。
但是，你知道吗？这个定理有着超过365种不同的证明方法。
本文将以从简到繁的方式，逐步探索这个数学定理的多样性与美妙。
1.初级证明勾股定理，在数学中又被称为毕达哥拉斯定理，最早出现在古希腊。
一个简单的证明方法是利用几何图形。
我们将一条直角边的长度设为a，另一条直角边的长度设为b，斜边的长度设为c。
根据勾股定理，我们有a²+b²=c²。
那么，我们可以通过构造一个正方形，将边长分别设为a、b和c，再利用面积的计算方法得到这个定理的证明。
2.三角函数证明在勾股定理的证明中，三角函数是常见且重要的工具。
我们可以通过正弦定理和余弦定理来推导勾股定理。
利用正弦定理得到sin A / a = sin B / b = sin C / c。
将这个结果代入余弦定理，得到a²+b²-2abcosC=c²。
由于直角三角形中cosC=0，所以最终得到a²+b²=c²。
3.解析几何证明解析几何是通过代数方法来解决几何问题的一种方法。
在勾股定理的证明中，我们可以利用平面直角坐标系来进行推导。
假设A点坐标为(0,0)，B点坐标为(a,0)，C点坐标为(0,b)，则C点的坐标为(a,b)。
通过距离公式和勾股定理的关系，我们可以得到a²+b²=c²。
4.复数证明复数是数学中一种有趣而重要的概念，在勾股定理的证明中也有其应用。
我们可以将直角边的长度表示为实数，斜边的长度表示为纯虚数。
通过对勾股定理进行代数操作，将三个数的平方相加，并最终等于零，从而证明了勾股定理。
5.数学归纳法证明数学归纳法是一种证明数学命题的方法。
勾股定理(毕达哥拉斯定理)及各种证明方法
勾股定理（毕达哥拉斯定理）勾股定理是一个初等几何定理，是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法，是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说，设直角三角形两直角边为a 和b ，斜边为c ，那么a ²+b ²=c ² ，即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ，b ，斜边长为c ，那么。
勾股定理的逆定理命题2 如果三角形的三边长a ，b ，c 满足，那么这个三角形是直角三角形。
【证法1】（赵爽证明）以a 、b 为直角边（b>a ）， 以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º，∴ ∠EAB + ∠HAD = 90º， ∴ ABCD 是一个边长为c 的正方形，它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形，它的面积等于.∴ ∴.【证法2】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等.即， 整理得 .【证法3】（1876年美国总统Garfield证明）以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形，它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形，它的面积等于∴ .∴.【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
勾股定理（毕达哥拉斯定理）及
各种证明方法
勾股定理（毕达哥拉斯定理）
勾股定理是一个初等几何定理，是人类早期
发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法，是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a2 + b2= c 2的正整数组（a, b, c）。
（3,4,5）就是勾股数。
也就是说，设直角三角形两直角边为a和b,斜边为c，那么a2+b2=c2，即直角三角形两直角边的平方和
等于斜边的平方。
勾股定理
命题1如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么”+b—
勾股定理的逆定理
命题2如果三角形的三边长a，b，c满足
= 3，那么这个三角形是直角三角形。
【证法1】（赵爽证明）
全等的直角三角形，则每个直角三角形的面积等 V Rt △ DAH 今 Rt △ ABE, A ZHDA = ZEAB ・ ••• ZHAD + ZHAD = 90°, :. ZEAB + ZHAD =
【证法2】（课本的证明）
做8个全等的直角三角形，设它们的两条直角边 长分别为a 、b,斜边长为c,再做三个边长分别
以a 、b 为直角边（b>a ）,
以c 为斜边作四个
于冲
把这四个直角三角形拼成如图所示形状
.
90°,
为a、b、c的正方形，把它们像上图那样拼
成两个正方形•从图上可以看到，这两个正方形的边长都是a + b，所以面积相等.
即，整理得宀F八
【证法3】（1876年美国总统Garfield 证明）以a、b为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于 >.把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上•
•・• Rt △ EAD也Rt △ CBE,「・ / ADE = / BEC.
•・• / AED + / ADE = 90o,二 / AED + / BEC = 90o.二 / DEC = 180c—90o= 90o.
••• △ DEC是一个等腰直角三角形，它的面积等于
/ .又•・•/ DAE = 90o, / EBC = 90o,二
AD// BC.・・・"
ABCD是一个直角梯形，它的面积等于
...知卄++护宀沪"
■ ■
【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。
他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。
由于好奇心驱使伽菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。
只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。
于是伽菲尔德便问他们在干什么？只见那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角
边分别为3和4，那么斜边长为
多少呢？”伽菲尔德答到：“是
5
呀。
”小男孩又问道：“如果两条直角边分别为5和乙那么这个直角三角形的斜边长又是多少？”伽菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方。
”小男孩又说道：“先生，你能说出其中的道理吗？”伽菲尔德一时语塞，无法解释了，心理很不是滋味。
于是伽菲尔德不再散步，立即回家，潜心探讨小男孩给他留下的难题。
他经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法。
1876年4月1日，伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年，伽菲尔德就任美国第二十任总统后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为"总统。
” 证法。
【证法4】（欧几里得证明）做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C B三点在一条直线上，连结BF、CD.过C 作
CLL DE 交 AB 于点 M 交 DE 于点 L. I AF = AC ， AB = AD , / FAB = / GAD
・•・△ FAB 也△ GAD
•・• △ FAB 的面积等于F ,△ GAD
勺面 积等于矩形ADLM 勺面积的一
半， ・•・矩形ADLM 的面积=4同理可证， 的面积=沪. •・•正方形ADEB 的面积=矩形ADLM 的面积+ 矩形MLEB 勺面积
.・• 沪，即 a -^=^.
【证法5】（利用相似三角形性质证明）
如图，在Rt △ ABC 中，设直角边 AC BC 的长度 分别为a 、b,斜边AB 的长为c,过点C 作CDLAB 垂足是D.在△ ADC 和△ ACB 中,
•・• / ADC= / ACB= 90o , / CAD= / BAC 二△ ADC
s △ ACB.
・•・ AD ： AC = AC : AB 即M". n
/ 、 / n 、 F 1 D « ■矩形MLEB
同理可证，△ CDB s △ ACB
从而有血=砂AB . :./匸亠毗~（血>58）•府■苗，即卩
【证法6】（邹元治证明）
以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于 >.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C G D三点在一条直线上.
••• Rt △ HAE 望Rt △ EBF,「. /
AHE=
Z BEF.
••• Z AEH + Z AHE = 90o,二Z AE
+ Z BEF = 90o.
••• Z HEF = 180o—90o= 90o.
•••四边形EFGH是一个边长为c的正方形.它的面积等于c2.
••• Rt △ GDH望Rt △ HAE,「. Z HGD = Z
EHA.
••• Z HG& Z GHD= 90o, • Z EHA+ Z GHD= 90o. 又••• Z GHE = 90o, • Z DHA = 90o+ 90o= 180o.
・•・ABCD是一个边长为a + b的正方形，它的面积等于（-+*r.
A ...低詳7 ...宀
■ ■
【证法7】（利用切割线定理证明）
在Rt △ ABC中，设直角边BC= a,
AC=
b,斜边AB = c.
如图，以B为圆心a为半径作圆，
交AB及AB的延长线分别于 D E,贝V BD = BE = BC = a.
因为/ BCA = 90o,点C在OB 上,
所以AC是。
B的切线.由切割线定理，得
即鼻鼾二X.
【证法8】（作直角三角形的内
切圆证明）
在Rt △ ABC中,设直角边BC= a ,
AC= b，斜边AB= c.作Rt △ ABC
的内切圆O Q切点分别为D E、F （如图）,设OO的半径为r.
•・• AE = AF , BF = BD, CD = CE,
CS-I-GD = r + r = 2r,即盘十丹一匚一",• I仏上
?
即 / "J亦 _*工+07)+^
心aw;, 又再十$»1；= 2°"+2
=：&42宀=>-tC> =「J逼.帝4A_
+«rj- Tub
* * ?
宀宀扌。