图的两种遍历
图的遍历算法

1图的遍历问题在实践中常常遇到这样的问题:给定n个点,从任一点出发对所有的点访问一次并且只访问一次。
如果用图中的顶点表示这些点,图中的边表示可能的连接,那么这个问题就可以表示成图的遍历问题,即从某个顶点出发,沿着某条搜索路径对图中每个顶点各做一次且仅做一次访问。
图的遍历操作和树的遍历操作功能相似,是图的一种基本操作,图的许多其它操作都是建立在遍历操作的基础上。
由于图结构本身的复杂性,所以图的遍历操作也比较复杂,主要表现在以下几个方面:(1) 在图结构中,没有一个确定的首结点,图中任意一个顶点都可以作为第一个被访问的结点。
(2) 在非连通图中,从一个顶点出发,只能够访问它所在的连通分量上的所有顶点,因此,还需要考虑如何选取下一个出发点以访问图中其余的连通分量。
(3) 在图结构中,如果有回路存在,那么一个顶点被访问后,有可能沿回路又回到该顶点。
⑷在图结构中,一个顶点可以和其它多个顶点相连,当这样的顶点访问过后,存在如何选取下一个要访问的顶点的问题。
基于以上分析,图的遍历方法目前有深度优先搜索(DFS)和广度优先搜索(BFS)两种算法。
下面将介绍两种算法的实现思路,分析算法效率并编程实现。
1.1深度优先搜索算法深度优先搜索算法是树的先根遍历的推广,它的实现思想是:从图G的某个顶点V o出发,访问V o,然后选择一个与V o相邻且没被访问过的顶点V i访问,再从V i出发选择一个与V i相邻且未被访问的顶点V j进行访问,依次继续。
如果当前被访问过的顶点的所有邻接顶点都已被访问,贝U退回已被访问的顶点序列中最后一个拥有未被访问的相邻顶点的顶点W,从W出发按同样的方法向前遍历,直到图中所有顶点都被访问。
其递归算法如下:Boolean visited[MAX_VERTEX_NUM]; // 访问标志数组Status (*VisitFunc)(int v); //VisitFunc是访问函数,对图的每个顶点调用该函数void DFSTraverse (Graph G Status(*Visit)(i nt v)){VisitF unc = Visit;for(v=0; vvG.vex num; ++v)visited[v] = FALSE; //访问标志数组初始化for(v=0; v<G .vex num; ++v)if(!visited[v])DFS(G v); //对尚未访问的顶点调用DFS}void DFS(Graph G int v){ //从第v个顶点出发递归地深度优先遍历图Gvisited[v]=TRUE; VisitFunc(v); // 访问第v 个顶点for(w=FirstAdjVex(G ,v); w>=0;w=NextAdjVex(G ,v,w))//FirstAdjVex返回v的第一个邻接顶点,若顶点在G中没有邻接顶点,则返回空(0)。
c语言中常用的查找

c语言中常用的查找C语言中常用的查找引言:在编程中,查找是一项非常常见且重要的操作。
无论是在数组、链表、树还是图等数据结构中,都需要进行查找操作来寻找特定的数据或者确定某个元素的存在与否。
C语言提供了多种查找算法和数据结构,本文将介绍C语言中常用的查找方法。
一、线性查找线性查找是最简单的查找方法之一,也称为顺序查找。
其基本思想是从数据集合的起始位置开始逐个比较待查找元素与集合中的元素,直到找到目标元素或者遍历完整个集合。
在C语言中,可以使用for循环或者while循环实现线性查找。
线性查找的时间复杂度为O(n),其中n为数据集合中元素的个数。
二、二分查找二分查找又称为折半查找,是一种高效的查找算法,但要求数据集合必须是有序的。
其基本思想是将数据集合分为两部分,然后通过与目标元素的比较来确定目标元素在哪个部分中,从而缩小查找范围。
重复这个过程直到找到目标元素或者确定目标元素不存在于数据集合中。
二分查找的时间复杂度为O(logn),其中n为数据集合中元素的个数。
三、哈希表查找哈希表是一种通过哈希函数将关键字映射到存储位置的数据结构,它能够以常数时间复杂度O(1)进行查找操作。
在C语言中,可以使用数组和链表的结合来实现哈希表。
哈希表的关键之处在于哈希函数的设计,良好的哈希函数能够将关键字均匀地映射到不同的存储位置,从而提高查找效率。
四、二叉搜索树查找二叉搜索树是一种常用的数据结构,它满足以下性质:对于任意节点,其左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值。
在C语言中,可以使用指针和递归的方式来实现二叉搜索树。
通过比较目标值与当前节点的值,可以确定目标值位于左子树还是右子树中,从而缩小查找范围。
五、图的遍历在图的数据结构中,查找操作通常是指遍历操作。
图的遍历有两种方式:深度优先搜索(DFS)和广度优先搜索(BFS)。
深度优先搜索通过递归的方式依次访问图中的每个节点,直到找到目标节点或者遍历完整个图。
第7章图的深度和广度优先搜索遍历算法
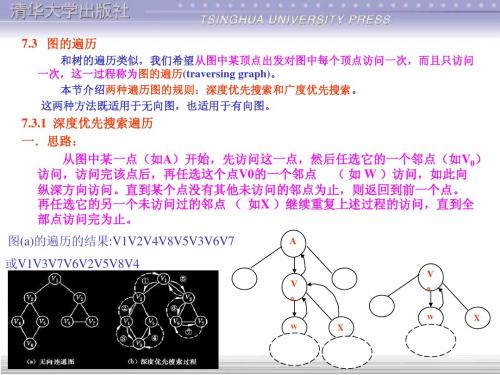
和树的遍历类似,我们希望从图中某顶点出发对图中每个顶点访问一次,而且只访问 一次,这一过程称为图的遍历(traversing graph)。 本节介绍两种遍历图的规则:深度优先搜索和广度优先搜索。 这两种方法既适用于无向图,也适用于有向图。
7.3.1 深度优先搜索遍历 一.思路: 从图中某一点(如A)开始,先访问这一点,然后任选它的一个邻点(如V0) 访问,访问完该点后,再任选这个点V0的一个邻点 ( 如 W )访问,如此向 纵深方向访问。直到某个点没有其他未访问的邻点为止,则返回到前一个点。 再任选它的另一个未访问过的邻点 ( 如X )继续重复上述过程的访问,直到全 部点访问完为止。 图(a)的遍历的结果:V1V2V4V8V5V3V6V7 或V1V3V7V6V2V5V8V4
p
v0 w x v 1
V
0
v 2
V
0
typedef struct {VEXNODE adjlist[MAXLEN]; // 邻接链表表头向量 int vexnum, arcnum; // 顶点数和边数 int kind; // 图的类型 }ADJGRAPH;
W W
X
X
7.3.2 广度优先搜索遍历 一.思路:
V
0
A V
0
W W
XXΒιβλιοθήκη 二.深度优先搜索算法的文字描述: 算法中设一数组visited,表示顶点是否访问过的标志。数组长度为 图的顶点数,初值均置为0,表示顶点均未被访问,当Vi被访问过,即 将visitsd对应分量置为1。将该数组设为全局变量。 { 确定从G中某一顶点V0出发,访问V0; visited[V0] = 1; 找出G中V0的第一个邻接顶点->w; while (w存在) do { if visited[w] == 0 继续进行深度优先搜索; 找出G中V0的下一个邻接顶点->w;} }
数据结构第七章-图

*
V0
V7
V6
V5
V4
V3
V2
V1
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一, 深度优先序列不是唯一的
V0
V1
V3
V2
V7
V6
V5
V4
V0,V1,V3,V4,V7,V2,V5,V6,
※求图G以V0为起点的的深度优先序列(设存储结构为邻接矩阵)
void DFSAL(ALGraph G, int i) {/*从第v个顶点出发,递归地深度优先遍历图G*/ /* v是顶点的序号,假设G是用邻接表存储*/ EdgeNode *p; int w; visited[i] =1; Visit(i); /*访问第v个顶点*/ for (p=G.vertices[i].firstarc;p;p=p->nextarc) {w=p->adjvex; /*w是v的邻接顶点的序号*/ if (!visited[w]) DFSAL(G, w); /*若w尚未访问, 递归调用DFS*/ } }/*DFSAL*/
在邻接表存储结构上的广度优先搜索
*
Q
V0
V1
V2
V3
V4
V7
V5
V6
V1
V2
V3
V0
V4
V7
V5
V6
V0
V7
V6
V5
V4
V3
V2
V1
7.3 图的遍历
7
0
1
2
V0
V2
V3
V1
data
firstarc
0
1
^
^
adjvex
next
3
dfs序列和bfs序列

dfs序列和bfs序列dfs序列和bfs序列是图遍历算法中的两种常见序列。
它们分别代表了深度优先搜索(Depth-First Search)和广度优先搜索(Breadth-First Search)在图中遍历节点的顺序。
1. DFS序列深度优先搜索是一种以深度为优先级的遍历算法。
它从图的起始节点开始,一直沿着一个分支遍历到底,然后回溯到前一个节点,再遍历下一个分支。
这样直到遍历完所有的节点。
DFS序列的生成是通过递归或栈的方式完成的。
在递归实现中,每次深入某个节点时,都对其邻接节点进行深度优先遍历,直到遍历完所有节点为止。
生成的DFS序列可以用一个数组来表示,序列中每个节点的顺序即为其被遍历到的顺序。
2. BFS序列广度优先搜索是一种以广度为优先级的遍历算法。
它从图的起始节点开始,首先遍历其所有的邻接节点,然后再逐层遍历下一个邻接节点的邻接节点。
这样依次遍历完所有的节点。
BFS序列的生成是通过队列的方式完成的。
首先将起始节点入队,然后从队列中依次取出节点,并将其所有未被访问的邻接节点入队,直到队列为空为止。
生成的BFS序列可以用一个数组来表示,序列中每个节点的顺序即为其被遍历到的顺序。
3. DFS序列和BFS序列的应用DFS序列和BFS序列在图遍历算法中具有不同的应用场景。
DFS适用于解决一些涉及路径搜索、连通性、拓扑排序等问题。
由于DFS的特点是往深层次搜索,因此在找到目标节点后可以停止搜索,适合在有限深度的图中应用。
而BFS适用于解决一些涉及最短路径、最小生成树、社交网络分析等问题。
由于BFS的特点是逐层遍历,因此可以保证找到的路径是最短路径,并且可以用于计算节点之间的距离。
总结:DFS序列和BFS序列是图遍历算法中常见的两种序列。
DFS以深度为优先级,递归或栈实现,适合解决路径搜索等问题。
BFS以广度为优先级,队列实现,适合解决最短路径等问题。
对于不同的应用场景,可以选择使用适合的算法序列来进行图遍历。
广度优先和深度优先的例子

广度优先和深度优先的例子广度优先搜索(BFS)和深度优先搜索(DFS)是图遍历中常用的两种算法。
它们在解决许多问题时都能提供有效的解决方案。
本文将分别介绍广度优先搜索和深度优先搜索,并给出各自的应用例子。
一、广度优先搜索(BFS)广度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,逐层扩展,先访问起始节点的所有邻居节点,再依次访问其邻居节点的邻居节点,直到遍历完所有节点或找到目标节点。
例子1:迷宫问题假设有一个迷宫,迷宫中有多个房间,每个房间有四个相邻的房间:上、下、左、右。
现在我们需要找到从起始房间到目标房间的最短路径。
可以使用广度优先搜索算法来解决这个问题。
例子2:社交网络中的好友推荐在社交网络中,我们希望给用户推荐可能认识的新朋友。
可以使用广度优先搜索算法从用户的好友列表开始,逐层扩展,找到可能认识的新朋友。
例子3:网页爬虫网页爬虫是搜索引擎抓取网页的重要工具。
爬虫可以使用广度优先搜索算法从一个网页开始,逐层扩展,找到所有相关的网页并进行抓取。
例子4:图的最短路径在图中,我们希望找到两个节点之间的最短路径。
可以使用广度优先搜索算法从起始节点开始,逐层扩展,直到找到目标节点。
例子5:推荐系统在推荐系统中,我们希望给用户推荐可能感兴趣的物品。
可以使用广度优先搜索算法从用户喜欢的物品开始,逐层扩展,找到可能感兴趣的其他物品。
二、深度优先搜索(DFS)深度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,沿着一条路径一直走到底,直到不能再继续下去为止,然后回溯到上一个节点,继续探索其他路径。
例子1:二叉树的遍历在二叉树中,深度优先搜索算法可以用来实现前序遍历、中序遍历和后序遍历。
通过深度优先搜索算法,我们可以按照不同的遍历顺序找到二叉树中所有节点。
例子2:回溯算法回溯算法是一种通过深度优先搜索的方式,在问题的解空间中搜索所有可能的解的算法。
回溯算法常用于解决组合问题、排列问题和子集问题。
例子3:拓扑排序拓扑排序是一种对有向无环图(DAG)进行排序的算法。
图的遍历技巧

图的遍历技巧
图的遍历是指按照一定的规则,从图的某个顶点出发,沿着边遍历图中的所有顶点,使得每个顶点都被访问一次且仅一次的过程。
常用的图的遍历技巧有以下两种:
1. 深度优先遍历(Depth First Search, DFS):从图的某个顶点出发,先访问该顶点,然后依次访问与该顶点相邻的未被访问过的顶点,并以此递归地进行遍历。
当不存在未被访问的相邻顶点时,回溯到上一个顶点,继续遍历其他未被访问的相邻顶点,直至所有顶点都被访问完。
2. 广度优先遍历(Breadth First Search, BFS):从图的某个顶点出发,先访问该顶点,然后依次访问与该顶点相邻的未被访问过的顶点,并将这些顶点按照入队的顺序加入队列中。
接下来再从队列中取出一个顶点,重复前述操作,直至队列为空。
这两种遍历技巧可以分别应用于不同场景的图问题。
深度优先遍历一般适用于需要探索整个图中某一支路径的问题,而广度优先遍历一般适用于需要确定最短路径或者按层遍历的问题。
第7章-2-(7.3图的遍历)

v2 v3
2 v2
v1 v4
v5
3 V3
v1 v6
v7
4 V4 v2 v8
5 v5 6 v6 7 v7 8 v8
v2 v8 v3 v7 v3 v6 v4 v5
v,1
v,2
v1 v,4
v5
v1
v2
v,8
v4
v,5
v2
v8
v,3
v,6
v7
0
1 v1
v2 v3
2 v2
v1 v4
v5
3 V3
v1 v6
v7
v,6
v7
v2
v,8
v3
v,7
v4
v,5
v2
v8
v3
v6
0
1 v1
v2 v3
2 v2
v1 v4
v5
3 V3
v1 v6
v7
4 V4 v2 v8
5 v5 6 v6 7 v7 8 v8
v2 v8 v3 v7 v3 v6 v4 v5
v,1
v,2
v,3
v1 v,4
v5
v1
v,6
v7
v2
v,8
v3
v,7
v4
v,5
v3
3 V3
v1 v6
v7
4 V4 v2 v8
5 v5
v2 v8
v1 v,4
v5
v2
v,8
6 v6 7 v7 8 v8
v3 v7 v3 v6 v4 v5
v4
v,5
v2
v8
0
v,1
1 v1
v2 v3
2 v2
v1 v4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入:
9 10 12 13 17 28 27 34 45 47 56 ram xy; var map:array[1..20,1..20] of integer; visited,q:array[1..100] of integer; //使用辅助队列Q和访问标志数组visited。 n,m,a,b,h,r,i,j:integer; procedure bfs(); //按广度优先非递归遍历图,n个顶点,编号为1..n。 var tmp:integer; begin while h<=r do begin tmp:=q[h]; //队头元素出队并置为tmp h:=h+1; write(tmp,' '); for j:=1 to n do if (map[tmp][j]=1) and (visited[j]=0) then //j为tmp的尚未访问的邻接顶点 begin visited[j]:=1;r:=r+1;q[r]:=j; end;//j入队列 end; end;
保证图中所有 顶点被访问
三、广(宽)度优先遍历
宽度优先遍历的基本思想为:
从图中某个顶点v0出发,访问此顶点。然后依次访问v0的 各个未被访问过的邻接结点,然后分别从这些邻接结点出发 宽度优先遍历图,直到图中所有和顶点v0连通的顶点都被访 问到。 若此时图中尚有顶点未被访问,则另选图中一个未曾被访 问的顶点作起始点,重复上述过程,直到图中所有顶点都被 访问到为止。
begin readln(n,m); for i:=1 to m do begin readln(a,b); map[a][b]:=1; map[b][a]:=1; end; for i:=1 to n do if visited[i]=0 then begin visited[i]:=1;work(i);end; end.
注意:
1、图中可能包含回路,因此在遍历过程中,一个顶点有可能被 重复访问,为此设置一个数组记录顶点是否被访问过。
var map:array[1..20,1..20] of integer; 2、图有可能不连通,必须保证图中所有顶点被访问。 for i:=1 to n do if visited[i]=0 then begin visited[i]:=1;work(i);end;
精品课件!
精品课件!
begin readln(n,m); h:=1;r:=1; //置空的辅助队列q for i:=1 to m do begin readln(a,b); map[a][b]:=1;map[b][a]:=1; end; for i:=1 to n do if visited[i]=0 then //i尚未访问 begin q[h]:=i; visited[i]:=1;bfs(); end; end.
二、深度优先遍历
深度优先遍历类似于树的先根遍历,其基本思想为:
从图中某个顶点v0出发,访问此顶点。然后依次从v0 未被访问的邻接结点出发深度优先遍历图,直到图中所有 和顶点v0连通的顶点都被访问到。 若此时图中尚有顶点未被访问,则另选图中一个未曾 被访问的顶点作起始点,重复上述过程,直到图中所有 顶点都被访问到为止。
输入:
9 10 12 13 17 28 27 34 45 47 56 89
输出: 127435689
program xy; var map:array[1..20,1..20] of integer; //邻接矩阵表示法(顺序存储) visited:array[1..20] of integer; //记录顶点是否被访问过 图的深度优先遍历类 n,m,a,b,i:integer; 似二叉树的先根遍历 procedure work(x:integer); var j:integer; begin write(x,' '); for j:=1 to n do if (map[x][j]=1) and (visited[j]=0) then 深度优先遍历 begin visited[j]:=1;work(j);end; end;
一、图的遍历 二、深度优先遍历 三、广(宽)度优先遍历
一、图的遍历 和树的遍历类似,可以从图的某个顶点出发访遍图中其余 顶点,且使每一个顶点仅被访问一次,这个过程称为图的 遍历。
图的遍历比树的遍历复杂。 树的遍历始于根结点,图中没有根结点。 图中可能存在回路。
常用的图遍历方法 深度优先遍历 宽度优先遍历
