偏微分方程论文
二阶偏微分方程的常规解与特殊解

株洲师范高等专科学校2010届毕业论文材料系、部:物理与电子工程系学生姓名:刘进萍指导教师:周昕职称:讲师专业:物理教育班级:07 物理教育2010年5月目录1、毕业论文课题任务书 (2)2、毕业论文开题报告 (4)3、指导教师评阅表 (8)4、评阅教师评阅表 (9)5、答辩及最终成绩评定表 (10)6、毕业论文 (11)2010届毕业论文课题任务书系:物理与电子工程系专业:物理教育株洲师范高等专科学校毕业论文开题报告系部_______物理与电子工程系____ 专业物理教育题目二阶偏微分方程的常规解与特殊解学生姓名__刘进萍学号04107103_指导教师周昕___职称__ 讲师_____2010年5月20日说明:开题报告作为毕业论文(设计)答辩委员会对学生答辩资格审查的依据材料之一,此报告应在导师指导下,由学生填写,将作为毕业论文(设计)成绩考查的重要依据,经导师签署意见及系审查后生效。
株洲师专2010届毕业论文指导教师评阅表系:物理与电子工程系株洲师专2010届毕业论文评阅教师评阅表系:物理与电子工程系株洲师专2010届毕业论文答辩及最终成绩评定表系(公章):物理与电子工程系株洲师范高等专科学校2007届毕业论文弦振动二阶偏微分方程的常规解与特殊解系、部:物理与电子工程系学生姓名:刘进萍指导教师:周昕职称讲师专业:物理教育班级:物理教育班完成时间:2010年5月弦振动二阶偏微分方程的常规解与特殊解物理与电子工程系物理教育专业2007级刘进萍指导老师周昕摘要:对于弦振动的二阶偏微分方程,一般采用分离变法来解。
如果我们考虑其物理意义,波在离振源X0处的振动就是振源在时间上推迟了t=X0/v, 从而将振源的振动方程引入推迟因子后代入偏微分方程中,一定会满足方程,则该振动方程就是此偏微分方程的解。
该种方法物理意义明确,求解过程相对简化。
关键词:二阶偏微分方程;推迟因子;弦振动;波的传播Abstract: For the partial differential equation of two ranks, we often use separation reform to solution. If we consider its physical significance, from the source X0 wave is the source of vibration in time delayed t = X0 / v, which will be the source of vibration equation introduced delay partial differential equations, the factor of offspring will meet equation, the vibration equation is the partial differential equations of the solution. This method has clear physical meaning and the solving process is relatively simple.Keywords:partial differential equation of two ranks; suspend gene; libration of string; transmit ion of wave前言在解弦振动的二阶偏微分方程时, 在数学上,一般采用分离变法来解,这是一种纯数学的方法。
偏微分方程论文

偏微分方程数值解法[摘要]偏微分方程课程主要介绍了求一阶拟线性偏微分方程、波动方程、热传导方程及位势方程的解析解。
本文受此启发,并结合所学数值计算方法知识,介绍几种偏微分方程的数值解法。
1.背景现实世界中,许多实际问题可归结为微分方程的定解问题。
很多情况下,人们无法或不方便求出这些问题的解析解,从而要求它们的数值解。
因此,需要了解偏微分方程的数值解法。
2.内容(一)双曲型方程∞≤≤∞-=x x x u ),()0,(ϕ初值条件将x-t 平面分割成矩形网格,2,1,0,,2,1,0,0=+==±±===j j t t t k kh x x j k τ用(k,j)表示网格节点(x k ,t j ),网格节点上的函数值为u(k,j)用差商表示导数 ),~(2),(),1()~,(2),()1,(,,j x u h h j k u j k u x u t k u j k u j k u t u x j k t j k ''--+=∂∂''--+=∂∂ττ ),~(62),1(),1()~,(62)1,()1,(2,2,j x u h h j k u j k u x u t k u j k u j k u t u x j k t j k '''---+=∂∂'''---+=∂∂ττ方程变为 0),(),(),1(),()1,(1=--++-+ττh R hj k u j k u a j k u j k u 略去误差项,得到差分方程0,,1,1,=-+-h u u a u u jk j k jk j k ++τ加上初始条件,构成差分格式kk j k j k j k j k u u u ar u u ϕ=--=0,,,1,1,)(++0=∂∂+∂∂=xu a t u Lu(二)抛物型方程 T t b xu b t u Lu ≤≤>=∂∂-∂∂=0,0022 )(g )t ,1(),(g )t ,0();10(),()0,(2),()0,(121x u x u x x x u x x x u ==≤≤=∞≤≤∞-=ϕϕ)初边值混合问题()初值问题(定解条件有两类:将x-t 平面分割成矩形网格,2,1,0,,2,1,0,0=+==±±===j j t t t k kh x x j k τ用(k,j)表示网格节点(x k ,t j ),网格节点上的函数值为u(k,j)用差商表示导数 ),~(12),1(),(2),1()~,(2),()1,()4(22,22,j x u h h j k u j k u j k u x u t k u j k u j k u t u x j k t j k --+-+=∂∂''--+=∂∂ττ则方程变为 0),(),1(),(2),1(),()1,(12=--+-+--+ττh R hj k u j k u j k u b j k u j k u 略去误差项,并令s =τ/h 2 得到差分方程)2(,1,,1,1,j k j k j k j k j k u u u bs u u -+-+=++边界条件差分化(第二、三类边界条件) ),~(2),(),(),~(2),0(),(1,1,0t x u h h t x u t x u x u t x u h h t u t h u x u x N N t x t ''+-=∂∂''--=∂∂- 得显式格式 ⎪⎩⎪⎨⎧===-===-=+-+=-,2,1,0)(),(1,,2,1)(,2,1,0,1,,2,1)2(2,1,00,,1,,1,1,j j g u j g u N k kh u j N k u u u bs u u j N jk j k j k j k j k j k ττϕ++(三)椭圆形方程),(f 2222y x yu x u u =∂∂+∂∂=∆边值问题⎪⎩⎪⎨⎧Γ∈=Ω∈=∂∂+∂∂=∆Γ),(),(),(),(f 2222y x y x u y x y x y u x u u ϕ将x-y 平面分割成矩形网格,2,1,0,,2,1,0,±±===±±===j j y y k kh x x j k τ用(k,j)表示网格节点(x k ,y j ),网格节点上的函数值为u(k,j) 用差商表示导数 )~,(12)1,(),(2)1,(),~(12),1(),(2),1()4(22,22)4(22,22y k u h j k u j k u j k u y u j x u h h j k u j k u j k u x u x j k x j k ττ--+-+=∂∂--+-+=∂∂方程变为j k f h R j k u j k u j k u h j k u j k u j k u ,122),()1,(),(2)1,(),1(),(2),1(=--+-++-+-+ττ 略去误差项,得到差分方程 j h j k j k j k j k j k j k f u u u s u u u h ,1,,1,2,1,,12)2(1)2(1=+-++--+-τ+。
2006级偏微分方程课程论文
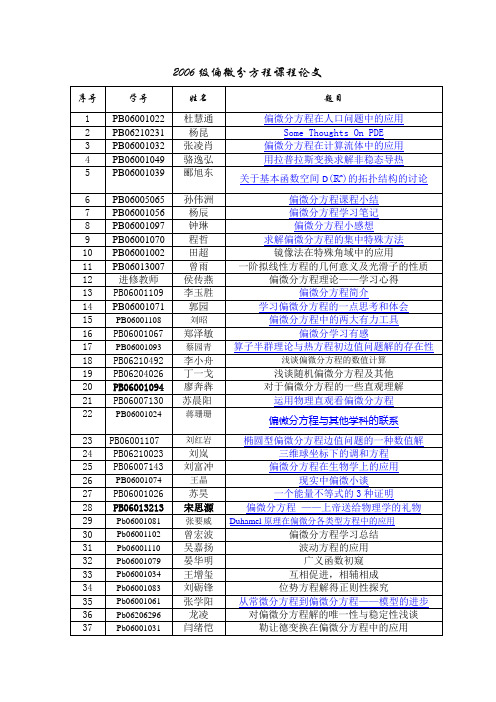
Pb06001059
李玥
狄拉克函数的物理应用
46
Pb06001018
王子腾
浅谈AMG方法求解PDE方程
47
Pb06009098
张可
关于高维波动非常初值问题的推广
48
Pb06001089
盛镇醴
分离变量法在偏微分方程中的应用
49
Pb06005018
潘慈辉
Green函数的求法及推广
50
PB06001065
55
PB06001047
崔晓月
基本解方法的推广
56
PB06001057
洪婧
圆形区域上的偏微分方程问题
57
PB06001060
吴越
热传导问题的一些研究
58
PB06204018
李应弘
共形映射在偏微分方程中的应用
59
PB06210447
温环宇
关于化简2阶线性偏微分方程的一些直观想法
60
PB06001015
40
Pb06001055
刘国庆
小议D’Alembert公式的推导
41
Pb06007209
张立成
关于波动方程的一些想法
42
Pb06013021
陈靖越
Fourier变化在求解偏微分方程中的应用
43
Pb06001046
黄潞
物理学与偏微分方程
44
Pb06001073
蒋琰
利用Duhamel原理解非齐次波动方程的齐次初边值问题
35
Pb06001061
张学阳
从常微分方程到偏微分方程——模型的进步
36
Pb06206296
基于偏微分方程的图像修复

potential research field which
Key
Words:image
inpainting;coherence
direction;tensor diffusion;total
variation
青岛人学硕士学位论文
学位论文独创性声明
本人声明,所呈交的学位论文系本人在导师指导下独立完成的研究成果。文中 依法引用他人的成果,均已做出明确标注或得到许可。论文内容未包含法律意义上
的分析和探讨。第二,在基于结构的图像修复方面,首先分析了基于TV模型的修复 方法在扩散迭代中所存在的扩散速度以及边界保持之间的矛盾,然后提出了一种基 于张量扩散的快速图像修复模型,可以有效的改善修复效果并减少运行时间。第三, 在基于流状线性结构的图像修复方面,针对传统的变分修复模型无法修复流状线性 结构图像,提出了一种流状线性结构图像修复模型.通过引入局部结构方向,并在局 部坐标系下建立新的修复模型,使它沿相干方向扩散来修复断裂特征。 综上所述,本文对数字图像修复技术进行了深入的研究,取得了一些有价值的 研究成果。数字图像修复仍然是一个较有潜力的研究领域,值得我们进行更深入的
on
traditional variational model beyond repair patch flow.1ike images of linear structures.we novel method for flow—like images of linear structures based the tensor
Processing based on decades,because of its strong
and the property of keeping the edge and texture details simultaneously.Its research areas include:image segmentation,image anisotropy
《偏微分方程分析的Laplace变换》论文

《偏微分方程分析的Laplace变换》论文
《Laplace变换的偏微分方程分析》
Laplace变换是一种用来分析偏微分方程解决问题的强大工具。
其主要目的是将时间域知识转换为频域知识,使得复杂的微分方程可以轻松解决。
Laplace变换不仅可以用于偏微分方程,
还可以用于积分方程,这两者是计算机科学中广泛使用的数学工具。
Laplace变换在偏微分方程分析中的应用是通过将偏微分方程
转换成一个常微分方程的问题,并且显式表达出所有的解,从而帮助偏微分方程的解决者。
由于Laplace变换是针对时域信
号的特性,有时会改变偏微分方程的现实表现形式,这可能会影响最终求解结果。
因此,在使用Laplace变换时应注意偏微
分方程的表达形式。
Laplace变换的主要优势在于它可以解决复杂的微分方程,允
许几乎立即求解这样的问题。
因此,它可以在许多情况下,如系统动态行为分析、热传导分析和控制系统分析等,都得到有效的应用,从而实现快速的解决数学问题的方法。
总的来说,Laplace变换是一种用于分析偏微分方程的非常有
用的工具,它可以帮助解决者更快地求解复杂的微分方程,并且可以解决多个问题。
应灵活使用Laplace变换,以便获得最
佳效果。
偏微分方程的应用

偏微分方程的应用作者:范俊杰来源:《科技视界》 2014年第31期范俊杰(武汉理工大学数学系,湖北武汉 430070)【摘要】本文在简要的介绍偏微分方程的发展历史的基础上,详细的讨论了其在弦振动及人口问题中的应用。
其目的在于了解偏微分方程曲折的发展史及其广阔的应用前景,从而激励读者深入的学习和研究偏微分方程。
【关键词】偏微分方程;弦振动;人口问题在科学技术日新月异的发展过程中,人们研究的许多问题用一个自变量的函数来描述已经不够精确了,所以不少问题必须用多个变量的函数来描述,才能够更精确地得到人们所需要的结果。
这样就产生了研究某些物理现象的理想的含有多个变量的函数及其偏导数的方程,这种方程就是偏微分方程。
实际上,偏微分方程的解一般有无穷多个,而在解决具体物理问题时,我们必须从众多一般解中找到能够满足题目给定的特殊条件的解,这样我们才能够了解具体问题的特殊性。
本文在简要的介绍偏微分方程的发展历史的基础上,详细的讨论了其在弦振动及人口问题中的应用。
1 偏微分方程的发展1746年,达朗贝尔在他的论文《张紧的弦振动时形成的曲线的研究》中,提议证明无穷多种和正弦曲线不同的曲线是振动的模式。
由此开创了偏微分方程这门学科。
和欧拉同时代的瑞士数学家丹尼尔·贝努利也研究了数学物理方面的问题,提出了解弹性系振动问题的一般方法,对偏微分方程的发展起了比较大的影响。
偏微分方程得到迅速发展是在十九世纪,那时候,数学物理问题的研究繁荣起来了,许多数学家都对数学物理问题的解决做出了贡献。
这里应该提一提法国数学家傅立叶,他在从事热流动的研究中,写出了《热的解析理论》,在文章中他提出了三维空间的热方程,也就是一种偏微分方程。
他的研究对偏微分方程的发展的影响是很大的[3]。
2 偏微分方程在某些具体问题中的应用2.1 偏微分方程在弦振动中的应用弦是一个力学系统,是一个质点组,故它的运动符合牛顿第二定律。
设弦在未受扰动时平衡位置是x轴,其上各点均以该点的横坐标表示。
HJB偏微分方程的数值计算

山东大学硕士学位论文HJB偏微分方程的数值计算姓名:曹海峰申请学位级别:硕士专业:概率论与数理统计指导教师:赵卫东20090507HJB偏微分方程的数值计算作者:曹海峰学位授予单位:山东大学1.学位论文吕峰推广的Lipschitz条件下的倒向随机微分方程及g—期望2004该文主要讨论了在一类推广的Lipschitz条件下的倒向随机微分方程和g期望及其相关性质.这个限制使得我们无法将倒向随机微分方程的相关理论应用于一个更广的范围.该文中,我们假设g满足如下形式的一类推广的Lipschitz条件:|g(t,y<,1>,z<,1>)-g(t,y<,2>,z<,2>)|≤r<,t>|y<,1>-y<,2>|+μ<,t>|z<,1>-z<,2>|在此假设之下,得到了倒向随机微分方程解的存在唯一性定理,相对于经典情况而言,在这种情形中,该文的结果对于解的可积性有一个更严格的要求;进一步的,该文还得到了在此条件之下的比较定理.以此为基础,类似于经典情形,定义了相应的g-期望,并以此为工具,得到了在此假设之下的倒向随机微分方程的逆比较定理.2.学位论文杨维强倒向随机微分方程和非线性期望在金融中的应用:风险度量,定价机制的估计以及期权定价2006倒向随机微分方程(BSDE)的线性形式首先由Bismut(1973)在引入,1990年Pardoux&Peng(1990)研究了Lipschitz条件下非线性倒向随机微分方程解的存在唯一性定理。
Duffie&Epstein(1992b)在研究随机微分效用过程中也独立地引进了一类倒向随机微分方程。
倒向随机微分方程在随机控制、偏微分方程、数理金融、经济等领域都有着广泛的应用。
经典的期望是一个线性泛函,在线性期望和可加测度之间存在一一对应的关系。
但是这种一一对应的关系在非线性情形下并不成立,一般地,给定一个非线性期望,我们仍然可以导出一个非可加概率测度,但是却存在无穷多的非线性期望满足这一关系。
几类非线性偏微分方程精确解的研究

几类非线性偏微分方程精确解的研究几类非线性偏微分方程精确解的研究摘要:非线性偏微分方程在数学和物理领域中有着广泛的应用,其求解是一个重要的研究方向。
精确解研究涉及到方法和技术,大大提高了求解的速度和精度。
本论文针对几类非线性偏微分方程进行研究,探讨其精确解。
首先,本文介绍了这些非线性偏微分方程的基本概念和性质,包括一些应用领域和模型的描述。
然后,我们提出了精确解研究的一般思路和流程,并阐述了具体实现方法。
接着,我们选择了几种典型的非线性偏微分方程,分别介绍其数学特性、求解方法、解的性质等方面,并通过实例进行验证和说明。
最后,我们评估了精确解研究的优缺点,探讨其未来发展方向。
关键词:非线性偏微分方程、精确解、方法、技术、数学特性。
正文:第一章绪论1.1 非线性偏微分方程的基本概念偏微分方程(Partial differential equation)是描述自然界中物理学、工程学、化学、社会学等学科中的数量关系的数学方法之一。
偏微分方程的解法往往是比较困难的,因此近年来许多研究者将精力集中在非线性偏微分方程的求解上。
非线性偏微分方程是指,未知函数出现在方程的高次项、积、除法、指数函数等时,即同一方程中出现有关函数和其偏导数的非线性项。
1.2 非线性偏微分方程的应用领域非线性偏微分方程的求解方法及其精度和速度在科学和工程应用中具有广泛的应用。
例如,在流体力学中,非线性偏微分方程可用于描述涡旋流、湍流、振荡流、波浪等。
在分子生物学中,非线性偏微分方程可用于描述分子扩散、蛋白质演化等。
在量子力学中,非线性偏微分方程可用于描述玻色、费米子体系等。
在统计学中,非线性偏微分方程可用于描述随机微分方程、布朗运动等。
1.3 非线性偏微分方程的模型如果要用非线性偏微分方程来描述一个现象,我们需要构造出一个非线性偏微分方程模型。
偏微分方程模型一般包含几个要素,例如:基本方程、边界条件、初始条件、材料参数等。
第二章精确解研究的一般思路和流程2.1 精确解的定义和种类精确解是指以公式的形式表示的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏微分方程数值解法
[摘要]偏微分方程课程主要介绍了求一阶拟线性偏微分方程、波动方程、热传导方程及位势方程的解析解。
本文受此启发,并结合所学数值计算方法知识,介绍几种偏微分方程的数值解法。
1.背景
现实世界中,许多实际问题可归结为微分方程的定解问题。
很多情况下,人们无法或不方便求出这些问题的解析解,从而要求它们的数值解。
因此,需要了解偏微分方程的数值解法。
2.内容
(一)双曲型方程
∞≤≤∞-=x x x u ),()0,(ϕ初值条件
将x-t 平面分割成矩形网格
,2,1,0,,2,1,0,0=+==±±===j j t t t k kh x x j k τ
用(k,j)表示网格节点(x k ,t j ),网格节点上的函数值为u(k,j)
用差商表示导数 ),~(2
),(),1()~,(2),()1,(,,j x u h h j k u j k u x u t k u j k u j k u t u x j k t j k ''--+=∂∂''--+=∂∂ττ ),~(62),1(),1()~,(6
2)1,()1,(2,2
,j x u h h j k u j k u x u t k u j k u j k u t u x j k t j k '''---+=∂∂'''---+=∂∂ττ
方程变为 0),(),(),1(),()1,(1=--++-+ττh R h
j k u j k u a j k u j k u 略去误差项,得到差分方程
0,,1,1,=-+-h u u a u u j
k j k j
k j k ++τ
加上初始条件,构成差分格式
k k j k j k j k j k u u u ar u u ϕ=--=0,,,1,1,)
(++
0=∂∂+∂∂=x
u a t u Lu
—
(二)抛物型方程 T t b x u
b t u
Lu ≤≤>=∂∂-∂∂=0,0022
)(g )t ,1(),(g )t ,0();10(),()0,(2),()0,(121x u x u x x x u x x x u ==≤≤=∞≤≤∞-=ϕϕ)初边值混合问题
()初值问题
(定解条件有两类:
将x-t 平面分割成矩形网格
,2,1,0,,2,1,0,0=+==±±===j j t t t k kh x x j k τ
用(k,j)表示网格节点(x k ,t j ),网格节点上的函数值为u(k,j) 用差商表示导数 )
,~(12
),1(),(2),1()
~,(2
),()1,()4(22,22,j x u h h j k u j k u j k u x u t k u j k u j k u t u
x j k t j k --+-+=∂∂''--+=∂∂ττ 则方程变为 0),()
,
1(),(2),1(),()1,(12=--+-+--+ττh R h j k u j k u j k u b j k u j k u
略去误差项,并令s =τ/h 2 得到差分方程
)2(,1,,1,1,j k j k j k j k j k u u u bs u u -+-+=++
边界条件差分化(第二、三类边界条件) )
,~
(2),(),
()
,~(2
),0(),(1,1,0t x u h h t x u t x u x u t x u h h t u t h
u x u x N N t x t ''+-=∂∂''--=∂∂-
得显式格式
⎪⎩⎪⎨⎧===-===-=+-+=-
,2,1,0)(),(1
,,2,1)(,2,1,0,1,,2,1)2(2,1,00,,1,,1,1,j j g u j g u N k kh u j N k u u u bs u u j N j k j k j k j k j k j k ττϕ++
(三)椭圆形方程
),(f 22
22y x y u
x u u =∂∂+∂∂=∆
—
边值问题
⎪⎩⎪⎨⎧Γ∈=Ω∈=∂∂+∂∂=∆Γ
),(),(),(),(f 2222y x y x u y x y x y u x u u ϕ
将x-y 平面分割成矩形网格
,2,1,0,,2,1,0,±±===±±===j j y y k kh x x j k τ
用(k,j)表示网格节点(x k ,y j ),网格节点上的函数值为u(k,j) 用差商表示导数 )~,(12)1,(),(2)1,(),~(12
),1(),(2),1()4(22,22)4(22,22y k u h j k u j k u j k u y u j x u h h j k u j k u j k u x u x j k x j k ττ--+-+=∂∂--+-+=∂∂
方程变为
j k f h R j k u j k u j k u h j k u j k u j k u ,12
2),()1,(),(2)1,(),1(),(2),1(=--+-++-+-+ττ 略去误差项,得到差分方程 j h j k j k j k j k j k j k f u u u s u u u h ,1,,1,2,1,,12)2(1)2(1=+-++--+-τ
+。
