电路原理作业第四章
电路原理(第2版)(范承志)第四章 谐振互感三相

1 L C ( ) tg 1 R
例3:某一电台信号频率f=990KHz,幅值U=100mV,欲通过 RLC串联谐振进行接收, 10, L 250H ,问:应调节电容C R 为多大?电路品质因数Q为多少?若接收信号附近有950KHz, 100mV 夹杂信号,试分析对接收的影响。 R L 解:对接收信号产生的谐振(调谐)
减小电阻或增大电感可使UL变大。电压放大。
对于电流源:采用并联谐振方法 。
IL R Q并 0 L I S
增大电阻或减小电感可使IL变大。电流放大。
3. 电路串并联谐振及应用
Z ab
1 j L2 ( ) j c j L1 1 j L2 j c
1 L2C
. U
R
a L1
di1 U 21 e21 M dt
同理: 当 i 2 变化时,引起 的变化, 二个线圈中产生感应电势, 线圈2 的自感电势: 用电压降表示:
di2 e22 L2 dt
di2 U22 e22 L2 dt
u12
线圈1 的互感电势
di2 e12 M dt
用电压降表示
g
. U
R
. I
外加电压全部降在电阻上,
端口电压与端口电流同相。
. U
C
记 0
1 LC
——电路谐振频率
谐振时 Z=R ,阻抗最小, 谐振电流最大
. U
. U
C
R
R
.L U
L
U I0 。 R
. U
. U
L
C
电感电压与电容电压幅值相同, 相位差180°(反相)。
g 1 g U L j 0 L I j I U c 0C g g
电路理论基础第四章习题解答西安电子科技大学出版社
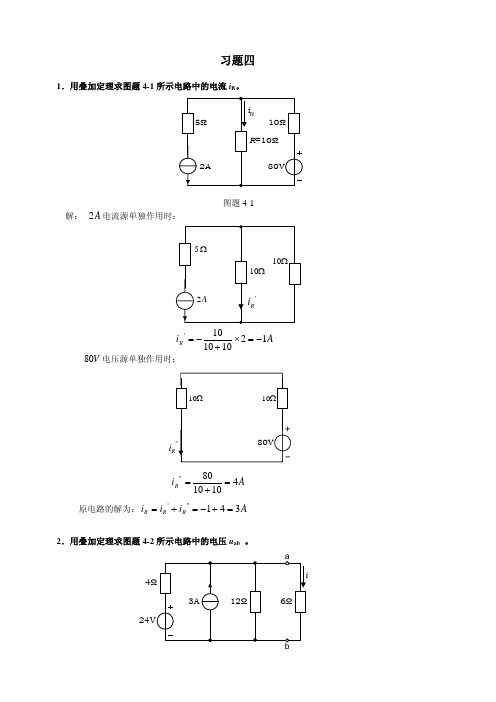
习题四1.用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解: A 2电流源单独作用时:A i R 12101010'−=×+−=V 80电压源单独作用时:i A i R 4101080''=+=原电路的解为:A i i i R R R 341'''=+−=+=2.用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解:V 24电压源单独作用时:Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时:Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为:V u u u ab ab ab 18612'''=+=+=3.用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解: A 6电流源单独作用时:ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时:Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为:()()A i i i 624'''−=−+−=+=4.图题4-4所示电路中,R =6Ω,求R 消耗的功率。
图题4-4解: 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u :12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻:eqRΩ=++×=426363eq R 原电路简化为:Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5.图题4-5所示电路中, R 1=1.5Ω R 2=2Ω,求(a )从a、b 端看进去的等效电阻;(b )i 1与i s 的函数关系。
电路分析第四章 电路定理

Uoc = U1 + U2
= -104/(4+6)+10 6/(4+6)
= -4+6=2V I a
Ri
+
(2) 求等效电阻Ri
Rx
a
Ri b
Uoc – b (3) Rx =1.2时,I= Uoc /(Ri + Rx) =0.333A I= Rx =5.2时, Uoc /(Ri + Rx) =0.2A Rx = Ri =4.8时,其上获最大功率。
计算; 2 加压求流法或加流求压法。
3 开路电压,短路电流法。
2 3 方法更有一般性。
(3) 外电路发生改变时,含源一端口网络的等效电路不变(伏安特性等效)。 (4) 当一端口内部含有受控源时,控制电路与受控源必须包 含在被化简的同一部分电路中。
21
第4章 电路定理
例1.
4 a Rx 6 + I b 10V
2.5A
10V 2 5V
?1A
?
这里替代后,两并联理想电压源 5V 5 1.5A 电流不确定,该支路不能被替代
14
第4章 电路定理
例.
3 + 1 Rx – U Ix + 0.5 0.5 若要使 I x 试求Rx。
1 8
I,
10V
–
I
0.5
解: 用替代:
1
1
I 0.5
8
I
1
0.5
又证:
ik
A
+ uk –
支 路 k
A
ik
+
–
uk
A
+ uk – uk
支 路 k
uk
电路分析第四章习题参考答案

4-2 试用外施电源法求图题4-2 所示含源单口网络VCR ,并绘出伏安特性曲线。
解:图中u 可认为是外加电压源的电压。
根据图中u 所示的参考方向。
可列出(3)(6)(5)20(9)50u i i A VA i V=Ω+Ω++=+4-5试设法利用置换定理求解图题4-5所示电路中的电压0u 。
何处划分为好?置换时用电压源还是电流源为好?解:试从下图虚线处将电路划分成两部分,对网路N 1有(节点法)1111967(11)uu u u i ⎧⎛⎫+-=⎪⎪+⎝⎭⎨⎪-++=-⎩ 整理得:1511714u i =- 对网络2N 有251133u i i i =⨯+⨯=解得3i A =,用3A 电流源置换N 1较为方便,置换后利用分流关系,可得:()121031V 1V u +=⨯⨯=4-9 求图题4-7所示电路的输入电阻R i ,已知0.99α=解: 施加电源t u 于输入端可列出网孔方程:12335121(25100)100 (1)100(100100101010)100.990(2)t i i u i i i +-=-++⨯+⨯-⨯=将(2)代入(1)得135ti u R i ==Ω4-14求图题4-10所示各电路的等效电路。
解解: 图(a):因电压的计算与路径无关,所以[5(1)]4(13)4ad ac cd ad ab bd u u u V V u u u V V=+=---=-=+=--=-图(b): 流出a 点的电流(521)8a i A =++=,流入b 点多的电流(541)8b i A =+-=。
所以ab 之间的等效电路为8A 的电流源,电流从b 端流出。
图(c):导线短接。
4-23 电路如图题4-15 所示,已知非线性元件A 的VCR 为2u i =。
试求u ,i ,i 1.解: 断开A ,求得等效内阻:1o R =Ω 开路电压a u 所满足的方程:()(11)12111/21c a c a u u u u +-⨯=⎧⎪⎨-⨯++=⎪⎩ 求得2a u V =,最后将A 接到等效电源上,如上图所示。
电路分析第四章

A
u
2 3
2 3i
8 9
v
-
0.5A
+
14 3
V
2 3
V
+
+
1V -
a
i
a
+
-
1V + 10 i1 2 N1 4 0.5A
a i1 1/3A b 图(c) 2 4 1/6A
图(d)
(3) 为求i1,将N2用1/3A电流源替代(图(c) 、(d))
4.1 叠加定理 (Superposition Theorem)
一、线性电路的齐次性和叠加性 线性电路:由线性元件和独立源构成的电路。 1.齐次性(homogeneity)(又称比例性,proportionality) 齐次性:若输入x(t) → 响应y(t) ,则输入K x(t) → Ky(t)
+ x(t) -
电 路
+ y(t) -来自+ Kx(t) -
+
电路
Ky(t) -
2.叠加性(superposition)
若输入x1(t) → y1(t)(单独作用) ,
x2(t) → y2(t) … xn(t) → yn(t) 则x1(t) 、x2(t) … xn(t) 同时作用时 响应y (t)= y1(t)+ y2(t)+ … +yn(t) + x1(t) -
3.替代后外电路及参数不能改变(只在一点等效)。
4. 3 互易定理 (Reciprocity Theorem)
例:
a
Us + 对(a): 对(b):
电路邱关源第四章

ik + 支 路 uk k –
+ uk –
ik
ik + uk R=uk/ik –
第4章 电路定理
2. 定理的证明
ik
A +支 uk 路
+
A
uk
–k
–
ik
+
A uk –
+支 uk 路 –k -
ห้องสมุดไป่ตู้uk
-
++
uk
第4章 电路定理
证毕!
例 求图示电路的支路电压和电流 5
5
解 i1 110 /5 (5 10) //10 i1 +
10 2
2 2
6
I1 (5 2) / 2 1.5A
u1 6 /1.2 5V I 1.5 0.5 1A
R 2/1 2Ω
第4章 电路定理
例5 已知: uab=0, 求电阻R
ab
解 uab 0
60 25
iab icd 0
用开路替代,得:
4
0.5A
+
30 20
42V R 10
ubd 20 0.5 10V -
i(+1) 2
10V -
1 +
+ + u(1) 2i(1) - -
2 i (2)
1 + 5A
+ u(2)
2i (2) -
-
10V电源作用: i(1) (10 2i(1) ) /(2 1) i(1) 2A
u(1) 1 i(1) 2i(1) 3i(1) 6V
5A电源作用: 2i(2) 1 (5 i(2) ) 2i(2) 0 i(2) 1A u(2) 2i(2) 2 (1) 2V
6Ω
电路理论 第4章

B
B
24
A
第 4 章
+ 20V _ 5Ω
+ _ 15V R3 5 Ω 3Ω
R4 4Ω B
I
有源二端网络等效为电 流源模型 ——诺顿定理 有源二端网络等效为电 压源模型—— 戴维南定理
有 源 二 端 网 络
R4 4Ω
I
等 效 电 源
R4 4Ω
第四章
第 4 章
电路分析方法之三
--电路定理法
叠加原理 等效电源定理 特勒根定理 互易定理
教学重点:替代定理
难点:线性电路的线性关系 戴维南定理 特勒根定理 运用多个定理的综合解题
1
§4-2 替代定理或置换定理
第 4 章
替代定理(又称置换定理): 在具有唯一解的线性网络中,若某条支路的电压UK (或电流IK)为已知,则这条支路可以用一个电压值为 UK的独立电压源(或用一个电流值为IK的独立电流源) 来替代,若替代后电路仍具有唯一解,则该网络所有支 路的电压和电流均保持不变。 说明: 1. 替代定理适用于线性、非线性电路、定常和时变电路。 2. 替代定理的应用必须满足的条件: 1) 原电路和替代后的电路必须有唯一解。 2) 被替代的K支路必须是独立的、和电路其它 部分应无耦 合及受控关系。
I1 2Ω I2 10A I 3 1Ω I4 4Ω 5Ω + 10V _
原电路 根据叠加定理
I1’’ 2Ω I2’’ I3’’ 1Ω I4’’ 4Ω 5Ω + 10V _
11
I 1 = I 1 ′ − I 1 ″, I 2 = I 2 ′ − I 2 ″ I3 = I3′ + I3 ″, I4 = I4 ′ + I4 ″
US"= 10I1 " + U1" =10×1.6 + 9.6 =25.6V US= US' +US"=-6+25.6=19.6V
电路原理部分习题解答

电路原理部分习题解答部分习题解答第⼀章部分习题1-1在题图1-1中,已知i=2+t A,且t=0时,,试求=?电场储能W C=?(其中C=1uF )题图1-1解:1-2题图1-2是⼀个简化的晶体管电路,求电压放⼤倍数,再求电源发出的功率和负载吸收的功率。
题图1-2解:,电源发出的功率:负载吸收的功率:1-4题图1-4电路中,=0.5A,=1A,控制系数r=10,电阻R=50。
⽅框内为任意电路(设不短路),试求电流I ?题图1-4解:,1-5电路各参数如题图1-5所⽰,试求电流I为多少?题图1-5解:如图,共有3个节点,6条⽀路,由KCL得:由得:,,节点,,解得:,,,,,1-15在题图1-15所⽰电路中,已知电流源=2A,=1A,R=5,=1,=2,试求电流I、电压U及电流源的端电压和各为多少?题图1-15解:由:1-16题图1-16所⽰电路中,电压源分别为=6V,=8V,R=7,试求电流I。
题图1-16解:,1-17如题图1-17所⽰电路中,发出功率为36W,电阻消耗的功率为18W,试求、、的值。
题图1-17解:,1-18题图1-18所⽰电路中,电压源E=12V,电流源=100mA,电压控制电压源的控制系数=1,=20,=100,试求和电流源发出的功率。
题图1-18解:,1-19题图1-19所⽰电路中,电压源E=20V,电阻==10,R=50,控制系数=5,试求I和。
题图1-19解:,,第⼆章部分习题2-1、题图2-1所⽰电路中,给定=1,=2,=3,=4,=5A,=6A,试⽤回路电流法求各⽀路电流。
题图2-1解:以R1 , R3 , R4所在⽀路为树,各⽀路电流:,2-2、题图2-2电路中,已知==2,==1,==3,=4,=6A,=1A,以,,,,⽀路为树,试求连⽀电流和。
题图2-2解:2-4、在题图2-4所⽰电路中,已知=2,=3,=4,=5,==2,=4V,试⽤⽹孔电流法求和。
题图2-4解:列写⽹孔电流⽅程:,代⼊数据解得:2-5、电路如题图2-5所⽰,已知=4,=5,=6,=7A,=8A, =9A,试⽤⽹孔电流法求各⽀路电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章“电路定理”练习题
4-2 应用叠加定理求题4-2图所示电路中电压u 。
+-
2Ω40Ωu 50V +
-
136V 8Ω
10Ω3A
+
-
题4-2图 题解4-2图 解:画出电源分别作用的分解电路,如图解4-2图(a )和(b )所示
对题解图4-2(a )应用结点电压法有
111113650()8240108210
n u ++=+++ 解得2u (1)113.650.10.0250.1
n u u +==++ =18.60.225
=24882.6673
V = 对题解图4-2(b )应用电阻串并联化简方法,可求得
10402(8)38161040331040183(8)21040i S u V ⨯⨯++=⨯=⨯=⨯+++ (2)16182323
i
s u u V -==-⨯=- 所以,由叠加定理得原电路的u 为
(1)(2)248824080333
u u u V =+=
-==
4-5应用叠加定理,按下列步骤求解题4-5图中a I 。
(1)将受控源参与叠加,画出三个分电路,第三分电路中受控源电压为a 6I ,a I 并非分响应,而为未知总响应;(2)求出三个
分电路的分响应a I '、a I ''、a I ''',a I '''中包含未知量a I ;(3)利用a a a a I I I I '''+''+'=解出a I 。
+-
6ΩI a 6I a +-36V
10Ω12Ω
12A
题4-5图
解:(1)将受控源参与叠加,3个分电路如题解4-5图(a )、(b)、(c )所示
(2)在分电路(a )中,'6124612
a I A A =⨯=+; 在分电路(
b )中,''362612
a I A =-=-+; 在分电路(c )中,'''61183
a a a I I I ==。
(3)由''''''1423a a a a a I I I I I =++=-+,可解得 3a I A =。
4-9 求题4-9图所示电路的戴维宁或诺顿等效电路。
b a 1A
2Ω2Ω
3V +-4Ω
(a ) 1'15V 6Ω7Ω+
-10Ω
9Ω
5Ω2Ω
(b )
题4-9图
解:(1) 求开路电压oc u 。
设oc u 参考方向如题4-9(a )图所示,由KVL 列方程 ()24I 32I 1)=0+++-(
解得 1I=-8
A 144()0.58
oc u I V =⨯=⨯-=- 求等效电阻eq R 。
将原图中电压源短路,电流源开路,电路变为题解4-9(a )图(a)应用电阻串并联等效,求得
(22)/42eq R =+=Ω
题解4-9 (a )图
画出戴维宁等效电路如题解4-9 (a )图(b )所示,应用电源等效变换得诺顿等效电 路如题解4-9 (a )图(c )所示,其中
0.50.252
oc sc eq u I A R -===- (2)本题电路为梯形电路,根据齐性定理,应用“倒退法”求开路电压oc u 。
设'10oc oc u u V ==,各支路电流如题4-9(b)图所示,计算得
'5510110
i i A === '22(210)112n n u u V ==+⨯=
''
244
12 2.455n u i i A ==== '''3345 2.41 3.4i i i i A ==+=+=
'''113277 3.41235.8n n n u u i u V ==⨯+=⨯+=
''
122
35.8 5.96766n u i i A ==== ''123 5.967 3.49.367i i i A =+=+=
''11999.36735.8120.1S S n u u i u V ==⨯+=⨯+=
故当5S u V =时,开路电压oc u 为
'5100.416120.1
oc oc u Ku V ==⨯= 将电路中的电压源短路,应用电阻串并联等效,求得等效电阻eq R 为
[](9/67)/52/10 3.505eq R =++=Ω
4-17 题4-17图所示电路的负载电阻L R 可变,试问L R 等于何值时可吸收最大功率?求此功
率。
L
题4-17图
解:首先求出L R 以左部分的等效电路。
断开L R ,设oc u 如题解4-17(a )所示,并把受控电流源等效为受控电压源。
由KVL 可得
11(22)86i i ++=
160.512i A =
= 故开路电压
111122812120.56oc u i i i i V =++==⨯=
把端口短路,如题解4-17图(b )所示应用网孔电流法求短路电流SC i ,网孔方程为 1111(22)2862(24)(28)0sc sc i i i i i i +-+=⎧⎨
-++-+=⎩ 解得
6342sc i A =
= 故一端口电路的等效电阻
643/2
oc eq sc u R i ===Ω 画出戴维宁等效电路,接上待求支路L R ,如题解4-17图(c )所示。
由最大功率传输定理知4L eq R R ==Ω时其上获得最大功率。
L R 获得最大功率为
22max 636 2.2544416
oc eq u P W R ====⨯
题解4-17。
