深圳西丽湖世纪星学校七年级数学下册第一单元《相交线与平行线》测试题(有答案解析)
七年级数学下册相交线与平行线测试题与答案

相 交 线 与 平 行 线 完卷时间:45分钟一、 填空题。
(每小题4分,共32分)1、若∠A与∠B 互为邻被角,且∠A=125°,则∠B=_________。
2、如图,OA ⊥OB 、∠A OC ∶∠BOC=2∶1,则∠AOC=_______,∠BO C=_________。
3、如图,直线AB 、CD 、EF 分别相交于点O, ∠A OE=25°,∠DOF=45°,则∠A OC =_______。
4、a 、b 、c是平面内的三条不同的直线,若a ∥c,b ∥c ,则a 与的位置关系是________。
5、如图,直线AB ∥CD ,E F与AB 、CD 分别相交于G、H, ∠BGF=118º,则∠E HD =______ 。
6、如图,∠A=120°,∠C=60°,EF 与AB 、CD∠EHC =70°,则∠AGH= ____。
7、命题“若∠1=30°,∠2=30°,则∠1=∠2”的题设是_______________,结论是_____________。
8、把命题“对顶角相等”改写成“如果------,那么-----” 的形式是______________________________________________。
二、选择题。
(每小题4分,共32分)9、如图,直线AB 、CD 、EF 相交于点O ,且AB⊥CD于O ∠BOE=70°,则∠FOD=()A、10° B、20° C 、30° D10、如图,直线D E经过点A ,则能判定DE ∥BC 的条件是A 、∠C=∠BADB 、∠C=∠BACC 、∠B+∠BA E=180° D、∠C +∠BAD=18011、下列命题中,正确的是 ( )A 、相等的角是对顶角B 、和为180°的两个角是邻补角C 、两条直线被第三条直线所截,同位角相等D 、在同一平面内垂直于同一条直线的两条直线平行 12、在同一平面内两条直线的位置关系可能是( )A 、相交或垂直B 、平行或垂直C 、相交或平行D 、不能确定13、同一平面内的三条直线a 、b 、c,若a ⊥b ,b ⊥c ,则a 与c 的位置关系是( ) A 、平行 B 、相交 C 、垂直 D 、不能确定14、如图,直线AB ∥CD,EF 与AB 、CD 分别相交于G 、H,∠BGH =2∠DHG, 则∠GHC = ( )A 、60°B 、100°C 、120°D 、130°15、如图,A B∥CD ∥E F,且CG ∥AF ,则图中与∠C 相等的角有 ( ) A 、6个 B 、5个 C 、4个 D、3个 16、平移改变了图形的( )A 、形状B 、大小 C、位置 D 、方向三、解答题。
七年级下册相交线与平行线测试题(含答案)

七年级下册相交线与平行线测试题(含答案)一、选择题1. 下列正确说法的个数是()①同位角相等②对顶角相等③等角的补角相等④两直线平行,同旁内角相等A . 1, B. 2, C. 3, D. 42. 下列说法正确的是()A.两点之间,直线最短;B.过一点有一条直线平行于已知直线;C.和已知直线垂直的直线有且只有一条;D.在平面内过一点有且只有一条直线垂直于已知直线.3. 下列图中∠1和∠2是同位角的是()A. ⑴、⑵、⑶,B. ⑵、⑶、⑷,C. ⑶、⑷、⑸,D. ⑴、⑵、⑸4. 如果一个角的补角是150°,那么这个角的余角的度数是( )A.30°B.60°C.90°D.120°5. 下列语句中,是对顶角的语句为( )A.有公共顶点并且相等的两个角B.两条直线相交,有公共顶点的两个角C.顶点相对的两个角D.两条直线相交,有公共顶点没有公共边的两个角6. 下列命题正确的是( )A.内错角相等B.相等的角是对顶角C.三条直线相交,必产生同位角、内错角、同旁内角D.同位角相等,两直线平行7. 两平行直线被第三条直线所截,同旁内角的平分线( )A.互相重合B.互相平行C.互相垂直D.无法确定8. 在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
下列图案中,不能由一个图形通过旋转而构成的是()A B C DA、3对B、4对C、5对D、6对10. 如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有( )A.5个B.4个C.3个D.2个11. 如图6,BO 平分∠ABC ,CO 平分∠ACB ,且MN ∥BC ,设AB =12,BC =24,AC =18,则△AMN 的周长为( )。
A 、30 B 、36 C 、42 D 、18 12. 如图,若AB ∥CD ,则∠A 、∠E 、∠D 之间的关系是 ( )A.∠A +∠E +∠D =180°B.∠A -∠E +∠D =180°C.∠A +∠E -∠D =180°D.∠A +∠E +∠D =270°二、填空题13. 一个角的余角是30º,则这个角的补角是 . 14. 一个角与它的补角之差是20º,则这个角的大小是 . 15. 时钟指向3时30分时,这时时针与分针所成的锐角是 . 16. 如图②,∠1 = 82º,∠2 = 98º,∠3 = 80º,则∠4 = 度.17. 如图③,直线AB ,CD ,EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE ,∠FOD = 28º,则∠BOE = 度,∠AOG = 度. 18. 如图④,AB ∥CD ,∠BAE = 120º,∠DCE = 30º,则∠AEC = 度.19. 把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB′= 70º,则∠OGC = . 20. 如图⑦,正方形ABCD 中,M 在DC 上,且BM = 10,N 是AC 上一动点,则DN + MN 的最小值为 .21. 如图所示,当半径为30cm 的转动轮转过的角度为120 时,则传送带上的物体A 平移的距离为 cm 。
七年级数学下册《相交线与平行线》单元测试卷(附答案)

七年级数学下册《相交线与平行线》单元测试卷(附答案)一、选择题(每题3分,共30分)1.如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是()A.垂线段最短B.两点确定一条直线C.两点之间,线段最短D.平行于同一条直线的两条直线平行2.如图,将一个含有30°角的直角三角尺放置在两条平行线a,b上.若∠1=135°,则∠2的度数为()A.95°B.110°C.105°D.115°3.如图,将△ABC沿BC方向平移1个单位得△DEF,若△ABC的周长等于10,则四边形ABFD 的周长为()A.12 B.10 C.9 D.84.下面四个图案中,能由如图经过平移得到的是()A.B. C. D.5.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为()A.16cm B.18cm C.20cm D.22cm6.如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是()A.垂直B.相等C.平分D.平分且垂直7.如图,下列说法错误的是()A.∠A与∠3是同位角B.∠4与∠B是同旁内角C.∠A与∠C是内错角D.∠1与∠2是同旁内角8.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于()A.4 B.5 C.6 D.以上都不对9.甲、乙、丙3人从图书馆各借了一本书(如下表所示),他们相约在每个星期天相互交换读完的书,经过数次交换后,他们都读完了这3本书.已知甲读的第三本书是乙读的第二本书,则丙读的第二本书是()甲乙丙书A书B书C A.书A B.书B C.书C D.无法确定10.下列各项正确的是()A.直线外一点到已知直线的垂线段叫做这点到直线的距离B.过一点有且只有一条直线与已知直线垂直C.同一平面内,两条直线的位置关系只有相交和平行两种D.有公共顶点且相等的两个角是对顶角二、填空题(每题3分,共24分)11.如图,已知∠1+∠2=180°,则图中与∠1相等的角共有_____个.12.如图,在图中标注的∠1、∠3、∠4、∠5中,当∠2 =∠_______时,AE∥BF.13.如图,已知a∥b,∠1=45°,则∠2=_________.14.“互补的两个角一定是同旁内角”是命题(填“真”或“假”).15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为.16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有个交点.17.如图所示,l1∥l2,点A,E,D在直线l1上,点B,C在直线l2上,满足BD平分∠ABC,BD⊥CD,CE平分∠DCB,若∠BAD=128°,那么∠AEC=.18.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E 交AF于点G,若∠CEF=70°,则∠GFD′=°.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.如图,直线AB与CD相交于点O,OE平分∠BOC,∠AOD=110°,求∠AOE的度数.20.已知,如图a∥b,c∥d,∠1=73°,求∠2和∠3的度数.21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.(1)写出两个不同的条件;(2)从(1)中选择一个来证明.22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.(1)试判断DE与BC的位置关系,并说明理由.(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.23.完成下列画图(1)如图,将△ABC向右平移4个单位,再向上平移2个单位长度,得到△A′B′C′,线段AB 与A′B′位置及数量关系是.(2)如图,一辆汽车在笔直的公路AB上由A向B行驶,M、是位于公路AB一侧的村庄.设汽车行驶到点P时,离村庄M的距离最小,请在图中公路AB上画出点P的位置,并说明数学原理.24.在ABC 中,D 是BC 边上一点,且CDA CAB ∠=∠,MN 是经过点D 的一条直线.(1)若直线MN AC ⊥,垂足为点E . ①依题意补全图1.②若70,CAB ︒∠=20DAB ︒∠=,则CAD ∠=________,CDE ∠=________. (2)如图2,若直线MN 交AC 边于点F ,且CDF CAD ∠=∠,求证:FD AB ∥.参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 CCABCDAAAC二、填空题:11.312.413.45°. 解析:∵a∥b,∠1=45°,∴∠2=∠1=45°.14.解:如图,∠1=∠2=90°,∵∠1+∠2=180°,∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,∴“互补的两个角一定是同旁内角”是假命题,故答案为:假.15.解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵GH∥EF,∴∠AEC=∠2=24°,∴∠1=∠ABC﹣∠AEC=36°.故答案为:36°.16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,∴8条直线两两相交,交点的个数最多为=28.故答案为:28.17.【分析】根据平行线的性质和角平分线的性质,可以得到∠AEC的度数,本题得以解决.【解答】解:∵l1∥l2,∴∠BAD+∠ABC=180°,∵∠BAD=128°,∴∠ABC=52°,∵BD平分∠ABC,∴∠DBC=26°,∵BD⊥CD,∴∠BDC=90°,∴∠BCD=64°,∵CE平分∠DCB,∴∠ECB=32°,∵l1∥l2,∴∠AEC+∠ECB=180°,∴∠AEC=148°,故答案为:148°.【点评】本题考查平行线的性质、角平分线的性质、垂线,解答本题的关键是明确题意,利用数形结合的思想解答.18.【分析】由AD∥BC可得∠AFE=∠CEF,∠CEF+∠DFE=180°,由翻折可得∠D'FE=∠DFE,进而求解.【解答】解:∵AD∥BC,∴∠AFE=∠CEF=70°,∵∠CEF+∠DFE=180°,∴∠DFE=180°﹣∠CEF=110°,由翻折可得∠D'FE=∠DFE=110°,∴∠GFD'=∠D'FE﹣∠AFE=110°﹣70°=40°,故答案为:40.【点评】本题考查角的相关计算,解题关键是掌握平行线的性质.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.【答案】解:∵∠AOD=110°,∴∠COB=110°,∠AOC=70°,∵OE平分∠BOC,∴∠COE=55°,∴∠AOE=70°+55°=125°.故答案为:∠AOE=125°.20.【答案】解:∵a∥b,∴∠1=∠2=73°,∵c∥d,∴∠3=180°-73°=107°.21.解:此题答案不唯一,合理即可.(1)添加∠FCB=∠CBE或CF∥BE.(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.证明:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠CBE,∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.22.解:(1)DE∥BC,理由如下:∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠5,∵∠3=∠B,∴∠5=∠B,∴DE∥BC,(2)∵DE平分∠ADC,∴∠5=∠6,∵DE∥BC,∴∠5=∠B,∵∠2=3∠B ,∴∠2+∠5+∠6=3∠B +∠B +∠B =180°, ∴∠B =36°, ∴∠2=108°, ∵∠1+∠2=180°, ∴∠1=72°.23.(1)解:如图,△A ′B ′C ′即为所求作;线段AB 与A ′B ′位置及数量关系分别是平行且相等, 故答案为:平行且相等. (2)解:如图,点P 即为所求.数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短, 24.(1)①如图所示.②70,CAB ︒∠=20DAB ︒∠=,50CAD ︒∴∠=.70CDA CAB ︒∠=∠=,18060C CAD CDA ︒︒∴∠=-∠-∠=.DE AC ⊥,第 11 页 共 11 页 9030CDE C ︒︒∴∠=-∠=. 故答案为50,︒30︒.(2)CDA CAB ∠=∠, 且,CDA CDF ADF ∠=∠+∠CAB CAD BAD ∠=∠+∠, CDF ADF CAD BAD ∴∠+∠=∠+∠. ,CDF CAD ∠=∠,ADF BAD ∴∠=∠FD AB ∴∥.。
七年级数学下册-相交线与平行线测试题(有答案)

《相交线与平行线》测试题 班级 学号 姓名 成绩一、填空题(每小题3分,共30分)1.如图1,直线AB 、CD 、EF 相交于O ,∠1=40°,∠2=60°,则∠3= .2.如图2,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4= .3.如图3,已知∠A=75°,∠B=105° 则_____∥_______.4.如图4,已知AB ∥CD ,∠B=30°,∠D=40°,则∠E=_____度.5.如图5,AC ⊥BC, 且BC=5,AC=12,AB=13,则点A 到BC 的距离是 点B 到点A 的距离是 .6.如图6,现有一条高压线路沿公路l 旁边建立,某村庄A 需进行农网改造,必须要从这条高压线上架接一条线路去村庄A ,为了节省费用,请你帮他们规划一下,并说明理由.理由是7.如图7,AB 、CD 相交于O ,OE 、OF 分别是∠AOD 和∠BOD 的平分线,试判断直线OE 、OF 的位置关系_________.8.如图8,两条直线a 、b 被第三条直线c 所截,如果a ∥b ,∠1=70°,则∠2=______.9.如图9,AB ∥CD ,AD ∥BC ,则图中与∠A 相等的角有_____个.10.在直线AB 上任取一点O ,过点O 作射线OC 、OD ,使OC ⊥OD ,当∠AOC =30°时,∠BOD 的度数是 .二、选择题 (每小题3分,共18分)11. 下列说法正确的是( )A.同一个平面内,不相交的两条线段是平行线B.同一个平面内,两条直线不相交就重合C.同一个平面内,没有公共点的两条直线是平行线D.不相交的两条直线是平行线 12. 已知两直线相交, 则下列结论成立的是 ( ) A .所构成的四个角中,有一个角是直角 B. 四个角都相等 C . 相邻的两个角互补 D. 对顶角互补13.如图10,已知∠1=∠B ,∠2=∠C ,则下列结论不成立的是( )A . AD ∥BC B.∠B=∠CC .∠2+∠B=180° D.AB ∥CD14.下列图形中,由AB ∥CD ,能得到∠1=∠2,的是( )15.如图11,B F E D O C A 1 2 3 图1 b a 2 c 1 4 3 图2A B C D 图3 A B C D E 图4 A B E A D E F D B F C B O C A D l 图6 C A A C B A 图5 图8 E B C F D A 图9 B CD A1 2 图10A BABC Rt 中,∠ACB=90°,DE 过点C ,且DE ∥AB ,若∠ACD=55°,则∠B 的度数是( )A .35°B .45°C .55°D .65°16. 下列说法中,正确的个数为( )(1)过一点有无数条直线与已知直线平行(2)如果a ∥b ,a ∥c ,那么b ∥c(3如果两线段不相交,那么它们就平行 (4)如果两直线不相交,那么它们就平行A.1个B.2个C.3个D.4个三、根据下列证明过程填空(每空1分,共18分)17.如图12,(1)因为∠A =_____(已知), 所以AC ∥ED ( )(2)因为∠2=_____(已知),所以AC ∥ED ( ) (3)因为∠A +_____=180°(已知),所以AB ∥FD ( ) (4)因为AB ∥_____(已知),所以∠2+∠AED =180°( ) (5)因为AC ∥_____(已知), 所以∠C =∠3( )18.如图13,∠1=∠2 ,CF ⊥AB ,DE ⊥AB ,求证:FG ∥BC 证明:因为 CF ⊥AB ,DE ⊥AB ( ) 所以 ∠BED=90° ,∠BFC=90°( )所以 ∠BED=∠BFC ( ) 所以 ED ∥FC ( ) 所以 ∠1=∠BCF ( )因为 ∠2=∠1 ( )所以 ∠2=∠BCF ( )所以 FG ∥BC ( )四、解答题19.画图题:把小船ABCD 通过平移后到''''D C B A 的位置,请你根据题中信息,画出平移后的小船位置.(5分)20.如图:已知∠1+∠2=180° , ∠3=110°, 求∠4的度数.(7分)21.如图:AB ,CD ,EF 相交于O 点,AB ⊥CD ,OG 平分∠AOE ,∠FOD=30°,求∠BOE 及∠AOG 的度数.(8分)3l 5643214l 2l 1l 1D B G F C A E 2C FA EB D 1 2 3 图12 图1322.如图:已知AB ∥DC ,AD ∥BC ,求证:∠B=∠D (8分)23.如图,AD ⊥BC 于D,EG ⊥BC 于G ,∠E =∠1,那么AD 平分∠BAC 吗?试说明理由(8分)参考答案:一、填空题1.80°提示:从图上可以知道∠1+∠2+∠3=180°,所以∠3=80°2.140°提示:∠1与∠2是对顶角,所以∠2=80°,又因为∠2=2∠3,所以∠3=40°,又因为∠4=180°-∠3,所以∠4=140°3.AD ∥BC 提示:因为∠A+∠B=1800,所以AD ∥BC4.70°提示:过点E 作EF 根据平行线的性质可知∠BED=∠BEF+∠FED=∠B+∠D=70°.5.AC ,AB ∥AB ,6.作图:过点A 作l 的垂线段最短.7.垂直8.110°9.3个 提示:分别是∠FDC ,∠C ,∠CBE.10.60°或120° 提示:点C 与D 在AB 的同侧或异侧两种情况.二、选择题11.C12.C 提示:只有当两直线垂直时A 、B 、D 才成立.13.B 提示:∠1=∠B 可得AD ∥BC ,∠2+∠B=180°根据∠C=∠2可得AD ∥BC 故选B14.B15.A 提示:DE ∥AB 所以∠B=∠BCE ,所以∠B=180°-90°-55°=35°16.A 提示:只有(2)对三、根据下列证明过程填空17.(1)∠BED 同位角相等,两直线平行(2)∠DFC 内错角相等,两直线平行(3)∠AFD 同旁内角互补,两直线平行(4)DF 两直线平行,同旁内角互补(5)ED 两直线平行,同位角相等18.已知,等式的性质,等量代换,同位角相等,两直线平行,两直线平行,同位角相等,已知,等量代换,内错角相等,两直线平行四、解答题19.将小船向左移9个格子,再向上移1个格子(画图略)20.解:因为∠1+∠2=180°O E C G F D B A A D C B A 4 C B E D G B 1 2 3所以l1∥l2所以∠3=∠6又因为∠4+∠6=180°所以∠4=180°-∠3又因为∠3=110°所以∠4=70°21.解:因为∠FOD=30°,∠COE与∠FOD是对顶角,所以∠EOC=30°因为AB⊥CD所以∠BOC=90°,∠BOE=∠BOC -∠EOC =60°因为∠AOE=90°+∠EOC=120°且OG平分∠AOE所以∠AOG=60°22.解:因为AB∥DC(已知)所以∠B+∠C=180°(两直线平行,同旁内角互补)因为AD∥BC(已知)所以∠D+∠C=180°(两直线平行,同旁内角互补)所以∠B=∠D(等角的补角相等)23.解:AD平分∠BAC理由:因为AD⊥BC于D,EG⊥BC于G所以EG∥AD(垂直于同一条直线的两直线平行)所以∠1=∠2(两直线平行,内错角相等)∠E=∠3(两直线平行,同位角相等)又因为∠E=∠1所以∠3=∠2(等量代换)所以AD平分∠BAC(角平分的定义)。
(完整word版)七年级数学下册_相交线与平行线测试题及答案

相交线与平行线测试题一、填空题1. 一个角的余角是30º,则这个角的补角是 .2. 一个角与它的补角之差是20º,则这个角的大小是 .3。
时钟指向3时30分时,这时时针与分针所成的锐角是。
4. 如图②,∠1 = 82º,∠2 = 98º,∠3 = 80º,则∠4 = 度。
5。
如图③,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD = 28º,则∠BOE = 度,∠AOG = 度。
6. 如图④,AB∥CD,∠BAE = 120º,∠DCE = 30º,则∠AEC = 度。
7. 把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB′= 70º,则∠OGC = 。
8. 如图⑦,正方形ABCD中,M在DC上,且BM = 10,N是AC上一动点,则DN + MN的最小值为。
9。
如图所示,当半径为30cm的转动轮转过的角度为120时,则传送带上的物体A平移的距离为cm 。
10。
如图所示,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余,将AB,CD分别平移到图中EF 和EG的位置,则△EFG为三角形,若AD=2cm,BC=8cm,则FG = 。
11。
如图9,如果∠1=40°,∠2=100°,那么∠3的同位角等于,∠3的内错角等于,∠3的12. 如图10,在△ABC 中,已知∠C =90°,AC =60 cm ,AB =100 cm ,a 、b 、c …是在△ABC 内部的矩形,它们的一个顶点在AB 上,一组对边分别在AC 上或与AC 平行,另一组对边分别在BC 上或与BC 平行。
若各矩形在AC 上的边长相等,矩形a 的一边长是72 cm ,则这样的矩形a 、b 、c …的个数是_ .二、选择题1。
下列正确说法的个数是( )①同位角相等 ②对顶角相等③等角的补角相等 ④两直线平行,同旁内角相等 A 。
七年级数学(下)《相交线与平行线》复习测试题 含答案
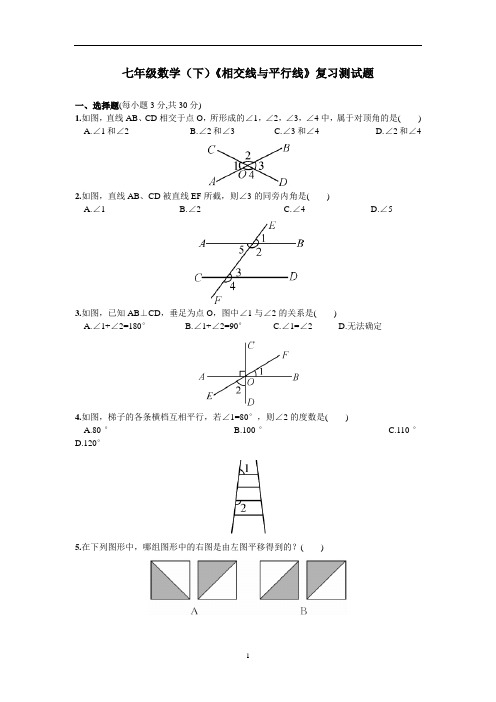
七年级数学(下)《相交线与平行线》复习测试题一、选择题(每小题3分,共30分)1.如图,直线AB、CD相交于点O,所形成的∠1,∠2,∠3,∠4中,属于对顶角的是( )A.∠1和∠2B.∠2和∠3C.∠3和∠4D.∠2和∠42.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( )A.∠1B.∠2C.∠4D.∠53.如图,已知AB⊥CD,垂足为点O,图中∠1与∠2的关系是( )A.∠1+∠2=180°B.∠1+∠2=90°C.∠1=∠2D.无法确定4.如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )A.80°B.100°C.110°D.120°5.在下列图形中,哪组图形中的右图是由左图平移得到的?( )6.命题:①对顶角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )A.1个B.2个C.3个D.4个7.平面内三条直线的交点个数可能有( )A.1个或3个B.2个或3个C.1个或2个或3个D.0个或1个或2个或3个8.下列图形中,由AB∥CD,能得到∠1=∠2的是( )9.如图,直线a∥b,直线c分别与a、b相交于点A、B.已知∠1=35°,则∠2的度数为( )A.165°B.155°C.145°D.135°10.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )A.∠1=∠2B.∠3=∠4C.∠5=∠BD.∠B+∠BDC=180°二、填空题(每小题4分,共20分)11.将命题“两直线平行,同位角相等”写成“如果……那么……”的形式是____________________.12.两条平行线被第三条直线所截,同旁内角的度数之比是2∶7,那么这两个角的度数分别是__________.13.如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A等于__________.14.如图,BC⊥AE,垂足为点C,过C作CD∥AB.若∠ECD=48°,则∠B=__________.15.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=__________度.三、解答题(共50分)16.(7分)如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的位置关系,并说明你的理由.解:BE∥CF.理由:∵AB⊥BC,BC⊥CD(已知),∴∠__________=∠__________=90°(垂直的定义).∵∠1=∠2(已知),∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.∴BE∥CF(____________________).17.(9分)如图,直线AB、CD相交于点O,P是CD上一点.(1)过点P画AB的垂线段PE;(2)过点P画CD的垂线,与AB相交于F点;(3)说明线段PE、PO、FO三者的大小关系,其依据是什么?18.(10分)如图,O是直线AB上一点,OD平分∠AOC.(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数;(2)若∠AOD和∠DOE互余,且∠AOD=13∠AOE,请求出∠AOD和∠COE的度数.19.(12分)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?20.(12分)如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.结论:(1)____________________;(2)____________________;(3)____________________;(4)____________________.选择结论:____________________,说明理由.参考答案变式练习1.C2.∵∠AOC=70°,∴∠BOD=∠AOC=70°.∵∠BOE∶∠EOD=2∶3,∴∠BOE=223×70°=28°.∴∠AOE=180°-28°=152°.3.C4.121°5.C6.8 复习测试1.D2.B3.B4.B5.C6.C7.D8.B9.C 10.A11.如果两直线平行,那么同位角相等12.40°,140°13.52°14.42°15.8016.ABC BCD 内错角相等,两直线平行17.(1)(2)图略;(3)PE<PO<FO,依据是垂线段最短.18.(1)∵OD平分∠AOC,∠AOC=60°,∴∠AOD=12×∠AOC=30°,∠BOC=180°-∠AOC=120°.(2)∵∠AOD和∠DOE互余,∴∠AOE=∠AOD+∠DOE=90°.∵∠AOD=13∠AOE,∴∠AOD=13×90°=30°.∴∠AOC=2∠AOD=60°.∴∠COE=90°-∠AOC=30°.19.(1)AE∥FC.理由:∵∠1+∠2=180°,∠2+∠CDB=180°, ∴∠1=∠CDB.∴AE∥FC.(2)AD∥BC.理由:∵AE∥CF,∴∠C=∠CBE.又∠A=∠C,∴∠A=∠CBE.∴AD∥BC.(3)BC平分∠DBE.理由:∵DA平分∠BDF,∴∠FDA=∠ADB.∵AE∥CF,AD∥BC,∴∠FDA=∠A=∠CBE,∠ADB=∠CBD.∴∠CBE=∠CBD.∴BC平分∠DBE.20.(1)∠PAB+∠APC+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠APC=∠PCD-∠PAB(4)∠APC=∠PAB-∠PCD(1)过P点作EF∥AB,∴EF∥CD,∠PAB+∠APF=180°.∴∠PCD+∠CPF=180°.∴∠PAB+∠APC+∠PCD=360°.。
七年级数学下学期相交线与平行线试题含答案

一、选择题1.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若//CD BE ,若1∠=α,则2∠的度数是( )A .3αB .1803α︒-C .4αD .1804︒-α 2.如图,//,AB CD ABK ∠的平分线BE 的反向延长线和DCK ∠的平分线CF 的反向延长线相交于点 24H K H ∠-∠=︒,,则K ∠=( )A .76︒B .78︒C .80︒D .82︒3.如图,////OP QR ST 下列各式中正确的是( )A .123180∠+∠+∠=B .12390∠+∠-∠=C .12390∠-∠+∠=D .231180∠+∠-∠=4.如图,已知//BC DE ,BF 平分ABC ∠,DC 平分ADE ∠,则下列判断:①ACB E ∠=∠;②DF 平分ADC ∠;③BFD BDF ∠=∠;④ABF BCD ∠=∠中,正确的有( )A .1个B .2个C .3个D .4个5.如图,直线12//l l ,23216∠+∠=°,则1∠的度数为( )A .216︒B .36︒C .44︒D .18︒6.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE 固定不动,将含30°的三角尺ABC 绕顶点A 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当15BAD ∠=︒时,//BC DE ,则BAD ∠(0180BAD ︒<∠<︒)其它所有可能符合条件的度数为( )A .60°和135°B .60°和105°C .105°和45°D .以上都有可能 7.如果,直线//AB CD ,65A ∠=︒,则EFC ∠等于( )A .105︒B .115︒C .125︒D .135︒8.如图,直线////AB CD EF ,点O 在直线AB 上,下列结论正确的是( )A .12390∠+∠-∠=︒B .12390∠+∠+∠=︒C .321180∠+∠-∠=︒D .132180∠+∠-∠=︒9.已知AB CD ∥,点E F ,分别在直线AB CD ,上,点P 在AB CD ,之间且在EF 的左侧.若将射线EA 沿EP 折叠,射线FC 沿FP 折叠,折叠后的两条射线互相垂直,则EPF ∠的度数为( )A .120︒B .135︒C .45︒或135︒D .60︒或120︒ 10.如图,已知AB ∥CD ,BE 和DF 分别平分∠ABF 和∠CDE ,2∠E-∠F=48°,则∠CDE 的度数为( ).A .16°B .32°C .48°D .64°二、填空题11.如图,//AC BD ,BC 平分ABD ∠,设ACB ∠为α,点E 是射线BC 上的一个动点,若:5:2BAE CAE ∠∠=,则CAE ∠的度数为__________.(用含α的代数式表示).12.如图,△ABC 中,∠C =90︒,AC =5cm ,CB =12cm ,AB =13cm ,将△ABC 沿直线CB 向右平移3cm 得到△DEF ,DF 交AB 于点G ,则点C 到直线DE 的距离为______cm .13.如图,已知AB CD ∥,CE 、BE 的交点为E ,现作如下操作:第一次操作,分别作ABE ∠和DCE ∠的平分线,交点为1E ,第二次操作,分别作1ABE ∠和1DCE ∠的平分线,交点为2E ,第三次操作,分别作2ABE ∠和2DCE ∠的平分线,交点为3E ,…第n 次操作,分别作1n ABE -∠和1n DCE -∠的平分线,交点为n E .若1n E ∠=度,那BEC ∠等于__________度.14.如图,有两个正方形夹在AB 与CD 中,且AB//CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为________度(正方形的每个内角为90°)15.如图,AB ∥CD ,OE 平分∠BOC ,OF ⊥OE ,OP ⊥CD ,∠ABO =40°,则下列结论:①∠BOE =70°;②OF 平分∠BOD ;③∠1=∠2;④∠POB =2∠3.其中正确的结论有______.(填序号)16.如图,四边形ABCD 的长条形纸带,AB //CD ,将长方形沿 EF 折叠,A 、D 分别于A ’、D '对应,若 ∠CFE =2∠CFD ',则∠AEF 的度数是___.17.如图,△ABC 沿AB 方向平移3个单位长度后到达△DEF 的位置,BC 与DF 相交于点O ,连接CF ,已知△ABC 的面积为14,AB =7,S △BDO ﹣S △COF =___.18.如图,//AB DE ,AD AB ⊥,AE 平分BAC ∠交BC 于点F .如果24CAD ∠=︒,则=E ∠__︒.19.一副三角板按如图所示(共定点A )叠放在一起,若固定三角板ABC ,改变三角板ADE 的位置(其中A 点位置始终不变),当∠BAD =___°时,DE ∥AB .20.如图,将一副三角板按如图放置,90,45,60BAC DAE B E ∠=∠=︒∠=︒∠=︒,则①13∠=∠;②2180CAD ∠+∠=︒;③如果230∠=︒,则有//AC DE ;④如果245∠=︒,则有//BC AD .上述结论中正确的是________________(填写序号).三、解答题21.已知,AB ∥CD ,点E 为射线FG 上一点.(1)如图1,若∠EAF =25°,∠EDG =45°,则∠AED = .(2)如图2,当点E 在FG 延长线上时,此时CD 与AE 交于点H ,则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系,请说明你的结论;(3)如图3,当点E 在FG 延长线上时,DP 平分∠EDC ,∠AED =32°,∠P =30°,求∠EKD 的度数.22.已知AB //CD .(1)如图1,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED .求证:∠BED =∠B +∠D ;(2)如图,连接AD ,BC ,BF 平分∠ABC ,DF 平分∠ADC ,且BF ,DF 所在的直线交于点F .①如图2,当点B 在点A 的左侧时,若∠ABC =50°,∠ADC =60°,求∠BFD 的度数.②如图3,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,请你求出∠BFD的度数.(用含有α,β的式子表示)23.已知AB∥CD,线段EF分别与AB,CD相交于点E,F.(1)请在横线上填上合适的内容,完成下面的解答:如图1,当点P在线段EF上时,已知∠A=35°,∠C=62°,求∠APC的度数;解:过点P作直线PH∥AB,所以∠A=∠APH,依据是;因为AB∥CD,PH∥AB,所以PH∥CD,依据是;所以∠C=(),所以∠APC=()+()=∠A+∠C=97°.(2)当点P,Q在线段EF上移动时(不包括E,F两点):①如图2,∠APQ+∠PQC=∠A+∠C+180°成立吗?请说明理由;②如图3,∠APM=2∠MPQ,∠CQM=2∠MQP,∠M+∠MPQ+∠PQM=180°,请直接写出∠M,∠A与∠C的数量关系.24.已知点C在射线OA上.(1)如图①,CD//OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD 与∠BO′E′的关系(用含α的代数式表示)(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.25.如图,已知AM //BN ,点P 是射线AM 上一动点(与点A 不重合),BC BD 、分别平分ABP ∠和PBN ∠,分别交射线AM 于点,C D .(1)当60A ∠=︒时,ABN ∠的度数是_______;(2)当A x ∠=︒,求CBD ∠的度数(用x 的代数式表示);(3)当点P 运动时,ADB ∠与APB ∠的度数之比是否随点P 的运动而发生变化?若不变化,请求出这个比值;若变化,请写出变化规律.(4)当点P 运动到使ACB ABD =∠∠时,请直接写出14DBN A +∠∠的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】由折叠的性质可知∠1=∠BAG ,2∠BDC +∠2=180°,根据BE ∥AG ,得到∠CFB =∠CAG =2∠1,从而根据平行线的性质得到∠CDB =2∠1,则∠2=180°-4∠1.【详解】解:由题意得:AG ∥BE ∥CD ,CF ∥BD ,∴∠CFB =∠CAG ,∠CFB +∠DBF =180°,∠DBF +∠CDB =180°∴∠CFB =∠CDB∴∠CAG =∠CDB由折叠的性质得∠1=∠BAG ,2∠BDC +∠2=180°∴∠CAG =∠CDB =∠1+∠BAG =2α∴∠2=180°-2∠BDC =180°-4α故选D.【点睛】本题主要考查了平行线的性质与折叠的性质,解题的关键在于能够熟练掌握相关知识进行求解.2.A解析:A【分析】分别过K 、H 作AB 的平行线MN 和RS ,根据平行线的性质和角平分线的性质可用ABK ∠和DCK ∠分别表示出H ∠和K ∠,从而可找到H ∠和K ∠的关系,结合条件可求得K ∠.【详解】解:如图,分别过K 、H 作AB 的平行线MN 和RS ,//AB CD ,//////AB CD RS MN ∴, 12RHB ABE ABK ∴∠=∠=∠,12SHC DCF DCK ∠=∠=∠, 180NKB ABK MKC DCK ∠+∠=∠+∠=︒,1180180()2BHC RHB SHC ABK DCK ∴∠=︒-∠-∠=︒-∠+∠, 180BKC NKB MKC ∠=︒-∠-∠180ABK DCK =∠+∠-︒,36021801802BKC BHC BHC ∴∠=︒-∠-︒=︒-∠,又24BKC BHC ∠-∠=︒,24BHC BKC ∴∠=∠-︒,1802(24)BKC BKC ∴∠=︒-∠-︒,76BKC ∴∠=︒,故选:A .【点睛】本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④//a b ,////⇒b c a c .3.D解析:D【详解】试题分析:延长TS ,∵OP ∥QR ∥ST ,∴∠2=∠4,∵∠3与∠ESR 互补,∴∠ESR=180°﹣∠3,∵∠4是△FSR 的外角,∴∠ESR+∠1=∠4,即180°﹣∠3+∠1=∠2,∴∠2+∠3﹣∠1=180°.故选D .考点:平行线的性质.4.B解析:B【分析】根据平行线的性质求出ACB E ∠=∠,根据角平分线定义和平行线的性质求出ABF CBF ADC EDC ∠=∠=∠=∠,推出//BF DC ,再根据平行线的性质判断即可.【详解】∵//BC DE ,∴ACB E ∠=∠,∴①正确;∵//BC DE ,∴ABC ADE ∠=∠,∵BF 平分ABC ∠,DC 平分ADE ∠, ∴12ABF CBF ABC ∠=∠=∠,12ADC EDC ADE ∠=∠=∠, ∴ABF CBF ADC EDC ∠=∠=∠=∠,∴//BF DC ,∴BFD FDC ∠=∠,∴根据已知不能推出ADF CDF ∠=∠,∴②错误;③错误;∵ABF ADC ∠=∠,ADC EDC ∠=∠,∴ABF EDC ∠=∠,∵//DE BC ,∴BCD EDC ∠=∠,∴ABF BCD ∠=∠,∴④正确;即正确的有2个,故选:B .【点睛】本题考查了平行线的性质和判定,角平分线定义的应用,能灵活运用平行线的性质和判定进行推理是解此题的关键.5.B解析:B【分析】记∠1顶点为A ,∠2顶点为B ,∠3顶点为C ,过点B 作BD ∥l 1,由平行线的性质可得∠3+∠DBC =180°,∠ABD +(180°-∠1)=180°,由此得到∠3+∠2+(180°-∠1)=360°,再结合已知条件即可求出结果.【详解】如图,过点B 作BD ∥l 1,∵12//l l ,∴BD ∥l 1∥l 2,∴∠3+∠DBC =180°,∠ABD +(180°-∠1)=180°,∴∠3+∠DBC +∠ABD +(180°-∠1)=360°,即∠3+∠2+(180°-∠1)=360°,又∵∠2+∠3=216°,∴216°+(180°-∠1)=360°,∴∠1=36°.故选:B .【点睛】本题考查了平行线的性质,正确作出辅助线,熟练掌握平行线性质是解题的关键. 6.D解析:D【分析】根据题意画出图形,再由平行线的性质定理即可得出结论.【详解】解:如图当AC ∥DE 时,45BAD DAE ∠=∠=︒; 当BC ∥AD 时,60DAB B ∠=∠=︒; 当BC ∥ AE 时,∵60EAB B ∠=∠=︒, ∴4560105BAD DAE EAB ∠=∠+∠=︒+︒=︒; 当AB ∥DE 时,∵ 90E EAB ∠=∠=︒, ∴4590135BAD DAE EAB ∠=∠+∠=︒+︒=︒. 故选:D . 【点睛】本题考查的是平行线的判定与性质,根据题意画出图形,利用平行线的性质及直角三角板的性质求解是解答此题的关键.7.B解析:B 【分析】先求∠DFE 的度数,再利用平角的定义计算求解即可. 【详解】 ∵AB ∥CD , ∴∠DFE =∠A =65°, ∴∠EFC =180°-∠DFE =115°, 故选B . 【点睛】本题考查了平行线的性质,平角的定义,熟练掌握平行线的性质是解题的关键.8.D解析:D 【分析】根据两直线平行,同旁内角互补可得∠1+∠AOF =180°,再根据两直线平行,内错角相等可得∠3=∠AOC ,而通过∠AOF =∠AOC-∠2,整理可得∠1+∠3-∠2=180°. 【详解】 解:∵AB ∥EF , ∴∠1+∠AOF =180°, ∵CD ∥AB , ∴∠3=∠AOC ,又∵∠AOF =∠AOC −∠2=∠3-∠2, ∴∠1+∠3-∠2=180°.【点睛】本题主要考查平行线的性质,从复杂图形中找出内错角,同旁内角是解题的关键.9.C解析:C 【分析】根据题意画出示意图,延长FP 交AB 于点Q ,根据折叠的性质和四边形的内角和进行分析解答. 【详解】解:根据题意,延长FP 交AB 于点Q ,可画图如下:∵AB CD ∥ ∴CFQ PQE ∠=∠∵将射线EA 沿EP 折叠,射线FC 沿FP 折叠, ∴,CFP PFM MEP PEQ ∠=∠∠=∠, ∵,FPE PQE PEQ EM FM ∠=∠+∠⊥,如第一个图所示,在四边形FPEM 中,36090PFM MEP FPE ∠+∠+∠=︒-︒, 得:2270FPE ∠=︒, ∴135FPE ∠=︒.如第二个图所示,在四边形FPEM 中,360(36090)90PFM MEP FPE ∠+∠+∠=︒-︒-︒=︒, 得:290FPE ∠=︒, ∴45FPE ∠=︒. 故选:C . 【点睛】本题考查的知识点是平行线的性质、折叠的性质、三角形的外角、四边形的内角和等知识.关键是利用平行线的性质以及四边形内角和进行解答.10.B【分析】已知BE和DF分别平分∠ABF和∠CDE,根据角平分线分定义可得∠ABE=12∠ABF,∠CDF=12∠CDE;过点E作EM//AB,点F作FN//AB,即可得////AB CD EM//FN,由平行线的性质可得∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,由此可得∠BED=∠BEM+∠DEM=∠ABE+∠CDE=12∠ABF+∠CDE,∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +12∠CDE,又因2∠BED-∠BFD=48°,即可得2(12∠ABF+∠CDE)-(∠ABF +12∠CDE)=48°,由此即可求得∠CDE=32°.【详解】∵BE和DF分别平分∠ABF和∠CDE,∴∠ABE=12∠ABF,∠CDF=12∠CDE,过点E作EM//AB,点F作FN//AB,∵//AB CD,∴////AB CD EM//FN,∴∠ABE=∠BEM,∠MED=∠EDC,∠ABF=∠BFN,∠CDF=∠DFN,∴∠BED=∠BEM+∠DEM=∠ABE+∠CDE=12∠ABF+∠CDE,∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +12∠CDE,∵2∠BED-∠BFD=48°,∴2(12∠ABF+∠CDE)-(∠ABF +12∠CDE)=48°,∴∠CDE=32°.故选B.【点睛】本题考查了平行线的性质,根据平行线的性质确定有关角之间的关系是解决问题的关键.二、填空题11.或【分析】根据题意可分两种情况,①若点运动到上方,根据平行线的性质由可计算出的度数,再根据角平分线的性质和平行线的性质,计算出的度数,再由,,列出等量关系求解即可得出结论;②若点运动到下方,根据解析:41203α︒-或36047α︒-【分析】根据题意可分两种情况,①若点E 运动到1l 上方,根据平行线的性质由α可计算出CBD ∠的度数,再根据角平分线的性质和平行线的性质,计算出BAC ∠的度数,再由5:2BAE CAE ∠∠=,BAE BAC CAE ∠=∠+∠,列出等量关系求解即可得出结论;②若点E运动到1l 下方,根据平行线的性质由α可计算出CBD ∠的度数,再根据角平分线的性质和平行线的性质,计算出BAC ∠的度数,再由5:2BAE CAE ∠∠=,BAE BAC CAE ∠=∠-∠列出等量关系求解即可得出结论. 【详解】解:如图,若点E 运动到l 1上方,//AC BD ,CBD ACB α∴∠=∠=,BC 平分ABD ∠,22ABD CBD α∴∠=∠=, 1801802BAC ABD α∴∠=︒-∠=︒-,又5:2BAE CAE ∠∠=,5():2BAC CAE CAE ∴∠+∠∠=, 5(1802):2CAE CAE α︒-+∠∠=, 解得180241205312CAE αα︒-∠==︒--; 如图,若点E 运动到l 1下方,//AC BD ,CBD ACB α∴∠=∠=,BC 平分ABD ∠,22ABD CBD α∴∠=∠=, 1801802BAC ABD α∴∠=︒-∠=︒-,又5:2BAE CAE ∠∠=,5():2BAC CAE CAE ∴∠-∠∠=, 5(1802):2CAE CAE α︒--∠∠=, 解得180236045712CAE αα︒-︒-∠==+. 综上CAE ∠的度数为41203α︒-或36047α︒-. 故答案为:41203α︒-或36047α︒-. 【点睛】本题主要考查平行线的性质和角平分线的性质,两直线平行,同位角相等.两直线平行,同旁内角互补.两直线平行,内错角相等,合理应用平行线的性质是解决本题的关键.12.【分析】根据平移前后图形的大小和形状不变,添加辅助线构造梯形,利用面积相等来计算出答案. 【详解】解:如图,连接AD 、CD ,作CH ⊥DE 于H ,依题意可得AD=BE=3cm , ∵梯形ACED 解析:7513【分析】根据平移前后图形的大小和形状不变,添加辅助线构造梯形,利用面积相等来计算出答案. 【详解】解:如图,连接AD 、CD ,作CH ⊥DE 于H ,依题意可得AD=BE=3cm , ∵梯形ACED 的面积()()2131235452S cm =⨯++⨯=, ∴()1153134522ADCDCESSCH +=⨯⨯+⨯⋅=, 解得7513CH =; 故答案为:7513. 【点睛】本题考查的是图形的平移和点到直线的距离,注意图形平移前后的形状和大小不变,以及平移前后对应点的连线相等.13.【分析】先过E 作EF ∥AB ,根据AB ∥CD ,得出AB ∥EF ∥CD ,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE ;根据∠ABE 和∠DCE 的平分线交点为E1, 解析:2n【分析】先过E 作EF ∥AB ,根据AB ∥CD ,得出AB ∥EF ∥CD ,再根据平行线的性质,得出∠B =∠1,∠C =∠2,进而得到∠BEC =∠ABE +∠DCE ;根据∠ABE 和∠DCE 的平分线交点为E 1,则可得出∠CE 1B =∠ABE 1+∠DCE 112=∠ABE 12+∠DCE 12=∠BEC ;同理可得∠BE 2C =∠ABE 2+∠DCE 212=∠ABE 112+∠DCE 112=∠CE 1B 14=∠BEC ;根据∠ABE 2和∠DCE 2的平分线,交点为E 3,得出∠BE 3C 18=∠BEC ;…据此得到规律∠E n 12n =∠BEC ,最后求得∠BEC 的度数. 【详解】如图1,过E 作EF ∥AB . ∵AB ∥CD , ∴AB ∥EF ∥CD , ∴∠B =∠1,∠C =∠2. ∵∠BEC =∠1+∠2, ∴∠BEC =∠ABE +∠DCE ; 如图2.∵∠ABE 和∠DCE 的平分线交点为E 1, ∴∠CE 1B =∠ABE 1+∠DCE 112=∠ABE 12+∠DCE 12=∠BEC . ∵∠ABE 1和∠DCE 1的平分线交点为E 2,∴∠BE 2C =∠ABE 2+∠DCE 212=∠ABE 112+∠DCE 112=∠CE 1B 14=∠BEC ;∵∠ABE 2和∠DCE 2的平分线,交点为E 3, ∴∠BE 3C =∠ABE 3+∠DCE 312=∠ABE 212+∠DCE 212=∠CE 2B 18=∠BEC ; …以此类推,∠E n 12n=∠BEC , ∴当∠E n =1度时,∠BEC 等于2n 度. 故答案为:2n .【点睛】本题考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.14.【详解】作IF ∥AB,GK ∥AB,JH ∥AB 因为AB ∥CD所以,AB ∥CD ∥ IF ∥GK ∥JH 所以,∠IFG=∠FEC=10° 所以,∠GFI=90°-∠IFG=80° 所以,∠KGF=∠解析:【详解】 作IF ∥AB,GK ∥AB,JH ∥AB 因为AB ∥CD所以,AB ∥CD ∥ IF ∥GK ∥JH 所以,∠IFG=∠FEC=10° 所以,∠GFI=90°-∠IFG=80° 所以,∠KGF=∠GFI=80° 所以,∠HGK=150°-∠KGF=70° 所以,∠JHG=∠HGK=70° 同理,∠2=90°-∠JHG=20° 所以,∠1=90°-∠2=70°故答案为70【点睛】本题考查了平行线的性质,正确作出辅助线是关键,注意掌握平行线的性质:两直线平行,内错角相等.15.①②③【分析】根据平行线的性质和∠ABO=40°,由两直线平行,同旁内角互补,可计算出∠BOC的度数,再根据角平分线的性质,可计算出∠BOC的度数,根据角平分线的性质可得出∠BOE的度数,可判断解析:①②③【分析】根据平行线的性质和∠ABO=40°,由两直线平行,同旁内角互补,可计算出∠BOC的度数,再根据角平分线的性质,可计算出∠BOC的度数,根据角平分线的性质可得出∠BOE 的度数,可判断①是否正确.根据OF⊥OE,由∠BOE的度数计算出∠BOF的度数,根据两直线平行,内错角相等的性质,得到∠BOD的度数,可计算出∠3的度数,可得出结论②是否正确,由②中的结论可判断③是否正确.根据平行线的性质,可得到∠OPB=90°,可计算出∠POB的度数,可得出④结论是否正确.【详解】解:∵AB∥CD,∠ABO=40°,∴∠BOC=180°﹣∠ABO=180°﹣40°=140°,∵OE平分∠BOC,∴∠B0E=12∠BOC=11402︒⨯=70°,故结论①正确;∵OF⊥OE,∠B0E=70°,∴∠BOF=90°﹣70°=20°,∵AB∥CD,∠ABO=40°,∴∠BOD=∠ABO=40°,∴∠FOD=∠BOD﹣∠BOF=20°,∴∠BOF=∠DOF,∴OF平分∠BOD,故结论②正确;由②的结论可得,∴∠1=∠2=20°,故结论③正确;∵OP⊥CD,∴∠OPB=90°,∴∠POB=90°﹣∠ABO=50°,∵2∠3=2×20°=40°,∴∠POB≠2∠3,故结论④错误.故答案为:①②③.【点睛】本题考查了平行线的性质、角平分线性质的应用,合理应用平行线的性质是解决本题关键.16.72゜【分析】先根据平行线的性质,由AB∥CD,得到∠CFE=∠AEF,再根据翻折的性质可得∠DFE=∠D′FE,由平角的性质可求得∠CFD′的度数,即可得出答案.【详解】解:∵AB∥CD,解析:72゜【分析】先根据平行线的性质,由AB∥CD,得到∠CFE=∠AEF,再根据翻折的性质可得∠DFE=∠D′FE,由平角的性质可求得∠CFD′的度数,即可得出答案.【详解】解:∵AB∥CD,∴∠CFE=∠AEF,又∵∠DFE=∠D′FE,∠CFE=2∠CFD′,∴∠DFE=∠D′FE=3∠CFD′,∴∠DFE+∠CFE=3∠CFD′+2∠CFD′=180°,∴∠CFD′=36°,∴∠AEF=∠CFE=2∠CFD′=72°.故答案为:72°.【点睛】本题主要考查了平行线的性质,翻折变换等知识,熟练应用平行线的性质进行求解是解决本题的关键.17.2【分析】如图,连接CD,过点C作CG⊥AB于G.利用三角形面积公式求出CG,再根据S△BDO﹣S△COF=S△CDB﹣S△CDF=求解即可.【详解】解:如图,连接CD ,过点C 作CG ⊥AB 于解析:2 【分析】如图,连接CD ,过点C 作CG ⊥AB 于G .利用三角形面积公式求出CG ,再根据S △BDO ﹣S △COF =S △CDB ﹣S △CDF =1122DB CG CF CG ⋅⋅-⋅⋅求解即可.【详解】解:如图,连接CD ,过点C 作CG ⊥AB 于G .∵S △ABC =12•AB •CG , ∴CG =2147⨯=4, ∵AD =CF =3,AB =7, ∴BD =AB ﹣AD =7﹣3=4,∴S △BDO ﹣S △COF =S △CDB ﹣S △CDF =1111443422222DB CG CF CG ⋅-⋅⋅=⨯⨯-⨯⨯=,故答案为:2. 【点睛】本题考查三角形的面积,平移变换等知识,解题的关键是学会用转化的思想思考问题.18.33 【分析】根据求出∠C=90°,再求出∠BAD=66°,根据角平分线性质得∠DAE=33°,由三角形的外角性质得∠ADE=114°,最后由三角形内角和定理可得结论. 【详解】 解:∵,, ∴∠解析:33 【分析】根据//AB DE 求出∠C=90°,再求出∠BAD=66°,根据角平分线性质得∠DAE=33°,由三角形的外角性质得∠ADE=114°,最后由三角形内角和定理可得结论. 【详解】解:∵//AB DE ,AD AB ⊥,∴∠180BAD D ∠+∠=︒,且90BAD ∠=︒ ∴90D ∠=︒∵∠CAD =24°∴∠BAC =90°-∠CAD =90°-24°=66°,∵AE 是∠BAC 的平分线∴∠EAB =11663322BAC ∠=⨯︒=︒ ∵//AB DE ,∴33E EAB ∠=∠=︒故答案为:33【点睛】此题主要考查了平行线的性质,角平分线的定义,准确识图,灵活运用相关知识是解题的关键.19.30或150【分析】分两种情况,根据ED ∥AB ,利用平行线的性质,即可得到∠BAD 的度数.【详解】解:如图1所示:当ED ∥AB 时,∠BAD=∠D=30°;如图2所示,当ED ∥AB 时,∠D解析:30或150【分析】分两种情况,根据ED ∥AB ,利用平行线的性质,即可得到∠BAD 的度数.【详解】解:如图1所示:当ED ∥AB 时,∠BAD =∠D =30°;如图2所示,当ED ∥AB 时,∠D =∠BAD =180°,∵∠D =30°∴∠BAD =180°-30°=150°;故答案为:30°或150°.【点睛】本题主要考查了平行线的判定,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由直线的平行关系来寻找角的数量关系.20.①②③④【分析】根据余角的概念和同角的余角相等判断①;根据①的结论判断②;根据平行线的判定定理判断③和④,即可得出结论.【详解】解:∵∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,解析:①②③④【分析】根据余角的概念和同角的余角相等判断①;根据①的结论判断②;根据平行线的判定定理判断③和④,即可得出结论.【详解】解:∵∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,故①正确;∵∠CAD+∠2=∠1+∠2+∠3+∠2=90°+90°=180°,故②正确;∵∠2=30°,∴∠1=60°=∠E,∴AC∥DE,故③正确;∵∠2=45°,∴∠3=45°=∠B,∴BC∥AD,故④正确;故答案为:①②③④.【点睛】本题考查的是平行线的性质和余角、补角的概念,掌握平行线的性质定理和判定定理是解题的关键.三、解答题21.(1)70°;(2)EAF AED EDG ∠=∠+∠,证明见解析;(3)122°【分析】(1)过E 作//EF AB ,根据平行线的性质得到25EAF AEH ∠=∠=︒,45EAG DEH ∠=∠=︒,即可求得AED ∠;(2)过过E 作//EM AB ,根据平行线的性质得到180EAF MEH ∠=︒-∠,180EDG AED MEH ∠+∠=︒-,即EAF AED EDG ∠=∠+∠;(3)设EAI x ∠=,则3BAE x ∠=,通过三角形内角和得到2EDK x ∠=-︒,由角平分线定义及//AB CD 得到33224x x =︒+-︒,求出x 的值再通过三角形内角和求EKD ∠.【详解】解:(1)过E 作//EF AB ,//AB CD ,//EF CD ∴,25EAF AEH ∴∠=∠=︒,45EAG DEH ∠=∠=︒,70AED AEH DEH ∴∠=∠+∠=︒,故答案为:70︒;(2)EAF AED EDG ∠=∠+∠.理由如下:过E 作//EM AB ,//AB CD ,//EM CD ∴,180EAF MEH ∴∠+∠=︒,180EDG AED MEH ∠+∠+=︒,180EAF MEH ∴∠=︒-∠,180EDG AED MEH ∠+∠=︒-,EAF AED EDG ∴∠=∠+∠;(3):1:2EAP BAP ∠∠=,设EAP x ∠=,则3BAE x ∠=,32302AED P ∠-∠=︒-︒=︒,DKE AKP ∠=∠,又180EDK DKE DEK ∠+∠+∠=︒,180KAP KPA AKP ∠+∠+∠=︒,22EDK EAP x ∴∠=∠-︒=-︒, DP 平分EDC ∠,224CDE EDK x ∴∠=∠=-︒,//AB CD ,EHC EAF AED EDG ∴∠=∠=∠+∠,即33224x x =︒+-︒,解得28x =︒,28226EDK ∴∠=︒-︒=︒,1802632122EKD ∴∠=︒-︒-︒=︒.【点睛】本题主要考查了平行线的性质和判定,正确做出辅助线是解决问题的关键.22.(1)见解析;(2)55°;(3)1118022αβ︒-+ 【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数;②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数.【详解】解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠, BF 平分ABC ∠,DF 平分ADC ∠, 1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒, 55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒;②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠,BF 平分ABC ∠,DF 平分ADC ∠, 1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=, 1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+. 答:BFD ∠的度数为1118022αβ︒-+. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质.23.(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①∠APQ+∠PQC=∠A+∠C+180°成立,理由见解答过程;②3∠PMQ+∠A+∠C=360°.【分析】(1)根据平行线的判定与性质即可完成填空;(2)结合(1)的辅助线方法即可完成证明;(3)结合(1)(2)的方法,根据∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,即可证明∠PMQ,∠A与∠C的数量关系.【详解】解:过点P作直线PH∥AB,所以∠A=∠APH,依据是两直线平行,内错角相等;因为AB∥CD,PH∥AB,所以PH∥CD,依据是平行于同一条直线的两条直线平行;所以∠C=(∠CPH),所以∠APC=(∠APH)+(∠CPH)=∠A+∠C=97°.故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH;∠APH,∠CPH;(2)①如图2,∠APQ+∠PQC=∠A+∠C+180°成立,理由如下:过点P作直线PH∥AB,QG∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG,∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∴∠APQ+∠PQC=∠APH+∠HPQ+∠GQP+∠CQG=∠A+∠C+180°.∴∠APQ+∠PQC=∠A+∠C+180°成立;②如图3,过点P作直线PH∥AB,QG∥AB,MN∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG∥MN,∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∠HPM=∠PMN,∠GQM=∠QMN,∴∠PMQ=∠HPM+∠GQM,∵∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,∴∠APM+∠CQM=∠A+∠C+∠PMQ=2∠MPQ+2∠MQP=2(180°﹣∠PMQ),∴3∠PMQ+∠A+∠C=360°.【点睛】考核知识点:平行线的判定和性质.熟练运用平行线性质和判定,添加适当辅助线是关键.24.(1)150°;(2)∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′【分析】(1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;(2)如图②,过O点作OF∥CD,根据平行线的判定和性质可得∠OCD、∠BO′E′的数量关系;(3)由已知推出CP∥OB,得到∠AOB+∠PCO=180°,结合角平分线的定义可推出∠OCD=2∠PCO=360°-2∠AOB,根据(2)∠OCD+∠BO′E′=360°-∠AOB,进而推出∠AOB=∠BO′E′.【详解】解:(1)∵CD∥OE,∴∠AOE=∠OCD=120°,∴∠BOE=360°-∠AOE-∠AOB=360°-90°-120°=150°;(2)∠OCD+∠BO′E′=360°-α.证明:如图②,过O点作OF∥CD,∵CD∥O′E′,∴OF∥O′E′,∴∠AOF=180°-∠OCD,∠BOF=∠E′O′O=180°-∠BO′E′,∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E′=360°-(∠OCD+∠BO′E′)=α,∴∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′.证明:∵∠CPO′=90°,∴PO′⊥CP,∵PO′⊥OB,∴CP∥OB,∴∠PCO+∠AOB=180°,∴2∠PCO=360°-2∠AOB,∵CP是∠OCD的平分线,∴∠OCD=2∠PCO=360°-2∠AOB,∵由(2)知,∠OCD+∠BO′E′=360°-α=360°-∠AOB,∴360°-2∠AOB+∠BO′E′=360°-∠AOB,∴∠AOB=∠BO′E′.【点睛】此题考查了平行线的判定和性质,平移的性质,直角的定义,角平分线的定义,正确作出辅助线是解决问题的关键.25.(1)120°;(2)90°-12x°;(3)不变,12;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN=180°-x°,根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=180°-x°,即∠CBD=∠CBP+∠DBP=90°-12x°;(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB:∠ADB=2:1;(4)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据角平分线的定义可得∠ABP=∠PBN=12∠ABN=2∠DBN,由平行线的性质可得12∠A+12∠ABN=90°,即可得出答案.【详解】解:(1)∵AM∥BN,∠A=60°,∴∠A+∠ABN=180°,∴∠ABN=120°;(2)∵AM∥BN,∴∠ABN+∠A=180°,∴∠ABN=180°-x°,∴∠ABP+∠PBN=180°-x°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=180°-x°,∴∠CBD=∠CBP+∠DBP=12(180°-x°)=90°-12x°;(3)不变,∠ADB:∠APB=12.∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1,∴∠ADB:∠APB=12;(4)∵AM∥BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠ABC,∠PBN=2∠DBN,∴∠ABP=∠PBN=2∠DBN=12∠ABN,∵AM∥BN,∴∠A+∠ABN=180°,∴12∠A+12∠ABN=90°,∴12∠A+2∠DBN=90°,∴14∠A+∠DBN=12(12∠A+2∠DBN)=45°.【点睛】本题主要考查平行线的性质和角平分线的定义,熟练掌握平行线的性质是解题的关键.。
七年级数学下册-相交线与平行线测试题及答案

七年级数学下册-相交线与平行线测试题及答案.doc相交线与平行线测试题一、填空题1.60º2.70º3.75º4.100º5.∠BOE = 76º。
∠AOG = 52º6.30º7.110º8.109.60π10.3cm11.∠3的同位角 = 140º。
∠3的内错角 = 40º。
∠3的同旁内角 = 140º12.4二、选择题1.D.42.D.在平面内过一点有且只有一条直线垂直于已知直线.3.B.⑵、⑶、⑷4.C.90°5.对顶角相等的语句为“对顶角互相相等”。
___(a)所示,五边形ABCDE是___十年前承包的一块土地示意图。
经过多年开垦荒地,现已变成图(b)所示的形状,但承包土地与开垦荒地的分界小路(即图(b)中折线CDE)还保留着。
___想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多。
请你用有关知识,按___的要求设计出修路方案。
(不计分界小路与直路的占地面积)1) 设计方案如下:首先,连接AE和BD,将五边形ABCDE分成三个部分。
然后,连接DE并延长到直路的位置,再连接CE和BC。
如图(c)所示,直路的位置为EF,其中EF与DE平行,且EF与BC垂直。
此时,EF将五边形分为左右两部分,且左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多。
2) 设计理由如下:首先,连接AE和BD是为了将五边形ABCDE分成三个部分,方便后续的计算。
连接DE并延长到直路的位置是为了确定直路的位置,使得EF与DE平行,方便计算面积。
连接CE和BC是为了确定EF与BC垂直,使得右边的土地面积与开垦的荒地面积一样多。
因此,这个修路方案符合___的要求。
解:(1) 根据已知条件,∠1=118°,∠2=∠3,a∥b,因此可以得出∠3=180°-∠1=62°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.如图,用直尺和三角尺画图:已知点P 和直线a ,经过点P 作直线b ,使//b a ,其画法的依据是( )A .过直线外一点有且只有一条直线与已知直线平行B .两直线平行,同位角相等C .同位角相等,两直线平行D .内错角相等,两直线平行2.如图,直线,a b 被直线c 所截,下列条件中不能判定a//b 的是( )A .25∠=∠B .45∠=∠C .35180∠+∠=︒D .12180∠+∠=︒ 3.如图,如果AB ∥EF ,EF ∥CD ,下列各式正确的是( )A .∠1+∠2−∠3=90°B .∠1−∠2+∠3=90°C .∠1+∠2+∠3=90°D .∠2+∠3−∠1=180° 4.下列命题中,属于真命题的是( )A .相等的角是对顶角B .一个角的补角大于这个角C .绝对值最小的数是0D .如果a b =,那么a=b5.如图,1∠与2∠是同位角的共有( )个A .1个B .2个C .3个D .4个6.已知//AB CD ,∠EAF=13∠EAB ,∠ECF=13∠ECD ,若∠E=66°,则∠F 为( )A .23°B .33°C .44°D .46°7.如图,直线l 与直线AB 、CD 分别相交于点E 、点F ,EG 平分BEF ∠交直线CD 与点G ,若168BEF ∠=∠=︒,则EGF ∠的度数为( ).A .34°B .36°C .38°D .68° 8.下列说法中,正确的是 A .相等的角是对顶角B .有公共点并且相等的角是对顶角C .如果1∠和2∠是对顶角,那么12∠=∠D .两条直线相交所成的角是对顶角9.如图,直线a ∥b ,则∠A 的度数是( )A .28°B .31°C .39°D .42° 10.如图,已知AB CD ∕∕,AF 交CD 于点E ,且,40BE AF BED ⊥∠=︒,则A ∠的度数是( )A .40︒B .50︒C .80︒D .90︒11.如图,将△ABE 向右平移50px 得到△DCF ,如果△ABE 的周长是400px(1px=0.04cm ),那么四边形ABFD 的周长是( )A .16cmB .18cmC .20cmD .21cm12.如图,A 、P 是直线m 上的任意两个点,B 、C 是直线n 上的两个定点,且直线m ∥n .则下列说法正确的是( )A .AC=BPB .△ABC 的周长等于△BCP 的周长 C .△ABC 的面积等于△ABP 的面积D .△ABC 的面积等于△PBC 的面积二、填空题13.如图,将一张长方形纸片按如图所示折叠,如果∠1=55°,那么∠2=_____°.14.如图,//EF AD ,//AD BC ,CE 平分BCF ∠,120DAC ∠=︒,20ACF ∠=︒,FEC ∠为______°.15.若∠A 与∠B 的两边分别平行,且∠A 比∠B 的3倍少40°,则∠B =_____度. 16.如图,点A 、B 为定点,直线l ∥AB,P 是直线l 上一动点,对于下列各值:①线段AB 的长;②△PAB 的周长;③△PAB 的面积;④∠APB 的度数,其中不会随点P 的移动而变化的是(填写所有正确结论的序号)______________.17.如图,已知12∠=∠,求证:A BCH ∠=∠.证明:∵12∠=∠(已知)23∠∠=(______)∴13∠=∠(等量代换)∴//CH (______)(同位角相等,两直线平行)∴A BCH ∠=∠(______)18.命题“若a 2>b 2则a >b ”是_____命题(填“真”或“假”),它的逆命题是_____. 19.运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识____________在生活中的应用. 20.如图,直线////a b c ,直角三角板的直角顶点落在直线b 上,若135∠=︒,则2∠等于_______.三、解答题21.如图是由相同边长的小正方形组成的网格图形,小正方形的边长为1个单位长度,每个小正方形的顶点都叫做格点,ABC 的三个顶点都在格点上,利用网格画图.(注:所画格点、线条用黑色水笔描黑)(1)过点A 画BC 的垂线,并标出垂线所过格点P ;(2)过点A 画BC 的平行线,并标出平行线所过格点Q ;(3)画出ABC 向右平移8个单位长度后A B C '''的位置;(4)A B C '''的面积为______.22.在一张地图上有、、A B C 三地,但地图被墨迹污染,C 地具体位置看不清楚,但知道C 地在A 地的北偏东30°方向,在B 地南偏东45°方向.(1)根据以上条件,在地图上画出C 地的位置;(2)直接写出ACB ∠的度数.23.如图,//AB CD ,直线EF 分别交AB ,CD 于E 、F 两点,且EG 平分BEF ∠,172∠=︒,求2∠的度数.24.三角形ABC 中,D 是AB 上一点,//DE BC 交AC 于点E ,点F 是线段DE 延长线上一点,连接FC ,180BCF ADE ∠+∠=︒.(1)如图1,求证://CF AB ;(2)如图2,连接BE ,若40ABE ∠=︒,60ACF ∠=︒,求BEC ∠的度数; (3)如图3,在(2)的条件下,点G 是线段FC 延长线上一点,若:7:13EBC ECB ∠∠=,BE 平分ABG ∠,求CBG ∠的度数.25.已知:直线GH 分别与直线AB ,CD 交于点E ,F .EM 平分BEF ∠,FN 平分CFE ∠,并且//EM FN .(1)如图1,求证://AB CD ;(2)如图2,2AEF CFN ∠=∠,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135︒.26.如图,直线AB ∥CD ,EB 平分∠AED ,170∠=︒,求∠2的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据平行线的判定定理即可得出结论.【详解】解:由画法可知,其画法的依据是同位角相等,两直线平行.故选:C .【点睛】本题考查了作图-复杂作图,熟知平行线的判定定理是解答此题的关键.2.D解析:D【分析】根据平行线的判定定理逐项判断即可.【详解】解:A. 由2∠和5∠是同位角,则25∠=∠ ,可得a//b ,故该选项不符合题意;B. 由4∠和5∠是内错角,则45∠=∠,可得a//b ,故该选项不符合题意;C. 由∠3和∠1相等,35180∠+∠=︒,可得a//b ,故该选项不符合题意;D. 由∠1和∠2是邻补角,则12180∠+∠=︒不能判定a//b ,故该选项满足题意. 故答案为D .【点睛】本题主要考查了平行线的判定,掌握同位角相等,两直线平行;同旁内角互补,两直线平行是解答本题的关键.3.D解析:D【分析】根据平行线的性质,即可得到∠3=∠COE ,∠2+∠BOE=180°,进而得出∠2+∠3-∠1=180°.【详解】∵EF ∥CD∴∠3=∠COE∴∠3−∠1=∠COE−∠1=∠BOE∵AB ∥EF∴∠2+∠BOE=180°,即∠2+∠3−∠1=180°故选:D .【点睛】本题考查了平行线的性质,两条直线平行:内错角相等;两直线平行:同旁内角互补. 4.C解析:C【分析】根据对顶角、补角、绝对值的定义与性质逐项判断即可得.【详解】A 、相等的角不一定是对顶角,此项是假命题;B 、一个角的补角不一定大于这个角,如这个角为130︒,其补角为50︒,小于这个角,此项是假命题;C 、由绝对值的非负性得:绝对值最小的数是0,此项是真命题;D 、如果a b =,那么a b =或=-a b ,此项是假命题;故选:C .【点睛】本题考查了对顶角、补角、绝对值、真命题与假命题,熟练掌握各定义与性质是解题关键.5.B解析:B【分析】根据同位角的概念对每个图形一一判断,选出正确答案即可.【详解】图1:1∠与2∠是同位角;图2:1∠与2∠不是同位角;图3:1∠与2∠不是同位角;图4:1∠与2∠是同位角;只有图1、图4中1∠与2∠是同位角.故选:B .【点睛】本题主要考查同位角的概念,熟记同位角的概念是解题关键.6.C解析:C【分析】如图(见解析),先根据平行线的性质、角的和差可得66EAB EC C D AE ∠+∠=∠=︒,同样的方法可得F FAB FCD ∠=∠+∠,再根据角的倍分可得,2323FAB EAB FCD ECD ∠=∠∠=∠,由此即可得出答案. 【详解】 如图,过点E 作//EG AB ,则////EG AB CD ,,EAB CE C A D G G E E ∴∠=∠∠∠=,66AEG EAB ECD CE A C G E ∴∠+=∠+=∠=∠∠︒,同理可得:F FAB FCD ∠=∠+∠,11,33EAF EAB ECF ECD ∠=∠∠=∠, ,2323FAB EAB FCD ECD ∴∠=∠∠=∠, ()266443333222F FAB FCD EAB ECD EAB ECD ∴∠=∠+∠=∠+∠=∠+∠=⨯︒=︒,故选:C .【点睛】本题考查了平行线的性质、角的和差倍分,熟练掌握平行线的性质是解题关键. 7.A解析:A【分析】由角平分线的性质可得∠GEB=12∠BEF=34°,由同位角相等,两直线平行可得CD ∥AB ,即可求解.∵EG平分∠BEF,∠BEF=34°,∴∠GEB=12∵∠1=∠BEF=68°,∴CD∥AB,∴∠EGF=∠GEB=34°,故选:A.【点睛】本题考查了平行线的判定和性质,角平分线的定义,灵活运用这些性质进行推理是本题的关键.8.C解析:C【分析】本题考查对顶角的定义,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.由此逐一判断.【详解】A、对顶角是有公共顶点,且两边互为反向延长线,相等只是其性质,错误;B、对顶角应该是有公共顶点,且两边互为反向延长线,错误;C、角的两边互为反向延长线的两个角是对顶角,符合对顶角的定义,正确.D、两条直线相交所成的角有对顶角、邻补角,错误;故选C.【点睛】要根据对顶角的定义来判断,这是需要熟记的内容.9.C解析:C【解析】试题分析:根据平行线的性质可得∠1=70°,再根据三角形的一个外角等于和它不相邻的两个内角的和可得∠A=70°-31°=39°.故选C.考点:平行线的性质10.B解析:B【分析】直接利用垂线的定义结合平行线的性质得出答案.解:∵,40BE AF BED ⊥∠=︒,∴50FED ∠=︒,∵AB CD ∕∕,∴50A FED ∠=∠=︒.故选B .【点睛】此题主要考查了平行线的性质以及垂线的定义,正确得出FED ∠的度数是解题关键. 11.C解析:C【分析】根据平移的性质可得DF=AE ,然后判断出四边形ABFD 的周长=△ABE 的周长+AD+EF ,然后代入数据计算即可得解.注意:1px = 0.04cm .【详解】∵1px = 0.04cm ,∴50px=2cm ,400px=16cm ,∵△ABE 向右平移2cm 得到△DCF ,∴DF=AE ,∴四边形ABFD 的周长=AB+BE+DF+AD+EF=AB+BE+AE+AD+EF=△ABE 的周长+AD+EF .∵平移距离为2cm ,∴AD=EF=2cm ,∵△ABE 的周长是16cm ,∴四边形ABFD 的周长=16+2+2=20cm .故选:C .【点睛】本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.12.D解析:D【分析】根据平行线之间的距离及三角形的面积即可得出答案.【详解】解:∵A 、P 是直线m 上的任意两个点,B 、C 是直线n 上的两个定点,且直线m ∥n , 根据平行线之间的距离相等可得:△ABC 与△PBC 是同底等高的三角形,故△ABC 的面积等于△PBC 的面积.故选D .【点睛】本题考查平行线之间的距离;三角形的面积.二、填空题13.110【分析】根据平行线的性质和折叠的性质可以得到∠2的度数本题得以解决【详解】如图:由折叠的性质可得∠1=∠3∵∠1=55°∴∠1=∠3=55°∵长方形纸片的两条长边平行∴∠2=∠1+∠3∴∠2=解析:110【分析】根据平行线的性质和折叠的性质,可以得到∠2的度数,本题得以解决.【详解】如图:由折叠的性质可得,∠1=∠3,∵∠1=55°,∴∠1=∠3=55°,∵长方形纸片的两条长边平行,∴∠2=∠1+∠3,∴∠2=110°,故答案为:110.【点睛】本题考查平行线的性质,解答本题的关键是明确题意,利用数形结合的思想解答. 14.20【分析】根据平行线的性质可得进而可得∠ACB =60°根据角平分线的性质和角的和差可得∠BCE 根据平行线的性质可得∠FEC 【详解】∵∴∵∴∵又∵∴∵平分∴∠BCE =∠ECF =∠BCF =20°∵∴∴解析:20【分析】根据平行线的性质可得180DAC ACB ∠+∠=︒,进而可得∠ACB =60°,根据角平分线的性质和角的和差可得∠BCE ,根据平行线的性质可得∠FEC .【详解】∵//AD BC ,∴180DAC ACB ∠+∠=︒.∵120DAC ∠=︒,∴180********ACB DAC ∠=︒-∠=︒-︒=︒.∵60BCF ACF ACB ∠+∠=∠=︒.又∵20ACF ∠=︒,∴602040BCF ACB ACF ∠=∠-∠=︒-︒=︒.∵CE 平分BCF ∠,∴∠BCE =∠ECF =12∠BCF =20° ∵//EF BC ,∴20FEC BCE ∠=∠=︒,∴20FEC ∠=︒.故答案为:20.【点睛】本题主要考查平行线的性质,涉及到角的和差,角平分线的性质,解题的关键是求得∠BCE . 15.55或20【分析】根据平行线性质得出∠A+∠B =180°①∠A =∠B②求出∠A =3∠B ﹣40°③把③分别代入①②求出即可【详解】解:∵∠A 与∠B 的两边分别平行∴∠A+∠B =180°①∠A =∠B②∵∠解析:55或20【分析】根据平行线性质得出∠A+∠B =180°①,∠A =∠B②,求出∠A =3∠B ﹣40°③,把③分别代入①②求出即可.【详解】解:∵∠A 与∠B 的两边分别平行,∴∠A+∠B =180°①,∠A =∠B②,∵∠A 比∠B 的3倍少40°,∴∠A =3∠B ﹣40°③,把③代入①得:3∠B ﹣40°+∠B =180°,∠B =55°,把③代入②得:3∠B ﹣40°=∠B ,∠B =20°,故答案为:55或20.【点睛】本题考查平行线的性质,解题的关键是掌握由∠A 和∠B 的两边分别平行,即可得∠A =∠B 或∠A +∠B =180° ,注意分类讨论思想的应用.16.①③【分析】求出AB 长为定值P 到AB 的距离为定值再根据三角形的面积公式进行计算即可;根据运动得出PA+PB 不断发生变化∠APB 的大小不断发生变化【详解】解:∵AB 为定点∴AB 长为定值∴①正确;∵点A解析:①③【分析】求出AB 长为定值,P 到AB 的距离为定值,再根据三角形的面积公式进行计算即可;根据运动得出PA+PB 不断发生变化、∠APB 的大小不断发生变化.【详解】解:∵A 、B 为定点,∴AB 长为定值,∴①正确;∵点A ,B 为定点,直线l ∥AB ,∴P 到AB 的距离为定值,故△APB 的面积不变,∴③正确;当P 点移动时,PA+PB 的长发生变化,∴△PAB 的周长发生变化,∴②错误;当P 点移动时,∠APB 发生变化,∴④错误;故选A .【点睛】本题考查了平行线的性质,等底等高的三角形的面积相等,平行线间的距离的运用,熟记定理是解题的关键.17.对顶角相等AG 两直线平行同位角相等【分析】根据对顶角的定义可得再根据平行线的判定可得CH//AG 最后由两直线平行同位角相等即可证明【详解】解:证明:∵(已知)(对顶角相等)∴(等量代换)∴(AG )(解析:对顶角相等,AG ,两直线平行,同位角相等.【分析】根据对顶角的定义可得23∠∠=,再根据平行线的判定可得CH//AG,最后由两直线平行、同位角相等即可证明.【详解】解:证明:∵12∠=∠(已知)23∠∠=(对顶角相等)∴13∠=∠(等量代换)∴//CH (AG )(同位角相等,两直线平行)∴A BCH ∠=∠(两直线平行,同位角相等).故答案为:对顶角相等,AG ,两直线平行,同位角相等.【点睛】本题考查了对顶角的定义、平行线的性质和判定定理等知识,灵活应用平行线的性质和判定定理是解答本题的关键.18.假若a >b 则a2>b2【分析】a2大于b2则a 不一定大于b 所以该命题是假命题它的逆命题是若a >b 则a2>b2【详解】①当a =-2b =1时满足a2>b2但不满足a >b 所以是假命题;②命题若a2>b2则解析:假 若a >b 则a 2>b 2【分析】a 2大于b 2则a 不一定大于b ,所以该命题是假命题,它的逆命题是“若a >b 则a 2>b 2”.【详解】①当a =-2,b =1时,满足a 2>b 2,但不满足a >b ,所以是假命题;②命题“若a 2>b 2则a >b ”的逆命题是若“a >b 则a 2>b 2”;故答案为:假;若a >b 则a 2>b 2.【点睛】本题主要考查判断命题真假、逆命题的概念以及平方的计算,熟记相关概念取特殊值代入是解题关键.19.垂线段最短【分析】根据题干跳远落点视为一个点直尺垂直踏板边缘可理解为作垂线然后用数学语言描述出来即可【详解】根据题意可知答案为:垂线段最短【点睛】本题考查点到直线距离在生活中的实际应用注意在书写答案 解析:垂线段最短【分析】根据题干,跳远落点视为一个点,直尺垂直踏板边缘可理解为作垂线,然后用数学语言描述出来即可.【详解】根据题意,可知答案为:垂线段最短【点睛】本题考查点到直线距离在生活中的实际应用,注意在书写答案时,尽量用“数学化”的语言来描述.20.【分析】如图利用平行线的性质得出∠3=35°然后进一步得出∠4的度数从而再次利用平行线性质得出答案即可【详解】如图所示∵∴∴∠4=90°−∠3=55°∵∴∠2=∠4=55°故答案为:55°【点睛】本解析:55︒【分析】如图,利用平行线的性质得出∠3=35°,然后进一步得出∠4的度数,从而再次利用平行线性质得出答案即可.【详解】如图所示,∵//a b ,135∠=︒,∴335∠=︒,∴∠4=90°−∠3=55°,∵////a b c ,∴∠2=∠4=55°.故答案为:55°.【点睛】本题主要考查了平行线的性质,熟练掌握相关概念是解题关键.三、解答题21.(1)见解析;(2)见解析;(3)见解析;(4)9.5【分析】(1)根据网格特点以A 为锐角顶点,对边为1,临直角边为5构造格点直角三角形,即可解答;(2)根据网格特点以A 为锐角顶点,对边为1,临直角边为5构造格点直角三角形,即可解答;(3)根据平移的性质,向右8个单位长度描出对应顶点,即可画出A B C '''; (4)由矩形法即可求出三角形面积.【详解】解:(1)如图所示,AP 是BC 的垂线;P 为所求格点;(2)如图所示,1//AQ BC ,1Q 、2Q 为所求格点;(3)如图所示,A B C '''为所求;(4)A B C '''的面积11119544151432222=⨯-⨯⨯-⨯⨯-⨯⨯=, 故答案为:192. 【点睛】 此题主要考查了应用设计与作图,正确掌握相关性质以及结合网格画出对应点是解题关键.22.(1)见详解;(2)105°.【分析】(1)过点A、B作正北方向,再据方位角的含义画射线BX和AY,两射线之交点即是C 地;(2)记过点A的正北方向线与射线BX之交点为D,先求得∠CDA的度数,最后由三角形内角和为180°计算得∠ACB的度数.【详解】(1)如下图,第一步过B作m的平行线BS,以B为顶点作射线BX,使∠SBX=45°;第二步过A作m的平行线AN交BX于点D,以A为顶点作射线AY,使∠NAY=30°;则射线BX与射线AY的交点就是C地.(2)如上图,由C地在B地南偏东45°方向得∠SBX=45°∵SB∥m,AN∥m∴SB∥AN∴∠ADC=∠SBX=45°由C地在A地的北偏东30°方向得∠NAY=30°,∴∠ACB=180°-∠ADC-∠NAY=180°-45°-30°=105°.【点睛】此题考查方位角、平行线等知识,其中理解方位角正确画出图形是关键.23.54°【分析】根据平行线的性质,求得∠BEF的度数,继而根据角平分线的定义以及平行线的性质,即可得出∠2的度数.【详解】∵AB//CD,∴∠1+∠BEF=180°,∵∠1=72°,∴∠BEF=180°-72°=108°,∵EG平分∠BEF,∴∠BEG=12∠BEF=12×108°=54°,又∵AB∥CD,∴∠BEG=∠2,∴∠2=54°.【点睛】考查了平行线的性质以及角平分线的定义,解题关键是运用:两直线平行,同旁内角互补;两直线平行,内错角相等.24.(1)证明见解析;(2)100°;(3)12°.【分析】(1)根据平行线的判定及其性质即可求证结论;(2)过E 作//EK AB 可得//CF AB ∥EK ,再根据平行线的性质即可求解;(3)根据题意设7EBC x ∠=︒,则13ECB x ∠=︒,根据∠AED +∠DEB +BEC =180°,可得关于x 的方程,解方程即可求解.【详解】(1)证明:∵DE ∥BC ,∴ADE B ∠=∠,又∵∠BCF +∠ADE =180°,∴180BCF B ∠+∠=︒,∴//CF AB ,(2)解:过E 作//EK AB ,∵//CF AB ,∴//CF EK ,∵//EK AB ,40ABE ∠=︒,∴40BEK ABE ∠=∠=︒,∵//CF EK ,60ACF ∠=︒,∴60CEK ACF ∠=∠=︒,又∵BEC BEK CEK ∠=∠+∠,∴4060100BEC ∠=︒+︒=︒,答:BEC ∠的度数是100°,(3)解:∵BE 平分ABG ∠, 40ABE ∠=︒,∴40EBG ABE ∠=∠=︒,∴:7:13EBC ECB ∠∠=,∴设7EBC x ∠=︒,则13ECB x ∠=︒,∵DE ∥BC ,∴7DEB EBC x ∠=∠=︒,13AED ECB x ∠=∠=︒,∵180AED DEB BEC ∠+∠+∠=︒,∴137100180x x ++=,∴4x =,∴728EBC x ∠=︒=︒,又∵EBG EBC CBG ∠=∠+∠,∴CBG EBG EBC ∠=∠-∠,∴402812CBG ∠=-=︒,答:CBG ∠的度数是12°.【点睛】本题考查平行线的判定及其性质,解题的关键是熟练掌握平行线的判定及其性质的有关知识.25.(1)见解析;(2)AEM ∠,GEM ∠,DFN ∠,HFN ∠【分析】(1)根据平行线的性质和判定可以解答;(2)由已知及(1)的结论可知∠CFN=45°,然后结合图形根据角度的加减运算可以得到解答.【详解】(1)证明:∵//EM FN ,∴EFN FEM ∠=∠.∵EM 平分BEF ∠,FN 平分CFE ∠,∴2CFE EFN ∠=∠,2BEF FEM ∠=∠. ∴CFE BEF ∠=∠.∴//AB CD .(2)由(1)知AB //CD ,∴∠AEF+∠CFE=180°,∵∠AEF=2∠CFN=∠CFE ,∴∠AEF=∠CFE=90°,∴∠CFN=∠EFN=∠FEM=∠BEM=45°,∠BEG=∠CFH=∠DFE=90°,∴∠AEM=∠GEM=∠HFN=∠DFN=90°+45°=135°,∴度数为135°的角有:AEM ∠、 GEM ∠、 DFN ∠、 HFN ∠.【点睛】本题考查平行线的判定和性质及角平分线的综合运用,熟练掌握平行线的判定和性质定理及角平分线的意义是解题关键.26.55︒.【分析】先根据对顶角相等可得170BAE ∠=∠=︒,再根据平行线的性质可得110AED ∠=︒,然后根据角平分线的定义可得55BED ∠=︒,最后根据平行线的性质即可得.【详解】170∠=︒,170BAE ∴∠=∠=︒,//AB CD ,180110AED BAE ∴∠=︒-∠=︒, EB 平分AED ∠,1552BED AED ∴∠=∠=︒, 又//AB CD ,255BED ∴∠=∠=︒.【点睛】 本题考查了对顶角相等、平行线的性质、角平分线的定义,熟练掌握平行线的性质是解题关键.。
