【六年级寒假班讲义】第7讲:一次方程组(学生版)
第七章一次方程组课件

第七章一次方程组课件1. 引言本章将介绍一次方程组的概念及解法。
一次方程组是由一系列一次方程组成的集合,其中每个方程的未知数个数相同。
解一次方程组即找到使得所有方程成立的未知数的取值。
2. 一次方程组的表示方法一次方程组可以通过矩阵的形式进行表示。
假设一次方程组有n个方程和n个未知数,可以表示为以下形式:a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ = b₁a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ = b₂...aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ = bₙ其中a₁₁, a₁₂, …, aₙₙ为系数,x₁, x₂, …, xₙ为未知数,b₁, b₂, …, bₙ为等式右侧的常数。
3. 一次方程组的解法一次方程组可以通过消元法或代入法进行求解。
3.1 消元法消元法是通过不断进行等式的加减运算,将方程组转化为更简单的形式。
主要步骤如下:•将方程组写成增广矩阵的形式。
•选择一个主元,通常选择第一行第一列的元素作为主元。
•将主元所在的列的其他元素都变为0,通过对行进行加减运算实现。
•重复以上步骤,将所有主元都变为1,得到方程组的最简形式。
•根据最简形式可以得到方程组的解。
3.2 代入法代入法是通过将一个方程的解代入到其他方程中,逐步缩小未知数的范围,最终得到方程组的解。
主要步骤如下:•选择一个方程,将其中一个未知数用其他未知数表示出来。
•将该未知数的表达式代入到其他方程中,将方程组转化为只有一个未知数的方程。
•解这个未知数的方程,得到该未知数的值。
•将该未知数的值代入到其他方程中,重复以上步骤,得到其他未知数的值。
4. 一次方程组的解的分类一次方程组可能有无穷多个解、唯一解或无解。
根据方程组的系数、常数项及未知数的个数可以进行分类。
•当方程组的未知数个数大于方程个数时,一般会有无穷多解。
•当方程组的未知数个数等于方程个数,并且方程组的系数矩阵满秩,方程组有唯一解。
【六年级寒假班讲义】第8讲:一次方程(组)和一次不等式(组)章节复习(学生版)
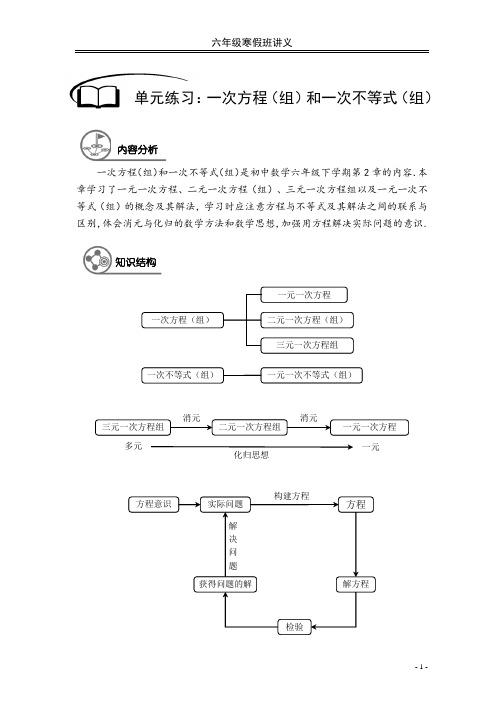
- 1 -一次方程(组)和一次不等式(组)是初中数学六年级下学期第2章的内容.本章学习了一元一次方程、二元一次方程(组)、三元一次方程组以及一元一次不等式(组)的概念及其解法,学习时应注意方程与不等式及其解法之间的联系与区别,体会消元与化归的数学方法和数学思想,加强用方程解决实际问题的意识.单元练习:一次方程(组)和一次不等式(组)内容分析知识结构一次方程(组)一次不等式(组)三元一次方程组一元一次方程二元一次方程(组) 一元一次不等式(组) 三元一次方程组一元一次方程二元一次方程组 消元消元多元一元化归思想实际问题检验解方程方程获得问题的解构建方程解决 问 题 方程意识- 2 -【练习1】 下列各式中,方程有( )个(1)633-+=-;(2)35x +=;(3)22ππ⨯=;(4)38a =;(5)7y =;(6)32p q -;(7)719nm +=;(8)1a a =+. A .3B .4C .5D .6【练习2】 下列各式中,一元一次方程有( )个(1)30x =;(2)437x y -=;(3)21303x -=;(4)()397y y --=;(5)23x -;(6)4x ≠. A .1B .2C .3D .4【练习3】 下列各式中,二元一次方程有( )个(1)2311x y -=;(2)23xy =-;(3)35m y+=;(4)25p q ->;(5)221x x +=;(6)21953m n -=.A .1B .2C .3D .4【练习4】 下列各式中,二元一次方程组有( )个(1)()()23111x y xy x y +=-⎧⎪⎨=+-⎪⎩;(2)31230x y x y +=⎧⎨-=⎩;(3)235x x y =⎧⎨+=-⎩;(4)3227x y x y -=+=+.A .1B .2C .3D .4【练习5】 二元一次方程组324526x y x y -=⎧⎨-=⎩的解是( )A .11x y =⎧⎨=-⎩B .112x y =-⎧⎪⎨=⎪⎩C .112x y =-⎧⎪⎨=-⎪⎩D .112x y =⎧⎪⎨=-⎪⎩【练习6】 如果0m n <<,那么下列各式中正确的是( )A .0.30.3m n <B .22m n <C .11m n <D .m n m n -<+选择题- 3 -【练习7】 下列判断中正确的是( )A .如果0x <,那么15x x <B .不等式35x ->-的解集是53x <C .如果113x <-,那么3x >-D .不等式组11x x >⎧⎨<⎩的解集为1x =【练习8】 若方程()2210a x bx c +++=是表示字母x 的一元一次方程,则( )A .12a =,0b ≠,c 为任意数 B .12a ≠,0b ≠,0c = C .12a =-,0b ≠,0c ≠D .12a =-,0b ≠,c 为任意数【练习9】 下列式子中一定正确的是( )A .23a a< B .a b a -< C .2a a >D .322x x-< 【练习10】 下列说法中错误的是( )A .方程ax b =的解是bx a=(0a ≠)B .如果ax b ->,则bx a<-(0a ≠)C .若2k =时,方程()22k x k -=无解D .8-是不等式32x ->一个解【练习11】 下列各对数值,是方程342x y +=的解的为( )A .012x y =⎧⎪⎨=-⎪⎩B .22x y =-⎧⎨=⎩C . 114x y =⎧⎪⎨=-⎪⎩D . 21x y =-⎧⎨=⎩【练习12】 某运输队运煤,第一天运了总量的27,第二天运煤恰好是第一天的23,还剩14 吨,设一共运煤x 吨,则可列出方程( )A .22214773x x x +⨯=-B .221473x x x ++=C .222114737x x x ⎛⎫+-=- ⎪⎝⎭D .22214773x x x +÷+=【练习13】 学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3 : 2,求两种球各有多少个?若设篮球有x 个,排球有y 个,则根据题意得到的方程组是( ) A .2332x y x y =-⎧⎨=⎩B .2332x y x y =+⎧⎨=⎩C .2323x y x y =-⎧⎨=⎩D .2323x y x y =+⎧⎨=⎩【练习14】 已知不等式组00x a x b -<⎧⎨-<⎩的解集为x a <,则不等式组00x a x b +>⎧⎨+>⎩的解集为( )A .x a <-B .x a >-C .x b >-D .x b <-- 4 - 【练习15】 323x y+=的正整数解的个数为( )个A .1B .2C .3D .4【练习16】 观察下列方程组,无解的是( )A .61x y x y -=⎧⎨+=-⎩B .52210x y x y -=-⎧⎨-=⎩C .5229x y x y -=⎧⎨+=⎩D .423x y x y +=⎧⎨-=⎩【练习17】 已知不等式组5x x m >⎧⎨>⎩的解集为5x >,则m 的取值范围是( )A .5m >B .5m ≥C .5m <D .5m ≤【练习18】 已知方程组35223x y k x y k+=+⎧⎨+=⎩,其中x 是y 的2倍,则k 的值是( )A .72-B .72C .0D .以上都不对【练习19】 如果关于x 的不等式32x a ->的所有正整数解之和为6,则a 的取值范围为( ) A .5a ≥-B .3a <-C .53a -<<-D .53a -≤<-【练习20】 如果关于x 的不等式组30310x m x m -->⎧⎨-+<⎩无解,那么m 的取值范围是( )A .2m <B .2m ≤C .2m >D .2m ≥【练习21】 若3350m x ---=是一元一次方程,则m =______.【练习22】 把方程5239x y -+=化成用含x 的式子表示y 的形式,得______________.【练习23】 用不等式表示:2x y+减去()21x --所得的差是非负数________________. 填空题- 5 -【练习24】 用不等号填空,并说明不等式变形过程.(1)若x y >,则4x -______4y -; (2)若235x +≤-,则3x ______7-; (3)若1233x x -≥-,则x ______2; (4)若x y >,则6x -______6y -; (5)若x y >,则2x -______2y -; (6)若x y >,0m >,则mx ______my ; (7)若m n ≥,20k +<,则mk ______nk .【练习25】 解集32x -≤<中的整数解为__________________.【练习26】 不等式组340731x x +>⎧⎨-≥-⎩的解集为____________________.【练习27】 判断:(1)如果a b >,那么3232a b ->-;( ) (2)如果a b <,那么22a b <;( ) (3)如果22a b >,那么a b >;( ) (4)如果a b >,那么a b >;( ) (5)如果1a >,那么a 比1a大;( ) (6)如果5a >,那么55a a -=-;( ) (7)如果144m <-,那么1m <-;( )(8)如果x y >,那么()()2211m x m y -->--.( ) 【练习28】 若0a b +<,且0ab >,则a ______0,b ______0.- 6 - 【练习29】 满足不等式()10484x x ++≤的最大整数解是_______.【练习30】 当x ______时,52x -的值是正的,此时最小的整数x =_______.【练习31】 如果43x y =⎧⎨=-⎩是方程436x ay -=的一个解,则a =______.【练习32】 如果3235351m n m n x y +--++=-是二元一次方程,那么m =______,n =_______.【练习33】 若357x -+=,则x =______.- 7 -【练习34】 若:5:3x y =,且x 与y 的和是10,则x =______,y =______.【练习35】 已知1y =是方程()1223m y y --=的解,那么关于x 的方程 ()()3225m x m x --=-的解是______.【练习36】 若关于x 、y 方程组352278x y ax y a -=⎧⎨+=-⎩的解互为相反数,则a =______.【练习37】 如果()222303x y x ⎛⎫+++-= ⎪⎝⎭,那么2016y =______.- 8 - 【练习38】 甲、乙两班共有88名学生,若从乙班调25人到甲班,则甲班人数是乙班人数的3倍,设甲班x 人,乙班y 人,可列出方程组_______________________,并解得甲班有______人,乙班有______人.【练习39】 有一个两位数,个位数字和十位数字之和是9,且这个两位数不大于63,求这个两位数.可设这个两位数的个位数字为x ,根据题意,可列不等式 ________________________,最后这个两位数为_______________________.【练习40】 若关于x 的不等式()22a x a +>+的解集是1x <,则a 的取值范围是______.- 9 -【练习41】 解方程:(1)1071253x x x +=--;(2)()()160%2180%22x x +-+=;(3)111257918643x ⎧⎫⎡+⎤⎛⎫+-+=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭; (4)1.88 1.5350.401.220.3x x x -----=.【练习42】 解不等式:(1)()23213x x +-≤;(2)()30%151%x x +<+;(3)()()11221225x x x ⎡⎤-+≤-⎢⎥⎣⎦; (4)()()0.20.30.40.50.10.21110.030.066x x --->+.解答题【练习43】解不等式组:(1)()()3241353324x xx x⎧-->-⎪⎨+≤+⎪⎩;(2)()210381274332xxxxx⎧---≤-⎪⎪⎨⎪-<+⎪⎩;(3)13222364553522x xx xx x⎧+>+⎪⎪+>+⎨⎪⎪-<-⎩;(4)()1226323112184xxx xx x⎧+>⎪⎪⎪+≥+⎨⎪+-⎪-<-⎪⎩.【练习44】解方程组:(1)521347a ba b+=-⎧⎨+=⎩;(2)5.3 4.7804.75.320x yx y+=⎧⎨+=⎩;- 10 -- 11 -(3)34135353x y z x y z x y z +-=⎧⎪-+=⎨⎪+-=⎩;(4)2636315764949x y z x y z x y z ++=⎧⎪++=⎨⎪-+=⎩.【练习45】 关于x 的方程()143321223x x x a x x +----=-的解是最小的质数的倒数,求a 的值.【练习46】 解方程:2015122320152016x x x +++=⨯⨯⨯.【练习47】若关于x、y的方程组2323ax byx y-=⎧⎨-=-⎩和3424y xax by-=⎧⎨+=-⎩有相同的解,求a、b的值.【练习48】甲、乙两人同时求7mx ny-=的整数解,甲求出一组解为34xy=⎧⎨=⎩,而乙把7mx ny-=中的7看成1,求出一组解为12xy=⎧⎨=⎩,求m、n的值.【练习49】已知关于x、y的方程组321431x y px y p+=+⎧⎨+=-⎩满足x > y,求p的取值范围.【练习50】解方程组:252821126x yy zz uu x+=⎧⎪+=⎪⎨+=⎪⎪+=⎩.- 12 -。
六年级寒假班第7讲一次方程组-学生版

一、引入经过前几次的学习,我们已经掌握了一元一次方程的解法,现在我们要学习一下一次方程组的解法。
一次方程组是一组由一次方程组成的方程集合,它有多个未知数和多个方程。
二、复习回顾一元一次方程的解法,我们要通过逆运算将未知数从方程中解出来。
例如,我们要解方程2x+3=9,我们可以将方程两边都减去3,得到2x=6,然后再让2x除以2,得到x=3,找出了方程的解x=3三、解一次方程组的方法1.平移消元法平移消元法是解一次方程组中常用的方法之一、它的基本思想是通过逐步消去未知数,使方程组变得简单。
我们通过一个例子来说明。
例题:解方程组2x+y=53x+2y=8解:首先我们可以通过消元法将方程组变得简单。
(1)将第二个方程的两边同时乘以2,得到方程6x+4y=16(2)然后将第一个方程的两边同乘以4,得到方程8x+4y=20。
(3)将第二个方程的两边减去第一个方程的两边,得到方程2x=4,解得x=2(4)将x的值代入第一个方程,得到2x+y=5,代入x=2,得到2*2+y=5,化简得到y=1所以,原方程组的解为x=22.代入消元法代入消元法也是解一次方程组的常用方法之一、它的基本思想是通过将一个方程的解代入另一个方程,逐步消去未知数。
我们通过一个例子来说明。
例题:解方程组3x+2y=7x-y=5解:我们可以将第二个方程化简成x=y+5,然后将x的值代入第一个方程,得到3(y+5)+2y=7,化简得到5y+15=7,解得y=-2将y的值代入第一个方程,得到3x+2(-2)=7,化简得到3x-4=7,解得x=11所以,原方程组的解为x=11四、练习题1.解方程组2x+y=8x-3y=1解:将第一个方程的两边同乘以3将第二个方程的两边同乘以2将第一个方程的两边减去第二个方程的两边,得到方程4x+9y=22将x的值代入第一个方程,得到2*4+y=8所以,原方程组的解为x=42.解方程组x+3y=52x-2y=2解:将第二个方程的两边同乘以3将第一个方程的两边同乘以2将第一个方程的两边减去第二个方程的两边,得到方程4x=-4将x的值代入第一个方程,得到-1+3y=5所以,原方程组的解为x=-13.解方程组3x-y=82x+y=3解:我们可以将第一个方程化简成y=3x-8,然后将y的值代入第二个方程,得到2x+(3x-8)=3,化简得到5x=11将x的值代入第一个方程,得到3*(11/5)-y=8所以,原方程组的解为x=11/5五、总结通过学习本次课程,我们掌握了解一次方程组的两种方法:平移消元法和代入消元法。
六年级寒假班第7讲一次方程组-教师版

第七讲一次方程组一、知识概述1.方程组的定义:方程组是由若干个方程组成的集合。
2.方程组的解:方程组的解是满足所有方程的变量值的组合。
3.一次方程组:方程组中所有方程的最高次数都是1的方程组叫做一次方程组。
4.一次方程组的解的个数:一次方程组的解的个数有以下几种情况:①有无穷多个解:当方程组中的方程是相互依赖的时候,方程组会有无穷多个解。
②有唯一解:当方程组中的方程是互相独立的时候,方程组会有唯一解。
③无解:当方程组中的方程出现矛盾的时候,方程组会无解。
二、课堂教学设计1.引入新知识:教师可以通过提问的方式,帮助学生回顾方程和方程解的概念,引出方程组的概念。
例如:方程是什么?方程有解吗?是否可能有多个解?2.讲解一次方程组的概念:通过举例子的方式,讲解一次方程组的概念。
例如:小明有3个苹果和4个梨,小红有2个苹果和5个梨。
请问小明和小红分别有几个苹果和几个梨?3.讲解一次方程组的解的个数:通过解析的方式,讲解一次方程组的解的个数。
例如:一个一次方程组有唯一解的条件是什么?为什么会有无穷多个解?为什么会无解?4.例题讲解:通过具体的例题,让学生熟悉一次方程组的解题思路和方法。
例如:小明有5个苹果和2个橘子,小红有3个苹果和4个橘子,苹果和橘子的总数一共有多少个?5.练习题:布置一些练习题,让学生独立完成。
例如:小明有若干个苹果和橘子,苹果的数量是橘子的3倍,若苹果的数量减去3等于橘子的数量,求苹果和橘子的总数。
6.拓展思考:引导学生思考更复杂的一次方程组问题,培养学生的分析和解决问题的能力。
例如:班级里有男生和女生,男生人数是女生人数的2倍,班级总共有30个学生,男生人数是多少?三、教学重点和难点教学重点:一次方程组的概念、解的个数和解题方法。
教学难点:引导学生理解一次方程组解的个数。
四、教学板书设计一次方程组解的个数:无穷多个解、唯一解、无解解题方法:代入法、消元法五、教具、教材准备教具:黑板、彩笔、教材教材:《小学数学》第六册六、教学过程1.复习导入:复习方程和方程解的概念。
六年级辅导讲义--一次方程组和一次不等式组

学而优教育学科教师辅导讲义就读学校年级授课次数学员姓名辅导科目数学学科教师吴老师课题第六章一次方程(组)和一次不等式授课日期授课时段教学目的1、方程的意义;一次方程的意义;一元一次方程的解法;不等式的意义及一元一次不等式解法;2、二元一次方程组及解法、三元一次方程组的解法;一元一次不等式(组)的解法;3、一次方程(组)的应用教学内容1、如果某未知数所取的某个值能使方程左右两边值相等,这这个未知数的值叫做原方程的解。
使方程成立的未知数的值叫作方程的解.方程的解的集合,叫作方程的解集.解方程就是求出方程的解集.2、只含有一个未知数且未知数的次数是一次的方程叫做一元一次方程(运用等式的性质及运算性质求解)。
任何一个一元一次方程总可以化为ax=b(a≠0)的形式,这是一元一次方程的标准形式(最简形式)。
3、解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项,化为最简形式ax=b;(5)方程两边同除以未知数的系数,得出方程的解.4、一元一次方程的应用一元一次方程的应用(根据题意中的数量关系,列方程解答;步骤:设、列、解、检、答)。
5、不等式及其性质1)用>,<,≥,≤,≠表示的关系式叫做不等式.2)不等式性质1:不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变。
3)不等式性质2:不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变。
4)不等式性质3:等式的两边同时乘以(或除以)同一个负数,不等式的方向改变。
6、一元一次不等式的解法只含有一个未知数且未知数的次数是一次的不等式叫做一元一次不等式。
在含有未知数的不等式中,能使不等式成立的未知数的值,叫做不等式的解。
不等式的解有无数个,不等式的解的全体叫做不等式解集。
求不等式的解集的过程叫做解不等式。
解一元一次不等式的一般顺序:(1)去分母(运用不等式性质2、3);(2)去括号;(3)移项(运用不等式性质1);(4)合并同类项;(5)将未知数的系数化为1 (运用不等式性质2、3);(6)有些时候需要在数轴上表示不等式的解集。
第6节---一次方程(组)

代 入 法
定义
防错提 醒 加 减 法
两个二元一次方程中同一未知数的系数相反或相等时,将 两个方程的两边分别相加或相减,从而消去这个未知数, 得到一个一元一次方程,这种求二元一次方程组的解的方 法叫做加减消元法,简称加减法
► 类型之四 二元一次方程组的解法 命题角度: 1.代入消元法; 2.加减消元法.
归类示例
► 类型之一 等式的概念及性质 命题角度: 1. 等式及方程的概念; 2. 等式的性质. 例1 如图①,在第一个天平上,砝码A 的质量等于砝码B 加上砝码C 的质量;如图②,在第二个天平上,砝码A 加上 砝码B的质量等于3个砝码C 的质量.请你判断:1个砝码A 2 与________ 个砝码C 的质量相等.
用方程或方程组解决实际问题,关键是先 分析出实际问题中的等量关系,一个方程需 要一个等量关系,方程组则需要两个等量关 系.
第6 讲 第7 讲 第8 讲 第9 讲 第10讲 第11讲
一次方程(组) 不等式(组) 分式方程 一元二次方程 方程(组)的综合应用 不等式(组)的综合应用
ቤተ መጻሕፍቲ ባይዱ
知能目标:1.了解解方程和方程的解的意义; 2.熟练掌握一次方程(组)的解法; 3.会利用方程(组)的解求方程(组)中的 待定系数; 4.会根据具体问题中的数量关系列出简单的 一次方程(组).
考点7
常见的几种方程类型及等量关系
基本量之间 路程=速度×时间 的关系 行程 相遇问题 全路程=甲走的路程+乙走的路程 问题 若甲为快者,则被追路程=甲走的路 追及问题 程-乙走的路程 流水问题 v 顺=v 静+v 水,v 逆=v 静-v 水 基本量之间 的关系 工作总量 工作效率= 工作时间
工程 (1)甲、乙合做的工作效率=甲的工作 问题 其他常用关 效率+乙的工作效率;(2)通常把工作 系量 总量看作“1”
第7讲六年级数学寒假教案--一元一次方程初步1.docx

六年级冲刺班数学讲义第7讲:一元一次方程初步复习巩固与错题再现一、甲、乙、丙三人一起买了9个面包,平分着吃,甲拿出了5个面包的钱,乙拿出了4个面包的钱,丙没有带钱,吃完一算,丙应该拿出6元钱,那么甲要收回多少钱?二、一个人上山每小时行驶4千米,下山按原路返回每小时行6千米,求他上下山的平均速度?三、甲数是乙、丙两数平均数的号,甲数是甲、乙、内三个数的平均数的儿分之儿?学习前言我们在之前已经学习过了简易方程的解法,这一类方程我们都是按照等式的性质来解的。
这里我们讲学习较为复杂的方程---------------- 元一次方程,实际上我们以前学习的方程都是一元一次方程,只是比较简单而已。
由于升学考试题目的多变性和复杂性,很多情况我们用列一元一次方程来解决问题会更加容易。
所以,同学们很有必要在升学考试前系统地学习下一元一次方程, 现在同学们认真地跟张老师一起好好学学吧!一元一次方程的一些概念正数与负数:像1,15,丄,1.35,100, 1.4......这样的数叫做正数。
像-1,-1,-0.79-100 (35)这样的数叫做负数,它的意义与正数的意义刚好相反,比如:“向前走10米计作+10, 那么后退10米就是T0 了”,再比如“今天的温度是8摄氏度计作+8,那么零下5摄氏度就是-5 了”……一元一次方程:像2兀+ 7 = 12,3兀-7 = 11,3/-7 = 5-兀,……这样的方程叫做一元一次方程。
一元一次方程的特点:只含有一个未知数,并且未知数的次数是一次,也就是说方程中不可能含有像:-,x2,x3……的式子,否则我们现在是没有办法解出来的。
通常在一元一次方程中会含有分母,括号,等号的两边都含有X等特点。
解一元一次方程的基本步骤*去分母:去分母时,方程两边乘以各分母的最小公倍数,如2, 3, 4的最小公倍数是:______________ ・去分母时,每一项都要乘以最小公倍数,特别是不含分母的项。
一次方程(组)教案

D日解方D D D D D D D D D D D D D D D D D D DDDDDD D D D D D D D DD DDDDD D D D D D D D D D D D D D D D D D D DDDDDD D D D D D D D D D DDDDD D D D D D D D D D D D D D D D D D D DDDDDDDD D D D D D D D D DDDDDDD DDDDDDD DDDDDDD概念:如果未知数所取的某个值能使方程左右两边的值相等,那么这个未知数的值叫做方程的解。
求方程解的过程叫做解方程口回顾:等式的性质DD等式两边同时加上(或减去)同一个数或同一个含有字母的式子,所得的结果仍是等式口DDD等式的性质DD等式两边同时乘以同一个数(或除以同一个不为零的数),所得的结果仍是等式口一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项口D D判断对错:DDDDDDDD,移项得口DDDDDDDDDDDDDDDDD,移项得KDDDDDDDDDDDDDDDD-DDDDDD,移项得DDDDDDDDDDDDDDDDDDDQ解方程:淬竺兀刈XXXUU解:去分母,得Dx=2(4x+5)+32去括号,得x=8x+10+32移项、化简,得7x=-42两边同时除以x的系数7,得x=-6所以,x=-6是原方程的解•解一元一次方程得一般步骤是:DDD去分母;DDD去括号;DDD移项;DDD化成DDD(D^D)的形式;UDD两边同时除以未知数的系数,得到方程的解口飘DDX练_一练:xxxxx xxxxxgxxXXDDDDD一元一次方程的应用:DDD某面粉仓库存放的面粉运出D%后,还剩余DDD千克,这个仓库原来有多少面粉?□D.本题中给出的已知量和未知量各是什么?DDD剩余面粉的重量:DDD千克口已运出面粉的百分比:DDDD□•已知量与未知量之间存在着怎样的等量关系?□□□□□□□□原来重量□运出重量□剩余重量口DD.若设原来面粉有口千克,则运出面粉可表示为多少千克?利用上述相等关系,如何列方程?D解:设原来有D千克面粉,那么运出了D千克口D由题意,得DDDD^DDDDDDDDDDDDDDDDDDD口所以,仓库原来有DDD千克面粉。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次方程组内容分析一次方程组是初中数学六年级下学期第2章第4节的内容.本讲主要讲解二元一次方程的概念,二元一次方程组和三元一次方程组的概念及其解法,同学们需要多多练习,做到能够灵活快速地解方程组.知识结构模块一:二元一次方程知识精讲1、二元一次方程含有两个未知数的一次方程叫做二元一次方程.2、二元一次方程的解使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.3、二元一次方程的解集二元一次方程的解有无数个,二元一次方程的解的全体叫做这个二元一次方程的解集.- 1 -- 2 -【例1】 下列方程中,哪些不是二元一次方程?并说明理由. (1)53x x +=;(2)239x y -=; (3)2x m +=; (4)413yx +=; (5)20xy +=;(6)321x y+=; (7)221x x +=-;(8)24x y z ++=.【例2】 若方程324235a b x y -+-=是关于x 、y 的二元一次方程,则a =______,b = ______.【例3】 以下各组数,______________(填序号)是方程34x y -=的解. (1)11x y =⎧⎨=⎩;(2)22x y =⎧⎨=⎩;(3)17x y =-⎧⎨=-⎩;(4)35x y =⎧⎨=-⎩.【例4】 已知x = 3,y = 5是关于x 、y 的方程31x ky -=一个解,求k 的值.【例5】 已知二元一次方程534x y -=-.(1)用含x 的代数式表示y ,y =______; (2)用含y 的代数式表示x ,x =______;(3)当1x =时,y =______;当1x =-时,y =______; (4)当2y =-时,x =______;当0y =时,x =______.【例6】 如果31n ax y +=是关于x 、y 的二元一次方程,求n 和a 的取值范围.例题解析- 3 -【例7】 若530x y -=,且0x ≠,那么3443x yx y-=+______.【例8】 求方程74100x y +=的正整数解.【例9】 某人只带2元和5元两种钱币,他要买一件27元的商品,若要恰好付清,请问他的付款方式共有哪几种?1、 二元一次方程组有几个方程组成的一组方程叫做方程组.如果方程组中含有两个未知数,且含未知数的次数都是一次,那么这样的方程叫做二元一次方程组. 2、 二元一次方程组的解在二元一次方程组中,使每个方程都适合的解,叫做二元一次方程组的解.模块二:二元一次方程组及其解法知识精讲3、代入消元法通过“代入”消去一个未知数,将方程组转化为一元一次方程,这种解法叫做代入消元法,简称代入法.4、加减消元法通过两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程,这种解法叫做加减消元法.【例10】以下方程组:(1)23xy=⎧⎨=⎩;(2)323xx y=⎧⎨+=⎩;(3)2323x yx y+=⎧⎨+=⎩;(4)423x yxy-=⎧⎨+=⎩;(5)23x yy z+=⎧⎨-=⎩;(6)34322x yx yx y-=⎧⎪+=⎨⎪-=⎩,哪些是二元一次方程组?【例11】判断下列两组数值是否是方程组34213y xx y-=⎧⎨=-⎩的解:(1)11xy=-⎧⎨=⎩;(2)35xy=-⎧⎨=-⎩.【例12】方程组2521x yx y+=⎧⎨-=⎩的解______是方程25x y+=的解;反之,方程25x y+=的解______是方程组2521x yx y+=⎧⎨-=⎩的解(填“一定”、“一定不”或“不一定”).例题解析- 4 -【例13】用代入消元法解下列方程组.(1)21234x yx y=+⎧⎨-=⎩;(2)54365x yx y+=⎧⎨-=⎩;(3)32222m nm n+=⎧⎨-=-⎩.【例14】用代入消元法解下列方程组.(1)2311543x yx y-=-⎧⎨-=-⎩;(2)122213yx yyx-⎧=-⎪⎪⎨+⎪=+⎪⎩.【例15】用代入消元法解下列方程组.(1)()()()()321824x y x yx y x y⎧++-=⎪⎨+--=-⎪⎩;(2)1311116411x yx y⎧⎛⎫+-=⎪⎪⎪⎝⎭⎨⎛⎫⎪+-=⎪⎪⎝⎭⎩.- 5 -【例16】用加减消元法解下列方程组.(1)62x yx y+=⎧⎨-=⎩;(2)231567x yx y+=⎧⎨-=⎩;(3)7423624x yx y+=⎧⎨-=⎩.【例17】选用适当的方法解下列方程组.(1)25342x yx y-=⎧⎨+=⎩;(2)633594x yx y-=-⎧⎨-=⎩;(3)3554235346x yx y--⎧+=⎪⎪⎨--⎪+=⎪⎩;(4)()()()31222331m nn m⎧-=+⎪⎨⎪+=-⎩.- 6 -- 7 -【例18】 若2211a b a b x y -+--=是二元一次方程,求a 、b 的值.【例19】 解方程组:201520176047201720156049x y x y +=⎧⎨+=⎩.【例20】 已知方程组451x y ax by -=⎧⎨+=-⎩和方程组34186218ax by x y -=⎧⎨+=⎩有相同的解,求a 、b 的值.【例21】 若方程组34412322x y m x y m +=-⎧⎪⎨-=+⎪⎩的解满足0x y +=,求m 的值.- 8 - 三元一次方程组二元一次方程组一元一次方程消元消元1、 三元一次方程组如果方程组中含有三个未知数,且含有未知数的项的次数都是一次,这样的方程组叫做三元一次方程组. 2、 解三元一次方程组的思想【例22】 下列方程组中,哪些是三元一次方程组?(1)623414253x y z x y z x y z ++=⎧⎪-+=⎨⎪+-=⎩; (2)234x y y z z x +=⎧⎪+=⎨⎪+=⎩;(3)231x y z =⎧⎪=⎨⎪=⎩;(4)3252x y z x y ++=⎧⎨+=⎩; (5)16x yz =⎧⎨=⎩; (6)2324x y z y z x ++=⎧⎨++=⎩.【例23】 解方程组:1425x x y x y z =⎧⎪+=⎨⎪-+=⎩.模块三:三元一次方程组及其解法知识精讲例题解析【例24】判断下列两组数值是否是方程组52621212x yy zx z-=⎧⎪-=-⎨⎪+=⎩的解:(1)35xyz=⎧⎪=-⎨⎪=-⎩;(2)225xyz=⎧⎪=⎨⎪=⎩.【例25】解方程组:(1)15321341813x y zx y zz-+=⎧⎪+-=-⎨⎪=⎩;(2)625114x y zx y zx y++=⎧⎪++=⎨⎪=⎩.【例26】解方程组:(1)261218x y zx yx z y++=⎧⎪-=⎨⎪+-=-⎩;(2)32522642730x y zx y zx y z++=⎧⎪--=⎨⎪+-=⎩.- 9 -【例27】解方程组:(1)344635511x y zx y zy z++=⎧⎪-+=-⎨⎪+=⎩;(2)2338456632456x y zx y zx y z++=⎧⎪++=⎨⎪++=⎩.【例28】解方程组:(1)14719x yy zx z+=-⎧⎪+=-⎨⎪+=⎩;(2)1151x y zy z xz x y+-=⎧⎪+-=⎨⎪+-=⎩.【例29】解方程组:12323434545151251532x x xx x xx x xx x xx x x++=⎧⎪++=⎪⎪++=-⎨⎪++=-⎪⎪++=⎩.- 10 -【习题1】 以下方程(1)320x xy y -+=;(2)3x y =;(3)4a b =;(4)5263y m +=; (5)23240x y -+=,其中二元一次方程有______个【习题2】 在方程511x ay -=中,如果12x y =⎧⎨=⎩是它的一个解,则a =______.【习题3】 已知一个二元一次方程,它的一个解为74x y =⎧⎨=⎩,则这个方程可以是_________________.【习题4】 将下列方程变形为用含y 的代数式表示x .(1)5210x y ++=; (2)492863x y -=; (3)25136yx-=.【习题5】 如果312327m n x y +++=是二元一次方程,那么m =______,n =______.随堂检测【习题6】 解方程组:(1)252138x y x y +=-⎧⎨+=⎩; (2)103178516x y x y +=⎧⎨-=-⎩;(3)()62324x y x y x y x y +-⎧+=⎪⎨⎪+-+=-⎩;(4)27323163213x y z x y z x y z ++=⎧⎪++=⎨⎪++=⎩.【习题7】 若2211a b a b x y -+--=是二元一次方程,求a 、b 的值.【习题8】 已知二元一次方程组45ax by bx ay +=⎧⎨+=⎩的解是21x y =⎧⎨=⎩,求a + b 的值.【习题9】方程组42132x yx y k-=⎧⎨+=⎩的解中x与y相等,求k的值.【习题10】已知方程组4360270x y zx y z--=⎧⎨+-=⎩,且0z≠,求345x y zx y z++--的值.【作业1】下列说法中,不正确的个数是()个(1)方程x = y不是二元一次方程;(2)二元一次方程21x y-=的解集是23xy=⎧⎨=⎩;(3)23xy=⎧⎨=⎩是二元一次方程21x y-=的一个解;(4)由于方程21x y-=有无数个解,所以任何一对x,y的值都是该方程的解.A.1个B.2个C.3个D.4个【作业2】已知一个二元一次方程5611x y-=,当x = 4时,y =______,当y = 4时,x =______,这个方程有______组解.课后作业【作业3】 已知方程51y x -=,请你在设计一个方程________________,使得这两个方程的公共解是253x y ⎧=⎪⎨⎪=⎩.【作业4】 若方程()23231a x b y -+-=-是二元一次方程,则a =______,b ______.【作业5】 若方程25x y +=有一组解中y 的值是x 的值的4倍,则x =______,y =______.【作业6】 解方程组:(1)231763172357x y x y +=⎧⎨+=⎩; (2)21243y x x x y -++==;(3)12334437x y x y -+⎧=⎪⎨⎪-=⎩; (4)3521545352x y z y z x z x y -+=⎧⎪-+=⎨⎪+-=-⎩.【作业7】已知()223320x y x y+-+-=,求x和y的值.【作业8】方程45100m n+=有______组自然数解.【作业9】已知方程组5354x yax y+=⎧⎨+=⎩与2551x yx by-=⎧⎨+=⎩有相同的解,求a、b的值.【作业10】已知方程组452x y mx y m+=+⎧⎨-=+⎩的解为正数,求m的取值范围.。
