四川省宜宾市叙州区第一中学校2020-2021学年高三上学期第一次月考数学(理)试题
2020-2021学年四川省宜宾市叙州区第一中学校高一上学期第一次月考数学试题(解析版)
（2）对于（1）中的函数 和函数 ，若对于任意的 ，总存在 ，使得 成立，求实数 的值.
【答案】（1）递减区间为 ，递增区间为 ，值域为 ；（2）
【解析】（1）把函数解析式中的分母变形为 ，利用分式的计算公式，函数解析式变形为 ，用 进行换元，得到新解析式为 这样根据已知所给的函数性质可以求出函数 的单调区间和值域.
若 （1） ，则在区间 上， ，在区间 上， ，
又由 为奇函数，则在区间 上， ，在区间 上， ，
则 即 ，即 或 或 ，
解可得： ，即不等式 的解集为 ， ；
故答案为： ．
【点睛】
本题考查函数的奇偶性与单调性的综合应用，涉及不等式的解法，属于中档题．
三、解答题
17．设集合A={a2，a＋1，-1}，B={2a－1，|a－2|，3a2＋4}，A∩B={-1}，求实数a的值．
∴函数f（x）的图象关于x=1对称，则f（x）在∈（1，+∞）上单调递增，
∴f（-1）=f（3）>f（2）＞f（1）
即f（-1）＞f（2）＞f（1）
故选B．
【点睛】
本题考查函数的对称性及单调性的应用，解题的关键是函数性质的灵活应用．
12．定义在 上的函数 满足 ， ， ，且当 时，有 ，则 的值为（）
A． B．
C． D．
【答案】B
【解析】由已知得函数f（x）图象关于x=1对称且在（-∞，1]上单调递减，在（1，+∞）上单调递增，从而可判断出大小关系.
【详解】
解：∵当x1，x2∈（-∞，1]（x1≠x2）时有（x1-x2）（f（x1）-f（x2））＜0，
∴f（x）在（-∞，1]上单调递减，
【精准解析】四川省宜宾市叙州区第一中学校2020届高三下学期第一次在线月考数学(理)试题
1
AB
1
AC
BO
BA
4 AO
4 3
AB
1
AC
44
所以
OAOB
AOBO
1 4
AB
1 4
AC
3 4
AB
1 4
AC
-2-
=
3
AB
2
1
AB
AC
1
2 AC
16
8
16
3 22 1 2 2 cos 60 1 22
16
8
16
3 4
故选 B
【点睛】本题考查向量的运算，解题的关键是找到一组基底，将所求向量用基底表示，然后
6
2
26
又因为 ＞0，所以 =
6
故选 B
【点睛】本题主要考查三角函数的图像平移变换，解题的关键是找到平移后的解析式，再结
【答案】B
【解析】
【分析】
先根据指数函数、对数函数的知识得到 a, b, c 所在的范围，进而可得 a, b, c 的大小关系．
【详解】由题意得
a
20.1
1, b
ln
1 2
0, c
log3
2
0,1
，
∴a c b．
故选 B．
【点睛】比较指数幂和对数的大小时，常用的方法是根据指数函数、对数函数的性质得到各
6.已知曲线
x2 a2
Hale Waihona Puke y2 b21（a0，b
0 ）的一条渐近线经过点 (
2,
6) ，则该双曲线的离
心率为（ ）
A. 2
B. 2
C. 3
D. 3
【答案】A
【解析】
四川省宜宾市叙州区第一中学2020届高三数学上学期期中试题理
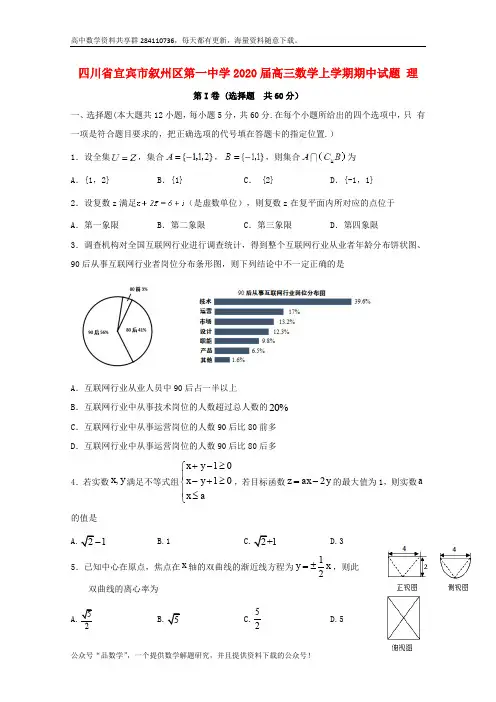
四川省宜宾市叙州区第一中学2020届高三数学上学期期中试题理第I卷 (选择题共60分）一、选择题(本大题共12小题，每小题5分，共60分.在每个小题所给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置.）1．设全集，集合，，则集合为A．{1，2} B．{1} C． {2} D．{-1，1}2．设复数z 满足（是虚数单位），则复数z在复平面内所对应的点位于A．第一象限B．第二象限C．第三象限D．第四象限3．调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图，则下列结论中不一定正确的是A．互联网行业从业人员中90后占一半以上B．互联网行业中从事技术岗位的人数超过总人数的20%C．互联网行业中从事运营岗位的人数90后比80前多D．互联网行业中从事运营岗位的人数90后比80后多4．若实数,x y满足不等式组1010x yx yx a+-≥⎧⎪-+≥⎨⎪≤⎩，若目标函数2z ax y=-的最大值为1，则实数a的值是1 B.1D.35．已知中心在原点，焦点在x轴的双曲线的渐近线方程为12y x=±，则此双曲线的离心率为C.52D.56．某几何体的三视图如图所示，则该几何体的体积为 A ．16163π-B ．32163π-C ．1683π- D ．3283π- 7．数列{}n a 为等比数列，且2113724a a a π+=，则212tan()a a =A．B． C．-D8．直线1y kx =+与曲线()1f x a nx b =+相切于点(1,2)P ,则a b += A.1B.4C.3D.29．将3名教师和3名学生共6人平均分成3个小组，分别安排到三个社区参加社会实践活动，则每个小组恰好有1名教师和1名学生的概率为 A ．13B ．25C ．12D ．3510．设函数()()sin f x A x =+ωϕ（,,A ωϕ是常数，0,0A ω>>).若()f x 在区间,62ππ⎡⎤⎢⎥⎣⎦上具有单调性，且2236f f f πππ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则()f x 的最小正周期为 A ．2π B ．πC ．32π D ．2π11．已知椭圆、双曲线均是以直角三角形ABC 的斜边AC 的两端点为焦点的曲线，且都过B 点，它们的离心率分别为12e e 、，则221211e e += A ．32B ．2C ．52D ．312．若函数()1sin 2cos 23f x x a x x =++在(),-∞+∞上单调递增，则a 的取值范围为 A.44,33⎡⎤-⎢⎥⎣⎦ B.41,3⎡⎤-⎢⎥⎣⎦C.4,13⎡⎤--⎢⎥⎣⎦D.[]1,1-第Ⅱ卷（非选择题共90分）二、填空题(本大题共4小题，每小题5分，满分20分） 13．已知5(2x 展开式的二项式系数之和为__________．14．已知向量,a b 满足()5a a b ⋅+=，且||2,||1a b ==，则向量a 与b 夹角余弦值为__________．15．已知抛物线C ：22(0)y px p =>的焦点为F ，准线l 与x 轴的交点为A ，P 是抛物线C上的点，且PF x ⊥轴.若以AF 为直径的圆截直线AP 所得的弦长为2，则实数p 的值为__________．16．在四面体ABCD 中，三组对棱棱长分别相等且依次为6、15，则此四面体ABCD的外接球的体积为________三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17 ~ 21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.） 17.（本大题满分12分）在ABC ∆中，,,a b c 分别为内角,,A B C 所对的边，已知cos a A R =，其中R 为ABC ∆外接圆的半径，S 为ABC ∆的面积， 222a c b +-=. (Ⅰ)求sin C ；（II ）若a b -=ABC ∆的周长． 18．（本大题满分12分）已知，正三角形PAD , 正方形ABCD ,平面PAD ⊥平面ABCD , E 为PD 的中点;(Ⅰ)求证: CD ⊥平面PAD（II ）求直线AC 与平面PCD 所成角的正弦值.19．（本大题满分12分）在某单位的食堂中，食堂每天以10元/斤的价格购进米粉，然后以4.4元/碗的价格出售，每碗内含米粉0.2斤，如果当天卖不完，剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料，得到食堂某天米粉需求量的频率分布直方图如图所示，若食堂某天购进了80斤米粉，以x （单位：斤）（其中50100x ≤≤）表示米粉的需求量， T （单位：元）表示利润. (Ⅰ)计算当天米粉需求量的平均数，并直接写出需求量的众数和中位数；(Ⅱ) 将T 表示为x 的函数；（Ⅲ）根据直方图估计该天食堂利润不少于760元的概率.20．（本大题满分12分）已知椭圆()2222:10x y C a b a b +=>>:20l x y -+=与以原点为圆心、椭圆C 的短半轴长为半径的圆O 相切． (Ⅰ)求椭圆C 的方程；（II ）是否存在直线与椭圆C 交于,A B 两点，交y 轴于点()0,M m ，使22OA OB OA OB +=-成立？若存在，求出实数m 的取值范围；若不存在，请说明理由．21．（本大题满分12分） 已知函数2()ln f x x mx x =--. (Ⅰ)若12x =是()f x 的一个极值点，求()f x 的最大值； （II ）若121,,x x e e ⎡⎤∀∈⎢⎥⎣⎦，12x x ≠，都有2112()()x f x x f x -1221()x x x x >-，求实数m 的取值范围.（二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22. [选修4-4：坐标系与参数方程]（10分）在直角坐标系xOy 中，直线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩（t 为参数），在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线1C ：2cos ρθ=，曲线2C ：2cos 3πρθ⎛⎫=- ⎪⎝⎭.(Ⅰ)求1C 与2C 交点的直角坐标；（II ）若直线l 与曲线1C ，2C 分别相交于异于原点的点M ，N ，求MN 的最大值. 23．选修4-5：不等式选讲已知函数()|1|,()|3|f x x g x x b =+=--+ （Ⅰ）解关于x 的不等式()30()f x a a R +->∈；（II ）若函数()f x 的图象恒在函数()g x 图象上方，求b 的取值范围.2019-2020学年度秋四川省叙州区一中高三期中考试理科数学试题参考答案1-5:CDDBA 6-10:DDCBB11-12:BA 13．3214．1215．16．288π17．（1）由正弦定理得：2sin 2sin cos a R A R A A R =∴=，，sin21A ∴=，又022A π<<，22A π∴=，则4A π=.1=sin 2S ac B，2221csin 32a cb a B +-=⋅，由余弦定理可得2cos sin ac B B =，tan B ∴=0B π<<，=3B π∴，()sin sin sin 43C A B ππ⎛⎫∴=+=+=⎪⎝⎭（2）由正弦定理得sin =sin a A b B ==，又a b -=a b ⎧=⎪∴⎨=⎪⎩42c ∴==， ABC ∴∆的周长2a b c ++=18．1)正方形ABCD 中,CD AD ⊥,由于平面PAD ⊥平面ABCD ,且交线为AD ,根据面面垂直的性质定理可知CD ⊥平面PAD .(2)过A 作AE PD ⊥,交点为E ,则AE PD ⊥,由于CD ⊥平面PAD 所以CD AE ⊥.由于PD CD D ⋂=,所以AE ⊥平面PCD ,故ECA ∠是直线AC 与平面PCD 所成的角.设正方形和等边三角形的边长都为1,则sin 4AE ECA AC ∠===.19．(Ⅰ)由频率分布直方图知()10550.015650.02750.03850.015950.0275.5⨯⨯+⨯+⨯+⨯+⨯=所以平均数为75.5，众数为75，中位数为75. (Ⅱ)一斤米粉的售价是4.4522⨯=元.当5080x ≤≤时， ()22108028020640T x x x =-⨯+-=- 当80100x <≤时， 22801080960T =⨯-⨯= 故20640,5080960,80100x x T x -≤≤⎧=⎨<≤⎩（Ⅲ）设利润T 不少于760元为事件A ，利润T 不少于760元时，即20640760x -≥. 解得70x ≥，即70100x ≤≤.由直方图可知，当70100x ≤≤时，()()100.030.0150.020.65P A =⨯++=.故该天食堂利润不少于760元的概率为0.65.20．（1）由已知得2222a b c b c a⎧⎪=+⎪⎪=⎨⎪⎪=⎪⎩，解方程组得a b c ===∴椭圆1C 的方程为22182x y +=，（2）假设存在这样的直线，由已知可知直线的斜率存在，设直线方程为y kx m =+，由22182y kx mx y =+⎧⎪⎨+=⎪⎩得()()()22222418480,16820*k x kmx m k m +++-=∆=-+>，设()()1122,,,A x y B x y ，则2121222848,4141km m x x x x k k -+=-=++， ()()()2222121212122841m k y y kx m kx m k x x km x x m k -=++=+++=+， 由22OA OB OA OB +=-得OA OB ⊥，即·0OAOB =，即12120x x y y +=，故228580k m =-≥，代入（*）式解得m >或m <． 21．（1）()1'21(0)f x mx x x=-->， 由题意得1'02f ⎛⎫=⎪⎝⎭，即210m --=，所以1m =， 所以()1'21f x x x =-- ()()211x x x--+=， 当102x <<时，()'0f x >；当12x >时，()'0f x <， 所以()f x 在10,2⎛⎫ ⎪⎝⎭上单调递增，在1,2⎛⎫+∞⎪⎝⎭上单调递减. 所以()max 12f x f ⎛⎫=⎪⎝⎭3ln24=--. （2）由题意得121,,x x e e⎡⎤∀∈⎢⎥⎣⎦，12x x ≠都有()()2112x f x x f x - ()1221x x x x >- ()111f x x x ⇔+ ()222f x x x >+，令函数()()f x g x x x=+ 2ln x mx xx x --=+ ln 1x mx x x =--+， 当12x x >时，()g x 在1,e e ⎡⎤⎢⎥⎣⎦上单调递增，所以()21ln '10x g x m x -=-+≥在1,e e ⎡⎤⎢⎥⎣⎦上恒成立，即21ln 1x m x -≤+在1,e e ⎡⎤⎢⎥⎣⎦上恒成立，令()21ln x h x x -=，1,x e e ⎡⎤∈⎢⎥⎣⎦，则()332ln '0xh x x -+=<， 所以()h x 在1,e e ⎡⎤⎢⎥⎣⎦上单调递减，故()()min 0h x h e ==，所以实数m 的取值范围为(],1-∞.同理，当12x x <时，()g x 在1,e e ⎡⎤⎢⎥⎣⎦上单调递减，所以()21ln '10x g x m x -=-+≤在1,e e ⎡⎤⎢⎥⎣⎦上恒成立，即21ln 1x m x -≥+在1,e e ⎡⎤⎢⎥⎣⎦上恒成立，令()21ln x h x x -=，1,x e e ⎡⎤∈⎢⎥⎣⎦，则()332ln '0xh x x-+=<， 所以()h x 在1,e e ⎡⎤⎢⎥⎣⎦上单调递减，故()2max 12h x h e e ⎛⎫== ⎪⎝⎭.所以实数m 的取值范围为)221,e ⎡++∞⎣，综上，实数m 的取值范围为][()2,121,e -∞⋃++∞.22．（1）曲线1C 的直角坐标方程为222x y x +=， 曲线2C的直角坐标方程为220x y x +--=.由222220x y x x y x ⎧+=⎪⎨+-=⎪⎩解得00x y =⎧⎨=⎩或322x y ⎧=⎪⎪⎨⎪=⎪⎩， 故1C 与2C 交点的直角坐标为(0,0)，3,22⎛⎫⎪ ⎪⎝⎭.（2）不妨设0απ≤<，点M ，N 的极坐标分别为1(,)ρα，2(,)ρα， 所以12||2cos 2cos 3MN πρραα⎛⎫=-=--⎪⎝⎭|2cos (cos )|ααα=-|cos |2cos 3πααα⎛⎫==+ ⎪⎝⎭，所以MN 的最大值2.23：（I ）：不等式()30f x a +->，即13x a +>-. 当3a =时，解集为()(),11,-∞-⋃-+∞; 当3a >时，解集为全体实数R ；当3a <时，解集为()(),42,a a -∞-⋃-+∞（II ）()f x 的图象恒在函数()g x 图象的上方，即13x x b +>--+对任意实数x 恒成立，即13b x x <++-恒成立，()min13b x x <++-，又因为13134x x x x ++-≥+-+=。
四川省宜宾市叙州区第一中学2020届高三数学上学期开学考试试题理
和是否“事先知道蕲春四宝有关系”？
（Ⅲ）从被询问的������名事先知道“蕲春四宝”的顾客中随机选取 2 名顾客，求抽到的女顾客
人数的分布列及其数学期望． 18.（本大题满分 12 分）
. ABC 的内角 A，B，C 的对边分别为 a，b，c，设 (sin B sin C)2 sin2 A sin B sin C ．
������2 = 60( 10.828
(2)由计算可得
40 × 20 × 24 × 36
，
所以在犯错误的概率不超过0.001的前提下，
认为购买“蕲春四宝”和“事先知道蕲春四宝有关系”
(3)������的可能取值为 0，1，2．
������(������ = 0) = ������28 = 7 ������(������ = 1) = ������18������116 = 32 ������(������ = 2) = ������126 = 30 = 10
时是否在来蕲春县之前就知道“蕲春四宝”，得到如下列联表：
男
女
总计
事先知道“蕲春四宝” 8
������
������
事先不知道“蕲春四宝”
������
4
36
总计
40
������
������
������(������2 ≥ ������0) ������0
0.010 6.635
0.005 7.879
0.001 10.828
������
A. 2������4
������ ‒
B. 2������ 4
������
C. 2������2
������ ‒
D. 2������ 2
四川省宜宾市叙州区第一中学2020届高三数学一诊模拟试题文
四川省宜宾市叙州区第一中学2020届高三数学一诊模拟试题文第I卷 (选择题共60分）一、选择题(本大题共12小题，每小题5分，共60分.在每个小题所给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置.）2?i|z|??z则，1．若复数1?i1010 D．3C．AB．．12??R?2,xx|x?A?y?lg(x?1)BA?B 2．已知集合的定义域，则为函数，集合(1,2)[1,2](1,2][1,2) D．．A． B．Cab 为实数，则的、是3．已知A．既不充分也不必要条D．充分不必要条件 B．必要不充分条件 C．充要条件件ABC?a?2,b?23,A?30?,则等于．在中，若 4B60?60?或12015030?或??°30A．． B ．D． C5．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入的值为2，则输出的值为． A．B．C．D- 1 -22yx1??F分别是椭圆的左、右焦点，且△PF．已知点P是椭圆＞2)上的一点，6F，F (a212124a的周长为12，则椭圆的离心率为1542 C．．．A DB．26527．某几何体的三视图如图所示，则该几何体的体积为30 24 D．．12 B．18 C．A?3??,则8．已知?2cos??cos()527171 D．． B． C． A??2552552(2,1)R Cl0):y??2px(qC A F，与抛物线的直线交于的焦点，9．已知过点是抛物线B5FA?FB?lABR两点，的斜率为为线段的中点，若，则直线1 D．3B．1C．2．A2ABCP??PA，的四个顶点都在半径为2的球面上，已知三棱锥10．2?BC?CA?2ABABCP?的体积为平面ABC，则三棱锥896C．．A ． BD．22 34?若三棱锥．已知三棱锥中，，，11,?ACAB?AC,ABBCD?BDBCDA??DCA?DBC?63，则三棱锥的最大体积为外接球的表面积为BCDA?2ππππ31243 C.D.A.B.812)xf'(0?f(1))(xf0?x0?x时，.（，且满足当12．已知偶函数）的导函数为x0?f(x)2xf'(x)?f(x)的取值范围是成立的，则使得(0,1)1,0)(?)(1,??1)(??,?(0,1)?1),(??A． C． B ．),??1 01(?,)(．D- 2 -90分）第Ⅱ卷（非选择题共分）5本大题共4小题，每小题分，满分20二、填空题(2x21?y?__________.的离心率是13．双曲线211?4xy?x?0，y?0的最小值为14．若，则______，且；yx 名学生参加成语知识14.为弘扬我国优秀的传统文化，某小学六年级从甲、乙两个班各选出7，乙班学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85y的值为生成绩的中位数是83，则．x，4GH?PH，?2PG那么随着PGPH如果三角形16上的顶点．平面上线段P的永远保持运动,三角形GPH面积的最大值等于_________.三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17 ~ 21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.）17.（12分）根据《中华人民共和国道路交通安全法》规定：“车辆驾驶员血液酒精溶度（单??80,20，属于酒后驾驶；血液浓度不低于80，/位mg/100ml）在属于醉酒驾驶。
四川省宜宾市叙州区第一中学2020届高三数学上学期第一次月考试题 理
四川省宜宾市叙州区第一中学2021届高三数学上学期第一次月考试题 理第I 卷(选择题 共60分）一、选择题(本大题共12小题，每小题5分，共60分.在每个小题所给出的四个选项中，只 有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置.） 1.已知集合{|1}A x y x ==-，(){}22|log B x y x x ==-，则A B ⋂=A. {|01}x x <<B. }1|{≥x xC. {|0}x x >D. }1|{>x x2.命题“，”的否定是A. B. C.D.3.等比数列{}n a 中，若0n a >，241a a =，7321=++a a a ，则公比q = A.14B.12C. 2D. 44.下列函数中，即是奇函数又是增函数的为 A. B. C.D.5.已知随机变量服从正态分布，若，则为A. 0.7B. 0.5C. 0.4D. 0.356.若变量满足约束条件则的最小值为 .A.B.C.D.7.七巧板是我国古代劳动人民的发明之一，被誉为“东方模板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图所示的是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自黑色部分的概率为A. B. C. D.8.已知某口袋中装有2个红球、3个白球和1个蓝球，从中任取3个球，则其中恰有两种颜色的取法种数为 A. B.C.D.9.若，则等于A. B. C. 2 D.10.已知，，，则下列选项正确的是 A.B.C.D. 11.设点为直线：上的动点，点，，则的最小值为 A.B.C. D.12.已知函数，若正实数满，则的最小值是 A. 1B.C. 9D. 18第Ⅱ卷（非选择题共90分）二、填空题(本大题共4小题，每小题5分，满分20分） 13.已知，，成等比数列，且，则_______．14.已知42sin =α，则=-)223sin(απ_______．15.若正数满足，则的最小值为__________．16.四棱锥中，底面为矩形，，，且，当该四棱锥的体积最大时，其外接球的表面积为_________.三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17 ~ 21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.）17.（本大题满分12分）已知数列满足，且成等差数列.（Ⅰ）求数列的通项公式；（Ⅱ）令，数列的前项和为，求的取值范围.18.（本大题满分12分）在一次高三年级统一考试中，数学试卷有一道满分10分的选做题，学生可以从，两道题目中任选一题作答.某校有900名高三学生参加了本次考试，为了了解该校学生解答该选做题的得分情况，计划从900名考生的选做题成绩中随机抽取一个容量为10的样本，为此将900名考生选做题的成绩按照随机顺序依次编号为001一900.（Ⅰ）若采用随机数表法抽样，并按照以下随机数表，以方框内的数字5为起点，从左向右依次读取数据，每次读取三位随机数，一行读数用完之后接下一行左端.写出样本编号的中位数；（Ⅱ）若采用系统抽样法抽样，且样本中最小编号为08，求样本中所有编号之和：（III）若采用分层轴样，按照学生选择题目或题目，将成绩分为两层，且样本中题目的成绩有8个，平均数为7，方差为4：样本中题目的成绩有2个，平均数为8，方差为1.用样本估计900名考生选做题得分的平均数与方差.19.（本大题满分12分）如图，已知四棱锥中，四边形为矩形，，，.（Ⅰ）求证：平面；（Ⅱ）设，求平面与平面所成的二面角的正弦值.20.（本大题满分12分）已知椭圆：的左、右焦点分别为，，椭圆的长轴长与焦距之比为，过的直线与交于，两点.（Ⅰ）当的斜率为时，求的面积；（Ⅱ）当线段的垂直平分线在轴上的截距最小时，求直线的方程.21.（本大题满分12分）设函数()()ln 1f x a x =+， ()1xg x e =-，其中a ∈R ， 2.718e =…为自然对数的底数．（Ⅰ）当0x ≥时， ()()f x g x ≤恒成立，求a 的取值范围； （Ⅱ）求证： 101095200010001791e << (参考数据： ln1.10.095≈)．（二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22. [选修4-4：坐标系与参数方程]（10分） 在平面直角坐标系中，直线的参数方程为为参数），以为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，点是曲线上的动点，点在的延长线上，且，点的轨迹为．（Ⅰ）求直线及曲线的极坐标方程；（Ⅱ）若射线与直线交于点，与曲线交于点（与原点不重合），求的最大值.23.设的最小值为.（10分）（Ⅰ）求的值；（Ⅱ）设，求的最小值.2021-2022度秋四川省叙州区一中高三开第一学月考试理科数学试题答案1.D2.B3.B4.C5.C6.C7.D8.C9.B 10.D 11.A12.A13.4 14.43 15.2 16.17.（1）由知数列是等比数列，且公比为.成等差数列，（2）易知单调递减，当时，的取值范围为18.解：（1）根据题意，读出的编号依次是：512，916（超界），935（超界），805，770，951（超界），512（重复），687，858，554，876，647，547，332.将有效的编号从小到大排列，得332，512，547，554，647，687，770，805，858，876，故中位数为.（2）由题易知，按照系统抽样法，抽出的编号可组成以8为首项，以90为公差的等差数列，故样本编号之和即为该数列的前10项之和.（3）记样本中8个题目成绩分别为，，…，2个题目成绩分别为，，由题意可知，，，，故样本平均数为.样本方差为.故估计该校900名考生该选做题得分的平均数为7.2，方差为3.56.19.（1）证明： BC SD ，BC CD则BC平面SDC, 又则AD平面SDC，平面SDCSC AD又在△SDC中，SC=SD=2, DC=AB，故SC2+SD2=DC2则SC SD ，又所以 SC平面SAD（2）解：作SO CD于O，因为BC平面SDC,所以平面ABCD平面SDC，故SO平面ABCD以点O为原点，建立坐标系如图.则S(0,0,),C(0，,0), A(2，-,0),B(2，,0)设E(2,y,0),因为所以即E((2,,0)令，则，，令，则，所以所求二面角的正弦值为20.解：（1）依题意，因，又，得，所以椭圆的方程为，设、，当时，直线：将直线与椭圆方程联立，消去得，，解得，，，所以.（2）设直线的斜率为，由题意可知，由，消去得，恒成立，，设线段的中点，设线段的中点，则，，设线段的垂直平分线与轴的交点为，则，得.，整理得：，，等号成立时.故当截距最小为时，，此时直线的方程为.21.解：(Ⅰ)令()()()()()1ln 10x H x g x f x e a x x =-=--+≥，则()()01x a H x e x x =-≥+' ①若1a ≤，则11x a e x ≤≤+， ()0H x '≥， ()H x 在[)0,+∞递增， ()()00H x H ≥=， 即()()f x g x ≤在 [)0,+∞恒成立，满足，所以1a ≤；②若1a >， ()1x a H x e x =-+'在[)0,+∞递增， ()()01H x H a ''≥=-且10a -< 且x →+∞时， ()H x '→+∞，则()00x ∃∈+∞，使()00H x '=， 则()H x 在[)00x ，递减，在()0x +∞，递增， 所以当()00x x ∈，时()()00H x H <=，即当()00x x ∈，时， ()()f x g x > ， 不满足题意，舍去；综合①，②知a 的取值范围为(],1-∞.(Ⅱ)由(Ⅰ)知，当1a =时， ()1ln 1xe x >++对0x >恒成立， 令110x =，则11010951ln1.1 1.0951000e >+≈> 即1010951000e >； 由(Ⅰ)知，当1a >时，则()H x 在[)00x ，递减，在()0x +∞，递增， 则()()000H x H <=，即()001ln 10xe a x --+<，又()00H x '=，即001x a e x =+， 令11011110a e =>，即0110x =，则110120001 1.1ln1.11791e <≈-， 故有101095200010001791e <<. 22.（1）消去直线l 参数方程中的t ，得，由，得直线l 的极坐标方程为， 故．由点Q 在OP 的延长线上，且，得，设，则，由点P是曲线上的动点，可得，即，所以的极坐标方程为．（2）因为直线l及曲线的极坐标方程分别为，，所以，，所以，所以当时，取得最大值，为．23.解：（Ⅰ）当时，当时，当时，当时，取得最小值（Ⅱ）由题意知当且仅当时，即等号成立，的最小值为.。
四川省宜宾市叙州区第一中学2020-2021学年高二上学期第一次月考数学(理)试题 Word版含答案
2020年秋四川省叙州区第一中学高二第一学月考试理科数学注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
第I 卷 选择题（60分）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给的四个选项中，只有一项是符合题目要求的。
1．设命题p ：x R ∀∈，3210x x --≤，则p ⌝为A ．x R ∀∈，3210x x --≥B ．x R ∀∈，3210x x -->C ．x R ∃∈，3210x x --≤D ．x R ∃∈，3210x x -->2．直线x - y + 3 = 0的倾斜角是A ．30°B ．45°C ．60°D ．90° 3．下列语句是存在量词命题的是A ．整数n 是2和5的倍数B ．存在整数n ，使n 能被11整除C ．若370x -=,则73x = D ．,()x M p x ∀∈ 4．双曲线的顶点到渐进线的距离等于A ．B ．C ．D ．5．已知集合{}2230A x x x =+-<，{}234B x x =+>-，则A B =A ．{}11x x -<<B ．{}21x x -<< C ．213x x ⎧⎫-<<⎨⎬⎩⎭ D ．{}32x x -<<- 6．经过圆x 2+y 2+2y =0的圆心C ，且与直线2x +3y −4=0平行的直线方程为 A ．2x +3y +2=0B ．2x +3y +3=0C ．2x +3y −3=0D ．3x −2y −2=0 7．已知2(1,0,2),(6,21,)a b λμλ=+=-，若a ∥b ，则λ与μ的值分别为A ．11,52B ．11,52-- C ．5,2 D ．5,2-- 8．若直线2=-y x 被圆4)(22=+-y a x 所解得的弦长为22，则实数a 的值为A ．1-或3B ．1或3C ．2-或6D ．0或4 9．已知圆22:2O x y +=与抛物线()2:20C y px p =>的准线相切，则p 的值为A B ．C ．2 D ．410．已知1F ，2F 是椭圆221:14x C y +=与双曲线2C 的公共焦点，A 是1C ，2C 在第二象限的公共点.若12AF AF ⊥，则2C 的离心率为A ．45B ．2C D。
四川省宜宾市叙州区第一中学校2021届高三上学期第一次月考数学(文)试题含答案
2020年秋四川省叙州区第一中学高三第一学月考试文科数学注意事项:1．答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后,再选涂其它答案标号.回答非选择题时，将答案写在答题卡上。
写在本试卷上无效.3．考试结束后，将本试卷和答题卡一并交回.第I 卷 选择题(60分）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给的四个选项中，只有一项是符合题目要求的.1．设集合{}2|30A x y x x ==-≤，{}|31xB x y ==>,则AB =A ．(0,3]B ．[0,)+∞C ．{}03x x <<D ．(0,)+∞2．设21iz i+=-，则z =A ．2B ．3C ．32D ．23．若1cos 24θ=，则22sin2cos θθ+的值为A ．78B ．1932C ．138D ．324．1614年纳皮尔在研究天文学的过程中为了简化计算而发明对数;1637年笛卡尔开始使用指数运算；1770年，欧拉发现了指数与对数的互逆关系，指出:对数源于指数，对数的发明先于指数,称为历史上的珍闻。
若522x =，lg 20.3010=,则x 的值约为 A ．1。
322 B ．1。
410 C ．1。
507D ．1.6695．已知函数()33f x x x =++1,若()2f a -=，则()f a 的值为A ．0B ．2-C ．2D ．1- 6．在ABC ∆中，1AC =，1AC AB ⋅=-，O 为ABC ∆的重心，则BO AC ⋅的值为A ．1B ．32C ．53D ．27．函数()()33lg xx f x x-=+⋅的图象大致为A ．B ．C ．D ．8．在ABC 中，若sin 2sin cos B A C =,那么ABC 一定是A ．等腰直角三角形B ．等腰三角形C ．直角三角形D ．等边三角形9．已知双曲线C ：()222210,0x y a b a b -=>>，斜率为2的直线与双曲线C 相交于点A 、B ，且弦AB 中点坐标为()1,1,则双曲线C 的离心率为 A ．2B 3C ．2D ．310．已知函数()()sin 202f x x πϕϕ⎛⎫=+<< ⎪⎝⎭的图象向左平移6π个单位长度后，图象关于y 轴对称，设函数()f x 的最小正周期为m ，极大值点为n ，则m n -的最小值是 A ．6πB ．3πC ．23π D ．53π 11．已知正四棱锥P ABCD -的高为2,22AB =过该棱锥高的中点且平行于底面ABCD 的平面截该正四棱锥所得截面为1111D C B A ,若底面ABCD 与截面1111D C B A 的顶点在同一球面上，则该球的表面积为A ．20πB ．203πC ．4πD ．43π 12．已知函数()22xx f x ae e x =-+有两个极值点1x ，2x ，若不等式()()1212x x f x f x e e t +<++恒成立，那么t 的取值范围是 A ．[)1,+∞﹣ B ．[)22ln 2,--+∞ C ．[)3ln 2,-+∞-D ．[)5,-+∞第II 卷 非选择题(90分）二、填空题：本题共4小题，每小题5分,共20分。
2020-2021学年四川省宜宾市叙州区第一中学校高一上学期第一次月考数学试题(解析版)
【答案】D
【解析】由抽象函数的性质可得 ，故可推测 为分段常数函数，从而由题意化简可得.
【详解】
，
，
所以 为分段常数函数，
又 ，
，
，
又 时， ，
当 时， ，
又 ，
，
故选：D.
【点睛】
本题考查了函数的性质的判断与应用，同时考查了抽象函数的应用，属于中档题.
二、填空题
13．已知 ，则 =_____________
（2）若不等式 的解集为 ,求 时 的值域.
【答案】（1） （2）
【解析】（1）二次函数 的对称轴为 ,且图象开口向上,函数 在 上是增函数,可得 ,即可求得答案;
（2）因为不等式 的解集为: ,故 和 是方程 的两个根,解得 , ,可得 ,即可求得答案.
【详解】
（1） 二次函数 的对称轴为 ,且图象开口向上
（2）由题意可知 的值域为 的值域的子集，这样可以求出实数 的值.
故选A．
【点睛】
本题考查函数单调性奇偶性的应用，关键是掌握函数的奇偶性与单调性的定义，属于基础题．
9．在如图所示的三角形空地中，欲建一个如图所示的内接矩形花园（阴影部分），则该矩形花园的面积的最大值为( )
A． B． C． D．
【答案】C
【解析】可设矩形的长为 ，宽为 ，则以长为底的三角形和该锐角三角形相似，再根据相似比求出 与 的关系式，表示出面积 关于 的关系式，即可求解
【详解】
（1）设 ，当 时 ，可得k=4，∴ ∴定义域为 ，t为常数， ；
（2）因为定义域中
函数 在 上单调递减，故 .
【点睛】
本题考查函数的应用问题，函数的解析式、二次函数的最值及分类讨论思想，牵扯字母太多，容易出错．
宜宾市叙州区第一中学2020届高三数学第一次适应性考试试题理含解析
所以 是等腰三角形， ，
又 ,
所以 ,
所以 ；
又 ， ，且 ,所以 ，
所以四边形 是矩形，
，所以矩形 的面积 ,
所以截面积 .
故选：B
【点睛】本题主要考查平面的基本性质，考查空间直线的关系，并涉及到余弦定理的应用，考查学生数形结合能力,属于中档题。
11。 如图， 为 的外心， , ， 为钝角， 是边 的中点，则 的值
当 时，由①得 ,即 ,又 ，
所以 ,此时 ，当 时, ，
当 即 时, 取最小值，无最大值，满足题意。
故选：C
【点睛】本题考查正弦型函数的图象及性质，考查学生的运算求解能力，是一道中档题.
9. 唐代诗人李顾的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题一“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营，怎样走才能使总路程最短?在平面直角坐标系中，设军营所在区域为 ，若将军从点 处出发，河岸线所在直线方程为 ，并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
先从CDEF中安排两位志愿者照顾乙，再从剩余的除去A的三位志愿者中选择两位照顾丙，计算得到答案。
【详解】先从CDEபைடு நூலகம்中安排两位志愿者照顾乙,有 种选择，
再从剩余 除去A的三位志愿者中选择两位照顾丙，有 种选择，剩余一位和A照顾甲，
故共有 种安排方法.
故答案为：18。
【点睛】本题考查了组合的应用，意在考查学生的计算能力和应用能力.
首先解一元二次不等式，根据代表元所满足的条件，求得集合A和集合B,之后利用补集和交集的定义求得结果.
【详解】集合 或 ,
四川省宜宾市叙州区第一中学2020届高三数学上学期期中试题文
四川省宜宾市叙州区第一中学2020届高三数学上学期期中试题文第I卷(选择题共60分）一、选择题(本大题共12小题，每小题5分，共60分.在每个小题所给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置.）1．设全集，集合，，则集合为A．{1，2} B．{1} C．{2} D．{-1，1}2．设复数z 满足（是虚数单位），则复数z在复平面内所对应的点位于A．第一象限B．第二象限C．第三象限D．第四象限3．调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图，则下列结论中不一定正确的是A．互联网行业从业人员中90后占一半以上B．互联网行业中从事技术岗位的人数超过总人数的20%C．互联网行业中从事运营岗位的人数90后比80前多D．互联网行业中从事运营岗位的人数90后比80后多4．若实数,x y满足不等式组1010x yx yx a+-≥⎧⎪-+≥⎨⎪≤⎩，若目标函数2z ax y=-的最大值为1，则实数a的值是1 B.1D.35．已知中心在原点，焦点在x 轴的双曲线的渐近线方程为12y x =±，则此双曲线的离心率为C.52D.5 6．某几何体的三视图如图所示，则该几何体的体积为 A ．16163π- B ．32163π- C ．1683π-D ．3283π-7．数列{}n a 为等比数列，且2113724a a a π+=，则212tan()a a =A．B． C．3-D8．已知1a =，2b =，且()a ab ⊥-，则向量a 在b 方向上的正射影的数量为A ．1BC ．12D．29．直线1y kx =+与曲线()1f x a nx b =+相切于点(1,2)P ,则a b += A.1B.4C.3D.210．已知函数()cos ,,32f x x x ππ⎛⎫=∈⎪⎝⎭，若方程()f x m =有三个从小到大排列的根123,,x x x ，且2213x x x =,则m 的值为A.12C.12-D. 11．已知椭圆、双曲线均是以直角三角形ABC 的斜边AC 的两端点为焦点的曲线，且都过B 点，它们的离心率分别为12e e 、，则221211e e += A ．32B ．2C ．52D ．312．若函数()1sin 2cos 23f x x a x x =++在(),-∞+∞上单调递增，则a 的取值范围为 A.44,33⎡⎤-⎢⎥⎣⎦ B.41,3⎡⎤-⎢⎥⎣⎦C.4,13⎡⎤--⎢⎥⎣⎦D.[]1,1-第Ⅱ卷（非选择题共90分）二、填空题(本大题共4小题，每小题5分，满分20分）13．设函数()()()()22,03,0x x x f x f x x ⎧-≤⎪=⎨->⎪⎩，则()5f 的值为________. 14．已知向量,a b 满足()5a a b ⋅+=，且||2,||1a b ==，则向量a 与b 夹角余弦值为__________．15．已知抛物线C ：22(0)y px p =>的焦点为F ，准线l 与x 轴的交点为A ，P 是抛物线C上的点，且PF x ⊥轴.若以AF 为直径的圆截直线AP 所得的弦长为2，则实数p 的值为__________．16．在四面体ABCD 中，三组对棱棱长分别相等且依次为6、15，则此四面体ABCD的外接球的体积为________三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17 ~ 21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.） 17.（本大题满分12分）某大学在开学季准备销售一种盒饭进行试创业，在一个开学季内，每售出1盒该盒饭获利润10元，未售出的产品，每盒亏损5元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了150盒该产品，以x （单位：盒，100200x ≤≤）表示这个开学季内的市场需求量，y （单位：元）表示这个开学季内经销该产品的利润．（1）根据直方图估计这个开学季内市场需求量x 的平均数和众数； （II ）将y 表示为x 的函数；（III ）根据频率分布直方图估计利润y 不少于1050元的概率.18．（本大题满分12分）在ABC ∆中，,,a b c 分别为内角,,A B C 所对的边，已知cos a A R =，其中R 为ABC ∆外接圆的半径，S 为ABC ∆的面积， 222a c b +-=. （Ⅰ）求sin C ；（II ）若a b -=ABC ∆的周长．19．（本大题满分12分）如图，多面体ABCDEF 中，ABCD 是菱形，60ABC ∠=︒，FA ⊥平面ABCD ，//ED FA ，且22AB FA ED ===.（Ⅰ）求证：平面FAC ⊥平面EFC ； （II ）求多面体ABCDEF 的体积.20．（本大题满分12分）已知椭圆()2222:10x y C a b a b +=>>:20l x y -+=与以原点为圆心、椭圆C 的短半轴长为半径的圆O 相切． （Ⅰ）求椭圆C 的方程；（II ）是否存在直线与椭圆C 交于,A B 两点，交y 轴于点()0,M m ，使22OA OB OA OB +=-成立？若存在，求出实数m 的取值范围；若不存在，请说明理由．21．（本大题满分12分）设函数()ln 1xf x e x =--.（Ⅰ）求证：函数()f x 存在极小值；（II ）若1,2x ⎡⎫∃∈+∞⎪⎢⎣⎭，使得不等式ln 0x e mx x x--≤成立，求实数m 的取值范围.（二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22. [选修4-4：坐标系与参数方程]（10分）在直角坐标系xOy 中，直线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩（t 为参数），在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线1C ：2cos ρθ=，曲线2C ：2cos 3πρθ⎛⎫=- ⎪⎝⎭.（Ⅰ）求1C 与2C 交点的直角坐标；（II ）若直线l 与曲线1C ，2C 分别相交于异于原点的点M ，N ，求MN 的最大值. 23．选修4-5：不等式选讲已知函数()|1|,()|3|f x x g x x b =+=--+ （Ⅰ）解关于x 的不等式()30()f x a a R +->∈；（II ）若函数()f x 的图象恒在函数()g x 图象上方，求b 的取值范围.参考答案1-5:CDDBA 6-10:DDDCC11-12:BA13．1214．1215．16．288π17．（1）平均数：()200.0051100.011300.0151500.01251700.0075190153⨯⨯+⨯+⨯+⨯+⨯=（盒）众数：150（2）由题意知：[)[]15750,100,150,1500,150,200,x x x N y x x N ++⎧-∈∈⎪=⎨∈∈⎪⎩ （3）[)[]100,15015020015750105015001050x x y x y ⎧⎧∈∈⎨⎨=-≥=≥⎩⎩，或故[]120,200x ∈10.10.9P ∴=-=。
四川省宜宾市叙州区第一中学2020-2021学年高二上学期第一次月考数学(理)试题
四川省宜宾市叙州区第一中学2020-2021学年高二上学期第一次月考数学（理）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．设命题p ：x R ∀∈，3210x x --≤，则p ⌝为（ ） A ．x R ∀∈，3210x x --≥ B ．x R ∀∈，3210x x --> C ．x R ∃∈，3210x x --≤D ．x R ∃∈，3210x x -->2．直线x - y + 3 = 0的倾斜角是（ ） A ．30°B ．45°C ．60°D ．90°3．下列语句是存在量词命题的是（ ） A ．整数n 是2和5的倍数 B ．存在整数n ，使n 能被11整除 C ．若370x -=,则73x =D ．,()x M p x ∀∈4．双曲线2214x y -=的顶点到渐近线的距离等于（ ）A B ．45C ．25D 5．已知集合{}2230A x x x =+-<，{}234B x x =+>-，则A B = （ ）A ．{}11x x -<< B ．{}21x x -<< C ．213x x ⎧⎫-<<⎨⎬⎩⎭D ．{}32x x -<<-6．经过圆2220x y y =++的圆心C ，且与直线2340x y +-=平行的直线方程为（ ）A ．2320x y ++=B ．2330x y ++=C ．2330x y +-=D ．3220x y --=7．已知2(1,0,2),(6,21,)a b λμλ=+=-，若a ∥b ，则λ与μ的值分别为（ ）A ．11,52B ．11,52--C ．5,2D ．5,2--8．若直线2x y -=被圆()224x a y -+=所截得的弦长为22则实数a 的值为（ ）9．已知圆22:2O x y +=与抛物线()2:20C y px p =>的准线相切，则p 的值为（ ）AB．C ．2 D ．410．已知1F ，2F 是椭圆221:14x C y +=与双曲线2C 的公共焦点，A 是1C ，2C 在第二象限的公共点.若12AF AF ⊥，则2C 的离心率为（ ） A ．45B．2CD11．点(),P x y 的坐标满足条件20400x y x y +-≥⎧⎪-≤⎨⎪≤⎩，若()1,1m =，()1,1n =-，且OP m n λμ=+，则2λμλ+的最大值为（ ）A ．2B ．3C ．4D ．512．已知椭圆2222:1(0)x y E a b a b+=>>右焦点为F (3,0)过点F 的直线交E 于A ，B 两点，若AB 的中点坐标为1(1,)2，则E 的离心率是（ ）A ．34BC．4D二、填空题13．如果关于x32ax >+的解集是非空集合{}4x x m <<，则m =______. 14．已知正数,a b ，121a b+=，则3ab 的最小值为_______ 15．圆22x y 2x 4y 30+++-=上到直线4x-3y=2__________个．16．1F 、2F 为E ：22221x y a b-=左右焦点，M E ∈，且212MF F F ⊥，1230MF F ∠=︒，则E 的离心率e =______.三、解答题17．求满足下列条件的直线的方程：(1)求与直线20x y -=平行，且过点(2)3，的直线方程；(2)已知正方形的中心为直线220x y -+=和10x y ++=的交点，其一边所在直线的方程为350x y +-=,求其他三边的方程.18．已知圆()()221:231C x y -++=，()()222:349C x y -+-=. （1）求两圆外公切线位于两切点（同一切线）之间的线段长；（2）设1C 与2C 的内公切线交于点P ，外公切线交于点Q ，求过点,P Q 的直线方程. 19．某玩具所需成本费用为p 元，且p 关于玩具数量x （套）的关系为：211000510p x x =++，而每套售出的价格为q 元，其中()(),xq x a a b bR =+∈． （1）问：玩具厂生产多少套时，使得平均成本最少？（2）若生产出的玩具能全部售出，且当产量为150套时利润最大，此时每套价格为30元，求a 、b 的值．（利润=销售收入-成本）．20．如图，PA ⊥底面ABCD ，四边形ABCD 是正方形，//,22DE AP AP AD DE ===.(Ⅰ)证明：平面//DCE 平面ABP ； (Ⅱ)求直线CP 与平面DCE 所成角的余弦值.21．已知O 为坐标原点，抛物线E ：22(0)x py p =>与直线l ：1y x =+交于点A ，B 两点，且3OA OB ⋅=-. （1）求抛物线E 的方程；（2）线段AB 的中点为Q ，过点Q 且斜率为k 的直线交抛物线E 于C ，D 两点，若直线OC ，OD 分别与直线2y =-交于M ，N 两点，当3MN =时，求斜率k 的值.22．已知椭圆()2222:10x y E a b a b +=>>的短轴长为2，直线l 过点()1,0-交椭圆E 于A B 、两点，O 为坐标原点．（1）求椭圆E的方程；面积的最大值．（2）求OAB参考答案1．D【解析】【分析】根据全称命题的否定是特称命题，即可写出．【详解】⌝：x Rp∃∈，3210-->．x x故选：D．【点睛】本题主要考查写出全称命题的否定，属于基础题．2．B【解析】由x－y＋2＝0，得y＝x＋2.其斜率为1，倾斜角为45°.选B.3．B【解析】【分析】“有一个”、“有些”、“存在一个”等表示部分的量词在逻辑中称为特称量词，通常用符号“x∃”表示“存在x”，这样的字眼在ACD中均没有，而只有B中有．【详解】解：对于A，无特称量词．对于B，命题：存在整数n，使n能被11整除，含有特称量词”存在” ,故B是特称命题．对于C，无特称量词．对于D，无特称量词．故选B．【点睛】本题主要考查特称命题的判断，发现特称量词是解决本题的关键，比较基础．4．A【解析】【分析】分别写出双曲线的顶点坐标和渐近线方程，利用点到直线的距离公式求解即可.双曲线2214x y -=的顶点为()2,0±.渐近线方程为：12y x =±. 双曲线2214x y -==. 故选A. 【点睛】本题主要考查了双曲线的几何性质，属于基础题. 5．B 【解析】 【分析】解不等式确定集合,A B ，再由交集定义求解． 【详解】{}2230{|31}A x x x x x =+-<=-<<，{}{}2342B x x x x =+>-=-，所以{|21}A B x x ⋂=-<<． 故选：B ． 【点睛】本题考查集合的交集运算，确定集合的元素是解题关键． 6．B 【解析】由圆x 2+y 2+2y =0得x 2+(y +1)2=1，圆心坐标为C (0,−1)， 直线2x +3y −4=0的斜率k =−23， ∴经过圆心C ，且与直线2x +3y −4=0平行的直线方程为y +1=−23x ，即2x +3y +3=0. 故选B. 7．A 【解析】根据两个向量平行，首先求得μ，然后求得λ的值. 【详解】由于//a b ，所以1210,2μμ-==，且121,265λλλ+==.故选：A. 【点睛】本小题主要考查根据空间向量平行求参数，属于基础题. 8．A 【解析】 【分析】利用垂径定理，结合点到线的距离公式求解. 【详解】由圆()224x a y -+=可知，圆心(),0a ，半径为：2，若直线2x y -=被圆()224x a y -+=所截得的弦长为则由垂径定理可知圆心到直线的距离：d =故d ==，解得4a =或0a =.故选：A. 【点睛】本题考查直线与圆相交时弦长的求解，考查点到线距离公式的应用，属于基础题. 9．B 【解析】 【分析】写出抛物线C 的准线方程，根据该准线与圆O 相切求出实数p 的值. 【详解】由题意可知，圆O的圆，抛物线C 的准线方程为2p x =-， 由于抛物线C 的准线方程与圆O相切，则2p=，解得p =【点睛】本题考查利用直线与圆相切求参数，同时也涉及了抛物线的准线方程，考查运算求解能力，属于基础题. 10．B 【解析】 【分析】设双曲线2C 的实轴长为2a ，焦距长为2c ，由题意求得c =根据双曲线和椭圆的定义、结合勾股定理可求a =c e a=. 【详解】设双曲线2C 的实轴长为2a ，焦距长为2c由题意得c在12Rt AF F △中，由勾股定理得22212412AF AF c +==在椭圆1C 中由定义得124AF AF +=∴221212+216AF AF AF AF +⋅=，故122AF AF ⋅=在双曲线2C 中由定义得212AF AF a -=∴2221212421248a AF AF AF AF =+-⋅=-=，解得a =∴双曲线2C 的离心率为c e a ===故选：B 【点睛】本题主要考查椭圆和双曲线的定义，考虑双曲线的离心率，属于中档题. 11．D 【解析】 【分析】根据向量线性运算的坐标公式，得到x y λμλμ=+⎧⎨=-⎩，由此代入题中的不等式组，可得关于λ、μ的不等式组.作出不等式组表示的平面区域，利用数形结合思想即可求解．【详解】解：()1,1m =，()1,1n =-，且OP m n λμ=+， 则()()()1,11,1,OP λμλμλμ=+-=+-，则x y λμλμ=+⎧⎨=-⎩，代入不等式20400x y x y +-≥⎧⎪-≤⎨⎪≤⎩，可得10400λλμλμ-≥⎧⎪+-≤⎨⎪-≤⎩， 作出不等式组表示的平面区域（阴影部分），又22λμμλλ+=+， 其中μλ表示点(),λμ与原点连线的斜率，当点(),λμ在A 点处斜率最大，由()1,3A 得：μλ的最大值为331=， 所以2λμλ+的最大值为235+=.故选D. 【点睛】本题主要考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，将条件转换为关于λ、μ的不等式组是解决本题的关键，属于中档题． 12．C 【解析】 【分析】设1122(,),(,)A x y B x y ，代入椭圆方程后相减可得出,a b 的关系，从而求得离心率． 【详解】设1122(,),(,)A x y B x y ，则22112222222211x y a bx y a b ⎧+=⎪⎪⎨⎪+=⎪⎩， 两式相减得：1212121222()()()()0x x x x y y y y a b +-+-+=，因为AB 的中点坐标为11,2⎛⎫⎪⎝⎭，所以122x x +=，121y y +=，代入后2122122y y b x x a -=--，所以22102213b a --=-，2222218b ac a a -==，所以c e a ==． 故选：C ． 【点睛】本题考查求椭圆的离心率，解题方法是点差法，在涉及到圆锥曲线弦的中点坐标时，常常利用点差法建立关系式. 13．36 【解析】 【分析】ax +32ax ﹣32＞0即﹣a 232＞0．当﹣a ＜0即a ＞0时，y=﹣a232是开口向下的抛物线，因为解集是非空集合{x |4＜x ＜m }，得到4和m 为y=0时的解，把4和m 代入求得a 和m 得解． 【详解】＞ax +32﹣ax ﹣32＞0即﹣a 2﹣32＞0 设y=﹣a232当﹣a ＜0即a ＞0时，y 是开口向下的抛物线．ax +32的解集是非空集合{x |4＜x ＜m }，所以4和m 为y=0时方程的两解，把4代入y 得：2﹣4a ﹣32=0解得a=18；把m 代入y﹣8m﹣32=0解得m=36． 故答案为：36 【点睛】本题考查一元二次不等式的应用，分类讨论思想，是中档题． 14．24 【解析】 【分析】根据题意，结合基本不等式得到121+=≥a b . 【详解】因为121+=≥a b 所以8ab ≥，因此324≥ab ， 当且仅当12a b=，即2a =，4b =时，取等号； 故答案为24 【点睛】本题主要考查由基本不等式求最值，熟记基本不等式即可，属于常考题型. 15．4 【解析】解：圆x 2+2x+y 2+4y-3=0的圆心（-1，-2），半径是4x-3y=2的距离是0，故圆上的点到直线x+y+1=0的共有4个．16【解析】 【分析】在12Rt MF F ∆中，根据边关系得到12122,2MF MF MF MF a =-=，112F F =，化简计算得到答案. 【详解】在12Rt MF F ∆中，1230MF F ∠=︒12122,2MF MF MF MF a =-=得到22MF a =11222F F c a =故==ce a【点睛】本题考查了离心率的计算，找到,,a b c 的数量关系是解题的关键.17．(1)240x y -+=；(2) 390x y -+=，330x y --=，370x y ++=. 【解析】 【分析】（1）过点()23，与直线20x y -=平行，斜率得到12k =，利用点斜式方程，即可求解； 由点斜式方程，可得直线方程是()1322y x -=-，即240x y -+=； （2）联立方程组，解得交点坐标为(1,0)-，分别设所求直线为30(5)x y m m ++=≠-， 【详解】（1）过点()23，与直线20x y -=平行，即所求直线的斜率为12k =， 由点斜式方程，可得直线方程是()1322y x -=-，即240x y -+=； （2）联立方程组22010x y x y -+=⎧⎨++=⎩，解得交点坐标为(1,0)-，设与边所在直线350x y +-=平行的边的方程为30(5)x y m m ++=≠-， 设与边所在直线350x y +-=垂直的边的方程为30x y n -+=，又由正方形的中心(1,0)-到直线350x y +-==， 所以点(1,0)-，==，解得7,9m n==或3n=-，所以其它边所在的直线方程分别为370x y++=，390x y-+=，330x y--=.【点睛】本题主要考查了两条直线的位置关系的应用，直线方程的求解，以及点到直线的距离公式的应用，着重考查了推理与运算能力，属于基础题.18．；(2)7170x y--=.【解析】试题分析：（1）先计算两圆位置关系，再由平面几何知识求出；（2）由平面几何知识可知，12,,,Q C P C四点共线，所以求出过12,C C点的直线方程即可．试题解析：（1）经计算可知两圆相离，设两圆的一条外公切线与两圆相切于,A B两点，连接1212,,C A C B C C，过点1C作12C H C B⊥于点H，由平面几何知识可知，12C HC∆为直角三角形，四边形1ABHC为矩形，且1222C C C H==.在12Rt C HC∆中，1C H==AB=..（2）由平面几何知识可知，12,,,Q C P C四点共线，∴过PQ的直线方程为()473y x-=-，即7170x y--=.19．（1）玩具厂生产100套时，平均成本最少；（2）25a=，30b=.【解析】【分析】（1）建立函数的解析式，利用基本不等式可求得函数的最值；（2）根据利润=销售收入-成本，求出利润函数，再利用当产量为150套时利润最大，此时每套价格为30元，结合二次函数的基本性质建立条件关系，即可求出a 、b 的值. 【详解】（1）由题意，每套玩具所需成本费用为2110005100010552510x xp x xx x ++==++≥=， 当且仅当100010x x=时，即当100x =时，每套玩具所需成本费用最少为25元； （2）利润()()2211110005510001010x y xq x p x a x x x a x b b ⎛⎫⎛⎫⎛⎫=-=+-++=-+-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，若生产的玩具能全部售出，且当产量为150套时利润最大，此时每套价格为30元，则51501121015030ab a b -⎧=⎪⎛⎫-⎪ ⎪⎨⎝⎭⎪⎪+=⎩，解得25a =，30b =. 【点睛】本题考查利用函数模型解决实际问题，同时也考查了利用基本不等式和二次函数求最值，考查计算能力，属于中等题.20．（1）见解析；（2）直线CP 与平面DCE. 【解析】分析：(1)先根据线面平行判定定理得//DC 平面ABP ，//DE 平面ABP .，再根据面面平行判定定理得结论，(2)先根据条件建立空间直角坐标系，设立各点坐标，根据方程组解得平面DCE 的一个法向量，利用向量数量积求得向量夹角，最后根据线面角与向量夹角互余关系得结果.详解： (Ⅰ)因为//DC AB ，AB ⊂平面ABP ，DC ⊄平面ABP ， 所以//DC 平面ABP . 同理可得，//DE 平面ABP . 又DC DE D ⋂=,所以平面//DCE 平面ABP .（Ⅱ）（向量法）以A 为坐标原点，,,AB AD AP 所在的直线分别为x 轴，y 轴，z 轴建立如下图所示的空间直角坐标系，由已知得，点(020)D ，，，()2,2,0C ,()0,2,1E ,()0,0,2P . 所以()2,2,2CP =--，()0,2,0AD =. 易证AD ⊥平面DCE ，则平面DCE 的一个法向量为()0,2,0AD =. 设直线CP 与平面DCE 所成角为θ，则(0,2,0·sin cos ,3AD CP AD CP AD CPθ====．则3cos 1sin 13θθ⎛⎫=-=-= ⎪ ⎪⎝⎭.即直线CP 与平面DCE . 点睛：利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.21．（1）24x y =（2）3k =-【解析】 【分析】（1）根据数量积求出参数p 的值即可得到所求方程．（2）求出点Q 的坐标为()2,3，然后再求出点C ，D 的坐标，进而得到直线OC ，OD 的方程，于是得到,M N 的坐标，最后根据3MN =可求出斜率k 的值． 【详解】（1）由221x py y x ⎧=⎨=+⎩消去y 整理得2220x px p --=，∵直线l 与抛物线交于两点，∴()248420p p p p ∆=+=+>，解得0p >或2p <-（舍去）．设()11,A x y ，()22,B x y ，则122x x p =-，∴()()222212121222212244x x p x x y y p p p p-=⋅===， ∵1212OA OB x x y y ⋅=+，∴213p -+=-，解得2p =，符合题意． ∴抛物线方程为E ：24x y =． （2）由（1）得2440x x --=， ∴124x x +=，124x x =-，∴()1212121126y y x x x x +=+++=++=， ∴A ，B 中点Q 为()2,3．设过点()2,3Q 斜率为k 的直线方程为()32y k x -=-，即23y kx k =-+，由2234y kx k x y=-+⎧⎨=⎩消去y 整理得248120x kx k -+-=， 其中()()2216481216120k k k ⎡⎤∆=--=-+>⎣⎦，故k R ∈．设233,4x C x ⎛⎫ ⎪⎝⎭，244,4x D x ⎛⎫ ⎪⎝⎭，则344x x k +=，34812x x k =-， 直线OC 的方程为34x y x =，令2y =-，得38x x =-，∴38,2M x ⎛⎫-- ⎪⎝⎭，同理得48,2N x ⎛⎫-- ⎪⎝⎭，∴3434348883x x MN x x x x -=-+====，解得3k =-，满足题意． ∴斜率k 的值为3-． 【点睛】本题主要考查用代数方法解决解析几何问题，由于解题过程会涉及到大量的计算，所以要合理运用“设而不求”、“整体代换”、“同理得”等方法的运用，同时也要充分利用曲线方程的特点进行代换，以减少变量的个数，起到简化运算、提高解题效率的作用．22．（1）2213x y +=；（2）.【解析】试题分析：（1）由题意得1b =，由 22{1c a a c ==+，得{a c ==2）设直线l 的方程为1x my =- ，将直线方程代入椭圆方程，消去x ，根据韦达定理代入三角形面积公式即可求得AOB的面积，再换元配方即可得出结论． 试题解析：（1）由题意得1b =，由22{1c a a c ==+，得{a c ==∴椭圆E 的标准方程为2213x y +=.（2）依题意可设直线l 的方程为1x my =-,由221{31x y x my +==-，得()223220m y my +--=，()224830m m ∆=++>，设()()1122,,A x y B x y 、，则12212223{23m y y m y y m +=+=-+，12112OABSy y =⨯⨯-==，设()233m t t +=≥，则OABS===∵3t ≥，∴1103t <≤， ∴当113t=，即3t =时，OAB ，此时0m =． 点睛：本题考查椭圆的方程与性质，考查直线与椭圆的位置关系、三角形面积的计算，考查计算能力；在解答本题的第（2）问时，关键是要利用几何关系得到12112OABSy y =⨯⨯-=并将其与韦达定理联立，这是解决圆锥曲线中面积问题的最常见方法.。
2020-2021学年四川省宜宾市叙州区第一中学校高一上学期第一次月考数学试题解析版
2020-2021学年四川省宜宾市叙州区第一中学校高一上学期第一次月考数学试题一、单选题1．若集合A ＝{}1，则下列关系错误的是（ ） A ．1A ∈ B ．A A ⊆C ．A φ⊆D ．A φ∈【答案】D【解析】根据元素与集合、集合与集合的关系可得答案. 【详解】 由A ＝{}1，A. 1A ∈，根据元素与集合的属于关系，正确；B. A A ⊆，根据集合与集合的包含关系，正确；C. A φ⊆，根据集合与集合的包含关系，正确D. A φ∈，应为集合与集合的包含关系，即A φ⊆，错误， 故选：D. 【点睛】本题考查元素与集合属于关系、集合与集合的包含关系，属于基础题. 2．集合{}*|5x x ∈<N 的另一种表示法是（ ） A ．{0,1,2,3,4} B ．{1,2,3,4}C ．{0,1,2,3,4,5}D ．{1,2,3,4,5}【答案】B【解析】题中所给集合中元素为小于5的正自然数，改用列举法表示即可. 【详解】集合{}*|5x x ∈<N 中元素为小于5的正自然数，可用列举法表示为{1,2,3,4}. 故选：B 【点睛】本题考查集合的表示方法，属于基础题. 3．函数()f x =的定义域是（ ）A．30,2⎛⎫⎪⎝⎭B．3,2⎡⎫+∞⎪⎢⎣⎭C．3,2⎛⎤-∞⎥⎝⎦D．3,2⎛⎫+∞⎪⎝⎭【答案】D【解析】直接求230x->即可；【详解】由题意得：3 2302x x->⇒>；故选：D.【点睛】本题主要考查了求函数的定义域问题.属于容易题.4．下列函数中，是偶函数，且在区间(0，1)上为增函数的是（）A．y＝|x| B．y＝1－xC．y＝1xD．y＝－x2＋4【答案】A【解析】通过函数的解析式，结合函数奇偶性和单调性的定义判断.【详解】选项B中，函数不具备奇偶性；选项C中，函数是奇函数；选项A，D中的函数是偶函数，但函数y＝－x2＋4在区间(0，1)上单调递减．故选：A.【点睛】本题主要考查函数的奇偶性和单调性，属于基础题.5．下列说法中，正确的是（）A．很小的实数可以构成集合B．自然数集N中最小的数是1C．空集的元素个数为零D．任何一个集合必有两个或两个以上的子集【答案】C【解析】A、根据集合的确定性进行判断；B、根据自然数的概念进行判断；C、根据空集的定义进行判断；D、根据子集的概念进行判断．【详解】对于A ，很小的实数不确定，不能构成集合，故A 不正确；对于B ，自然数集N 中最小的数是0，故B 不正确；对于C ，空集不含有任何元素，故C 正确；对于D ，空集只有1个子集，故D 不正确，故选C. 【点睛】本题考查命题真假的判定，考查空集、集合的含义，考查集合中元素的性质，属于基础题．6．已知集合1|0,4x A x B N x +⎧⎫=≥=⎨⎬-⎩⎭，则A B 中元素的个数为( ) A ．2 B ．3C ．4D ．5【答案】C【解析】化简集合A ，求出交集即可得到结果. 【详解】11|0|0[1,4)44x x A x x x x ++⎧⎫⎧⎫=≥=≤=-⎨⎬⎨⎬--⎩⎭⎩⎭,B N =，∴{}0,1,2,3A B =,∴元素个数为4个，故选：C 【点睛】本题主要考查了分式不等式，集合的交集，属于容易题.7．下列函数()f x 中，满足对任意()12,0,x x ∈+∞，当x 1<x 2时，都有()()12f x f x >的是（ ） A ．()2f x x =B ．()1f x x=C ．()f x x =D ．()21f x x =+【答案】B【解析】根据题意，结合函数解析式，选择在()0,+∞上单调递减的函数即可. 【详解】由12x x <时，()()12f x f x >，所以函数()f x 在()0,∞+上为减函数的函数. A 选项，2y x 在()0,∞+上为增函数，不符合题意.B 选项，1y x=在()0,∞+上为减函数，符合题意.C 选项，y x =在()0,∞+上为增函数，不符合题意.D 选项，()21f x x =+在()0,∞+上为增函数，不符合题意. 故选：B. 【点睛】本题考查常见函数单调性的判断，属简单题.8．若函数()y f x =为奇函数，且在(),0∞-上单调递增，若()20f =，则不等式()0f x >的解集为( )A ．()()2,02,∞-⋃+B ．()(),22,∞∞--⋃+C ．()(),20,2∞--⋃D ．()()2,00,2-⋃【答案】A【解析】根据题意，由奇函数的性质可得f （﹣2）=﹣f （2）=0，结合函数的单调性分析可得在区间（﹣∞，﹣2）上，f （x ）＜0，在（﹣2，0）上，f （x ）＞0，再结合函数的奇偶性可得在区间（0，2）上，f （x ）＜0，在（2，+∞）上，f （x ）＞0，综合即可得答案． 【详解】根据题意，函数y=f （x ）为奇函数，且f （2）=0， 则f （﹣2）=﹣f （2）=0，又由f （x ）在（﹣∞，0）上单调递增，则在区间（﹣∞，﹣2）上，f （x ）＜0，在（﹣2，0）上，f （x ）＞0， 又由函数y=f （x ）为奇函数，则在区间（0，2）上，f （x ）＜0，在（2，+∞）上，f （x ）＞0， 综合可得：不等式f （x ）＞0的解集（﹣2，0）∪（2，+∞）； 故选A ． 【点睛】本题考查函数单调性奇偶性的应用，关键是掌握函数的奇偶性与单调性的定义，属于基础题．9．在如图所示的三角形空地中，欲建一个如图所示的内接矩形花园（阴影部分），则该矩形花园的面积的最大值为( )A ．120B ．210C ．225D ．300【答案】C【解析】可设矩形的长为x ，宽为y ，则以长为底的三角形和该锐角三角形相似，再根据相似比求出x 与y 的关系式，表示出面积S 关于,x y 的关系式，即可求解 【详解】设矩形的长为x ，宽为y ，则以长为底的三角形和该锐角三角形相似，可得30303030x y y x -=⇒=-，则矩形面积()()23015225S xy x x x ==-=--+，当矩形长15x =时，面积S 最大，为225 故选C 【点睛】本题考查以三角形为载体建立的一元二次函数求最值问题，找出长与宽的等量代换关系是解题关键10．函数()()2231f x ax a x =+-+在区间()2,-+∞上单调递减，则实数a 的取值范围是（ ） A ．[]3,0- B ．(],3-∞- C ．[)3,0- D ．[]2,0-【答案】A【解析】讨论0a =和0a ≠两种情况，分别计算得到答案. 【详解】当0a =时，()61f x x =-+显然满足题意；当0a ≠时，要使()f x 在区间()2,-+∞上单调递减，需满足032a a a<⎧⎪-⎨≤-⎪⎩，解得30a -≤<．综上所述：可知实数a 的取值范围是[]3,0-． 故选A ．【点睛】本题考查了函数的单调性，把握开口方向和对称轴是解题的关键.11．已知函数f （x ）（x ∈R ）满足f （x ）=f （2-x ），且对任意的x 1，x 2∈（-∞，1]（x 1≠x 2）有（x 1-x 2）（f （x 1）-f （x 2））＜0．则（ ） A ．()()()211f f f <-< B ．()()()121f f f <<- C ．()()()112f f f <-< D ．()()()211f f f <<-【答案】B【解析】由已知得函数f （x ）图象关于x=1对称且在（-∞，1]上单调递减，在（1，+∞）上单调递增，从而可判断出大小关系. 【详解】解：∵当x 1，x 2∈（-∞，1]（x 1≠x 2）时有（x 1-x 2）（f （x 1）-f （x 2））＜0， ∴f （x ）在（-∞，1]上单调递减， ∵f （x ）=f （2-x ），∴函数f （x ）的图象关于x=1对称，则f （x ）在∈（1，+∞）上单调递增， ∴f （-1）=f （3）>f （2）＞f （1） 即f （-1）＞f （2）＞f （1） 故选B ． 【点睛】本题考查函数的对称性及单调性的应用，解题的关键是函数性质的灵活应用． 12．定义在R 上的函数()f x 满足(0)0f =，()(1)1f x f x +-=，1()()52xf f x =，且当1201x x ≤≤≤时，有12()()f x f x ≤，则1()2010f 的值为（ ） A ．116B ．120C ．125D ．132【答案】D【解析】由抽象函数的性质可得()111111,,2252f f f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，故可推测()f x 为分段常数函数，从而由题意化简可得. 【详解】()()()00,11f f x f x =+-=，∴()()1111111,,122522f f f f ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭，所以()f x 为分段常数函数，又()152x f f x ⎛⎫= ⎪⎝⎭， ()542351111111...152525232f f f f ⎛⎫⎛⎫⎛⎫∴===== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，4341111111 (25)2252232f f f ⎛⎫⎛⎫⎛⎫=⋅=== ⎪ ⎪ ⎪⨯⎝⎭⎝⎭⎝⎭， 又1201x x ≤<≤时，()()12f x f x ≤，∴当5411,525x ⎡⎤∈⎢⎥⨯⎣⎦时，()132f x =， 又54111,2010525⎡⎤∈⎢⎥⨯⎣⎦， 11201032f ⎛⎫∴=⎪⎝⎭， 故选：D. 【点睛】本题考查了函数的性质的判断与应用，同时考查了抽象函数的应用，属于中档题.二、填空题13．已知2()1f x x x =++，则(1)f x +=_____________ 【答案】233x x ++ 【解析】直接代入即得解. 【详解】由题得22(1)(1)1133f x x x x x +=++++=++. 故答案为：233x x ++ 【点睛】本题主要考查求复合函数的解析式，意在考查学生对这些知识的理解掌握水平.14．设{}28150A x x x =-+=，{}10B x ax =-=，若A B B =，则实数a 组成的集合C =________. 【答案】110,,35⎧⎫⎨⎬⎩⎭【解析】解出集合A ，由A B B =，可得出B A ⊆，然后分B =∅和B ≠∅两种情况讨论，可得出实数a 的值. 【详解】{}{}281503,5A x x x =-+==，且A B B =，B A ∴⊆.当B =∅时，则0a =，此时B A ⊆成立；当B ≠∅时，则0a ≠，此时{}110B x ax a ⎧⎫=-==⎨⎬⎩⎭，则有13a =或15a =，解得13a =或15a =.因此，110,,35C ⎧⎫=⎨⎬⎩⎭.故答案为：110,,35⎧⎫⎨⎬⎩⎭. 【点睛】本题考查利用集合的包含关系求参数，解题时要对含参集合分空集和非空集合两种情况讨论，考查分类讨论思想的应用，属于基础题.15．已知31,0()1,0x x f x x x-≥⎧⎪=⎨-<⎪⎩，若()f a a >，则实数a 的取值范围是____.【答案】1(,0)(,)2-∞⋃+∞【解析】根据题意，当0a ≥时，解31a a ->；当0a <时，解1a a->，即可得出实数a的取值范围. 【详解】当0a ≥时，由()f a a >得31a a ->，解得12a >，又0a ≥， 所以12a >；当0a <时，由()f a a >得1a a->，又0a <，所以0a <恒成立， 故0a <，故答案为：1(,0)(,)2-∞⋃+∞. 【点睛】本题主要考查了分段函数，解不等式及分类讨论的思想，属于中档题. 16．已知定义在R 上的函数()f x 满足：①(1)0f =；②对任意x ∈R 的都有()()f x f x -=-；③对任意的12,(0,)x x ∈+∞且12x x ≠时，都有()()12120f x f x x x ->-.记2()3()()1f x f xg x x --=-，则不等式()0g x ≤的解集______.【答案】[]1,0-【解析】根据题意，分析可得函数()f x 为奇函数且(0)0f =，结合单调性的定义可得()f x 在(0,)+∞上为增函数，结合f （1）0=以及函数奇偶性的性质分析可得()0f x >与()0f x <的x 的取值范围，转化为()010f x x <⎧⎨->⎩或()010f x x >⎧⎨-<⎩或()010f x x =⎧⎨-≠⎩，可得x 的取值范围，即可得答案． 【详解】根据题意，()f x 满足对任意x ∈R 的都有()()f x f x -=-，即函数()f x 为奇函数，则有(0)0f =；又由对任意的1x ，2(0,)x ∈+∞且12x x ≠时，总有1212()()0f x f x x x ->-，即函数()f x 在(0,)+∞上为增函数，若f （1）0=，则在区间(0,1)上，()0f x <，在区间(1,)+∞上，()0f x >， 又由()f x 为奇函数，则在区间(,1)-∞-上，()0f x <，在区间(1,0)-上，()0f x >，则()0g x 即2()3()5()()011f x f x f x g x x x --==--，即()010f x x <⎧⎨->⎩或()010f x x >⎧⎨-<⎩或()010f x x =⎧⎨-≠⎩， 解可得：10x -，即不等式()0g x 的解集为[1-，0]； 故答案为：[]1,0-． 【点睛】本题考查函数的奇偶性与单调性的综合应用，涉及不等式的解法，属于中档题．三、解答题17．设集合A ={a 2，a ＋1，-1}，B ={2a －1，|a －2|，3a 2＋4}，A ∩B ={-1}，求实数a 的值． 【答案】０【解析】根据A ∩B ={-1}知道－1∈B .而|a －2|＞０，3a 2＋4＞０ 故2a －1＝－１，解出a 的值，再带入检验即可． 【详解】A ∩B ={-1}∴－1∈B .而|a －2|＞０，3a 2＋4＞０∴2a －1＝－１ a ＝０此时 A ={０，1，－1} Ｂ＝｛－１，２，４｝符合题意 【点睛】本题考查集合的运算和分类讨论思想，属于基础题．18．设{}22150A x x x =-->，{}121B x a x a =+≤≤-，且R B C A ⊆，求实数a 的取值范围.【答案】 3.a ≤【解析】求解不等式可得：{}35R C A x x =-<<，利用子集关系分类讨论集合B =∅和B ≠∅两种情况可得实数a 的取值范围是{}|3a a ≤. 【详解】{}22150{|3A x x x x x =-->=<-或5}x >， {}35R C A x x ∴=-≤≤，{}121B x a x a =+≤≤-，且R B C A ⊆，当B =∅时，121a a +>-，解得： 2.a <当B ≠∅时，12113215a a a a +≤-⎧⎪+>-⎨⎪-≤⎩，或12113215a a a a +≤-⎧⎪+≥-⎨⎪-<⎩即23a ≤≤.综上所述，实数a 的取值范围为 3.a ≤ 19．已知函数()2f x x ax b =++.（1）若函数()f x 在()1,+∞上是增函数,求实数a 的取值范围；（2）若不等式()0f x ≤的解集为{}|02x x ≤≤,求[]0,3x ∈时()f x 的值域. 【答案】（1）[2,)-+∞（2）[1,3]-【解析】（1）二次函数2()f x x ax b =++的对称轴为2ax =-,且图象开口向上,函数()f x 在(1,)+∞上是增函数,可得12a-≤,即可求得答案; （2）因为不等式()0f x ≤的解集为:{|02}x x ≤≤,故10x =和22x =是方程20x ax b ++=的两个根,解得2a =-,0b =,可得2()2f x x x =-,即可求得答案.【详解】 （1）二次函数2()f x x ax b =++的对称轴为2ax =-,且图象开口向上 又函数()f x 在(1,)+∞上是增函数,∴12a-≤, 解得:2a ≥-,即实数a 的取值范围是[2,)-+∞. （2）不等式()0f x ≤的解集为:{|02}x x ≤≤,故10x =和22x =是方程20x ax b ++=的两个根,∴20220b a b =⎧⎨++=⎩解得:2a =-,0b =,∴2()2f x x x =-,函数2()2f x x x =-的对称轴为:1x = 当1x =时()f x 最小为(1)1f =-;当3x =时,()f x 最大为(3)3f =. ∴()f x 在[0,3]值域为[1,3]-. 【点睛】本题主要考查了根据二次函数单调区间求参数范围和二次函数的值域,解题关键是掌握二次函数的基础知识和已知一元二次不等式的解求参数的解法,考查了分析能力和计算能力,属于中档题. 20．已知函数()f x =的定义域为A ，函数2()g x x=（12x ≤≤）的值域为B .（1）求AB ；（2）若{}|21C y a y a =<<-，且C B ⊆，求实数a 的取值范围.【答案】（1）{}2；（2）32⎛⎤-∞ ⎥⎝⎦，.【解析】（1）求出集合A 、B ，然后利用交集的定义可求出AB ；（2）分C =∅和C ≠∅两种情况讨论，结合C B ⊆得出关于实数a 的不等式组，解出即可. 【详解】（1）由202x x -≥⇒≥ ，∴{}[)22,A x x =≥=+∞， ∵2()g x x=（12x ≤≤）是减函数 ∴(2)()(1)g g x g ≤≤，即1()2g x ≤≤， ∴{}[]121,2B y y =≤≤=， ∴{}2A B ⋂=；（2）由（1）可知{}12B y y =≤≤，又C B ⊆， ①当C =∅时，满足C B ⊆，此时21≥-a a ，∴1a ≤，②当C ≠∅时，由C B ⊆，得：213112212a a a a a <-⎧⎪≥⇒<≤⎨⎪-≤⎩， 综上，a 的取值范围32⎛⎤-∞ ⎥⎝⎦，.【点睛】本题考查交集的运算，考查利用集合的包含关系求参数的取值范围，考查分类讨论思想的应用，属于常考题.21．某公司有价值10万元的一条流水线，要提高该流水线的生产能力，就要对其进行技术改造，改造就需要投入，相应就要提高产品附加值，假设附加值y 万元与技术改造投入x 万元之间的关系满足：① y 与10x -和x 的乘积成正比；② 当5x =时，100y =；③02(10)x t x ≤≤-，其中t 为常数，且1[,1]2t ∈.（1）设()y f x =，求出()f x 的表达式，并求出()y f x =的定义域； （2）求出附加值y 的最大值，并求出此时的技术改造投入的x 的值. 【答案】（1）()410y x x =-，200,21t x t ⎡⎤∈⎢⎥+⎣⎦；（2）()()max 5100f x f ==. 【解析】（1）列出f （x ）的表达式，求函数的定义域时，要注意条件③的限制性． （2）本题为含参数的二次函数在特定区间上求最值，结合二次函数的图象及单调性解决，注意分类讨论． 【详解】（1）设()10y k x x -＝，当5x ＝ 时100y =，可得k=4，∴410y x x =-（） ∴定义域为200,21t t ⎡⎤⎢⎥+⎣⎦，t 为常数，1,12t ⎡⎤∈⎢⎥⎣⎦； （2）因为定义域中202012020,,1,5,,12122132t t t t t t⎡⎤⎛⎫⎡⎤=∈∴∈ ⎪⎢⎥⎢⎥++⎣⎦⎝⎭⎣⎦+函数()()241045100y x x x =-=--+在205,3⎡⎤⎢⎥⎣⎦上单调递减，故()()max 5100f x f ==.【点睛】本题考查函数的应用问题，函数的解析式、二次函数的最值及分类讨论思想，牵扯字母太多，容易出错． 22．已知函数ty x x=+有如下性质：如果常数0t >，那么该函数在(上是减函数，在)+∞上是增函数.（1）已知24123()21x x f x x --=+，()2g x x a =--，[0,1]x ∈，利用上述性质，求函数()f x 的单调区间和值域.（2）对于（1）中的函数()f x 和函数()g x ，若对于任意的[]10,1x ∈，总存在[]10,1x ∈，使得()()21g x f x =成立，求实数a 的值.【答案】（1）递减区间为1[0,]2，递增区间为1[,1]2，值域为[4,3]--；（2）32a =【解析】（1）把函数解析式中的分母变形为2(21)8(21)4x x +-++，利用分式的计算公式，函数解析式变形为241234()2182121x x f x x x x --==++-++，用21u x =+进行换元，得到新解析式为48y u u=+-这样根据已知所给的函数性质可以求出函数()f x 的单调区间和值域.（2）由题意可知()f x 的值域为()g x 的值域的子集，这样可以求出实数a 的值. 【详解】（1）241234()2182121x x f x x x x --==++-++，设21u x =+，[0,1]x ∈，则13u ≤≤，则48y u u=+-，[1,3]u ∈，由已知性质得， 当12u ≤≤，即102x ≤≤时，()f x 单调递减，所以递减区间为1[0,]2，当23u ≤≤，即112x ≤≤时，()f x 单调递增，所以递增区间为1[,1]2，由(0)3f =-，1()42f =-，11(1)3f =-，得()f x 的值域为[4,3]--.（2）由于()2g x x a =--为减函数，故[]()12,2g x a a ∈---，[]0,1x ∈，由题意，()f x 的值域为()g x 的值域的子集，从而有12423a a --≤-⎧⎨-≥-⎩所以32a =.【点睛】本题考查了根据所给函数的性质解决新问题的能力，根据函数解析式的特征合理变形是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
四川省宜宾市叙州区第一中学校2020-2021学年高三上学期第一次月考数学（理）试题
学校_________ 班级__________ 姓名__________ 学号__________
一、单选题
1. 设集合，，则（）A．B．C．D．
2. 设，则（）
A．2 B．3
C．D．
3. 若，则的值为（）
A．B．C．D．
4. 1614年纳皮尔在研究天文学的过程中为了简化计算而发明对数；1637年笛卡尔开始使用指数运算；1770年，欧拉发现了指数与对数的互逆关系，指出：
对数源于指数，对数的发明先于指数，称为历史上的珍闻.若，
，则的值约为（）
A．1.322 B．1.410
C．1.507 D．1.669
5. 二项式的展开式中的系数是，则（）
A．1
D．
B．C．
6. 在中，，，为的重心，则的值为
A．1
D．2
B．C．
7. 函数的图象大致为（）
A．B．
C．D．
8. 为了考察、两种药物预防某种疾病的效果，某研究所进行动物试验，已知参与两种药物试验的服药和未服药的动物数量相同，图1是药试验结果对应的等高条形图；图2是药试验结果对应的等高条形图．下列说法正确的是（）
A．服用药物患病比例高于未服药物的患病比例
B．服用药物对预防该疾病没有效果
C．在对药物的试验中，患病小动物约占总数的
D．对该疾病的预防作用药物比药物更有效
9. 已知双曲线，斜率为2的直线与双曲线相交于点、，且弦中点坐标为，则双曲线的离心率为（）
A．2 B．C．D．3
10. 已知函数的图象向左平移个单位长度后，
图象关于轴对称，设函数的最小正周期为，极大值点为，则
的最小值是（）
A．B．C．D．
11. 已知正四棱锥的高为2，，过该棱锥高的中点且平行于底面的平面截该正四棱锥所得截面为，若底面与截面的顶点在同一球面上，则该球的表面积为（）
A．
B．C．
D．
12. 给出下列命题，其中真命题为（）
①用数学归纳法证明不等式时，当
时，不等式左边应在的基础上加上；
②若命题：，，则：，；
③若，，，则；
④随机变量，若，则.
A．①②④B．①④C．②④D．②③
二、填空题
13. 已知数列的前项和为，，，则＝_____．
14. 用1、2、3、4、5、6六个数字组成的没有重复数字的六位数，要求任何相邻两个数字的奇偶性不同，且1和2相邻，这样的六位数的个数是
____________．
15. 已知函数，若（a），则实数的取值范围是__.
16. 已知函数，，用max{m，n}表示m，n中的最大值，设．若在上恒成立，则实数a的取值范围为_____
三、解答题
17. 在锐角中，内角、、所对的边分别为，且直线为函数图像的一条对称轴．
（1）求；
（2）若恒成立，求实数的最小值．
18. 为抑制房价过快上涨和过度炒作，各地政府响应中央号召，因地制宜出台了系列房价调控政策.某市拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度，在20～60岁的人群中随机调查100人，调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如图所示：
（1）由以上统计数据填列联表，并判断能否在犯错误的概率不超过0.05
的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异？
（2）若以44岁为分界点，从不支持“房产限购”的人中按分层抽样的方法抽
取8人参加政策听证会，现从这8人中随机抽2人.记抽到44岁以上的人数为，求随机变量的分布列及数学期望.
0.100 0.050 0.010 0.001
2.706
3.841 6.635 10.828
19. 如图1，在矩形中，，，点在线段上，
.把沿翻折至的位置，平面，连结，
点在线段上，，如图2.
（1）证明：平面；
（2）当三棱锥的体积最大时，求二面角的余弦值.
20. 已知椭圆C：点的离心率为，且经过点. （1）求C的方程；
（2）若不过坐标原点的直线与椭圆C相交于点M，N两点，且满足
，求面积最大时直线的方程..
21. 已知函数.
（1）求函数的极值；
（2）是否存在实数a，使方程有两个不同的实数根？若存在，求出实数a的取值范围；若不存在，请说明理由.
22. 在极坐标系中，已知曲线C1：ρ＝2cosθ和曲线C2：ρcosθ＝3，以极点O为坐标原点，极轴为x轴非负半轴建立平面直角坐标系．
（1）求曲线C1和曲线C2的直角坐标方程；
（2）若点P是曲线C1上一动点，过点P作线段OP的垂线交曲线C2于点Q，求线段PQ长度的最小值．
23. 已知均为实数，且 .
（Ⅰ）求的最小值；
（Ⅱ）若对任意的恒成立，求实数的取值范围.。