动态规划算法-01背包问题
动态规划与回溯法解决0-1背包问题

0-1背包动态规划解决问题一、问题描述:有n个物品,它们有各自的重量和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?二、总体思路:根据动态规划解题步骤(问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成)找出01背包问题的最优解以及解组成,然后编写代码实现。
原理:动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。
但不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
过程:a) 把背包问题抽象化(X1,X2,…,Xn,其中 Xi 取0或1,表示第i 个物品选或不选),V i表示第i 个物品的价值,W i表示第i 个物品的体积(重量);b) 建立模型,即求max(V1X1+V2X2+…+VnXn);c) 约束条件,W1X1+W2X2+…+WnXn<capacity;d) 定义V(i,j):当前背包容量j,前i 个物品最佳组合对应的价值;e) 最优性原理是动态规划的基础,最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略”。
判断该问题是否满足最优性原理,采用反证法证明:假设(X1,X2,…,Xn)是01背包问题的最优解,则有(X2,X3,…,Xn)是其子问题的最优解,假设(Y2,Y3,…,Yn)是上述问题的子问题最优解,则理应有(V2Y2+V3Y3+…+V n Yn)+V1X1 > (V2X2+V3X3+…+VnXn)+V1X1;而(V2X2+V3X3+…+VnXn)+V1X1=(V1X1+V2X2+…+VnXn),则有(V2Y2+V3Y3+…+VnYn)+V1X1 > (V1X1+V2X2+…+VnXn);该式子说明(X1,Y2,Y3,…,Yn)才是该01背包问题的最优解,这与最开始的假设(X1,X2,…,Xn)是01背包问题的最优解相矛盾,故01背包问题满足最优性原理;f) 寻找递推关系式,面对当前商品有两种可能性:第一,包的容量比该商品体积小,装不下,此时的价值与前i-1个的价值是一样的,即V(i,j)=V(i-1,j);第二,还有足够的容量可以装该商品,但装了也不一定达到当前最优价值,所以在装与不装之间选择最优的一个,即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i) }其中V(i-1,j)表示不装,V(i-1,j-w(i))+v(i) 表示装了第i个商品,背包容量减少w(i)但价值增加了v(i);由此可以得出递推关系式:1) j<w(i) V(i,j)=V(i-1,j)2) j>=w(i) V(i,j)=max{ V(i-1,j),V(i-1,j-w(i))+v(i) }number=4,capacity=7四、构造最优解:最优解的构造可根据C列的数据来构造最优解,构造时从第一个物品开始。
动态规划之01背包问题(最易理解的讲解)
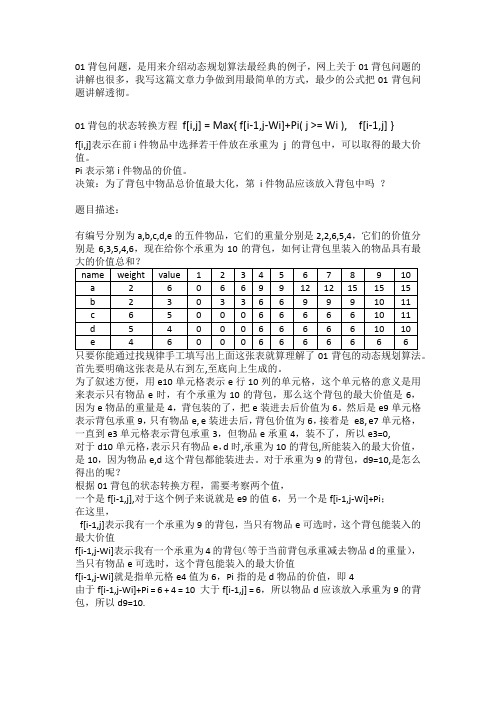
01背包问题,是用来介绍动态规划算法最经典的例子,网上关于01背包问题的讲解也很多,我写这篇文章力争做到用最简单的方式,最少的公式把01背包问题讲解透彻。
01背包的状态转换方程f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }f[i,j]表示在前i件物品中选择若干件放在承重为j 的背包中,可以取得的最大价值。
Pi表示第i件物品的价值。
决策:为了背包中物品总价值最大化,第i件物品应该放入背包中吗?题目描述:有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最首先要明确这张表是从右到左,至底向上生成的。
为了叙述方便,用e10单元格表示e行10列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为10的背包,那么这个背包的最大价值是6,因为e物品的重量是4,背包装的了,把e装进去后价值为6。
然后是e9单元格表示背包承重9,只有物品e, e装进去后,背包价值为6,接着是e8, e7单元格,一直到e3单元格表示背包承重3,但物品e承重4,装不了,所以e3=0,对于d10单元格,表示只有物品e,d时,承重为10的背包,所能装入的最大价值,是10,因为物品e,d这个背包都能装进去。
对于承重为9的背包,d9=10,是怎么得出的呢?根据01背包的状态转换方程,需要考察两个值,一个是f[i-1,j],对于这个例子来说就是e9的值6,另一个是f[i-1,j-Wi]+Pi;在这里,f[i-1,j]表示我有一个承重为9的背包,当只有物品e可选时,这个背包能装入的最大价值f[i-1,j-Wi]表示我有一个承重为4的背包(等于当前背包承重减去物品d的重量),当只有物品e可选时,这个背包能装入的最大价值f[i-1,j-Wi]就是指单元格e4值为6,Pi指的是d物品的价值,即4由于f[i-1,j-Wi]+Pi = 6 + 4 = 10 大于f[i-1,j] = 6,所以物品d应该放入承重为9的背包,所以d9=10.。
动态规划——01背包问题

动态规划——01背包问题⼀、最基础的动态规划之⼀01背包问题是动态规划中最基础的问题之⼀,它的解法完美地体现了动态规划的思想和性质。
01背包问题最常见的问题形式是:给定n件物品的体积和价值,将他们尽可能地放⼊⼀个体积固定的背包,最⼤的价值可以是多少。
我们可以⽤费⽤c和价值v来描述⼀件物品,再设允许的最⼤花费为w。
只要n稍⼤,我们就不可能通过搜索来遍查所有组合的可能。
运⽤动态规划的思想,我们把原来的问题拆分为⼦问题,⼦问题再进⼀步拆分直⾄不可再分(初始值),随后从初始值开始,尽可能地求取每⼀个⼦问题的最优解,最终就能求得原问题的解。
由于不同的问题可能有相同的⼦问题,⼦问题存在⼤量重叠,我们需要额外的空间来存储已经求得的⼦问题的最优解。
这样,可以⼤幅度地降低时间复杂度。
有了这样的思想,我们来看01背包问题可以怎样拆分成⼦问题:要求解的问题是:在n件物品中最⼤花费为w能得到的最⼤价值。
显然,对于0 <= i <= n,0 <= j <= w,在前i件物品中最⼤花费为j能得到的最⼤价值。
可以使⽤数组dp[n + 1][w + 1]来存储所有的⼦问题,dp[i][j]就代表从前i件物品中选出总花费不超过j时的最⼤价值。
可知dp[0][j]值⼀定为零。
那么,该怎么递推求取所有⼦问题的解呢。
显⽽易见,要考虑在前i件物品中拿取,⾸先要考虑前i - 1件物品中拿取的最优情况。
当我们从第i - 1件物品递推到第i件时,我们就要考虑这件物品是拿,还是不拿,怎样收益最⼤。
①:⾸先,如果j < c[i],那第i件物品是⽆论如何拿不了的,dp[i][j] = dp[i - 1][j];②:如果可以拿,那就要考虑拿了之后收益是否更⼤。
拿这件物品需要花费c[i],除去这c[i]的⼦问题应该是dp[i - 1][j - c[i]],这时,就要⽐较dp[i - 1][j]和dp[i - 1][j - c[i]] + v[i],得出最优⽅案。
0-1背包问题

• 因为本题的目标是求解储蓄罐内可以达到的最小金 额,所以初始化时所有dp都为INF(无穷大),且 dp[0]=0。(如果要求解储蓄罐内可以达到的最大金 额,那么应该初始化为-1)。本题的解为dp[n][m], 如果dp[n][m]为INF,则说明m克是一个不可达的状 态。
• 本题dp数组一维,下标为硬币重量。
SPACE ELEVATOR
• 试题来源:USACO 2005 March Gold • 在线测试:POJ 2392
• 奶牛们要上太空了!它们计划建造一座太空电梯作 为它们登上太空的轨道:电梯是一个巨大的、由块 组成的塔,有K(1K400)种不同类型的块用于建 造塔。类型i的块的高度为hi(1hi100),块的数量 为ci(1ci10)。由于宇宙射线可能造成的损害,在 塔中,由类型i的块组成的部分不能超过最大高度ai (1ai40000)。
• 由于本题的数据范围较大,而long long可以存 储19位,因此,将超过19位的部分称为高位部 分(如果存在),19位以内的部分称为低位部 分。设两个long long类型的变量dp1[ ]和dp2[ ], 其中dp1[ ]存储高位部分,dp2[ ]存储低位部分。 这样,就可以按照题目要求的数据规模存储和 输出方式数了。
多重背包
• 多重背包问题描述如下:给定n种物品和一个 载荷能力为M的背包,物品i重量为wi,数量为 numi , 价 值 为 pi , 其 中 wi>0 , pi>0 , numi>0 , 1in;求解将哪些物品装入背包,可使得使 背包里所放物品的总重量不超过M,且背包中 物品的价值总和达到最大。
4种常见的动态规划模型

例谈四种常见的动态规划模型动态规划是解决多阶段决策最优化问题的一种思想方法,本文主要结合一些例题,把一些常见的动态规划模型,进行归纳总结。
(一)、背包模型可用动态规划解决的背包问题,主要有01背包和完全背包。
对于背包的类型,这边就做个简单的描述:n个物品要放到一个背包里,背包有个总容量m,每个物品都有一个体积w[i]和价值v[i],问如何装这些物品,使得背包里放的物品价值最大。
这类型的题目,状态表示为:f[j]表示背包容量不超过j时能够装的最大价值,则状态转移方程为:f[j]:=max{f[j-w[i]]+v[i]},边界:f[0]:=0;简单的程序框架为:beginreadln(m,n);for i:=1to n do readln(w[i],v[i]);f[0]:=0;for i:=1to m dofor j:=1to n dobeginif i>=w[j]then t:=f[i-w[j]]+v[j];if t>f[i]then f[i]:=t;end;writeln(f[m]);end.这类型的题目应用挺广的(noip1996提高组第4题,noip2001普及组装箱问题,noip2005普及组采药等),下面一个例子,也是背包模型的简单转化。
货币系统(money)【问题描述】母牛们不但创建了他们自己的政府而且选择了建立了自己的货币系统。
他们对货币的数值感到好奇。
传统地,一个货币系统是由1,5,10,20或25,50,100的单位面值组成的。
母牛想知道用货币系统中的货币来构造一个确定的面值,有多少种不同的方法。
使用一个货币系统{1,2,5,10,..}产生18单位面值的一些可能的方法是:18×1,9×2,8×2+2×1,3×5+2+1等等其它。
写一个程序来计算有多少种方法用给定的货币系统来构造一个确定的面值。
【输入格式】货币系统中货币的种类数目是v(1≤v≤25);要构造的面值是n(1≤n≤10,000);第1行:二个整数,v和n;第2..v+1行:可用的货币v个整数(每行一个)。
动态规划——背包问题python实现(01背包、完全背包、多重背包)

动态规划——背包问题python实现(01背包、完全背包、多重背包)参考:⽬录描述:有N件物品和⼀个容量为V的背包。
第i件物品的体积是vi,价值是wi。
求解将哪些物品装⼊背包,可使这些物品的总体积不超过背包流量,且总价值最⼤。
⼆维动态规划f[i][j] 表⽰只看前i个物品,总体积是j的情况下,总价值最⼤是多少。
result = max(f[n][0~V]) f[i][j]:不选第i个物品:f[i][j] = f[i-1][j];选第i个物品:f[i][j] = f[i-1][j-v[i]] + w[i](v[i]是第i个物品的体积)两者之间取最⼤。
初始化:f[0][0] = 0 (啥都不选的情况,不管容量是多少,都是0?)代码如下:n, v = map(int, input().split())goods = []for i in range(n):goods.append([int(i) for i in input().split()])# 初始化,先全部赋值为0,这样⾄少体积为0或者不选任何物品的时候是满⾜要求dp = [[0 for i in range(v+1)] for j in range(n+1)]for i in range(1, n+1):for j in range(1,v+1):dp[i][j] = dp[i-1][j] # 第i个物品不选if j>=goods[i-1][0]:# 判断背包容量是不是⼤于第i件物品的体积# 在选和不选的情况中选出最⼤值dp[i][j] = max(dp[i][j], dp[i-1][j-goods[i-1][0]]+goods[i-1][1])print(dp[-1][-1])⼀维动态优化从上⾯⼆维的情况来看,f[i] 只与f[i-1]相关,因此只⽤使⽤⼀个⼀维数组[0~v]来存储前⼀个状态。
那么如何来实现呢?第⼀个问题:状态转移假设dp数组存储了上⼀个状态,那么应该有:dp[i] = max(dp[i] , dp[i-v[i]]+w[i])max函数⾥⾯的dp[i]代表的是上⼀个状态的值。
分支界限方法01背包问题解题步骤

分支界限方法是一种用于解决优化问题的算法。
在动态规划算法中,分支界限方法被广泛应用于解决01背包问题。
01背包问题是一个经典的动态规划问题,其解题步骤如下:1. 确定问题:首先需要明确01背包问题的具体描述,即给定一组物品和一个背包,每个物品有自己的价值和重量,要求在不超过背包容量的情况下,选取尽可能多的物品放入背包,使得背包中物品的总价值最大。
2. 列出状态转移方程:对于01背包问题,可以通过列出状态转移方程来描述问题的求解过程。
假设dp[i][j]表示在前i个物品中,背包容量为j时能够获得的最大价值,则状态转移方程可以表示为:dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+v[i])3. 初始化边界条件:在动态规划中,需要对状态转移方程进行初始化,一般情况下,dp数组的第一行和第一列需要单独处理。
对于01背包问题,可以初始化dp数组的第一行和第一列为0。
4. 利用分支界限方法优化:针对01背包问题,可以使用分支界限方法来优化动态规划算法的效率。
分支界限方法采用广度优先搜索的思想,在每一步选择最有希望的分支,从而减少搜索空间,提高算法的效率。
5. 实际解题步骤:根据上述步骤,实际解决01背包问题的步骤可以概括为:确定问题,列出状态转移方程,初始化边界条件,利用分支界限方法优化,最终得到问题的最优解。
分支界限方法在解决01背包问题时起到了重要的作用,通过合理的剪枝策略,可以有效地减少动态规划算法的时间复杂度,提高问题的求解效率。
分支界限方法也可以应用于其他优化问题的求解过程中,在算法设计和实现中具有重要的理论和实际意义。
在实际应用中,分支界限方法需要根据具体问题进行灵活选择和调整,结合动态规划和剪枝策略,以便更好地解决各类优化问题。
掌握分支界限方法对于解决复杂问题具有重要的意义,也是算法设计和优化的关键技术之一。
分支界限方法在解决01背包问题的过程中,具有重要的作用。
01背包实验报告

算法设计与分析实验报告0_1背包一.问题描述假设有n件物品,每件物品有各自的重量W1,W2,……,Wn和与之对应的价值V1,V2,……,Vn。
设背包的容量为c,在不超过背包容量的前提下,求出获得最大价值总和的方案。
(0-1背包的情况下物品不可分割,只能选择放入,或者不放入背包中)。
二.求解思路1.贪心策略问题开始阶段,将所有物品按价值从高到低排列,每一次往背包里放入不超过背包容量的价值最大的物品,直到没有物品可放入为止。
但事实证明,由于物品的不可分割性,0-1背包并不适合贪心策略。
例:假设背包的容量为50,共有三件物品(重量,价值):(10,60),(20,100),(30,120)。
若使用贪心策略,则会选择一个(30,120)和一个(20,100)。
得到的价值总和是220。
而稍加计算便可知选取两个(20,100)和一个(10,60)可以得到更大的价值总和260。
因此贪心策略不能给出0-1背包的最优解。
后话:即使是普通背包问题(物品可分割),每次选择价值最大的物品也不能得到最优解。
正确的贪心策略应是:每次选择单位重量下价值最大的物品。
由于本次实验主要讨论的是0-1背包问题,这里就不给出该贪心策略的证明。
2.动态规划(1)证明0-1背包问题具有最优子结构性质:假设(x1,x2,……,xn)是容量为c的背包的一组最优解,其中xi的取值为0或1,表示是否放入背包中。
则必有(x2,x3,……,xn)为如下子问题的一组最优解:sum{xi*wi} (2<=i<=n)<=c-x1*w1利用反证法证明,假设(y1,y2,……,yn)是该子问题的一组最优解而(x2,x3,……,xn)不是。
则sum{yi*vi} > sum{xi*vi} (2<=i<=n)那么就可得到:x1*v1+ sum{yi*vi} > x1*v1+ sum{xi*vi} (2<=i<=n)则(x1,y2,……,yn)是原问题的最优解,而(x1,x2,……,xn)不是,与假设矛盾。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
intn = 5;//物品个数
//c[i][j]表示前i个物品能装入容量为Wj的背包中的最大价值
intc[][] =newint[n+1][m+1];
intpath[][] =newint[n+1][m+1];
//初始化第一列和第一行
for(inti=0;i<c.length;i++){
动态规划算法是非常有效的算法技术,那么什么时候使用它呢?或者说其运用场景是什么?若求解问题具有一下性质,可以考虑使用动态规划法:
1、最优子结构:如果一个问题的最优解中包含其子问题的最优解,就是说该问题具有最优子结构。这时候贪婪算法可能也使用求解此类问题
2、重叠子问题:重叠子问题是指用来求解问题的递归算法可以反复的解同样的问题,而不是总在产生新的问题,即当一个递归算法不断的调用同一个问题时,就说该问题包含重叠子问题,此时若使用分治法递归求解时,则每次遇到子问题都会视为新问题,会极大降低效率,而动态规划法对每个子问题仅计算一次,把解保存到在一个需要时就可以查看的表中
根据上述分析,设c[i , w]表示背包容量为w时i个物品最优解的总价值,得到公式:
0i = 0或w = 0
C[i , w ] =c[i – 1, w] wi > w
max{ c[i–1 ,w–wi ] + vi , c[i – 1,w]} i > 0且wi <= w
2、根据物品的件数i = 5、包的容量W = 17规划“价值”分布矩阵,如下图所示:
{
int i,w;
//为二维数组申请空间
int** c = (int**)malloc(sizeof(int *)*(n+1));
for(i=0;i<=n;i++)
c[i] = (int *)malloc(sizeof(int)*(W+1));
//初始化二维数组
for(w=0;w<=W;w++)
c[0][w]=0;
for(i=1;i<=n;i++)
{
c[i][0]=0;
for(w=1;w<=W;w++)
{
//如果背包剩余重量大于物品重量
if(Weights[i-1]<=w)
{
if(Values[i-1]&> c[i-1][w])
{
//重量为w的背包中放入该物品
c[i][w]=Values[i-1]+c[i-1][w-Weights[i-1]];
动态规划算法通常用于求解具有某种最优性质的问题。这类问题中,可能会有许多可行的解,每个解对应个值,我们希望找到最大值或者最小值的那个解,其步骤如下:
1、找出最优值的性质,并分析其结构特征
2、递归定义最优解的值
3、自底向上的方式计算出最优值
4、根据计算最优值得到的信息,构造一个最优解
步骤1—2是基本步骤,在只需求出最优值的情况下步骤4可以省略。若需要求子问题的最优解,则必须执行步骤4,此时在步骤3中计算最优值时,通常记录等多的信息,以便在步骤4中根据所记录的信息快速构造出一个最优解
}else{
c[i][Wj] = c[i-1][Wj];
}
}
}
}
for(inti=0;i<c.length;i++){
for(intj=0;j<c[0].length;j++){
System.out.print(c[i][j]+" ");
}
System.out.println();
}
inti=c.length-1;
intj=c[0].length-1;
while(i>0&&j>0){
if(path[i][j] == 1){
System.out.print("第"+i+"个物品装入");
j -= goods_weight[i-1];
}
i--;
}
}
2、C/C++代码实现如下:
int** demo(int n, int W ,int* Weights,float* Values)
c[i][Wj] = c[i-1][Wj];
else{
if(c[i-1][Wj]<c[i-1][Wj-goods_weight[i-1]]+goods_value[i-1]){
c[i][Wj] = c[i-1][Wj-goods_weight[i-1]]+goods_value[i-1];
path[i][Wj] = 1;
c[i][0] = 0;
}
for(inti=0;i<c[0].length;i++){
c[0][i] = 0;
}
//通过公式迭代计算
for(inti=1;i<c.length;i++){
for(intWj=1;Wj<c[0].length;Wj++){
if(goods_weight[i-1]>Wj)
(1)物品价值重量关系表
(2)物品件数—价值分布矩阵
(二)程序实现
1、Java语言代码实现如下:
publicstaticvoidmain(String[] args) {
int[] goods_weight = {3,4,7,8,9};//物品重量
int[] goods_value = {4,5,10,11,13};//物品价值
动态规划法求解0-1背包问题
一、动态规划法的设计思想
动态规划法是数学--“运筹学”中一个决策分析的实现,广泛运用在计算机算法、企业决策、市场营销等领域
动态规划法是将待求解的问题分成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合用动态规划法求解的问题,经过分解的子问题往往不是独立的。若用分治法求解这类问题,则相同的子问题会被求解多次,以至于最后解决问题需要消耗指数级别的时间。然而,不同子问题的数目常常只有多项式量级。如果能够保存已经解决的子问题的答案,在需要时再找出已经求得的答案,这样就可以避免大量的重复计算,从而得到多项式时间的算法。为了达到这个目的,可以使用个表来记录已经解决子问题的答案,不管子问题以后是否被用到,只要它计算过,就将其结果填入表中,这就是动态规划法的基本思路
}else{
//重量为w的背包中不放入该物品
c[i][w]=c[i-1][w];
}
}else{
c[i][w] = c[i-1][w];
}
}
}
return c;
}
11
13
重量w
3
4
7
8
9
(一)、求解思路
1、使用矩阵规划出最优解
把求解过程看作是一系列的决策过程,即决定哪些物品应该放入背包,哪些物品不放入背包
(1)如果一个问题的最优解包含了物品n,即Xn=1,那么其余的X1,X2,….Xn-1一定构成子问题1,2,……n-1在容量为W-wn时的最优解
(2)如果这个最优解不包含物品n,即Xn=0,那么其余X1,X2….,Xn-1一定构成子问题1,2….,n-1在容量为W时的最优解
二、动态规划法案例:0-1背包问题
有n个物品,第i个物品的价值为Vi,重量为Wi,其中Vi和Wi均为非负数,背包容量为W,W为非负数。现考虑如何选择装入背包的物品,使装入背包的物品总价值最大。假设商品有5件,n=5,容量为17,W=17
要装入的物品及其价值如下表所示:
物品编号
1
2
3
4
5
价值v
4
5
10
