8角度调制习题及答案0
通信原理第三章测试题

一.填空 1.对DSB —SC 信号,当采用插入导频法进行载波同步时,插入的条件是( )。
2.残留边带滤波器的传输特性H (w )应该是( )。
3.AM 系统在( )情况下会出现门限效应。
4.什么是门限效应?AM 信号瞎用包络检波法为什么会产生门限效应? 5.在残留边带调制系统中,为了不失真地恢复信号,其传输函数H (w )应满足( )。
6.在解调过程中,( )的解调方式会产生门限效应,产生门限效应的原因是( )。
7.当调频指数满足( )时称为窄带调频。
8.相干解调器由( )和( )组成,信号与噪声可以分开处理,故没有门限效应。
9.门限效应是由包络检波器的( )作用所引起的。
10.什么是频分复用? 填空答案:1.载频处、正交插入2.在载频两边具有互补对称特性 3.在包络检波时且小信噪比时4小信噪比时,解调输出信号无法与噪声分开,有用信号“淹没”在噪声中,这时候输出信噪比不是按比例地随着输入信噪比下降,而是急剧恶化。
这种现象称为门限效应。
5.H ()()c c H H ωωωωωω++-=≤常数, 6.非相干解调 非线性应用 7.1f m <<8.相乘器 低通滤波器 9.非线性解调 10.利用调制技术将各路信息信号调制到不同载频上,使各路信号的频谱搬移到各自的子通道内,合成后送入信道传输。
在接收端,采用一系列不同中心频率的带通滤波器分离出各路已调信号,解调后恢复各路相应的基带信号。
1.常见的幅度调制方式:(调幅<AM>)、(双边带<DSB>)、(单边带<SSB>)、(残留边带<VSB>)。
2.如果把语音信号0.3-3.4kHZ 直接通过天线发射,那么天线的长度为(22km ) 3.基带信号控制高频载波的过程叫(调制)4.要保证Ao+f (t )总是正的,对于所有的t ,必须要求( )5.( )越大,说明这种调制制度的抗干扰性能越好。
《数字通信原理》第2章习题(不含答案)

(1)FM 波的表达式;(2)FM 波的频率偏移;(3) 调制信号频率提高到 2×103Hz 时的频率偏移。 45. 有一个 2MHz 的载波受一个 20kHz 单频正弦信号调频,峰值频偏为 10kHz,求: (1) 调频信号的频带带宽; (2) 调制信号幅度加倍后调频信号的带宽; (3) 调制信号频率加倍后调频信号的带宽。
上可以用调制信号与载波信号直接____________得到。
6. 非线性调制是不满足线性调制条件的调制,__________调制和__________调制都是非线
性调制。
7. 对__________调制而言,已调信号的频谱不再是原调制信号频谱的线性搬移,而是频谱
的非线性变换,会产生与频谱搬移不同的新的频率成分。
在频谱结构上,它的频谱完全是基带信号的频谱在频域内的简单搬移,由于这种搬移是线
性的,因此,这种调制通常又称为________。
5. 线性调制的特点是已调信号的频谱与调制信号的频谱相比,在形状上____________,即
不改变调制信号的____________,但在频谱的幅值上差一个倍数。另外,线性调制在数学
A.AM
B.DSB
C.SSB D.VSB
28. 在同等条件下,抗噪性能最好的调制技术是( )。
A.AM
B.DSB
C.SSB D.FM
29. 以下说法正确的是( )。
A.若对调制信号先进行微分,再进行调频则得到调相信号
B.若对调制信号先进行微分,再进行调相则得到调频信号
C.若对调制信号先进行积分,再进行调频则得到调相信号
A.0.3 kHz B.10 kHz
C.5 kHz
D.0.6 kHz
25. 相干解调中,相干载波与已调信号的载波必须( )。
高频电子线路(第八章 角度调制与解调)PPT课件

例题8.1
已知一个信c号 o2s表 [1达 00 (式 t022为 t)]
2 求其瞬时相率 位。 和瞬时频
解 :瞬时 (t) 2 相 10 位 (t2 0 2 t) 0 2
(t) d(t) 2 10 (2 t0 2 ) 0 40 (t 0 1 )0 dt
注意这是一个加的速矢转,量 波 动形示意图为
式中(3) PM波瞬时频偏:
(t)kp
dv(t) dt
(4)最大频偏: kp| ddv(tt)|max
16
调频与调相的关系
t
a F(M t)A 0co0 ts k [f 0v ()d]
a P( M t)A 0co0 ts k [p v (t)]
比较二式 :如会 果发 我 h(t现 )们 0tv 对 ()d这个信号
第八章 角度调制与解调
(包括调频与调相)
1
本章结构
§8.1 概述 §8.2 调角波的性质
调制信号vΩ为标准余弦时调频调相的表达式 调制指数、最大频偏的概念和计算 频带宽度的计算
§8.3 调频方法概述 §8.4 直接调频电路简介 §8.5 调频信号的解调
2
§8.1 概述
任意余弦波信号: v 0 ( t) V 0 m c o s (0 t 0 ) V 0 m c o s( t)
(t)t0
但是如果矢量的旋转速度“时快时慢”, 那么如何求瞬时相位呢?
7
瞬时频率(续)
我们定义,矢量在任意时刻旋转的速度
(t) 为这个旋转矢量的瞬时角频率,简
称瞬时频率
则瞬时相位 (t)0t()d0
两边t求 同导 时 d(t)得 对 (t)
dt
即 : 瞬 时 频 率 是 瞬 时 相 位 函 数 的 的 导 函 数
角度调制与解调答案

6.5 调频振荡回路由电感 L 和变容二极管组成, L 2μH,变容二极管的参数为: Co 225pF , =1 2 ,
U D 0.6V , U Q
4
6V ,调制信号 u (t ) 3sin10 t 。求输出 FM 波时:
( 1)载波 f o ;( 2)由调制信号引起的载频漂移
fo ;( 3)最大频率偏移 fm ;( 4)调频灵敏度 k f 。
偏移 m 。
解:( 1) FM : f (t)
k f u (t )
3
5 10
Hale Waihona Puke 2cos(242000t ) 10 cos(2
∴ fm 104 Hz 10kHz
mf
fm 104 5
F 2000
2000t ) ( F 2000Hz )
( 2) PM : (t ) k pu (t ) 2.5 2cos(2 2000t ) 5cos(2 2000t ) ( F 2000Hz )
3
3sin3 10 t
3
10 t ](V)
6.4 已知调制信号为 u (t) U cos2 103 t , m f mp 10 ,求此时 FM 波和 PM 波的带宽。 若 U 不 1 / 10
变, F 增大一倍,两种调制信号的带宽如何变化?若
F 不变, U 增大一倍,两种调制信号的带宽如
何变化?若 U 和 F 都增大一倍,两种调制信号的带宽又如何变化?
1 m f , mp 不变;
2
∴ BFM BPM
2(mf 2(mp
( 3) FM: m f
1)F
1)F kfU
F
2(5 1) 2 103=24 103 (Hz) 2(10 1) 2 103 =44 103(Hz)
高频电子线路最新版课后习题解答第七章——角度调制与解调答案

第七章 思考题与习题7.1 什么是角度调制?解:用调制信号控制高频载波的频率(相位),使其随调制信号的变化规律线性变化的过程即为角度调制。
7.2 调频波和调相波有哪些共同点和不同点,它们有何联系?解:调频波和调相波的共同点调频波瞬时频率和调相波瞬时相位都随调制信号线性变化,体现在m f MF ∆=;调频波和调相波的不同点在:调频波m f m f k V Ω∆=与调制信号频率F 无关,但f m f k V M Ω=Ω与调制信号频率F 成反比;调相波p p m M k V Ω=与调制信号频率F 无关,但m f m f k V Ω∆=Ω与调制信号频率F 成正比;它们的联系在于()()d t t dtϕω=,从而具有m f MF ∆=关系成立。
7.3 调角波和调幅波的主要区别是什么?解:调角波是载波信号的频率(相位)随调制信号的变化规律线性变化,振幅不变,为等福波;调幅波是载波信号的振幅随调制信号的变化规律线性变化,频率不变,即高频信号的变化规律恒定。
7.4 调频波的频谱宽度在理论上是无限宽,在传送和放大调频波时,工程上如何确定设备的频谱宽度? 解:工程上确定设备的频谱宽度是依据2m BW f =∆确定7.5为什么调幅波调制度 M a 不能大于1,而调角波调制度可以大于1?解:调幅波调制度 M a 不能大于,大于1将产生过调制失真,包络不再反映调制信号的变化规律;调角波调制度可以大于1,因为f fcmmV M k V Ω=。
7.6 有一余弦电压信号00()cos[]m t V t υωθ=+。
其中0ω和0θ均为常数,求其瞬时角频率和瞬时相位解: 瞬时相位 00()t t θωθ=+ 瞬时角频率0()()/t d t dt ωθω==7.7 有一已调波电压1()cos()m c t V A t t υωω=+,试求它的()t ϕ∆、()t ω∆的表达式。
如果它是调频波或调相波,它们相应的调制电压各为什么?解:()t ϕ∆=21A t ω,()()12d t t A t dtϕωω∆∆==若为调频波,则由于瞬时频率()t ω∆变化与调制信号成正比,即()t ω∆=()f k u t Ω=12A t ω,所以调制电压()u t Ω=1fk 12A t ω 若为调相波,则由于瞬时相位变化()t ϕ∆与调制信号成正比,即 ()t ϕ∆=p k u Ω(t )所以调制电压()u t Ω=1pk 21A t ω 由此题可见,一个角度调制波可以是调频波也可以是调相波,关键是看已调波中瞬时相位的表达式与调制信号:与调制信号成正比为调相波,与调制信号的积分成正比(即瞬时频率变化与调制信号成正比)为调频波。
现代通信原理(罗新民)指导书 第六章 角度调制系统 习题详解

①已调信号的平均功率;
②最大频率偏移;
③最大相位偏移;
④已调信号的近似带宽;
⑤判断该已调信号是FM波还是PM波。
解: 已调信号的平均功率为
②信号瞬时频率为
因此信号最大频偏为
瞬时相位偏移为
因此信号最大相位偏移为
根据卡森带宽,
根据已调信号表达式判断是FM波还是PM波,主要依据是瞬时相偏与调制信号成正比还是瞬时频偏与调制信号成正比。根据题目所给,在未知调制信号是正弦波还是余弦波的情况下,该已调信号既可能是正弦波作FM调制,也可能是余弦波作PM调制。因此,不能判断是FM波还是PM波。
6-2用频率为10kHz,振幅为1V的正弦基带信号,对频率为100MHz的载波进行频率调制,若已调信号的最大频偏为1MHz,试确定此调频信号的近似带宽。如果基带信号的振幅加倍,此时调频信号的带宽为多少?若基带信号的频率加倍,调频信号的带宽又为多少?
解: 由题目可知 , 。根据卡森带宽公式可以得到调频信号的带宽近似为
解: 采用类似教材上推导单音频调制的方法,可将已调信号展开为
所以调频波的频谱由若干根离散谱线组成,每根谱线幅度为 ,位于 , ; 未调载波谱线幅度为 。
由贝塞尔函数查表,得
。
可算出大于未调载波幅度1%的边频分量的幅度:
,( );
;
, ;
。
以上即为调频波中的各谱线对应的幅度(再×A ),频谱图如下所示:
第六章角度调制系统
6-1设角度调制信号
①若 为FM波,且 ,试求调制信号 ;
②若 为PM波,且 ,试求调制信号 ;
③试求最大频偏 及最大相位移 。
解: FM已调信号瞬时相位为 ,对其取导数得到瞬时角频率为
高频电子线路 第6章 习题答案

第6章角度调制与解调电路6.1已知调制信号38cos(2π10)V u t Ω=⨯,载波输出电压6o ()5cos(2π10)V u t t =⨯,3f 2π10rad/s V k =⨯ ,试求调频信号的调频指数f m 、最大频偏m f ∆和有效频谱带宽BW ,写出调频信号表示式[解]3m 3m 2π108810Hz2π2πf k U f Ω⨯⨯∆===⨯3m33632π1088rad2π102(1)2(81)1018kHz ()5cos(2π108sin 2π10)(V)f f o k U m BW m F u t t t Ω⨯⨯===Ω⨯=+=+⨯==⨯+⨯6.2已知调频信号72()3cos[2π105sin(2π10)]V o u t t t =⨯+⨯,3f 10πrad/s V k = ,试:(1)求该调频信号的最大相位偏移f m 、最大频偏m f ∆和有效频谱带宽BW ;(2)写出调制信号和载波输出电压表示式。
[解](1)5f m =5100500Hz=2(+1)2(51)1001200Hzm f f m F BW m F ∆==⨯==+⨯=(2)因为mf f k U m Ω=Ω,所以352π1001V π10f m fm U k ΩΩ⨯⨯===⨯,故27()cos 2π10(V)()3cos 2π10(V)O u t t u t t Ω=⨯=⨯6.3已知载波信号m c ()cos()o u t U t ω=,调制信号()u t Ω为周期性方波,如图P6.3所示,试画出调频信号、瞬时角频率偏移()t ω∆和瞬时相位偏移()t ϕ∆的波形。
[解]FM ()u t 、()t ω∆和()t ϕ∆波形如图P6.3(s)所示。
6.4调频信号的最大频偏为75kHz ,当调制信号频率分别为100Hz 和15kHz 时,求调频信号的fm 和BW 。
[解]当100Hz F =时,37510750100m f f m F ∆⨯===2(1)2(7501)100Hz 150kHzf BW m F =+=+⨯=当15kHz F =时,33751051510m f f m F ∆⨯===⨯32(51)1510Hz 180kHzBW =+⨯⨯=6.5已知调制信号3()6cos(4π10)V u t t Ω=⨯、载波输出电压8()2cos(2π10)V o u t t =⨯,p 2rad /V k =。
8-1 角度调制的基本概念
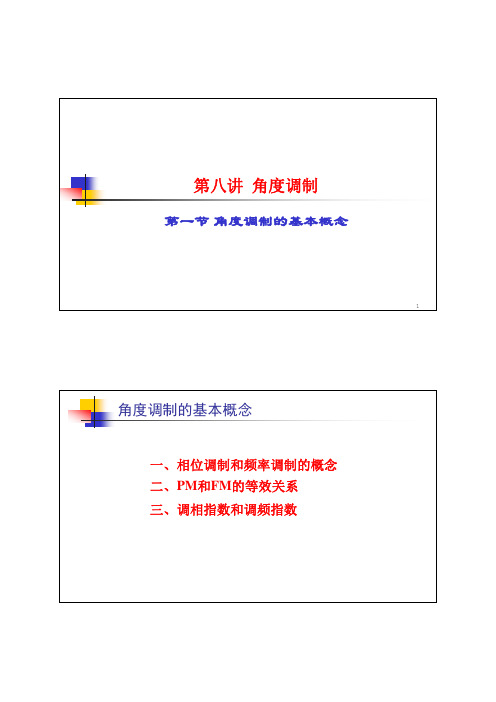
¾ PM是瞬时相位偏移随调制信号m(t)线性变化;
¾ FM是瞬时相位偏移随m(t)的积分呈线性变化。
讨论:如果预先不知道调制信号m(t)的具体形式,能否判
断已调信号是调相信号还是调频信号?
7
角度调制的基本概念
¾ 单频信号的PM和FM信号波形
m(t )
m(t )
ω(t) ωc
t
t
ω (t)
ωc
sPM (t )
Kp - 调相灵敏度(单位是rad/V),表示单位调制信号幅 度引起PM信号的相位偏移量
5
角度调制的基本概念
频率调制(FM)
瞬时频率偏移随调制信号而线性变化dϕ (Fra bibliotek) dt=
K
f m(t)
∫ ϕ ( t ) = K f
t m (τ )dτ
−∞
∫ sFM ( t ) = A cos[ω c t + K f
第八讲 角度调制
第一节 角度调制的基本概念
1
角度调制的基本概念
一、相位调制和频率调制的概念 二、PM和FM的等效关系 三、调相指数和调频指数
角度调制的基本概念
一、相位调制和频率调制的概念
任意一个幅度不变的 正弦函数
c (t) = A cosθ (t)
正弦波的 瞬时相位
θ
(t)
=
∫t ω −∞
(τ
)dτ
ω (t ) = dθ (t )
dt
正弦波的瞬时角 频率
未调制载波 c ( t ) = A cosθ ( t ) = A cos ⎡⎣ωct + θ0 ⎤⎦
角度调制信号 sm (t ) = A cos[ωct + ϕ (t )]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章 角度调制与解调思 考 题8.1 已知载波f c =100MH Z ,载波电压振幅U cm =5V ,调制信号u Ω(t )= ( cos2π×103t +2cos2π×500t )V 。
试写出下述条件调频波的数学表达式:(1) 频灵敏度K f =1kH Z /V 。
(2)频偏△f m =20kH Z 。
解:(1)⎥⎦⎤⎢⎣⎡+=⎰Ωtt f c cm t FM dt u k t U u 0)()(cos ω⎥⎦⎤⎢⎣⎡⨯⋅⨯+⨯⋅⨯+⨯⨯⨯=⎥⎦⎤⎢⎣⎡⨯+⨯+=⎰⎰t t t tdt k tdt k t f t tf f c 5002sin 50022000102sin 10210001010014.32cos 55002cos 2102cos 2cos 5336003πππππππ()t t t 5002sin 64.0102sin 16.01028.6cos 538⨯+⨯+⨯=ππ(2)因为max )(2t u k f f m m Ω=∆=∆πω所以V KHz t u f k m f /8.622102014.32)(23max =⨯⨯⨯=∆=Ωπ所以()tt t dt t u k t U t u tf c cm FM 5002sin 40102sin 101028.6cos 5)(cos )(380⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+=⎰Ωππω8.2 载波振荡频率f c =25MH Z ,振幅U cm =4V ;调制信号为单频余弦波,频率为F =400H Z ;最大频偏△f m =10kH Z 。
(1) 分别写出调频波和调相波的数学表达式。
(2) 若调制频率变为2 kH Z ,其他参数均不变,再分别写出调频波和调相波的数学表达式。
解:(1)因为F m f f m ⋅=∆,所以rad KHz KHz F f m m f 254.010==∆=所以:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 251057.1cos 42sin 252cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()t t t m t U t u P c cm PM 38105.2sin 251057.1cos 4cos cos )(⨯+⨯=Ω+=ω(2)如果F=2KHz ,则rad KHzKHzm m P f 5210=== 近而可写出调频波和调相波的数学表达式:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 51057.1cos 42sin 52cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()t t t m t U t u P c cm PM 38105.2sin 51057.1cos 4cos cos )(⨯+⨯=Ω+=ω8.3若调频波的中心频率f c =100MH Z ,最大频偏△f m =75kH Z ,求最高调制频率F max 为下列数值时的m f 和带宽:(1) F max =400 H Z ;(2) F max =3kH Z ;(3) F max =15kH Z 。
解:(1)rad KHzKHzF f m m f 5.1874.075max ==∆=,()KHz F f BW m 8.1502max =+∆= (2)rad KHz KHzF f m m f 25375max ==∆=,()KHz F f BW m 1562max =+∆= (3)rad KHzKHzF f m m f 51575max ==∆=,()KHz F f BW m 1802max =+∆=8.4 设调角波的表达式为u (t )=5cos(2×106πt +5cos2×103πt )V 。
(1) 求载频f C 、调制频率F 、调制指数m 、最大频偏△f m 、最大相偏△ϕm 和带宽。
(2) 这是调频波还是调相波?求相应的原调制信号(设调频时K f =2kHz/V ,调相时K p=1rad/v)。
解:(1)MHz f C C 1210226=⨯==πππω,KHz F 1210223=⨯=Ω=πππ rad m 5=,KHz KHz F m f f m 515=⨯=⋅=∆,()KHz KHz KHz BW 12152=+= rad m m 5==∆ϕ(2)可能是调频波,也可能是调相波。
如果看成调频波:t t u π3102sin 5.2)(⨯-=Ω 如果看成调相波:t t u π3102cos 5)(⨯=Ω8.5 若调角波的调制频率F =400Hz ,振幅U Ωm =2.4V ,调制指数m=60rad 。
(1) 求最大频偏△f m 。
(2) 当F 降为250Hz ,同时U Ωm 增大为3.2V 时,求调频和调相情况下调制指数各变为多少?解:(1)KHz KHz mF f m 244.060=⨯==∆ (2)由V KHz k U k m f mf f /10=Ω=Ω得所以可得当F 降为250Hz ,同时U Ωm 增大为3.2V 时rad m f 12825.02.310=⨯=由V rad k U k m P m P P /25==Ω得所以可得当F 降为250Hz ,同时U Ωm 增大为3.2V 时rad m P 802.325=⨯= 8.6 若载波u c(t)=10cos2π×50×106tV ,调制信号为u Ω(t)=5sin2π×103tV ,且最大频偏△f m =12kHz ,写出调频波的表达式。
解:由题可知:rad Ff m U mf C cm 12102101038=∆=⨯=Ω==ππω 所以:()t m t U t u f C cm FM Ω+=sin cos )(ω()t t 38102sin 1210cos 10⨯+=ππ8.7 用正弦调制的调频波的瞬时频率为f (t)=(106+104cos2π×103t)Hz ,振幅为10V ,试求:(1) 该调频波的表达式。
(2) 最大频偏△f m 、调频指数m f 、带宽和在1Ω负载上的平均功率。
(3) 若将调制频率提高为2×103Hz ,f(t)中其他量不变,△f m 、m f 、带宽和平均功率有何变化?解:(1)由题得:)102cos 1010(2)()(3406t dt t t tt⨯+==⎰⎰ππωϕt t 36102sin 10102⨯+⨯=ππ 所以()t t t u FM ππ36102sin 10102cos 10)(⨯+⨯=(2)WR U P KHzF f BW rad KKF f m KHz t u f L cm av m m f m 5021002122)(21011010)(2max max ====+∆===∆===∆Ω(3)不变W p KHzKHz BW radm KHzf av f m 5024)210(2521010==+====∆ 8.8 调制信号为余弦波,当频率F =500Hz 、振幅U Ωm =1V 时,调角波的最大频偏△f m1=200Hz 。
若U Ωm =1V ,F =1kHz ,要求将最大频偏增加为△f m2=20kHz 。
试问:应倍频多少次(计算调频和调相两种情况)?解:根据题目已知的条件可得rad F f m m m P f 4.05002001==∆==(1)对于调频波由Ω⋅=Ωmf f U k m 得k f =2×3.14×200,所以在U Ωm =1V ,F =1kHz时,KHz F U k f mf m 2.0100010001200=⨯⨯=∙Ω⋅=∆Ω,所以要将最大频偏增加为△f m2=20kHz ,则应倍频100次。
(2)对于调相波由m P P U k m Ω=得k p =0.4,所以在U Ωm =1V ,F =1kHz 时,KHz F U k f m P m 4.0114.0=⨯⨯=⋅⋅=∆Ω,所以要将最大频偏增加为△f m2=20kHz ,则应倍频50次。
8.9在变容管直接调频电路中,如果加到变容管的交流电压振幅超过直流偏压的绝对值,则对调频电路有什么影响?答:如果加到变容管的交流电压振幅超过直流偏压的绝对值,则在信号的一个周期内的某些时间,变容二极管有可能会正向导通,则失去结电容随反偏电压变化的特性,因而不能实现调频。
8.10双失谐回路斜率鉴频器的一只二极管短路或开路,各会产生什么后果?如果一只二极管极性接反,又会产生什么会果?答:如果一只二极管开路,则电路相当于单失谐回路鉴频器;如果一只二极管短路,则输出的低频调制信号中将叠加有调幅-调频波;如果一只二极管接反,则两检波器输出电压大小相等,极性相同,在输出端相互抵消,输出电压为零。
习图5—1中,0360MHz f =,变容管的3γ=,0.6V V Ω=,cos v t Ω=Ω。
(1)分析电路工作原理,画出交流等效电路。
(2)已知当6V Q V =-时,20pF jQ C =。
求2?L = (3)求m f ∆及调制灵敏度(/m Q f V ∆)。
解:(1)该电路是1C 、2C 、变容二极管和电感L 组成的电容三端式振荡器。
当v Ω改变变容管反向偏置电压时,变容管j C 随之变化,从而振荡频率随v Ω规律变化而实现调频。
(2)12120.51pF 0.513C C C C C ===++ 203'0.33pF 1203jQ jQCC C C C ∑==≈++262120110.59μH (2)'(236010)0.3310L f C ππ-∑===⨯⨯⨯⨯(3)0(1)j j r DC C v V γ=+ ()c o s r Q v t V V t Ω=+Ω 0(1cos )cos (1)j j jQ Q DC C C m t V V tV γγ-Ω==+Ω+Ω+其中 00(1)j Q DC C V V γ=+ 110.1560.6 6.6Q D V m V V Ω===≈++ j j CC C C C ∑=+()t ωωω=====0ω==0v Ω=时的载频)11jQ jQC p C C =≈+ 20.016jQCp C C =≈+()t ωω=将()t ω在cos 0t Ω=处展开成泰勒级数,有:220222202220012111()[1cos (1)cos ]24211111[1(1)cos (1)cos 2]82282cos cos 2t p m t p m t p m p m t p m t t t ωωωγγγωγγγγγωωωω==+Ω+--Ω+=+--+Ω+--Ω+=+∆+∆Ω+∆Ω+习图5—2中,哪个电路能实现包络检波?哪个电路能实现鉴频?01f 和02f 如何配置?解:(a )图中两谐振回路的谐振曲线如图所示。
