K的几何意义
反比例函数K的几何意义

反比例函数K的几何意义反比例函数是一种特殊的数学函数形式,具有形如y=k/x的表达式,其中k是一个常数。
在这个函数中,x和y之间存在一种特殊的关系:当x增大时,y会减小,反之亦然。
因此,反比例函数的几何意义可以通过分析函数图像和实际例子来理解。
首先,我们可以通过绘制反比例函数的图像来揭示其几何意义。
考虑一个简单的例子:y=1/x。
对于这个函数,我们可以观察到以下几个重要的特点:1.图像总是通过第一象限的正半轴和第三象限的负半轴。
这是因为除数不能为零,所以函数在x=0时无定义。
2.图像与两条坐标轴的交点确定了函数的极值点:当x趋近于正无穷或负无穷时,y趋近于零。
这也表示当x趋近于零时,y趋近于正或负无穷。
3.图像是关于y=x和y=-x的直线对称的。
这是因为当x和y的值交换时,函数的值保持不变。
通过上述特点,我们可以揭示反比例函数的几何意义。
函数的图像形状类似于一组双曲线的分支,其中的曲线与两条坐标轴无法相交,而它们的渐近线分别与坐标轴平行。
这暗示了反比例函数的一个重要特点:随着一个变量的增加,另一个变量会减少。
例如,在y=1/x的情况下,我们可以看到当x增加时,y会减小。
1.电阻和电流:欧姆定律表明电阻与电流成反比例关系。
当电流增大时,电阻减小。
这可以解释为,当电阻较低时,电流可以更容易地通过电路,导致电流增加。
2.时间和任务完成率:假设一个人在一段时间内完成了一定数量的任务。
如果任务数量保持不变,增加时间将导致任务完成率降低。
这是因为在更长的时间内,完成的任务数量将更少。
3.运动速度和到达时间:当我们维持一定的目的地距离不变时,提高行驶速度将缩短到达目的地所需的时间。
这是因为较高的行驶速度意味着我们每单位时间所覆盖的距离更多。
这些例子揭示了反比例函数在现实生活中的广泛应用,从电路设计到时间管理,以及交通规划等等。
通过理解反比例函数的几何意义,我们可以更好地理解和应用这个数学概念。
总而言之,反比例函数是一种数学函数形式,其几何意义可以通过分析函数图像和实际例子来理解。
反比例函数中比例系数k的几何意义

反思小结
在反比例函数 y 10 的图象上,有一系列点A1,A2, x A3…..An,An+1,若A1横坐标为2,且以后每点的 横坐标与它前一个点的横坐标的差都为2. 现分别 过点A1,A2,A3…..An,An+1作X轴与Y轴的垂线 段,构成若干个矩形如图10所示,将图中阴影部 分的面积从左到右依次记为S1、S2、S3、…Sn, 5 5 15 2 5 2 (5 _____, ) 则S1=________, S +S +S =____ S1+S2 2 1 2 3 4 2 5 10 n 2 (5 ) +S3+….+Sn=________________.( 用n的代数式表 n 1 n 1 A 示)
C
S SOAD SABD SBCD SOCD 4 1 4
达标测试
已知几何图形的面积S,求比例系数k
5、如图,已知双曲线 (k>0) 经过矩形OABC边AB的中点F,交BC于点E, 且四边形OEBF的面积为2,则k的值为( B )。
y
y
k x
A 1
所以
B 2
C 4
S OAB 4
O
y
已知几何图形的面积S,求比例系数k k y 变式、如图,已知双曲线 x ( k>0 )经
B
D
C E A
x
而
SOAB SOBC SOAC
即
S ODE 1 S OAB 1 4 k 3 2
1 k 2
相似三角形的面积比 等于相似比的平方 k 4;
k 0 k 4
k 0 k 4
4 y x
达标测试
4、如图,在平面直角坐标系中, 点O为原点,菱形OABC的对角线 OB在x轴上,顶点A在反比例函数 2 的图像上,求菱形的面积。 y B
反比例函数中K的几何意义课件

k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中,k值决定了图 像的形状和位置。当k>0时,图像出 现在第一象限和第三象限;当k<0时 ,图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时,图像分布在第一象限和第三象限;当k<0时,图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展,反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域,如经济学、生物学等,以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念,与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系,以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小,反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用,如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解,但仍有许多未知的性质等待我们去发 现和研究。例如,反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质:当 x 增大时,y 值会减小;当 x 减小 时,y 值会增大。这是因为 xy =
k 的关系。
在图像上,反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的,且无限接近于坐标轴
。
Part
02
k的几何意义
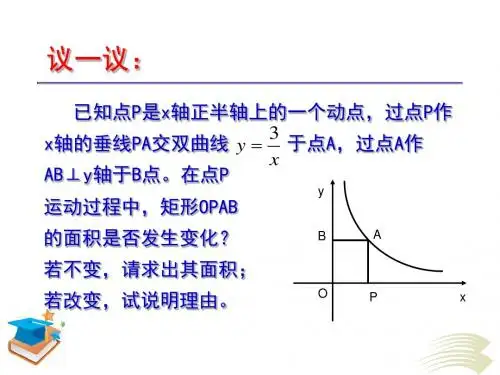
已知点P是x轴正半轴上的一个动点,过点P作 3 x轴的垂线PA交双曲线 y 于点A,过点A作 x AB⊥y轴于B点。在点P
运动过程中,矩形OPAB 的面积是否发生变化?
y B A
若不变,请求出其面积;
若改变,试说明理由。
O P x
K的几何意义:
过双曲线 y 足分别为A、B,则
k (k 0) 上一点P(m,n)分别作x轴,y轴的垂线,垂 x
x
∴y= 2x-2
综合运用:
(2)根据图象写出反比例函数的值大于一次函数 y 的值的x的取值范围.
(2)观察图象得: 当x<-1或0<x<2时, 反比例函数的值大 于一次函数的值.
M(2,m)
-1 0 2
x
N(-1,-4)
A 、 C 两点 .AB⊥x轴于B,CD⊥y轴于 D(如图 ),则四边形
ABCD的面积为( (A )1 (C )2 )
D C y A O B
3 (B ) 2 (D ) 5 2
x
3:已知点A(0,2)和点B(0,-2),点
1 P在 y 函数的图象上,如果△PAB的 x
面积是6,求P的坐标。
综合运用:
S矩形OAPB =OA· AP=|m| · |n|=|k|
y .P(m,n)
B
.P(m,n) .P(m,n)
A
o
x
变式一:
如图,点P是反比例函数图象上的一点,过点P 分别向x轴、y轴作垂线,若阴影部分面积为12,则 12 y = 这个反比例函数的关系式是__________ x 。
y
p
N
o x
M
变式二:
解:(1)∵点N(-1,-4)在反比例函数图象上 ∴k=4, 又∵点M(2,m)在反比例函数 图象上 ∴m=2 ∴M(2,2)
[整理版]正比例函数K的几何意义专
![[整理版]正比例函数K的几何意义专](https://uimg.taocdn.com/299fe77a82c4bb4cf7ec4afe04a1b0717fd5b32a.webp)
当k>0时,直线从左下方向右上方倾斜,倾斜角α为锐角;当k<0时,直线从左 上向右下方倾斜,倾斜角α为钝角。
直线斜率与面积关系
斜率K与三角形面积
在直角坐标系中,若直线y=kx与x轴、y轴围成一个三角形,则该三角形的面积S 与斜率k之间存在关系S=1/2*|k|。
斜率K与平行四边形面积
VS
方法二
利用相似三角形的性质,若两个三角形相 似,则它们的对应边成比例。设两个相似 三角形的对应边分别为$l_1, l_2$和$l_1', l_2'$,则有$frac{l_1}{l_1'} = frac{l_2}{l_2'}$。若这两个三角形的一条 边与x轴平行,那么这条边的长度比就等 于两三角形的斜率之比,即$frac{k}{k'} = frac{l_1}{l_1'} = frac{l_2}{l_2'}$。
工程学中效率与工作量关系
工作效率与工作量关系
在工程学中,工作效率η通常与工作量W成正比关系。高效率意味着在相同时间内可以完成更多的工 作,即η=kW,其中k为比例系数。
机器性能与工作负载关系
机器的性能表现通常与其工作负载成正比。当机器承受的负载增加时,其性能表现也会相应提升,以 保持稳定的工作效率,即P=kW,其中k为比例系数。
正比例函数与反比例函数关系
01
正比例函数和反比例函数是两种不同类型的函数,它
们之间没有直接的转化关系。
02
正比例函数的自变量和因变量之间是线性关系,而反
比例函数的自变量和因变量之间是倒数关系。
03
在平面直角坐标系中,正比例函数的图像是一条过原
点的直线,而反比例函数的图像是一条双曲线。
26.1.2反比例函数k的几何意义

预备铃响进教室,全体做到静快齐 学习用品准备好,心宁神定坐姿正 细心听讲不插话,眼到耳到心更到
自主学习并不难,学辅资料好帮手 勤做笔记勤思考,圈点勾画有取舍 独立作业勤动脑,不要抄袭不拖延
米斯拉说:“数学是人类思考中最高的成 就” 培根说:“数学是打开科学大门的钥匙” 黑格尔说:“数学是上帝描述自然的符号”
A. 面积分别为S1 , S 2 , S3 , 则有 __ A.S1 = S2 = S3 B. S1 < S2 < S3 C. S3 < S1 < S2 D. S1 > S2 >S3
y
A S1 B
C
o
S2 S3 A1 B1 C1
x
3 y 5.如图,A,B是双曲线 上的点,分别经过A,B两点向X x
三角形的面积是不变的,为:
SOAP
1 1 1 OA AP | m | | n | | k | 2 2 2
y P(m,n) y
P(m,n)
o A x o
A
x
2 1.如图,点P是反比例函数 y 图象上的 x 一点,PD⊥x轴于D.则△POD的面积为 1 .
y P o
D
x
2.如图,点P是反比例函数图象上的一点,过点P分别向 x轴、y轴作垂线,若阴影部分面积为1,则这个反比例
1 1 1 OB AB | x || y | xy 4 2 2 2
B
o x
k 设P(m, n)是 双 曲 线 y (k 0)上 任 意 一 点 ,有 : x (1) 过 Px 作 x轴 的 垂 线 ,垂 足 为 A, A, 则 则它与坐标轴形成的 过 P 作 轴的垂线,垂足为
拓 展 提 高
反比例函数K的几何意义求面积
例3:反比例函数
y1
m x
与一次函数
y2
kx
b
交于
点A(1,8 ) 和B (4,n),
求:⑴这两个函数的解析式;
⑵三角形⊿AOB的面积。 S△AOB=S△AOD-S△BOD
S AOB S MOB S AOM
S△AOB=S△MOD-S△AOM-S△BOD
y
MA
B o E FDx
SAOB S梯形AEFB
变式练习1:如图C是AB的中点,反比例函数 y 6 (x 0)
x
在第一象限的图象经过A( 2,3)、C(6,1)两点,
求:△OAB面积
C是A B的中点。
SAOC SCOB
SAOC SCOE
D
E
SAOC S梯形ADE(C 等量代换)
SAOB 2S梯形ADEC
直击中考 ☞
如图,直线AB过点A(m, 0)、B(0, n)(其中 m>0, n>0).反比例函数 y p(p>0)
x
的图象与直线AB交于C、D两点,连结OC、OD. (1)已知m+n=10,△AOB的面积为S, 问:当n何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC、 △COD、△DOB的面积都相等 时,求p的值。
——成都明成学校、王莉
-
回顾与思考
图中的这些矩形面积有什么特点? y
y k x
O
x
回顾与思考
反比例函数中“k”的几何意义
结论1: S矩形 = k
k 结论2: S直角三角形 = 2
面积与P在反比例函数图像上的位置无关
y P(x,y)
y
反比例函数函数K的几何意义
反比例函数函数K的几何意义首先,反比例函数的几何意义可以通过其函数图像来展示。
对于y=k/x的函数形式来说,我们可以通过绘制此函数的图像来可视化这种比例关系。
这个图像是一个二维平面上的曲线,被称为双曲线。
双曲线是一种特殊的曲线,它的形状与抛物线类似,但却没有顶点。
相反,双曲线的中心是坐标轴上的原点(0,0)。
双曲线的形状取决于k的值。
当k是正值时,双曲线会与x和y轴相交于第一和第三象限,而当k是负值时,双曲线会与x和y轴相交于第二和第四象限。
因此,双曲线的图像有两个分支,分别位于坐标轴的正负两个象限中。
双曲线的特殊性质之一是它的渐近线。
在反比例函数图像中,存在两条直线,它们并不相交于双曲线,但又无限靠近它。
这些直线被称为双曲线的渐近线。
通过计算可以得知,当x趋向于正无穷或负无穷时,y趋向于0。
因此,我们可以得出结论,双曲线的两条渐近线为y=k和y=-k。
这意味着双曲线可以无限接近这两条直线,但永远不会与其相交。
渐近线提供了双曲线在远离原点时的大致变化趋势。
反比例函数的另一个几何意义是它对于比例函数的补充。
比例函数y=kx表示两个变量之间的正比关系,而反比例函数则表示它们之间的反比关系。
这两种函数形式都比较简单,易于理解和分析。
它们反映了不同的实际情况和数学模型,因此在实际应用中都有各自的用途。
在物理学中,反比例函数经常用于描述两个物理量之间的关系。
例如,牛顿第二定律F=ma(力等于质量乘以加速度)可以写成F=k/a的形式,其中k是一个常数。
这就是一个反比例关系,表示物体的质量越大,所需施加的力就越小。
类似地,欧姆定律V=IR(电压等于电流乘以电阻)可以被写成V=k/R的形式,也是反比例关系的一个例子。
反比例函数还可以用于解决实际问题,尤其是涉及到比例关系的问题。
通过建立反比例函数模型,我们可以预测和控制变量之间的关系,并做出相应的决策。
例如,在经济学中,我们可以使用反比例函数来研究价格和需求之间的关系。
反比例函数K的几何意义
【山东·全国考题回访】
1.(2014·济南中考)如图,△OAC和△BAD都是等
如图,过y轴正半轴上的任意一点P,作x轴 的平行线,分别与反比例函数y=-4/x和 y=2/x交于点A和点B,若点C是x轴上任意一 点,连接AC、BC,则△ABC的面积为
点B,D在反比例函数y=b/x(b<0)的图象上,
AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,
AB与CD的距离为5,则a-b的值是
则S△OBC=
1·(-x)·22y=6.解得k=xy=-6. 2
答案:-6
如图,直线l⊥x轴于点P,且与反比例函数 y1=k1/x(x>0)及y2=k2/x(x>0)的图像分别交于点A, B,连接OA,OB,已知△OAB的面积为3,则k1-k2 的值等于( )
如图△P1OA1,△P2A1A2是等腰直角三角形,点P1, P2在函数y=4/x(x>0)的图象上,斜边OA1,A1A2 都在x轴上,则点A2的坐标是______.
答案:6
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同 时落在反比例函数的图象上,猜想是哪两个点, 并求矩形的平移距离和反比例函数的解析式.
(1)∵四边形ABCD是矩形,平行于x轴,且AB=2,AD=4, 点A的坐标为(2,6). ∴AB=CD=2,AD=BC=4, ∴B(2,4),C(6,4),D(6,6);
腰直角三角形,∠ACO=∠ADB=90°,反比例函数 y= k 在第一象限的图象经过点B,若OA2-AB2=12, 则kx的值为_______.
1.2反比例函数k的几何意义(第4课时)
A
B
C S2 S3 o A1 B1 C1 S1
x
k 已知,点P是反比例函数 y 图象上一 x
点,作PA⊥ x轴 于A,若 S△AOP是3,则这
个反比例函数的解析式为(
)
谢谢大家,再见
方形,反比例函数 y
y
B A
k 的 x
的图象过点B,则k的值为(
) C
解: S正方形OABC 1 k
2
o
x
k 1
又 该反比例函数图象位于 第二、四象限
k 0
k 1
注意: 当图像在第一、三象限时,K>0; 当图像在第二、四象限时,K<0、。
3.如图,S矩形 OAPB= ____,S △OAP= y
A C E
B o x
D
如图,已知,A,B是双曲线
(1)若A(2,3),求K的值
k y (k 0) x
上的两点,
(2)在(1)的条件下,若点B的横坐标为3, 连接OA,OB,AB,求△OAB的面积。
y
A
B o
x
(3)若A,B两点的横坐标分别为a,2a,线段AB的延长 线交X轴于点C,若 SAOC 6 ,求K的值 y
k y (k 0) x
上的两点,
(2)在(1)的条件下,若点B的横坐标为3, 连接OA,OB,AB,求△OAB的面积。
y
A
B o
C x (5,0)
如图,已知,A,B是双曲线 (1)若A(2,3),求K的值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数K的几何意义专题
一.教学分析
反比例函数知识看似简单,好像就只有定义,图像,性质,但在实际的中考中,它常与图形的面积交汇在一起,是中考的热点之一.本节内容在这一章中也占据着举足轻重的地位,是一次函数的延续和二次函数的基础,在初中函数的学习中起着承上启下的作用.
﹙一﹚、教学目标
1.知识目标;
(1)、理解K的几何意义,会由已知条件求函数解析式和简单图形的面积
(2)、熟练掌握反比例函数的图像和性质,灵活运用K的几何意义.
2.能力目标;
在教学过程中引导学生自主探索、思考及想象,经历探索K的几何意义的过程,发展学生分析归纳和概括的能力,
3.情感目标;
通过学习,培养学生积极参与和勇于探索的精神,科学的学习态度,同时通过多媒体演示激发学生学习的兴趣.
﹙二﹚、教学重点:K的几何意义的探究与运用
教学难点:灵活运用K的几何意义.
﹙三﹚教学方法:自主探究、合作交流、讲练结合
教学模式问题——探究——总结——应用
﹙四﹚、教学准备:多媒体课件.
二、考点分析:
反比例函数是历年中考数学的一个重要考点章节,且多以大题的形式出现,常常结合三角形,四边形等相关知识综合考察.所以,应该引起广大学生的重视.反比例函数中k的几何意义也是其中一块很重要的知识章节,常在中考选择题,计算大题中进行考察.这类考题大多考点简单但方法灵活,目的在于考察学
生的数学图形思维.
本次专题目的在于让学生掌握反比例函数中k的几何意义这一知识要点,灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路.
三、学情分析
反比例函数的图象是学生中学阶段首次遇到的非线性函数的图象,而且反比例函数的图象还是不连续的断开的两支曲线,而学生的认知结构中仅有正比例、一次函数即所谓的线性函数的作图经验,逐步学习利用数形结合的思想分析问题和解决问题,提高解决问题的能力.
四、授课内容:
(一):反比例函数与矩形面积
这就说明,过双曲线上任意一点作x轴、y轴的垂线,所得到的矩形的面积为常数|k|.这是系数k几何意义,明确了k的几何意义,会给解题带来许多方便.设计意图:利用多媒体直观展示图形的变化,吸引学生的注意力,激发学生的学习兴趣.
推广:反比例函数与三角形面积
如图1,设点P(a,b)是双曲线上任意一点,作P A⊥x轴于A点,PB⊥y 轴于B点,则矩形PBOA的面积是(三角形P AO和三角形PBO的面积都是).
设计意图:两个题目让学生经历由特殊到一般,由猜想到归纳,教给学生考虑
问题的方法,同时渗透了数形结合思想与分类讨论的数学思想 . (二 ) 例题讲解
千里之行 始于足下
例题1.如图,点P 是反比例函数 图象上的一点,PD ⊥x 轴于D .则△POD 的面积为 .
例2:如图所示,直线l 与双曲线)0(k y >=
k x 交A 、B 两点,P 是AB 上的点,试比较⊿AOC 的面积S 1,⊿BOD 的面积S 2,⊿POE 的面积S 3的大小:
设计意图:这几个题目为了及时掌握总结的知识点,加深印象,强化学生的数形结合能力.
例3 如图,点A ,B 是双曲线 上的点,过点A 、B 两点分别向x 轴、y 轴作垂线,若S 阴影=1,则S 1+S 2=
例4. 在反比例函数2y x
=(0x >)的图象上,有点1234P P P P ,,,,它们的横坐标依次为1,2,3,4.分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分的面积从
左
到右依次为123S S S ,,,则123S S S ++= . 2y x
=
x y O P 1 P 2 P 3
P 4 1 2 3 4
设计意图:对面积类题目进行了一次升华,目的是使课堂面向全体学生,照顾优
等生,提高分析能力.培养学生的表达能力和分析能力,树立合作学习的理念.趁热打铁,大显身手
1. 已知点A是反比例函数上的点,过点A作
AP⊥x轴于点P,已知△AOP的面积3,则k的值是()
A.6 B.-6 C.-3 D.3
2 3 4题
设计意图:灵活运用k的几何意义解决面积类题目进行了一次升华,培养学生的表达能力和分析能力,树立合作学习的理念.
(三) 根据中心对称解题
的图象相交于A、C两点,AB⊥例题6.正比例函数y=x与反比例函数y=1
x
x轴于B,CD•⊥x轴于D,如图所示,则四边形ABCD的为
_______.
例题7
设计意图:让学生感受知识间的联系,双曲线具有轴对称性,中心对称性,妙用其图像的对称性,有利于我们理清思路,快速解题,它是一个重要的解题技巧.
五.中考题型精选
设计意图:这个简单而有用的结论,较好的体现了数形结合.是解决反比例函数问题的有力的侗剧,因而备受各地中考命题人的关注和青睐,在中考中,反比例函数方面的考题多与一次函数,三角形,特殊四边形等知识综合来进行考查,常以中低难度的选择题,填空题的形式出现.
六.课堂练习
1 若A(m,n)是反比例函数图象上的一动点,其中0<m<3,点B的坐标(3,2),过点A作直线AC∥x轴,交y轴于点C;过点B作直线BD∥y轴交x轴于点D,交直线AC 于点E,当四边形OBEA的面积为6时,请判断线段AC与AE的大小关系,并说明理由.
2、已知反比例函数y=12/x与一次函数y=kx-7的图象都经过点P(m,2),函数y=kx-7的图象交y轴于点Q.试求这个一次函数的解析式及△OPQ的面积.
设计意图:检查学习效果,巩固所学知识,作业面向全体,照顾大多数,同时也要注意培养优等生,选拔数学人才,激励学生深入研究,给学生发展空
间.七、课时总结:
让学生谈谈本节课有哪些收获?
设计意图:对本节课的内容进行一次系统回顾,进一步加深印象,巩固所学知识,加强学生的表达能力.
八、作业布置
●若A(m,n)是反比例函数图象上的一动点,其中0<m<3,点B的坐标(3,2),过点A
作直线AC∥x轴,交y轴于点C;过点B作直线BD∥y轴交x轴于点D,交直线AC于点E,当四边形OBEA的面积为6时,请判断线段AC与AE的大小关系,并说明理由.●设计意图:检查学习效果,巩固所学知识,作业面向全体,照顾
大多数,同时也要注意培养优等生,选拔数学人才,激励学生深入研究,给学生发展空间.
●九板书设计
●
●
●
●
●教学设计说明:
●本节课的设计力求体现使学生“学会学习,为学生终身学习做准备”的理念,
努力实现学生的主体地位,使数学教学成为一种过程教学,并注意教师角色的转变,为学生创造一种宽松和谐、适合发展的学习环境,创设一种有利于思考、讨论、探索的学习氛围,根据学生的实际水平,选择恰当的教学起点和教学方法.由此我采用“问题——探究——总结——应用”的学科教学模式,把主动权充分的还给学生,让学生在自己已有经验的基础上提出问题,明确学习任务,教师引导学生观察、发现、猜想、操作、动手实践、自主探索、合作交流,寻找解决的办法并最终探求到真正的结果,从而体会到数学的奥
妙与成功的快乐.。
