幂函数及其性质
幂函数知识点
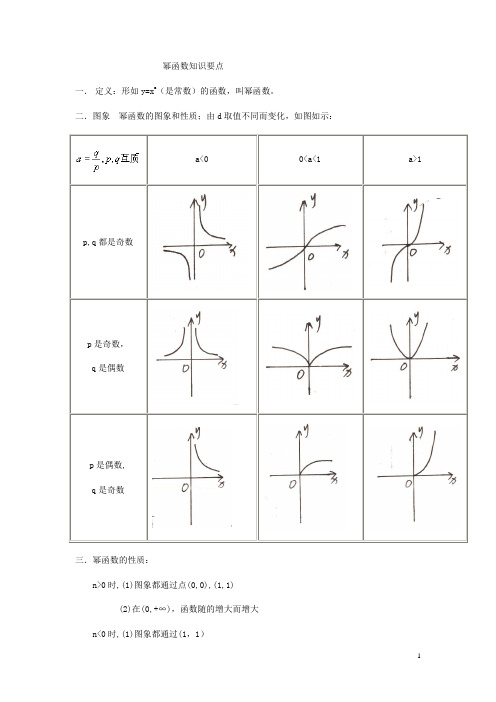
幂函数知识要点一．定义：形如y=x a（是常数）的函数，叫幂函数。
二．图象幂函数的图象和性质；由d取值不同而变化，如图如示：三．幂函数的性质：n>0时,(1)图象都通过点(0,0),(1,1)(2)在(0,+∞)，函数随的增大而增大n<0时,(1)图象都通过(1，1）(2)在(0,+∞)，函数随x的增加而减小(3)在第一象限内，图象向上与y轴无限地接近，向右与x轴无限地接近。
注意事项：1．判断幂函数的定义域的方法可概括为（对指数）“先看正负，是负去零，再看奇偶，是偶非负”2．根据幂函数的定义域，值域及指数特点画其图象。
函数位于第一象限的图象在“n>1”时，往上翘；0<n<1,往右拐;n<0向下滑。
四．例析：分析：底数分别不同而指数相同，可以看作是和。
两个幂函数，利用幂函数的单调性质去理解。
解：(1)(0,+∞)是递增的又∵1.1<1.4 ∴利用幂函数的性质比较数的大小。
例3．比较的大小。
分析：三个量比较大小，先考虑取值的符号。
启示：当直接比较大小难以进行时，可以考虑借助一些中间量特殊值，如0，1或其他数来解决。
分析：在指数运算中，注重运算顺序和灵活运用乘法合成。
启示：此处化简过程可与初中代数式的运算联系。
五．自测题：1.计算的值（）2．下列命题中正确的是（）A.当n=0时，函数y=x n的图象是一条直线B.幂函数的图象都经过(0,0),(1,1)两点C.若幂函数y=x n的图象关于原点对称，则y=x n在定义域内y随x的增大而增大D.幂函数的图象不可能在第四象限3．实数a,b满足0<c<b<1,则下列不等式正确的是（）A．a b<ba B．a-b<b-b C．a-a<b-b D．b b<a a4．在幂函数y=x a,y=x b,y=x c,y=x d在第1象限的图象中(右图)，的大小关系为（）A．a>b>c>d B．d>b>c>a C．d>c>b>aD．b>c>d>a5．下列函数中是幂函数的是）6．设幂函数y=x n的图象经过(8,4)，则函数y=x n的值域为_______。
幂函数的性质
幂函数的性质幂函数是数学中常见的一种函数形式，由x的幂次和常数项构成。
幂函数的一般形式可以表示为f(x) = ax^n + b，其中a、n和b为常数，且n为正整数。
幂函数具有独特的性质，包括定义域、值域、奇偶性、单调性以及图像特点等，下面将详细探讨幂函数的各种性质。
一、定义域幂函数的定义域取决于幂指数n的奇偶性：当n为奇数时，幂函数的定义域为实数集；当n为偶数时，幂函数的定义域取决于系数a的正负性：- 若a>0，则幂函数的定义域为非负实数集，即x ≥ 0；- 若a<0，则幂函数的定义域为空集，即不存在实数使幂函数的结果为负数。
二、值域幂函数的值域也与幂指数n的奇偶性和系数a的正负性相关：当n为奇数时，幂函数的值域为全体实数；当n为偶数时，幂函数的值域取决于系数a的正负性：- 若a>0，则幂函数的值域为非负实数集，即f(x) ≥ 0；- 若a<0，则幂函数的值域在实数轴上存在最大值，即存在一个唯一的实数C使得f(x) ≤ C。
三、奇偶性幂函数的奇偶性由幂指数n来决定：当n为偶数时，幂函数为偶函数，即f(x) = f(-x)，图像关于y轴对称；当n为奇数时，幂函数为奇函数，即f(x) = -f(-x)，图像关于原点对称。
四、单调性幂函数的单调性与幂指数n的奇偶性和系数a的正负性相关：当n为正整数且n为奇数时，幂函数在整个定义域上单调递增或单调递减；当n为正整数且n为偶数时，幂函数在定义域上存在极值点，若系数a>0，则为单调递增，若系数a<0，则为单调递减。
五、图像特点幂函数的图像具有一些特点：当n为正整数时：- 当n为奇数时，幂函数的图像经过点(0, 0)且从第三象限经过第一象限，右上倾斜；- 当n为偶数时，幂函数的图像经过点(0, 0)，右侧在y轴上方且上升（a>0）或下降（a<0）。
综上所述，幂函数的性质主要包括定义域、值域、奇偶性、单调性以及图像特点。
高一数学《幂函数》PPT课件
根据n, m, p的取值不同，图像形状各 异。
03
幂函数运算规则与技巧
同底数幂相乘除法则
01
02
03
同底数幂相乘
底数不变，指数相加。公 式：a^m × a^n = a^(m+n)
同底数幂相除
底数不变，指数相减。公 式：a^m ÷ a^n = a^(m-n)
举例
2^3 × 2^4 = 2^(3+4) = 2^7；3^5 ÷ 3^2 = 3^(5-2) = 3^3
在幂函数中，指数a可以取任意实数，但不同的a值会导致函数性质的不
同。学生需要注意区分不同a值对应的函数性质。
02 03
函数定义域
幂函数的定义域与指数a的取值有关。例如，当a≤0时，函数定义域为 非零实数集；当a>0且a为整数时，函数定义域为全体实数集。学生需 要注意根据指数a的取值来确定函数的定义域。
计算圆的面积
$S=pi r^2$，$r$为圆半 径，利用幂函数表示圆的 面积与半径关系。
增长率、衰减率问题中应用
细菌增长模型
假设细菌以固定比例增长，则细 菌数量与时间关系可用幂函数表
示。
放射性物质衰变
放射性物质衰变速度与剩余质量 之间的关系可用幂函数描述。
投资回报计算
投资回报率与时间关系可用幂函 数表达，用于预测未来收益。
利用积的乘方法则进行化简
如(ab)^n = a^n × b^n
举例
化简(x^2y)^3 ÷ (xy^2)^2，结果为x^4y
04
幂函数在生活中的应用举例
面积、体积计算中应用
计算正方形面积
$S=a^2$，其中$a$为正 方形边长，利用幂函数表 示面积与边长关系。
幂函数及其性质
[跟进训练]
1.(1)在函数 y＝x12，y＝2x2，y＝x2＋x，y＝1 中，幂函数的个数为(
)
A．0
B．1
C．2
D．3
(2) 若 函 数
f(x) 是 幂 函 数 ， 且 满 足
f(4) ＝ 3f(2) ， 则
f
1 2
的
值
等
于
________．
(1)B
1 (2)3
[(1)∵y＝x12＝x－2，
＝12log23＝13.]
幂函数的图象及应用
【例 2】 (教材改编题)点( 2，2)与点－2，－21分别在幂函数 f(x)，g(x)的图象上，问当 x 为何值时，有：
(1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)<g(x)．
解：设 f(x)＝xα，g(x)＝xβ. ∵( 2)α＝2，(－2)β＝－12，∴α＝2，β＝－1， ∴f(x)＝x2，g(x)＝x－1.分别作出它们的图象，如图所示．由图象 知， (1)当 x∈(－∞，0)∪(1，＋∞)时，f(x)>g(x)； (2)当 x＝1 时，f(x)＝g(x)； (3)当 x∈(0,1)时，f(x)<g(x)．
m2＋2
2．已知 f(x)＝(m＋1)x 是幂函数，则 m＝( )
A．2
B．1
C．3
D．0
D [由题意可知 m＋1＝1，即 m＝0， ∴f(x)＝x2.]
3．已知幂函数f(x)＝xα的图象过点2，
22，则f(4)＝
________.
1 2
[由f(2)＝ 22可知2α＝ 22，
即α＝－12，
∴f(4)＝4－12＝12.]
幂函数性质的综合应用
幂函数知识点总结
幂函数知识点总结幂函数是数学中常见的一类函数，主要应用于数据分析和物理学中。
它有着独特的数学性质，并且能够解释一系列规律性的现象，因此在各个领域中都有着广泛的应用。
本文将综合介绍幂函数的基本性质、作用机制和表达方式，以及其在实际应用中的各种特性。
一、基本性质幂函数（Power Function）是一类函数，通常定义为 y=x^n，其中x为变量，n为常数。
它同样也是一种一元函数，因为它只有一个变量X，表示函数值由变量X决定。
二、作用机制幂函数的作用机制主要体现在它的图象与数轴上。
因为x的增大会使得y的值也会加大，所以函数的图象通常是一条上凸的曲线。
这条曲线在原点处发散无限，而且具有明显的拐点，即抛物线的最高点。
此外，幂函数的作用机制还表现出了其“加速增长”的性质。
从图象上看，在抛物线最高点处，x增大时，y值会比较稳定，但是在x值增大之后，y值会变化得越来越快，这也是函数的最显著特征。
三、表达方式幂函数的表达方式很简单，一般情况下，以n来表示其幂的值，并且幂的值可以是整数、实数或负数，但必须保证x的值不等于0，这里说明由于x不等于0才有意义，因为若x等于0时，n为任意值，y都等于0.例如：y=x^2，即平方函数，n=2；y=x^3，即立方函数，n=3；y=x^2，即倒数平方函数，n=2.四、实际应用1、数据分析：幂函数在数据分析中应用十分广泛，其特有的“加速增长”性质，让数据分析者能够以规律的路径追求特定的结果。
例如，可以利用幂函数进行回归分析，以拟合给定数据；此外，可以利用幂函数构建概率模型，更好地研究联系型数据间的关系；2、物理学：幂函数在物理学中也有着广泛应用，可以用来模拟夸克的衰变过程，更好地理解物质的衰变规律；另外，也可以利用幂函数，研究物体受力的加速度变化，以及质量变化对物体运动的影响等。
综上所述，幂函数是一类重要的函数，它的基本性质、作用机制和表达方式构成了幂函数的基本框架，而在实际应用中，幂函数又有着广泛的用途，能够用于数据分析和物理学等领域，从而帮助人们更好地理解客观事物的变化规律。
幂函数的定义及性质
幂函数的定义及性质幂函数是数学中常见的一类函数形式，它的定义如下：定义：对于给定的实数a（a≠0）和非零实数b，幂函数f(x)=a⋅x^b。
其中，a称为幂函数的系数，b称为幂函数的指数，x称为幂函数的自变量，f(x)称为幂函数的因变量。
在幂函数的定义中，a是幂函数的系数，可以取任意非零实数。
系数a决定了函数的纵向伸缩变换，当a>0时，幂函数的图像在y轴上方，当a<0时，幂函数的图像在y轴下方。
指数b是幂函数的指数，决定了函数的横向伸缩变换以及函数的形状。
当b>1时，幂函数增长更为迅速；当0<b<1时，幂函数增长逐渐变缓；当b=1时，幂函数变为线性函数；当b<0时，幂函数变为倒数函数。
幂函数的性质如下：1. 定义域和值域：幂函数的定义域为所有使得指数函数值存在的实数。
当a>0且b>0时，幂函数的值域为(0,+∞)；当a<0且b为奇数时，幂函数的值域为(-∞,0)；当a<0且b为偶数时，幂函数的值域为[0,+∞)。
2. 对称性：a⋅(-x)^b = (-a)⋅x^b，即幂函数关于y轴对称。
3. 单调性：幂函数在定义域上单调递增或递减，取决于系数a和指数b的正负情况。
4. 奇偶性：当b为整数时，幂函数的奇偶性与系数a的奇偶性一致；当b为分数时，幂函数的奇偶性与a的正负性一致。
5. 渐近线：当b>0时，幂函数的图像有一条水平渐近线y=0；当b<0时，幂函数的图像有两条渐进线，分别是x轴和y轴。
6. 函数的图像：幂函数的图像形状随着系数a和指数b的取值而变化，可以是上凸、下凸、对称或非对称的。
以上是幂函数的定义及性质的介绍。
幂函数作为一类常见的函数形式，具有广泛的应用领域，在数学、物理、经济等学科中都有重要的作用。
通过对幂函数的研究和理解，我们可以更好地理解函数的变化规律和函数图像的特点，为解决实际问题提供数学工具和思路。
幂函数的图像和性质 纪福双【打印】
（1）幂函数的定义: （2）幂函数的图象
纪福双
一般地，函数 y x 叫做幂函数，其中 x 为自变量， 是常数．
（3）幂函数的性质： ①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图 象关于 y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第 一象限． ②过定点：所有的幂函数在 (0, ) 都有定义，并且图象都通过点 (1,1) ． ③单调性：如果 0 ，则幂函数的图象过原点，并且在 [0, ) 上为增函数．如果 0 ，则幂函数的图象在 (0, ) 上为减函数，在第一象限内，图象无限接近 x 轴与 y 轴． ④奇偶性：当 为奇数时，幂函数为奇函数，
大行不倦呕心沥血传道授业解惑！大思行广打通大脑思维的任督二脉，大行无疆捍卫中国文化最后良心！第 1 页
q p q p
q p
⑤图象特征： 幂函数 y x , x (0, ) ，当 ，若 x 1 ，其图象在直线 y x 上方，当 1时，若 0 x 1 ，其
图象在直线 y x 上方，若 x 1 ，其图象在直线 y x 下方．
q （其 p 中 p, q 互质， p 和 q Z ） ，若 p 为奇数 q 为奇
当 为偶数时， 幂函数为偶函数． 当 数时，则 y x 是奇函数【简称：奇，奇，奇】 ， 图像位于一三象限，关于原点对称。若 p 为奇 数 q 为偶数时， 则 y x 是偶函数， 【简称： 偶， 奇，偶】 ，图像位于一二象限，关于关于 y 轴对 称。 ； 若 p 为偶数 q 为奇数时， 则 y x 是非奇 非偶函数【简称：奇，偶，非】 ，图像只在第一 象限．
幂函数图像及性质知识点总结(最新)
幂函数图像及性质知识点总结
一、幂函数图像及性质
1、正值性质
当α>0时，幂函数y=xα有下列性质：
（1）图像都经过点（1,1）（0,0）；
（2）函数的图像在区间[0,+∞）上是增函数；
（3）在第一象限内，α>1时，导数值逐渐增大；α=1时，导数为常数；0<α<1时，导数值逐渐减小，趋近于0。
2、负值性质
当α<0时，幂函数y=xα有下列性质：
（1）图像都通过点（1,1）；
（2）图像在区间（0，+∞）上是减函数；（内容补充：若为X-2，易得到其为偶函数。
利用对称性，对称轴是y轴，可得其图像在区间（-∞，0）上单调递增。
其余偶函数亦是如此）。
（3）在第一象限内，有两条渐近线（即坐标轴），自变量趋近0，函数值趋近+∞，自变量趋近+∞，函数值趋近0。
3、零值性质
当α=0时，幂函数y=xa有下列性质：
1、y=x0的图像是直线y=1去掉一点（0,1）。
它的图像不是直线。
二、什么是幂函数
幂函数属于基本初等函数之一，一般y=xα（α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。
例如函数y=x0 、y=x1、y=x2、y=x-1（注：y=x-1=1/x、y=x0时x≠0）等都是幂函数。
【幂函数图像及性质知识点总结】
1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a
1
学习目标
一、知识目标： 1.通过实例了解并记住幂函数的概念. 2.结合几个常见幂函数的图象观察图象特征并能
自行发现幂函数的性质. 3.记住幂函数的性质并会应用. 能力目标： 通过观察图象特征来归纳函数性质, 从而培养学生数形结合的能力. 情感目标： 通过观察图象体会数学的简洁美.
2.当α为奇数时,幂函数为奇函数, 当α为偶数时,幂函数为偶函数.
3.如果α>0,则幂函数 在(0,+∞)上为增函数;
α>1a=1
0<α<1
如果α<0,则幂函数
α<0
在(0,+∞)上为减函数。
a
22
练习：利用单调性判断下列各值的大小。
（1）5.20.8 与 5.30.8 （(23）) 0.20.3-2与 0.30.3-2
3
y 1 y x 2
2
(
( 1 ( y x - -
- - 6 - 4 2 2 4 6
-1
(-
-2
-3
-4
a
20
幂函数的定义域、值域、奇偶性和单调性，随常 数α取值的不同而不同.
y = x y = x2
1
y x2
y x1
R R 奇偶性 奇函数
R [0，+∞）
偶函数
R [0，+∞） ， 0 （ 0， +） R [0，+∞） ， 0 （ 0， +）
只要把点带入解析式中即可求出a，也就可以求 出函数的解析式。
待定系数法
a
7
解：设所求幂函数的解析式为y x
(3, 3)因为点在函数图像上，所以代
入解析式得： 3 3a 1
a 2
1
y x2
a
8
1
3.如果函数f (x) = (m2+2m－2) xm21 2n3
是幂函数，求实数m,n的值。
解：由题意得
定义域：{x x 0}
值 域：{y y 0}
奇偶性：在{x x 0}上是奇函数
单调性：在(0,)上是减函数
在(a,0)上是减函数
18
下面将5个函数的图像画在同一坐标系中
(1) yx (2) y x2 (3) y x3
(4)
1
y x2
(5) y x1
a
19
( 4 y x 3 ( y x 2
奇函数
非奇非偶 函数
奇函数
在（－∞,0]
在R上 上是减函
是增函 数，在(0,
数
+∞）上是
增函数
a
在R上 是增函 数
在(0，+∞) 上是增函数
在( －∞,0)， (0, +∞）上是 减函数
（1，1） 21
小结： 幂函数的性质:
幂函数的定义域、值域、奇偶性和单调性，随 常数α取值的不同而不同.
１.所有幂函数的图象都通过点(1,1);
a
2
一、幂函数的概念的引入
阅读课本第85页的具体实例（1）－（5）， 思考下列问题：
1.它们的解析式分别是什么？若用 x 表示自
y 变量, 表示 x 的函数,上述五个函数解析式
分别是什么?
a
3
问题引入：函数的生活实例
问题1：如果张红购买了每千克1元的苹果w千克，
那么她需要付的钱数p =w元，这里p是w的函数 。yx
值，则相应图象依次为:__C4__C_2__C_3 C1
1
一般地，幂函数的图象在直线x=1
的右侧，大指数在上，小指数在下，
指大图高
a
27
思考4：根据上述五个函数的图象，你能
归纳出幂函数 y x a 在第一象限的图
象特征吗？
α>1
y
1.图象都过点(1,1)
α=1
2.α>0时图象过原点且上升，
0<α<1
的平均速度v = t 1 km/s
，这里v是t的函数 。
y
1
x
若将它们的自变量全部用x来表示,函数值用
y来表示,a则它们的函数关系式将是:y
a
x4
以上问题中的函数有什么共同特征？
(1) y=x (2) y=x2
（1）都是函数；
（2）均是以自变量为底的 幂；
(3) y=x1/2
（3）指数为常数；
a
23
练习(4) 1） 1 . 3 0 .5 ＜ 1 . 5 0 .5
2） 5 . 1 2 ＜ 5.09 2
3）
1
0 .5 4
1
＞ 0 .4 4
4）
2
0 .7 3
2
＞ 0 .8 3
a
24
例例 21：.证明幂 f(x)函 x数 在 [0, )上是增 . 函数
证 : 任 x 明 1 ,x 2 取 [ 0 , ) 且 , x 1 x 2 ,则
(4) y=x3 (5) y=x-1
（4）自变量前的系数为1; （5）幂前的系数也为1。
一般地，函数y= x 叫做幂函数，其中x是自
变量，α是常数.
注意:幂函数中α的可以为任意实数.
a
5
一、幂函数的定义： 一般地，我们把形如 y x 的函数叫做
幂函数，其中 x为自变量，为常数。
y x 中 x前面的系数是1，后面没有其它项。
m2 2m 2 1 m2 1 0 2n 3 0
解 得 m3,n3.
a
2
9
二、幂函数与指数函数比较
a为底数 指数 幂值
α为指数 底数
幂值
判断一个函数是幂函数还是指数函数的切入点：
看未知数x是指数还是底数
指数a函数
幂函1数0
二、五个常用幂函数的图像和性质
(1) yx (2) y x2 (3) y x3
f(x1)f(x2)x1x2
(
x1
x2)(
x1
x2)
x1 x2
x1 x2 x1 x2
方法技巧:分子有理化
因 0 x 1 为 x 2 , 所 x 1 x 2 以 0 ,x 1 x 2 0 ,
所 以 f(x1)f(x2) 即幂函 af(x)数 x在 [0, )上的25 增. 函
1
(4) y x 2 (5) y x1
a
11
函数 yx的图像
定义域： R
值 域： R
奇偶性：在R上是奇函数
单调性：在aR上是增函数
12
函数 y x2的图像
定义域： R
值 域：[0,)
奇偶性：在R上是偶函数
单调性：在[0,)上是增函数
在(,0]上是减函数
a
13
用描点法作出函数y=x3的图象.
问题2：如果正方形的边长为a，那么正方形的面积
是S = a²， 这里S是a的函数。
y x2
问题3：如果立方体的边长为a，那么立方体的体积
是V = a³， 这里V是a的函数 。
问
题
4:
如
果
1
正
方
形
场
地
的
面
积
为
S
，
那
y 么正
3
方x
形
的
边问长题a5=：S如2，果某这人里tas是内S骑的车函行数进。了1km，那么他y 骑x车12
例3 若m412 32m12,
则求m的取值范围.
解:
幂函数f
(x)
x
1
2的定义域是(0,
)
且在定义域上是减函数,
0 3 2m m 4
1 m 3 ,即为m的取值范围.
3
2
a
26
练习3: 如图所示，曲线是幂函数 y = xk 在第一象
限内的图象，已知 k分别取 1 , 1 , 1 , 2 四个 2
a
29
作业: 利用单调性判断下列各值的大小。
(1)1.30.5与 1.50.5 (2)5.12与 5.092
1
1
(3)1.794与1.814
a
30
再见!
a
31
a
14
函数 y x3的图像
定义域： R
值 域： R
奇偶性：在R上是奇函数
单调性：在aR上是增函数
15
1
1
y x 2 用描点法作出函数y x 2 的图象.
a
16
1
函数 y x 2 的图像
定义域：[0,)
值 域： [0,)
奇偶性： 非奇非偶函数
单调性：在[a0,)上是增函数
17
函数 y x1 的图像
练习1：判断下列函数哪几个是幂函数？
（1）y 3x; (2)y x2; (3)y 2x2; (4)y x2 1;
(5)y 1
思考：指数函数y=ax与幂
答案（2x）（5）函数y=xα有什么区别？
a
6
2.已知幂函数y = f (x)的图象经过点
（3 ，3 ），求这个函数的解析式。
分析：例题要求函数的解析式，首先由题知， 此函数是幂函数，也就符合幂函数的一般形 式 y x ，而且我们知道图像(过2点, 2 )
α<0时图象不过原点且下降， 1x=1 的右侧指大图高. o 1
x
a
28
小结:
1．记住幂函数的定义；
2．掌握幂函数的图象和性质；
3．能利用幂函数的性质解决有关问题; 4．这节课我们从观察图象入手,运用自然语言描述
了函数的图象特征,最后抽象到运用数学语言和符 号刻画了相应的数量特征. 这是一个循序渐进的 过程,这也是数学学习和研究中经常使用的方法.
2.5 5 与 2.7 5