七年级数学探索三角形全等的条件4
探索三角形全等的条件4预习与思考
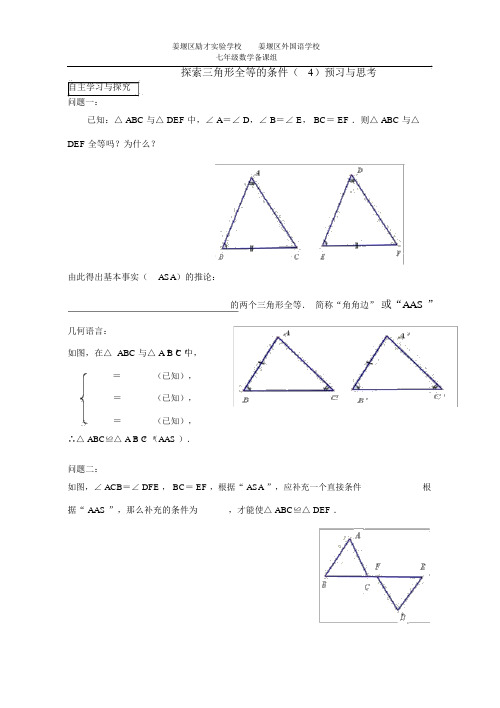
探索三角形全等的条件(4)预习与思考自主学习与探究问题一:已知:△ ABC 与△ DEF 中,∠ A=∠ D,∠ B=∠ E, BC= EF .则△ ABC 与△DEF 全等吗?为什么?由此得出基本事实(ASA)的推论:的两个三角形全等.简称“角角边”或“AAS ”几何语言:如图,在△ ABC 与△ A B C 中,=(已知),=(已知),=(已知),∴△ ABC≌△ A B C (AAS ).问题二:_________ 根如图,∠ ACB=∠ DFE , BC= EF ,根据“ ASA ”,应补充一个直接条件据“ AAS ”,那么补充的条件为_____,才能使△ ABC≌△ DEF .问题三:如图, BE=CD ,∠ 1=∠ 2,你能运用 AAS证明△ ABE≌△ ACD 吗?你还能得到哪些线段相等?问题四:已知:如图,△ ABC≌△ABC,AD 和 AD分别是△ ABC 和△ABC中 BC 和 BC 边上的高.求证:AD = A D .收获与困惑探索三角形全等的条件(4)教案例:对问题四的变式:变式 1: 已知:如图,△ABC≌△ A B C ,AD 和 A D 分别是△ ABC 和△ A B C 中∠ A 和∠ A’的角平分线.求证: AD=A D .变式 2: 已知:如图,△ABC≌△ A B C ,AD 和 A D 分别是△ ABC 和△ A B C 的 BC 和 B C 边上的中线.求证: AD=A D .例 2.( 课本第 21 页第 1 题 ) 已知:如图,∠ A=∠ D ,∠ ACB=∠ DBC ,求证: AB= DC.例 3: 课本第 21 页第 2 题(略)例 4.如果∠ B= ∠C, AD 平分∠ BAC,(1) 求证: AB=AC B(2) 连结 BC交 AD于 E,你能发现AD与 BC的关系吗?DAC探索三角形全等的条件(4)达标自测班级学号姓名自测内容1.已知△ ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是()A .甲和乙B.乙和丙C.只有乙D.只有丙2.如图,已知∠ A= ∠ C, BE ∥ DF ,若要用“ AAS ”证△ ABE ≌△ CDF,则还需添加的一个条件是.(只要填一个即可)BA DA CF ED B C(第 3题)(第 2题)3.如图,已知∠A= ∠ D ,∠ ABC= ∠ DCB ,AB=6, 求 DC 的长度.4.如图, AB⊥ BC, AD⊥ DC,∠ BAC=∠CAD . 求证: AB=AD .5.如图,如果 AF = EC,那么根据所给的数据信息,图中的两个三角形全等吗?请说明理由.6.如图,已知∠1=∠ 2,∠ 3=∠ 4, EC= AD ,求证: AB = BEDE3C421A B7. 已知:如图,△ABC≌△A BC ,AD 和 A D 分别是△ ABC 和△A BC的 BC 和 B C边上的中线.求证: AD=A D .10..如图 AB 、CD 相交于点 O,,OA=OB , OC=OD , EF 是过 O 点的任意一条直线,且交 AC 于点 E,交 BD 于点 F,请回答:(1) AC 和 BD 有什么关系?(2)求证: OE=OF。
七年级数学下册 第4章 三角形 4.3 探索三角形全等的条件课件 (新版)北师大版

例2 (2017四川宜宾中考)如图4-3-2,已知点B、E、C、F在同一条直线 上,AB=DE,∠A=∠D,AC∥DF.试说明:BE=CF.
图4-3-2 分析 由AC∥DF可得∠ACB=∠F,又∠A=∠D,AB=DE,可以利用AAS 得到△ABC≌△DEF,根据全等三角形的对应边相等可得BC=EF,都减 去EC即可得BE=CF.
AD BC,
因为DAB CBA,所以△ABD≌△BAC(SAS).
AB AB,
知识点一 判定三角形全等的条件——边边边 1.如图4-3-1,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判 定△ABC和△FED全等,下面的4个条件中:①AE=FB;②AB=FE;③AE= BE;④BF=BE,可利用的是 ( )
AB=DE,BC=EF (2)已知两角
思路一(找第三边)
思路二(找角)
首先找出AC=DF,然后应用“SSS”判定全等
①找夹角:首先找出∠B=∠E,然后应用 “SAS”判定全等;②找直角用“HL”判定 全等(后面会学到)
思路一(找夹边)
思路二(找角的对边)
首先找出AB=DE,然后应用“ASA”判定全 等
A.①或②
B.②或③
图4-3-1 C.①或③ D.①或④
答案 A 由题意可得,要用“SSS”进行△ABC和△FED全等的判定, 只需AB=FE,若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,故①可 以;显然②可以;若添加③AE=BE或④BF=BE,均不能得出AB=FE,故③④ 不可以,故选A.
架不变形,他至少要再钉上
根木条.
()
图4-3-5
A.0 解析 答案
B.1 C.2 D.3 连接AC或BD,构成三角形,三角形具有稳定性. B
数学:11.3探索三角形全等的条件(第4课时)教案(苏科版七年级下)

第11章图形的全等
课时分配
本课(章节)需5课时
本节为第4课时
为本学期总第课时
探索三角形全等的条件(4)
教学目标
1、角平分线的尺规作图
2、“sss公理”的灵活应用
重点
角平分线作图原理及“sss公理”的灵活应用
难点
原理的应用
教学方法
采用启发式和讨论式教学
课型
新授课
教具
投影仪
教师活动
学生活动
情境创设:
第145页“想一想”请你说明它的道理。(教具)
新课讲解:
由此,我们就得到了作角平分线的方法。已知∠AOB你能用直尺和圆规作出它的角平分线吗?
例题1:书第145页
分析:如何说明∠B=∠E?
具备什么样的已知条件?
补充:除了∠B=∠E,你还可以发现哪些结论?
练习:第146页第1、2、3题
教学素材:
A组题:
作业
板书设计
复习例1板演
………………
………………
………………
………………
………………
教学后记
如图,点A、B、C、D在同一条直线上,AB=CD,△EAC和△FDB全等吗?为什么?
B组题:
如图,点B、C、F、E在同一条直线上,BF=EC.
(1)至少添加哪些条件,可使△ABC和△DEF全等?为什么?
(2) 若△ABC和△DEF全等,则还可以进一步得到哪些结论?
学生思考,讨论并作答
学生自读完成,师指导
苏科版-数学-七年级下册-《探索三角形全等的条件(4)》学案

《探索三角形全等的条件(4)》学案课型:新课课后作业:一、基础类一、选择题1.下列各组所列的条件中,不能判△ABC和△DEF全等的是()A.AB=DE,∠C=∠F,∠B=∠E B.AB=EF,∠B=∠F,∠A=∠EC.∠B=∠E,∠A=∠F,AC=DE D.BC=DE,AC=DF,∠C=∠D2.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板。
你认为下列四个答案中考虑最全面的是()A.带其中的任意两块去都可以B.带1、2或2、3去就可以了C.带1、4或3、4去就可以了D.带1、4或2、4或3、4去均可二、填空题1.如图,已知:AB、CD相交于点O,AO=BO,要判定图中两个三角形全等, 只需再补充一个条件:(1)__________ ( )(2)__________ ( )(3)__________ ( )2.如图,要用“SAS”说明ΔABC≌ΔA DC,若AB=AD,则需要添加的一个条件是.要用“ASA”说明ΔABC≌ΔADC,若∠ACB=∠ACD,则需要添加的一个条件是.三、解答题1.如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断D是BC边上的中线.2.如图,已知∠1=∠2,∠3=∠4,BC=BD,求证AB=BE.3.如图:在“①AD⊥BC,②∠1=∠2,③点D是BC的中点”中,任选两个作为条件,能否得出结论AB=AC?试试你的能力!解:条件:_______________结论:证明:4.已知:如图,△ABC和△CDE都是等边三角形,AD和BE相交于点F.⑴在图①中,点B、C、D三点在同一直线上,试说明AD和BE的大小关系,并确定它们所成的锐角的度数;⑵当△CDE绕点C沿逆时针方向旋转到图②位置时,⑴中的结论还成立吗?请说明理由.二、拓展类等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N (1)你能找到一对三角形的全等吗?并说明理由.(2)BM,CN,MN之间有何关系?并说明理由.若将直线l旋转到如下图的位置,其他条件不变,那么BM,CN,MN之间又有何关系?请说明理由.。
北师大版七年级数学下册4.3.2 探索三角形全等的条件

如图,∠A=∠D,要使△ABC≌△DBC,还需要补充一个条件:
利用“角边角“判定两三角形全等:
所以△BEC≌△CDA(AAS).
解:因为AD是△ABC的中线,所以BD=CD.
因为CF⊥AD,BE⊥AE,
所以∠CFD=∠BED=90°.
BED=CFD,
)
在△BDE和△CDF中,因为
BDE=CDF,
利用“角角边“判定两三角形全等:
又因为OE⊥AB,OF⊥CB,所以∠OEB=∠OFB.
在△BAC和△EAD中,因为
如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AE=BF,那么△AEC≌△BFD的理由是(
所以CE=AD=5 cm,BE=CD,
所以△BDE≌△CDF(AAS).
利用“角边角“判定两三角形全等:
两角及其 夹边
分别相等的两个三角形全等(简写成“角边角”
或“ASA”).
几何语言:
在△ABC与△A'B'C'中,
∠=∠',
='',所以△ABC≌ △A'B'C' (
∠=∠',
ASA
).
1.〈厦门〉已知:如图,点B,F,C,E在一条直线上,∠A=
∠D,AC=DF,且AC∥DF.
试说明:△ABC≌△DEF.
在探索三角形全等条件及其应用过程中,能够进行有条理地思考并进行简单地推理.
如图,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AE=BF,那么△AEC≌△BFD的理由是(
)
∠ACB=∠F
B.
所以△BEC≌△CDA(AAS).
的判定方法看缺什么条件,再去说明什么条件,简言
七年级数学下册第四章4.3.1-4.3.3教案

第四章 三角形4.6探索三角形全等的条件(第1课时)教学目标1.探索三角形全等的“边边边”的条件,会利用“边边边”的条件判断两个三角形全等2.知道三角形的稳定性 教学重、难点重点:利用“边边边”的条件判断两个三角形全等 难点:利用“边边边”的条件判断两个三角形全等 教学过程一、情境导入【温习旧知】已知△ABC ≌△A ′B ′C ′,找出其中相等的边与角.图中相等的边是: 相等的角是: 【自学指导】活动一:只给一个条件画三角形 1.画一个边长为3厘米的三角形。
2.画一个内角为45°的三角形。
与你的小组成员交流,只给一个条件,大家画出的三角形全等吗?活动二:只给两个条件画三角形1.画一个边长为3厘米,内角为45°的三角形。
2.画两个内角分别为30°和50°的三角形。
3.画一个两边长分别为2厘米和3厘米的三角形。
与你的小组成员交流,,只给两个条件,大家画出的三角形全等吗?C 'B 'A 'C B A活动三:给出三个条件画三角形给出三个条件画三角形,你能说出有几种可能的情况吗?归纳:有四种可能.即:三内角、三条___、两边一内角、两_____一边. 1.画三个内角分别为30°,60°和90°的三角形。
把你画的三角形与同伴画的三角形进行比较,它们全等吗?2.画三条边长分别为3cm 、4cm 、5cm 的三角形。
把你画的三角形与同伴画的三角形进行比较,它们全等吗?结论:(1)_______________的两个三角形全等,简写为_________或_________.(2)用三根木条钉成三角形框架,它的大小和形状是固定不变的,•而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的__________.二、思考探究,获取新知 问题一:如图, △ABC 是一个钢架,AB=AC,AD 是连接点A 与BC 中点D 的支架,求证: △ABD ≌ △ACD问题二: 已知:如图AB=CD,AD=BC.则∠A 与∠C 相等吗?为什么?三、精讲延伸DB1.已知:如图,AD=BC ,AE=FC ,DF=BE 。
4.3.2 利用“角边角”“角角边”判定三角形全等 北师版数学七年级下册课件
∴△∠ACB=C∠≌F△. DEF(ASA ).
例4 如图,已知:在△ABC中,∠BAC=90°, AB=AC,直线m经过点A,BD⊥直线m,CE⊥直 线m,垂足分别为点D、E.试说明: (1)△BDA≌△AEC;
解:(1)∵BD⊥m,CE⊥m,
所以AB=A'B'(全等三角形对应边相等),
D′ C′
∠ABD=∠A'B'D'(全等三角形对应角相等).
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证), ∠ABD=∠A'B'D'(已证),
全等三角形对应边上 的高也相等.
∴ △ABC≌△ A′ B′ C′ (AAS). B ′
C′
例3:在△ABC和△DEF中,∠A=∠D,∠B= ∠E,
BC=EF.求说明:△ABC≌△DEF.
解: 在△ABC中,∠A+∠B+∠C=180°. ∴ ∠C=180°-∠A-∠B. 同理 ∠F=180°-∠D-∠E. 又 ∠A=∠D,∠B= ∠E, ∴ ∠C=∠F.
思考: 这里的条件与1中的条件有什么相同点与不同点?
你能将它转化为1中的条件吗?
60°
75°
归纳总结
两角分别相等且其中一组对角的对边相等的两个三角形 全等.简写成“角角边”或“AAS”.
A
在△ABC和△A′B′C′中,
∠A=∠A′(已知),
∠B=∠B′ (已知),
专题探索三角形全等的条件(SSS和SAS)(知识讲解)数学七年级下册(北师大版)
专题4.10 探索三角形全等的条件(SSS 和SAS )(知识讲解)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).特别说明:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).特别说明:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、用“SSS”和“SAS”直接证明三角形全等➽➼证明✮✮求值1.如图,已知:AB =AC ,BD =CD ,E 为AD 上一点.(1) 求证:△ABD △△ACD ;(2) 若△BED =50°,求△CED 的度数.【答案】(1) 证明见分析 (2) 50CED ∠=︒【分析】(1)根据SSS 即可证明△ABD △△ACD ;(2)只要证明△EDB △△EDC (SAS ),即可推出△BED =△CED ,进而得到答案. (1)证明:在△ABD 和△ACD 中, AB ACBDCD AD AD ⎧⎪⎨⎪⎩===,△△ABD △△ACD (SSS );(2)解:△△ABD △△ACD ,△△ADB =△ADC ,在△EDB 和△EDC 中,DB DC BDE CDE DE DE ⎧⎪∠∠⎨⎪⎩===,△△EDB △△EDC (SAS ),△△BED =△CED ,△△BED =50°,△△CED =△BED =50°.【点拨】本题考查全等三角形的判定和性质,解题的关键是根据图形题意,熟练掌握两个三角形全等判定与性质.举一反三:【变式1】如图,点A 、M 、N 、C 在同一条直线上,AB CD =,BN DM =,AM CN =,求证:AB CD ∥.【分析】根据AB CD =,BN DM =,AM CN =,利用SSS 定理证明ABN CDM ≌,从而得到A C ∠=∠,再根据内错角相等,两直线平行,AB CD ∥得证.解:证明:∵AM CN =∴AM MN CN MN∴AN CM =在ABN 和CDM 中AB CD BN DM AN CM =⎧⎪=⎨⎪=⎩,∴()ABN CDM SSS △≌△∴A C ∠=∠∴AB CD ∥(内错角相等,两直线平行)【点拨】本题考查了三角形全等的判定方法和性质,以及平行线的判定,解题关键是掌握全等三角形的判定方法,运用全等三角形的性质证明线段和角相等.【变式2】如图,已知AB AC =,AD AE =,BD CE =,求证:312.【分析】利用SSS 可证明△ABD△△ACE ,可得△BAD=△1,△ABD=△2,根据三角形外角的性质即可得△3=△BAD+△ABD ,即可得结论.解:在△ABD 和△ACE 中,AB=AC AD=AE BD=CE ⎧⎪⎨⎪⎩,△△ABD△△ACE ,△△BAD=△1,△ABD=△2,△△3=△BAD+△ABD ,△△3=△1+△2.【点拨】本题考查全等三角形的判定与性质及三角形外角性质,熟练掌握判定定理及外角性质是解题关键.2.已知:如图,AB AC =,F ,E 分别是AB AC ,的中点,求证:ABE ACF ≌.在ABE 与△AB AC A A AE AF =⎧⎪∠=∠⎨⎪=⎩ABE △≌△【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:ASAAAS 、、【变式1】如图,点D 在BC 上,,ADB B BAD CAE ∠=∠∠=∠.(1) 添加条件:____________(只需写出一个),使ABC ADE ≅;(2) 根据你添加的条件,写出证明过程.【答案】(1) AC AE = (2) 见分析【分析】(1)根据已知条件可得AB AD =,BAC DAE ∠=∠,结合三角形全等的判定条件添加条件即可;(2)结合(1)的条件,根据三角形全等的判定条件添加条件进行证明即可.解:(1)添加的条件是:AC AE =,故答案为AC AE =;(2)△,ADB B ∠=∠△AB AD =,△BAD CAE ∠=∠△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,又AC AE =△ABC ADE ≅【点拨】本题主要考查了三角形全等的判定,确定出三角形全等判定条件是解答本题的关键.【变式2】如图所示,DC CA ⊥,EA CA ⊥,CD AB =,CB AE =,求证:(1) BCD EAB ≌△△;(2) DB BE ⊥.【分析】(1)利用SAS 判定定理证明三角形全等即可;(2)由()≌DCB BAE SAS △△,可得∠=∠DBC BEA ,∠=∠BDC EBA ,再利用90DBC BDC ∠+∠=︒,可得90∠+∠=︒DBC EBA ,即90DBE ∠=︒,所以DB BE ⊥.解:(1)证明:△DC CA ⊥,EA CA ⊥,△90∠=∠=︒DCB BAE ,在DCB △和BAE 中,CD AB DCB BAE CB AE =⎧⎪∠=∠⎨⎪=⎩△()≌DCB BAE SAS △△. (2)证明:由(1)可知()≌DCB BAE SAS △△, △∠=∠DBC BEA ,∠=∠BDC EBA ,△90DBC BDC ∠+∠=︒,△90∠+∠=︒DBC EBA ,即90DBE ∠=︒,△DB BE ⊥.【点拨】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.类型二、用“SSS”和“SAS”间接证明三角形全等➽➼证明✮✮求值3.已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,求证:△ABC≌≌DEF .【分析】首先根据AF=DC ,可推得AF ﹣CF=DC ﹣CF ,即AC=DF ;再根据已知AB=DE ,BC=EF ,根据全等三角形全等的判定定理SSS 即可证明△ABC△△DEF .解:△AF=DC ,△AF ﹣CF=DC ﹣CF ,即AC=DF ;在△ABC 和△DEF 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩△△ABC△△DEF (SSS )举一反三: 【变式1】如图,已知:PA=PB,AC =BD ,PC =PD ,△PAD 和△PBC 全等吗?请说明理由.【分析】由AC=BD ,利用线段的和差关系可得AD=BC ,利用SSS 即可证明△PAD△△PBC.解:△AC =BD ,△AC+CD=BD+CD ,即AD =BC ,又△PA =PB ,PC =PD ,△△PAD△△PBC(SSS)【点拨】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题关键.【变式2】如图,点D ,A ,E ,B 在同一直线上,EF =BC ,DF =AC ,DA =EB .试说明:△F =△C .【分析】根据SSS 的方法证明△DEF△△ABC,即可得到结论.解:因为DA =EB , 所以DE =AB.在△DEF 和△ABC 中, 因为DE =AB ,DF =AC ,EF =BC ,所以△DEF△△ABC(SSS),所以△F =△C.【点拨】本题考查了全等三角形的判定和性质,属于简单题,找到证明全等的方法是解题关键.4.如图,在ABCD 中,点E 、F 在BD 上,ABE 与CDF 全等吗?若全等,写出证明过程;若不全等,请你添加一个条件使它们全等,并写出证明过程.(1) 你添加的条件是__________.(2) 证明过程: 【答案】(1) BE DF =,答案不唯一; (2) 证明见分析; 【分析】(1)根据选择的全等三角形判定方法添加合适的条件即可;(2)由四边形ABCD 是平行四边形得到AB CD ∥,AB CD =,得ABE CDF ∠=∠,再用上添加的条件,即可证明结论.(1)解:BE DF =(答案不唯一)故答案为:BE DF =(答案不唯一)(2)证明:△四边形ABCD 是平行四边形,△AB CD ∥,AB CD =,△ABE CDF ∠=∠,在ABE 和CDF 中,AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩,△ABE CDF △≌△(SAS ).【点拨】此题考查了平行四边形的性质、全等三角形的判定等知识,熟练掌握全等三角形的判定是解题的关键.举一反三:【变式1】如图,在ABC 和ADE 中,AB AD =,AC AE =,且BAD CAE ∠=∠,求证:ABC ADE △≌△.【分析】根据BADCAE ∠=∠可得BAC DAE ∠=∠,再根据SAS 即可证明.证明:△BAD CAE ∠=∠,△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,在ABC 和ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC ADE △≌△.【点拨】本题主要考查了用SAS 证明三角形全等,解题的关键是通过BAD CAE ∠=∠得出BAC DAE ∠=∠.【变式2】图,BE CF =,AC DF =,AC DF ∥.求证:ABC DEF ≌△△.【分析】首先根据BE CF =可得BC EF =,再由AC DF ∥可得ACB F ∠=∠,然后利用定理证明ABC DEF ≌即可.证明:△BE CF =,△BE EC CF EC ++=,即BC EF =,△AC DF ∥,△ACB F ∠=∠, 在ACB △和DFE △中,BC EF ACB F AC DF =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC DEF ≌.【点拨】此题主要考查了全等三角形的判定和平行线的性质,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.注意:AAA SSA 、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.类型三、全等的性质与“SSS”和“SAS”综合➽➼证明✮✮求值 5.已知:如图,在ABC 中,AB AC AD =,是BC 边上的中线.求证:AD BC ⊥(填空).证明:在三角形ABD ACD 和中,△()()()______________BD AB ⎧=⎪⎪=⎨⎪⎪⎩已知已知公共边,△ ≌ ( ).△ADB ∠= (全等三角形的对应角相等).△1902ADB BDC ∠∠︒==(平角的意义). △(垂直的意义).【答案】,,,,SSS DC AC AD AD ABD ACD ADC AD BC =∠⊥,△△,,【分析】证明()SSS ADB ADC ≌△△.推出ADB ADC ∠∠=,可得结论. 证明:△AD 是BC 边上的中线,△BD CD =,在三角形ABD △和ACD 中,【变式1】如图:AB AC =,BD CD =,若28B ∠=︒,求C ∠的度数.【答案】28︒ 【分析】连接AD ,利用“SSS ”证明ABD ACD △≌△,即可得到答案.解:连接AD ,在ABD △和ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,()SSS ABD ACD ∴≌C B ∴∠=∠,28B ∠=︒,28C ∴∠=︒.【点拨】本题考查了全等三角形的判定和性质,正确作辅助线构造全等三角形是解题关键.【变式2】已知:如图,AC BD =,AD BC =,AD ,BC 相交于点O ,过点O 作OE AB ⊥,垂足为E .求证:(1) ABC BAD ≌.(2) AE BE =.【分析】(1)利用SSS 证明ABC BAD ≌;(2)根据全等三角形的性质得出DAB CBA ∠=∠,则OA OB =,根据等腰三角形的性质可得出结论.(1)证明:在ABC 和BAD 中,AC BD BC AD AB BA =⎧⎪=⎨⎪=⎩,△ABC BAD ≌(2)证明:△ABC BAD ≌△CBA DAB ∠=∠,△OA OB =,△OE AB ⊥,△AE BE =.【点拨】此题考查了全等三角形的判定与性质,利用SSS 证明ABC BAD ≌是解题的关键.6.如图,在ABC 中,CM 是AB 边上的中线,8AC =,12BC =,求CM 的取值范围.【答案】210CM <<【分析】倍长中线CM 至点N ,构造BNM ,易得ACM BNM ≅△△,再利用三角形的三边关系找到CN 的取值范围,进而得到CM 的取值范围.解:如图,延长CM 到点N ,使CM MN =,连接BN ,在ACM △和BNM 中,CM NM AMC BMN AM BM =⎧⎪∠=∠⎨⎪=⎩,∴ACM BNM ≅△△(SAS ),∴8AC BN ==, 在BCN △中,BC BN CN BC BN -<<+,∴128128CN -<<+,即420CN <<,∴4220CM <<,即210CM <<.【点拨】本题考查了全等三角形的性质与判定以及三角形的三边关系,解决本题的关键是倍长中线构造全等三角形.举一反三:【变式1】如图,已知在ABC 与ADE 中,90BAC DAE AB AC AD AE ∠=∠=︒==,,,点C ,D ,E 三点在同一条直线上,连接BD .图中的CE BD 、有怎样的数量和位置关系?请证明你的结论.【答案】CE BD =,证明见分析【分析】根据SAS 证明ACE ABD ≌△△,即可得到CE BD =.解:CE BD =,证明:△90BAC DAE ∠=∠=︒,△BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠,在ACE △和ABD △中AC AB CAE BAD AE AD =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE ABD ≌△CE BD =.【点拨】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.【变式2】如图已知AOB 和MON △都是等腰直角三角形.(1) 如图1,连接AM ,BM ,此时AM ,BN 的数量关系为___________请说明理由.(2) 若将MON △绕点O 顺时针旋转,如图2,当点N 恰好在AB 边上时,求证:222BN AN MN +=.【答案】(1) AM BN =,理由见分析(2) 见分析 【分析】(1)由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =(2)连接AM ,由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =,再求得90MAN ∠=︒,利用勾股定理即可得到222BN AN MN +=解:(1)AM BN =,理由如下:△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ON AOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =(2)如下图,连接AM ,△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,45B BAO ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ONAOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =,45B MAO ∠=∠=︒,△90MAN MAO BAO ∠=∠+∠=︒,△222AM AN MN +=,△222BN AN MN +=【点拨】本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质及勾股定理,熟练掌握全等三角形的判定和性质是解决问题的关键。
北师大版七年级数学下册教学课件4.3 探索三角形全等的条件——边角边
∴∵A∠DA=是∠△7EA.,B如C的图角,平分已线,知CA=CB,AD=BD, M,N分别是CA,CB的中点,试说明:
∴△ABC≌△EFD,
已知:如D图M,A=BD=ANC,.BD=CD,E为AD上一点,
∴ 【归纳】两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”. 解: 连接CD,如图所示; AM=BN (重庆中考)如图,△ABC和△DEF分别在线段AE的两侧,点D、C在线段AE上,AC=DE, AB∥EF, AB=EF.
∠A=∠D ∴∠A=∠BB.
∴DM=DN.
又∵M,N分别是CA,CB的中点,
活动5 课堂小结
内 容
边角边 应 用 注 意
有两边及夹角对应相等的两个三角形全等(简写成“SAS”)
为证明线段和角相等提供了新的证法
1.已知两边,必须找“夹角” 2. 已知一角和这角的一夹边,必须找这角的另一夹边
∴∠BAD五=∠、EA作C. 业布置与教学反思
∴△AFD≌△CEB(SAS).
D
F C
练习
6.已知:如图,AB=AC,AD是△ABC的角平分线,
试说明:BD=CD. 解: ∵AD是△ABC的角平分线, ∴ ∠BAD=∠CAD, 在△ABD和△ACD中,
AB=AC(已知), ∠BAD=∠CAD(已证), AD=AD (已证), ∴△ABD≌△ACD (S∴ASB)D=. CD.
证明:∵AD是∠BAC的角平分线(已知) ∴∠BAD=∠CAD(角平分线的定义) ∵AB=AC(已知) ∠BAD=∠CAD(已证)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴BD=CD(全等三角形对应边相等)
A
BDC
北师大版七年级数学下册课件4.探索三角形全等的条件边边边
不一定全等 不一定全等 不一定全等
3cm
30°
50°
30°
50° 3cm
结论: 有两个条件对应相等不能保证三角形全等.
30° 3cm
30°
3cm
新知探究
探究活动3:三个条件可以吗? (1)有三个角对应相等的两个三角形;
30°
60°
30°
60°
结论:三个内角对应相等的三角形不一定全等.
新知探究
(2)三边对应相等的两个三角形会全等吗?
七年级数学北师版·下册
第四章 三角形
4.3.1 边边边
教学目标 1.探索三角形全等条件.(重点) 2.“边边边”判定方法和应用.(难点)
新课导入
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应 提供多少个数据,才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有 的边长和所有的角度吗?
课堂小测
3.如图 ,AB=AE,AC=AD,BD=CE,求证:△ABC ≌△AED.
证明:因为BD=CE,
所以BD-CD=CE-CD,
所以BC=ED .
在△ABC和△AED中,
AC=AD(已知), AB=AE(已知), BC=ED(已证),
所以△ABC≌△AED(SSS).
=×
×=
课堂小测
4. 如图,AC=FE,AD=FB,BC=DE. 求证:(1)△ABC≌△FDE ; (2)∠C= ∠E.
证明:(1)因为 AD=FB,
所以 AB=FD(等式性质).
在△ABC 和△FDE 中,
AC=FE(已知), BC=DE(已知), AB=FD(已证),
A。 ?CD=源自E?=。B
F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
佛像本是凝固的历史,在郑老师的解说里,佛像雕成之后,明洪武23年间(1390),有护法者为之建堂覆盖,明万历年间又有护法者重建,明泰昌元年间(1620年),一位叫叶向高的居士募缘增建 石佛阁,可清同治元年(1826年),石佛阁毁坏,清末,又有护法者要重新建阁,但几经磋商,还是决定将佛像耸立于天地之间,于是才有了裸露于眼前的十根耸立的石柱,辉映眼前石柱上的楷书“愿 天常生好人,愿人常行好事”…….可不知为什样流动,波澜起伏,那是一百个工匠心灵的现实,是他们和生活在他们 身边芸芸众生心灵的现实:在深受灾难、饥饿、生老病死困扰的娑婆世界,他们的人生经历了怎样的波澜起伏?当无常无时无刻不在摧残弱小生命,使他们和他们周遭的众生不得不向上苍发出呼救,吕 姓财主的召唤是不是恰逢其时?来到瑞岩山,在一钻一钻的雕刻中,他们看到了什么,他们是不是在专注于当下的一刻,找到了内心的佛,从而找到内心的安详?!在故事里,是吕姓财主四处寻找工匠, 可我在想,是不是工匠们共同发自内心的寻找,才有了吕姓财主的出现,就像有了吕姓财主和九十九个工匠的共同发心,才有了第一百个弥勒佛形象的示现一样……
