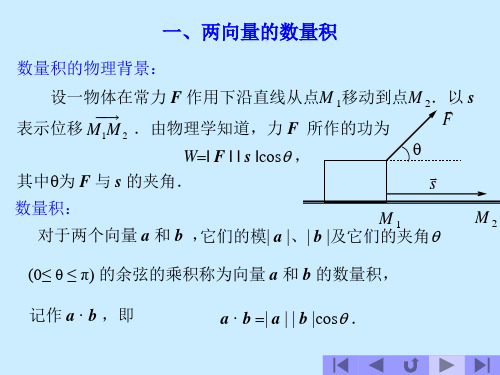
向量积的物理背景
《向量数量积的物理背景与定义》 知识清单

《向量数量积的物理背景与定义》知识清单一、向量数量积的物理背景在物理学中,我们常常会遇到力做功的问题。
当一个力作用在物体上,并使物体在力的方向上产生位移时,力就对物体做了功。
例如,一个水平向右的力 F 作用在一个物体上,使物体在水平方向上移动了一段距离 s,力 F 与位移 s 之间的夹角为θ。
那么力 F 所做的功 W 就可以表示为:W =|F| ×|s| × cosθ 。
这里的|F| 表示力 F 的大小,|s| 表示位移 s 的大小,cosθ 则反映了力的方向与位移方向之间的关系。
从这个物理模型中,我们可以抽象出向量数量积的概念。
力 F 和位移 s 都是向量,它们的数量积就与力做功的大小密切相关。
再比如,在电学中,电场强度 E 与电荷 q 移动的位移 s 的数量积,也可以表示电场力对电荷做功的大小。
通过这些物理实例,我们能够更加直观地理解向量数量积的实际意义,并且认识到它在描述物理现象和解决物理问题中的重要性。
二、向量数量积的定义1、定义已知两个非零向量 a 和 b,它们的夹角为θ(0 ≤ θ ≤ π),则数量|a| ×|b| × cosθ 叫做 a 与 b 的数量积(或内积),记作 a·b ,即 a·b =|a| ×|b| × cosθ 。
如果其中有一个向量为零向量,那么规定它们的数量积为 0 。
2、几何意义向量数量积 a·b 的几何意义是:数量积 a·b 等于 a 的长度|a| 与 b 在 a 方向上的投影|b|cosθ 的乘积,或者等于 b 的长度|b| 与 a 在 b 方向上的投影|a|cosθ 的乘积。
以 a·b 为例,假设向量 b 在向量 a 方向上的投影为向量 p ,则 p 的长度为|b|cosθ ,那么 a·b =|a| ×|p| 。
3、性质(1)交换律:a·b = b·a这意味着两个向量进行数量积运算时,其顺序不影响结果。
高等数学数量积向量积
两向量夹角的余弦的坐标表示:
当a 0 、b 0 时,由于 a ·b | a | | b |cos ,所以
cos a b
| a || b |
axbx ayby azbz
ax2
a
2 y
az2
bx2 by2 bz2
.
例1 已知三点M(1,1,1)、A(2,2,1)和B(2,1,2),求AMB .
3
二、两向量的向量积
向量积的物理背景:
设O为一根杠杆L的支点. 有一个力F 作用于这杠杆上P点处.
F 与 OMPA的夹角为 . 由力学规定,力 F 对支点O的力矩是一向
量 M , 它的模
|
M
||OMPA
|
|
F
|sin
,
F
而 M 的方向垂直于 MOPA与 F 所决定的 O
平面, M 的指向是的按右手规则从
线速度.
解 w 平行于 l 轴, w 的方向由右手规则确定.
设点M 到旋转轴 l 的距离为a ,再在 l 轴上任取一点O作向量
r
OMMA
,
并以
表示w
与
r
的夹角,
那么
w
a| r |sin .
设线速度为 v ,那么 v 的大小为
| v || w | a| w || r |sin ;
v a
M
v垂直于 w与 r ,又 v 的指向是使 w 、r 、v 符合右手规则.因此有
为了邦助记忆,利用三阶行列式符号,上式可写成
i jk ab ax ay az (ay bzaz by)i(az bx ax bz)j(ax byay bx)k.
bx by bz
例2 已知三角形ABC的顶点分别是A(1,2,3)、B(3,4,5)、 C(2,4,7),求三角形ABC的面积.
向量数量积的物理背景与定义ga

(3)已知向量a, b ,向量|a|=4,<a, b>=600,则向量a在向量b上的正射影的数量
解:4cos600=2
解:OA1=5COS600=5×( ½)=5/2
-5/2
四.向量的数量积(内积)
定义: 叫做向量a和b的数量积(或内积)
3
的夹角是
与
AD
AB
∵
练习3
已知|a|=3, |b|=5,且a·b=-12,求a在b方向上的正射影的数量及b在a方向上的正射影的数量。
解:因为
所以a在b方向上的正射影的数量是
b在a方向上的正射影的数量是
(1)
01
A 锐角三角形
06
C
05
D
02
C 钝角三角形
04
D 不能确定
07
A 锐角三角形
2.3.1 向量数量积的物 理背景与定义
单击添加副标题
单击此处添加文本具体内容,简明扼要地阐述你的观点
一.力做功的计算
位移S A θ
θ表示力F的方向与位移S的方向的夹角。
如果一个物体在力F作用下产生位移S,那么F所做的功为:
( )
(×)
( )
(×)
(×)
(×)
练习4
课堂小结
1.两个向量的夹角
2.向量在轴上的正射影
正射影的数量
3.向量的数量积(内积)
a·b=
4.两个向量的数量积的性质:
(1). ab ab = 0
(2). aa = |a|2或
(3). cos =
范围0≤〈a ,b〉≤π;
平面向量数量积的物理背景及其含义

例2.已知|a|6,|b|4,a与b夹角为60,
解
:(a
2b)(·a
- 3b)
求:(1)(a2b)(a3b)
a·a a·b 6b·b
|
a
|2
a ·b
6
|
b
|2
(2)a2b|. | a |2 | a |·| b | cosθ 6 | b |2 36 12 96 72
例3.已知|a|3,|b|4,且a与b不共线.
b a
a+b
OM
Nc
则: (a + b) ·c = ON |c|
= (OM + MN) |c|
= OM|c| + MN|c|
= a·c + b·c .
典型例题
( 1)(ab)2
2
2
a 2abb
22
(2)(ab)(ab)a b
例1.已知向量a,b,求证下列各式
证明:(1)(a+b)2=(a+b)·(a+b) =(a+b)·a+(a+b)·b =a·a+b·a+a·b+b·b =a2+2a·b+b2.
6
WORKHARVEST
W=|F| |S|cosθ 其中 θ是F与S的夹角
数量积的定义
已知两个非零向量a 和b ,它们的夹
角为 ,我们把数量 |a||b|c叫os做a 与b 的
数量积(或内积),记作a · b ,即
(1)两向量的数量积是一个数量,
注
意 (2) a · b不能写成a×b ,‘·’不能省.
特别地: aa |a|2或 |a|aa求模的方法
求 角
(3)cos
|
ab a || b
(4)|a
|
向量数量积的物理背景及定义

A1 a1 O1
则a l a cos
︱a︱cosθ 的几何意义:
A
对于两个非零向量a与b,设其夹角为θ , a ︱a︱cosθ 叫做向量a在b方向上的 b 正射影的数量, θ B O |a|cosθ A1 ︱b︱cosθ的几何意义呢?
向量数量积 a · 的几何意义 b
1、向量的夹角的概念
(0 )
B
叫做向量
b
怎样找向量 的夹角? b
记作 a, b
和 a
b的夹角.
a
O
特殊情况:
a
A
注意:在两向量的夹角 定义中,两向量必须是 同始点的
O b B 0 a 与 b 同向
a
A B b
a
O A
a 与 b 反向
(×)
(×)
(×) ( )
(×) (×)
课堂小结
向量的夹角 共始点 向量在轴上的正射影
al a cos a , l
向量的数量积的定义,几何意义,性质。
a b a b cos a, b
我们学到 了什么?
向量 a 与b 的数量积等于a 的长度 |a| 与b 在a 的方向上的正射影的数量| b | cosθ的积.
θ为直角时, | b | cos a , b =0
A
B1
O
a A
θ为锐角时, | b | cos a , b >0
θ为钝角时, | b | cos a , b <0
当夹角为 0 0 和180° ,结果是什么呢?
2.3.1向量数量积 的物理背景与定 义
我们学过功的概念,即一个物体在力F的 作用下产生位移s(如图) F s
向量数量积的物理背景与定

若a是一个单位向量,则a · a = 1。
向量数量积的几何意义
向量数量积表示两个向量的“相似度” 或“一致性”。当两个向量同向时, 数量积为最大值;当垂直时,数量积 为0;其他情况下,数量积介于0和最 大值之间。
向量数量积可以用于描述两个向量在 方向上的关系,例如在物理中可以表 示力或速度之间的角度关系,在工程 中可以用于分析结构的稳定性等。
05
CHAPTER
向量数量积的物理意义
动能定理
动能定理描述了物体在力的作用下运动时,动能的变化与 力所做的功之间的关系。具体来说,物体动能的增加等于 力所做的功。在物理学中,向量数量积可以用来表示力与 位移之间的点乘运算,从而计算力所做的功。
公式:$W = Fmathbf{cdot}s$,其中$W$表示力所做的功, $F$表示力的大小和方向,$mathbf{cdot}$表示点乘运算, $s$表示位移。
03
CHAPTER
向量数量积的应用
力的合成与分解
力的合成
通过向量数量积,可以将多个力合成一个合力,计算合力的效果。例如,在物理实验中,经常需要将多个力合成 一个合力,以研究物体的运动状态。
力的分解
在物理问题中,有时需要将一个已知力分解为若干个分力。通过向量数量积,可以将一个力分解为沿不同方向的 分力,以便进一步分析。
04
CHAPTER
向量数量积的运算
向量数量积的运算律
交换律
$vec{A} cdot vec{B} = vec{B} cdot vec{A}$
结合律
$(vec{A} + vec{B}) cdot vec{C} = vec{A} cdot vec{C} + vec{B} cdot vec{C}$
2.3.1 向量数量积的物理背景与定义

张喜林制2.3.1 向量数量积的物理背景与定义考点知识清单1.两个向量的夹角:已知两个非零向量a 、b ,作,,b a ==则AOB ∠称作向量a 和向量b 的夹角,记作(a ,b ),并规定其范围是 当2,π=b a 时,我们说向量a 和向量b 互相垂直,记作.b a ⊥2.向量在轴上的正射影:已知向量a 和轴L ,作,a =过点0,A 分别作轴f 的垂线,垂足分别为,,11A O 则11A O 叫做向量a 在轴L 上的正射影(简称射影),该射影在轴L 上的坐标,称作a 在轴L 上的数量或在轴L 的方向上的数量,即 ,其中l a 是a 在轴L 上正射影的数量. 3.向量的数量积(内积)定义: 4.向量内积的性质:(1)如果e 是单位向量,则=⋅=⋅a e e a,0)2(=⋅⇒⊥b a b a 且;0b a b a ⊥⇒=⋅,||)3(2a a a =⋅即>=<b a ,cos )4( ||)5(b a ⋅ .||||b a要点核心解读1.向量数量积的物理背景——力做功的计算.如图2 -3 -1 -1.一个力F 使物体发生位移s 所做的功W 可以用下式计算..cos ||||θF s W =其中θcos ||F 就是F 在物体位移方向上的分量的数量,也就是力F 在物体位移方向上正射影的数量. 2.两个向量的夹角已知两个非零向量a ,b (如图2 -3 -1 -2所示),作,,b a ==则AOB /称作向量a 和向量b 的夹角,记作),,(b a 并规定,),(0π≤≤b a在这个规定下,两个向量的夹角被唯一确定了,并且有.,,>>=<<a b b a当2,π>=<b a 时,我们说向量a 和向量b 互相垂直,记作,b a ⊥在讨论垂直问题时,规定零向量与任意向量垂直.3.向量在轴上的正射影已知向量a 和轴L 如图2 -3 -1 -3.作,a =过点0、A 分别作轴L 的垂线,垂足分别为,11A O 、,则向量11A O 叫做向量a 在轴L 上的正射影(简称射影),该射影在轴L 上的坐标,称作a 在轴L 上的数量或在轴L 的方向上的数量.a =在轴L 上正射影的坐标记作,l a 向量a 的方向与轴L 的正向所成的角为θ,则由三角函数中的余弦定义有.cos ||θa a l =4.向量的数量积(内积)定义><b a b a ,cos ||||叫做向量a 和向量b 的数量积(或内积),记作a ×b ,即.,cos ||||><=⋅b a b a b a5.平面向量的数量积的性质(1)如果e 是单位向量,则;,cos ||><=⋅=⋅e a a a e e a,0)2(=⋅⇒⊥b a b a 且;0b a b a ⊥⇒=⋅,||)3(2a a a =⋅即;||a a a ⋅=;||||,cos )4(b a ba b a ⋅>=<.||||||)5(b a b a ≤⋅典例分类剖析考点1求数量积的问题[例1] 已知.3||,4||==b a 当b a b a b a 与③②①,,//⊥的夹角为60时,分别求a 与b 的数量积. [解析] ①当b a //时,若a 与b 同向,则a 与b 的夹角∴=,0 θ||a b a =⋅;120cos 34cos .||=⨯⨯= θb若a 与b 反向,则a 与b 的夹角为,180o =θ;12)1(34180cos ||||-=-⨯⨯=⋅=⋅∴o b a b a②当a ⊥b 时,向量a 与b 的夹角为,90;003490cos .||||=⨯⨯=⋅=⋅∴ b a b a③当a 与b 的夹角为60时..6213460cos .||||=⨯⨯=⋅=⋅∴ b a b a [点拨] 若||||b a ⋅是一个定值k ,则当这两个向量的夹角从0变化到o180时,两向量的数量积从k 减到-k ,其图象恰好为从O 到霄的半个周期内的余弦图象,对于图形中的问题要注意区分图形中的角与向量的夹角.1.如图2—3 -1-4,在边长为1的等边三角形ABC 中,设,a BC =,,c AB bCA == 试求 a c c b b a ..++⋅的值.考点2 向量的夹角与垂直关系的运算[例2] 已知,9,1||,36||-=⋅==b a b a 则=),(b a ( )120.A 150.B 60.C 30.D[试解] .(做后再看答案,发挥母题功能) [解析] 利用||||,cos b a ba b a ⋅>=<及,),(0π≤≤b a 求⋅),(b a解:⋅-=⨯-=⋅>=<231369||||,cos b a b a b a又.150,,180),(0 >=∴<≤≤b a b a [答案] B[点拨] 两个向量夹角的范围是⋅],0[π2.(1)向量a 、b 满足4222-=⋅--b a b a 且,4||,2||==b a 则=),(b a(2)若0是△ABC 所在平面内一点,且满足=-|||,2|-+则△ABC 的形状为( ). A .等腰直角三角形 B .直角三角形 C .等腰三角形 D .等边三角形考点3 向量的投影问题[例3] 如图2-3 -1-5,在等腰三角形ABC 中,=AB D ABC AC ,30,2 =∠=是BC 的中点, 求:(1)C 在方向上的投影;(2)在D 方向上的投影.[解析] 如图2 -3 -1-5所示,连接AD ,在等腰三角形ABC 中,=∠==ABC AC AB ,2D ,30是BC的中点,所以⨯===⊥230cos ,AB BD CD BC AD .323=作CB 的延长线BE ,则与的夹角为-=∠180ABE .150=∠ABCCD BA =)1(方向上的投影是=-⨯=)23(2150cos || ;3- BA CD 在)2(方向上的投影是=-⨯=)23(3150cos || ⋅-23[点拨] 向量的投影是一个实数,它可正、可负、可为零,其性质符号取决于两向量之间的夹角,因此在正确理解向量投影定义的同时,找准两个向量之间的夹角是关键.b a a 与,4||.3=的夹角为,30 则a 在b 方向上的投影为考点4 内积性质的简单应用[例4] 已知,5||||==b a 向量a 与b 的夹角为,3π求.|||,|b a b a -+ [解析] 解法一:由数量积公式2||a a =求解.,25||,25||2222====b b a a,2253cos55cos ||||=⨯⨯==⋅πθb a b a .352525252)(222=++=⋅++=+=+∴b a b a b a b a同样可求 b a b a b a b a ⋅-+=-=-2)(||2.5252525=-+=解法二:由向量线性运算的几何意义求作菱形ABCD ,使,3.5π=∠==DAB AD AB设,,b A a A ==如图2 -3 -1 -6.则,5||||||===-A B b a.355232||2||||=⨯⨯===+A b a[点拨] (1)利用数量积求解长度问题是数量积的重要应用,要掌握此类问题的处理方法:①22||a a a a =⋅=;||a a a ⋅=或.2)(||22b b a a b a b a +⋅±=±=±②由关系式=2a ,||2a 可使向量的长度与向量的数量积互相转化,因此欲求+a ||,b 可求),()(b a b a +⋅+将此式展开.由已知,5||||==b a 即b a b b a a ⋅=⋅=⋅,25 也可求得,225将上面各式的值代入,即可求得被求式的值. (2)利用向量线性运算的几何意义转化到求平面几何的长度的计算.4.(1)已知向量a ,b 满足==||,13||b a ,24||,19=+b a 求.||b a -(2)已知a 、b 均为单位向量,它们的夹角为,60那么+a |=|3b ( ).7.A 10.B 13.C 4.D学业水平测试1.下列命题,正确的是( ).A .若,0=⋅b a 则00==b a 或B .若,0=⋅b a 则b a //C .若,b a ⊥则0=⋅b a ||.a a aD >⋅对任意向量恒成立 2.已知,135,,4||,212 >=<=-=⋅b a a b a 则=||b ( )12.A 3.B 6.C 33.D3.以下等式中恒成立的有( ).① b a b a ⋅=⋅ ② ;||;||22a a a a a ==⋅③④⋅+⋅-=-)2()2(222b a b a b aA.l 个B.2个 C .3个 D.4个4.向量a 、b 满足,3||,2||==b a 且,7||=+b a 则=⋅b a5.已知,2||,1||==b a 且),2()(b a b a λλ-⊥+a 与b 的夹角为,60则=λ6.在△ABC 中,设,,,c AB b CA a BC ===若..a c c b b a ⋅=⋅=求证:△ABC 为正三角形,高考能力测试(测试时间:45分钟测试满分:100分) 一、选择题(5分×8 =40分)1.在△ABC 中,C B A ∠∠∠、、的对边分别为1,3,==b a c b a 、、,30=∠C 则=B .343.A 323.B 343.-C 323.-D 2.△ABC 中,.A B A ⋅+⋅+一定是( )A .小于0B .大于0.C .小于或等于零D .大于或等于零3.设a 、b 、c 是任意的非零平面向量,且相互不共线,则下列结论正确的有( )..(|;||||];0)()(b b a b a b a c c b a ③②①-≤-=⋅⋅-⋅⋅b a c a c ⋅⋅-⋅)()不与C 垂直;=-⋅+)23()23(b a b a ④.||4||922b a -A .①②B .②③C .③④D .②④ 4.若,5||,4||,32041||==-=-b a b a 则a 与b 的数量积为( ).310.A 310.-B 210.C 10.D5.若四边形ABCD 满足,0)(,0=⋅-=+AC AD AB CD AB 则该四边形一定是( ).A .直角梯形B .菱形C .正方形D .矩形 6.(2009年福建高考题)设a ,b ,c 为同一平面内具有相同起点的任意三个非零向量,且满足a 与b 不共线,|,|||,c a c a =⊥则||c b ⋅的值一定等于( ).A .以a ,b 为两边的三角形的面积B .以b ,c 为两边的三角形的面积C .以a ,b 为邻边的平行四边形的面积D .以b ,c 为邻边的平行四边形的面积 7.已知非零向量AC AB 与满足0)||||(=⋅+AC AC AB 且.||AB ⋅,21||=AC 则△ABC 为( ). A .三边均不相等的三角形 B .直角三角形 C .等腰非等边三角形 D .等边三角形 8.(2011年全国大纲理)设向量a ,b ,c 满足.,1||||a b a ==,21-=b ,60, >=--<c b c a 则∣C ∣的最大值等于( ).2.A3.B 2.C 1.D二、填空题(5分x4 =20分)9.(2008年江苏高考题)a ,b 的夹角为,3||,1||,120==b a则=-|5|b a10.(2010年天津高考题)如图2-3 -1 -7,在△ABC 中,,AB AD ⊥BC =,1||=AD 则=⋅.11.设向量a ,b ,c 满足.,)(,0b a c b a c b a ⊥⊥-=++若=||a 222||||||,1c b a ++则的值是 12.(2008年陕西高考题)关于平面向量a ,b ,c ,有下列三个命题:①若,c a b a ⋅=⋅则;c b =②若//),6,2(),,1(a b k a -==;3,-=k b 则③非零向量a 和b 满足|,|||||b a b a -==则a 与b a +的夹角为.60 其中真命题的序号为____(写出所有真命题的序号).三、解答题(10分x4 =40分)13.如图2-3 -1-8,已知正六边形,654321P P P P P P 求下列向量的数量积.;)2(;)1(41213121P P P P P P P P ⋅⋅.)4(;)3(61215121P P p p P P P P ⋅⋅14.已知,0||2||=/=b a 且关于x 的方程0||2=⋅++b a x a x 有实根,求a 与b 的夹角的取值范围.15.已知向量,60,, =∠==AOB b O a 且.4||||==b a (1)求|;||,|b a b a -+(2)求b a +与a 的夹角及b a -与a 的夹角.16.已知),1,(),1,2(λ=--=b a 若a 与b 的夹角α为钝角,求A 的取值范围.。
平面向量数量积的物理背景及其含义

平面向量数量积的物理背景及其含义在我们的日常生活中,有些东西就像水和空气,虽然看不见,但却无时无刻不在影响着我们。
就拿平面向量的数量积来说吧,听起来可能有点儿复杂,其实它就是一种简单又有趣的概念,来,咱们一起聊聊这件事。
想象一下,你在操场上跟朋友打篮球。
你投篮的时候,用力的角度、力量的大小,都会影响到篮球的飞行轨迹。
数量积就像是你在这场游戏里的秘密武器,能帮助你理解这股力量和方向的结合。
简单点说,数量积就是把两个向量结合在一起,得出一个数值,告诉你这两个向量之间的关系。
比如,力的方向和移动的方向,如果你力气大但方向错了,那球就算飞得再快,也未必能进篮。
这就好比你走路的时候,前面有个障碍,你必须调整自己的方向,不然就撞上去了。
再举个例子,你在海边晒太阳,风在吹,你的沙滩椅子被风推得摇摇晃晃。
这个时候,你得考虑风的方向和力量,才能舒服地躺在那里。
如果你朝着风的方向靠,就算风再大,也不会把你推倒。
数量积就像是这个时候的指南针,告诉你该如何调整自己,才能迎风而行。
这种感觉真的是妙不可言,恰如其分。
说到这里,你可能会想,这个数量积到底有什么用呢?嘿,别小看它。
它在物理学、工程学和计算机科学中,都起着至关重要的作用。
拿物理来说,力和位移的数量积,能直接帮我们算出做功的大小。
这就意味着,咱们可以通过简单的计算,明白做事情的效率。
想想看,如果你在搬家,要搬一个重重的箱子,你使出的力气和箱子移动的方向正好一致,结果就是一口气就能把它搬上车。
但要是你使力的方向偏了,可能搬半天也没动,这可就太尴尬了。
再看看工程领域,设计师们在绘制建筑图纸的时候,数量积也能大显身手。
想要确保建筑的稳定性和安全性,设计师得考虑每一个结构的受力情况。
而数量积恰好能帮助他们判断,哪个方向的力量最大,从而做出最好的设计选择。
这就像是在搭积木,搭得越稳,玩得越开心。
再说计算机科学,这可是个神奇的领域。
机器学习、计算机图形学中,数量积用得相当频繁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)cos〈a,b〉= |a||b| (|a||b|≠0). (5)|a·b| ≤ |a||b|.
2.3.1 向量数量积的物理背景与定义
9
预习导学
[知识链接]
挑战自我,点点落实
如图,一个物体在力F的作用下产生位移 s,且力F与
位移 s 的夹角为θ,那么力F所做的功W怎么计算?
W=|F1|·|s|
∴cos〈A→B,B→C〉=cos(180°-B)=-cos B=-153. ∴A→B·B→C=|A→B|·|B→C|cos(180°-B)
=13×5×-153=-25.
2.3.1 向量数量积的物理背景与定义
16
练习2. 已知正三角形ABC的边长为1,求:
(1)A→B·A→C;
(2)A→B·B→C;
F1
= |F|cos θ ·|s|
=|F||s|cos θ= F·s
2.3.1 向量数量积的物理背景与定义
10
课堂小结 1.了解平面向量数量积的物理背景,即物体在力F的作用下 产生位移s所做的功。 2.向量在轴上的正射影及其数量。 3.掌握了平面向量数量积的定义,会数量积求向量的夹角 4.总结了平面向量数量积的性质,会用其解决问题。
→→ (3)BC·AC.
解 (1)∵A→B与A→C的夹角为 60°. ∴A→B·A→C=|A→B||A→C|cos 60°=1×1×12=12.
(2)∵A→B与B→C的夹角为 120°.
∴A→B·B→C=|A→B||B→C|cos 120°=1×1×-12=-12. (3) B→C·A→C=|B→C||A→C|cos 60°=1×1×12=12.
2.3.1 向量数量积的物理背景与定义
11
课堂讲义
重点难点,个个击破
判断正误,并简要说明理由. (1)a·0=0;(2)0·a=0;(3)a与b是两个单位向量,则a2=b2. 解 上述3个命题中只有(3)正确; 对于(1):两个向量的数量积是一个实数,应有a·0=0; 对于(2):应有0·a=0; 对于(3):|a|=|b|=1⇒a2=b2=1.
13
练习3 已知a、b、c是三个非零向量,则下列问题中
真命题的个数为( )
①a·b=±|a|·|b|⇔a∥b;②a、b反向⇔a·b=-|a|·|b|;
③a⊥b⇔|a+b|=|a-b|;④|a|=|b|⇔|a·c|=|b·c|.
A.1
B.2Biblioteka C.3D.42.3.1 向量数量积的物理背景与定义
14
练习4 已知a,b是两个非零向量|a|=3,|b|=4,|a·b|=6,
求a与b的夹角。
练习5 已知向量a,b的夹角为120,且|a|=4,|b|=2 求 (1) |a+b| (2) |3a-4b|.
2.3.1 向量数量积的物理背景与定义
15
练习 1.在△ABC 中,|A→B|=13,|B→C|=5,|C→A|=12,则A→B·B→C的
值是________.
解析
易知|A→B|2=|B→C|2+|C→A|2, C=90°. cos B=153,
2.3.1 向量数量积的物理背景与定义
4
例1
(1)
已知
|O→A|=5,〈O→A,l〉=60°,求
→ OA
在l上正射影的数量OA1
(2)
已知|O→B|=5,〈O→B,l〉=120°,求
→ OB
在l上正射影的数量OB1
2.3.1 向量数量积的物理背景与定义
5
思考:当θ为锐角,钝角,0°,90°,180°角时,向量在轴上 正射影的数量是怎样的?
例2 已知|a|=3,|b|=4, a与b的夹角θ=135°,求a·b
2.3.1 向量数量积的物理背景与定义
8
平面向量数量积的性质
(1)e是单位向量,则a·e=e·a=|a|cos〈a,e〉. (a≠0).
(2)a⊥b⇒a·b= 0 ,反之a·b=0 ⇒a⊥b(a≠0,b≠0). (3)a·a= |a|2 或|a|= a·a .
2
1.两个向量的夹角 (1)已知两个非零向量a,b(如图所示),作 O→A=a, O→B=b,则 ∠AOB 称作向量a和向量b的夹角, 记作〈a,b〉, 并规定它的范围是[0,π].
任意向量
思考 正∆ABC中,〈A→B,A→C〉= 60〈°, A→B,B→C〉=120°, 〈A→C,B→C〉=60°.
2.3.1 向量数量积的物理背景与定义
3
2.向量在轴上的正射影 已知向量 a 和轴 l,作 O→A=a,过点O,
A分别作轴l的垂线,垂足分别为O1,A1,则 向量 O——1A→1叫做向量 a 在轴 l上的正射影(简称
射影),该射影在轴l上的坐标,称作 a 在轴 l上的数量,或 a
在轴 l 上正射影的数量.记为al, al=|a|cos θ
2.3.1 向量数量积的物理背景与定义
17
练习4 已知a,b是两个非零向量|a|=3,|b|=4,|a·b|=6,求
a与b的夹角。
2.3.1 向量数量积的物理背景与定义
18
练习5 已知向量a,b的夹角为120,且|a|=4,|b|=2 求 (1) |a+b| (2) |3a-4b|.
2.3.1 向量数量积的物理背景与定义
2.3.1 向量数量积的物理背景与定义
12
练习 1.在△ABC 中,|A→B|=13,|B→C|=5,|C→A|=12,则A→B·B→C的
值是________.
练习 2.已知正三角形ABC的边长为1,求:
(1)A→B·A→C;
(2)A→B·B→C;
→→ (3)BC·AC.
2.3.1 向量数量积的物理背景与定义
6
跟踪演练 已知|p|=2,|q|=3,且p与q的夹角θ=120°,则
向量p在q方向上的正射影的数量为
;向量q在p
方向上的正射影的数量为
。
2.3.1 向量数量积的物理背景与定义
7
平面向量数量积的基本概念
|a||b|cos 〈a,b〉叫做向量a和b的数量积(或内积),记 作a·b. 即 a·b=|a||b|cos〈a,b〉.
19
第二章——
2.3.1 向量数量积的物理背景与定义
预习导学
[知识链接]
挑战自我,点点落实
如图,一个物体在力F的作用下产生位移 s,且力F与
位移 s 的夹角为θ,那么力F所做的功W怎么计算?
W=|F1|·|s|
F1
= |F|cos θ ·|s|
=|F||s|cos θ.
2.3.1 向量数量积的物理背景与定义
(1)当θ为锐角时,正射影和轴 l 同向, al=|a|cos θ >0. (2)当θ为钝角时,正射影和轴 l 反向,al=|a|cos θ <0.
(3)当 θ= 0° 时, al=|a|; 当 θ= 180° 时, al=-|a|.
(4)当 θ= 90° 时, al=0.
2.3.1 向量数量积的物理背景与定义
