第二章参数估计习题修改
参数估计习题参考答案

参数估计习题参考答案班级:姓名:学号:得分一、单项选择题:1、关于样本平均数和总体平均数的说法,下列正确的是 ( B )(A)前者是一个确定值,后者是随机变量(B)前者是随机变量,后者是一个确定值(C)两者都是随机变量(D)两者都是确定值2、通常所说的大样本是指样本容量( A )(A)大于等于30 (B)小于30 (C)大于等于10 (D)小于103、从服从正态分布的无限总体中分别抽取容量为4,16,36的样本,当样本容量增大时,样本均值的标准差将( B )(A)增加(B)减小(C)不变(D)无法确定4、某班级学生的年龄是右偏的,均值为20岁,标准差为4.45.如果采用重复抽样的方法从该班抽取容量为100的样本,那么样本均值的分布为( A )(A)均值为20,标准差为0.445的正态分布(B)均值为20,标准差为4.45的正态分布(C)均值为20,标准差为0.445的右偏分布(D)均值为20,标准差为4.45的右偏分布 5. 区间估计表明的是一个( B )(A)绝对可靠的范围(B)可能的范围(C)绝对不可靠的范围(D)不可能的范围 6. 在其他条件不变的情形下,未知参数的1-α置信区间,( A )A. α越大长度越小B. α越大长度越大C. α越小长度越小D. α与长度没有关系7. 甲乙是两个无偏估计量,如果甲估计量的方差小于乙估计量的方差,则称( D )(A)甲是充分估计量(B)甲乙一样有效(C)乙比甲有效(D)甲比乙有效8. 设总体服从正态分布,方差未知,在样本容量和置信度保持不变的情形下,根据不同的样本值得到总体均值的置信区间长度将( D )(A)增加(B)不变(C)减少(D)以上都对9.在其他条件不变的前提下,若要求误差范围缩小1/3,则样本容量( C )(A)增加9倍(B)增加8倍(C)为原来的2.25倍(D)增加2.25倍 10设容量为16人的简单随机样本,平均完成工作时间13分钟,总体服从正态分布且标准差为3分钟。
庞皓计量经济学第二章练习题及参考解答
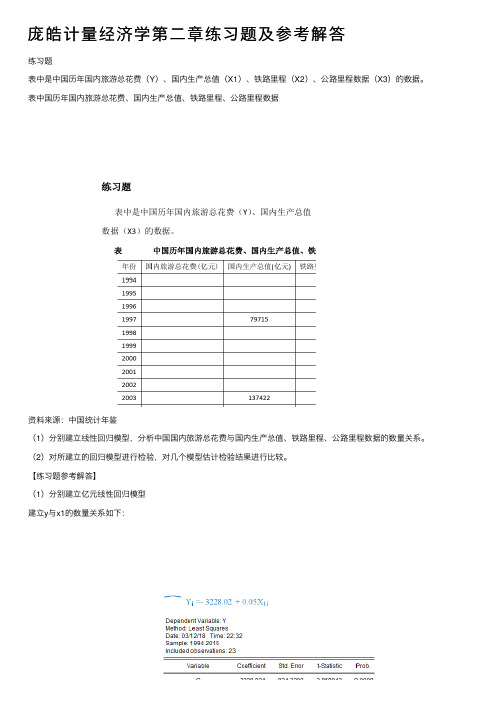
庞皓计量经济学第⼆章练习题及参考解答练习题表中是中国历年国内旅游总花费(Y)、国内⽣产总值(X1)、铁路⾥程(X2)、公路⾥程数据(X3)的数据。
表中国历年国内旅游总花费、国内⽣产总值、铁路⾥程、公路⾥程数据资料来源:中国统计年鉴(1)分别建⽴线性回归模型,分析中国国内旅游总花费与国内⽣产总值、铁路⾥程、公路⾥程数据的数量关系。
(2)对所建⽴的回归模型进⾏检验,对⼏个模型估计检验结果进⾏⽐较。
【练习题参考解答】(1)分别建⽴亿元线性回归模型建⽴y与x1的数量关系如下:建⽴y与x2的数量关系如下:建⽴y与x3的数量关系如下:(2)对所建⽴的回归模型进⾏检验,对⼏个模型估计检验结果进⾏⽐较。
关于中国国内旅游总花费与国内⽣产总值模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显着性检验表明,GDP对中国国内旅游总花费有显着影响。
同理:关于中国国内旅游总花费与铁路⾥程模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显着性检验表明,铁路⾥程对中国国内旅游总花费有显着影响。
关于中国国内旅游总花费与公路⾥程模型,由上可知,,说明所建模型整体上对样本数据拟合较好。
对于回归系数的t检验:,对斜率系数的显着性检验表明,公路⾥程对中国国内旅游总花费有显着影响。
为了研究浙江省⼀般预算总收⼊与地区⽣产总值的关系,由浙江省统计年鉴得到如表所⽰的数据。
年份⼀般预算总收⼊(亿元)地区⽣产总值(亿元)年份⼀般预算总收⼊(亿元)地区⽣产总值(亿元)Y X Y X 1978199819791999198020001981200119822002198320031984200419852005198620061987200719882008198920091990201019912011199220121993 2013 1994 2014 1995 2015 1996 2016 1997(1)建⽴浙江省⼀般预算收⼊与全省地区⽣产总值的计量经济模型,估计模型的参数,检验模型的显着性,⽤规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2017年,浙江省地区⽣产总值为52000亿元,⽐上年增长10%,利⽤计量经济模型对浙江省2017年的⼀般预算收⼊做出点预测和区间预测(3)建⽴浙江省⼀般预算收⼊的对数与地区⽣产总值对数的计量经济模型,估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义。
统计学习题答案参数估计

第5章参数估计●1. 从一个标准差为5的总体中抽出一个容量为40的样本,样本均值为25。
(1)样本均值的抽样标准差等于多少?(2)在95%的置信水平下,允许误差是多少?解:已知总体标准差σ=5,样本容量n=40,为大样本,样本均值=25,(1)样本均值的抽样标准差===0。
7906(2)已知置信水平1-=95%,得=1。
96,于是,允许误差是E ==1.96×0.7906=1.5496。
●2.某快餐店想要估计每位顾客午餐的平均花费金额,在为期3周的时间里选取49名顾客组成了一个简单随机样本.(3)假定总体标准差为15元,求样本均值的抽样标准误差;(4)在95%的置信水平下,求允许误差;(5)如果样本均值为120元,求总体均值95%的置信区间。
解:(1)已假定总体标准差为=15元,则样本均值的抽样标准误差为===2.1429(2)已知置信水平1-=95%,得=1.96,于是,允许误差是E ==1.96×2.1429=4.2000。
(3)已知样本均值为=120元,置信水平1-=95%,得=1.96,这时总体均值的置信区间为=120±4。
2=可知,如果样本均值为120元,总体均值95%的置信区间为(115。
8,124.2)元。
●3.某大学为了解学生每天上网的时间,在全校7500名学生中采取不重复抽样方法随机抽取36人,调查他们每天上网的时间,得到下面的数据(单位:小时):3.3 3。
1 6。
2 5.8 2。
3 4。
1 5.4 4。
5 3。
24。
4 2。
0 5。
4 2。
6 6。
4 1.8 3.5 5.7 2。
32。
1 1.9 1.2 5.1 4.3 4。
2 3.6 0。
8 1。
54。
7 1。
4 1.2 2。
9 3。
5 2.4 0.5 3.6 2。
5求该校大学生平均上网时间的置信区间,置信水平分别为90%、95%和99%。
解:⑴计算样本均值:将上表数据复制到Excel表中,并整理成一列,点击最后数据下面空格,选择自动求平均值,回车,得到=3。
参数估计习题参考答案

参数估计习题参考答案班级: __________ 姓名: ______________学号: __________ 得分 ___________、单项选择题:1、关于样本平均数和总体平均数的说法,下列正确的是(A )增加 (B )减小 (C )不变 (D )无法确定4.某班级学生的年龄是右偏的,均值为 20岁,标准差为4.45.如果采用重复抽样的方法从该班抽取容量 为100的样本,那么样本均值的分布为(A )(A )均值为20,标准差为0.445的正态分布(B )均值为20,标准差为4.45的正态分布 (C )均值为20,标准差为0.445的右偏分布(D )均值为20,标准差为4.45的右偏分布5. 区间估计表明的是一个(B )(A )绝对可靠的范围(B )可能的范围 (C )绝对不可靠的范围(D )不可能的范围 6. 在其他条件不变的情形下,未知参数的 1-a 置信区间,(A )C. a 越小长度越小D. a 与长度没有关系7.甲乙是两个无偏估计量,如果甲估计量的方差小于乙估计量的方差,则称(D )(A )甲是充分估计量(B )甲乙一样有效(C )乙比甲有效 (D )甲比乙有效8.设总体服从正态分布,方差未知,在样本容量和置信度保持不变的情形下,根据不同的样本值得到总 体均值的置信区间长度将(D )(A )增加 (B )不变(C )减少 (D )以上都对9 •在其他条件不变的前提下,若要求误差范围缩小 1 / 3,则样本容量(C )(A )增加9倍 (B )增加8倍 (C )为原来的2.25倍 (D )增加2.25倍10设容量为16人的简单随机样本,平均完成工作时间13分钟,总体服从正态分布且标准差为若想对完成工作所需时间构造一个90%置信区间,则 (A)A.应用标准止态概率表查出 z 值B.应用 t-分布表查出t 值C.应用一项分布表查出 p 值D.应用泊松分布表查出 入值11. 100(1- a % 是(C)A.置信限B.置信区间C.置信度D.可靠因素12. 参数估计的类型有(D(A )点估计和无偏估计(B )无偏估计和区间估计 (C )点估计和有效估计(D )点估计和区间估计13、抽样方案中关于样本大小的因素,下列说法错误的是 (C )A 、总体方差大,样本容量也要大B 、要求的可靠程度高,所需样本容量越大(A )前者是一个确定值,后者是随机变量 (B )前者是随机变量,后者是一个确定值 (C )两者都是随机变量(D )两者都是确定值2、通常所说的大样本是指样本容量(A )大于等于30 ( B )小于30(C )大于等于103、从服从正态分布的无限总体中分别抽取容量为4,16, 36标准差将(A )(D )小于10的样本,当样本容量增大时,样本均值的(B )A. a 越大长度越小B. a 越大长度越大 3分钟。
参数估计习题及答案

参数估计习题及答案参数估计在统计学中是一个重要的概念,它涉及到根据样本数据来估计总体参数的过程。
下面,我将提供一些参数估计的习题以及相应的答案,以帮助学生更好地理解这一概念。
习题一:假设有一个班级的学生数学成绩,我们从这个班级中随机抽取了10名学生的成绩,得到样本均值 \(\bar{x} = 85\),样本标准差 \(s = 10\)。
请估计总体均值 \(\mu\)。
答案:根据样本均值 \(\bar{x}\) 来估计总体均值 \(\mu\),我们可以使用以下公式:\[ \hat{\mu} = \bar{x} \]因此,\(\hat{\mu} = 85\)。
习题二:在习题一中,如果我们想要估计总体方差 \(\sigma^2\),我们应该如何操作?答案:总体方差 \(\sigma^2\) 通常使用样本方差 \(s^2\) 来估计,样本方差的计算公式为:\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]其中 \(n\) 是样本大小,\(x_i\) 是第 \(i\) 个观测值。
在这个例子中,\(n = 10\),\(\bar{x} = 85\),\(s = 10\)。
因此,我们可以使用以下公式来估计总体方差:\[ \hat{\sigma}^2 = s^2 = \frac{1}{10-1} \times 10^2 = 100 \]习题三:一个工厂生产的产品长度服从正态分布,样本均值为 \(\bar{x} =50\) 厘米,样本标准差为 \(s = 2\) 厘米。
如果我们知道总体均值\(\mu\) 为 \(50\) 厘米,我们如何估计总体标准差 \(\sigma\)?答案:根据已知的样本均值 \(\bar{x}\) 和样本标准差 \(s\),我们可以使用以下公式来估计总体标准差 \(\sigma\):\[ \hat{\sigma} = s \]因此,\(\hat{\sigma} = 2\) 厘米。
应用多元统计分析课后习题答案高惠璇第二章部分习题解答学习资料

1 2 [y ( 1 7 )2 (y 2 4 )2]
g(y1,y2)
设函数 g(y1, y2) 是随机向量Y的密度函数.
15
第二章 多元正态分布及参数的估计
(3) 随机向量
YYY12~N274,
I2
(4) 由于 XX X121011Y Y12CY
1 0 1 1 7 4 3 4 , 1 0 1 1 I2 1 0 1 1 1 1 2 1
e e d x e 2
2
1 2 (x 1 7 )2
9
第二章 多元正态分布及参数的估计
1 1 2(2x1 22x2 16 5 x1 2 1x4 14)91 2(x2x17)2
e e dx 2
2
2 1e 2 1 e dx 1 2(x1 28x1 1)6
1 2(x2x17)2 2
1(
1 e2
(22)(22)0
可得Σ的特征值 1 2 (1 )2 , 2 (1 ).
22
第二章 多元正态分布及参数的估计
λi (i=1,2)对应的特征向量为 1
1
l1
2 1 2
l1
2 1 2
由(1)可得椭圆方程为 2(1y 1 2)b22(1y 2 2)b21
其 b 2 中 2 la n ( 2 ) [ | |1 /2 ] 2 l2 n2 [ 1 2 a ]
解二:比较系数法 设 f(x 1,x2)2 1ex 1 2 p (2 x 1 2x2 2 2 x 1x2 2x 1 2 1x2 4 6) 5
2 1 2 11 2ex 2 p 1 2 2 2 1 (1 2)[2 2(x 1 1)2 2 1 2(x 1 1)x (2 2) 1 2(x2 2)2]
《参数估计习题》word版

参数估计习题一、填空题1、设总体2(,)X Nμσ,若2σ已知,总体均值μ的置信度为1α-的置信区间为:x x⎛-+⎝,则λ=;2、设由来自正态总体2(,0.9)X N μ的样本容量为9的简单随机样本,得样本均值5x=,则未知参数μ的置信度0.95的置信区间为;3、设12,X X为来自总体2(,)X Nμσ的样本,若1211999CX X+为μ的一个无偏估计,则C=;4、设12,,,nX X X为来自正态总体2(,)Nμσ的样本,,a b为常数,且0a b<<,则随机区间2211()(),n ni ii iX Xb aμμ==⎡⎤--⎢⎥⎣⎦∑∑的长度L的数学期望为;5、设ˆθ是未知参数θ的估计量,若称ˆθ为θ的无偏估计量,则ˆ()Eθ=;6、设12ˆˆ,θθ为总体未知参数θ的两个无偏估计量,若称1ˆθ比2ˆθ更有效,则1ˆ()Dθ1ˆ()Dθ;7、设θ为总体的未知参数,若由样本确定的两个统计量1ˆθ和2ˆθ,且12ˆˆθθ<,对于预先给定的α值(01α<<),满足12ˆˆ{}1Pθθθα<<=-,则称随机区间12ˆˆ(,)θθ为θ的1α-或100(1)%α-置信区间,其中为置信上限,为置信下限,称为置信度;8、设12,,,nX X X为来自正态总体2(,)Nμσ的一个样本,样本均值11niiX Xn==∑是的无偏估计量;9、设12,,,nX X X是取自总体X的一个样本,2()D Xσ=,则2211()1niiS X Xn==--∑为的无偏估计量;10、设12,,,n x x x 是取自总体2(,)XN μσ的一组样本值,则2σ的置信度为(1)α-的置信区间是 。
二、 选择题 1、 设总体2(,)XN μσ,其中2σ已知,则总体均值μ的置信区间长度l 与置信度1α-的关系是( ).1-.1-.1-.A l B l C l D ααα当缩小时,缩短 当缩小时,增大当缩小时,不变 以上说法均错2、 设总体2(,)XN μσ,2σ已知,若样本容量n 和置信度1α-均不变,则对于不同的样本观测值,总体均值μ的置信区间的长度( )....A B C D 变长 变短 不变 不能确定3、 设随机变量12,,,n X X X 相互独立且同分布2(,)XN μσ,11ni i X X n ==∑,2211()1ni i S X X n ==--∑,2()i D X σ=,则2S ( ) 2....A B C D σσμ是的有效估计 是的无偏估计是的无偏估计 不能确定4、设ˆθ是未知参数θ的估计量,如果ˆ()E θθ=,则称ˆθ为θ的( ) ....A B C D 有偏估计量 无偏估计量一致估计量有效估计量5、设总体X 的分布中,未知参数θ的置信度为1α-的置信区间是[]12,T T ,即12()1P T T θα≤≤=-,则下列说法正确的是( )1212121212.[,].[,]..[,]A T T t t ,t t B T T C D T T θθααθθθ∈对,的观测值,必有 以的概率落入区间区间以1-的概率包含 的数学期望E()必属于6、α越小,则1α-就越大,θ落在区间12ˆˆ,θθ⎡⎤⎣⎦内的概率就越大。
第二章参数估计

第二章 参数估计【学习目标】1、掌握矩估计的替代原则;会求已知分布中未知参数的矩估计(值)2、熟练掌握极大似然估计的思想及求法3、估计量的评价标准:无偏性、有效性、相合性的定义4、统计量的无偏性的判断;两个无偏估计的有效性判断;会用Fisher 信息量及c-R 下界进行统计量的UMVUE 充分性判断5、掌握区间估计的定义6、单个正态总体均值的区间估计(包括方差已知、方差未知);单个正态总体方差的区间估计(包括均值已知、均值未知)7、两个正态总体均值差的区间估计(方差未知);两个正态总体方差比的区间估计 8、单侧置信区间的求法 【典型例题讲解】例1、设1,,n X X 是来自均匀分布(,1)U θθ+的总体的容量为n 的样本,其中θ-∞<<+∞为未知参数,试证:θ的极大似然估计量不止一个,例如1(1)ˆXθ=,2()ˆ1n X θ=-,3(1)()11ˆ()22n XXθ=+-都是θ的极大似然估计。
解:(,1)U θθ+分布的密度函数为11()0x f x θθ≤≤+⎧=⎨⎩其他似然函数(1)()11()0n x x L θθθ≤≤≤+⎧=⎨⎩其他由于在(1)()1n x x θθ≤≤≤+上()L θ为常数,所以凡是满足:(1)()ˆˆ1n x x θθ≤≤≤+的ˆθ均为θ的极大似然估计。
从而(1)1(1)ˆX θ=满足此条件,故1(1)ˆX θ=是θ的极大似然估计;(2)由于()(1)1n X X -≤,故2()(1)()2ˆˆ11n n X X X θθ=-≤≤=+,所以2()ˆ1n Xθ=-为θ的极大似然估计;(3)由于()(1)1n X X -≤,故(1)()(1)12n X X X +-≤,(1)()()12n n X X X ++≥,从而有3(1)()(1)()(1)()31111ˆˆ()()12222n n n XXXXXXθθ=+-≤≤≤++=+,故3ˆθ也为θ的极大似然估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,0 x , 7.设母体X具有均匀分布密度 从中抽得容量为6的子样数值 1.3,0.6,1.7,2.2,0.3,1.1,试求母体平均数和方差 的最大似然估计量的值. 解: X U (0, ) , 的最大似然估计 ^ max x 2.2 i ^ ^ EX , 1.1 f ( x)
e x , x 0
0, x 0
(
x
0
1
)
Ex
xf ( x)dx xe
dx
x
用样本 x 估计Ex,则有 x
1
^ 1 ,
2.设母体X具有几何分布,它的分布列为 P{X=k}=(1-p)k-1p,k=1,2,… 先用矩法求p的估计量,再求p的最大似然估 计. 解 :( 1)矩法估计
i
Dx
2
n
13.设X1,X2,…,Xn是具有泊松分布 P ( ) 母体 的一个子样。试验证:子样方差 S *2 是 的无偏估计;并且对任一值 [0,1], X (1 )S*2 也是 的无偏估计,此处 X 为子样的平均 数 解: P(), EX , DX , E X , ES *2 X
f(x)= () { ex ) 0 ( x解: e , x 0
第二章 参数估计 1.设母体X具有负指数分布,它的分布密度 为 e x , x 0 f(x)= 0, x 0 其中 0 。试用矩法求的估计量。 解:x e( ) f(x)=
0, x 0
2
s 40 1000 1.96 992.2 10 n s 40 1000 1.96 1007.8 10 n
区间为(992.2,1007.8)小时.
19.随机地从一批钉子中抽取16枚,测得其长 度(单位:cm)为 2.14,2.10,2.13,2.15,2.13,2.12,2.13,2.10,2.15,2. 12,2.14,2.10,2.13,2.11,2.14,2.11。设钉长分布 为正态的,试求母体平均数 的置信概率 为90%的置信区间 :(1)若已知 0.01(cm); (2)若 未知。 解:n=16, x 2.125, s* 0.017 x (1)若已知 0.01(cm) ,构造函数u / n N (0,1) 给定置信概率90%,有 P{ u u } 1 2 0 0 即 P( x u x u ) 1
2
12
4.设母体X的分布密度为 f(x)=
x ,0 x 1
0, 其他
1
其中
0
(1) 求 的最大似然估计量; (2)用矩法求 的估计量. 1 x ,0 x 1 解:
x f ( x)
1最大似然估计 L xi 1 n xi 1
3 3 3 3 3 3
3 5 1 1 ^ 2 1 5 ^ 1 ^ 1 D1 ( ) 2 ( ) 2 , D2 ( ) 2 ( ) 2 , D3 ( ) 2 ( ) 2 3 3 9 4 4 8 2 2 2
^ 方差最小为有效 3
n i 1
^ 对形如 xi xi , 且 xi 1时, E ,以 x 为最有效
( xi ) 2 2 ( xi 1 )( xi ) ( xi ) 2
i i
E( xi1 )( xi ) 0
n 1 i 1 2 2 i i
i
i
i
E ( xi 1 xi ) E ( xi 1 ) 2 E ( xi 1 )( xi ) E ( xi ) 2
2
n
置信区间为( x u
2
0
n
2
n
)为(2.125 0.0041)
(2)若 未知 x 构造函数 T * t (n 1) 给定置信概率90%,查得 t0.05 (15) 1.7531 ,有
p( T t (n 1)) 1
S / n
∴母体平均数 * 的置信概率为90%的置信 s ( x t0.05 (15) ) ,即(2.125±0.0075) 区间为
E( X (1 )S *2 ] EX (1 )ES *2 (1 )
N (, 2 ) 的一个子 14 .设X1,X2,…,Xn为母体
C ( X i 1 X i )2 样。试选择适当常数C,使
n 1 i 1
为
2
的无偏估计。 解: ( x x )2 [( x ) ( x )]2 i1 i i 1 i
n
2
21.假定每次试验时,出现事件A的概率p相 同但未知。如果在60次独立试验中,事件A 出现15次,试求概率p的置信区间(给定置 信概率为0.95)。 m m m x 解:n=60,m=15,x~“0-1”分布, n , s n (1 n ) x p 近似 构造函数u N (0,1) 给定置信概率95%,有P{ u u } 1
ln L n ln ( 1) ln xi
i
i 1 i 1
0, 其他 n
( 0)
n
d ln L n ^ n ln xi 0, d i ln xi
i
2矩法估计
EX
用
X 用估计EX
x f ( x)dx x x dx
1 ,a x b ba 0, 其他
其中a,b是未知参数,试用矩法求a与b的估计 量. ab 1 X U [a, b], EX , DX (b a ) 2 解:
2 12
用 X 和 aS b分别估计EX和DX 得 X 2 ^ X 3S a (b a ) 2 ^ X 3S b S2
x 近似 N (0,1) 用 x 估计 ,构造函数 u s/ n 给定置信概率 1 ,有 P{ u u } 1
即
P( x u
2
置信下限 x u 置信上限 x u
s s 2 x u ) 1 n n 2
2
整批电子管的平均寿命置信概率为95%的置信
3 3 1 3 2 (2)^ 4 X 1 4 X 2 1 1 (3)^ X 1 X 2 3 2 2
都是 的无偏估计,并求出每个估计量的 方差。问哪一个方差最小? 2 1 2 1 2 1 解:^ E ( x1 x2 ) Ex1 Ex2 E 1 ^ 同理: 2和^都是 的无偏估计。 3
L (1 p) xi 1 p (1 p)
i 1
n
xi n
i
pn
ln L ( xi n) ln(1 p) n ln p
i
d ln L n 1 i 0,^ p dp 1 p p x
n xi
3.设母体X具有在区间[a,b]上的均匀分布,其 分布密度为 f(x)=
2
e
(
i
ln L n ln 2 n ln
i d ln L n i 2 0 d
x
i
2
) e
i
x
^ 1 x 得 n
i
i
E xi E X
x f ( x)dx
x
1 1 x e dx 2 x e dx 2 2 0
似然函数
L f ( xi ) e ( xi )
为了使L达到最大, xi n 0 ,尽可能小, i 尽可能大,而^ xi , min xi x(1)
1i n
d ln L ln L ( xi n ), 0无解 d i
12设母体X服从正态分布 N (,1),( X1, X 2 ) 是 从此母体中抽取的一个子样。试验证下面三 个估计量 2 1 (1)^ X 1 X 2 1
2
给定置信概率1
n
/ n
,有 u ,使
2
2
P{ u u } 1
即
P( x u
2
x u
2u
2
n
) 1
置信区间长度
n
2
L
n 4 u / L
2 2 2
2
23.从正态母体中抽取一个容量为n的子样, * 算得子样标准差 s 的数值。设(1)n=10, s * =5.1(2)n=46, s * =14。试求母体标准差 的置信概率为0.99的置信区间。 X N (, 2 ), , 2未知 解: (1)n=10, s*2 5.1 (n 1) s*2 *2 2 2 2 (n 1) 用 s 估计 ,构造函数 2 给定置信概率1 =99%,查表得
2
s/ n
即
m 1m m m 1m m p( u (1 ) p u (1 )} 1 n nn n n nn n 2 2
故p的置信概率为95%的置信区间为 (0.25±0.11)
22.对于方差 为已知的正态母体,问需抽 取容量n为多大的子样,才使母体平均数 的置信概率为1 的置信区间的长度不大 于L? 解: X N (, 2 ), 2已知 x 构造函数 u N (0,1)
x
1 1 E E ( xi ) E xi n i n i
^ 是 的无偏估计.
6.设母体X具有分布密度
k
f(x)= (k 1)!
0, 其他
x k 1e x , x 0
