积分变换第1讲傅里叶(Fourier)级数展开共48页文档
合集下载
积分变换__第1.傅里叶变换

1 j t 证:f ( t ) F ( )e d 2 1 j0 t j t j t 2 d ( )e d e e . 0 0 2 即e j0t 和2d ( 0 )构成了一个傅氏变换对。
由上面两个函数的变换可得
0, t 0 , 证明: 例6 单位阶跃函数 u (t ) 1, t 0
1 1 F d ( ) 证: j 2
1
1 jt d ( ) e d j 1 1 1 jt j t d ( ) e d e d 2 2 j
t
3.若f ( t )为无穷次可微的函数,则有
d ' ( t ) f ( t )d t - f ' ( 0) , d ( t ) f ( t )d t ( -1) f
(n) n (n)
一般地,有
( 0).
例3 证明:1和2d ()构成傅氏变换对.
F 1 1 e 证法1:
jt
dt s t e js ds 2d .
证法2:若F()=2d (), 由傅氏逆变换可得
1 f (t ) 2
2d ( )e d e
j t
jt
0
1
例4 证明e j0t 和2d ( 0 )构成一个傅氏变换对。
单位脉冲函数及其傅氏变换就可以求出它们的傅
氏变换. 所谓广义是相对于古典意义而言的, 在广 义意义下, 同样可以说,原象函数f(t) 和象函数F() 构成一个傅氏变换对.
例5 求正弦函数f (t)=sin0t的傅氏变换。
F ( ) F [ f ( t )] e jt sin 0 t d t
傅立叶(Fourier)级数的展开方法

快速傅立叶变换(FFT)法
定义
FFT法是一种基于数学和计算机技术的快速计算傅立叶级数展开式的 方法。
步骤
首先,将函数进行离散化处理,然后利用分治策略将问题分解为多个 子问题,最后通过递归和数学公式计算出傅立叶级数的系数。
优点
FFT法计算速度快,适用于大规模数据的傅立叶变换计算。
缺点
对于非周期函数,FFT法可能存在误差和稳定性问题。
图像处理
在图像处理中,傅立叶变换是常用的工具,通过将图像分解为不同 频率的成分,可以实现图像的滤波、去噪、压缩等操作。
控制系统
在控制工程中,傅立叶级数可以用于分析系统的频域响应,从而优 化控制系统的设计和性能。
在金融问题中的应用
要点一
周期性分析
在金融领域,傅立叶级数可以用于分析具有周期性的金融 数据,如股票价格、汇率等,从而预测未来的走势。
唯一性证明
唯一性定理的证明涉及到数学分析中的一些高级技巧,如反证法、数学归纳法 等。
三角函数的正交性
正交性定义
在一定条件下,三角函数系中的函数都互相垂直,即它们的内积为0。这就是三角函数 的正交性。
正交性的应用
正交性是傅立叶级数展开的基础,因为只有当三角函数系是正交的时,我们才能将一个 周期函数表示为一个傅立叶级数。同时,正交性在解决物理问题、信号处理等领域也有
傅立叶级数的复数形式
傅立叶级数的复数形式是将函数表示 为复指数函数的线性组合,通过复数 运算,可以简化计算过程并方便地处 理函数的频域性质。
VS
复数形式的傅立叶级数在信号处理、 通信等领域中具有重要应用,可以用 于信号的频谱分析和滤波等操作。
02 傅立叶级数的性质
收敛性
傅立叶级数在$L^2$空间中收敛
第一节傅立叶级数与傅里叶积分

2
ej jnω0t
代入 (A) 式并整理得
fT
(t)
a0 2
(an
n1
2
jbn
e jnω0t
an
2
jbn
e jnω0t
).
推导
fT
(t)
a0 2
(an
n1
2
jbn
e jnω0t
an
2
jbn
e
jnω0t
).
令
c0
a0 2
,
cn
an jbn , 2
cn
an
jbn 2
,
则有
fT (t ) e cn jnω0t ,
特点 (1) 周期性
(2) 正交性
T/2
T/2m (t ) n (t )d t 0 ,
T/2
T/2 k (t ) l (t )d t 0 ,
T/2
T/2
k
(t )
l
(t)d
t
0,
(k l)
由 {k (t)}, { k (t)} 组合叠加可以生成周期为 T 的复杂波。
问题 对于任何一个周期为 T 的(复杂)函数 fT (t),能否:
(B)
n
其中,
cn
1 T
T /2 T /2
fT (t ) e jnω0td t ,
n 0, 1, 2,
定义 称 (B) 式为 Fourier 级数的指数形式。
注意 (1) 分解式是惟一的。 (2) 计算系数 cn 时, 其中的积分可以在任意 一个长度为 T 的区间上进行。
(3) 采用周期延拓技术,可以将结论应用到 仅仅定义在某个有限区间上的函数。
fT
ej jnω0t
代入 (A) 式并整理得
fT
(t)
a0 2
(an
n1
2
jbn
e jnω0t
an
2
jbn
e jnω0t
).
推导
fT
(t)
a0 2
(an
n1
2
jbn
e jnω0t
an
2
jbn
e
jnω0t
).
令
c0
a0 2
,
cn
an jbn , 2
cn
an
jbn 2
,
则有
fT (t ) e cn jnω0t ,
特点 (1) 周期性
(2) 正交性
T/2
T/2m (t ) n (t )d t 0 ,
T/2
T/2 k (t ) l (t )d t 0 ,
T/2
T/2
k
(t )
l
(t)d
t
0,
(k l)
由 {k (t)}, { k (t)} 组合叠加可以生成周期为 T 的复杂波。
问题 对于任何一个周期为 T 的(复杂)函数 fT (t),能否:
(B)
n
其中,
cn
1 T
T /2 T /2
fT (t ) e jnω0td t ,
n 0, 1, 2,
定义 称 (B) 式为 Fourier 级数的指数形式。
注意 (1) 分解式是惟一的。 (2) 计算系数 cn 时, 其中的积分可以在任意 一个长度为 T 的区间上进行。
(3) 采用周期延拓技术,可以将结论应用到 仅仅定义在某个有限区间上的函数。
fT
傅里叶积分变换

1 j j 2 2
通过傅氏逆变换,可求得指数衰减函数的积分表达 式。由(3)式,并利用奇偶数的积分性质,可得
f (t) F 1 F ()
1
F (
)e
j
t
d
2
1 j e j td
2 2 2
1
(
j )(cost j sin t)d
2 2 2 2 2
0
2 2
由傅氏积分定理,可得到一个含参量广义积分的 结果:
0,
t 0;
cos t sin t
0
2 2
d
2
,
t 0;
e t , t 0
4.单位脉冲函数(狄拉克--Dirac函数)
设
0 ,
(t)
1
t 0或 t , 0t
定义单位脉冲函数为
(t
)
lim
0
(t)
单位脉冲函数的一些性质:
() 的傅氏逆变换为u(t) 。
f (t) F-1 F()
1
2
1
j
()e jt d
1
()ejt d
1
sin td
2
2
1 1 sin td
20
由于
0
sin
td
0,2
,t t
0; 0
2
,
t0
故
f (t) 1 1
2
sin 0
td
1
2 1 2
1
j ( 0 ) t
2 j
1 2
2j
( 0 ) 2
( 0 )
j ( 0 ) ( 0 )
我们可以看出引入δ-函数后,一些在普 通意义下不存在的积分,有了确定的数 值。工程技术上许多重要函数的傅氏变 换都可以利用δ-函数及其傅氏变换很方 便地表示出来,并且使许多变换的推导 大大地简化。
ZGP-积分变换第一讲 Fourier积分 (1)

求 f (t) 的积分表达式的步骤:
() 1 F () F [ f (t )]
() 2 f (t ) F 1[ F ( )]
26
Fourier 变换的概念
0, 例 求函数 f (t ) t e ,
t 0 的 Fourier 变换及其 t 0
指数衰减函数
积分表达式,其中 0.
信号
Fourier变换
频谱函数
1
第一章 Fourier 变换
§1.1 §1.2 §1.3 §1.4 §1.5 Fourier 积分 Fourier 变换 Fourier 变换的性质 卷积与相关函数 Fourier 变换的应用
2
§1.1 Fourier 积分
• 函数的 Fourier 级数展开 • Fourier 积分公式
成立,而左端的 f(t) 在间断点 t 处的值用
f (t 0) f (t 0) 2
来替代.
Fourier积分公式的 指数形式
15
Fourier 积分定理及应用
若 f(t)为奇函数,则
若 f(t)为偶函数,则
f (t )dt 0
f (t )dt 2 f (t )dt
其中
2 , T
2 T2 a0 T fT (t ) dt , T 2
2 T2 an T fT (t ) cos ntdt (n 1, 2,) T 2 2 T2 bn T fT (t ) sin ntdt (n 1, 2,) T 2 1, x [ , 0) f ( x) 0, x [0, 6)
f ( )e i d eit d
1.1 Fourier积分【VIP专享】

正交 , 即其中任意两个不同的函数之积在 上的积分等于 0 . 证:
同理可证 :
但是在三角函数系中两个相同的函数的乘积在 上的积分不等于 0 . 且有
研究周期函数实际上只须研究其中的一个周期 内的情况即可, 通常研究在闭区间[T/2,T/2]内函数变 化的情况. 并非理论上的所有周期函数都可以用傅里 叶级数逼近, 而是要满足狄利克雷(Dirichlet)条件, 即 在区间[T/2,T/2]上:
则可以合写为一个式子,
1
cn T
T
2 T
fT (t )e jntdt
(n 0, 1, 2,L )
2
若令
则上式可以写为
这就是Fourier级数的复指数形式,或者写为
接下来讨论非周期函数的展开问题。
任何一个非周期函数 f (t) 都可以看成是由某个 周期函数 fT(t) 当T时转化而来的。
作周期为T 的函数 fT (t), 使其在[T/2,T/2]之内 等于 f (t), 在[T/2,T/2]之外按周期T 延拓到整个数轴 上, 则T 越大, fT (t)与 f (t) 相等的范围也越大, 这就说 明当T时, 周期函数 fT(t) 便可转化为 f (t), 即有
n
n
n1
2
T
, 或T
n
,
如图
(n
nபைடு நூலகம்
n1
2
T
, 或T
n
)
{
{ { {
O 1 2 3
所以 f (t)又可写为
n-1n
当 t 固定时,
记为
,即
则有
当
是参数 n 的函数,
又
(n )
1
2
f
同理可证 :
但是在三角函数系中两个相同的函数的乘积在 上的积分不等于 0 . 且有
研究周期函数实际上只须研究其中的一个周期 内的情况即可, 通常研究在闭区间[T/2,T/2]内函数变 化的情况. 并非理论上的所有周期函数都可以用傅里 叶级数逼近, 而是要满足狄利克雷(Dirichlet)条件, 即 在区间[T/2,T/2]上:
则可以合写为一个式子,
1
cn T
T
2 T
fT (t )e jntdt
(n 0, 1, 2,L )
2
若令
则上式可以写为
这就是Fourier级数的复指数形式,或者写为
接下来讨论非周期函数的展开问题。
任何一个非周期函数 f (t) 都可以看成是由某个 周期函数 fT(t) 当T时转化而来的。
作周期为T 的函数 fT (t), 使其在[T/2,T/2]之内 等于 f (t), 在[T/2,T/2]之外按周期T 延拓到整个数轴 上, 则T 越大, fT (t)与 f (t) 相等的范围也越大, 这就说 明当T时, 周期函数 fT(t) 便可转化为 f (t), 即有
n
n
n1
2
T
, 或T
n
,
如图
(n
nபைடு நூலகம்
n1
2
T
, 或T
n
)
{
{ { {
O 1 2 3
所以 f (t)又可写为
n-1n
当 t 固定时,
记为
,即
则有
当
是参数 n 的函数,
又
(n )
1
2
f
第01章 Fourier变换_2012
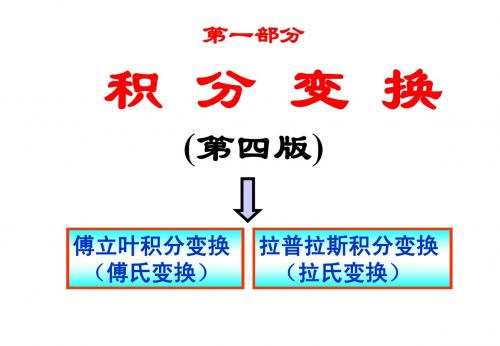
1 f (t ) 2p
+ f ( )e - j d e jt d - -
+
这个公式称为函数f (t)的Fourier积分公式,其中f (t)函数 应满足Fourier 收敛定理。
Fourier积分
四、Fourier积分定理 若函数f (t)在(-∞,+∞)上满足下列条件: 1°在任一有限区间满足Dirichlet条件; + 2°在无限区间上绝对可积: - f (t ) dt 则积分 F ( ) - f (t )e - jt dt 存在,并且在f (t)的连续点处
例
题
1, t 1 例1:已知如下的函数 f (t ) ,求其Fourier 0, 其它 积分表达式,并证明:
p 2 + sin cos t p d 0 4 0 f(t) t 1 t 1 t 1
1
-1
o
1
t
例
题
于是有:
方法1:直接根据Fourier积分公式证明,对于连续点有:
p
1
+
0 +
+ f ( ) cos (t - )d d -
1
(cos t cos + sin t sin )d d p - -1 2 + 1 cos d cos td p - 0 2 + sin cos t d
+
为
1 f (t0 + 0) + f (t0 - 0) 2
1 f (t ) 2p
+
-
F ( )e jt dt,而在f
傅立叶(Fourier)级数的展开方法-82页PPT精选文档
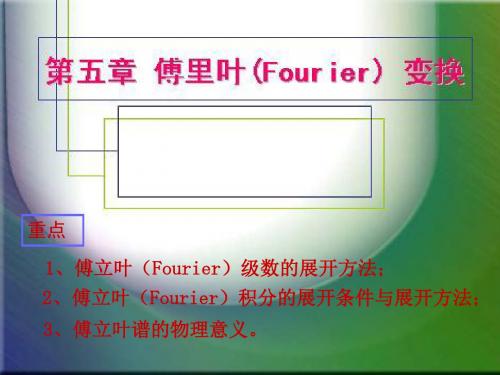
b 1l
n l l
f xsin nxdx
(n1,2,3 ).
称为傅里叶系数
3、函数以傅立叶级数展开是在函数空间中以三角函数
为基进行分解
x
2x
kx
基
矢
1, cos , cos ,.
量
x 2x
kx
sin , sin ,... sin ,...
2
2
在连续点处收敛于f(x)。
f (x)
x
不计点x (2 k 1 ) (k 0 , 1 , 2 ...函.数)是周期为2π,且是奇函
数。
则
2
2
bk
0
f(x)sinkxdx
0
xsinkxdx
2(1)k1 (k1,2,3...)
k
f(x) 2(1)k1sinkx
例1 设f(x)函数是周期为2π周期函数,它在[π,π]
表达式
1 (x0)
f(x)
1
(0x)
将f(x)展为傅立叶级数。
解 函数满足狄氏条件,它在x=kπ(k=0,1,-1,2,-2…)
点不连续,收敛于 1 1 0 2
在连续点上收敛于f (x) f ( x)
x
则
2l l
说明
1、三角函数族是两两正交的
l kx
cos d x 0
l
l
(k 0),
l kx
sin d x 0
l
l
l kx nx
cos cos d x 0 (k n)
l
l
l
l kx nx
sin sin dx0 (kn),
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
w w fT (t)a 2 0n 1(a nco snt b nsin nt)(1 .1 )
为求出a0,计算[fT,1],即
T
2 -T
fT(t)dt
2
T 2 -T 2
a0 dt 2
(an
n1
T
2 cosnwtdt
-T
bn
2
T 2
sinnwtdt)a0
cosnwt
T
2 cos2 nwtdt
T 2
1cos2nwt
dt
T
-T 2
-T 2
2
2
sinnwt
T
2 sin2 nwtdt
T 2
1-cos2nwt
dt
T
-T 2
-T 222Fra bibliotek因此, 任何满足狄氏条件的周期函数fT(t), 可表 示为三角函数形式的傅利叶级数如下:
j(n - m )
1
e- j( n-m )p [e j2( n-m )p - 1] 0
j(n - m )
p
cos(n - m ) j sin(n - m ) d -p
p
p
- pc o s ( n - m )d - ps in ( n - m )d 0 ( n m )
T
[f,g] 2 f(t)g(t)dt -T 2
一个函数f(t)的长度为
T
|| f || [ f , f ] 2 f 2 ( t ) d t -T 2
而施瓦兹不等式成立 :
[f,g] f g
T
即 2 f ( t ) g ( t ) d t -T 2
这样可令
T
T
2 f 2 ( t ) d t 2 g 2 ( t ) d t
数.
第一类间断点和第二类间断点的区别:
第二类间断点
第一类间断点
不满足狄氏条件的例子: f (t) tgt
存在第二类间断点
f (t) sin(1) t
在靠近0处存在着无限多个极点值.
而在工程上所应用的函数, 尤其是物理量的变 化函数, 全部满足狄氏条件. 实际上不连续函 数都是严格上讲不存在的, 但经常用不连续函 数来近似一些函数, 使得思维简单一些.
T
-T 2
2
即a0
2 T
T 2 -T 2
fT(t)dt
为求an, 须计算[fT(t), cosnwt], 即
T
2 -T
f T ( t ) cos
2
nwtd t
T 2
a0
cos
2 - T 2
nwtd t
T
am
2 cos
-T
m w t cos
nwtd t
m 1
2
4个正弦波的逼近
100个正弦波的逼近
研究周期函数实际上只须研究其中的一个周 期内的情况即可, 通常研究在闭区间[-T/2,T/2] 内函数变化的情况.
并非理论上的所有周期函数都可以用傅里叶 级数逼近, 而是要满足狄利克雷(Dirichlet)条 件, 即在区间[-T/2,T/2]上
1. 连续或只有有限个第一类间断点 2. 只有有限个极值点 这两个条件实际上就是要保证函数是可积函
在区间[-T/2,T/2]上满足狄氏条件的函数的全 体也构成一个集合, 这个集合在通常的函数加 法和数乘运算上也构成一个线性空间V, 此空 间的向量就是函数, 线性空间的一切理论在此 空间上仍然成立. 更进一步地也可以在此线性 空间V上定义内积运算, 这样就可以建立元素 (即函数)的长度(范数), 及函数间角度, 及正交 的概念. 两个函数f和g的内积定义为:
由此不难验证
T
2 cos nwt d t 0 -T 2
(n 1,2,3,),
T
2 sin nwt d t 0 -T 2
(n 1,2,3,),
T
2 sin nwt cos mwt d t 0 -T 2
(n, m 1,2,3,),
T
2 sin nwt sin mwt d t 0 -T 2
-T
-T
2
2
cos [ f , g ] 是 f , g间 的 夹 角 余 弦 , f g
则 如 果 [ f ,g] 0称 为 f与 g正 交 .
而在区间[-T/2,T/2]上的三角函数系
{1, coswt, sinwt, cos 2wt, sin 2wt, ...,
cos nwt, sin nwt, ...} 是两两正交的, 其中w=2p/T, 这是因为 cos nwt和sin nwt都可以看作是复指数函数ejnwt
n
T
bm
2 sin
-T
m w t cos
nwtd t
m 1
2
a n
T
2 cos
-T 2
2 nwt d t
T an 2
即
an
2 T
T
2 -T
f T ( t ) cos
2
nwtd t
同理, 为求bn, 计算[fT(t), sin nwt], 即
积分变换
第1讲
积分变换
傅里叶(Fourier)级数展开
在工程计算中, 无论是电学还是力学, 经常要 和随时间而变的周期函数fT(t)打交道. 例如:
t
具有性质fT(t+T)=fT(t), 其中T称作周期, 而1/T代表单 位时间振动的次数, 单位时间通常取秒, 即每秒重 复多少次, 单位是赫兹(Herz, 或Hz).
的线性组合. 当nm时,
p T 2
ejnwte-jmwtdt
T
p ej(n-m)d
0
-T 2
2 -p
其中wt2Tpt,则d2pTdt,dt2Tpd
这是因为
p e j(n-m ) d
1
p
e j( n-m )
-p
j(n - m )
-p
1
[e j(n-m )p - e- j(n-m )p ]
最常用的一种周期函数是三角函数
fT(t)=Asin(wt+j) 其中w=2p/T
t
而Asin(wt+j)又可以看作是两个周期函数 sinwt和coswt的线性组合
Asin(wt+j)=asinwt+bcoswt
人们发现, 所有的工程中使用的周期函数都可 以用一系列的三角函数的线性组合来逼近.
方波
(n, m 1,2,3, , n m),
T
2 cos nwt cos mwt d t 0 (n, m 1,2,3, , n m), -T 2
而{1, coswt, sinwt, ..., cos nwt, sin nwt, ...}的函
数的长度计算如下:
T
1 1 2 2 dt T -T 2
