函数展开成傅里叶级数(课堂PPT)
合集下载
高等数学课件--D12_7傅里叶级数

目录 上页
π
2012-10-12
同济版高等数学课件
0
返回 结束
下页
2 ( cos n π 1) n π
2
4 ( 2 k 1) π
2
, n 2k 1
n 2k ( k 1 , 2 , )
0
,
π
π 2
1
π π
f ( x ) sin nx d x
1 5
目录 上页 下页 返回 结束
定理 1. 组成三角级数的函数系 正交 , 即其中任意两个不同的函数之积在 上的积分等于 0 . 证: π 1 cos nx d x π 1 sin nx d x 0
π π
π cos k x cos nx d x
1 2 π
π
cos( k n) x cos( k n) x d x 0
f ( x) a0 2 (an cos nx bn sin nx)
n 1
①
右端级数可逐项积分, 则有 ② 证: 由定理条件, 对①在
π
逐项积分, 得
π π
f ( x) d x 2 d x an cos nx d x bn sin nx d x n 1 π π π π a0
2012-10-12 同济版高等数学课件
目录 上页 下页 返回 结束
f ( x)
4 π
sin x
sin 3 x 3
sin 5 x 5
sin 7 x 7
sin 9 x 9
]
说明: 1) 根据收敛定理可知,
1 1 2
y
1
π
2012-10-12
同济版高等数学课件
0
返回 结束
下页
2 ( cos n π 1) n π
2
4 ( 2 k 1) π
2
, n 2k 1
n 2k ( k 1 , 2 , )
0
,
π
π 2
1
π π
f ( x ) sin nx d x
1 5
目录 上页 下页 返回 结束
定理 1. 组成三角级数的函数系 正交 , 即其中任意两个不同的函数之积在 上的积分等于 0 . 证: π 1 cos nx d x π 1 sin nx d x 0
π π
π cos k x cos nx d x
1 2 π
π
cos( k n) x cos( k n) x d x 0
f ( x) a0 2 (an cos nx bn sin nx)
n 1
①
右端级数可逐项积分, 则有 ② 证: 由定理条件, 对①在
π
逐项积分, 得
π π
f ( x) d x 2 d x an cos nx d x bn sin nx d x n 1 π π π π a0
2012-10-12 同济版高等数学课件
目录 上页 下页 返回 结束
f ( x)
4 π
sin x
sin 3 x 3
sin 5 x 5
sin 7 x 7
sin 9 x 9
]
说明: 1) 根据收敛定理可知,
1 1 2
y
1
方波信号f(t)展开为傅里叶级数.ppt
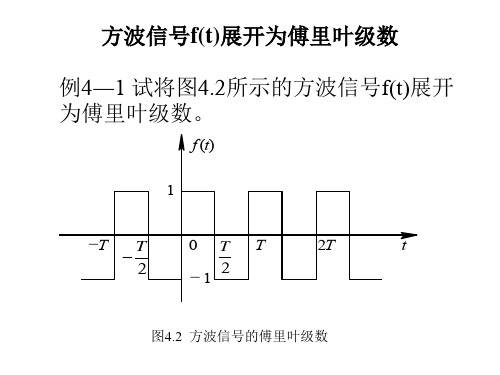
(j)
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
F() f (t)e jtdt eat e jtdt
1
j
2 T
2
f (t)cos(2nft)dt
2 T
0 T
2
(1)cos(2nft)dt 2
T
T 2 0
1 cos(2nft)dt
2 T
1
2 nf
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2nft)dt
2 T
o 2
τ 2
t
(a )
F(j )
2
-
4
-
2
o
4
(b )
F( )
( )
-
4
-
2
o
2 4
-
4
-
2
o 2 4
-
(c)
(d )
图 3.4-1 (a) 门函数; (b) 门函数的频谱; (c) 幅度谱; (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
- 2/
2/
-/ 2 0 / 2
t
01j
1
jarctan
ea
a22
其振幅频谱及相位频谱分别为
F ( ) 1 2 2
( ) arctan
单边指数信号的频谱
例4―4 求单边指数信号的频谱。 解 单边指数信号是指
f (t) eatu(t),a 0
F() f (t)e jtdt eat e jtdt
1
j
2 T
2
f (t)cos(2nft)dt
2 T
0 T
2
(1)cos(2nft)dt 2
T
T 2 0
1 cos(2nft)dt
2 T
1
2 nf
[ sin(2 nft)]
0 T
2
2 T
1
2 nf
[sin(2 nft)]
T
2 0
0
bn
2 T
T
2 T
2
f (t)sin(2nft)dt
2 T
o 2
τ 2
t
(a )
F(j )
2
-
4
-
2
o
4
(b )
F( )
( )
-
4
-
2
o
2 4
-
4
-
2
o 2 4
-
(c)
(d )
图 3.4-1 (a) 门函数; (b) 门函数的频谱; (c) 幅度谱; (d) 相位谱
矩形脉冲信号gτ(t)的频谱
例4―3 求矩形脉冲信号gτ(t)的频谱。
g(t)
F()
1
- 2/
2/
-/ 2 0 / 2
t
高等数学-第七版-课件-12-7 傅里叶级数

在 例3 将函数
上的傅里叶展开式
u
展开成傅里叶级数, 其中E 是正的常数 . O t
傅里叶级数
一、三角级数 二、函数展开成傅里叶级数
三、正弦级数和余弦级数
傅里叶级数
一、三角级数 二、函数展开成傅里叶级数
三、正弦级数和余弦级数
周期为2 的奇、偶函数的傅里叶级数 对周期为 2 的奇函数 f (x) , 其傅里叶系数为
a0 f ( x) an cos nx bn sin nx 2 n 1
①
② 定义 由公式 ② 确定的 称为函数f(x)
的傅里叶系数 ; 以f (x)的傅里叶系数为系数的三角级数 a0 an cos nx bn sin nx 称为f(x)的傅里叶级数 . 2 n 1
x
分别展开成正弦级数和余弦级数.
将定义在[0,]上的函数展开成正弦级数与余弦级数 展开思路 在
奇延拓 (偶延拓) 傅里叶展开 在
上有定义 上, 上为奇函数(偶函数)
定义在 在
(0, π] 上 F ( x ) f ( x ) 的正弦级数 (余弦函数) 展开式
y
例6 将函数
O 分别展开成正弦级数和余弦级数.
2) 在一个周期内至多只有有限个极值点, 则 f (x) 的傅里叶级数收敛 , 并且 当x 为f (x)的连续点时,级数收敛于 f ( x );
当x 为f (x)的间断点时,级数收敛于
1 [ f ( x ) f ( x )]. 2
例1 设 f (x) 是周期为 2 的周期函数 , 它在 上的表达式为
引言
简单的周期运动 ( A:振幅 :角频率
?
复杂的周期运动
:初相 )
《傅里叶级数》课件

FFT基于分治策略,将大问题分解为小问题,从而显著提高了计算效率。
FFT的出现极大地促进了数字信号处理领域的发展,尤其在实时信号处理 和大数据分析方面。
小波变换与傅里叶级数的关系
01
小波变换是一种时间和频率的局部化分析方法,用于多尺度信 号处理和分析。
02
小波变换与傅里叶级数都是信号的频域表示方法,但小波变换
频域处理
傅里叶变换将图像从空间域转换到频域,使得图 像的频率特征更加明显,便于进行滤波、增强等 操作。
图像压缩
通过分析图像的频谱,可以去除不重要的频率成 分,从而实现图像的压缩,节省存储和传输资源 。
图像去噪
傅里叶变换在图像去噪中发挥了重要作用,通过 滤除噪声对应的频率成分,可以有效去除图像中 的噪声。
傅里叶级数提供了一种将 复杂信号分解为简单正弦 波的方法,有助于理解和 处理信号。
频谱分析
通过傅里叶变换,可以分 析信号的频率成分,这在 通信、音频处理等领域有 广泛应用。
滤波器设计
利用傅里叶级数或其变换 形式,可以设计各种滤波 器,用于提取特定频率范 围的信号或抑制噪声。
图像处理中的应用
1 2 3
数值分析中的应用
求解微分方程
傅里叶级数在数值分析中常用于 求解初值问题和偏微分方程,通 过离散化和变换,将复杂问题转 化为易于处理的简单问题。
数值积分与微分
傅里叶级数在数值积分和微分中 也有应用,可以将复杂的积分或 微分运算转换为易于计算的离散 形式。
插值与拟合
傅里叶级数可以用于多项式插值 和函数拟合,通过选取适当的基 函数,可以构造出精度较高的插 值函数或拟合模型。
04
傅里叶级数的扩展知识
离散傅里叶变换
离散傅里叶变换(DFT)是连续傅里叶变换的离 散化形式,用于将时域信号转换为频域信号。
FFT的出现极大地促进了数字信号处理领域的发展,尤其在实时信号处理 和大数据分析方面。
小波变换与傅里叶级数的关系
01
小波变换是一种时间和频率的局部化分析方法,用于多尺度信 号处理和分析。
02
小波变换与傅里叶级数都是信号的频域表示方法,但小波变换
频域处理
傅里叶变换将图像从空间域转换到频域,使得图 像的频率特征更加明显,便于进行滤波、增强等 操作。
图像压缩
通过分析图像的频谱,可以去除不重要的频率成 分,从而实现图像的压缩,节省存储和传输资源 。
图像去噪
傅里叶变换在图像去噪中发挥了重要作用,通过 滤除噪声对应的频率成分,可以有效去除图像中 的噪声。
傅里叶级数提供了一种将 复杂信号分解为简单正弦 波的方法,有助于理解和 处理信号。
频谱分析
通过傅里叶变换,可以分 析信号的频率成分,这在 通信、音频处理等领域有 广泛应用。
滤波器设计
利用傅里叶级数或其变换 形式,可以设计各种滤波 器,用于提取特定频率范 围的信号或抑制噪声。
图像处理中的应用
1 2 3
数值分析中的应用
求解微分方程
傅里叶级数在数值分析中常用于 求解初值问题和偏微分方程,通 过离散化和变换,将复杂问题转 化为易于处理的简单问题。
数值积分与微分
傅里叶级数在数值积分和微分中 也有应用,可以将复杂的积分或 微分运算转换为易于计算的离散 形式。
插值与拟合
傅里叶级数可以用于多项式插值 和函数拟合,通过选取适当的基 函数,可以构造出精度较高的插 值函数或拟合模型。
04
傅里叶级数的扩展知识
离散傅里叶变换
离散傅里叶变换(DFT)是连续傅里叶变换的离 散化形式,用于将时域信号转换为频域信号。
9.7.傅里叶级数ppt

①
f (x)dx
1 2
a0dx
[
(ak cos kx bk sin kx)]dx
k 1
1 2
a0dx
ak cos kxdx k 1
bk sin kxdx k 1
a0
1 2
2
,
a0
1
f (x)dx
(2) 求an .
f
( x)cos nxdx
a0 2
cos nxdx
an n , bn n .
练习题
一、设周期为2 的周期函数f ( x) 在[ , ) 上的表达式
为
f
(
x
)
bx ax
, ,
0
x
x
0
(常数a b 0)试将
其展开成傅里叶级数 .
二、将下列函数 f ( x) 展开成傅里叶级数:
1、
f
(x)
e x ,
x
0;
1,0 x
2、 f ( x) sin(arcsin x).
1) 在一个周期内连续或只有有限个第一类间断点; 2) 在一个周期内只有有限个极值点, 则 f (x) 的傅里叶级数收敛 , 且有
f (x) ,
f (x) f (x) , 2
x 为连续点 x 为间断点
其中 an , bn 为 f (x) 的傅里叶系数 .
特别地,当 x为端点 x 时, 收敛于 f ( 0) f ( 0). 2
n1
令
an An sinn , bn An cosn ,
得函数项级数
a0 2
(an
n1
cos nx
bn
sin nx)
称上述形式的级数为三角级数.
第十一章 第5节 傅立叶级数PPT课件

f(x )d x a 2 0 d x n 1 a n co n x d s x b n sn ix n d x
a0
11
af0(x n)c 11 ao nk x fd s (cxx)o dksa xx2 0 c onc sxdo k xx d s bx n coksxsinnxdx
,
an
则得函数项级数
Ansinn, bnAncons, tx
a20k 1(anconsxbnsinx)
称上述级数为三角级数 .
8
定理 1 组成三角级数的函数系
1 , cosx,sin x , cos2x , sin2x , ,consx,sinnx,
在 [ , ]上正交 , 即其中任意两个不同的函数之积在
sikn xsin n xdx0(kn)
(k n)
9
但是在三角函数系中两个相同的函数的乘积在
[ , ]上的积分不等于 0 . 且有
11dx
2
co2snxdx
sin2nxdx
(n1,2,)
co2snx1co2snx si2nnx1co2snx
2
2
10
三. 周期为 2 的周期函数的傅立叶级数
利用正交性
ak
co2skxdx
ak
ak1 f(x)cokxsdx (k1,2,)
类似地, 用 sin k x 乘①式两边,(x n )1s(aik nx n cd ox snx(kb n1 s,i2 nn, x)) ① 12
a20n 1anconx sbnsin nx
an1
f(x)consxdx
o
x
1
(P298 例1 )
10 (1)consxd1x0 1consxdx
傅立叶(Fourier)级数的展开方法PPT幻灯片课件

k
ck
1 2l
l l
i kx
f ( x)e l dx
例5 把锯齿波f(x)在(0,T)这个周期上可表示
为f(x)=Hx/T,试把它展为复数形式的傅立叶 级数。
f (x)
解 函数曲线如图 x
T
27
周期为 2l T , l T
2
ck
1 2l
l l
i 2kx
f ( x)e T dx
1
T
H
i
xe
方法
将函数 f(x)解析延拓到[-l,l]区间,再将[-l,l] 区间的函数再延拓到[-∞∞]区间上,构成周期函数 g(x),其周期为2l
例4 定义在(0,l)上的函数f(x)=a(1-x/l),将
该函数展开为傅立叶级数。
解 函数曲线如图
f (x)
a x
l
21
延拓到(- l,l)后再周期延拓,如图做偶延拓:
16
三、定义在有限区间上的函数的傅里叶展开
工程以及物理上用到的函数一般是定义在有限区间上的. 1、定义在 [-l, l] 上的函数 f(x)展开;
方法 将函数 f(x)解析延拓到[-∞,∞]区间, 构成的周期函数g(x),其周期为2l
f (x)
l
l
f (x)
l
l
x x
17
f (x)
l
l
x
f (x)
x
l
l
仅在 [-l,l]上,g(x)≡f(x).
例3 在(-1,1)上定义了函数f(x)为:
x
f
(
x)
1
1
(1,0)
(0, 1 ) 2
( 1 ,1) 2
高数-傅里叶级数2.ppt

2
例 4.将函数 f (x) x2( x) 展开成傅里叶级数。
解:把 f ( x) 在(,] 上作周期延拓,
a0
1
1 f ( x)dx
x2dx 22 , 3
an
1
f ( x)cosnxdx 1
x2cosnxdx
(1)n n2
4(n1,
2,
)
,
bn
1
x2sinnxdx0 ,
如例 1:
即 S(
x 时,
xxn)1((10x),,n,)1xx时n2ys(,innn.x,1(),f 1()n10n2)2sinf n(x0f)
(x) x ,
0 2
。
3 2 o 2 3 y
3 2 o 2 3
x f (x)的图象. x S(x)的图象.
把 f (x) 在[, ] 上展开为傅里叶级数的步骤为 (1)用狄氏条件判断 f ( x) 能否展开为傅里叶级数; (2)求出傅里叶系数; (3)写出傅里叶级数并注明在何处收敛于f ( x) ; (4)画出 f ( x) 和S( x) 的图形(至少画出三个周期),
并写出 S( x)的表达式 。
例
2.设
f
(x)
以2
为周期,且
f
(
1,
x)
1,
x0 , 0 x
将 f ( x) 展开为傅里叶级数,并求其和函数S( x) 。
解: f ( x) 满足狄氏条件。求傅里叶系数:
a0
1
f
( x)dx
1
0
dx
1
0
dx0
,
1
10
1
an f ( x)cosnxdx (1)cosnxdx 0 cosnxdx
例 4.将函数 f (x) x2( x) 展开成傅里叶级数。
解:把 f ( x) 在(,] 上作周期延拓,
a0
1
1 f ( x)dx
x2dx 22 , 3
an
1
f ( x)cosnxdx 1
x2cosnxdx
(1)n n2
4(n1,
2,
)
,
bn
1
x2sinnxdx0 ,
如例 1:
即 S(
x 时,
xxn)1((10x),,n,)1xx时n2ys(,innn.x,1(),f 1()n10n2)2sinf n(x0f)
(x) x ,
0 2
。
3 2 o 2 3 y
3 2 o 2 3
x f (x)的图象. x S(x)的图象.
把 f (x) 在[, ] 上展开为傅里叶级数的步骤为 (1)用狄氏条件判断 f ( x) 能否展开为傅里叶级数; (2)求出傅里叶系数; (3)写出傅里叶级数并注明在何处收敛于f ( x) ; (4)画出 f ( x) 和S( x) 的图形(至少画出三个周期),
并写出 S( x)的表达式 。
例
2.设
f
(x)
以2
为周期,且
f
(
1,
x)
1,
x0 , 0 x
将 f ( x) 展开为傅里叶级数,并求其和函数S( x) 。
解: f ( x) 满足狄氏条件。求傅里叶系数:
a0
1
f
( x)dx
1
0
dx
1
0
dx0
,
1
10
1
an f ( x)cosnxdx (1)cosnxdx 0 cosnxdx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1777年,欧拉在天文学的研究中,用三角函数的正交性 得到了将函数表示成三角函数时的系数. 也就是现今教科书中傅立叶级数的系数.
3
在历史上,三角级数的出现和发展与求解微分方程 是分不开的. 1753年.丹贝努利首先提出将弦振动方程的解表示为 三角级数的形式, 这为傅立叶级数题奠定了物理基础,促进了它的发展. 1822年,傅立叶在 «热的解析理论»一书中 对于欧拉和贝努利等人就一些孤立的,特殊的情形 采用的三角级数方法进行加工处理,发展成一般理论. 傅立叶指出: 任意定义在 (π, π ) 上的有界函数 f (x) 可以展开成级数
an,
则
an
1
f ( x)cos nxdx
(n 1,2,3,).
(3) 求 bn.
f ( x)sin nxdx a0
sin nxdx
2
(利用正交性)
[ak
cos kx sin nxdx bk
sin kxsin nxdx]
bn,
k 1
则
bn
1
f ( x)sin nxdx
但是在三角函数系中两个相同的函数的乘积在
上的积分不等于 0 . 且有
11dx
2
cos2
n xdx
sin
2
nx
dx
cos2 nx 1 cos 2nx , sin2 nx 1 cos 2nx
2
2
7
机动 目录 上页 下页 返回 结束
二、函数展开成傅里叶级数
问题: 1. 若函数能展开成三角级数,ai ,bi是什么? 2. 展开的条件是什么?
一.三角级数 三角函数系的正交性
在高等数学学习当中,接触两类基函数:
u ( x) x n 1,x,x2 ,x 3 x n n
sin nx
u n
(
x)
cos
nx
1,sin x,cos x,sin 2x,cos 2xsin nx,cos nx
函数在一点的性质 f ( x) an ( x x0 )n
bn An cosn, t x,
得级数
a0 2
(an
n1
cos nx
bn
sin nx)
称为三角级数.
2
1757年,法国数学家克莱罗在研究太阳引起的摄动时,
大胆地采用了三角级数表示函数:
f (x) A0 2 An cos nx .
n1
其中
An
1 2π
2πx
.
1759年,拉格朗日在对声学的研究中使用了三角级数.
设 f (x) 是周期为2π 的周期函数,
且能展开成三角级数
(1)
求 a0.
f
(x)
a0 2
(ak
k 1
cos kx
bk
sin kx)
π f ( x)dx
π
π a0 dx π 2
π
[
π
(ak cos kx bk sin kx)]dx
k 1
8
π a0 dx π 2
π
π ak cos kxdx k 1
11
代入傅里叶系数的三角级数称为傅里叶级数
a0 2
(an
n1
cos nx
bn
sin nx)
问题: 在什么条件下函数可以展开成傅里叶级数?
f
(x)
条件?
a0 2
(an
n1
cos nx
bn
sin nx)
狄利克雷于1829年第一次对于傅立叶级数的收敛性 给出了严格的证明.
得到了现今教科书中的所谓狄利克雷判定准则.
正交 , 即其中任意两个不同的函数之积在
上的积分等于 0 .
证:
1
cos
nx d
x
1
sin
nx d
x
0
cos k x cos nx dx
1 2
cos(k
n)
x
cos(k
n)
x
d
x
0
同理可证 : sin k x sin nx dx 0 cos k x sin nx dx 0 (k n )
6
机动 目录 上页 下页 返回 结束
12
定理(收敛定理, 展开定理) 设 f (x) 是周期为2的
周期函数, 并满足狄利克雷( Dirichlet )条件:
1) 在一个周期内连续或只有有限个第一类间断点;
2) 在一个周期内只有有限个极值点,
则 f (x) 的傅里叶级数收敛 , 且有
注意: 函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多.
n1
f (x) ;
2. 设 x (π, π ) 是 f (x) 的间断点,则有
S(x) 1 [ f (x 0) f (x 0)] ; 2
3.当x π , π 时, 有
S(x) 1 [ f ( 0) f ( 0)] .
2
14
例1. 设 f (x) 是周期为 2 的周期函数 , 它在
n0
周期函数(整体性质) Fourier级数
三角级数 表达周期函数
1
(一)三角级数 表达周期函数
简单的周期运动 :
复杂的周期运动 :
f (t) A0 An sin(nt n )
n1
谐波分析
A0 ( An sinn cosnt An cosn sin nt)
n1
令
a0 2
A0 ,
an An sinn ,
π
π bk sin kxdx k 1
a0 2, 2
则
a0
1 π
π
f ( x)dx .
π
(2) 求 an.
f ( x)cos nxdx a0
cos nxdx
2
(利用正交性)
π
[ak
cos kx cos nxdx bk
sin kxcosnxdx]
k 1
9
an
cos2 nxdx
4
f (x)
a
~
0 (a cos nx b sin nx ) .
2
n1
n
n
其中
an
1 π
π
π
f
( x) co sn xdx
(n
0,1,2...)
,
bn
1 π
π
π
f
( x) s in n xdx
(n
1,2...)
.
5
(二)、三角函数系的正交性
1,cos x,sin x,cos 2x,sin 2x,cos nx,sin nx,
(n 1,2,3,).
10
傅里叶系数
an
1
f ( x)cos nxdx,
(n 0,1,2,)
bn
1
f ( x)sin nxdx,
(n 1,2,)
或
an
1
2 0
f ( x)cos nxdx,
bn
1
2 0
f ( x)sin nxdx,
(n 0,1,2,) (n 1,2,)
f (x) ,
x 为连续点
f (x)
f ( x ) , x 为间断点
2
其中 an , bn 为 f (x) 的傅里叶系数 . ( 证明略 )
13
简介 目录 上页 下页 返回 结束
既
1. 设 x0 (π, π ) 是 f (x) 的连续点, 则有
S(x) :
a0 2
(an cos nx bn sin nx)
