方差与协方差理解
统计学中的方差分析与协方差分析的比较

统计学中的方差分析与协方差分析的比较统计学是研究数据收集、分析和解释的一门学科,方差分析和协方差分析是其中两个重要的统计方法。
在本文中,我们将比较这两个方法的基本原理、适用范围和使用方法。
一、基本原理1. 方差分析方差分析(ANOVA)是一种用于比较两个或更多组之间的差异的统计方法。
它通过将总体方差分解为组内差异和组间差异,并通过检验组间差异是否显著来判断组间是否存在统计学上的差异。
2. 协方差分析协方差分析(ANCOVA)是一种结合方差分析和线性回归分析的统计方法。
它通过在方差分析中添加一个或多个协变量来控制实验组间潜在的混杂因素,并进一步检验组间差异的统计学意义。
二、适用范围1. 方差分析方差分析广泛应用于实验设计和观察研究中,特别适用于比较多个组的均值是否有显著差异。
例如,一个研究人员想要比较不同教育水平的人在某项测试中的平均得分是否有差异,方差分析可以被用来解决这个问题。
2. 协方差分析协方差分析主要针对一些协变量对实验结果的影响进行调整。
它适用于那些存在其他可能影响结果的潜在因素的研究,如年龄、性别、教育水平等。
通过添加这些协变量作为回归分析的自变量,可以更准确地评估组间差异的统计学显著性。
三、使用方法1. 方差分析方差分析通常包括以下几个步骤:a. 界定研究对象和问题;b. 选择合适的方差分析模型;c. 收集所需的数据;d. 进行方差分析,计算组间和组内的方差;e. 利用统计方法检验组间差异的显著性;f. 根据结果进行结论和解释。
2. 协方差分析协方差分析的步骤包括:a. 选择适当的协方差模型,并确定潜在的影响因素;b. 收集数据,并测量协变量和实验结果;c. 进行协方差分析,控制协变量的影响;d. 利用统计方法检验组间差异的显著性;e. 根据结果进行解释并得出结论。
四、总结方差分析和协方差分析是统计学中常用的两种方法,其应用范围和使用方法存在差异。
方差分析适用于比较多个组之间的差异,而协方差分析则主要用于控制潜在的混杂因素。
方差和协方差

⽅差和协⽅差1.⽅差⽅差是各个数据与平均数之差的平⽅和的平均数。
(⽅差⽅差,就是平⽅了数据与平均数之差)在中,⽅差(英⽂Variance)⽤来度量和其数学期望(即)之间的偏离程度。
例⼦:1, 5 ,9 ⽅差⼤ 4,5,6⽅差就⼩。
2.协⽅差在和中,协⽅差⽤于衡量两个变量的总体误差。
⽽是协⽅差的⼀种特殊情况,即当两个变量是相同的情况。
期望值分别为E(X) = µ 与E(Y) = ν的两个实数随机变量X与Y之间的协⽅差定义为:COV(X,Y)=E[(X-E(X))(Y-E(Y))]=EXY-EX*EY直观上来看,协⽅差表⽰的是两个变量总体误差的⽅差,这与只表⽰⼀个变量误差的⽅差不同。
如果两个变量的变化趋势⼀致,也就是说如果其中⼀个⼤于⾃⾝的期望值,另外⼀个也⼤于⾃⾝的期望值,那么两个变量之间的协⽅差就是正值。
如果两个变量的变化趋势相反,即其中⼀个⼤于⾃⾝的期望值,另外⼀个却⼩于⾃⾝的期望值,那么两个变量之间的协⽅差就是负值。
如果X与Y是统计独⽴的,那么⼆者之间的协⽅差就是0,因为两个独⽴的随机变量满⾜EXY=EXEY。
但是,反过来并不成⽴。
即如果X与Y的协⽅差为0,⼆者并不⼀定是统计独⽴的。
(⽐如Y是X的绝对值并且E(X)=0的情况,如果X的正负分布⾜够“均匀”,那么就有可能EXY=EX*EY=0;换句话说,Y和X的变化趋势没关系,但是Y和X绝对值的变化趋势⼀样。
总结:协⽅差描述了”Y和X的步调⼀致性“的⼤⼩?)协⽅差cov(X,Y)的度量单位是X的协⽅差乘以Y的协⽅差。
⽽取决于协⽅差的相关性,是⼀个衡量的的数。
协⽅差为0的两个称为是不相关的。
方差、标准差、协方差和Pearson相关系数及其间的关系

方差、标准差、协方差和Pearson相关系数及其间的关系方差、协方差和Pearson相关系数在机器学习的理论概念中经常出现,本文主要理一下这几个概念及其相互间的关系。
(一)方差:方差是每个样本值与全体样本值的平均数之差的平方值的平均数,公式如下:上式中mui为样本均值。
方差可以反应样本数据的离散程度,由上式可以看出,方差越大,样本离散程度也越大。
机器学习中,如果某一特征值的离散程度很小,即表示该特征取值很少,可以认为样本在这个特征上基本没有差异,那这个特征对于样本区分没有什么作用,可以将这个特征去除,从而做到特征选择。
(二)标准差:标准差即方差的开平方,不展开了,下面是公式:(三)协方差:协方差描述的是两个变量间的相关性,计算公式如下:也可以用以下公式表示,两者是等价的:cov(X, Y) = E[(X-E[X])(Y-E[Y])]上式中E[ ]表示求期望,其中E[X]为X特征期望或均值,E[Y]为Y 特征期望或均值。
对比方差和协方差的公式可以看出两者很像,但方差的结果是大于等于0的,当等于0时,说明样本的x特征取值唯一,反应的样本的x特征的离散程度;协方差的取值则可以大于零也可以小于零,当大于零时,说明对应的两个变量x和y与其均值相比都同大于或同小于,即两个变量的变化趋势相同(正相关);当小于零时,说明对应的两个变量x和y不同时大于或小于其均值,即两个变量的变化趋势相反(负相关);而当均方根接近零时,说明两个变量基本没有相关性,接近相互独立。
从以上描述可以看出,协方差可以衡量两个变量相关性大小,绝对值越大,说明越相关。
但是,却不好比较多个变量与另外同一个变量间相关性的相对大小,因为量纲没有统一。
为了便于比较不同变量与另外同一个变量间相关性的相对大小,Pearson相关系数被提出了。
Pearson相关系数:如上所述,Pearson相关性系数是为了比较不同变量与另外同一变量间相关性的相对大小,这里要注意的是:Pearson相关性系数衡量的是定距变量间的线性关系,可以用Pearson相关系数来进行特征特征选择。
第四章方差与协方差

随机变量的数学期望(均值), 它体现了随机 变量取值的平均水平, 是随机变量的一个重要的 数字特征.
但是在很多场合, 仅仅知道平均值是不够的.
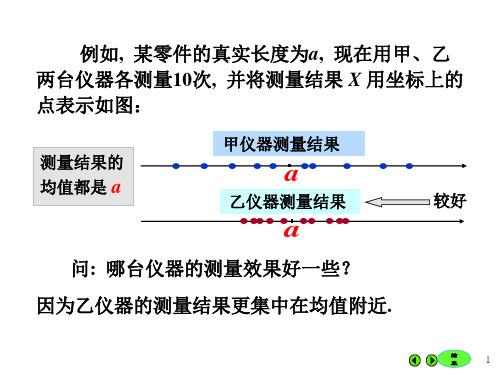
例如, 某零件的真实长度为a, 现在用甲、乙 两台仪器各测量10次, 并将测量结果 X 用坐标上的 点表示如图:
测量结果的 均值都是 a
为此需要引进另一个数字特征, 用它来度量 随机变量在其中心 (即均值) 附近取值的离散程度 (或集中程度). 这个数字特征就是: 方差.
我们该用怎样的量去度量这种偏离程度呢?
X − E(X) ? E[ X − E(X) ] ? E{ [ X − E(X) ]2 }
E[ | X − E(X) | ] ?
若 X 的取值比较集中, 则方差较小; 若 X 的取值比较分散, 则方差较大 .
如: 据以往记录, 甲乙两射手命中环数 X、Y 的分布律为
X
6
7
8
9
10
0.1
P 0.1 0.2 0.4 0.2 可以算出:
及
Y
6
7
8
9
10
0.2
P 0.2 0.2 0.2 0.2
8.0, 6 0 . 1 7 0 . 2 8 0 . 4 9 0 . 2 10 0 . 1 E (X) E ( Y ) 8 . 0 , 两人命中环数的平均水平相同, 从中看不出两人射击技术的 高低; 2 1 )20 .2 ( 2 )20 .1( ( X ) E {[ X E ( X )] } 但 D
一、方差( variance )的定义
随机变量 X 的平方偏差 [ X − E(X) ]2 的均值
E { [ X E ( X ) ]}
方差与协方差
n
n
从而 E( X ) E( X i ) np, D( X ) D( X i ) npq.
E(Y 2)
1
dx
1 y2 8x ydy 2 ,
0x
3
D(Y ) E(Y 2 ) [E(Y )]2 2 .
75
结 束
7
三. 常见分布的期望与方差
(1) X ~ B(n, p) , 则 E( X ) n p , D( X ) n pq .
(2) X ~ P( ) , 则 E( X ) , D( X ) .
2 2b b2 令 1
4 3 3 2
, 解得 b = 0, a = 2, E( X ) = 2/3
36
18 或b = 2, a = −2, E( X ) = 1/3 .
结 束
6
例:
设 (X, Y) 的概率密度为 试求 D( X ), D( Y ) .
f
( x,
y)
8x 0,
y, 0 x 其它.
(2) 设 X 与 Y 相互独立, 则
D(X+Y) = D(X) + D(Y), D(X−Y) = D(X) + D(Y).
进一步, 若 X1 ,… , Xn 相互独立, 则对任意常数
c1 ,…, cn 有: D( c1 X1+ … + cn Xn ) = c12 D( X1 ) + … + cn2 D( Xn ).
(3) D(X) = 0 的充要条件是 X 以概率 1 取常数 C , 即 P{X = C } = 1 .
结 束
9
例: X ~ B(n, p) , 则 E( X ) n p , D( X ) n pq .
方差和协方差转换公式

方差和协方差转换公式方差和协方差,这俩家伙在统计学里可算是重要角色啦。
咱们先来说说方差,它衡量的是一组数据的离散程度。
比如说,咱们班同学的考试成绩,方差大就说明成绩参差不齐,有高有低;方差小呢,就表示大家成绩都比较接近。
那协方差又是啥呢?它反映的是两个变量的总体的误差。
就像我观察过的一件事儿,有一次我们搞小组活动,要统计每个小组完成任务的时间和质量。
时间和质量就是两个变量,通过计算它们的协方差,就能知道这两者之间的关系是正相关还是负相关。
咱们来具体讲讲方差和协方差的转换公式。
方差的公式大家都比较熟悉,就是每个数据与均值的差的平方的平均值。
而协方差的公式呢,是两个变量与各自均值的差的乘积的平均值。
这转换公式就像是一座桥梁,能让我们在方差和协方差之间自由穿梭。
比如说,我们知道了一组数据的方差,通过一些巧妙的计算,就能得到它与另一个变量的协方差。
我记得有一次,我在研究股票市场的数据。
不同股票的价格波动就是一组变量,通过计算它们的方差和协方差,就能更好地分析风险和相关性。
当时我为了搞清楚这些,那可是熬了好几个晚上,对着一堆数据反复琢磨。
再说说在实际应用中,方差和协方差转换公式用处可大了。
比如在金融领域,分析投资组合的风险;在医学研究中,判断不同治疗方法的效果和相关性。
总之,方差和协方差转换公式虽然看起来有点复杂,但只要我们多琢磨、多练习,就能把它运用得得心应手,让它成为我们解决问题的有力工具。
就像我们在学习和生活中遇到的其他难题一样,只要用心,都能搞定!。
方差分析及协方差分析
方差分析及协方差分析方差分析和协方差分析是统计学中常用的两种分析方法,用于研究变量之间的关系和差异。
本文将分别介绍方差分析和协方差分析的基本概念、原理和应用。
一、方差分析(Analysis of Variance)1.基本概念:方差分析是一种通过对不同组之间的差异进行分析,来揭示组间差异是否非随机的统计方法。
它可以用于比较两个或更多个组的均值是否有显著差异。
2.原理:方差分析的原理基于对总体变异的分解。
总体变异可以分解为组间变异和组内变异。
组间变异表示不同组之间的差异,而组内变异表示组内个体之间的差异。
方差分析通过计算组间变异与组内变异之间的比值来判断组间差异是否显著。
3.适用场景:方差分析适用于有一个自变量和一个或多个因变量的情况。
常见的应用场景包括:比较不同药物对疾病影响的效果、比较不同教学方法对学生成绩的影响等。
4.步骤:方差分析的步骤包括:确定研究目的和假设、选择适当的方差分析模型、计算方差分析统计量和p值、进行结果解释。
二、协方差分析(Analysis of Covariance)1.基本概念:协方差分析是一种结合方差分析和线性回归分析的方法。
它通过控制一个或多个连续变量(协变量)对组间差异进行调整,来比较不同组之间的差异。
协方差分析不仅考虑到组间差异,还考虑到了协变量的影响。
2.原理:协方差分析的基本原理是通过线性回归模型来估计组间均值的差异,同时考虑协变量的影响。
通过计算协方差矩阵和相关系数,可以得到组间差异的调整后的统计结果。
3.适用场景:协方差分析适用于有一个自变量、一个或多个因变量,以及一个或多个连续变量的情况。
常见的应用场景包括:比较不同药物对疾病影响的效果,并控制患者年龄和性别等协变量。
4.步骤:协方差分析的步骤包括:确定研究目的和假设、选择适当的协方差分析模型、建立回归模型、计算协方差分析统计量和p值、进行结果解释。
总结:方差分析和协方差分析都是常用的统计分析方法,用于研究组间差异和变量之间的关系。
方差协方差理解
方差协方差理解方差和协方差是在数据分析中常用的两个统计量,它们可以用来衡量数据的分散程度以及不同变量之间的关系。
在本文中,我们将解释方差和协方差的概念、计算方法以及在统计分析中的应用。
方差方差是指数据分布的离散程度。
例如,如果我们有一组数据,它们分别为9、10、11、12、13,那么这些数据的平均值为11。
方差就是每个数据点与平均值的差的平方的平均值。
数学上,方差可以表示为:$$\sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n}$$其中,$\sigma^2$表示方差,$ n $表示数据的数量,$ x_i $是第 $ i $个数据点,$ \mu $是所有数据的平均值。
我们可以使用这个公式来计算任何一组数据的方差。
在这个例子中,方差为2。
方差可以用来衡量数据的分散程度。
如果一组数据的方差很大,说明这些数据彼此之间的差距比较大。
如果方差很小,说明这些数据的差距比较小,说明这些数据比较集中。
协方差是衡量两个变量之间关系的统计量。
例如,如果我们有两组数据,分别是X和Y。
协方差可以用来衡量这两组数据之间的线性关系程度。
协方差可以表示为:其中,$\sigma_{XY}$表示X和Y的协方差,$ n$表示数据的数量,$ x_i $和$ y_i $分别是X和Y的第 $ i $个数据点,$ \overline{X} $和$ \overline{Y} $分别是X和Y的平均值。
协方差的值有三种可能:正值表示两个变量之间具有正的线性关系;负值表示两个变量之间呈负的线性关系;值为零说明没有线性关系。
在其他情况下,协方差的大小反映了这两个变量之间的强度和方向。
但是,协方差不能比较不同单位的变量。
因此,我们通常使用相关系数来描述变量之间的关系。
相关系数是协方差的标准化表达。
我们可以使用以下公式来计算相关系数:其中,$ r_{XY} $表示X和Y的相关系数,$ \sigma_{XY} $表示协方差,$ \sigma_X $和$ \sigma_Y $分别表示X和Y的标准差。
4,2.方差与协方差
a
a
较好
乙仪器测量结果 就上述结果可评价两台仪器的优劣, 乙仪器较好,
因为乙仪器的测量结果更集中在均值附近。
为此需要引进另一个数字特征, 中心附近取值的离散(集中)程度.
用它来度量随机变量在其 这个数字特征就是: 方差.
一、方差的定义
随机变量 X 的方差为
(3)设X与Y 相互独立, 则
D(X+Y)=D(X)+D(Y), D(X−Y)=D(X)+D(Y).
进一步,若 X1 ,… , Xn 相互独立, 则
D(X1+ … +Xn)=D(X1)+ … +D(Xn) .
(4) D(X)=0的充要条件是X 以概率1取常数C , 即
P{X=C }=1 .
例: X ~ B( n, p) , 则 E ( X ) n p , D( X ) n pq . 解: X 表示 n 重伯努利试验中 “成功”的次数,
记作
D( X ) E { [ X E ( X ) ] 2 }
而
D( X )
( X ) 叫做 X 的标准差或均方差。
方差刻划了随机变量的取值对于其数学期望的离散程度 . 若 X 的取值比较集中,则方差较小; 若 X 的取值比较分散,则方差较大 . 若方差 D(X)= 0, 则 X 以概率 1 取常数值 .
1
1
y
y=x
1
1 E ( X ) dx x 8 x ydy , 0 x 3
2
1 1 2
D( X ) E ( X ) [ E ( X )]
4 E (Y ) 0 dx x y 8 x ydy , 5 1 1 2 2 2 E (Y ) dx y 8 x ydy , 0 x 3 2 2 2 . D(Y ) E (Y ) [ E (Y )] 75
协方差的直观理解
协⽅差的直观理解1.协⽅差⽅差是描述⾃⾝偏离其均值的程度。
协⽅差⽤来描述两个变量间的变化关系,协⽅差⽤来度量两个随机变量关系的统计量cov(X,Y)=E[(X−E[X])(Y−E[Y])]cov(X,Y)=E[(X−µx)(Y−µy)]E[x] 代表期望,⼀般置X的均值公式:如果有X,Y两个变量,每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到⼀个乘积,再对这每时刻的乘积求和并求出均值eg:⽐如有两个变量X,Y,观察t1-t7(7个时刻)他们的变化情况。
我们发现在每⼀个时刻,X-µ,和Y-µ 都是同号的,如果是反向的:X-µ,和Y-µ 的乘积就是负号,当然上⾯说的是两种特殊情况,很多时候X,Y的运动是不规律的,⽐如:这种情况下很可能在某⼀个时刻乘积是正,另外⼀个时刻乘积⼜为负数了,将每⼀个时刻的乘积加到⼀起,其中的正负会抵消,最后平均得出值就是协⽅差,通过协⽅差的⼤⼩,就可以判断两个变量同向或者反向的程度了。
总结⼀下,如果协⽅差为正,说明X,Y同向变化,协⽅差越⼤说明同向程度越⾼;如果协⽅差为负,说明X,Y反向运动,协⽅差越⼩说明反向程度越⾼。
拓展如果同向变化,但是X⼤于均值,Y⼩于均值,那乘积是负数的。
可见t1时刻 X-µ,和Y-µ 负号相反,乘积为负。
但是如果从整体来说依然要计算其他时间的值,然后在吧7个时间的值求均值,所以某⼀时刻的为负数不代表整体是反向的。
要结合整体来判断。
相关系数翻译⼀下:就是⽤X、Y的协⽅差除以X的标准差和Y的标准差。
所以,相关系数也可以看成协⽅差:⼀种剔除了两个变量量纲影响、标准化后的特殊协⽅差。
既然是⼀种特殊的协⽅差,那它:1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协⽅差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,⽽只是单纯反应两个变量每单位变化时的相似程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2方差、协方差与相关系数2.1方差例1比较甲乙两人的射击技术,已知两人每次击中环数分布为p 89<67 89 10^巴.Q10.6 01 丿” :vQ1 0.2 0.4 0.2 01 丿问哪一个技术较好?首先看两人平均击中环数,此时 E =E =8,从均值来看无法分辩孰优孰劣 •但从直观上 看,甲基本上稳定在 8环左右,而乙却一会儿击中 10环,一会儿击中6环,较不稳定.因此 从直观上可以讲甲的射击技术较好 .上例说明:对一随机变量,除考虑它的平均取值外,还要考虑它取值的 离散程度.称-E为随机变量 对于均值E的离差(deviation ),它是一随机变量.为了给出一个描述离散程度的数值,考虑用E -E,但由于E-E = ^ -E=0对一切随机变量均成立,即'2的离差正负相消,因此用 E -E 是不恰当的.我们改用E E描述取值的离散程度,这就是方差Vat=EZ 叮deviatio n ).2方差是随机变量函数(一 一E 」)的数学期望,由§的⑸式,即可写出方差的计算公式(x 「E )2P 「二 xj,离散型, 巴 产(x-E®2dFKx) f 「(x-E©2pKx)dx ,连续型.Var - ■ = a-= L -°0进一步,注意到E G —E © 2 = EF -2春 +(E : )2] = E ©2 -(E © )2即有许多情况,用(3)式计算方差较方便些 例1(续)计算例1中的方差Var 与Var .定义12存在,为有限值, 就称它是随机变量 ■的方差(varianee),记作 Var -,但Var •的量纲与 不同,为了统一量纲,有时用Var,称为的标准差(standard(1)Var_E 2_ E■. 2 - 解利用⑶式 匚 2 ' X :P( ―) 222E = i =7 X0.1+8 X 0.8+9 >0.1=64.2,2 2Var =E _ E=64.2-- 82=0.2.2 2同理,Var = E- E= 65.2-64 = 1.2 > Var ,所以 取值较 分散. 术较好.例2这说明甲的射击技试计算泊松分布 P (入的方差.-■ k E 2八 k 2—e k z0 k!:: kk e _ 心(k-1)!:' -k:"■ k所以设 服从[a, b ]上的均匀分布 U [a, b ],求Var .b 2 1dx 」a 2ab b b —aVar1a 2ab b 2 _ 1 a b 3 _221 I 2b _ a I 12设■服从正态分布N a,;",求Var .解此时用公式⑵,由于E 二a-boVar 询违厂"a)-□02 - ::2ze dz2 二 sf2 ,-bo-be2 2\ -ze" z /2 +r—z /2 ■e dzI-oO这就得(4)式.切贝雪夫不等式无论从证明方法上还是从结论上都有一定意义 」:,E —与E ,;内的概率小于等于Var/ ;2,或者说, 落在区间E一 ;,E ;内的概率大于1-Var / ;2,从而只用数学期望和方差就可对上述概率进 行估计.例如,取 £ =3 Var ,则P (|— E q 兰^/VO ^ 比1 —Var ”(37V0^ (〜089P (|EE| E3 '、V ar )=卩(|“| 乞3 扌胡.997 ).性质1Var- =0的充要条件是 P(手C )=1,其中C 是常数.证 显然条件充分.反之,如果Var= 0,记E = C,由切贝雪夫不等式E 巴>P(冷E| - £=0对一切正数£成立.从而2可见正态分布中参数 C 就是它的方差,二就是标准差• 方差也有若干简单而重要的性质 •先介绍一个不等式•切贝雪夫(Chebyshev)不等式若随机变量的方差存在,则对任意给定的正数P (|E —E © ")兰Var L/y恒有⑷证设•的分布函数为F x ,则P (|E-E 律让仁込dF(x) <"E )2|X -E |_ ;dF(x)1-j 2「(x-E )2dF(x)= Var / 2.事实上,该式断言 落在当然这个估计还是比较粗糙的(当N a,' 时,在第二章曾经指出,P G=c)=1_P(G_c =0)=1「lim_P -c -1 n =1性质2设c,b 都是常数,则Var(c+b)=c2VarVar(c+b)=E(c +b-E(c +b))?=E(c+b-c E-b )2c 2E( -E )2=c 2Var性质 3 若 c= E [则Var :: E -c.证 因Var=E 2 -(E )[而 E( E C )2 = E 2-2C E+c 2,度最小.n nVar (迟 Ej 迟 Var® 送 E& — E ©"® — 性质4 i 土 = i 4 +2 1丄::j 岂特别若1,川,n 两两独立,则nn n ni )yi 7 i )、2 (' ( i -E i ))2i 珀=E ( i £-E ( i =1 ) =E i 叫n(、(i -E i )2( i -E J(〔 -E J)=E i 仝i _i ::j 』n' Var i ' E( i -E J( j -E j )=i 仝+21 生,得证⑹式成立.当1,川,n 两两独立时,对任何1- I > j -n有E i j — E i E j , 故E( i -E i )( j -E j )=E( i i E j - j E i E i E j )-i - i - E E - i=E i j i j =0,这就得证(7)式成立.利用这些性质,可简化某些随机变量方差的计算 例5设E 服从二项分布B(n, p),求Var.解 如§例12构造rhlll,n,它们相互独立同分布,此时两边相减得 Var - E - c 2 = _ E2_c ::: 0.这说明随机变量E 对数学期望E的离散证 Var(若 E (; -E ;)(二j 一E 了)< +处就称Va 「£ =E¥_(E £)2 =i 2”p+°2 q_p 2=pq.由于相互独立必是两两独立的,由性质 4nnw $ =Var(E 耳)=瓦 Var©Vari j ynpq设随机变量i 川I ,n 相互独立同分布,E i = a , V a r i^2解由§性质2和本节性质•作为各i 的算术平均,它的数学期望与各 i 的数学期望相同,但方差只有i 的1/ n 倍.这一事实在数理统计中有重要意义 例7设随机变量E 的期望与方差都存在,Va「・°.令*_-E ^Var £1称它为随机变量E 的标准化•求E 与Var 解由均值与方差的性质可知2.2协方差数学期望和方差反映了随机变量的分布特征•对于随机向量(J",n ),除去各分量的期望和方差外,还有表示各分量间相互关系的数字特征 一协方差•定义2记-i 和的联合分布函数为F j (X, y ).—1仁(i =1,HI,n ).记二=n y,求 ^,Var"_s nE_「n v=a,1 nVar 一 KF ,,1 2 n •• J n这说明在独立同分布时,E — EC_)5/Var -=0VarVar( _ E )VarVar Var(8)E( i —E J( j —E j )二:;.:;(x-E i )(y — E j )dF j (x,y) 为 _i ' j 的协方差(covarianee),记作 Cov( _i ^j ).显然,Cov j=Vari•公式⑹可改写为nn ' i'、Var i ' Cov( i , j )Var (v )=第+21L ::j _n容易验证,协方差有如下性质: 性质 1 Cov( , ) = Cov( ,)=E -E E.性质2设a,b是常数,则Cov( a ,b )二 abCov(,)nnCov(E 守)=Z Cov&n)性质3yi 吕其中 b j =Cov (qt j )C 11 C 1n则C •的协方差阵为CBC ,其中B 是E 的协方差阵.J 1,川,J\C m1C mn5对于n 维随机向量 可写出它的协方差阵b21■ aGb12b1nb 2nB = E (©_E : X©_E :)" = <bmb n2bnn(9)由性质1可知B 是一个对称阵,且对任何实数t j jn' b jk t j t kj,k 1八 WE( j - E j )( k - E k )二 E(' t j ( j - E j ))2 一0 j,心 jw即随机向量 性质4设E 的协方差阵B 是非负定的.因为EC (C ) =E^ C nCE'c',所以CBC •的第i,j元素就是C的第i元素与第j元素的协方差.2.3相关系数协方差虽在某种意义上表示了两个随机变量间的关系,但C°v ,的取值大小与纲有关.为避免这一点,用E的标准化随机变量(见例7)来讨论.定义3称_ E( -E )( -E )r =Cov( , ) . Va^~Var_为E ,的相关系数(correlation coefficient).为了讨论相关系数的意义,先看一个重要的不等式柯西一许瓦茨(Cauchy—Schwarz)不等式对任意随机变量E 有E幼2兰E©2E H2等式成立当且仅当存在常数t。
使P(H =t°E)=1.证对任意实数tu (t)二E(t - )2二t2E 2—2tE E 2是t的二次非负多项式,所以它的判别式(E孕)2 _E:2E H2兰0J证得(11)式成立.(11)式中等式成立当且仅当多项式U (t)有重根t o,即u(to )=E(to© -巧2=0.又由(3)Var (t o©」戶E(t o—耳)J故得V a rt o - = °同时有E t o - =o.所以由方差的性质1P t o •一=0 二1,此即(12)式.由此即可得相关系数的一个重要性质.E的量(1o)(11)(12)—1(13)9 / 12性质1对相关系数r 有r■ =1当且仅当P-E --E 「-Var, Varr' =-1当且仅当PE— =-1 1 J Var - J Va L(14)证由(11)式得闱=|E 广[兰 J E :承= J var r'Var " =1J. * *证得(13)式成立•证明第二个结论•由定义r r E.由柯西-许瓦兹不等式的证 明可知,|rT"等价于u(t) =t 2E -2tE * * E 有重根V * * K * 2 * * |. * *t o =2E /(2e)=E •因此由(12)式得「二1当且仅当巩 二)=1 ; r = 一1当且仅当注 性质1表明相关系数r = -1时,E 与 以概率1存在着线性关系•另一个极端是r = o ,此时我们称 E 与不相关(uncorrected). 性质2对随机变量E 和,下列事实等价:(1) Cov( E ,)=0;(2) E 与不相关;⑶ E;⑷ Var(工+耳)=Var :+Var 11证 显然(1)与⑵等价.又由协方差的性质1得(1)与⑶等价.再由(6)式,得(1)与⑷等价. 性质3若E 与独立,则E 与不相关.显然,由E 与n 独立知 ⑶成立,从而E 与 不相关■ 但其逆不真.例8设随机变量B 服从均匀分布U [0, 2兀],手cosT ,H=si n J 显然哼+^才,故三与口 不独立•但+2-2 —1cos d =0 02 二2 —1E二 Es -=0sin 士d '0E = Ecos vs in :二故Cov \ =E ~E E =0 ,即E 与不相关.注性质2不能推广到n -3个随机变量情形.事实上从n -3个随机变量两两不相关只nn能推得Var(「)K r i ,不能推得E 1川 mE n .反之,从这两个等式也不能推得1,l|l , n 两两不相关.具体例子不列出了 .对于性质3,在正态分布情形,独立与不相Cov ,= 一 (x-a)(y-b)p(x,y)dxdy=0+r j '- 2. 故得E =Ecosv总是 致的,这将在下面进行讨论设(E )服从二元正态分布N a,b;Gf 2,r,试求Cov,和—2二丁2 *1 - r 2Q Q Q Q;;(x-a )(y-b) exp1 2(1-「2)a 1a 2丿弊 dxdyz4_r 口t=口°2 ,则 -a= z rt J =-(x , y)_ ;-^2 W 讯z,t); 1;一 2Cov ,2「.1-r 2:::: 2(zt rt )-z 2/2(1 -r 2)dzdtL f t L /2dt.2 ■: s•2二 d -r 2广Z €~/2(1上违-ad丄 2 -t 2/2t edt____dt2: 一2:'e-2/2^2)dz-oOCov(,)屮ar^VarH这就是说二元正态分布中参数r就是E ,的相关系数.所以对二元正态分布,E、等价于r = 0•但在第二章已证E与相互独立等价于r = 0.这样我们有性质4对二元正态分布,两个分量不相关与相互独立是等价的2.4矩矩(mome nt)是最广泛的一种数字特征,常用的矩有两种,一种是原点矩,对正整数m k =E k称为E的k阶原点矩.数学期望就是一阶原点矩.另一种是中心矩,对正整数k,称C k -E )k为E的k阶中心矩.方差是二阶中心矩.除此以外,三阶与四阶中心矩也是常用的, 表示随机变量的性状.往往用他们的相对值.,3/2称C3 / C2为偏态系数,当它大于0时为正偏态,小于0时则为负偏态.称c4/c2 -3为峰态系数,当它大于0时表明该分布密度比正态分布更为尖峭例10设E为服从正态分布N (0,二2)的随机变量,此时E = 0,且特别m4二C4 =3二4.故不论b为多少,正态分布的偏态系数与峰态系数都为0.我们可以用原点矩来表示中心矩:kC k = 'r为反过来,我们也可以用中心矩来表示原点矩:不相关它们分别p,1 3 川(n-1);「n = 2k 1, n 二2k.I r r(—1) gm」m n2 r r(-1)m C k_p .J 丿k m k =- r =6我们也定义:-阶绝对矩M k =E 「其中〉是实数.对于例10中的随机变量E| |"「2和宀』*I1 3 |丨I (n -1);」,n =2k 利用上述结果,可以求出其他某些分布的矩E nx n $e ;2:2dx 乂 「x|x1「2:2dx a 2一皿因此, n = 2k 1,2k.:|x|n 2 2dx因此,1 3 W (n - 1)T特别,如果'服从参数为’的指数分布,那么 对于k -1, E k根据递推关系得2 :: n 2 - 2;:2x R(X )re^2 2,x 0 ,那么 JI 特别, E “2, 2- 2.因此, 方差 2 7. 2 丸=(2 __)a 2 2 再如, 马克斯威尔分布具有密度p(x)二 x 2「2— 0,那么 如瑞利分布,具有密度 ..22k (k 1)F k 1 n 二 2k,n =2k 1.例11. K 2 ak!即指数分布的任意阶矩存在。
