机械原理课件之四杆机构受力分析
合集下载
铰链四杆机构分析PPT课件

平面连杆机构与分类
平面连杆机构的组成
.
1
平面连机构的组成
• 平面连杆机构 :各构件是用销轴、滑道等方式连接起来的,各构件间的相对 运动均在同一平面内或互相平行的平面内。最简单的平面连杆机构是由四个 杆件组成的,简称平面四杆机构。由四个构件通过转动铰链联结而成的机构, 称为铰链四杆机构。
.
2
• 可以看出一般铰链四杆机构有四部分组成 • 1机架:固定不动 • 2连架杆2个:与机架相连,他是四杆机构
.
29
应用
.
30
铰链四杆机构的演化及应用
• 在生产实际应用中还广泛应用其它形式的四杆机构,可以 认为是通过改变某些构件的形状、相对长度,或不同的构 件作为机架等方法,来得到铰链四杆机构的一些其它的演 化形式,以下介绍常用的一些演化形式。
• 一:曲柄滑块机构 曲柄滑块机构是有曲柄摇杆机构演化得来的
• 在曲柄滑块机构(曲柄摇杆机 构)中,若曲柄很短,可将转 动副B的尺寸扩大到超过曲柄长 度,则曲柄AB就演化成几何中 心B不与转动中心A重合的圆盘, 该圆盘称为偏心轮,含有偏心 轮的机构称为偏心轮机构。
.
39
偏心轮极位
.
40
应用实例
• 偏心轮机构结构简单,偏心轮 轴颈的强度和刚度大,广泛用 于曲柄长度要求较短、冲击在 和较大的机械中,如图所示为 用于破碎机中的偏心轮机构。
• 以摇杆为主动件的
• 摇杆的摆动运动也可以转换为曲柄的整周回转运动。图示为缝纫机的 踏板机构,当踏板作往复摆动时,通过连杆使曲柄作整周转动。
.
11
双曲柄机构
• 在铰链四杆机构中,若两个连架杆都是曲柄时,此种四杆机构即称为 双曲柄机构。
• 下图为双曲柄机构原理图
平面连杆机构的组成
.
1
平面连机构的组成
• 平面连杆机构 :各构件是用销轴、滑道等方式连接起来的,各构件间的相对 运动均在同一平面内或互相平行的平面内。最简单的平面连杆机构是由四个 杆件组成的,简称平面四杆机构。由四个构件通过转动铰链联结而成的机构, 称为铰链四杆机构。
.
2
• 可以看出一般铰链四杆机构有四部分组成 • 1机架:固定不动 • 2连架杆2个:与机架相连,他是四杆机构
.
29
应用
.
30
铰链四杆机构的演化及应用
• 在生产实际应用中还广泛应用其它形式的四杆机构,可以 认为是通过改变某些构件的形状、相对长度,或不同的构 件作为机架等方法,来得到铰链四杆机构的一些其它的演 化形式,以下介绍常用的一些演化形式。
• 一:曲柄滑块机构 曲柄滑块机构是有曲柄摇杆机构演化得来的
• 在曲柄滑块机构(曲柄摇杆机 构)中,若曲柄很短,可将转 动副B的尺寸扩大到超过曲柄长 度,则曲柄AB就演化成几何中 心B不与转动中心A重合的圆盘, 该圆盘称为偏心轮,含有偏心 轮的机构称为偏心轮机构。
.
39
偏心轮极位
.
40
应用实例
• 偏心轮机构结构简单,偏心轮 轴颈的强度和刚度大,广泛用 于曲柄长度要求较短、冲击在 和较大的机械中,如图所示为 用于破碎机中的偏心轮机构。
• 以摇杆为主动件的
• 摇杆的摆动运动也可以转换为曲柄的整周回转运动。图示为缝纫机的 踏板机构,当踏板作往复摆动时,通过连杆使曲柄作整周转动。
.
11
双曲柄机构
• 在铰链四杆机构中,若两个连架杆都是曲柄时,此种四杆机构即称为 双曲柄机构。
• 下图为双曲柄机构原理图
机械原理之四杆机构受力分析PPT课件
FR12、 FR32
第21页/共30页
FR32= - FR12= FR21
3).取构件3为分离体——其上作用有:FR23、 FR43、 M3
由力平衡条件得: FR43= - FR23= FR21
M3 = FR23L´
C
FR23
3
L
M3
ω1 1 D
FR43
第22页/共30页
例 如图所示为一曲柄滑块机构,设各构件的尺寸(包括转动副的半径)已知,各
式中
xI, yI——力作用点I的坐标, xK, yK——取矩点K的坐标。
第16页/共30页
4) 各构件的力平衡方程式
•对于构件1分别根据
•对于构件2有
•对于构件3有
可得
第17页/共30页
以上共列出九个方程式,故可解出上述各运动副反力和平衡力的九个力 的未知要素。又因为以上九式为一线性方程组,因此可按构件1、2、3上待 定的未知力Mb, R41x, R41y, R12x, R12y, R23x, R23y, R34x, R34y的次序整理成以下的 矩阵形式:
3求rc取构件3为分离体并取该构件上的诸力对d点取矩规定力矩的方向逆时针者为正顺时针者为负则于是得同理取构件2为分离体并取诸力对b点取矩则因此可得3求rd根据构件3上的诸力平衡条件4求rb根据构件2上的诸力平衡条件5求ra同理根据构件1的平衡条件得至此机构的受力分析进行完毕
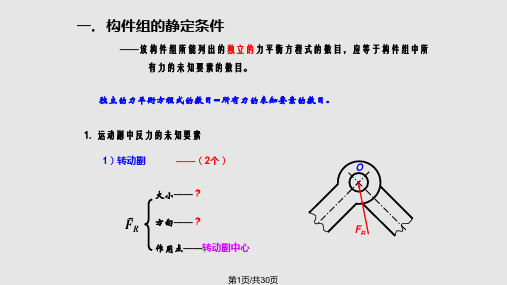
一. 构件组的静定条件
——该构件组所能列出的独立的力平衡方程式的数目,应等于构件组中所 有力的未知要素的数目。
A
ω23
C
FR32
3
M3
4D
解:1).求构件2所受的两力FR12、FR32的方位。
2).取曲柄1为分离体——其上作用有:
第21页/共30页
FR32= - FR12= FR21
3).取构件3为分离体——其上作用有:FR23、 FR43、 M3
由力平衡条件得: FR43= - FR23= FR21
M3 = FR23L´
C
FR23
3
L
M3
ω1 1 D
FR43
第22页/共30页
例 如图所示为一曲柄滑块机构,设各构件的尺寸(包括转动副的半径)已知,各
式中
xI, yI——力作用点I的坐标, xK, yK——取矩点K的坐标。
第16页/共30页
4) 各构件的力平衡方程式
•对于构件1分别根据
•对于构件2有
•对于构件3有
可得
第17页/共30页
以上共列出九个方程式,故可解出上述各运动副反力和平衡力的九个力 的未知要素。又因为以上九式为一线性方程组,因此可按构件1、2、3上待 定的未知力Mb, R41x, R41y, R12x, R12y, R23x, R23y, R34x, R34y的次序整理成以下的 矩阵形式:
3求rc取构件3为分离体并取该构件上的诸力对d点取矩规定力矩的方向逆时针者为正顺时针者为负则于是得同理取构件2为分离体并取诸力对b点取矩则因此可得3求rd根据构件3上的诸力平衡条件4求rb根据构件2上的诸力平衡条件5求ra同理根据构件1的平衡条件得至此机构的受力分析进行完毕
一. 构件组的静定条件
——该构件组所能列出的独立的力平衡方程式的数目,应等于构件组中所 有力的未知要素的数目。
A
ω23
C
FR32
3
M3
4D
解:1).求构件2所受的两力FR12、FR32的方位。
2).取曲柄1为分离体——其上作用有:
机械四杆机构演示文稿ppt

班级:D机制123 制作人:吴日晓 李雪 陈琪
内容概要:
在铰链四杆机构中,若两个连架杆,一为曲柄,另一个为摇杆,则此
铰链四杆机构称为曲柄摇杆机构。
在曲柄摇杆机构中,一般两连架杆一为主动件,一为从动件,我们知
道,当从动件连架杆与连杆处于共线(拉直共线或重叠共线)位置时,
主要应用于把转动变为摆动或把摆动变为转动的场合,如:飞剪、传
送带送料机构、牛头刨床横向进给机构、雷达调整机构、缝纫机脚踏
机构和复摆式腭式破碎机等。
死点位置
曲柄摇杆机构当满足最短杆与最长杆的长度之和等于另外两杆长度之
和时,即有死点位置存在。
曲柄主动时,曲柄摇杆机构具有死点位置的条件为:最短杆与最长杆
的长度之和等于另外两杆长度之和“由此亦可得,曲柄主动时,曲柄摇 杆机构无死点位置的条件为:最短杆与最长杆的长度之和小于另外两 杆长度之和
1、选择应用程序下面的机构,如图19 图19 进入机构运动仿真环境, 窗口左侧出现运动仿真特征树,右侧显示运动分析工具栏。
2、设置主动件。单击工具按钮“伺服电机”,在弹出的窗口中,选 择曲柄与机架的铰接轴作为运动轴,即指定曲柄为主动件,来产生回 转运动,然后点轮廓,把位置改为速度,A处输入10,意思为10度/秒, 确定
副。此时,如果取最短杆为机架,则得到双曲柄机构;若取最短杆的 任何一个相连构件为机架,则得到曲柄摇杆机构;如果取最短杆对面 构件为机架,则得到双摇杆机构。
曲柄摇杆机构
尺寸:
曲柄 连杆 摇杆 机架 摆角 极位夹角 行程速比系数
20 140 40 130
运动仿真图
最短杆为曲柄,曲柄转动带动摇杆摆动,实现急回特性。
曲柄摇杆机构条件
内容概要:
在铰链四杆机构中,若两个连架杆,一为曲柄,另一个为摇杆,则此
铰链四杆机构称为曲柄摇杆机构。
在曲柄摇杆机构中,一般两连架杆一为主动件,一为从动件,我们知
道,当从动件连架杆与连杆处于共线(拉直共线或重叠共线)位置时,
主要应用于把转动变为摆动或把摆动变为转动的场合,如:飞剪、传
送带送料机构、牛头刨床横向进给机构、雷达调整机构、缝纫机脚踏
机构和复摆式腭式破碎机等。
死点位置
曲柄摇杆机构当满足最短杆与最长杆的长度之和等于另外两杆长度之
和时,即有死点位置存在。
曲柄主动时,曲柄摇杆机构具有死点位置的条件为:最短杆与最长杆
的长度之和等于另外两杆长度之和“由此亦可得,曲柄主动时,曲柄摇 杆机构无死点位置的条件为:最短杆与最长杆的长度之和小于另外两 杆长度之和
1、选择应用程序下面的机构,如图19 图19 进入机构运动仿真环境, 窗口左侧出现运动仿真特征树,右侧显示运动分析工具栏。
2、设置主动件。单击工具按钮“伺服电机”,在弹出的窗口中,选 择曲柄与机架的铰接轴作为运动轴,即指定曲柄为主动件,来产生回 转运动,然后点轮廓,把位置改为速度,A处输入10,意思为10度/秒, 确定
副。此时,如果取最短杆为机架,则得到双曲柄机构;若取最短杆的 任何一个相连构件为机架,则得到曲柄摇杆机构;如果取最短杆对面 构件为机架,则得到双摇杆机构。
曲柄摇杆机构
尺寸:
曲柄 连杆 摇杆 机架 摆角 极位夹角 行程速比系数
20 140 40 130
运动仿真图
最短杆为曲柄,曲柄转动带动摇杆摆动,实现急回特性。
曲柄摇杆机构条件
机械原理之四杆机构受力分析共32页文档

机械原理之四杆机构受 力分析
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 观而不 盲目。 ——马 克思
谢谢你的阅读
❖ 知就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 观而不 盲目。 ——马 克思
谢谢你的阅读
❖ 知就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
机械原理四连杆机构 ppt课件

ppt课件
12
1.急回运动
如图4-4所示为一曲柄摇杆机构, 其曲柄AB在转动一周的过程中,有两 次与连杆BC共线。在这两个位置,铰 链中心A与C之间的距离AC1和AC2分别 为最短和最长,因而摇杆CD的位置C1D 和C2D分别为其两个极限位置。摇杆在
两极限位置间的夹角称为摇杆的摆角。
ppt课件
13
有时死点来实现工作,如图4-6所示
工件夹紧装置,就是利用连杆BC与摇杆
CD形成的死点,这时工件经杆1、杆2传
给杆3的力,通过杆3的传动中心D。此力
则这时连杆加给曲柄的力将通过铰链中
心A,即机构处于压力角=90(传力角 =0)的位置时,驱动力的有效力为0。
此力对A点不产生力矩,因此不能使曲柄 转动。机构的这种位置称为死点。
ppt课件
25
死点会使机构的从动件出现卡死或 运动不确定的现象。可以利用回转机构 的惯性或添加辅助机构来克服。如家用 缝纫机中的脚踏机构,图4-3a。
23
若BCD由锐角变钝角,机构运 动将在BCD(min)和BCD(max)位置两次 出现传动角的极小值。两者中较小的
一个即为该机构的最小传动角min。
ppt课件
24
3.死点
对于图4-4所示的曲柄摇杆机构,如 以摇杆3 为原动件,而曲柄1 为从动件, 则当摇杆摆到极限位置C1D和C2D时,连 杆2与曲柄1共线,若不计各杆的质量,
非传动机构,<40,但不能过小。
ppt课件
21
确 定 最 小 传 动 角 min 。 由 图 4-5 中
∆ABD和∆BCD可分别写出
BD2=l12+l42-2l1l4cos BD2=l22+l32-2l2l3cosBCD
机械原理四连杆机构全解

2.导杆机构 图4-16a)所示为 曲柄滑块机构。
若取曲柄为机架, 则为演变为导杆机构, 如图4-16b)所示。
若AB<BC,则杆2和杆4均可作整周回转, 故称为转动导杆机构。若AB>BC,则杆4 均只能作往复摆动,故称为摆动导杆机构。
图4-17牛头刨床的摆动导杆机构
又如图4-18为牛头刨床回转导杆机 构,当BC杆绕B点作等速转动时,AD 杆绕A点作变速转动DE杆驱动刨刀作变 速往返运动。
图4-19自卸卡车翻斗机构及其运动简图
4.定块机构
图4-16a)所示 曲柄滑块机构。 若取杆 3 为固定件, 即可得图 4-16d )所示 的固定滑块机构或称 定块机构。 这种机构常用于 如图4-20所示抽水唧筒 机构中。
图4-20所示为抽水唧筒机构及其运动简图
5.偏心轮机构
图4-21a所示为偏心轮机构。杆1为 圆盘,其几何中心为B。因运动时该圆 盘绕偏心A转动,故称偏心轮。 A、B之 间的距离e称为偏心距。
l 1+ l 4≤l2+ l3 (4-6)
将以上三式两两相加可得:
l 1≤l 2 l 1≤l 3 l 1≤ l 4
上述关系说明:曲柄存在的必要条件: (1) 在曲柄摇杆机构中,曲柄是最短杆; (2) 最短杆与最长杆长度之和小于或等 于其余两杆长度之和。
如何得到不同类型的铰链四杆机构?
根据以上分析可知: 当各杆长度不变时,取不同杆为 机架就可以得到不同类型的铰链四杆 机构。
当BCD为钝角时,传动角=180BCD ,BCD(max)对应传动角的另一 极小值。
若BCD由锐角变钝角,机构运 动将在BCD(min)和BCD(max)位置两次 出现传动角的极小值。两者中较小的 一个即为该机构的最小传动角min。
连杆机构-4.铰链四杆机构-PPT文档资料
c o s F F t F n Fsin
压力角愈小,机构的传力效果愈好。所以, 衡量机构传力性能,可用压力角作为标志。
Fn
F
Ft vC
在连杆机构中,为度 量方便,常用压力角 的余角即连杆与从动 件间所夹的锐角(传 动角)检验机构的传 力性能。
传动角愈大,机构的传力性能愈好,反之则不利于机构 中力的传递。机构运转过程中,传动角是变化的,机构 出现最小传动角的位置正好是传力效果最差的位置,也 是检验其传力性能的关键位置。
2.按给定的行程速比系数设计四杆机构
设计具有 急回特性 的四杆机 构,关键 是要抓住 机构处于 极限位置 时的几何 关系,必 要时还应 考虑其他 辅助条件。
例:已知摇杆长度L=100,摆角 =50 和行程速比 系数k=1.4,试设计曲柄摇杆机构。 解: 由给定的行程速比系 数求出极位夹角 : C1
9.3平面四杆机构的设计
设计类型 :
1.实现给定的运动规律:给定行程速 比系数以实现预期的急回特性、实现 连杆的几组给定位置等。 2.实现给定的运动轨迹:要求连杆上 某点沿着给定轨迹运动等。
设计目标 :
根据给定的运动条件,选定机构的类 型,确定机构中各构件的尺寸参数。
设计方法 :图解法、实验法和解析法等。
9.2 铰链四杆机构的基本性质
1.急回特性 :
—摇杆的摆角, —极位夹角。
为描述从动摇杆的急 回特性,在此引入行 程速比系数 K,即:
K =
180
180
+
-
பைடு நூலகம்
K值的大小反映了急回运动特性的显著程度。K值的大 小取决于极位夹角 , 角越大,K值越大,急回运动 特性越明显;反之,则愈不明显。当时 0 ,K=1 , 机构无急回特性。
机械原理四连杆机构全解PPT课件
第37页/共87页
§4-2 铰链四杆机构的演化
一、铰链四杆机构的曲柄存在条件 铰链四杆机构中是否存在曲柄,取决于机构各杆的相对长度和机架的选
择。如图4-13所示的机构中,杆1为曲柄,杆2为连杆,杆3 为摇杆,杆4为机架, 各杆长度以l1、l2、l3、l4表示。为了保证曲柄1整周回转,曲柄1必须能顺利通过与 机架4共线的两个位置AB’和AB’’。
第51页/共87页
2.导杆机构 图4-16a)所示为曲柄滑块机构。
若取曲柄为机架,则为演变为导 杆机构,如图4-16b)所示。
若AB<BC,则杆2和杆4均可作整周回转,故称为转动导杆机构。若AB>BC,则杆4 均只能作往复摆动,故称为摆动导杆机构。
第52页/共87页
图4-17牛头刨床的摆动导杆机构
曲柄摇杆机构
双曲柄机构 双摇杆机构
第5页/共87页
一、 曲柄摇杆机构
在铰链四杆机构中,若两个连架杆,一个为曲柄,另一个为摇杆,则 此铰链四杆机构称为曲柄摇杆机构。
图4-2所示为调整雷达天线俯仰角的曲柄摇杆机构。曲柄1缓慢地匀速转 动,通过连杆2使摇杆3在一定的角度范围内摇动,从而调整天线俯仰角的大小。
第19页/共87页
在实际应用中,为度量方便起见,
常用压力角的余角来衡量机构传力性 能的好坏,称为传力角。显然值越大 越好,理想情况是=90。
一般机械中,=40~50。
大功率机构,min=50。
非传动机构,<40,但不能过小。
第20页/共87页
确 定 最 小 传 动 角 min 。 由 图 4-5 中
第25页/共87页
图4-6 利用死点夹紧工件的夹具
第26页/共87页
二、双曲柄机构 两连架杆均为曲柄的铰链四杆机构称为双曲柄机构。
§4-2 铰链四杆机构的演化
一、铰链四杆机构的曲柄存在条件 铰链四杆机构中是否存在曲柄,取决于机构各杆的相对长度和机架的选
择。如图4-13所示的机构中,杆1为曲柄,杆2为连杆,杆3 为摇杆,杆4为机架, 各杆长度以l1、l2、l3、l4表示。为了保证曲柄1整周回转,曲柄1必须能顺利通过与 机架4共线的两个位置AB’和AB’’。
第51页/共87页
2.导杆机构 图4-16a)所示为曲柄滑块机构。
若取曲柄为机架,则为演变为导 杆机构,如图4-16b)所示。
若AB<BC,则杆2和杆4均可作整周回转,故称为转动导杆机构。若AB>BC,则杆4 均只能作往复摆动,故称为摆动导杆机构。
第52页/共87页
图4-17牛头刨床的摆动导杆机构
曲柄摇杆机构
双曲柄机构 双摇杆机构
第5页/共87页
一、 曲柄摇杆机构
在铰链四杆机构中,若两个连架杆,一个为曲柄,另一个为摇杆,则 此铰链四杆机构称为曲柄摇杆机构。
图4-2所示为调整雷达天线俯仰角的曲柄摇杆机构。曲柄1缓慢地匀速转 动,通过连杆2使摇杆3在一定的角度范围内摇动,从而调整天线俯仰角的大小。
第19页/共87页
在实际应用中,为度量方便起见,
常用压力角的余角来衡量机构传力性 能的好坏,称为传力角。显然值越大 越好,理想情况是=90。
一般机械中,=40~50。
大功率机构,min=50。
非传动机构,<40,但不能过小。
第20页/共87页
确 定 最 小 传 动 角 min 。 由 图 4-5 中
第25页/共87页
图4-6 利用死点夹紧工件的夹具
第26页/共87页
二、双曲柄机构 两连架杆均为曲柄的铰链四杆机构称为双曲柄机构。
机械原理四连杆机构分析
图4-6 利用死点夹紧工件的夹具
二、双曲柄机构
两连架杆均为曲柄的铰链四杆机构称 为双曲柄机构。
图4-7 插床双曲柄机构
BD2=l22+l32-2l2l3cosBCD 由此可得
l l l l 2l1l 4 cos cosBCD 2l 2 l3
2 2 2 3 2 1 2 4
当=0和180时,cos=+1和-1, BCD分别最小和最大(见图4-4)。 当BCD为锐角时,传动角=BCD, 是传动角的最小值,也即BCD(min) ;
曲柄摇杆机构 双曲柄机构
双摇杆机构
一、 曲柄摇杆机构
在铰链四杆机构中,若两个连架杆, 一个为曲柄,另一个为摇杆,则此铰链 四杆机构称为曲柄摇杆机构。
图4-2所示为调整雷达天线俯仰角的 曲柄摇杆机构。曲柄1缓慢地匀速转动, 通过连杆2使摇杆3在一定的角度范围内 摇动,从而调整天线俯仰角的大小。
图4-2 雷达天线俯仰角调整机构
第四章 连杆机构
平面连杆机构是将各构件用转动 副或移动副联接而成的平面机构。
最简单的平面连杆机构是由四个 构件组成的,简称平面四杆机构。它 的应用非常广泛,而且是组成多杆机 构的基础。
§4-1 铰链四杆机构的基本形式 和特性
全部用回转副组成的平面四杆机构 称为铰链四杆机构,如图4-1所示。
连杆
机架
连 架 杆
图4-1 铰链四杆机构
图中,机构的固定件4称为机架;与 机架用回转副相联接的杆1和杆3称为连 架杆;不与机架直接联接的杆2称为连杆。 另外,能做整周转动的连架杆,称为曲 柄。仅能在某一角度摆动的连架杆,称 为摇杆。
Байду номын сангаас
对于铰链四杆机构来说,机架和连杆 总是存在的,因此可按照连架杆是曲柄还 是摇杆,将铰链四杆机构分为三种基本型 式:
机械原理课件-3.3平面四杆的工作特性
1、平面四杆机构有曲柄的条件
C
b
B
c d
连架杆AB为曲柄 铰链A和B都为整转副
D
a
A
1、平面四杆机构有曲柄的条件 课堂练习
C
b
B
c d
D
a
A
当a=10、b=17、c=22、d=28时,问此四杆机 构的类型?
1、平面四杆机构有曲柄的条件
•推论1:
• 当Lmax+LminL(其余两杆长度之和)时 –最短杆是连架杆之一 ——曲柄摇杆机构 –最短杆是机架 –最短杆是连杆 •推论2: • 当Lmax+Lmin>L(其余两杆长度之和)时 ——双摇杆机构 ——双曲柄机构 ——双摇杆机构
2 2 2 2
C b B a A d c
cosd =
2bc
分析 =0 cos =1 cos d d min
=180° cos = –1 cos d d max d min 或 d max 可能最小
d
D
曲柄摇杆机构,当曲柄主动时,在曲柄与机架共线的两个位置 之一,传动角最小.
=
V工
=
180º +
t工 = t回
C
C1 C2
=
180º-
1
=
1
180º-
B
b
c
B2
K=
180º+ 180º- (K1) K+1
a
1
B1
d
K-1 = ——— 180º
A 2
D
3、压力角和传动角
压力角 传动角
从动杆(运动输出件)受力点的力作用线与该点速度方位 线所夹锐角. (不考虑摩擦)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S2 G2
3
E D
n FR 63
按F作力多边形 由力多边形得:
h3 FR4 3
n FR 12
h2
t FR 63
FR6 5
F
t
f
F nR12 F
n R63
f
R12
FR4 5
F S5 5
FI5
Fb F if FR 6 1 F hi
F tR63
a
G5
FR63
f
FR32 FI5
√ √
√ √
√
?
√
?
x
B A
1
S2 G2
3
E
4
G
1
x
F S5 5
FI5
D
6
aF
Fr
G5
取 力 比 例 尺 μF ( N / mm ) 作力多边形
t FR 12
h1
2
2 FI2 C h2
B
n FR 12
S2 G2
3
E D
n FR 63
h3 FR4 3
由力多边形得:
h2
t FR 63
FR45 F ea FR65 F de
M1 FR41
FR12 M1
ω23
C
3
B
ω21 ω1 1 A
2
FR32 M3
4
D
B
FR21 L
ω1 1
A
由力平衡条件得: FR41= - FR21
且有:M1 = FR21LFR21= M1/L
3).取构件2为分离体——其上作用有: FR12、 FR32
FR32= - FR12= FR21
3).取构件3为分离体——其上作用有:FR23、 FR43、 M3
4) 各构件的力平衡方程式
•对于构件1分别根据
可得
•对于构件2有
•对于构件3有
以上共列出九个方程式,故可解出上述各运动副反力和平衡力的九个力 的未知要素。又因为以上九式为一线性方程组,因此可按构件1、2、3上待 定的未知力Mb, R41x, R41y, R12x, R12y, R23x, R23y, R34x, R34y的次序整理成以下的 矩阵形式:
——求解保证原动件按预定运动规律运动时所需要的驱动力(矩) 已知驱动力(矩) 平衡力(矩)
——求解机构所能克服的生产阻力
一. 构件组的静定条件
——该构件组所能列出的独立的力平衡方程式的数目, 应等于构件组中所有力的未知要素的数目。 独立的力平衡方程式的数目 =所有力的未知要素的数目。 1. 运动副中反力的未知要素 1)转动副 ——(2个)
方向 :√ 大小 : ? √ √ √ √ √ √ √ √ √ √ √
F tR63
Fr
G5 f
F nR12 F nR63
f
F tR12
?
a
G5 FR45 Fr
FR63
FR43
f
FR32 FI5
FR12 FI2
g
G2
h
按F作力多边形
由力多边形得:
e
b
FR65
c
FR12 F hf
FR63 F fa
FR6 5 FR4 5
F S5 5
FI5
a
FR45 G5
Fr
e
FI5
G5
b
Fr
c
d
FR65
再分析杆组2、3 构件2:ΣMC = 0 t l G h F h 0 FR 12 2 2 2 I2 1
t FR 12
t FR 12
h1
2
2 FI2 C h2
B
n FR 12
S2 G2
而Rji=-Rij, 所以各运动副中的反力统一写成Rij的形式(即反力Rji用-Rij表示之)。
3) 力矩的统一表达式:作用于构件上任一点 I
上的力PI对该构件上另一点K之矩(规定逆时 针方向时为正,顺时针方向时为负 ) ,可表
示为下列统一的形式
式中
xI, yI——力作用点I的坐标, xK, yK—— 取矩点 K 的坐标。
R32
R23
R43
R34
滑块4 在Q、R34及R14三个力的作用下平衡
B
1
S2
G2
3
E
4
F S5 5 Fr G5
G
x 6
D
速度图
加速度图
构件2:
FI 2 m2aS2 (G2 / g )a ps2 t / l J n c / l M J J a I 2 S 2 S CB 2 S2 a 2 2 2 2
(FI2与aS2反向,MI2与2反向) 构件5:
于是得
同理,取构件2为分离体,并取诸力对B点取矩,则
因此可得
(3) 求RD 根据构件3上的诸力平衡条件
(4)求RB
根据构件2上的诸力平衡条件
(5)求RA
同理,根据构件1的平衡条件 得
至此,机构的受力分析进行完毕。
2 矩阵法
如图为一四杆机构,图中 1 、 2 、 3 分别为作用于质心 S1 、 S2 、 S3 处的已知 外力(含惯性力), M1 、 M2 、 M3 为作 用于各构件上的已知外力偶矩(含惯性 力偶矩),另外,在从动件上还受着一 个已知的生产阻力矩Mr。现需确定各运 动副中的反力及需加于原动件 1 上的平 衡力偶矩Mb。 如图所示先建立一直角坐标系, 以便将各力都分解为沿两坐标轴 的两个分力,然后再分别就构件 1 、 2 及 3 列出它们的力的平衡方程式。 又为便于列矩阵方程,
上式可以简化为
[C ]{ R }=[D ]{P }
式中 {P }——已知力的列阵;
{R }——未知力的列阵;
[D ]——已知力的系数矩阵; [C ]——未知力的系数矩列阵。
对于各种具体机构,都不难按上述的步骤进行分析,即按顺序对
机构的每一活动构件写出其力平衡方程式,然后整理成为一个线性方 程,并写成矩阵方程式。利用上述形式的矩阵方程式,可以同时求出 各运动副中的反力和所需的平衡力,而不必按静定杆组逐一进行推算, 而且根据这种矩阵方程式便于利用标准程序且计算机解算。
加于主动件1上的平衡力矩Mb。
(1) 首先建立一直角坐标系,并将各
构件的杆矢量及方位角示出,如图
所示。然后再设各运动副中的反力 为
(2)首解运动副:机构中首解副的条件是:组成该运动副的两个构件上的作用
外力和力矩均为已知者。在本实例中,运动副C为应为首解副。
(3)求RC
取构件3为分离体,并取该构件上的诸力对 D点取矩(规定力矩的方向逆时针 者为正,顺时针者为负) ,则
FR32 F fe
最后取构件1为分离体
x
2
FI2 C h2 2
B A
1
S2 G2
3
E
4
F1 0 FR 21 Fb FR61 0
G
1
x
F S5 5
FI5
D
6
aF
Fr
G5
方向 :√ 大小 : √
√ ?
√ ?
t FR 12
h1
2
2 FI2 C h2
B
1) 可解性分析:在四杆机构中,共有四个低副,每个低副中的反力都有两个
未知要素 (即反力的大小及方向 ),此外,平衡力尚有一个力的未知要素, 所以在此机构中共有九个未知要素待定;而另一方面,在此机构中,对三
个活动构件共可列出九个平衡方程,故此机构中所有的力的未知要素都是
可解的。 2) 反力的统一表示:用运动副中反力 Rij ,表示构件 i作用于构件 j上的反力,
O
大小——?
FR
方向——? 作用点——转动副中心
FR
2)移动副
——(2个) 大小——?
K
Hale Waihona Puke FR方向——垂直移动导路 作用点——? ——(1个)
FR
FR
n
C
3)平面高副
大小——?
n
FR
方向——公法线
作用点——接触点
2. 构件组的静定条件 设某构件组共有n个构件、pl个低副、 ph个高副 一个构件可以列出3个独立的力平衡方程,n个构件共有3n 个力平衡方程 一个平面低副引入2个力的未知数, pl个低副共引入2pl个力 的未知数 一个平面高副引入1个力的未知数, ph个低副共引入 ph个力 的未知数
解 : 1)根据已知条件作
出各转动副处的摩擦
R23
圆(如图中虚线小圆
所示)。
R43
2)取二力杆连杆3为研究对象 构件3在B、C两运动副处分别受到R23及R43的作用
R23和R43分别切于该两处的摩擦圆外,且R23=-R43。
3)根据R23及R43的方向,定出R32 及R34的方向。 4)取滑块4为分离体
此时可取滑块5为分离体,列方程
n FR 63
G5 Fr FI 5 FR45 FR65 0
√ √ √ √ √ ? √ ?
方向:√ 大小:√
G5 Fr FI 5 FR45 FR65 0
2
FI2 C h2 2
方向:√
大小:√
§3-5 考虑摩擦时机构的力分析
考虑摩擦时,机构受力分析的步骤为: 1 )计算出摩擦角和摩擦圆半径,并画出摩擦圆;
2)从二力杆着手分析,根据杆件受拉或受压及该杆相对于另一
杆件的转动方向,求得作用在该构件上的二力方向; 3)对有已知力作用的构件作力分析; 4)对要求的力所在构件作力分析。 掌握了对运动副中的摩擦分析的方法后,就不难在考虑有
