光学第2章习题及答案
《应用光学》第2章课后答案全文

12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距 为f1′,第二组透镜的焦距为f2′,物平面位于第一组透镜 的物方焦面上,求该倒像系统的垂轴放大率。
解:
1
1
1
1
F2
1
1
第一组透镜
第二组透镜
1
第二组透镜
13. 由两个同心的反射球面(二球面球心重合)构成的光学系 统,按照光线反射的顺序第一个反射球面是凹的,第二个 反射球面是凸的,要求系统的像方焦点恰好位于第一个反 射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d之间的关系。
B′
面,如图示.
l ′ = 2f′
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l = −f′
B
……
F
F′
A
H H′
像平面在像 空间无限远 处.
l′=∞
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l f' 2
B′
r1 无穷远物点
r2
r1/2
最终像点
11 2
l2 l2 r2
l2
l2
2 r2
(l2l2 )
14. 假定显微镜物镜由相隔20mm的两个薄透镜组构成,物平 面和像平面之间的距离为180mm,放大率β=-10×,要求近 轴光线通过二透镜组时的偏角Δu1和Δu2相等,求二透镜 组的焦距。
y n1u1 u1 10
l = −f′
B
……
F′
F
H H′
A
像平面在像 空间无限远 处.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
应用光学习题(第二章)

个面对不晕像点。
n2 n2 n 1 l2 r2 r2 n2 n n2 n2 l2 r2 n 1r2 n2
1 n n 1 n 1 r1 - r2 r1 r2 n n n 由于 d始终都是大于零的,所 以r1 r2 (由于 r1 0,r2 0,且 r1 r2,该透镜为负弯月型透 镜)
1 n2
S1
S1与S2重合,所以 r2 l2 l2
d l1 l2
n
r1
C1 l2 l2 l1 r2 l1
C2
n1 n1 1 n 而 l1 r1 r1 n1 n 1 n d r1 r2 n
b. 同心球面透镜 物像点重合且位于两个 球面的共同曲率中心 C1,C 2点上Leabharlann 所以编号出处
2_004
P193_7
什么是不晕透镜?当透 镜成无球差点实像点时 ,应采用 什么样的结构形式 ?
答: ( 1)所谓不晕透镜,是轴 上物点单色光成像时, 不产生球差的透镜
(2) 由于不晕条件,物象点 在透镜的同一侧,所以 不晕透镜 分为两种情况:一种是 实物成虚像,而另一种 是虚物成实像。 该题中得到实像点时, 采用的就是虚物成实像 的形式(会聚光入射) r1 0,r2 0 a. 正弯月单透镜 r1 r2 r1 r2,所以第一个面对球心 C 1点在 C2点的左边
,S2,S 同心球面透镜构成不晕 透镜C ( ,S1,S1 2 C1 2)
n1 1
1 n2
C1 C2
n
r1 l1 l1 r2 l2 l2
,S2与S2重合 S1,S1 d r1 r2
编号
出处
2_005
光学第二章习题解答

∆y = y2 − y1 ≈ 2 f ′
λ
b
− f′
λ
b
= f′
λ
b
∆y ⋅ b 0.02 × 0.885 ɺ λ= = = 5900 A f′ 300
(2)波长为 波长为0.1nm的x射线时,相邻最小值间的距离为 射线时, 波长为 的 射线时
′λ 300 × 0.1×10−9 f ∆y = = 0.02 b −6 −4 = 1.5 × 10 m = 1.5 × 10 cm
主焦点
还有次焦点: 还有次焦点:± f ′ /3,
± f ′ /5, ± f ′ / 7⋯
故:光强极大值出现在轴上 1/3m,1/5m,1/7m……1/(2k+1)m等处 , , 等处
2.6 波长为 的点光源波带片成一个像点,该波带 波长为λ的点光源波带片成一个像点 的点光源波带片成一个像点, 个透明奇数半波带(1, , )。另外 有100个透明奇数半波带 ,3,5 ……199)。另外 个透明奇数半波带 )。 100个不透明偶数半波带。比较用波带片换上同样焦 个不透明偶数半波带。 个不透明偶数半波带 距和口径的透镜时像点的强度比I: 距和口径的透镜时像点的强度比 :I0 解:(1) 只有 ) 只有100个透明奇数半波带透过 个透明奇数半波带透过
∵
θ3 < θ 2
∴
二级和三级光谱部分重叠 二级和三级光谱部分重叠
2.14 用波长为 用波长为589nm的单色光照射一衍射光栅, 的单色光照射一衍射光栅 的单色光照射一衍射光栅, 其光谱的中央最大值和第二十级主最大值之间的衍 射角为15 10′。试求该光栅1cm内的缝数是多少? 15° cm内的缝数是多少 射角为15°10′。试求该光栅 cm内的缝数是多少? 解: 由光栅方程 d sin θ = jλ
物理光学第二章答案

第二章光的干涉作业1、在杨氏干涉实验中,两个小孔的距离为1mm,观察屏离小孔的垂直距离为1m,若所用光源发出波长为550nm和600nm的两种光波,试求:(1)两光波分别形成的条纹间距;(2)两组条纹的第8个亮条纹之间的距离。
2、在杨氏实验中,两小孔距离为1mm,观察屏离小孔的距离为100cm,当用一片折射率为1.61的透明玻璃贴住其中一小孔时,发现屏上的条纹系移动了0.5cm,试决定该薄片的厚度。
3、在菲涅耳双棱镜干涉实验中,若双棱镜材料的折射率为1.52,采用垂直的激光束(632.8nm)垂直照射双棱镜,问选用顶角多大的双棱镜可得到间距为0.05mm 的条纹。
4、在洛埃镜干涉实验中,光源S1到观察屏的垂直距离为1.5m,光源到洛埃镜的垂直距离为2mm。
洛埃镜长为40cm,置于光源和屏的中央。
(1)确定屏上看见条纹的区域大小;(2)若波长为500nm,条纹间距是多少?在屏上可以看见几条条纹?5、在杨氏干涉实验中,准单色光的波长宽度为0.05nm,平均波长为500nm,问在小孔S1处贴上多厚的玻璃片可使P ’点附近的条纹消失?设玻璃的折射率为1.5。
6、在菲涅耳双面镜的夹角为1’,双面镜交线到光源和屏的距离分别为10cm 和1m 。
设光源发出的光波波长为550nm ,试决定光源的临界宽度和许可宽度。
7、太阳对地球表面的张角约为0.0093rad ,太阳光的平均波长为550nm ,试计算地球表面的相干面积。
8、在平行平板干涉装置中,平板置于空气中,其折射率为1.5,观察望远镜的轴与平板垂直。
试计算从反射光方向和透射光方向观察到的条纹的可见度。
9、在平行平板干涉装置中,若照明光波的波长为600nm ,平板的厚度为 2mm ,折射率为1.5,其下表面涂上高折射率(1.5)材料。
试问:(1)在反射光方向观察到的干涉圆环条纹的中心是亮斑还是暗斑?(2)由中心向外计算,第10个亮环的半径是多少?(f=P P ’20cm)(3)第10个亮环处的条纹间距是多少?10、检验平行平板厚度均匀性的装置中,D是用来限制平板受照面积的光阑。
工程光学习题参考答案第二章理想光学系统
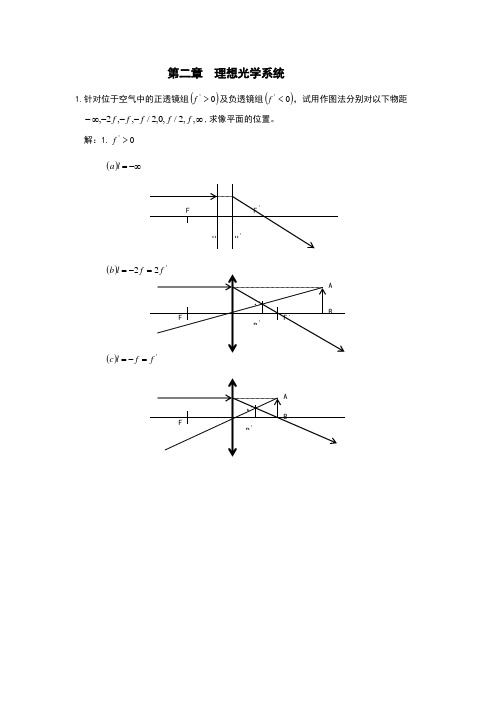
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′= (3)x ′= (4)x ′= (5)x ′=(6)x ′=3.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
光学第二章习题

第二章习题一、选择题:2008.在菲涅耳圆屏衍射的几何阴影中心处( B )(A)永远是个亮点,其强度只与入射光强有关。
(B)永远是个亮点,其强度随着圆屏的大小而变。
(C)有时是亮点,有时是暗点。
2014.一波长为500nm的单色平行光,垂直射到0.02cm宽的狭缝上,在夫琅禾费衍射花样中心两旁第二条暗纹之间的距离为3mm,则所用透镜的焦距为( D )(A)60mm (B)60cm (C)30mm (D)30cm2026.一个衍射光栅宽为3cm,以波长为600nm的光照射,第二级主极大出现于衍射角为300处。
则光栅的总刻度线数为A(A)1.25*104 (B)2.5*104 (C)6.25*103 (D)9.48*1032028.X 射线投射在间距为d的平行点阵面的晶体中,试问发生布拉格晶体衍射的最大波长为多少?D(A)d/4 (B)d/2 (C)d (D)2d2128. 菲涅尔圆孔衍射实验表明,几何光学是波动光学在一定条件下的近似,如果从圆孔露出来的波面对所考察的点作出的的半波带的数目为K,这种条件下可表达成:( D )(A)衍射波级数K~0;(B)衍射波级数K=1;(C)衍射波级数K〉1;(D)衍射波级数K〉〉1。
2129. 用半波带法研究菲涅尔圆孔的衍射的结果说明,圆孔轴线上的P点的明暗决定于:(C )(A)圆孔的大小;(B)圆孔到P点的距离;(C)半波带数目的奇偶;(D)圆孔半径与波长的比值。
2130 用半波带法研究菲涅尔圆孔衍射时,圆孔线上P点的明暗决定于:(D )(A)圆孔的直径;(B)光源到圆孔的距离;(C)圆孔到P的距离;(D)圆孔中心和边缘光线到P点的光程差。
2131 一波带片主焦点的光强约为入射光强的400倍,则波带片的开带数为:( A )(A)10;(B)20;(C)40;(D)100。
2132 在夫琅和费单缝衍射中,当入射光的波长变大时,中央零级条纹:(B )(A)宽度变小;(B)宽度变大;(C)宽度不变;(D)颜色变红。
光学作业答案
I = 0.37% ,此时接近消反射。 I0
2π λ0 λ0 = π , λ0 = 500nm λ 2 λ
(2)反射两光束相位差
δ=
2π
λ
2n 2 h =
将 λ = 400nm 和 λ = 700 nm 分别代入上式,得到相位差分别是 1.375πrad 和 0.7857πrad 20.砷化镓发光管制成半球形,以增加位于球心的发光区对外输出功率,减少反射损耗,已 知砷化镓发射光波长 930nm,折射率为 3.4,为了进一步提高光输出功率,常在球形表面涂 一层增透膜。 (1)不加增透膜时,球面的强度反射率多大? (2)增透膜折射率和厚度应取多大? (3)如果用氟化镁(1.38)作为增透膜,能否增透?强度反射率多大? (4)如果用硫化锌(2.35) ,情况又如何? 解:
此光学系统成像在 L1 之右 10cm 处。
, s1, s2 10 10 = − = −1 , V2 = − = − = 2, 横向放大率分别为 V1 = − −5 s1 10 s2
总放大率 V = V1 • V2 = −2 27.用作图法求本题各图中的 Q 像。 (a)
(b)
(c)
(d)
35.(1)用作图法求图中光线 1 共轭线 (2)在图上标出光具组节点 N,N’位置
与屏幕交点(零级)随之移动,即以 M 为中心转了角 β ≈ δs / B ,反映在屏幕上零级位移
C δs ,即幕上条纹总体发生一个平移。 B (5)设扩展光源 b,即其边缘两点间隔 δs = b ,若这两套条纹错开的距离(零级平移量) δx = Δx ,则幕上衬比度降为零,据此有, B+C C δx = b , Δx = λ 2aB B 令 δx = Δx ,
36.已知 1-1’是一对共轭光线,求光线 2 的共轭线。
物理光学与应用光学习题解第二章
第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
光学教程第二版习题答案(一至七章)
∴ d1
=
h1 − h2 tan u1′
= 1.5 −1 0.015
= 33.33mm
tan u2 ′ = tan u2
+
h2 f 2′
= 0.015 +
1 = 0.011
− 250
∴d2
=
h2 − h3 tan u2 ′
1 − 0.9 =
0.011
= 9.091mm
2-13 一球形透镜,直径为 40mm,折射率为 1.5,求其焦距和主点位置。
= −200mm
lH
= dϕ2 ϕ
= 50 × 5 = −100mm − 2.5
2-11
有三个透镜,
f1′
= 100mm,
f2′
= 50mm,
f
′
3
=
−50mm,其间隔 d1
= 10mm,
d 2 = 10mm ,设该系统处于空气中,求组合系统的像方焦距。
解:设 h1 = 100mm, u1 = 0 ,则:
tan u3′
= tan u3 +
h3 f3′
= 2.8 +
62 − 50
= 1.56
∴组合系统的像方焦距为:
f
′=
h1 tan u3′
100 =
1.56
= 64.1mm
2-12
一个三 片型望远镜 系统,已知
f
′
1
= 100mm,
f
′
2
=
−250mm ,
f
′
3
= 800mm,入
射平行光在三个透镜上的高度分别为: h1 = 1.5mm, h2 = 1mm , h3 = 0.9mm ,试求合成
工程光学基础 习题参考答案-第二章_02
3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
f 2 ' = −240mm
8、一短焦距物镜 一短焦距物镜, 焦距物镜,已知其焦距为 35mm,筒长 L=65mm,工作距离 l k ' = 50mm ,按 最简单结构的薄透镜系统考虑, 最简单结构的薄透镜系统考虑,求系统结构。 求系统结构。 解: (仿照 (仿照 P32 P32 例 2) 利用正切计算法,设 h1 = 100mm ,有公式:
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得:
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题答案2—1 铯的逸出功为,试求: (1)铯的光电效应阈频率及阈值波长; (2)如果要得到能量为的光电子,必须使用多少波长的光照射 解:光电效应方程212m mv h =ν-Φ (1) 由题意知 0m v = 即 0h ν-Φ=14151.9 4.59104.13610ev Hz h ev s -Φν===⨯⨯⋅ 1.24652.61.9c hc nm Kev nm evλ⋅====νΦ(2) ∵ 21 1.52m mv ev =∴ 1.5cev h h λ=ν-Φ=-Φ 1.24364.71.5 1.5 1.9hc nm Kevnm ev ev evλ⋅===+Φ+2-2 对于氢原子、一次电离的氢离子He +和两次电离的锂离子Li ++,分别计算它们的:(1)第一、第二玻尔轨道半径及电子在这些轨道上的速度;(2)电子在基态的结合能; (3)由基态带第一激发态所需的激发能量及由第一激发态退激到基态所放光子的波长。
解:(1)由波尔理论及电子的轨道半径公式r 1为氢原子第一波尔半径22201122204()(197.3)0.0530.511e e c r a nm nm m e m c e 6πε====≈/4πε⨯10⨯1.44h h 氢原子第二波尔半径可知:He +(Z=2)Li + + (Z=3)电子在波尔轨道上的速率为 21n n r r z=221140.212r n r r nm===112210.0265220.1062ar nmr a nm====112210.0176320.07053ar nmr a nm====nzv cn=α于是有 H :61161212.19101371.1102v c m s m s cv m s 8--=α=⨯3⨯10/=⨯⋅α==⨯⋅He +:6116122 4.3810102v c m s cv m s --=α=⨯⋅2α==2.19⨯⋅ Li+ +:6116123 6.5710102v c m s c v m s--=α=⨯⋅3α==3.28⨯⋅ (2) 电子在基态的结合能E k 在数值上等于原子的基态能量 由波尔理论的能量公式 可得故有 H : 13.6k E ev =He +: 213.6254.4k E ev =⨯=Li ++: 213.63122.4k E ev =⨯=(3)以电压加速电子,使之于原子碰撞,把原子从基态激发到较高能态,用来加速电子的电势差称为激发电势,从基态激发到第一激发态得相应的电势差称为第一激发电势。
212122113.6(1)2E V z e ∆==- 对 H : 12113.6(1)10.24V v =⨯-=He + : 212113.62(1)40.84V v =⨯⨯-=Li ++ : 212113.63(1)91.84V v =⨯⨯-=共振线(即赖曼系第一条)的波长: 121212E E hcE hc -=∆=λ H : 12 1.24121.610.2nm kevnm ev λ⋅==He +: 12 1.2430.440.8nm kev nm ev λ⋅==Li ++: 12 1.2413.591.8nm kev nm evλ⋅==21()2n e z E m c n=-α221()13.62k e E m cz z ev 1=∣E∣=α=2—3 欲使电子与处于基态的锂离子Li ++发生非弹性散射,试问电子至少具有多大的动能解:Li + +基态能量为 211()122.42e E m cz ev α=-=- 从基态到第一激发态所需能量为ev Z E 8.91434.122)211(6.132212=⨯=-⨯⨯=∆,故电子必须具有的动能.2—4 运动质子与一个处于静止的基态氢原子作完全非弹性的对心碰撞,欲使锂原子发射出光子,质子至少应多大的速度运动解: 方法一:欲使基态氢原子发射光子,至少应使氢原子以基态激发到第一激发态122110.2E E E ev ∆=-=V根据第一章的推导,入射粒子m 与靶M 组成系统的实验室系能量E L 与E C 之间的关系为:c L ME E M m=+∴所求质子的动能为:212121(1)220.42k c M m mE mv E E E evM M+===+∆=∆=V 所求质子的速度为: )(1026.610673.1106.14.2022142719---⋅⨯=⨯⨯⨯⨯==s m m E v k 方法二: 质子与基态氢原子碰撞过程动量守恒,则()v m m v m H P P +=10 ⇒ 10v m m m v HP P+=1021022102121)(2121E m m m v m v m m v m E H P H P H P P =+⋅=+-=∆ eV E E E v m E P 4.20)(22211221010=-=∆==)/(1026.62421010s m c cm E v P ⨯=⋅=MeV c m P 9382=其中 (1)原子在热平衡条件下处于不同能量状态的数目是按波尔兹曼分布的,即处于能量为E n 的激发态的原子数为:1()11n E E kTn n g N N e g --/=式中N 1是能量为E 1状态的原子数,k 为玻尔兹曼常量,g n 和g 1为相应能量状态的统计权重。
试问:原子态的氢在一个大气压、20℃温度的条件下,容器必须多大才能有一个原子处在第 一激发态已知氢原子处于基态和第一激发态的统计权重分别为g 1=2和g 2=8。
(2)电子与室温下的氢原子气体相碰撞,要观察到H α线,试问电子的最小动能为多大2—6 在波长从95nm 到125nm 的光带范围内,氢原子的吸收光谱中包含哪些谱线 解:对于min 95nm λ=,有22min1111()1R n λ=-1 4.8n ===∵ min 95nm λ=的波长的光子不足以将氢原子激发到n=5的激发态,则在min 95nm λ=以内有一光子可将氢原子激发到n=4的激发态 ∴ n 1=4同理有:2 1.9n === ∵ 对应于n=1的辐射光子的波长应比125nm 更长,在波段以外 ∴ n 2=2又∵ 氢原子的吸收谱对应于赖曼系 ∴ 在(95∽125nm )波段内只能观察到3条 即(1,2)(1,3)(1,4)m n m n m n ν==ν==ν==%%%1232—7 试问哪种类氢离子的巴耳末系和赖曼系主线的波长差等于解:赖曼系主线:22213(1)24RZ RZ ν=-=%赖巴耳末主线:2222115()2336RZ RZ ν=-=%巴 二主线波长差:nm RZ RZ RZ RZ 7.1331588)20108(151345362222==-⨯=-=-=∆赖巴λλλ 278888415133.715109737.3110133.7Z R nm -===⨯⨯⨯⨯⨯ 2Z ∴=即He 原子的离子。
2—8 一次电离的氢原子He +从第一激发态向基态跃迁时所辐射的光子,能量处于基态的氢原子电离,从而放出电子,试求该电子的速度。
解:He +从E 2→E 1跃迁辐射的光子的能量为22121(1)32h E E RcZ Rhc ν=-=--= 氢原子的电离能为 10()E E E Rhc Rhc ∞=-=--= ∴ 电离的电子的能量为 32k E Rhc Rhc Rhc =-=该电子的速度为63.0910v m s ====⨯/ 2—9 电子偶素是由一个正电子和一个电子所组成的一种束缚系统,试求出:(1)基态时两电子之间的距离;(2)基态电子的电离能和由基态到第一激发态的激发能;(3)由第一激发态退激到基态所放光子的波长。
解:电子偶素可看作类氢体系,波尔理论同样适用,但有关公式中的电子质量必须采用体系的折合质量代替,对电子偶素,其折合质量为:2e e e m M mm M μ==+(1)22001122442220.0530.106e r a nm nm e m eπεπε====⨯=μh h (2)电离能为 1i A E E E R hc ∞=-=式中 1121A e R R R mM∞∞==+ 于是 7611 1.097373110 1.2410 6.8022i E R hc ev ev -∞==⨯⨯⨯⨯=则电离电势为 6.80i i EV v e==第一激发电势为 222121211()312 5.102A R hcZ E R hc V v e e e∞-∆∆==== (3)共振线波长为31212 1.2410243.15.10hc nm evnm E evλ⨯⋅===∆2—10 μ-子是一种基本粒子,除静止质量为电子质量为电子质量的207倍外,其余性质与电子都一样。
当它运动速度较慢时,被质子俘获形成μ子原子,试计算:(1)μ子原子的第一波尔轨道半径;(2)μ子原子的最低能量;(3)μ子原子赖曼线系中的最短波长。
解:(1)μ子原子可看作类氢体系,应用波尔理论,其轨道半径为22024n n r e Z πε=μh 式中 2072071836186.020********e e e e m M m m m M ⨯μ===++ 其第一波尔半径为24011240.053 2.8510186.0186.0186.0e a nm r nm m e πε-====⨯h (2)μ子原子的能量公式为 2211()186.0()22n e z z E c m c nnαα=-μ=-⨯ 最低能量 1n =,2311186.0()186.013.6 2.53102e E m c ev ev α=-⨯=-⨯=-⨯(3)由波长公式 hcEλ=∆3min3max 1 1.24100.490( 2.5310)hc hc nm ev nm E E E ev λ∞⨯⋅====∆---⨯ 2—11 已知氢和重氢的里德伯常量之比为 728,而它们的核质量之比为m H /m D = 20,试计算质子质量与电子质量之比。
解:由 1A e AR R m M ∞=+,可知 10.9997281eH D e D H m R M m R M +==+ 又∵ 0.50020HD M M =,∴0.5002010.9997281eHe Hm M m M +=+则30.4995281836.5 1.8100.000272H e M m ==≈⨯ 2—12 当静止的氢原子从第一激发态向基态跃迁放出一个光子时,(1)试求这个氢原子所获得的反冲速率为多大(2)试估计氢原子的反冲能量与所发光子的能量之比。
解:(1)所发光子的能量ev ev Rhc E E h 2.106.1343)2111(2212=⨯=-=-=ν光子的动量 cevc h h P 2.10===νλ 氢原子的反冲动量等于光子动量的大小,即ch P M v Hν==反 s m s mc m h H v 26.31031067.110602.12.1082719=⨯⨯⨯⨯⨯==--ν反(3) 氢原子的反冲能量为J J v m E H k 2722721087.8)26.3(1067.12121--⨯=⨯⨯⨯==反 91927104.510602.12.101087.8---⨯=⨯⨯⨯=νh E k2—13 钠原子的基态为3s ,试问钠原子从4P 激发态向低能级跃迁时,可产生几条谱线(不考虑精细结构)解:不考虑能级的精细结构,钠原子的能级图如下:根据辐射的选择定则1±=∆l ,可知,当钠原子从4P 态向低能级跃迁时可产生6条光谱。
