《新编基础物理学》第15章习题解答和分析
《新编大学物理》(上、下全册)桑建平教材习题答案解析武汉大学出版社

第1章 质点运动学一、选择题 题1.1 : 答案:[B]提示:明确∆r 与r ∆的区别题1.2: 答案:[A]题1.3: 答案:[D]提示:A 与规定的正方向相反的加速运动, B 切向加速度, C 明确标、矢量的关系,加速度是d dtv题1.4: 答案:[C] 提示: 21r r r ∆=-,12,R R r j ri ==-,21v v v ∆=-,12,v v v i v j =-=-题1.5: 答案:[D]提示:t=0时,x=5; t=3时,x=2得位移为-3m ;仅从式x=t 2-4t+5=(t-2)2+1,抛物线的对称轴为2,质点有往返题1.6: 答案:[D]提示:a=2t=d dt v,2224t v tdt t ==-⎰,02tx x vdt -=⎰,即可得D 项题1.7:答案:[D]北v 风v 车1v 车2提示: 21=2v v 车车,理清=+v v v 绝相对牵的关系二、填空题 题1.8:答案: 匀速(直线),匀速率题1.9:答案:2915t t -,0.6 提示: 2915dxv t t dt==-,t=0.6时,v=0题1.10:答案:(1)21192y x =-(2)24t -i j 4-j(3)411+i j 26-i j 3S提示: (1) 联立22192x t y t=⎧⎨=-⎩,消去t 得:21192y x =-,dx dydt dt =+v i j (2) t=1s 时,24t =-v i j ,4d dt==-va j (3) t=2s 时,代入22(192)x y t t =+=+-r i j i j 中得411+i j t=1s 到t=2s ,同样代入()t =r r 可求得26r∆=-i j ,r 和v 垂直,即0∙=r v ,得t=3s题1.11: 答案:212/m s 提示:2(2)2412(/)dv d x a v x m s dt dt=====题1.12: 答案:1/m sπ提示: 200t dvv v dt t dt =+=⎰,11/t vm s ==,201332tv dt t R θπ===⎰,r π∆==题1.13:答案:2015()2t v t gt -+-i j 提示: 先对20(/2)v t g t =-r j 求导得,0()y v gt =-v j 与5=v i 合成得05()v gt =-+-v i j 合 201=5()2t v t gt -+-∴⎰r v i j t合0合dt=题1.14: 答案:8, 264t提示:8dQ v R Rt dt τ==,88a R τ==,2264n dQ a R t dt ⎛⎫== ⎪⎝⎭三、计算题 题1.15:解:(1)3t dv a t dt == 003v tdv tdt =∴⎰⎰ 232v t ∴= 又232ds v t dt == 20032stds t dt =∴⎰⎰ 312S t =∴ (2)又S R θ= 316S tRθ==∴(3)当a 与半径成45角时,n a a τ=2434n v a t R == 4334t t =∴t =∴题1.16:解:(1)dv a kv dt ==- 0v tdv kdt v =-∴⎰⎰, 0ln v kt v =-(*) 当012v v =时,1ln 2kt =-,ln 2t k=∴ (2)由(*)式:0ktv v e-=0kt dxv e dt -=∴,000xtkt dx v e dt -=⎰⎰ 0(1)kt v x e k-=-∴第2章 质点动力学一、选择题 题2.1: 答案:[C]提示:A .错误,如:圆周运动B .错误,m =p v ,力与速度方向不一定相同 D .后半句错误,如:匀速圆周运动题2.2: 答案:[B]提示:y 方向上做匀速运动:2y y S v t t == x 方向上做匀加速运动(初速度为0),Fa m=22tx v a d t t ==⎰,223tx x t S v dt ==⎰ 2223t t =+∴S i j题2.3: 答案:[B]提示:受力如图MgF杆'F 猫mg设猫给杆子的力为F ,由于相对于地面猫的高度不变'F mg = 'F F = 杆受力 1()F Mg F M m g =+=+ 1()F M m g a M M+==题2.4 :答案:[D] 提示:a a A22A BA B m g T m a T m a aa ⎧⎪-=⎪=⎨⎪⎪=⎩ 得45A a g = (2A B a a =,通过分析滑轮,由于A 向下走过S ,B 走过2S) 2A B a a =∴题2.5: 答案:[C]提示: 由题意,水平方向上动量守恒, 故 0(cos 60)()1010m mv m v =+ 共 0=22v v 共题2.6: 答案:[C] 提示:RθθRh-R由图可知cos h RRθ-=分析条件得,只有在h 高度时,向心力与重力分量相等所以有22cos ()mv mg v g h R Rθ=⇒=- 由机械能守恒得(以地面为零势能面)22001122mv mv mgh v =+⇒=题2.7: 答案:[B]提示: 运用动量守恒与能量转化题2.8: 答案:[D] 提示:v v y由机械能守恒得2012mgh mv v =⇒=0sin y v v θ=sin Gy Pmgv mg ==∴题2.9: 答案: [C]题2.10: 答案: [B]提示: 受力如图fT F由功能关系可知,设位移为x (以原长时为原点)2()xF mg Fx mgx kxdx x kμμ--=⇒=⎰弹性势能 2212()2p F mg E kx kμ-==二、填空题题2.11: 答案:2mb提示: '2v x bt == '2a v b == 2F m a m b==∴题2.12:答案:2kg 4m/s 2 提示:4N 8Nxy 0由题意,22/x a m s = 4x F N =8y F N = 2Fm k g a== 24/y y F a m s m==题2.13: 答案:75,1110提示: 由题意,32()105F a t m ==+ 27/5v adt m s ⇒==⎰ 当t=2时,1110a =题2.14: 答案:180kg提示:由动量守恒,=m S -S m 人人人船相对S ()=180kg m ⇒船题2.15: 答案:11544+i j 提示:各方向动量守恒题2.16:答案: ()mv +i j ,0,-mgR提示:由冲量定义得 ==()()mv mv mv --=+I P P i j i j 末初- 由动能定律得 0k k E W E ∆=⇒∆=,所以=0W 合 =W m g R -外题2.17: 答案:-12提示:3112w Fdx J -==⎰题2.18:答案: mgh ,212kx ,Mm G r - h=0,x=0,r =∞ 相对值题2.19: 答案: 02mgk ,2mg,题2.20: 答案: +=0A∑∑外力非保守力三、计算题 题2.21:解:(1)=m F xg L 重 ()mf L xg L μ=- (2)1()(1)ga F f x g m Lμμ=-=+-重(3)dv a v dx =,03(1)v LL g vdv x g dx Lμμ⎡⎤=+-⎢⎥⎣⎦⎰⎰,v =题2.22: 解:(1)以摆车为系统,水平方向不受力,动量守恒。
大学物理15章答案

第15章 磁介质的磁化15.1 一均匀磁化的磁介质棒,直径为25mm ,长为75mm ,其总磁矩为12000A·m 2.求棒的磁化强度M 为多少?[解答]介质棒的面积为S = πr 2,体积为 V = Sl = πr 2l ,磁矩为p m = 12000A·m 2,磁化强度为m m p p M V V ∑==∆32312000(2510/2)7510π--=⨯⨯⨯=3.26×108(A·m -1).15.2一铁环中心线的周长为30cm ,横截面积为1.0cm 2,在环上密绕线圈共300匝,当通有电流32mA 时,通过环的磁通量为2.0×10-6Wb ,求:(1)环内磁感应强度B 的值和磁场强度H 的值;(2)铁的磁导率μ、磁化率χm 和磁化强度M .[解答](1)根据公式B = Φ/S 得磁感应强度为642.0101.010B --⨯=⨯= 0.02(T).根据磁场的安培环路定理∑⎰=⋅,d I L l H由于B 与d l 的方向相同,得磁场强度为3230032103010NI H l --⨯⨯==⨯= 32(A·m -1).(2)根据公式B = μH ,得铁的磁导率为0.0232B H μ=== 6.25×10-4(Wb·A -1·m -1).由于μ = μr μ0,其中μ0 = 4π×10-7为真空磁导率,而相对磁导率为μr = 1 + χm ,所以磁化率为470 6.251011496.4410m μχμπ--⨯=-=-=⨯.磁化强度为M = χm H = 496.4×32 = 1.59×104(A·m -1).15.3一螺绕环中心周长l = 10cm ,线圈匝数N = 200匝,线圈中通有电流I = 100mA .求:(1)管内磁感应强度B 0和磁场强度H 0为多少?(2)设管内充满相对磁导率μr = 4200的铁磁质,管内的B 和H 是多少?(3)磁介质内部由传导电流产生的B 0和由磁化电流产生的B`各是多少?[解答](1)管内的磁场强度为302200100101010NI H l --⨯⨯==⨯= 200(A·m -1).磁感应强度为B = μ0H 0 = 4π×10-7×200 = 2.5×10-4(T).(2)当管内充满铁磁质之后,磁场强度不变H = H 0 =200(A·m -1).磁感应强度为B = μH = μr μ0H= 4200×4π×10-7×200 = 1.056(T).(3)由传导电流产生的B 0为2.5×10-4T .由于B = B 0 + B`,所以磁化电流产生的磁感应强度为B` = B - B 0 ≈1.056(T).15.4一根无限长的直圆柱形铜导线,外包一层相对磁导率为μr 的圆筒形磁介质,导线半径为R 1,磁介质外半径为R 2,导线内有电流I 通过(I 均匀分布),求:(1)磁介质内、外的磁场强度H 和磁感应强度B 的分布,画H-r ,B-r 曲线说明之(r 是磁场中某点到圆柱轴线的距离);(2)磁能密度分布.[解答](1)导线的横截面积为S 0 = πR 12,导线内的电流密度为 δ = I/S 0 = I/πR 12.在导线内以轴线的点为圆心作一半径为r 的圆,其面积为 S =πr 2,通过的电流为 ΣI = δS = Ir 2/R 12.根据磁场中的安培环路定理∑⎰=⋅,d I L l H环路的周长为l = 2πr ,由于B 与d l 的方向相同,得磁场强度为 212I Ir H l R π∑==,(0≦r ≦R 1).在介质之中和介质之外同样作一半径为r 的环路,其周长为l = 2πr ,包围的电流为I ,可得磁场强度为2I I H l r π∑==,(r ≧R 1).导线之内的磁感应强度为00121,(0)2Ir B H r R R μμπ==≤≤;介质之内的磁感应强度为0012,()2r r I B H H R r R r μμμμμπ===≤≤;介质之外的磁感应强度为002,()2I B H r R r μμπ==≥. (2)导线之内的磁能密度为200001122m w H μ=⋅=B H 2201241,(0)8I r r R R μπ=≤≤;介质之中的磁能密度为220111222m r w H H μμμ=⋅==B H201222,()8r I R r R r μμπ=≤≤;介质之外的磁感应强度为220022211,()228m I w H r R r μμπ=⋅==≥B H .15.5一根磁棒的矫顽力为H c = 4.0×103A·m -1,把它放在每厘米上绕5匝的线圈的长螺线管中退磁,求导线中至少需通入多大的电流?[解答]螺线管能过电流I 时,产生的磁感应强度为 B = μ0nI . 根据题意,螺线管产生的磁场强度至少要与磁棒的矫顽力大小相等,但方向相反,因此 B = μ0H c ,所以电流强度为I = H c /n = 4.0×103/500 = 8(A).15.6 同轴电缆由两个同轴导体组成.内层是半径为R 1的圆柱,外层是半径分别为R 2和R 3的圆筒,如图所示.两导体间充满相对磁导率为μr 2的均匀不导电的磁介质.设电流强度由内筒流入由外筒流出,均匀分布是横截面上,导体的相对磁导率为μr 1.求H 和B 的分布以及i m 为多少?[解答](1)导体圆柱的横截面积为S 0 = πR 12,圆柱体内的电流密度为δ = I/S 0 = I/πR 12.在圆柱体内以轴线的点为圆心作一半径为r 的圆,其面积为 S = πr 2,通过的电流为 ΣI = δS = Ir 2/R 12.根据磁场中的安培环路定理∑⎰=⋅,d I L l H环路的周长为l = 2πr ,由于B 与d l 的方向相同,得磁场强度为图15.6212I Ir H l R π∑==,(0≦r ≦R 1).磁感应强度为1010212r r IrB H R μμμμπ==,(0≦r ≦R 1).(2)在介质之中同样作一半径为r 的环路,其周长为l = 2πr ,包围的电流为I ,可得磁场强度为2I I H l r π∑==,(R 1≦r ≦R 2).磁感应强度为20202r r IB H r μμμμπ==,(R 1≦r ≦R 2).磁化强度为220(1)(1)2r r I BM H H r μμμπ-=-=-=.磁化面电流的线密度为 i m = M ×n 0,n 0是介质表面的法向单位矢量.在介质的两个圆形表面,由于M 与n 0垂直,i m = |M ×n 0| = M .在介质的内表面,由于r = R 1,所以磁化电流为21(1)2r m Ii R μπ-=.在介质的外表面,由于r = R 2,所以22(1)2r m Ii R μπ-=.(3)导体圆筒的横截面积为S` = π(R 32 - R 22),圆筒内的电流密度为δ` = I/S`.在圆筒内以作一半径为r 的圆,其面积为 S = π(r 2 - R 22), 圆所包围的电流为``SI I S I I S δ=-=-∑22223222223232(1)R r r R I I R R R R --=-=--, 根据安培环路定理∑⎰=⋅,d I L l H 得磁场强度为 2232232()22()I R r I H r R R r ππ-∑==-,(R 2≦r ≦R 3).磁感应强度为22103102232()2()r r I R r B H R R r μμμμπ-==-,(R 2≦r ≦R 3).(4)在圆筒之外作一圆,由于包围的电流为零,所以磁场强度和磁感应强度都为零.15.7在平均半径r = 0.1m ,横截面积S = 6×10-4m 2铸钢环上,均匀密绕N = 200匝线圈,当线圈内通有I 1 = 0.63安的电流时,钢环中的磁通量Φ1 = 3.24×10-4Wb .当电流增大到I 2 = 4.7安时,磁通量Φ2 =6.18×10-4Wb ,求两种情况下钢环的绝对磁导率.[解答]钢环中的磁感应强度为 B = Φ/S ;根据安培环路定理∑⎰=⋅,d I L l H 得磁场强度为H = NI /2πr .根据公式B = μH ,得绝对磁导率为2B r H NIS πΦμ==.(1)在第一种情况下4420.1 3.24102000.63610πμ--⨯⨯⨯=⨯⨯⨯= 2.69×10-3(H·m -1) .(2)在第二种情况下4420.1 6.1810200 4.7610πμ--⨯⨯⨯=⨯⨯⨯= 6.88×10-4(H·m -1) .15.8 一矩磁材料,如图所示.反向磁场一超过矫顽力H c ,磁化方向立即翻转.用矩磁材料制造的电子计算机中存储元件的环形磁芯,其外径为0.8mm ,内径为0.5mm ,高为0.3mm .若磁芯原来已被磁化,方向如图所示,现在需使磁芯从内到外的磁化方向全部翻转,导线中脉冲电流I 的峰值至少需要多大?设磁性材料的矫顽力H c 12π=⨯103(A·m -1).[解答]直线电流I 产生磁感应强度为B = μ0I /2πr ,产生的磁场为 H = B/μ0 = I /2πr .为了磁芯从内到外的磁化方向全部翻转,电流在磁芯外侧r = 0.4mm 处产生的磁场应该为 H = H c ,即 H c =I /2πr ,图15.8所以,脉冲电流为I = 2πrH c33120.410100.4(A)2ππ-=⨯⨯⨯=。
《新编大学物理》(上、下册)习题答案

第1章 质点运动学一、选择题 题1.1 答案:[B]提示:明确∆r 与r ∆的区别题1.2: 答案:[A]题1.3: 答案:[D]提示:A 与规定的正方向相反的加速运动, B 切向加速度, C 明确标、矢量的关系,加速度是d dtv题1.4: 答案:[C] 提示: 21r r r ∆=-,12,R R r j r i ==-,21v v v ∆=-,12,v v v i v j =-=-题1.5: 答案:[D]提示:t=0时,x=5; t=3时,x=2得位移为-3m ;仅从式x=t 2-4t+5=(t-2)2+1,抛物线的对称轴为2,质点有往返题1.6: 答案:[D]提示:a=2t=d dt v,2224t v tdt t ==-⎰,02tx x vdt -=⎰,即可得D 项题1.7:答案:[D]北v 风v 车1v 车2提示: 21=2v v 车车,理清=+v v v 绝相对牵的关系二、填空题 题1.8:答案: 匀速(直线),匀速率题1.9:答案:2915t t -,0.6 提示: 2915dxv t t dt==-,t=0.6时,v=0题1.10:答案:(1)21192y x =-(2)24t -i j 4-j(3)411+i j 26-i j 3S提示: (1) 联立22192x t y t =⎧⎨=-⎩,消去t 得:21192y x =-,dx dydt dt =+v i j (2) t=1s 时,24t =-v i j ,4d dt==-va j (3) t=2s 时,代入22(192)x y t t =+=+-r i j i j 中得411+i j t=1s 到t=2s ,同样代入()t =r r 可求得26r∆=-i j ,r 和v 垂直,即0∙=r v ,得t=3s题1.11: 答案:212/m s 提示:2(2)2412(/)dv d x a v x m s dt dt=====题1.12: 答案:1/m s22π提示: 200t dvv v dt t dt =+=⎰,11/t vm s ==,201332tv dt t R θπ===⎰,222r R π∆==题1.13:答案:2015()2t v t gt -+-i j 提示: 先对20(/2)v tg t =-r j 求导得,0()y v gt =-v j 与5=v i 合成得05()v gt =-+-v i j 合 201=5()2t v t gt -+-∴⎰r v i j t合0合dt=题1.14: 答案:8, 264t提示:8dQ v R Rt dt τ==,88a R τ==,2264n dQ a R t dt ⎛⎫== ⎪⎝⎭三、计算题 题1.15:解:(1)3t dv a t dt == 003v tdv tdt =∴⎰⎰ 232v t ∴=又232ds v t dt == 20032stds t dt =∴⎰⎰ 312S t =∴(2)又S R θ= 316S t R θ==∴ (3)当a 与半径成45角时,n a a τ=2434n v a t R == 4334t t =∴ 34t S =∴题1.16:解:(1)dv a kv dt ==- 0v tdvkdt v =-∴⎰⎰, 0ln v kt v =-(*)当012v v =时,1ln 2kt =-,ln 2t k=∴ (2)由上式:0kt v v e-=0kt dxv e dt -=∴,000xtkt dx v e dt -=⎰⎰ 0(1)kt v x e k-=-∴第2章 质点动力学一、选择题 题2.1: 答案:[C]提示:A .错误,如:圆周运动B .错误,m =p v ,力与速度方向不一定相同 D .后半句错误,如:匀速圆周运动题2.2: 答案:[B]提示:y 方向上做匀速运动:2y y S v t t == x 方向上做匀加速运动(初速度为0),Fa m=22tx v a d t t ==⎰,223tx x t S v dt ==⎰ 2223t t =+∴S i j题2.3: 答案:[B]提示:受力如图MgF杆'F 猫mg设猫给杆子的力为F ,由于相对于地面猫的高度不变'F mg = 'F F = 杆受力 1()F Mg F M m g =+=+1()F M m g a M M+==题2.4 :答案:[D] 提示:Ba BTTa A Tmg22A BAB m g T m a T m a a a ⎧⎪-=⎪=⎨⎪⎪=⎩ 得45A a g = (2A B a a =,通过分析滑轮,由于A 向下走过S ,B 走过2S) 2A B a a =∴题2.5: 答案:[C]提示: 由题意,水平方向上动量守恒, 故 0(cos60)()1010m mv m v =+共 0=22v v 共题2.6: 答案:[C] 提示:RθθRh-R由图可知cos h RRθ-=分析条件得,只有在h 高度时,向心力与重力分量相等所以有22cos ()mv mg v g h R Rθ=⇒=- 由机械能守恒得(以地面为零势能面)2200112()22mv mv mgh v gh g h R =+⇒=+-题2.7: 答案:[B]提示: 运用动量守恒与能量转化题2.8: 答案:[D] 提示:θv 0v x v y由机械能守恒得20122mgh mv v gh =⇒= 0sin y v v θ=sin 2Gy Pmgv mg gh θ==∴题2.9: 答案: [C]题2.10: 答案: [B]提示: 受力如图fT Fx由功能关系可知,设位移为x (以原长时为原点)2()xF mg Fx mgx kxdx x kμμ--=⇒=⎰弹性势能 2212()2p F mg E kx kμ-==二、填空题题2.11: 答案:2mb提示: '2v x bt == '2a v b == 2F m a m b==∴题2.12:答案:2kg 4m/s 2 提示:4N 8Nxy 0由题意,22/x a m s = 4x F N =8y F N = 2Fm k ga== 24/y y F a m s m==题2.13: 答案:75,1110提示: 由题意,32()105F a t m ==+ 27/5v adt m s ⇒==⎰ 当t=2时,1110a =题2.14: 答案:180kg提示:由动量守恒,=m S -S m 人人人船相对S ()=180kg m ⇒船题2.15: 答案:11544+i j 提示:各方向动量守恒题2.16:答案: ()mv +i j ,0,-mgR提示:由冲量定义得 ==()()mv mv mv --=+I P P i j i j 末初- 由动能定律得 0k k E W E ∆=⇒∆=,所以=0W 合 =W m g R -外题2.17: 答案:-12提示:3112w Fdx J -==⎰题2.18:答案: mgh ,212kx ,MmG r - h=0,x=0,r =∞ 相对值题2.19: 答案:02mg k ,2mg ,0mg k题2.20: 答案: +=0A∑∑外力非保守力三、计算题 题2.21:解:(1)=m F xg L 重 ()mf L xg L μ=- (2)1()(1)ga F f x g m Lμμ=-=+-重(3)dv a v dx =,03(1)v LL g vdv x g dx L μμ⎡⎤=+-⎢⎥⎣⎦⎰⎰,2(2)3v Lg μ=-题2.22: 解:(1)以摆车为系统,水平方向不受力,动量守恒。
《新编基础物理学》十四和十五章光学习题解和分析

十四章 几何光学习题和解答14-1.如题图14-1所示,一束平行光线以入射角θ射入折射率为n ,置于空气中的透明圆柱棒的端面.试求光线在圆柱棒内发生全反射时,折射率n 应满足的条件.分析:一次折射,一次反射;利用端面折射角和内侧面入射角互余及全反射条件即可求解。
解:设光线在圆柱棒端面的折射角为γ,在内侧面的入射角为'θ,根据折射定律,有'sin 'cos sin sin 222θθγθn n n n -===光线在界面上发生全反射的条件为1'sin ≥θn∴发生全反射时,n 必须满足θ2sin 1+≥n14-2.远处有一物点发出的平行光束,投射到一个空气中的实心玻璃球上.设玻璃的折射率为50.1=n ,球的半径为cm r 4=.求像的位置.分析:利用逐步成像法,对玻璃球的前后两个球面逐一成像,即可求得最后像的位置.用高斯成像公式时,应注意两个球面的顶点位置是不同的.cm r r cm r r 4,421-=-===.解:cm cm r n n f 12)415.15.1(1'11=⨯-=-=cm cm f n f 8)5.112('111-=-=-=cm f p p p f p f 12'',,1''1111111==∞==+ 或用-∞====-=-1111111111,1,5.1','''p n n n r n n p n p ncm p p 12',415.11'5.111=-=∞--对玻璃球前表面所成的像,对后表面而言是物,所以cm cm r p p 4)812(2'212=-=+=cm cm r n f 8)]4(5.111[11'22=-⨯-=-=cm cm nf f 12)85.1('22-=⨯-=-=cm cm f p f p p p f p f 2)12484('',1''222222222=+⨯=-==+ 或用1',5.1,'''222222222===-=-n n n r n n p n p n题图14-1cm p p 2',45.1145.1'122=--=-像在球的右侧,离球的右边2cm 处.14-3.如题图14-3所示的一凹球面镜,曲率半径为40cm ,一小物体放在离镜面顶点10cm 处.试作图表示像的位置、虚实和正倒,并计算出像的位置和垂轴放大率.分析:利用凹面镜的半径可确定焦距,以知物距,由球面镜的物像公式和横向放大率公式可求解。
物理15 章知识点总结

物理15 章知识点总结1. 运动的描述在第15章中,我们首先学习了关于运动的描述,即如何用物理量来描述物体的运动。
物体的运动状态可以由位置、速度和加速度来描述。
位置是物体所处的空间位置,速度是物体在某一时刻的位移变化率,加速度是速度的变化率。
在运动学中,我们常常使用位移、速度和加速度的概念来描述物体的运动状态。
2. 牛顿定律第15章还介绍了牛顿运动定律,分别是牛顿第一定律、牛顿第二定律和牛顿第三定律。
牛顿第一定律指出,物体静止或匀速直线运动,若受到的合外力为零,则保持静止或匀速直线运动的状态。
牛顿第二定律表明,物体的加速度正比于其所受的合外力,与物体的质量成正比。
牛顿第三定律阐述了相互作用的两个物体之间,彼此受力大小相等、方向相反的原理。
3. 动量和动量守恒在物理第15章中,我们还学习了动量和动量守恒的概念。
动量是物体的运动惯性,是物体质量和速度的乘积。
动量守恒定律表明,一个系统的总动量在相互作用过程中不变。
这一定律在解释物体的碰撞和反冲等现象时非常有用,能够帮助我们理解这些现象背后的物理规律。
4. 能量能量是物理学中一个重要的概念,也是我们在第15章中学习的知识点之一。
能量可以分为动能和势能两种形式,动能是物体由于运动而具有的能量,势能是物体在外力作用下具有的能量。
在物理学中,能量守恒定律是一个非常重要的定律,它表明一个封闭系统的能量在相互作用过程中保持不变。
5. 功和功率在第15章中,我们还学习了关于功和功率的概念。
功是力对物体做的功,是力在物体上的作用引起的能量转化。
功率是功对时间的比值,表示单位时间内能量的转换率。
功和功率的概念在工程和日常生活中有着广泛的应用,对于理解各种机械运动和能量转换过程具有重要意义。
6. 动能和机械能在第15章中,我们还学习了动能和机械能的概念。
动能是物体由于运动而具有的能量,是物体质量和速度平方的乘积。
机械能包括动能和势能两部分,是描述物体在外力作用下的能量状态。
大学物理答案第15章
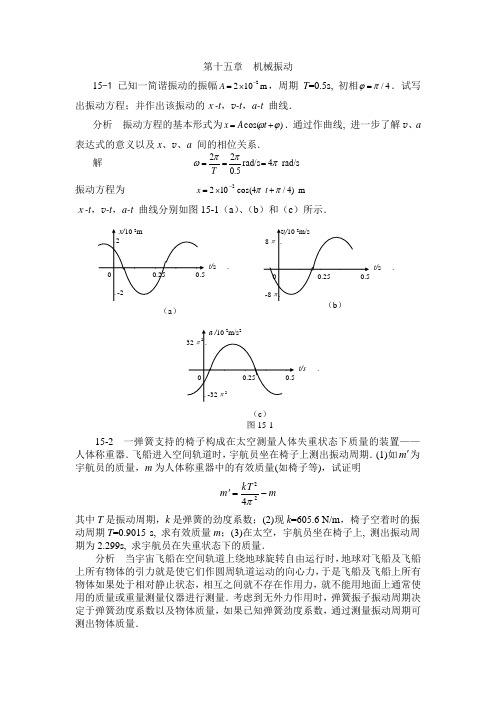
第十五章 机械振动15-1 已知一简谐振动的振幅m 1022-⨯=A ,周期T =0.5s, 初相4/πϕ=.试写出振动方程;并作出该振动的x-t ,v -t ,a-t 曲线.分析 振动方程的基本形式为)cos(ϕω+=t A x .通过作曲线, 进一步了解v 、a表达式的意义以及x 、v 、a 间的相位关系.解 rad/s 4 rad/s 5.022πππω===T振动方程为m)4/4cos(1022ππ+⨯=-t xx15-2 一弹簧支持的椅子构成在太空测量人体失重状态下质量的装置——人体称重器.飞船进入空间轨道时,宇航员坐在椅子上测出振动周期.(1)如m '为宇航员的质量,m 为人体称重器中的有效质量(如椅子等),试证明mkT m -='224π其中T 是振动周期,k 是弹簧的劲度系数;(2)现k =605.6 N/m ,椅子空着时的振动周期T =0.9015 s, 求有效质量m ;(3)在太空,宇航员坐在椅子上, 测出振动周期为2.299s, 求宇航员在失重状态下的质量.分析 当宇宙飞船在空间轨道上绕地球旋转自由运行时,地球对飞船及飞船上所有物体的引力就是使它们作圆周轨道运动的向心力,于是飞船及飞船上所有物体如果处于相对静止状态,相互之间就不存在作用力,就不能用地面上通常使用的质量或重量测量仪器进行测量.考虑到无外力作用时,弹簧振子振动周期决定于弹簧劲度系数以及物体质量,如果已知弹簧劲度系数,通过测量振动周期可测出物体质量.解 (1) 弹簧振子系统振动周期为km m T +'=π2 (1)宇航员的质量为 m kT m -='224π(2) 椅子空着时,0='m ,由(1)式得kg 66.12kg 6.605142.349015.042222=⨯⨯==πkT m(3) kg 50.68kg 66.12kg 142.34299.26.60542222=-⨯⨯=-='m kT m π15-3 一质量为0.20kg 的质点作简谐振动,其振动方程为 x =0.60cos(5t -π/2), 其中x 以m 为单位, t 以s 为单位.求:(1)质点的初速度;(2)质点在正向位移一半处所受的力.分析 物体振动速度tx d d =v , 物体所受恢复力x m ma F 2ω-==,方向指向平衡位置.解 (1)据已知)2/5(60.0π-=t x ,得t t t A tx 5cos 3)2/5sin(560.0)sin(d d =-⨯-=+-==πϕωωv当t=0时,得 v 0=3 m/s(2) 正向最大位移一半处,x =0.30 m ,所受的力为N 5.1N 3.052.022-=⨯⨯-=-==x m ma F ω方向指向平衡位置.15-4 一物体沿x 轴作简谐振动,振幅为0.12m ,周期为2s ,当t =0时,位移为0.06m ,且向x 轴正方向运动.求(1)该物体的振动方程;(2)t =0.5s 时,物体的位置、速度、加速度;(3)在x =-0.06m 处,且向x 轴负方向运动时,物体的速度、加速度,以及物体从这一位置回到平衡位置所需的时间.分析 求解振动方程的难点是确定振动物体的初相ϕ.初相取决于计时起点t =0时物体的位置和速度.确定初相可用三角函数法或旋转矢量法.解 (1) 已知振幅为A = 0.12 m ,角频率为πππω===222Trad/s ,t = 0时初始位置和初速度分别为x 0=A cos ϕ =0.06 (1)v 0=ϕωsin A - >0 (2)从(1)式得2112.006.0cos 0===Ax ϕ得 33ππϕ或-=从(2)式得0sin <ϕ,所以应取3/πϕ-=此外,由t = 0时初始位置和初速度可以确定其旋转矢量如图15-4所示,即3/πϕ-=.振动方程为m)3/cos(12.0ππ-=t x(2) t =0.5s 时, x =)3/cos(12.0ππ-t =0.104 mv m/s188.0)3/sin(12.0-=--=πππt22m/s03.1)3/cos(12.0-=--=πππt a(3) 在1x =-0.06 m 处,物体向x 轴负向运动时,设1t t =,则06.0)3/cos(11-=-=ππt A x m (3)v 1)3/sin(1ππω--=t A < 0 (4)从(3)式得 2112.006.0)3/cos(11-=-==-Ax t ππ解得 ππππππn n t 2322323/1+-+=-或 (n =0,1,2…)又从(4)式得 0)3/sin(1>-ππt 应取 ππππn t 2323/1+=- (n =0,1,2…)故 )12(1+=n tm/s 592.0 m/s 326.0211=-= a v设回到平衡位置时2t t =,则0)3/cos(22=-=ππt A x (5)v 2)3/sin(2ππω--=t A >0 (6)从(5)式得 ππππn t 2233/2+=-或ππππn t 223/2+=- (n =1,2…)从(6)式得 )3/sin(2ππ-t <0 应取 ππππn t 2233/2+=- (n =1,2…)65)12(2++=n t回到平衡位置所需时间 s 83.0s 6512==-=t t t ∆15-5 一个质点作简谐振动,其振动方程为x =0.24cos(πt /2+π/3)m ,其中x 以m 计, t 以s 计.试用旋转矢量法求出质点由初始状态运动到 x =-0.12m, v <0状态所需的最短时间.分析 根据振动方程,当0t =0时旋转矢量A 与Ox 于x =-0.12m, v <0状态时,A 32π,如图15-5所示.因此,从0t 位置转到新位置偏转3/π解 如图15-5所示, t '时刻的相位为πϕ32=A 沿逆时针方向从0t 位置转过角度3/π所需的时间为s 32231=÷ππ15-6 作简谐振动的单摆在一个周期内的几个运动状态如图15-6所示.(1)若以(a )图所示的状态为计时起点;(2)若以(b )图所示的状态为计时起点,问单摆的初相位和其它各图所示状态的相位各为何值?分析 应从本题得出的结论是: 初相与计时起点(即初始条件)有关; 相位与与计时起点无关而与振动物体的瞬时状态有关.解 (1)以图(a )状态为计时起点,t =0时m m cos θϕθθ==得0=ϕ,因此对图(b)有0)cos(=+=ϕωθθt m (1)0)sin(d d <+-=ϕωωθθt tm(2)从(1)式得 2πϕω±=+t从(2)式得 )s i n (ϕω+t >0 所以图(b)的相位应取 2)(πϕω=+t同理,对图(c) πϕω=+)(t 对图(d)3)(πϕω=+t0cos ==ϕθθm (3)0sin d d <-=ϕωθθm t(4)(3)式(4)式联立,解得 2πϕ=同理,对图(c) πϕω=+)(t 对图(d) 23)(πϕω=+t对图(a) 0)(=+ϕωt15-7 一物块在水平面上作简谐振动,振幅为0.1m ,在距平衡位置0.06m 处速度为0.4m/s ,(1)求振动周期;(2)当速度为±0.12m/s 时,位移为多少?(3)若有另一物体置于该振动物块之上,当物块运动至端点时正好滑动,问摩擦系数μ为多大?分析 当所讨论问题涉及物体正好要滑动的条件时,由于物体尚未滑动,所受摩擦力仍为静摩擦力,静摩擦力方向与物体运动趋势方向相反.解 (1)设物块的振动方程为)cos(1.0ϕω+=t x物块位于06.01=x m 时, 速度v 1= 0.4m/s, 即x 1=A )cos(ϕω+t =0.06 m (1) v 1=)sin(ϕωω+-t A =0.4 m/s (2)以上两式平方相加, 代入A =0.1m ,解得 5=ωrad/s 26.12==ωπT s(2)由 v 2=)sin(ϕωω+-t A =±0.12 得 24.0)sin( =+ϕωt971.0)(sin 1)cos(2±=+-±=+ϕωϕωt t 则位移为x 2=0.1)cos(ϕω+t =±9.7×10-2m(3)物块运动至端点时正好物体开始滑动,即最大恢复力等于最大静摩擦力,物块受力如图15-7所示,因最大静摩擦力mg F μ=f ,最大恢复力A m F 2max ω=,得mg A m μω=226.08.91.05 22=⨯==gA ωμ15-8 一个轻弹簧在60N 的拉力作用下可伸长30cm , 将一物体悬挂在弹簧下端,并在它上面放一小物体,它们的总质量为4kg , 待其静止后再把物体向下拉10cm , 然后释放. 问(1)此小物体是停在振动物体上还是离开它? (2)如果使放在振动物体上的小物体与振动物体分离, 则振幅A 需满足什么条件? 二者在何位置开始分离?分析 根据胡克定律,由弹簧在外力作用下的形变量可以求出弹簧的劲度系数.当两物体脱离接触时,它们之间的正压力等于零,以此为条件可以判断小物体是否停在振动物体上. 解 (1) 根据胡克定律,得N/m 200N/m 3.060Δ===lF k由定义得 rad/s50rad/s 4200===mk ω弹簧、物体和小物体组成一个弹簧振子系统,把物体下拉10cm 后释放,故该弹簧振子的振幅为A =0.1m .设小物体质量为m ,小物体随系统一起运动,最大加速度为A a 2ω=,小物体受力情况如图15-8所示,当达最高点时,所受物体的正压力有最小值,即Am ma F mg N 2ω==+ (1)当A =0.1m 时,得 N 2.192=-=-=kA mg A m mg F N ω 即F N > 0 ,因而小物体仍停留在振动物体上.(2) 两物体脱离接触条件为0N =F ,代入(1)式得m196.0m 508.92==='ωgA即振幅大于0.196m ,两物体将在平衡位置上方分离,分离的位置即在0.196m 处.15-9 如图15-9(a )所示,在一个倾角为θ的光滑斜面上,固连一原长为L ,劲度系数为k ,质量忽略不计的弹簧,弹簧与质量为m 的重物相连,求重物作简谐振动的平衡位置和周期.分析 平衡位置是系统所受合外力为零的位置. 在建立振动方程时,一般都把取平衡位置为坐标原点.放在斜面上的弹簧振子处于静止状态时,物体所受弹簧的弹性力与重力沿斜面向下的分量大小相等,方向相反.解 弹簧和物体组成一个弹簧振子系统.物体受力情况如图15-9(b )所示.设在平衡位置弹簧的伸长量为0x ,有0sin 0=-kx mg θ 解得 k mg x θsin 0=即处于平衡位置时弹簧长度为0x L +. 根据定义,弹簧振子系统作简谐振动的角频率为mk =ω周期为 km T π2=15-10 如图15-10(a)所示,密度计玻璃管的直径为d ,浮在密度为ρ的液体中.若在竖直方向轻轻推一下,任其自由振动,试证明:若不计液体的沾滞阻力,密度计的运动是简谐振动;设密度计的质量为m , 试求振动周期.分析 若物体运动为简谐振动,应该具有如下特征:物体所受合外力与位移成正比而方向相反,即加速度与位移成正比而方向相反;或者位移是时间的余弦F F(a) (b)图15-9函数或正弦函数.解 密度计受力分析如图15-10(b)所示.设密度计截面积为S , 当处于平衡状态时,设浸入水中部分高度为h , 浮力则为ghS F ρ=B ,有0=-ghS mg ρ(1) 取平衡位置为坐标原点,向下为x 轴正向,当密度计向下位移为x 时,有22d d )(t xm S x h g mg =+-ρ (2) 由(1)和(2)式得gxS t x m ρ-=22d d 即加速度与位移成正比而方向相反,因此运动为简谐振动,且有g m dT mg d mgS ρππρρω4 2===15-11 如图15-11,劲度系数为k 的轻弹簧上端与质量为m 的平板相连,下端与地固连.另一质量为m '的物体,从h 高处自由落下,与平板发生完全非弹性碰撞后一起运动. 若以平板开始运动为计时起点,取向下为坐标正向,求振动的周期,振幅和初相位.分析 m '与m 发生完全非弹性碰撞后一起运动,与轻弹簧组成振动系统, 平衡位置是(m '+ m )所受合外力为零的位置,并选取为坐标原点.以发生碰撞后平板开始运动为计时起点,此时平板m 的坐标就是系统的初位移0x ,碰后(m '+ m )的共同速度v 0就是系统的初速度,而且可以依据碰撞中动量守恒求出.解 m '自由下落, 以gh 2的速度与m 发生完全非弹性碰撞,设碰后m '+ m 的共同速度为v 0,方向向下,应用动量守恒定律,得)(2m m gh m +'='v 0v 0mm gh m +''=2m '、m和弹簧组成振动系统,设m '+m 所受合外力为零时,弹簧的压缩量为x ∆,此位置是系统的平衡位置,则有0Δ)(=-+'x k g m m (1)取系统的平衡位置为坐标原点,向下为x 轴正向,当m '+m 位移为x 时,有d d )()()(22tx m m x x k g m m +'=+-+'∆ (2)由(1)和(2)式得0d d 22=+'+x mm k t x且有 km m T mm k +'=+'=πω2取m '与m 相碰的瞬间为振动的初始时刻t =0,有mm gh m kmg x +''=-=2 00v即 kmg A x -==ϕcos 0 (3)mm gh m A +''=-=2sin 0ϕωv (4)(3)与(4)式联立,得振动的周期和初相位分别为)(212020gm m kh kg m x A +'+'=⎪⎭⎫ ⎝⎛+=ωvgm m kh mm x )(2tan 0+''=-=ωϕv又因ϕ , 0 , 000><v x 在第三象限,则)(2 tanarc πϕ++''=gm m kh mm15-12 弹簧下端挂一物体后,弹簧伸长量为2108.9-⨯m , 若令物体上下振动,(1)求振动周期;(2)使其在平衡位置上方0.1m 处由静止开始运动,求振幅、初相及振动方程.(3)使其在平衡位置以0.8m/s 向上的初速度开始运动,求振幅、初相及振动方程.分析 计算结果表明,同一系统在不同初始条件下的振动方程不同. 解 (1)设挂上物体达平衡时弹簧的伸长量为x ∆, 根据胡克定律和平衡条件有mgx k =∆由定义得 10===xgmk ∆ω rad/s 63.02==gx T ∆πs(2)如图15-12所示,取平衡位置为坐标原点, 向上为x 轴正向.初始条件为: t =0时, x 0=0.1m v 0=0,即1.0cos 0==ϕA x (1)0sin 0=-=ϕωA v (2) 由(1)和(2)式联立解得m 1.01.022020==⎪⎭⎫ ⎝⎛+=ωv x A0=ϕ振动方程为 t x 10cos 1.0= m(3) 初始条件为:t =0时,x 0=0 v 0=0.8,即cos 0==ϕA x (3)08.0sin 0>=-=ϕωA v (4)由(3)和(4)式联立解得A =2020⎪⎭⎫ ⎝⎛+ωv x 0.08m从(3)式得 2πϕ=或 23πϕ=从(4)式得 0sin <ϕ 所以取 23πϕ=振动方程为 )2310cos(08.0π+=t x m15-13 如图15-13(a )所示的弹簧,其一端固定在天花板上,另一端挂着质量都是1.0kg 的两个物体A 和B .当物体静止时,弹簧伸长量为2108.9-⨯m , 如果物体B 突然脱落掉下,不计弹簧质量,(1)求物体A 的振动周期;(2)若从物体B 脱落时开始计时,求物体A 的振幅、初相和振动方程.分析 虽然弹簧下悬挂着两物体,但由于物体B 脱落,振动系统实为弹簧和 物体A 组成. 据题意, 物体B 脱落之时t=0,因此物体A 的位置为系统的初始位置,且物体B 从静止状态脱落,系统初速度为0.解 物体B 脱落之前,两个物体A 和B 处于重力和弹簧的弹性力作用下的平衡状态,弹簧伸长量为m 108.9Δ2-⨯=l ,则l k mg Δ2=N/m200N/m 108.98.912Δ22=⨯⨯⨯==-lmg k物体B 脱落后,物体A 和弹簧组成弹簧振子系统,设平衡位置处弹簧伸长量为0l ,则 00=-kl mg (1) 取平衡位置为坐标原点,向下为x 轴正向,如图15-13(b )所示,当物体A 位移x 时,应用牛顿第二定律,得220d d )(tx ml x k mg =-- (2)由(1)和(2)式得22d d tx mkx =-由定义得 rad/s2100.1200===mk ω s44.02==ωπT0=t 时,物体B 脱落,有m 109.4ΔΔ200-⨯==-=-=kmg kmg l l l x即 m 109.4cos 20-⨯==ϕA x (3) 0sin 0=-=ϕωA v (4)(3)和(4) 式联立解得 2220109.4)(-⨯=+=ωv x A m从(3)式0=ϕ,满足(4)式, 所以 0=ϕ振动方程为 t x 210cos 109.42-⨯= m讨论: (1)我们现在是取向下为x 轴正向,如果取向上为正,则初相为π,振动方程有所不同.这就是解题中强调要给出坐标取向的理由.(2)如果A 、B 质量不等,例如A B m m 2=,会有不同的l Δ值,则初始条件0x 不同,将导致振动特征参量的改变.15-14 如图15-14(a )所示,一质量可忽略的盘挂在劲度系数为k 的轻弹簧之下,一质量为m 的物体自h 高处自由下落至盘中,并与盘粘在一起作简谐振动. 设m =0.1kg ,k =4.9 N/m ,h =0.3m ,若以物体刚落至盘中时为计时起点,求系统的振动方程.解 如图15-14(b), 弹簧、质量为m 的物体和盘组成振动系统.取平衡位置为坐标原点, 向上为x 轴正向.平衡时弹簧伸长为0l l-,平衡方程为)(0=--l l k mg(1)当盘的位移为x 时,应用牛顿第二定律,得220d d )(tx ml x l k mg=-+- (2)由(1)和(2)式,得 22d d tx mkx=-由定义得71.09.4===mk ω rad/s质量为m 的物体与盘相碰时, t =0,弹簧伸长量为m 2.0m 9.48.91.0k0=⨯-=-=mg x相碰时,物体下落速度为gh 2,忽略盘质量,应用动量守恒定律,碰后物与盘的共同速度方向向下,大小为m/s 3.2m/s 3.08.922=⨯⨯==gh v即 x 0=ϕcos A =0.2 m (3)ϕωsin 0A -=v <0 (4)(3)和(4)式联立解得220)(ωv +=x A =0.4 m从(3)式得21cos 0==Ax ϕ,3πϕ±=.从(4)式得0sin >ϕ,所以应取3πϕ=振动方程为 )37cos(4.0π+=t xm15-15 单摆长为l ,小球质量为m ,带有电荷+q ,悬挂在场强大小为E 、方向由左向右的均匀电场中,如图15-15(a )所示.(1)求小球处在平衡位置时悬线与竖直向下方向所成的角;(2)假设单摆对平衡位置的偏角很小,求单摆的周期.分析 由于带电小球受到均匀电场的电场力作用,合外力为零的平衡位置将与铅垂位置有一偏角.解 (1)如图15-15(b )所示, 小球受重力m g 、静电力E q 和张力F T 作用,设平衡位置偏角为0θ,则0cos 0T =-θF mgsin 0T =-qE F θmg qEarctan 0=θ (1) (2)当摆线从平衡位置偏离θ角时,与铅垂位置偏角为)(0θθ+,应用牛顿第二定律,得小球切向运动微分方程为2220200d d d )(d )sin()cos(tmltmlmg qE θθθθθθθ=+=+-+ (2)由(1)式可得0tan θmg qE =代入(2)式,得2200d d ]cos )sin(sin )[cos(cos tmlmg θθθθθθθθ=+-+应用三角函数公式,得θθθsin cos d d 022l g t-=当θ很小时,θθ≈sin,得θωθθθ222cos d d -=-=l g t表明角加速度与角位移成正比,且方向相反,因此小球作简谐振动,并得222222222 cos Eq gm ml T mlEq gm l g +=+==πθω15-16 劲度系数分别为1k 和2k 的两根弹簧串在一起,竖直地悬挂着,下面挂一质量为m 的小球,作成一个在竖直方向振动的弹簧振子.试求其振动周期.分析 这是两根弹簧串联(首尾相连)的问题.处理这类连接体问题仍要用隔离物体法.当两弹簧质量均可忽略时,无论处于运动或静止状态,两弹簧中的弹性力相等,并等于相互作用力. 解 两根串联弹簧和小球组成振动系统. 隔离物体,对小球作受力分析如图15-16所示.取平衡位置为坐标原点,向下为x 轴正向.设平衡时弹簧1的伸长量为10x ,弹簧2的伸长量为20x ,小球受力平衡方程为101=-x k mg (1)两弹簧连接处相互作用力等大而反向,即0202101=-x k x k (2)小球相对于平衡位置下移x 时,设弹簧1伸长量为1x ,弹簧2伸长量为2x ,应用牛顿第二定律,得2211d d tx mx k mg =- (3)两弹簧连接处相互作用力等大而反向,即2211x k x k =,因201021x x x x x ++=+,得 )(20102121x x x k k k x +++=代入(3)式得 22212101d d )(tx mx k k k x k mg =++- (4)由(1)和(4)式,得222121d d tx mx k k k k =+-表明加速度与位移成正比,且方向相反,因此小球作简谐振动,并得)(2 )(21212121k k k k m T k k m k k +=+=πω15-17 两弹簧劲度系数分别为1k =1N/m , 2k =3N/m .在光滑的水平面上将此二弹簧分别连接到质量为m =0.1kg 的物体的两端,弹簧的其余两端分别固定在支柱1P 及2P 上,如图15-17所示.今使物体有一向右初位移m10320-⨯=x ,向右初速度m/s10402-⨯=v ,(1)试证物体作简谐振动;(2)求振动方程(设物体在振动中,两弹簧始终处于被拉伸状态).分析 当物体运动时,两弹簧的形变量大小相同,并等于物体的位移量. 解 以物体为研究对象, 受力如图15-17所示. 设平衡时两弹簧伸长量分别为1l 、2l ,有2211l k l k = (1) 取平衡位置为坐标原点,向右为x轴正向.当物体向右位移为x 时,应用牛顿第二定律,得221122d d )( )(tx mx l k x l k =+-- (2)由(1)和(2)式得2221d d )(-tx mx k k =+由定义,得 r a d /s102rad/s 1.0421==+=mk k ω已知t =0时, m/s 1040 m 1032020--⨯=⨯=v x即 ϕcos 0A x = = m 1032-⨯ (3)v 0= ϕωsin A - >0 (4)(3)和(2)式联立,解得220)(ωv +=x A =2×10-2m从(3)式得23cos 0==Ax ϕ,6πϕ±=,从(4)式得ϕsin <0,则应取6πϕ-=所以振动方程为 m )6102cos(1022π-⨯=-t x15-18 已知某简谐振动的振动曲线如图15-18(a),试求此简谐振动的振动方程.分析 振动曲线是振动物体位移x 与时间t 的关系曲线.从振动曲线上可得出振幅和初始条件.由图15-18(a)可以看出,当t 稍大于零时,物体将向x 轴负向运动,所以物体初速度v 0< 0.由旋转矢量图可以比较容易地确定振动的角频率,即旋转矢量1s 内转过的角度便是角频率.解 由图15-18(a)看出,A = 2 m ,32πϕ=.t =1s 时的位移和速度分别为)cos(1ϕω+=t A x = 0 (1)v 1= )sin(ϕωω+-t A <0 (2)(1)式给出cos )(ϕω+t = 0,得2)(πϕω=+t ,显然满足(2)式,即为1s 时的相位.旋转矢量图如图15-18(b)所示,t =0时的旋转矢量为)0(=t A ,可以看出,1s 内A 沿逆时针方向转过的角度即角频率为rad/s61123ππππω=++=振动方程为 )32611cos(2ππ+=t xm15-19 (1)、(2)两个简谐振动的周期相同,振动曲线如图15-19.求(1)、(2)两个简谐振动的相位差. 分析 根据振动曲线可以判断指定点的相位.若两振动的相位差012>-ϕϕ,通常说,振动2的相位比振动1超前或振动1的相位比振动2落后.解 从图15-19知,振动(1)的初始条件是10cos ϕA x ==0 (1)v 0= 0sin 1>-ϕωA (2)由(1)式得 21πϕ±=由(2)式得 0sin 1<ϕ 则振动(1)的初相应取 21πϕ-=振动(2)的初始条件是20cos ϕA x = =A (3)v 0= 2sin ϕωA -=0 (4)由(3)式得02=ϕ,满足(4)式,即为振动(2)的初相.因两振动的角频率相同, 所以振动(1)与振动(2)相位差为2π-, 且振动(1)比振动(2)相位落后2π.15-20 一质量为0.1kg 的物体作振幅为0.01m 的简谐振动,最大加速度为0.042m/s .试求(1)振动的周期;(2)总的振动能量;(3)物体在何处时,其动能和势能相等?分析 作简谐振动的弹簧振子系统机械能守恒, 动能和势能都随时间周期变化且相互转换,这是系统运动过程中只有重力、弹性力等保守力作功,外力和非保守内力不作功的条件下才成立的.实际的振动系统起码要受到阻力作用, 因而必定有能量的损耗,系统机械能不守恒.解 (1)由A a m 2ω= 得s 14.3s 04.001.022===ππma A T(2)总振动能量为J102J 01.004.01.02121215-m22⨯=⨯⨯⨯===A maAm E ω(3)设动能和势能相等时, 物体距平衡位置x 远, 则 2P 21kx E =又由 mk E E E ===2k P , 21ω得 m 1007.7m 04.01.001.010235--⨯=⨯⨯⨯==mma EA x15-21 质点作简谐振动,已知振动频率为ν, 则振动动能变化的频率为多少?当其位移为振幅的一半时,其动能为总能量的几分之几?分析 只要大致勾画出k E -t 和x-t 曲线轮廓,便可得出动能变化频率与振动频率间关系.解 振动动能为)]2(2cos 1[41 )2(sin 2122222k t A m t A m E πνωπνω-==所以振动动能变化频率为ν2,k E -t 曲线如图15-21所示.当 A x 21=时, 振动势能为)21(41)2(2122p kA A k E ==此时振动动能为)21(43)21(4121222P k kA kA kA E E E =-=-= 即为总能量的3/4.15-22 两同方向简谐振动,其振动方程分别为)4110cos(106, )4310cos(1052221ππ+⨯=+⨯=--t x t x式中x 以m 为单位,t 以s 为单位.(1)求合振动的振幅和初相;(2)若另有一同方向简谐振动)10cos(10723ϕ+⨯=-t x ,问 ϕ为何值时,合振动 31x x +的振幅为最大; 又 ϕ为何值时,合振动 32x x +的振幅为最小?(3)用旋转矢量法表示(1)、(2)的结果.分析 先体会给出的两个振动方程,哪里体现了同方向?哪里体现了同频率?作两个同方向同频率振动合成,最简单的方法是旋转矢量法(不妨也尝试一下解析法),只要画出了合成矢量,简单的几何关系便给出合振动的振幅及初相.本题的另一部分是讨论振动加强减弱条件,这为后面讨论机械波、光波的干涉加强减弱作舖垫.解 (1)如图15-22,两矢量间夹角为2π所以合振动振幅m 107.81 m106522222221--⨯=⨯+=+=A A A合振动初相8484465 tanarc 0'=+=πϕ(2) 合振动A 再与第三个振动合成.据振动叠加条件, πϕϕk 21±=-时合振动有极大值,即ππϕk 243±=(k =0,1,2…)当πϕϕ)12(1+±=-k 时合振动有极小值, 即ππϕ)12(43+±=k (k =0,1,2…)15-23 有两个同方向同频率的简谐振动,其合振动的振幅为0.2m ,相位与第一振动的相位差为π61,若第一振动的振幅为1103-⨯m ,用旋转矢量法求第二振动的振幅及第一、第二两个振动的相位差.分析 本题与上题相反, 为已知合振动求分振动. 解 作旋转矢量如图15-23所示,由几何关系得m1.030cos 212122=︒-+=AA A A A再由)cos(2122122212ϕϕ-++=A A A A A 解得20)cos(1212πϕϕϕϕ=-=-15-24 示波管的电子束受到两个互相垂直的电场的作用,若电子在两个方向上的位移分别为t A x ωcos =和)cos(ϕω+=t A y .求在0=ϕ、30=ϕ、90=ϕ各种情况下,电子在荧光屏上的轨道方程,并分别说明电子沿轨道的运动方向.分析 这是两个频率相同、振动方向相互垂直简谐振动的合成. 解 轨道方程为)(sin )cos(21221221222212ϕϕϕϕ-=--+A A xy Ay Ax因 A A A ===-2112 ϕϕϕϕϕ2222sin cos 2A xy y x =-+当0=ϕ时,得x=y ,为一过原点的直线.说明电子沿直线作往返运动.当 30=ϕ时,得 222413Axy y x =-+为一椭圆,且运动方程为)30cos(cos+==t A y t A x ωω当 90=t ω时,电子位于)21,0(A -处,此后瞬间x <0, y <0,电子位于第三象限内,表明电子顺时针转动.当 90=ϕ时,得 222A y x =+ 为一圆.且运动方程为)90cos(cos+==t A y t A x ωω当0=t ω时, 电子位于)0, (A 处, 此后瞬间x >0, y <0,电子位于第四象限内, 表明电子仍顺时针转动.。
大学物理第十五章狭义相对论基础课后习题答案及复习内容

第十五章狭义相对论基础一、基本要求1. 理解爱因斯坦狭义相对论的两个基本假设。
2. 了解洛仑兹变换及其与伽利略变换的关系;掌握狭义相对论中同时的相对性,以及长度收缩和时间膨胀的概念,并能正确进行计算。
3. 了解相对论时空观与绝对时空观的根本区别。
4. 理解狭义相对论中质量和速度的关系,质量和动量、动能和能量的关系,并能分析计算一些简单问题。
二、基本内容1.牛顿时空观牛顿力学的时空观认为,物体运动虽然在时间和空间中进行,但时间的流逝和空间的性质与物体的运动彼此没有任何联系。
按牛顿的说法是“绝对空间,就其本性而言,与外界任何事物无关,而永远是相同的和不动的。
”,“绝对的,真正的和数学的时间自己流逝着,并由于它的本性而均匀地与任何外界对象无关地流逝着。
”以上就构成了牛顿的绝对时空观,即长度和时间的测量与参照系无关。
2.力学相对性原理所有惯性系中力学规律都相同,这就是力学相对性原理(也称伽利略相对性原理)。
力学相对性原理也可表述为:在一惯性系中不可能通过力学实验来确定该惯性系相对于其他惯性系的运动。
3. 狭义相对论的两条基本原理(1)爱因斯坦相对性原理:物理规律对所有惯性系都是一样的,不存在任何一个特殊的(例如“绝对静止”的)惯性系。
爱因斯坦相对论原理是伽利略相对性原理(或力学相对性原理)的推广,它使相对性原理不仅适用于力学现象,而且适用于所有物理现象。
(2)光速不变原理:在任何惯性系中,光在真空中的速度都相等。
光速不变原理是当时的重大发现,它直接否定了伽利略变换。
按伽利略变换,光速是与观察者和光源之间的相对运动有关的。
这一原理是非常重要的。
没有光速不变原理,则爱因斯坦相对性原理也就不成立了。
这两条基本原理表示了狭义相对论的时空观。
4. 洛仑兹变换()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧--='='='--='2222211c u xc u t t z z y y c u ut x x (K 系->'K 系)()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧-'+'='='=-'+'=2222211c u x c u t t z z y y c u t u x x (K 系->'K 系) 令u c β=,γ=①当0→β,γ=1得ut x x -=',,',','t t z z y y ===洛仑兹变换就变成伽利略变换。
新编物理基础学全册(王少杰版)课后习题答案及详解

新编物理基础学全册课后习题详细答案王少杰,顾牡主编第一章1-1.质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t 对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kxv v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvv dt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kxv v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r表达式。
对运动学方程求一阶导、二阶导得()v t 和()a t ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
画图略 (2)质点的位置可表示为:22(48)r ti t j =+- 由/v dr dt =则速度:28v i tj =+ 由/a dv dt =则加速度:8a j =则:当t=1s 时,有24,28,8r i j v i j a j =-=+=当t=2s 时,有48,216,8ri j v i j a j =+=+=1-4.一质点的运动学方程为22(1)x t y t ==-,,x 和y 均以m 为单位,t 以s 为单位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第15章 早期量子论15-1 某物体辐射频率为146.010Hz ⨯的黄光,问这种辐射的能量子的能量是多大? 分析 本题考察的是辐射能量与辐射频率的关系. 解: 根据普朗克能量子公式有:-3414196.6310 6.010 4.010(J)h εν-==⨯⨯⨯=⨯15-2 假设把白炽灯中的钨丝看做黑体,其点亮时的温度为K 2900. 求:(1) 电磁辐射中单色辐出度的极大值对应的波长; (2) 据此分析白炽灯发光效率低的原因.分析 维恩位移定律告诉我们,电磁辐射中单色辐出度的极大值对应的波长与温度的乘积等于一个常量.由此可以直接由维恩位移定律求解. 解 (1)由维恩位移定律,得-3-72.89810=9.9910(m)=999(nm)2900b T λ⨯==⨯(2)因为电磁辐射中单色辐出度的极大值对应的波长在红外区域,所以白炽灯的发光效率较低。
15-3 假定太阳和地球都可以看成黑体,如太阳表面温度T S =6000K ,地球表面各处温度相同,试求地球的表面温度(已知太阳的半径R 0=6.96×105km ,太阳到地球的距离r =1.496×108km )。
分析 本题是斯忒藩—玻尔兹曼定律的应用。
解: 由 40T M σ=太阳的辐射总功率为2428482002644 5.671060004(6.9610)4.4710(W)S S S P M R T R πσππ-===⨯⨯⨯⨯⨯=⨯地球接受到的功率为62226221117 6.3710() 4.4710()422 1.496102.0010(W)S E E E S P R P R P d d ππ⨯===⨯⨯⨯=⨯ 把地球看作黑体,则 24244E E E E E R T R M P πσπ==290(K)E T ===15-4 一波长nm 2001=λ的紫外光源和一波长nm 7002=λ的红外光源,两者的功率都是400W 。
问:(1)哪个光源单位时间内产生的光子多? (2)单位时间内产生的光子数等于多少?分析 本题考察光的粒子性及光源的功率与单位时间发射的光子数间的关系. 解: (1)光子的能量λνchh E ==设光源单位时间内产生的光子数为n ,则光源的功率hcw n nhcnE w λλ===, 可见w 相同时,λ越大,n 越大,而12λλ>,所以红外光源产生的光子数多。
(2)紫外光源)(个==s /1002.41031063.61020040020834911⨯⨯⨯⨯⨯⨯=--hc w n λ 红外光源)(个==s /1008.141031063.61070040020834922⨯⨯⨯⨯⨯⨯=--hc w n λ 15-5 在天体物理中,一条重要辐射线的波长为21cm ,问这条辐射线相应的光子能量等于多少?分析 本题考察光子能量的计算。
解: 光子能量34825626.63103109.510(J) 5.910(eV)2110cE h h νλ----⨯⨯⨯==⨯=⨯⨯== 即辐射线相应的光子能量为65.910eV -⨯15-6 一光子的能量等于电子静能,计算其频率、波长和动量。
在电磁波谱中,它属于哪种射线?分析 本题考察光的粒子性的物理量的计算。
解: 电子静能2311614009.11109108.2010(J)E m c --==⨯⨯⨯=⨯则光子14200348.2010 1.2410(Hz)6.6310E h ν--⨯===⨯⨯ 81220310 2.4210(m)1.2410cλν-⨯===⨯⨯ 34221126.6310 2.7310(kg m s )2.4210hp λ----⨯===⨯⋅⋅⨯ 它属于γ射线。
15-7 钾的光电效应红限波长是550nm, 求钾电子的逸出功.分析 本题考察的是爱因斯坦光电效应方程.根据红限波长,可以求出与该波长相应的光子能量, 这个能量就是该金属 的逸出功. 解:由爱因斯坦光电效应方程A m hv +=2max v 21 当光电子的初动能为零时, 有:34819090 6.6310310 3.61610(J) 2.26(eV)55010hcA hv λ---⨯⨯⨯====⨯=⨯15-8 波长为200nm 的紫外光照射到铝表面,铝的逸出功为4.2eV 。
试求: (1)出射的最快光电子的能量; (2)截止电压; (3)铝的截止波长;(4)如果入射光强度为2.02W m -⋅,单位时间内打到单位面积上的平均光子数。
分析 本题考察的是爱因斯坦光电效应方程。
解: (1) 入射光子的能量为:3481996.63103109.9310(J) 6.20(eV)20010cE h h νλ---⨯⨯⨯==⨯=⨯== 由光电效应方程可得出射的最快光电子的能量为:1 6.20 4.20 2.00(eV)2hcm A λ=-=-=2max v (2) 截止电压为:01 2.00(eV)2 2.00(V)m U e e===2maxv(3) 铝的截止波长可由下式求得:00 6.20200295.2(nm 4.20c hc hv v A A λλ====⨯=) (4) 光强I 与光子流平均密度N 的关系为I =Nhv , 所以有:1821192.0 2.0210(m s )9.9310I N hv ---===⨯⋅⨯15-9 光照射到金属表面的入射光波长从1λ减小到2λ(1λ和2λ均小于该金属的红限波长). 求(1)光电子的截止电压改变量.(2)当nm 2951=λ,nm 2652=λ时截止电压的改变量。
分析 本题考察光电效应方程的应用. 解 (1) 截止电压A h m eU m -==ν2021v 对1λ,有e A e hc U -=101λ 对2λ,有eA e hc U -=202λ 两式相减得21211201020)()11(λλλλλλe hc e hc U U U -=-=-=∆ (2) 当nm 2951=λ,nm 2652=λ时,(V)476.01026510295106.110)265295(1031063.6)(9919983421210=⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯=-=∆-----λλλλe hc U15-10 试求波长cm 1075-⨯=λ的红光光子的能量、动量和质量.分析 本题考察的是光子的能量、动量和质量与光子的波长之间的关系.解 光子的能量3481976.6310310 2.8410()710hch ενλ---⨯⨯⨯====⨯⨯J 光子的动量3428176.63109.4710(kg m s )710h p λ----⨯===⨯⋅⋅⨯ 光子的质量19362162.84103.1610(kg)910m c ε--⨯===⨯⨯15-11 用波长为λ的单色光照射某一金属表面时, 释放的光电子最大初动能为30eV , 用波长为2λ的单色光照射同一表面时, 释放的光电子最大初动能为10eV . 求能引起这种金属表面释放电子的入射光的最大波长.分析 本题考察的是爱因斯坦光电效应方程.根据不同波长的入射光产生的光电子的动能的大小,可以求出该金属的逸出功的大小,从而求出相应的入射光的波长. 解: 设A 为该金属的逸出功, 则有:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=A hc E A hcE A hck k 0212λλλ 因此可以得到:010eV,4hcA Aλλ=== 即能引起该金属表面释放电子的最大波长为λ4.15-12 波长0.100nm 0=λ的X 射线在碳块上受到康普顿散射, 求在900方向上所散射的X 射线波长以及反冲电子的动能。
分析 本题考察康普顿散射公式。
根据散射角的大小可以求出散射波长, 然后根据散射前后的总的能量守恒可以求出反冲电子的动能。
解: 由康普顿散射公式00(1cos )0.0024(1cos )(nm)hm cλλλθθ∆=-=-=- 可知散射波长为:00.0024(10)0.1000.1024(nm)λλλ=∆+=-+=根据能量守恒 , 电子的动能应等于散射前后光子的能量之差, 即:170011() 4.6610(J)291(eV)E hv hv hc λλ-=-=-=⨯=15-13 在康普顿散射中,入射光子的波长为0.003nm, 反冲电子的速度为0.6c , c 为真空中的光速. 求散射光子的波长及散射角.分析 本题散射前后能量守恒, 由反冲电子和入射光子的能量差就可以求出散射光子的波长, 然后根据康普顿散射公式求出散射角. 解: 反冲电子的能量为:202022020225.06.01c m c m c c c m c m mc =-⎪⎭⎫ ⎝⎛-=-=ε根据能量守恒, 该能量同时也等于入射光子能量的减少, 所以有:20025.0c m hchc==-ελλ由此可以解出散射光子的波长为:2200.0043nm 0.25h h m c λλ==-根据康普顿散射公式可得:2sin 2200θλλc m h =- 所以可求出散射角为:o '6224θ=15-14 设康普顿散射实验的反射光子波长为0.0711nm, 求: (1) 这些光子的能量多大?(2) 在θ=1800处, 散射光子的波长和能量多大? (3) 在θ=1800处, 电子的反冲能量多大? 分析 本题考察康普顿散射公式.解: (1) 348150116.6310310 2.810(J)7.1110ch ελ---⨯⨯⨯=⨯⨯== (2) 3412318022 6.6310 4.8610(m)9.1110310h m c λ---⨯⨯∆===⨯⨯⨯⨯ 1107.59610(m)λλλ-=∆+=⨯相应的散射光子的能量为:34815116.6310310 2.6210(J)7.59610ch ελ---⨯⨯⨯=⨯⨯== (3) 160 1.810J e E εε-=-=⨯15-15 一光子与自由电子碰撞,电子可能获得的最大能量为6 keV ,求入射光子的波长和能量(用J 或eV 表示)。
分析 本题考察康普顿散射的规律。
解 光子反向弹回时(πθ=),电子将获得最大的能量343180 6.6310(1cos )(1cos )0.0048(nm)9.1110310h m c λθπ--⨯∆-=⨯-=⨯⨯⨯= 电子获得的能量)()11(0000λλλλλλλνν∆+∆=∆+-='-=hc hc h h E k整理后得0020=∆-∆+kE hc λλλλ 解得入射光波长nm 00786.02220==k E hc λλλλ∆+⎪⎭⎫ ⎝⎛∆+∆- 入射光子能量1402.5310J 158(keV)hcE λ-==⨯=15-16.用里德伯常量R 表示氢原子光谱的最短波长.分析 本题考察的是氢光谱的波数公式.氢原子光谱的最短波长为n=∞能级向n=1能级的跃迁而产生.解 R R =⎪⎭⎫ ⎝⎛∞-=22min1111λ所以有min λ15-17 计算氢原子的电离电势和第一激发电势. 分析 本题考察的是氢原子的能级公式. 解: 由氢原子能级光子公式213.6eV n E n=-因此电离能:10(13.6)13.6(eV)E E E ∞=-=--=所以电离电势:/13.6V U E e ==从基态到第一激发态所需要能量为:()()222113.6/213.6/110.2(eV)E E E ∆=-=---=所以第一激发电势为10.2V . 15-18 试求(1) 氢原子光谱巴尔末线系辐射的、能量最小的光子的波长; (2) 巴尔末线系的线系极限波长. 分析 本题考察的是氢光谱的波数公式.解: (1) 巴尔末线系为氢原子的高激发态向n =2的能级跃迁产生的谱线系, 因此能量最小的谱线对应于由n =3的能级向n =2的能级的跃迁。
