§310三角函数的诱导公式(二)
1.3.1三角函数的诱导公式2

玛纳斯县一中
温故知新
任意角三角函数的定义
定 义
图
单 位 圆 中
y P(x,y) 。 α
一 般 地
P(x,y)
sin
cos
y
x
y x
tan
| OP | r(r 0) y r x r y x
想一想,记一记
角度a 弧度a sina 0°
6
2. 填写下表:
45° 60° 90° 180° 270°
cosa tana
归纳总结
y α 的终边
P(x,y)
.
x
诱导公式(一):
o
sin( k 2 ) sin cos( k 2 ) cos t an( k 2 ) t an (k z )
α的终边
角终边关于y轴对称
x
o
x
归纳总结
sin( 2k ) sin
公式一:
公式二:
cos( 2k ) cos (k Z ) tan( 2k ) tan
公式三:
sin( ) sin cos( ) cos tan( ) tan
2.以诱导公式一~四为基础,还可以 产生一些派生公式, 如sin(2π -α )=-sinα 等.
课本P29
1,4. 1
再见!
用公式三或一
任意正角的 三角函数
用公式一
0 到 360 的角
o
o
用公式 二或四
的三角函数
锐角三 角函数
学以致用 例2.化简
cos(180 ) sin( 360) sin( 180) cos(180 )
高一数学(三角函数的诱导公式 2)

3p 3p sin( - a ), cos( - a ), 2 2 3p 3π sin( + a ), cos( +α) 2 2
公式五: 公式五:
sin (
π
2
−α) = cosα −α) = sin α
cos(
π
2
sin(
π
2
+α) = cosα +α) = −sin α
公式六: 公式六:
cos(
π
2
形成结论
kπ 所有诱导公式可统一为 ±α(k ∈Z) 2 的三角函数与α的三角函数之间的关系 的三角函数之间的关系. 的三角函数与 的三角函数之间的关系
它们之间的关系归纳为: 它们之间的关系归纳为:
奇变偶不变,符号看象限. 奇变偶不变,符号看象限.
典例讲解
化简: 例1 化简:
11 π sin(2π -α)cos(π +α)cos( +α)cos( -α) 2 2 9π cos(π -α)sin(3π -α)sin(- π -α)sin( +α) 2
y
π
2 −α 的终边
π
y=x
α的终边
O
x
y
π
2
−α 的终边
(y, P2(y,x) α的终边
O
P1(x ,y) x
),则关 设角α的终边上有一点P1(x,y),则关 π 于直线y=x y=x对称的角 的终边上的点P 于直线y=x对称的角 −α 的终边上的点P2的 2 坐标如何? 坐标如何?
形成结论
2
cos(180 +α) ⋅ sin(α + 360 ) 2. o o sin(-α-180 ) ⋅ cos(-180 -α)
高中数学 人教A版必修4 第1章 1.3三角函数的诱导公式(二)

研一研·问题探究、课堂更高效 (2)诱导公式五的推导:
§1.3(二)
π 问题 1 若 α 为任意角,那么 -α 的终边与角 α 的终边有怎 2 样的对称关系? 本 课 π 时 答 角 α 的终边与 -α 的终边关于直线 y=x 对称. 栏 2 目 π 开 问题 2 设角 α 与单位圆交于点 P(x, y), 则 - 2 关
y.
所以,对任意角 α
sin α .
π 都有:sin2-α=
cos α
π ,cos2-α=
研一研·问题探究、课堂更高效
探究点二 诱导公式六
π ,cos2+α=
§1.3(二)
(1)诱导公式六: π sin2 +α= cos α
本 课 时 栏 目 开 关
填一填·知识要点、记下疑难点
§1.3(二)
2.诱导公式五~六的记忆 π π -α, +α 的三角函数值,等于 α 的异名三角函数值, 2 2 本
课 时 栏 目 开 关
前面加上一个把 α 看成锐角时原函数值的符号, 记忆口诀 为“函数名改变,符号看象限”.
研一研·问题探究、课堂更高效
§1.3(二)
α 与单位圆交于点 P′,写出点 P′的坐标.
答 P′(y,x).
研一研·问题探究、课堂更高效
§1.3(二)
问题 3 根据任意角三角函数的定义,完成下列填空:
本 课 时 栏 目 开 关
sin α= y ,cos α= x ;
π sin2 -α=
x
π ,cos2-α=
§1.3(二)
本 课 时 栏 目 开 关
§1.3(二)
【学习要求】 1.掌握诱导公式五、六的推导,并能应用于解决简单的求值、化 简与证明问题. 本 课 时 2.对诱导公式一至六,能作综合归纳,体会出六组公式的共性与 栏 目 个性,培养由特殊到一般的数学推理意识和能力. 开 关 现问题、解决问题的能力.
1.3 三角函数的诱导公式(二) 教案+习题
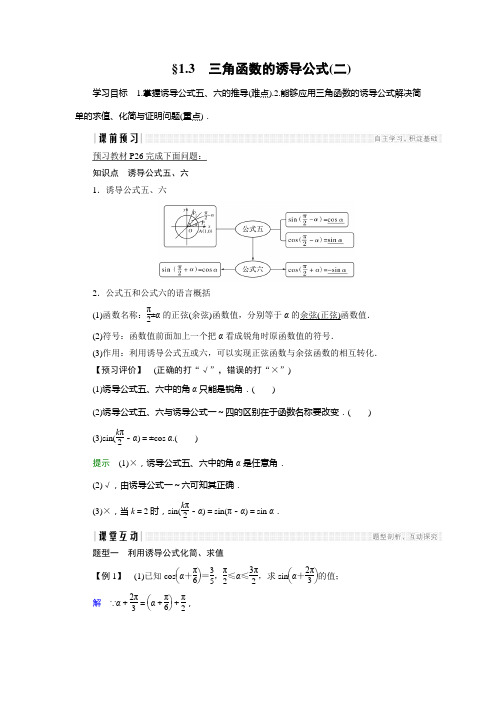
§1.3 三角函数的诱导公式(二)学习目标 1.掌握诱导公式五、六的推导(难点).2.能够应用三角函数的诱导公式解决简单的求值、化简与证明问题(重点).预习教材P26完成下面问题: 知识点 诱导公式五、六 1.诱导公式五、六2.公式五和公式六的语言概括(1)函数名称:π2±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值.(2)符号:函数值前面加上一个把α看成锐角时原函数值的符号.(3)作用:利用诱导公式五或六,可以实现正弦函数与余弦函数的相互转化. 【预习评价】 (正确的打“√”,错误的打“×”) (1)诱导公式五、六中的角α只能是锐角.( )(2)诱导公式五、六与诱导公式一~四的区别在于函数名称要改变.( ) (3)sin(k π2-α)=±cos α.( )提示 (1)×,诱导公式五、六中的角α是任意角. (2)√,由诱导公式一~六可知其正确.(3)×,当k =2时,sin(k π2-α)=sin(π-α)=sin α.题型一 利用诱导公式化简、求值【例1】 (1)已知cos ⎝⎛⎭⎫α+π6=35,π2≤α≤3π2,求sin ⎝⎛⎭⎫α+2π3的值; 解 ∵α+2π3=⎝⎛⎭⎫α+π6+π2,∴sin(α+2π3)=sin ⎣⎡⎦⎤⎝⎛⎭⎫α+π6+π2=cos ⎝⎛⎭⎫α+π6=35. (2)化简:sin (2π+α)cos (π-α)cos (π2-α)cos (7π2-α)cos (π-α)sin (3π-α)sin (-π+α)sin (5π2+α).解 原式=sin α·(-cos α)·sin α·(-sin α)(-cos α)·sin α·(-sin α)·cos α=tan α.规律方法 求值问题中角的转化方法 任意负角的三角函数――→用公式一或三任意正角的三角函数――→用公式一0~2π的角的三角函数――→用公式二或四、或五或六锐角三角函数【训练1】 已知cos(π6-α)=23,求下列各式的值:(1)sin(π3+α);(2)sin(α-2π3).解 (1)sin(π3+α)=sin[π2-(π6-α)]=cos(π6-α)=23.(2)sin(α-2π3)=sin[-π2-(π6-α)]=-sin[π2+(π6-α)] =-cos(π6-α)=-23.题型二 利用诱导公式证明恒等式【例2】 求证:tan (2π-α)sin (-2π-α)cos (6π-α)sin ⎝⎛⎭⎫α+3π2cos ⎝⎛⎭⎫α+3π2=-tan α.证明 左边=tan (-α)·sin (-α)·cos (-α)sin ⎣⎡⎦⎤2π-⎝⎛⎭⎫π2-α·cos ⎣⎡⎦⎤2π-⎝⎛⎭⎫π2-α=(-tan α)·(-sin α)·cos αsin ⎣⎡⎦⎤-⎝⎛⎭⎫π2-αcos ⎣⎡⎦⎤-⎝⎛⎭⎫π2-α=sin 2α-sin ⎝⎛⎭⎫π2-αcos ⎝⎛⎭⎫π2-α=sin 2α-cos α·sin α=-sin αcos α=-tan α=右边.∴原等式成立.规律方法 证明等式的常用方法利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有: (1)从一边开始,使得它等于另一边,一般由繁到简. (2)左右归一法:即证明左右两边都等于同一个式子.(3)针对题设与结论间的差异,有针对性地进行变形,以消除差异. 【训练2】 求证:2sin ⎝⎛⎭⎫θ-3π2cos ⎝⎛⎭⎫θ+π2-11-2sin 2(π+θ)=tan (9π+θ)+1tan (π+θ)-1. 证明 左边=-2sin ⎝⎛⎭⎫3π2-θ·(-sin θ)-11-2sin 2θ=2sin ⎣⎡⎦⎤π+⎝⎛⎭⎫π2-θsin θ-11-2sin 2θ=-2sin ⎝⎛⎭⎫π2-θsin θ-11-2sin 2θ=-2cos θsin θ-1cos 2θ+sin 2θ-2sin 2θ =(sin θ+cos θ)2sin 2θ-cos 2θ=sin θ+cos θsin θ-cos θ. 右边=tan θ+1tan θ-1=sin θ+cos θsin θ-cos θ.∴左边=右边,故原等式成立.【例3】 已知cos α=-45,且α为第三象限角.(1)求sin α的值;(2)求f (α)=tan (π-α)·sin (π-α)·sin (π2-α)cos (π+α)的值.解 (1)因为α为第三象限角,所以sin α=-1-cos 2α=-35.(2)f (α)=(-tan α)·sin α·cos α-cos α=tan α·sin α=sin αcos α·sin α =sin 2αcos α=(-35)2×(-54)=-920. 【迁移1】 本例条件不变,求f (α) =sin (5π-α)cos (7π2-α)tan (-π+α)-tan (-19π-α)sin (-α)的值.解 f (α)=sin α·(-sin α)·tan αtan α·(-sin α)=sin α=-35.【迁移2】 本例条件中“cos α=-45”改为“α的终边与单位圆交于点P (m ,154)”,“第三象限”改为“第二象限”,试求sin (α-π2)sin (π+α)-sin (3π2-α)+1的值.解 由题意知m 2+(154)2=1, 解得m 2=116,因为α为第二象限角,故m <0, 所以m =-14,所以sin α=154,cos α=-14. 原式=-cos α(-sin α)-(-cos α)+1=14-154-14+1=-3+156.规律方法 用诱导公式化简求值的方法(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行切化弦,以保证三角函数名最少.(2)对于π±α和π2±α这两套诱导公式,切记运用前一套公式不变名,而运用后一套公式必须变名.课堂达标1.sin 165°等于( ) A .-sin 15° B .cos 15° C .sin 75°D .cos 75°解析 sin 165°=sin(90°+75°)=cos 75°. 答案 D2.已知sin(α+π4)=13,则cos(π4-α)的值为( )A .223B .-223C .13D .-13解析 cos(π4-α)=cos[π2-(α+π4)]=sin(α+π4)=13.答案 C3.代数式sin 2(A +45°)+sin 2(A -45°)的化简结果是________. 解析 原式=sin 2(A +45°)+sin 2(45°-A ) =sin 2(A +45°)+cos 2(A +45°)=1. 答案 14.若cos α=15,且α是第四象限角,则cos(α+5π2)=________.解析 由题意得sin α=-1-cos 2α=-265,所以cos(α+5π2)=-sin α=265.答案2655.已知sin(5π-θ)+sin ⎝⎛⎭⎫52π-θ=72,求sin 4⎝⎛⎭⎫π2-θ+cos 4⎝⎛⎭⎫32π+θ的值. 解 ∵sin(5π-θ)+sin ⎝⎛⎭⎫52π-θ =sin(π-θ)+sin ⎝⎛⎭⎫π2-θ =sin θ+cos θ=72,∴sin θcos θ=12[(sin θ+cos θ)2-1]=12⎣⎡⎦⎤⎝⎛⎭⎫722-1=38, ∴sin 4⎝⎛⎭⎫π2-θ+cos 4⎝⎛⎭⎫32π+θ=cos 4θ+sin 4θ =(sin 2θ+cos 2θ)2-2sin 2θcos 2θ =1-2×⎝⎛⎭⎫382=2332.课堂小结1.学习了本节知识后,连同前面的诱导公式可以统一概括为“k ·π2±α(k ∈Z )”的诱导公式.当k 为偶数时,得α的同名函数值;当k 为奇数时,得α的异名函数值,然后前面加一个把α看成锐角时原函数值的符号.2.诱导公式反映了各种不同形式的角的三角函数之间的相互关系,并具有一定的规律性,“奇变偶不变,符号看象限”,是记住这些公式的有效方法.3.诱导公式是三角变换的基本公式,其中角α可以是一个单角,也可以是一个复角,应用时要注意整体把握、灵活变通.基础过关1.已知sin α=14,则cos(α+π2)=( )A .14B .-14C .154D .-154解析 cos(α+π2)=-sin α=-14.答案 B2.若sin(180°+α)+cos(90°+α)=-a ,则cos(270°-α)+2sin(360°-α)的值是( ) A .-23aB .-32aC .23aD .32a解析 由条件得-sin α-sin α=-a ,故sin α=a2,原式=-sin α-2sin α=-3sin α=-32a .答案 B3.已知cos(π2+φ)=32,且|φ|<π2,则tan φ等于( )A .-33B .33C .- 3D . 3解析 由cos(π2+φ)=-sin φ=32,得sin φ=-32,又∵|φ|<π2,∴φ=-π3,∴tan φ=-3.答案 C4.若sin(α+π12)=13,则cos(α+7π12)=________.解析 cos(α+7π12)=cos[π2+(α+π12)]=-sin(α+π12)=-13.答案 -135.化简sin ⎝⎛⎭⎫15π2+αcos ⎝⎛⎭⎫α-π2sin ⎝⎛⎭⎫9π2-αcos ⎝⎛⎭⎫3π2+α=________.解析 原式=sin (32π+α)·cos (π2-α)sin (π2-α)sin α=(-cos α)·sin αcos α·sin α=-1.答案 -16.已知sin α是方程5x 2-7x -6=0的根,且α为第三象限角,求 sin ⎝⎛⎭⎫α+3π2·sin ⎝⎛⎭⎫3π2-α·tan 2(2π-α)·tan (π-α)cos ⎝⎛⎭⎫π2-α·cos ⎝⎛⎭⎫π2+α的值.解 因为5x 2-7x -6=0的两根为x =2或x =-35,所以sin α=-35,又因为α为第三象限角,所以cos α=-1-sin 2α=-45.所以tan α=34.故原式=(-cos α)·(-cos α)·tan 2α·(-tan α)sin α·(-sin α)=tan α=34.7.设tan ⎝⎛⎭⎫α+8π7=m . 求证:sin ⎝⎛⎭⎫α+15π7+3cos ⎝⎛⎭⎫α-13π7sin ⎝⎛⎭⎫-α+20π7-cos ⎝⎛⎭⎫α+22π7=m +3m +1.证明 左边=sin ⎣⎡⎦⎤π+⎝⎛⎭⎫α+8π7+3cos ⎣⎡⎦⎤⎝⎛⎭⎫α+8π7-3πsin ⎣⎡⎦⎤4π-⎝⎛⎭⎫α+8π7-cos ⎣⎡⎦⎤2π+⎝⎛⎭⎫α+8π7=-sin ⎝⎛⎭⎫α+8π7-3cos ⎝⎛⎭⎫α+8π7-sin ⎝⎛⎭⎫α+8π7-cos ⎝⎛⎭⎫α+8π7=tan ⎝⎛⎭⎫α+8π7+3tan ⎝⎛⎭⎫α+8π7+1=m +3m +1=右边. ∴原等式成立.能力提升8.若f (sin x )=3-cos 2x ,则f (cos x )等于( ) A .3-cos 2x B .3-sin 2x C .3+cos 2xD .3+sin 2x解析 f (cos x )=f (sin(π2-x ))=3-cos 2(π2-x )=3-cos(π-2x )=3+cos 2x .答案 C9.α为锐角,2tan(π-α)-3cos ⎝⎛⎭⎫π2+β=-5,tan(π+α)+6sin(π+β)=1,则sin α=( ) A .355B .377C .31010D .13解析 由条件可知-2tan α+3sin β=-5①,tan α-6sin β=1②, ①式×2+②式可得tan α=3, 即sin α=3cos α,又sin 2α+cos 2α=1,α为锐角, 故可解得sin α=31010.答案 C10.已知tan(3π+α)=2,则sin (α-3π)+cos (π-α)+sin (π2-α)-2cos (π2+α)-sin (-α)+cos (π+α)=________.解析 ∵tan(3π+α)=2,∴tan α=2, ∴原式=sin αsin α-cos α=tan αtan α-1=22-1=2. 答案 211.定义:角θ与φ都是任意角,若满足θ+φ=90°,则称θ与φ“广义互余”.已知sin(π+α)=-14,下列角β中,可能与角α“广义互余”的是________(填上所有符合的序号).①sin β=154;②cos(π+β)=14;③tan β=15; ④tan β=155. 解析 ∵sin(π+α)=-sin α, ∴sin α=14,若α+β=90°,则β=90°-α,故sin β=sin(90°-α)=cos α=±154,故①满足; ③中tan β=15,即sin β=15cos β,又sin 2β+cos 2β=1,故sin β=±154,即③满足,而②④不满足. 答案 ①③12.是否存在角α,β,α∈⎝⎛⎭⎫-π2,π2,β∈(0,π),使等式 ⎩⎪⎨⎪⎧sin (3π-α)=2cos ⎝⎛⎭⎫π2-β,3cos (-α)=-2cos (π+β)同时成立.若存在,求出α,β的值;若不存在,说明理由.解 由条件,得⎩⎪⎨⎪⎧sin α=2sin β, ①3cos α=2cos β. ②①2+②2,得sin 2α+3cos 2α=2, ③ 又因为sin 2α+cos 2α=1,④由③④得sin 2α=12,即sin α=±22,因为α∈⎝⎛⎭⎫-π2,π2,所以α=π4或α=-π4. 当α=π4时,代入②得cos β=32,又β∈(0,π),所以β=π6,代入①可知符合.当α=-π4时,代入②得cos β=32,又β∈(0,π),所以β=π6,代入①可知不符合.综上所述,存在α=π4,β=π6满足条件.13.(选做题)已知sin ⎝⎛⎭⎫-π2-α·cos ⎝⎛⎭⎫-5π2-α=60169,且π4<α<π2,求sin α与cos α的值. 解 sin ⎝⎛⎭⎫-π2-α=-cos α, cos ⎝⎛⎭⎫-5π2-α=cos ⎝⎛⎭⎫2π+π2+α=-sin α. ∴sin α·cos α=60169,即2sin α·cos α=120169.① 又∵sin 2α+cos 2α=1,②①+②得(sin α+cos α)2=289169,②-①得(sin α-cos α)2=49169.又∵α∈⎝⎛⎭⎫π4,π2,∴sin α>cos α>0, 即sin α+cos α>0,sin α-cos α>0, ∴sin α+cos α=1713,③ sin α-cos α=713,④③+④得sin α=1213,③-④得cos α=513.。
§1.3三角函数的诱导公式(2)

第一章 §1.3 三角函数的诱导公式 第二课时学习目标:(1)理解识记诱导公式(2)理解和掌握公式的内涵及结构特征,会初步运用诱导公式求三角函数的值 (3)会进行简单三角函数式的化简和证明。
预习导航:要求:在上课前认真阅读教材,完成导学案上的预习导航,并将不懂知识进行标注 1. 写出诱导公式一~四?观察这四组公式共同特点是?2、 公式五3、 公式六公式五~六可以概括如下:4、点P 1(x,y )关于直线y=x 对称的点P 2的坐标如何? 探究问题(一) 诱导公式五思考1:sin (90°-60°)与sin60°的值相等吗?相反吗?思考2:sin (90°-60°)与cos60°,cos(90°-60°)与sin60°的值分别有什么关系?据此,你有什么猜想?思考3:如果α为锐角,你有什么办法证明ααπcos )2sin(=-与ααπsin )2cos(=-?思考4:若α为一个任意角,那么απ-2的终边与α的终边有什么对称关系?思考5:设角α的终边与单位圆的交点为P 1(x,y ),则απ-2的终边与单位圆的交点为P 2(x,y ),根据三角函数的定义,你能获得那些结论?探究问题(二)απ+2的诱导公式思考1:απ-2与απ+2有什么内在联系?思考2:根据相关诱导公式推导,3sin(),2πα- 3sin(),2πα+ 3cos(),2πα-)23cos(απ+探究问题(三) 公式的应用 例1: 化简:)29)sin(-)sin(--)sin(3-cos()-211)cos(2)cos()cos(-sin(2απαπαπαπαπαπαπαπ+++课堂小结:1.这节课学到了什么2.各小组表现如何课下作业:课本P28 练习7)60(sin 1)60(cos )30(tan 1ααα++++-31)30(sin =-α 32)6(cos =-απ)32(sin πα-例3 已知 ,求 的值。
三角函数诱导公式(二)

cosπ2-θ=sin θ,cosπ2+θ=-sin θ, 所以 B,D 项与 cos32π-θ的值相等.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
4.若 sin(180°+α)+cos(90°+α)=-41,则 cos(270°-α)+2sin(360°-α)的值为
=1-c2os2θ=sin22θ=右边,
∴原等式成立.
三、诱导公式的综合应用
例 3 已知 sin(π-α)-cos(π+α)= 32,求下列各式的值: (1)sin32π+αcosα-π2;
解 由 sin(π-α)-cos(π+α)= 32, 得 sin α+cos α= 32, 两边平方整理得 2sin αcos α=-79, ∴sin αcos α=-178, ∴cos α-sin α =± cos α-sin α2=± 1-2sin αcos α
√ A.-16
B.-38
1 C.6
3 D.8
解析 由 sin(180°+α)+cos(90°+α)=-14, 得 sin α=18,
cos(270°-α)+2sin(360°-α)=-sin α-2sin α=-3sin α=-38.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
(2)已知 sinπ3-α=12,则 cosπ6+α的值为__12__. 解析 cosπ6+α=cosπ2-π3-α =sinπ3-α=12.
延伸探究 1.将本例(2)的条件改为 sinπ3+α=12,求 cos56π+α的值.
解 cos56π+α=cosπ2+π3+α =-sinπ3+α=-12.
=co-s θsi·nsiθn·θc·otsanθ θ
1.3三角函数的诱导公式(二)

课 题:1.3正弦、余弦的诱导公式(二)教学目的:学会关于90︒ k ± α两套诱导公式,并能应用,进行简单的三角函数式的化简及论证。
教学重点:诱导公式教学难点:诱导公式的灵活应用授课类型:新授课课时安排:1课时教 具:多媒体、实物投影仪教学过程:一、讲解新课:诱导公式5:(课件1.3.7)sin(90︒ -α) = cos α, cos(90︒ -α) = sin α.tan(90︒ -α) = cot α, cot(90︒ -α) = tan α. sec(90︒ -α) = csc α, csc(90︒ -α) = sec α诱导公式6:(课件1.3.8) sin(90︒ +α) = cos α, cos(90︒ +α) = -sin α.tan(90︒ +α) = -cot α, cot(90︒ +α) = -tan α. sec(90︒ +α) = -csc α, csc(90︒+α) = sec α如图所示 sin(90︒ +α) = M’P’ = OM = cos αcos(90︒ +α) = OM’ = PM = -MP = -sin α或由6式:sin(90︒ +α) = sin[180︒- (90︒ -α)] = sin(90︒ -α) = cos αcos(90︒ +α) = cos[180︒- (90︒ -α)] = -sin(90︒ -α) = -cos α二、讲解范例: 例1)2cos()5cos()2sin()4sin()cot()2tan()23cos()2sin(απαπαπαπαπαπαπαπ+-+--=+-+---+k k k 求证: 证:α-ααα=α+α-α+α=sin cos cos sin cot tan sin cos 左边 α-ααα=α+α-αα-=s i n c o s c o s s i n s i n c o s c o s s i n 右边 左边 = 右边 ∴等式成立例2的值。
三角函数的诱导公式(二)

§1.3 三角函数的诱导公式(二)【使用说明及学法指导】1.先精读一遍教材P25-P27,用红色笔进行勾画。
再针对预习案二次阅读并回答;2.若预习完可对合作探究部分进行认真审题,做不完的正课时再做,对于变式部分BC层可以不做;3.找出自己的疑惑和需要讨论的问题准备课上讨论质疑;【学习目标】1.掌握诱导公式并能灵活应用进行化简求值,提高和渗透化归数学思想;2.积极讨论,踊跃展示,大胆质疑,探究诱导公式的应用规律;3.以极度热情投入学习,享受学习数学的快乐;+( 2kα∈的关系,记忆口诀“奇变偶不变,符号看象4之间角的三角函1.将下列三角函数化为045之间的三角函数(1)sin115= (2)cos105= (3)tan110= (4)sin85=2.求值(1)19sin()4π-= (2)4tan()3π-= (3)cos()2πα-= (4) sin()2πα-=例1、 (1)化简)2cos()23sin()27cos()2sin()23sin()sin()3tan(απαππααπαπαπαπ++--+---(2)求证:对任意的整数k1)212cos()232sin()212cos()212sin(-=--∙++++∙-+απαπαπαπk k k k变式练习:已知C B A ,,是ABC ∆的三个内角,求证: (1)A C B A cos )2cos(-=++(2) 2cos 2sin AC B =+ (3) 43tan 4tan CB A +-=+π例2.(1)已知方程sin(α - 3π) = 2cos(α - 4π),求)sin()23sin(2)2cos(5)sin(ααπαπαπ----+-的值。
(2)已知31)3sin(=+απ,求)65cos(απ+值变式练习:已知)23sin()sin()23sin()2cos()2cos()(απαππααπαπα+∙--+-∙-∙+=f (1)化简)(αf(2)若α是第三象限角,且51)23cos(=-πα,求)(αf 的值课堂小结一、选择题1、sin(α-2π)= ( ) A .sin(23π+α) B .cos(2π+α) C .cos(2π-α) D .sin(2π+α)2、如果sin(π+α)=-21,那么cos(α-π23)= ( ) A .-21 B .21 C .-23 D .233、)75(sin 2cos )(cos f x x f ,则== ( )A .21 B .21- C .23 D .23- 4、式子)690sin(630sin )585cos(︒-+︒︒-的值是 ( )A .22B .2C .32D .-325、已知31)4sin(=-πα,则)4cos(απ+的值等于 ( )A .232B .-232 C .31D .-31二、填空题6、化简___________________28sin 36tan 54tan 62sin 020002=+⋅+.7、54cos 53cos 52cos5cosππππ+++= . 8、)(sin ,17cos )(cos x f x x f 求若==______________.三、解答题9、已知的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.10 三角函数的诱导公式(二)
教学目标:教学知识点:正弦、余弦的诱导公式.
教学过程:
一、复习回顾
诱导公式一~四 (1)公式一:sin(α+2k π)=______,cos(α+2k π)=______,tan(α+2k π)=______,其中k ∈Z .
(2)公式二:sin(-α)=_________,cos(-α)=_________,tan(-α)=________.
(3)公式三:sin(π-α)=________,cos(π-α)=________,tan(π-α)=________.
(4)公式四:sin(π+α)=________,cos(π+α)=________,tan(π+α)=________.
二、新授
诱导公式五~八
(1)公式五:=-)2sin(
απ ,=-)2cos(απ
,=-)2tan(απ . (2)公式六:=+)2sin(απ ,=+)2cos(απ ,=+)2
tan(απ . (3)公式七:=-)23sin(απ ,=-)23cos(απ ,=-)2
3tan(απ . (4)公式八:=+)23sin(απ ,=+)23cos(απ ,=+)2
3tan(απ . 总结:①诱导公式五~八的记忆απ±2,απ±2
3的三角函数值,等于α的________三角函数值,前面加上一个把α看成锐角时原函数值的________.
②诱导公式一~八记忆口诀为: .
三、应用举例
例1.化简)2
5sin()2cos()5tan()4cos()23cos()3sin(πααππααππααπ-+-+--
例2.①若sin ⎝⎛⎭⎫α+π12=13,则cos ⎝⎛⎭
⎫α+7π12=________. ②若sin(3π+α)=-12
,则cos ⎝⎛⎭⎫72π-α=________.
例3.已知3
1)75cos(=+αο,且οο90180-<<-α,求)15cos(α-ο的值.
例4.①已知f (sin x )=cos 3x ,则f (cos 10°)的值为______.
②(cos )cos17,(sin )f x x f x =若求.
作业: 班级 姓名 学号
1.化简)2
cos()2sin()sin()cos(αππααππα+---= . 2.化简)
3tan()2sin()
sin()2cos(απαπ
απαπ-++-= . 3.已知sin ⎝⎛⎭⎫α-π4=13,则cos ⎝⎛⎭
⎫π4+α的值等于________. 4.已知cos(75°+α)=13
,则sin(α-15°)+cos(105°-α)的值是________. 5.已知41)6sin(=+π
x ,则)3
(sin )65sin(2x x -+-ππ= . 6.代数式sin 2(A +45°)+sin 2(A -45°)的化简结果是________.
7.sin 21°+sin 22°+…+sin 288°+sin 289°=________.
8.已知tan(3π+α)=2,则sin (α-3π)+cos (π-α)+sin ⎝⎛⎭⎫π2-α-2cos ⎝⎛⎭⎫π2+α-sin (-α)+cos (π+α)
=________. 9.已知函数满足x 2cos )x (cos f =,则)15(sin f ︒= .
10.已知x x x f 3cos tan 1)(tan -=,则=)tan 1(x
f .
11.已知51)4sin(
-=-x π,且20π<<x ,求)4
sin(x +π的值.
12.设a =+)78tan(πα,求)7
22cos()720sin()713cos(3)715sin(πααππααπ+---++.。
