二项式定理公开课课件

合集下载

二项式定理公开课27534省名师优质课赛课获奖课件市赛课一等奖课件

对于某个k (k∈{ 0,1,2,…,n }), 相应旳项an-kbk是由
n-k个（a+b）中选a, k个（a+b）中选b得到旳.因为b选定后,
a旳选法也随之拟定, 所以, an-kbk出现旳次数相当于
从n个(a+b)中取k个b旳组合数 Cnk , 这么,(a+b)n旳展开式中， ankbk共有Cnk个，将它们合并同类项, 就得到二项展开式:
每个(a+b)在相乘时有两种选择，选a或选b，而且每个
(a+b)中旳a或b都选定后，才干得到展开式旳一项。
对(a+b)2展开式旳分析
(a+b)2＝ (a+b) (a+b) 展开后其项旳形式为：a2 ， ab ， b2
这三项旳系数为各项在展开式中出现旳次数。考虑b
每个都不取b旳情况有1种，即C20 ,则a2前旳系数为C20 恰有1个取b旳情况有C21种，则ab前旳系数为C21 恰有2个取b旳情况有C22 种，则b2前旳系数为C22
A C160
B C160
C C150
D C150
1.知识收获：二项式定理；二项式定理旳体现式及展开式旳通项、二项式系数与系数旳概念。
二项式定理
第 k 1项旳二项式系数通项
a b n Cn0an Cn1an1b Cnkankbk Cnnbn
二项式
二项式展开式
2.措施收获：正确区别“项旳系数”和“二项式系
7100
C1 100
799
Cr 100
7100r
C 99 100
71
C 100 100
70
∴8100被7除旳余数是1，所以 8100 天后旳这
一天是星期四.

新教材选择性必修二7.4.1二项式定理课件(37张)

9．二项式(x＋y)5的展开式中，含x2y3的项的系数是________；二项式系数是
__________.(用数字作答)
【解析】根据二项式的展开式通项公式可得Tr＋1＝C
r 5
x5－ryr，可得含x2y3的项为C
3 5
x2y3，所以其系数为10，二项式系数为C53 ＝10.
答案：10 10
10．设n∈N*，则C1n ＋Cn2 6＋C3n 62＋…＋Cnn 6n－1＝________．
x－2x n 展开式中第3项的系数比第2项的系数大162.
(1)n的值；
(2)求展开式中含x3的项，并指出该项的二项式系数．
【解析】(1)因为T3＝C2n (
x
)n－2－2x
2
＝4C2n
n－6 x2
，
T2＝C1n (
x
)n－1－2x
＝－2C1n
n－3 x2
，
依题意得4C2n ＋2Cn1 ＝162，所以2Cn2 ＋Cn1 ＝81，所以n2＝81，n＝9.
二项式定理二项式定理
基础认知·自主学习
【概念认知】
二项式定理
(a＋b)n＝ C 0 n a n ＋ C 1 n a n － 1 b ＋＋ C n r a n － r b r ＋＋ C n n b n ( n N * ) ．这个公式叫作二项式定
理，右边的多项式叫作(a＋b)n的二项展开式，它一共有_n_＋__1_项，其中
【解析】(1)根据题意得：C1m ＋Cn1 ＝7，即 m＋n＝7①，
f(x)的展开式中的x2的系数为C2m
＋C2n
m（m－1）＝2
n（n－1）＋2
m2＋n2－m－n
＝
2

二项式定理一等奖完整ppt课件

在数学中的地位和作用
二项式定理是组合数学中的基本定理之一，它描述了两个向量的和的n次幂的展开式。
在组合数学中，二项式定理被广泛应用于排列、组合、概率论等领域。同时，它也是多项式定理的基础之一。
03
二项式定理的证明方法
ቤተ መጻሕፍቲ ባይዱ 数学归纳法
数学归纳法是一种证明二项式定理的有效方法。首先，我们需要证明当n=1时，二项式定理成立。然后，假设当n=k时，二项式定理成立，再证明当n=k+1时，二项式定理也成立。通过这个递推关系，我们可以得出结论：当n为任意正整数时，二项式定理都成立。
二项式系数的应用
举例说明二项式系数在解决实际问题中的应用，如概率计算、统计学等。
06
总结与展望
二项式定理的重要性和影响
重要的数学工具
二项式定理是数学中重要的工具之一，在代数学、数论、组合数
学等学科中都有广泛的应用。
解决问题的关键
二项式定理可以解决一些经典的数学问题，如组合问题、概率问题等，为人们提供了重要的解题
思路和方法。
对其他学科的影响
二项式定理不仅在数学学科中有重要的地位，还对其他学科如物理学、工程学、计算机科学等产
生了深远的影响。
与其他数学分支的联系和相互渗透
01
与代数学的联系
二项式定理与代数学中的多项式理论密切相关，可以看作是多项式的一
种推广和应用。
02
与组合数学的相互渗透
二项式定理与组合数学有着密切的联系，它可以用来解决一些组合问题
数学归纳法的关键步骤是：第一步，证明基础情况（n=1）成立；第二步，假设归纳基础（n=k）成立，并由此推断归纳步骤（n=k+1）成立。第三步，根据归纳步骤得出结论，证明二项式定理对所有正整数n都成立。

《二项式定理》公开课课件

n
展开式的二项式系数和为
64.
（1）求 n （2）求展开式中的常数项（3）求展开式中所有的有理项
小结
(a b)n Cn0an C1nan1b Crnanrbr Cnnbn
———二项式定理 (n N )
二项式系数
展开式特征
通项公式
系数
谢谢大家！
敬请各位老师指导！
2
(a+b)32= (a+b) (a+b) (a+b)
项
a23 a12b11 ab1b2 2 b3
系数
都取取取
不一两三
取个个个
b
b
b
b
C302 C213 C232 C33
结果：(a+b)32=C320a32+C312a2bb++CC223b2a2b2+C33b3
合情推理
(a+b)2=C20a2+C21a1b1+C22b2 (a+b)3=C30a3+C31a2b1+C23a1b2+C33b3 (a+b)4 =C40a4+C41a3b1+C24a2b2+C34a1b3+C44b4 (a+b)n= Cn0an+Cn1an-1b1+ … +Cnran-rbr + … +Cnnbn
解:(1)依题意 Cn0 C1n Cn2 Cnn 2n 64 , ∴n=6
通项公式为
T r
1＝C6r
3
x
6r
2
1
3
x
r
Cr6
r 62r
1 x 3 2

二项式定理说课稿公开课一等奖课件省赛课获奖课件

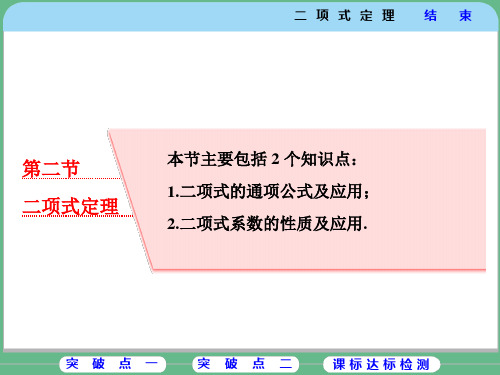
的展开式中含
x32的项的系数为
30，则
a＝
A. 3
B．－ 3
C．6
() D．－6
[解析] (2)∵Tr＋1＝Cr5(x2)5－r－x23r＝(－2)rCr5·x10－5r，由 10 －5r＝0，得 r＝2，∴T3＝(－2)2C25＝40.
(3)Tr＋1＝Cr5( x)5－r·－xar＝Cr5(－a)rx5－22r，由5－22r＝32，解得 r＝1.由 C15(－a)＝30，得 a＝－6.故选 D.
[答案] C
突破点一
突破点二
课标达标检测
二项式定理结束
(2)(2016·安徽安庆二模)将x＋4x－43 展开后，常数项
是________．
[解析]
x＋4x－43＝
x－
2 6 x
展开式的通项是
Ck6
( x)6－k·－ 2xk＝(－2)k·Ck6( x)6－2k.
令 6－2k＝0，得 k＝3.
所以常数项是 C36(－2)3＝－160.
[答案] (2)C (3)D
突破点一
突破点二
课标达标检测
二项式定理结束
(4)
x－ 1 24
8 x
的展开式中的有理项共有________项．
[解析]
(4)
x－ 1 8 24 x
的展开式的通项为
Tr ＋ 1 ＝
Cr8·( x)8－r2－4 1xr＝－12rCr8x16－4 3r(r＝0,1,2，…，8)，为使
突破点一
突破点二
课标达标检测
二项式定理结束
[方法技巧] 求解形如(a＋b)n(c＋d)m 的展开式问题的思路
(1)若 n，m 中一个比较小，可考虑把它展开得到多个，如(a＋b)2(c＋d)m＝(a2＋2ab＋b2)(c＋d)m，然后展开分别求解．

二项式定理ppt课件

$(a+b)^4$ 的中间项是什么？
$(a-b)^5$ 的展开式中，$a^4$ 的系数是多少
？
深化习题
01
02
03
04
深化习题1
利用二项式定理展开 $(a+b)^5$，并找出所有项
的系数。
深化习题2
求 $(a+b+c)^3$ 的展开式中 $a^2b$ 的系数。
深化习题3
利用二项式定理证明 $(a+b)^n$ 的展开式中，中
组合数学是研究组合问题的一门数学分支，与二项式定理密切相关。
在二项式定理的推导过程中，组合数学原理提供了组合数的计算方法和组合公式的应用。
通过组合数的计算，我们可以得到二项式展开的各项系数，进一步验证二项式定理的正确性。
幂级数的展开与收敛
幂级数是数学分析中的重要概念，与二项式定理的推导密切相关
微积分中的应用
二项式定理在微积分中有着广泛的应用，如在求极限、求导和积分等运算中。
概率论中的应用
在概率论中，二项式定理可以用于计算组合数学中的一些概率分布，如二项分布和超几何分布等。
05
习题与思考题
基础习题
基础习题1
基础习题2
基础习题3
基础习题4
$(a+b)^2$ 的展开式是什么？
$(a-b)^3$ 的展开式是什么？
概率分布
利用二项式定理，可以推导二项分布的概率分布函数和概率密度函数。
概率推断
在贝叶斯推断中，二项式定理可以用于计算后验概率和预测概率。Leabharlann 二项式定理在组合数学中的应用
01
组合数的计算
利用二项式定理，可以计算组合数$C(n, k)$，即从n个不同元素中取出

第十章第三节二项式定理课件(共47张PPT)

赋值法求系数和的应用技巧 (1)“赋值法”对形如(ax＋b)n，(ax2＋bx＋c)m(a，b，c∈R)的式子求其展开式的各项系数之和，常用赋值法，只需令 x＝1 即可；对形如(ax＋by)n(a， b∈R)的式子求其展开式各项系数之和，只需令 x＝y＝1 即可． (2)若 f(x)＝a0＋a1x＋a2x2＋…＋anxn，则 f(x)展开式中各项系数之和为 f(1)，偶次项系数之和为 a0＋a2＋a4＋…＝f（1）＋2f（－1），奇次项系数之和为 a1＋a3＋a5＋…＝f（1）－2f（－1） .令 x＝0，可得 a0＝f(0).
令
x＝1
代入2x－
1 x
6
＝1；
故所有项的系数之和为 1；故选 AC.]
求形如(a＋b)n(n∈N*)的展开式中与特定项相关的量 (常数项、参数值、特定项等)的步骤
(1)利用二项式定理写出二项展开式的通项公式 Tr＋1＝Crn an－rbr，常把字母和系数分离开来(注意符号不要出错)；
(2)根据题目中的相关条件(如常数项要求指数为零，有理项要求指数为整数)先列出相应方程(组)或不等式(组)，解出 r；
故选 B.]
3．(x＋1x －2)6(x>0)的展开式中含 x3 项的系数为________．
解析：
法一：因为(x＋1x －2)6＝(
x
－
1 x
)12，所以其展开式的通项公
式为 Tr＋1＝C1r2 (
x
)12－r(－
1 x
)r＝Cr12
(－1)r(
x )12－2r＝Cr12 (－1)rx6－r，由 6
1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)Ckn an－kbk 是二项展开式的第 k 项．( ) (2)在二项展开式中，系数最大的项为中间一项或中间两项．( ) (3)(a＋b)n 的展开式中，每一项的二项式系数与 a，b 无关．( ) (4)(a＋b)n 某项的系数是该项中非字母因数部分，包括符号等，与该项的二项式系数不同．( ) 答案： (1)× (2)× (3)√ (4)√

二项式定理(一)课件

03 二项式定理的扩展与推广
二项式定理的扩展形式
01
02
03
04
二项式定理的扩展形式包括二项式定理的逆用、二项式定理的变形以及二项式定理的推广
。
二项式定理的逆用是指将二项式定理中的幂次和系数互换，
从而得到新的等式。
二项式定理的变形是指通过改变二项式定理中的幂次或系数
，从而得到新的等式。
二项式定理的推广是指将二项式定理应用到更广泛的情况，例如应用到多项式、分式等。
解析
根据二项式定理，$(a + b)^{2}$ 可以展开为 $a^{2} + 2ab + b^{2}$，与给定的等式一致。
习题二：证明题
题目
证明 $(a - b)(a + b) = a^{2} - b^{2}$。
解析
首先展开 $(a - b)(a + b)$，得到 $a^{2} - b^{2}$，与给定的等式一致。
习题三：综合应用题
题目
计算 $(a + b + c)^{3}$ 的展开式。
解析
根据二项式定理，$(a + b + c)^{3}$ 可以展开为 $a^{3} + 3a^{2}b + 3ab^{2} + b^{3} + c^{3} + 3ac^{2} + 3bc^{2} + 3ab^{2}c + 3ac^{2}b$。
利用组合数的性质和二项式展开式的性质来推导公式。
公式证明的过程
基础步骤
当$n=0$和$n=1$时，公式成立。
归纳步骤
假设当$n=k$时公式成立，证明当$n=k+1$时公式也成立。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

因此, an-kbk出现的次数相当于
k Cn , 这样,(a+b)n的展开式中，从n个(a+b)中取k个b的组合数 k 将它们合并同类项, 就得到二项展开式: a nk bk 共有Cn 个，
0 1 k n (a b)n Cn an Cn an1b Cn ank bk Cn bn
n
（三）、存疑设问——突破难点
推陈出新
(a b) a b
1
(a b) a 2ab b
2
2
2
(a b)
3
?
(a b)4 = ?
(a b)5 = ?
……
对 (a b)2 展开式的分析
(a+b)2是2个(a+b)相乘，即(a+b)2= (a+b)* (a+b) = (a + b)* (a + b)=aa+ab+ba+bb 每个(a+b)在相乘时有两种选择，选a或选b，而且每个 (a+b)中的a或b都选定后，才能得到展开式的一项。由分步乘法计数原理，在合并同类项之前， (a+b)2的展开式共有2*2=22项，而且每一项a,b次数和都是2且每一项都是都是 a2-kbk(k=0,1,2) 的形式。
n
Cnk k 0,1,2 n 称为二项式系数，其中各项的系数
k 式中的 Cn a nk bk 叫做二项展开式的通项，它是二项
展开式的第 k
1 项,记作: Tk 1
C a b
k n
n k
k
第 k 1 项的二项式系数
通项
n n n
a b
n
C a C a b C a b C b
6 A C10
.
B
6 C10
5 C C10
D
5 C10
课堂练习：
1 4 2、（1）求 (2 x ) 的二项展开式. x
（2）求
(1 2x)
7
的二项展开式.
(3)求
1 7 (x ) x
的展开式中x 项的系数
3
= C30a3 +C31a2b+C32ab2 +C33 b3
(a+b)4＝ (a+b) (a+b) (a+b) (a+b)＝？
问题：
1)．(a+b)4展开后各项形式分别是什么？ a4 a3b a2b2 ab3 b4 2)．各项前的系数代表着什么？
各项前的系数代表着这些项在展开式中出现的次数
3)．你能分析说明各项前的系数吗？
香河一中秦淑霞
（二）、创设情境——引出问题问题:今天是星期五,
7天后的这一天是星期几呢？ 15天后的这一天呢？
算法：用各个数除以7，看余数是多少，再用五加余数来推算
若今天是星期五,再过8100天后的那一天是星期几?
8 除以7的余数是多少？
100
8
100
(7 1)

100
（a b) (n N )的展开式是什么？
0 n n k n
1 n 1 n
n k k
n n n
二项式展开式
2.方法收获：正确区分“项的系数”和“二项式系数” 3.思维收获归纳猜想的数学思想从特殊 —— 一般 —— 特殊，类比思想，
P 习题1.3的第2、4（1）（2）布置作业： 37
课本P31练习： 7 1.写出 p q 的展开式.
对(a+b)2展开式的分析
(a+b)2＝ (a+b) (a+b) 展开后其项的形式为：a2 ， ab ， b2
这三项的系数为各项在展开式中出现的次数。考虑b
每个都不取b的情况有1种，即C20 ,则a2前的系数为C20 恰有1个取b的情况有C21种，则ab前的系数为C21 恰有2个取b的情况有C22 种，则b2前的系数为C22 (a+b)2 = a2 +2ab+b2 ＝C20 a2 + C21 ab+ C22 b2 (a+b)3=a3 + 3a2b+3ab2 + b3
(n N * )
二项式定理（binomial theorem)
0 1 k n (a b)n Cn an Cn an1b Cn ank bk Cn bn
二项式
二项展开式
(n N )
这个公式叫做二项式定理,左边的多项式叫做二项式, 右边的多项式叫做 a b 的二项展开式，
T3 C52 (2 x) 2 40x 2 二项式系数为 52 10 C
3 x 3项T4 C5 (2 x)3 -80x 3
x 3项系数 - 80
• 引例：今天是星期五，若 8100 天后的这一天是星
期几呢？
0 1 r 解: 8100 7 1 100 C100 7100 C100 799 C100 7100r （）
b （）b
k
n
(a b) C a C a b C a
n 0 n n k n
1 n1 n
n k
b C b
k
n n n
(n N )
*
证明:
(a+b)n是n个(a+b)相乘,每个(a+b)在相乘时有两种选择选a 或选b,而且每个(a+b)中的a或b都选定才能得到展开的一项。在合并同类项之前,由分步乘法计数原理,(a+b)n的展开式共有2n项,而且每一项都是 an-kbk(k=0，1，2，…，n) 的形式. 对应的项an-kbk是由对于某个k (k∈{ 0,1,2,…,n }), n-k个（a+b）中选a, k个（a+b）中选b得到的.由于b选定后, a的选法也随之确定,
(1 + x) = 1 + C x + C x + + C x + + C x
在上式中，令 x = 1，则有：
n

1 n
2 2 n
r r n
n n n
2 = C + C + C ++ C ++ C
n
0 n
1 n
2 n
r n
n n
例1:求(1 2 X ) 的展开式
5
解：（ 2 x)5 1
0 n n
1 n1 n
k n k k n
二项式
二项展开式
0 1 2 n 1.系数规律：C n、C n、C n、、C n
2.指数规律：（1）各项的次数均为n；（2）a的次数按降幂排列，由n降到0， b的次数按升幂排列，由0升到n. 3.项数规律：展开式共有n+1个项
在二项式定理中，令a=1，b=x，则有：
请同学们猜一猜:
(a b)
尝试猜想
5
= ?
......(a b)
n
= ?
(a b) ? (n N )
n *
知识，只有以我们自主探索的方式获得才显得更为珍贵。
初步归纳
猜想:(a+b)n展开式又是怎样的呢？
(a b) （）a （）a b （）a
n n n1 n k
0 1 3 4 5 C5 (2 x) 0 C5 (2 x)1 C52 (2 x) 2 C5 (2 x)3 C（2 x) 4 C5 (2 x)5 5
1 10x 40x 2 80x 3 80x 4 32x 5
（求 1 2 x) 5 展开式第三项以及其二项式系数，求x3项的系数
2.求 2a 3b 的展开式的第三项.
6
3.求
3b 2a
3
6
的展开式的第三项.
4. x 2 x

7
3 C7 _ , 35 的展开式的第四项的二项式系数是
3 C7 23 280. 第四项的系数是
5、选择题： x 1 的展开式的第 6 项的系数是 D
10
99 100 C100 71 C100 70
被7除的余数是1，因此 8 一天是星期六.
∴8
100
100
天后的这
1.知识收获：二项式定理；二项式定理的表达式及展开式的通项、二项式系数与系数的概念。第 k 1 项的二项式系数通项二项式定理
a b
二项式
n
C a C a b C a b C b
3)．你能分析说明各项前的系数吗？
(a+b)4= (a+b) (a+b) (a+b) (a+b)
项： a4 a3b a2b2 ab3 b4
都不取 b 系数：C
0 4
取一个 b
取两个 b
取三个 b
取四个 b
C
1 4
C
2 4
C
3 4
C
4 4
(a+b)4=C40a4 +C41a3b +C42a2b2 +C43ab3 +C44b4 结果：