变位系数经验公式分配计算

变位系数计算公式

变位系数计算公式变位系数（coefficient of variation，简称CV）是描述数据离散程度的一种统计指标，它用于衡量数据的变异性，反映数据相对平均值的波动程度。

变位系数越小，表示数据的波动程度越小，反之则越大。

计算变位系数的公式为：CV=(标准差/平均值)×100其中，标准差是描述数据变异程度的一个指标，平均值是数据的平均值。

变位系数的数值无单位，可以用百分比表示，一般乘以100。

变位系数的计算步骤如下：1.计算数据的平均值，即将所有数据相加后除以数据的个数。

2.计算标准差，标准差是描述数据波动程度的一个指标，计算公式为数据每个值与平均值的差的平方和的均值的平方根。

（1）计算每个数据与平均值的差值，即（数据-平均值）。

（2）将差值的平方相加。

（3）将差值的平方和除以数据个数。

（4）对结果进行开方。

例如，有一组数据：5、10、15、20、25、要计算这组数据的变位系数，按照上述步骤进行计算如下：1.平均值=（5+10+15+20+25）/5=75/5=152.计算标准差：（1）（5-15）^2+（10-15）^2+（15-15）^2+（20-15）^2+（25-15）^2=500。

（2）500/5=100。

（3）√100=10。

3.计算变位系数：CV=（标准差/平均值）×100=(10/15)×100=66.67%。

通过计算得出的变位系数为66.67%，表示这组数据的波动程度相对较大。

变位系数的应用：变位系数主要用于比较两个或多个数据集的变异程度，可以帮助研究者选择样本数据、评估质量控制的有效性等。

在一些领域，变位系数还可以用于衡量不同因素对数据波动的影响程度，进而进行决策和优化。

例如，在金融领域中，可以使用变位系数来评估不同投资组合的风险和收益的相对关系。

总之，变位系数是一种用于衡量数据离散程度的指标，它结合了数据的平均值和标准差，能够综合考虑数据的中心趋势和波动程度。

齿轮转位系数

变位齿轮传动的设计步骤设计变位齿轮时，根据不同的已知条件，可采用不同的设计步骤。

（1）已知z1、z2、m、α、ha*和c*时，其设计步骤为：1）选择传动类型，若z1+z2 < 2zmin，必须采用正传动，否则可考虑其它传动类型；2）选择两齿轮的变位系数；3）计算两齿轮的几何尺寸；4）验算重合度及轮齿强度。

（2）已知z1、z2、m、a'、α、ha*和c*时，其设计步骤为：1）计算啮合角α'cosα'=（a/a')cosα2）选择两齿轮的变位系数invα'=2tgα(x1+x2)/(z1+z2) + invαx1+x2=(z1+z2)(invα'-invα)/2tgαx1≥ha*(zmin-z)/zmin，x2≥ha*(zmin-z)/zmin3）计算两齿轮的几何尺寸4）验算重合度及轮齿强度（3）已知i、m、a'、α、ha*和c*时，其设计步骤为：1）确定两齿轮的齿数因a'=acosα/cosα'=[m(z1+z2)/2]cosα/cosα'=[mz1(1+i)/2]cosα/cosα' 故z1≈2a'/(i+1)m 取整数，z2=iz1 取整数。

思考题：1)某机器中的一对外啮合标准圆柱直齿轮，小齿轮轮齿严重磨损，拟报废，大齿轮轮齿磨损较轻，拟修复。

试问采用什么方法可使传动能恢复使用？2）图示为一单联滑移齿轮机构，已知基本参数为m=3mm,z1=18,z2=30,z3=27。

试问有几种设计方案？哪种方案较好？3）吊车行走机构中有一对标准直齿轮传动，已知z1=13,z2=47,m=3mm,齿轮1因根切经常断齿。

试问采用什么方案来解决这个问题？例用齿条插刀加工一个直齿圆柱齿轮。

已知被加工齿轮轮坯的角速度ω1=5 rad/s，刀具的移动速度为0.375m/s，刀具的模数m=10mm，压力角α=200。

1）求被加工齿轮的齿数z1；2）若齿条分度线与被加工齿轮中心的距离为77mm,求被加工齿轮的分度圆齿厚；3）若已知该齿轮与大齿轮2相啮合时的传动比i12=4，无侧隙准确安装时的中心距a'=377mm，求这两个齿轮的节圆半径r1'、r2'及啮合角α'。

变位斜齿轮变位系数计算公式

变位斜齿轮变位系数计算公式
1、定义
斜齿轮变位系数是指斜齿式传动系统的主动齿轮和从动齿轮之间实际的变位系数．斜齿轮变位系数是确定斜齿传动系统输出转速与输入转速之比的重要参数．
2、基本理论
斜齿轮变位系数的计算可以根据斜齿轮传动原理得出，斜齿轮传动系统中以滚动轮组的形式相互啮合，当主动轮齿面与从动轮齿面的啮合滚动过程中，一步步完成传动，斜齿轮变位系数的计算公式为：
K=T2/T1=√(cosα2/cosα1)
其中：K-变位系数；T1、T2-主动轮和从动轮的转速；α1、α2-主动轮和从动轮上压力角的大小；
3、计算步骤
(1)确定从动轮的压力角α2,从动轮压力角的大小主要受主动轮和从动轮的齿数和形状的影响。

压力角α2综合考虑主从轮的齿数及形状，是将从动轮的中心线与从动轮对应齿面的交边连线与从动轮的法线的夹角。

(2)确定主动轮的压力角α1,主动轮压力角的大小将直接影响到斜齿轮传动系统的变位系数。

压力角α1由主动轮的齿数及形状决定，可以根据从动轮的压力角确定。

(3) 由转速比率确定斜齿轮变位系数K，根据上式知，斜齿轮变位系数K=T2/T1=√(cosα2/cosα1)
4、示例
以下计算题示例：。

变位系数经验公式分配计算

变位系数经验公式分配计算变位系数是衡量变态程度的一种指标，也叫离散系数，表示数据的离散程度。

它是标准差与均值之比，用来描述数据的相对离散程度。

变位系数的公式如下：CV=(σ/μ)*100%其中，CV表示变位系数，σ表示标准差，μ表示均值。

根据变位系数的定义，当数据相对离散程度较高时，变位系数的值较大；当数据相对离散程度较低时，变位系数的值较小。

变位系数适用于比较不同数据集之间的离散程度，对于均值较小的数据集，可能会出现变位系数过大的情况，这是由于变位系数的计算公式中分子中的标准差通常比均值大的缘故。

在实际应用中，变位系数经常用于财务、经济、人口、生物统计学等领域，以辅助对数据的分析和比较。

下面以一个例子来计算变位系数：假设有一组数据：2,4,6,8,10首先，计算数据的均值μ：μ=(2+4+6+8+10)/5=6然后计算数据的标准差σ：σ=√(((2-6)^2+(4-6)^2+(6-6)^2+(8-6)^2+(10-6)^2)/5)=√(4+4+0+4+4)/5=√16/5=√3.2≈1.79最后，根据变位系数的公式计算：CV=(1.79/6)*100%≈29.83%因此，这组数据的变位系数为29.83%。

通过计算变位系数，我们可以得出结论：这组数据相对离散程度较高。

需要注意的是，变位系数只是一种衡量变态程度的指标，它的计算结果并不能完全代表数据集的离散程度。

在实际应用中，我们应该结合其他统计指标和实际情况进行综合分析。

变位系数的计算公式简单易懂，计算过程也相对简单。

通过计算变位系数，我们可以直观地了解数据的离散程度，有助于辅助对数据进行分析和比较。

在实际应用中，变位系数是一种简单而有用的统计指标。

变位系数计算公式

变位系数计算公式
变位系数是用来衡量其中一数据的离散程度的统计量，它可以用来描述一组数据中的离散程度，是比较常用的统计描述方法之一、变位系数的计算公式如下：
变位系数=(标准差/平均值)*100%
其中，标准差表示数据集合中各个数据偏离平均数的程度，平均值表示数据集合中各个数据的平均水平。

通过将标准差与平均值相比较，可以判断数据的离散程度，即数据分布的紧密程度。

变位系数的值越大，表示数据的离散程度越大；反之，值越小，表示数据的离散程度越小。

当变位系数等于0时，表示数据完全没有离散，即所有数据都相等；当变位系数等于100%时，表示数据的离散程度最大，即所有数据都不相等。

下面以一组数据为例，来计算变位系数：
假设有一组数据：1,2,3,4,5
首先，计算平均值：
平均值=(1+2+3+4+5)/5=3
然后，计算标准差：
标准差=√((1-3)²+(2-3)²+(3-3)²+(4-3)²+(5-3)²)/5
=√(4+1+0+1+4)/5
=√(10/5)
=√2
≈1.414
最后，计算变位系数：
变位系数=(标准差/平均值)*100%
≈(1.414/3)*100%
≈47.14%
因此，这组数据的变位系数约为47.14%，表示数据的离散程度较大。

需要注意的是，变位系数只适用于连续变量，且对数据的标度敏感。

在计算变位系数之前，建议先判断数据是否满足这两个条件。

此外，在不
同领域中使用变位系数时，也会根据具体情况进行微调或修改公式，以适
应特定的数据特征和需求。

齿轮变位系数计算公式

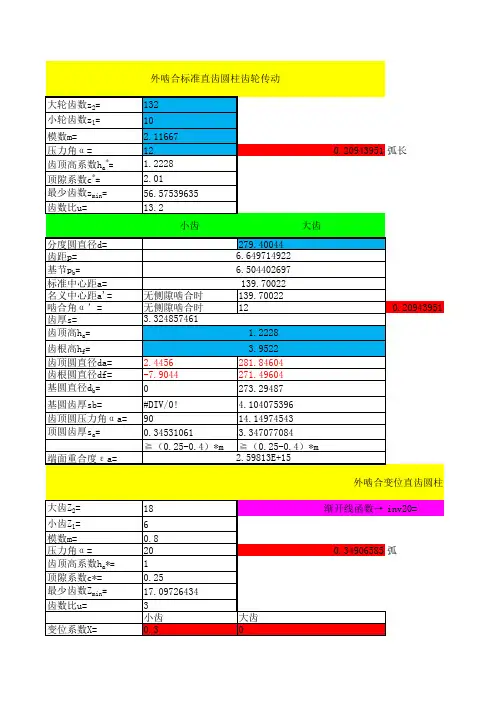
齿顶高ha=
0.664884418
齿根高hf=
0.76
齿顶圆直径da=
6.129768836
齿根圆直径df=
3.28
基圆直径db=
4.51052458
齿距p=
基圆齿距pb=
齿厚s=
1.431342774
基圆齿厚sb=
1.412247101
齿顶圆压力角αa= 42.62181966
顶圆齿厚sa=
端面重合度εa=
#NUM!
校验干涉
应满足
渐开线干涉
1
≧
小齿轮过渡曲线干涉
≧
由表2-11查 #NUM!
外啮合标准斜齿（人字齿）圆柱齿轮传动
大轮齿数z2=
9
小轮齿数z1=
9
法向模数mn=
1.5
法向压力角αn=
30
螺旋角β=
25
端面模数mt=
1.655066878
端面压力角αt=
32.49858487
法向齿顶高系数han*= 1 法向顶隙系数cn*= 0.25
1.743355127
1.622393438
27.87834641
0.295868875
直齿外齿轮
公法线长度
公法线长度的计算 Wk=
标准齿轮 9.70116265
直齿外齿轮斜齿外齿轮
跨测齿数公法线长度跨测齿厚
k= Wkn= k=
5.055555556
直齿外齿轮
公法线长度跨测齿数
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=

变位斜齿轮变位系数计算公式

变位斜齿轮变位系数计算公式
解析它
变位斜齿轮是一种被广泛应用的特殊传动机构，它采用变位斜齿轮把传动精度提高到很高水平，它有变位系数，即求和运算角有助于计算精度和能量。

变位斜齿轮变位系数计算公式是：
C = KPM⋅(1 + β)
其中：C是变位斜齿轮的变位系数。

KPM是变位斜齿轮的齿数比。

β是变位斜齿轮的偏移率。

变位斜齿轮的变位系数是用来表示几种不同的变位系统的变位精度的量度，可以帮助我们计算每次传动的角度。

首先，我们需要知道变位斜齿轮的齿数比KPM，这里KPM=m：n，m和n分别表示变位斜齿轮齿对对接轮齿数，一般情况下m和n之间的商值会被假定为m：n，但是也可以选择精确表示方式，即将KPM的分母的值精确的计算出来。

第二，计算变位斜齿轮的偏移率β。

变位斜齿轮的偏移率β表示一次转动角度有一定的偏差，普通斜齿轮只可能有β=0，但变位斜齿轮由于变位对齿形的改变，导致了其转动角度有不同的
偏差，这里β的精确值取决于斜齿轮的变位样式，但也可以满足一定精度要求使用来估计为0.01或者更小的值。

最后根据以上变位斜齿轮变位系数计算公式，就可以计算出变位斜齿轮的变位系数C值，从而评估出变位斜齿轮的变位精度并满足精度要求。

变位系数计算范文

变位系数计算范文变位系数（coefficient of variation）是一种用于衡量数据的离散程度的统计量。

它可以用于比较不同样本或群体之间的变异性，而不受数据尺度的影响。

变位系数的计算公式为：变位系数 = （标准差 / 平均值）* 100%。

下面将通过一个实际案例演示如何计算变位系数。

假设我们想比较两个城市A和B的每月平均气温的变异性。

我们收集了这两个城市过去一年的每个月的平均气温数据。

以下是数据表格：城市A 城市B1月10 82月12 103月15 134月18 155月22 186月26 227月30 248月28 229月25 2010月20 1611月15 1212月10 81.计算每个城市的平均气温。

首先，我们将每个城市的气温加总，然后除以12（表示12个月）得到平均气温。

城市A的平均气温=（10+12+15+18+22+26+30+28+25+20+15+10）/12=19.5城市B的平均气温=（8+10+13+15+18+22+24+22+20+16+12+8）/12=16.52.计算每个城市的标准差。

标准差是用来衡量数据的离散程度的指标。

城市A的标准差=√[（（10-19.5）^2+（12-19.5）^2+...+（10-19.5）^2）/12]=7.57城市B的标准差=√[（（8-16.5）^2+（10-16.5）^2+...+（8-16.5）^2）/12]=5.273.计算每个城市的变位系数。

变位系数是标准差和平均值的比率，乘以100%。

城市A的变位系数=（7.57/19.5）*100%=38.87%城市B的变位系数=（5.27/16.5）*100%=31.94%通过计算，我们发现城市A的平均气温的变异性较大，因为其变位系数较大。

而城市B的平均气温的变异性较小，因为其变位系数较小。

变位系数的值越小，表示数据的离散程度越小，相对的，变位系数的值越大，表示数据的离散程度越大。

圆柱齿轮啮合变位系数分配

变位系数变位系数x是径向变位系数，加工标准齿轮时，齿条形刀具中线与齿轮分度圆相切。

加工变位齿轮时齿条形刀具中线与齿轮分度圆相切位置偏移距离xm，外移x为正，内移x为负。

除了圆锥齿轮有时采用切向变位xt外，圆柱齿轮一般只采用径向变位。

变位系数x的选择不仅仅是为了凑中心距，而主要是为了提高强度和改善传动质量。

变位齿轮的主要功用如下：(1)减小齿轮传动的结构尺寸，减轻重量在传动比一定的条件下，可使小齿轮齿数zl＜zmin，从而使传动的结构尺寸减小，减轻机构重量。

(2)避免根切，提高齿根的弯曲强度当小齿轮齿数z1＜zmin时，可以利用正变位避免根切，提高齿根的弯曲强度。

x≥xmin=(Z-Zmin)/Zmin，对α=20o时，Zmin=17。

(3)提高齿面的接触强度采用啮合角α’＞α的正传动时，由于齿廓曲率半径增大，故可以提高齿面的接触强度。

(4)提高齿面的抗胶合耐磨损能力采用啮合角α’＞α的正传动，并适当分配变位系数xl、x2，使两齿轮的最大滑动率相等时，既可降低齿面接触应力，又可降低齿面间的滑动率以提高齿轮的抗胶合和耐磨损能力。

(5)配凑中心距当齿数z1、z2不变的情况下，啮合角α’不同，可以得到不同的中心距，以达到配凑中心距的目的。

(6)修复被磨损的旧齿轮齿轮传动中，小齿轮磨损较重，大齿轮磨损较轻，可以利用负变位把大齿轮齿面磨损部分切去再使用，重配一个正变位小齿轮，这就节约了修配时需要的材料与加工费用。

选择变位系数的基本原则(1)润滑条件良好的闭式齿轮传动当齿轮表面的硬度不高时(HBS＜350)，即对于齿面未经渗碳、渗氮、表面淬火等硬化处理的齿轮，齿面疲劳点蚀或剥伤为其主要的失效形式，这时应选择尽可能大的总变位系数x，即尽量增大啮合角，以便增大啮合节点处齿廓的综合曲率半径，减少接触应力，提高接触强度与疲劳寿命。

当轮齿表面硬度较高时(HBS＞350)，常因齿根疲劳裂纹的扩展造成轮齿折断而使传动失效，这时，选择变位系数应使齿轮的齿根弯曲强度尽量增大，并尽量使相啮合的两齿轮具有相近的弯曲强度。

变位系数计算公式

变位系数计算公式
变位系数是描述土壤颗粒粒径分布不均匀程度的指标，通常用于评估土壤的颗粒分布情况，从而判断土壤的物理性质和水力性质。

下面将详细介绍变位系数计算公式的内容。

变位系数的计算公式是：
Cc = (D60-D10)/(D30)^2
其中，Cc表示变位系数，D10、D30和D60分别为从小到大排列的颗粒直径分别为10%、30%和60%的颗粒的直径。

这个公式不仅适用于评估土壤颗粒的分布情况，也适用于评估河床物质颗粒的分布情况。

在实际应用中，我们可以通过以下步骤来计算变位系数：
1. 从小到大排列颗粒的直径，记录下10%、30%和60%的颗粒的直径；
2. 带入计算公式，计算出变位系数的值。

变位系数的值越小，说明土壤颗粒分布越均匀，土壤的物理和水力性质越好。

相反，变位系数的值越大，说明土壤颗粒分布不均匀，土壤物理和水力性质也越差。

在实际应用中，变位系数可以用于评估土壤的通透性、渗透性、压缩性等性质。

通常来说，变位系数越小的土壤，其通透性和渗透性
越好，而变位系数越大的土壤，其压缩性越强，易产生土壤沉降和淤
积等问题。

总之，变位系数是评估土壤物理性质和水力性质的一个重要指标，它的计算公式简单易懂，操作简便。

通过对土壤的变位系数进行评估，可以更好地了解土壤的性质，为农业、工程和环境等领域的实际应用
提供更可靠的依据。

变位系数经验公式分配计算

渐开线函数渐开线函数传动比 invα t invα t' i 0.01490438 0.0149044 1
说明： 1、若齿轮的主要形式为断裂则按公式：（硬齿面）若齿轮的主要形式为点蚀则按公式：（软齿面调质齿轮）若齿轮的主要形式为胶合则按公式：（一些高速齿轮）解决多对齿轮结构上的矛盾，又要尽可能增强齿轮的承载能力，还要力求齿轮副的齿根强度以及滑动系数相等或接近，端面重合度又不能小于1.3
=（XnΣ /（(Z2/Z1)+1））*((Z1+12)/(Z1+2))+8/(Z2+8) =XnΣ /（(Z2/Z1)+1）+((Z2/Z1)-1)/((Z2/Z1)+1+0.4*Z2）
Xn1
=XnΣ /（(Z2/Z1)+1）+7*((Z2/Z1)-1)/（10*((Z2/Z1)+1）)
齿顶高系数顶隙系数法向模数 ha*(han*) C*(Cn*) Mn 1 0.25 1.5
小齿轮 Z1 32
大齿轮 Z2 32
压力角 α （α n） 20 0.34906585
基本参数螺旋角 β 0 0
啮合角 α '
渐开线函数 invα n
计算值渐开线函数总变位系数 invα n' XnΣ 0.000
Xn1 0.251 情况情况情况情况 1 2 3 4
Xn2 -0.251 Xn1 Xn1 Xn1 Xn1 0 0.2 0 0 Xn2 Xn2 Xn2 Xn2
2、 3、
4、
基本参数变位前中心距 A 48
实际中心距 A' 48
计算值端面啮合角 α t 0.34906585 20

变位系数_精品文档

变位系数一、引言变位系数（Coefficient of variation），简称CV，是统计学中用于衡量数据变异程度的一种指标。

它能够比较不同样本或总体的变异性大小，无论其绝对数值大小如何。

变位系数的计算通常是通过将标准差除以平均值而得到。

变位系数的应用广泛，在金融、经济、生物学、医学等领域都有重要作用。

通过计算变位系数，我们可以比较不同样本或总体的相对稳定性，从而更好地理解数据的变化情况。

本文将介绍变位系数的计算方法、应用场景以及其在实际问题中的作用。

二、计算方法变位系数（CV）的计算公式如下：CV = （标准差 / 平均值）× 100%其中，标准差是衡量数据集中观测值的离散程度的一种统计指标，而平均值则是数据集的中心位置。

通过将标准差除以平均值，我们可以得到一个相对指标，用以表示数据的变异程度。

三、应用场景1. 金融领域在金融领域，变位系数常用于衡量资产的风险水平。

通过计算不同资产的变位系数，投资者可以比较它们的波动性，从而作出更为明智的投资决策。

一般来说，变位系数越大，该资产的风险越高。

2. 经济领域在经济学中，变位系数可用于评估不同国家或地区的经济波动性。

通过比较不同地区的变位系数，我们可以了解到哪些地区的经济相对稳定，哪些地区的经济波动较大。

这对于投资者和政策制定者都十分重要。

3. 生物学领域在生物学领域，变位系数可以帮助研究人员分析和比较不同物种的遗传变异性。

通过计算不同物种的变位系数，我们可以了解它们的遗传多样性，从而对物种的进化和适应能力有更深入的理解。

4. 医学领域在医学研究中，变位系数被广泛应用于评估不同治疗方法或药物的疗效稳定性。

通过比较不同治疗组的变位系数，研究人员可以判断哪种治疗方法更为稳定有效，从而为临床实践提供依据。

四、在实际问题中的作用变位系数在实际问题中有着重要的作用，以下是几个例子：1. 质量控制在制造业中，变位系数可用于衡量产品质量的稳定性。

通过计算不同生产批次的变位系数，制造商可以判断生产过程是否稳定，以及产品是否符合质量要求。

齿轮的变位系数

齿轮的变位系数变位系数x是径向变位系数，加工标准齿轮时，齿条形刀具中线与齿轮分度圆相切。

加工变位齿轮时齿条形刀具中线与齿轮分度圆相切位置偏移距离xm，外移x为正，内移x为负。

除了圆锥齿轮有时采用切向变位xt外，圆柱齿轮一般只采用径向变位。

变位系数x的选择不仅仅是为了凑中心距，而主要是为了提高强度和改善传动质量。

变位齿轮的主要功用如下：(1)减小齿轮传动的结构尺寸，减轻重量在传动比一定的条件下，可使小齿轮齿数zl＜zmin，从而使传动的结构尺寸减小，减轻机构重量。

(2)避免根切，提高齿根的弯曲强度当小齿轮齿数z1＜zmin时，可以利用正变位避免根切，提高齿根的弯曲强度。

x≥xmin=(Z-Zmin)/Zmin，对α=20o时，Zmin=17。

(3)提高齿面的接触强度采用啮合角α’＞α的正传动时，由于齿廓曲率半径增大，故可以提高齿面的接触强度。

(4)提高齿面的抗胶合耐磨损能力采用啮合角α’＞α的正传动，并适当分配变位系数xl、x2，使两齿轮的最大滑动率相等时，既可降低齿面接触应力，又可降低齿面间的滑动率以提高齿轮的抗胶合和耐磨损能力。

(5)配凑中心距当齿数z1、z2不变的情况下，啮合角α’不同，可以得到不同的中心距，以达到配凑中心距的目的。

(6)修复被磨损的旧齿轮齿轮传动中，小齿轮磨损较重，大齿轮磨损较轻，可以利用负变位把大齿轮齿面磨损部分切去再使用，重配一个正变位小齿轮，这就节约了修配时需要的材料与加工费用。

选择变位系数的基本原则(1)润滑条件良好的闭式齿轮传动当齿轮表面的硬度不高时(HBS＜350)，即对于齿面未经渗碳、渗氮、表面淬火等硬化处理的齿轮，齿面疲劳点蚀或剥伤为其主要的失效形式，这时应选择尽可能大的总变位系数x，即尽量增大啮合角，以便增大啮合节点处齿廓的综合曲率半径，减少接触应力，提高接触强度与疲劳寿命。

当轮齿表面硬度较高时(HBS＞350)，常因齿根疲劳裂纹的扩展造成轮齿折断而使传动失效，这时，选择变位系数应使齿轮的齿根弯曲强度尽量增大，并尽量使相啮合的两齿轮具有相近的弯曲强度。

齿轮变位系数计算公式

1.743355127
1.622393438
27.87834641
0.295868875
直齿外齿轮
公法线长度
公法线长度的计算 Wk=
标准齿轮 9.70116265
直齿外齿轮斜齿外齿轮
跨测齿数公法线长度跨测齿厚
k= Wkn= k=
5.055555556
直齿外齿轮
公法线长度跨测齿数
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=
14.212488
齿根圆直径df=
11.14560191
基圆直径db=
12.5630209
法向齿距pn=
端面齿距pt=
5.199545947
法向基圆齿距pbn=
端面基圆齿距pbt=
基圆螺旋角βb=
21.46902352
法向齿厚sn=
2.35619449
端面齿厚st=
2.599772973
端面基圆齿厚sbt= 2.474242055
0.003117051
0.019 要查出，我没查，用时一定要
0.01
查
弧长
αa1
αa2
1.570796327 0.246959646
位直齿圆柱齿轮传动 0.014904
给定x∑求a' 0.320442451
αa1 0.743891086
αa2 0.479274389
inv20= invαa1= invαa2=
变位系数X=
18
6 0.8 20 1 0.25 17.09726434 3 小齿 0.3

变位系数

变位系数变位系数x是径向变位系数，加工标准齿轮时，齿条形刀具中线与齿轮分度圆相切。

加工变位齿轮时齿条形刀具中线与齿轮分度圆相切位置偏移距离xm，外移x为正，内移x为负。

除了圆锥齿轮有时采用切向变位xt外，圆柱齿轮一般只采用径向变位。

变位系数x的选择不仅仅是为了凑中心距，而主要是为了提高强度和改善传动质量。

变位齿轮的主要功用如下：(1)减小齿轮传动的结构尺寸，减轻重量在传动比一定的条件下，可使小齿轮齿数zl＜zmin，从而使传动的结构尺寸减小，减轻机构重量。

(2)避免根切，提高齿根的弯曲强度当小齿轮齿数z1＜zmin时，可以利用正变位避免根切，提高齿根的弯曲强度。

x≥xmin=(Z-Zmin)/Zmin，对α=20o时，Zmin=17。

(3)提高齿面的接触强度采用啮合角α’＞α的正传动时，由于齿廓曲率半径增大，故可以提高齿面的接触强度。

(4)提高齿面的抗胶合耐磨损能力采用啮合角α’＞α的正传动，并适当分配变位系数xl、x2，使两齿轮的最大滑动率相等时，既可降低齿面接触应力，又可降低齿面间的滑动率以提高齿轮的抗胶合和耐磨损能力。

(5)配凑中心距当齿数z1、z2不变的情况下，啮合角α’不同，可以得到不同的中心距，以达到配凑中心距的目的。

(6)修复被磨损的旧齿轮齿轮传动中，小齿轮磨损较重，大齿轮磨损较轻，可以利用负变位把大齿轮齿面磨损部分切去再使用，重配一个正变位小齿轮，这就节约了修配时需要的材料与加工费用。

选择变位系数的基本原则(1)润滑条件良好的闭式齿轮传动当齿轮表面的硬度不高时(HBS＜350)，即对于齿面未经渗碳、渗氮、表面淬火等硬化处理的齿轮，齿面疲劳点蚀或剥伤为其主要的失效形式，这时应选择尽可能大的总变位系数x，即尽量增大啮合角，以便增大啮合节点处齿廓的综合曲率半径，减少接触应力，提高接触强度与疲劳寿命。

当轮齿表面硬度较高时(HBS＞350)，常因齿根疲劳裂纹的扩展造成轮齿折断而使传动失效，这时，选择变位系数应使齿轮的齿根弯曲强度尽量增大，并尽量使相啮合的两齿轮具有相近的弯曲强度。

标准齿轮的变位系数

标准齿轮的变位系数齿轮是一种常见的机械传动装置，广泛应用于各种机械设备中。

在齿轮传动中，齿轮的变位系数是一个重要的参数，它直接影响着齿轮传动的性能和工作效率。

本文将对标准齿轮的变位系数进行详细介绍，以便读者更好地了解和应用这一参数。

1. 变位系数的定义。

变位系数是指齿轮齿廓的修形量与标准齿廓尺寸的比值。

它反映了齿轮齿廓的修形程度，是齿轮传动中一个重要的参数。

通常情况下，变位系数越小，齿轮的传动效率越高，噪音和振动也会相应减小。

2. 变位系数的计算。

标准齿轮的变位系数可以通过以下公式进行计算：\[ C_x = \frac{X X_n}{m} \]其中，\( C_x \)为变位系数，\( X \)为修形量，\( X_n \)为标准齿廓尺寸，\( m \)为模数。

通过这个公式，我们可以很方便地计算出标准齿轮的变位系数。

3. 变位系数的影响。

变位系数直接影响着齿轮传动的性能。

当变位系数较小时，齿轮的传动效率较高，噪音和振动较小，但制造成本较高。

而当变位系数较大时，齿轮的传动效率较低，噪音和振动较大，但制造成本较低。

因此，在实际应用中，需要根据具体的传动要求和成本考虑，选择合适的变位系数。

4. 变位系数的优化。

为了提高齿轮传动的性能，我们可以通过优化变位系数来实现。

一种常见的优化方法是采用修形滚刀进行齿轮的加工，通过精确控制修形滚刀的参数，可以实现齿轮齿廓的精密修形，从而降低变位系数，提高传动效率，减小噪音和振动。

5. 结语。

标准齿轮的变位系数是齿轮传动中一个重要的参数，它直接影响着齿轮传动的性能和工作效率。

通过合理计算和优化变位系数，可以实现齿轮传动的性能提升，从而满足不同工程应用的需求。

希望本文对读者对标准齿轮的变位系数有所帮助，谢谢阅读！。

变位系数资料

变位系数在未来音乐教育的发展趋势
未来音乐教育的发展
• 音乐教育理念的更新 • 音乐教育方法的改进 • 音乐教育资源的拓展
变位系数在未来音乐教育中的应用
• 音乐理论教育的创新 • 音乐创作教育的实践 • 音乐分析教育的拓展 • 音乐教育研究的深化
THANK YOU FOR WATCHING
谢谢观看
变位系数的分类与特点
变位系数的分类
• 按照音程类型分类 • 按照和弦功能分类 • 按照音乐风格分类
变位系数的特点
• 描述音高关系的一致性 • 反映音乐风格的差异性 • 具有音乐分析的价值
03
变位系数在音乐创作中的应用
变位系数在旋律创作中的应用
旋律的变位系数分析
• 旋律的音高与节奏 • 旋律的变位系数计算 • 旋律的风格与特点
节奏的变位系数分析
• 节奏的时值与拍子 • 节奏的变位系数计算 • 节奏的风格与特点
节奏分析中的变位系数应用
• 节奏的评价与鉴赏 • 节奏的变位系数比较 • 节奏的传承与创新
05
变位系数的实践与拓展
变位系数的实践案例分析
音乐创作的实践案例
• 旋律创作的变位系数应用 • 和声创作的变位系数应用 • 节奏创作的变位系数应用
DOCS SMART CREATE
变位系数：音乐理论的基本概念与应用
CREATE TOGETHER
DOCS
01
音乐理论的基本概念及重要性
音乐理论的发展历程及背景
音乐理论的起源
• 古希腊时期的音乐理论 • 中世纪的音乐理论 • 文艺复兴时期的音乐理论
音乐理论的发展
• 巴洛克时期的音乐理论 • 古典主义时期的音乐理论 • 浪漫主义的音乐理论 • 现代音乐理论