基于李雅普诺夫方法设计的模型参考自适应系统Matlab仿真
多轴同步收放卷系统建模与自适应控制

多轴同步收放卷系统建模与自适应控制石贤可;温盛军【摘要】针对工业生产中广泛存在的张力控制问题,以西门子系列PLC和变频器组成的多轴同步收放卷系统为研究对象,采用动力学建模方法,建立了收放卷系统的动力学模型,并基于该模型设计了以李雅普诺夫稳定性理论为依据的模型参考自适应张力控制器.MATLAB仿真和实验均表明,与PID控制器相比,该模型参考自适应张力控制器在系统启动、升速以及减速阶段均具有更好的动态性能和鲁棒性.【期刊名称】《中原工学院学报》【年(卷),期】2019(030)003【总页数】8页(P82-89)【关键词】多轴同步;张力控制;模型参考自适应;李雅普诺夫【作者】石贤可;温盛军【作者单位】中原工学院电子信息学院,河南郑州 450007;中原工学院中原彼得堡航空学院,河南郑州 450007【正文语种】中文【中图分类】TP273多轴同步收放卷系统是工业现场中经常使用的电气控制系统,收放卷系统在钢铁厂、造纸厂、印刷厂、纺织漂染厂、食品厂、燃料电池厂应用广泛,涉及轧制、拉拔、压花、涂层、印染、清洗以及卷绕等工序,其作用是控制卷材的张力,使其保持稳定[1]。
曾有学者利用动力学建模方法得出了多轴同步收放卷系统开卷机构的数学模型,并认为,多轴同步收放卷系统张力控制的关键是解决速度对张力影响较大的问题[2-3]。
陈耀等针对PID (Proportion Integration Differentiation)算法不能解决控制模型突变时动态响应不佳问题,设计了模糊PID控制器[4]。
马文明等研究了内模控制算法在多轴同步张力控制系统中的应用[5]。
智能控制算法在多轴同步张力控制系统中的应用,从不同程度上解决了张力控制系统存在的问题。
本文通过推导多轴同步收放卷系统的数学模型,设计基于模型参考自适应算法的张力控制器,试图解决以PID算法为张力控制器时系统启动、升减速阶段存在的张力波动过大问题;并且将该控制器应用于收放卷系统,采集相关数据,观察收放卷系统升减速阶段的张力变化,以确定该控制器的应用效果。
李雅普诺夫稳定性的Matlab实现

1 -1 -1
P -1
3
2
-1 2 5
对称矩阵的定号性(正定性)的判定(6/12)
Matlab程序m5-1如下。
P=[1 -1 -1; -1 3 2; -1 2 -5];
1 -1 -1
P -1 3
2
-1 2 5
result_state=posit_def(P); % 采用合同变换法判定矩阵定号性 switch result_state(1:5) % 运用开关语句,分类陈述矩阵正定否的判定结果
对称矩阵的定号性(正定性)的判定(9/12)
函数max()的主要调用格式为: [C,I]=max(A) D=max(A,B)
对第1种调用格式,若输入A为向量,输出的C为向量A的各 元素中最大值,输出I为该最大值在向量中的位置; 若A为矩阵,则C为矩阵A的各列的各元素中最大值,输 出I为这些最大值在各列的位置,这里输出C和I均为1 维数组。 如,执行语句 [C,I]=max([1 -2 3; -4 5 -6]); 后,C和I分别为[1 5 3]和[1 2 1]。
对称矩阵的定号性(正定性)的判定(10/12)
对第2种调用格式的输入A和B须为维数大小相同的矩阵 或向量,输出D为A和B两矩阵同样位置的元素的最大值组 成的矩阵。 如,执行语句 C=max([1 -2 3; -4 5 -6], [-1 2 -3; 4 -5 6]); 后,C为如下矩阵
1 2 3 4 5 6
Ch.5 李雅普诺夫稳定性 分析
目录
概述 5.1 李雅普诺夫稳定性的定义 5.2 李雅普诺夫稳定性的基本定理 5.3 线性系统的稳定性分析 5.4 非线性系统的稳定性分析 5.5 Matlab问题 本章小结
基于分数阶参考模型的半主动悬架自适应控制

基于分数阶参考模型的半主动悬架自适应控制摘要:基于分数阶微积分理论,提出一个以含分数阶次力与位移传递函数定义的悬架为参考模型的磁流变阻尼半主动控制悬架自适应控制模型。
通过最优控制方法得到参考悬架的最佳参数,由于分数阶微积分的引入,使得参考模型更加精确。
采用李雅普诺夫稳定性理论设计得到模型参考自适应控制的自适应控制律,并用Oustaloup逼近算法解算分数阶微积分因子。
Matlab/Simulink仿真结果表明,与传统的被动悬架相比,悬架的平顺性和舒适性有一定的提高,且能保证一定的系统鲁棒性,但悬架动位移稍有增大。
关键词:悬架分数阶自适应控制仿真中图分类号:TP13;U461.4 文献标识码:A 文章编号:1674-098X(2015)12(a)-0244-04Abstract:According to the fractional calculus theory,an adaptive control model of a semi-active control suspension with magneto rheological (MR)damping is established ,which the reference suspension model is defined a fractional force and displacement transfer function. The optimal parameters of the reference suspension are obtained by the optimal control method. Due to the introduction of fractional calculus,makesthe reference model more accurate. A model reference adaptive control method based on Lyapnov stability theory is used to design adaptive controller,and the solution of fractional calculus factor is realized by the Oustaloup’s approximation algorithm. The Matlab/Simulink simulation results indicate that,compared with the traditional passive suspension,the primary performances of the new suspension is improved and the system robustness can be guaranteed,but the suspension dynamic displacement increased slightly.Key Words:Fractional Order;adaptive Control;Simulation;Suspension20世纪90年代初法国Alain Oustaloup教授[1]基于分数阶传递函数具有等相位特性提出的一种鲁棒控制理论(即“Commmande Robuste d’Ordre Non Entier”,其中CRONE是其首字母缩写)。
系统辨识与自适应控制MATLAB仿真第5章模型参考自适应控制

[ky]
k
(t)
(t)
(5-13)
10
由式(5-13)和上式有
(t) k(t) (t)
(5-14)
式中,k(t) k(t) k。 于是可以看到,当 k(t) k 时, (t) 0
现给出规范化的性能指标函数:
J
(k)
1 2
2 (t)
m2
式中,m 1 2(t) 为规范化信号。
按优化理论,k变化使 J (k) 极小的方向应按负梯度确定:
梯度设计法来叙述。
例5.1.3 设有被控对象式(5-1),仍采用参考模型式(5-2)
和控制器结构式(5-6)。设aˆp (t) 是未知对象参数 ap的估计值,式
(5-6)中的 k(t) 由下式计算:
k(t) aˆp (t) am
(5-16)
为了产生参数估计aˆp (t) ,选择一个稳定的滤波器
系统辨识与自适应控制 MATLAB仿真
第5章模型参考自适应控制
1
模型参考自适应控制是一种不同于自校正控制的另一类自适应 控制形式。根据被控对象结构和控制要求,设计参考模型,使其输 出表达对输入指令的期望响应,然后通过模型输出与被控对象输出 之差来调整控制器参数,使差值趋向于零,也就是使对象输出向模 型输出靠近,最终达到完全一致。根据控制器参数更新方法的不 同,模型参考自适应控制可分为直接自适应控制和间接自适应控制 两种。推演参数自适应规律的方法有两种:梯度法和稳定理论法。 5.1简单自适应控制系统
本节目的:1)给出直接自适应控制和间接自适应控制的概 念;2)自适应控制系统的两种基本设计方法:李亚普诺夫法和2梯
度法。
5.1.1直接自适应控制
直接自适应控制是指控制器参数直接从一个自适应规律中获取
基于李雅普诺夫方法设计的模型参考自适应系统Matlab仿真
基于李雅普诺夫方法设计的模型参考自适应系统Matlab仿真
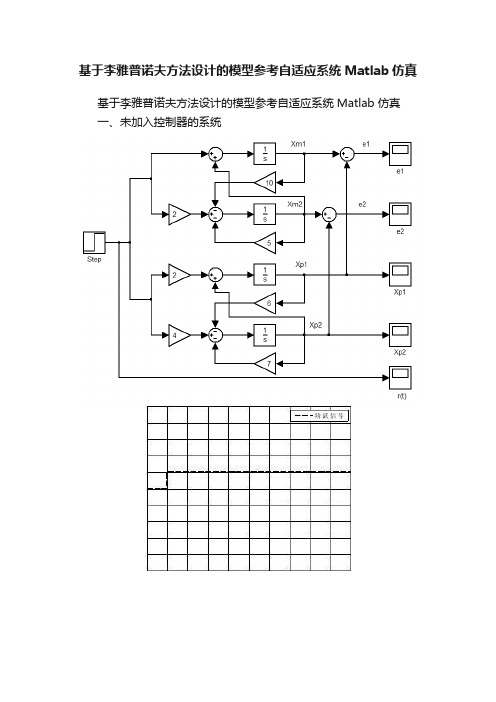
基于李雅普诺夫方法设计的模型参考自适应系统Matlab 仿真
一、未加入控制器的系统
其中,上半部分为参考模型,下半部分为控制系统,分别使用阶跃信号和方波信号输入,便可得到相应的输出。
1. 阶跃信号下的输出
2. 方波信号下的输出
仿真时间(s )
幅值
阶跃输入
仿真时间(s )
幅值
广义状态误差
仿真时间(s )
幅值控制对象状态变量
二、加入了自适应控制器的系统
其中,上半部分为参考模型,下半部分为控制系统,仍然使用和先前相同的阶跃信号和方波信号输入,便可得到相应的输出。
仿真时间(s )
幅值
广义状态误差
仿真时间(s )
幅值
控制对象状态变量
仿真时间(s )
幅值
方波输入
1. 阶跃信号下的输出
2. 方波信号下的输出
使用李雅普诺夫方法设计自适应控制器后,可以看到系统的误差明显减小了,同时系统的稳定性也得到了提升。
仿真时间(s )幅值
广义状态误差
仿真时间(s )幅值
广义状态误差
仿真时间(s )幅值
控制对象状态变量
仿真时间(s )幅值
控制对象状态变量。
自适应控制第4章

25
(3)一般n阶定常线性系统
数学模型: e=ym-yr满足:
试取
(4.3.20) (4.3.21) (4.3.22) (4.3.23)
26
得自适应律:
(4.3.24)
或
(4.3.25)
可以看出,得到的自适应律依赖于整个状态向量X(t),即,自适 应控制律不仅与广义误差e(t)有关,而且与e(t)的各阶导数有 关,为自适应律的实现带来极大不便。
选定指标泛函:
(4.2.4)
(4.2.5)
(4.2.6) (4.2.7) (4.2.8)
8
广义误差对输入的开环传函:
对Kc求偏导: 另根据参考模型 比较(12)、(13):
(4.2.9)
(4.2.10) (4.2.11) (4.2.12) (4.2.13) (4.2.14)
(4.2.15)
可调增益Kc的自适应律—MIT自适应规则(1958 年MIT提出)
9
自适应系统的 数学模型
图4.2.3 MIT可调增益自适应系统
开环广义误差方程
参考模型方程 (4.2.16)
参数调节方程(自适应律)方程 10
凡是用可凋增益构成自适应系统,都可套用 上述模型。
缺点:设计过程中未考虑稳定性问题 因此,求得自适应律后,尚需进行稳定性校验,
以确保广义误差e在了司环回路中能收敛于 某一允许的数值。 补充假设: ✓ 参考模型与可调系统的初始偏差较小; ✓ 自适应速度不能太快(即u不能过大)。
综合出只与e(t)有关的自适应律。选择李亚普诺夫函数时增 加一约束条件:
自适应律简化为:
(4.3.26) (4.3.27)
基于MATLAB控制系统的仿真与应用毕业设计论文

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用,通过对控制系统进行深入的理论分析和实际应用研究,提出一种有效的控制系统设计方案,并通过实验验证其正确性和有效性。
本文对控制系统的基本理论进行了详细的阐述,包括控制系统的定义、分类、性能指标以及设计方法。
我们以一个具体的控制系统为例,对其进行分析和设计。
在这个过程中,我们运用MATLAB软件作为主要的仿真工具,对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。
在完成理论分析和实际设计之后,我们进一步研究了基于MATLAB 的控制系统仿真方法。
通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析,我们提出了一种高效的仿真策略。
我们将所设计的控制系统应用于实际场景中,通过实验数据验证了所提出方案的有效性和可行性。
本论文通过理论与实践相结合的方法,深入探讨了基于MATLAB 控制系统的仿真与应用。
基于Lyapunov稳定性理论的模型参考自适应控制

基于Lyapunov稳定性理论的模型参考⾃适应控制0 引⾔中,Lyapunov 稳定性理论就是设计⾃适应率的有效⼯具。
这种基于稳定性理论的设计保证了系统的稳定[3],所以受到更⼴泛的应⽤。
⾃适应控制的定义到⽬前为⽌尚未统⼀,争议也⽐较多。
综合起来⾃ 2 基于Lyapunov稳定性理论设计控制规律适应控制系统主要有三个特征[1]:1)在线进⾏系统结构和参数的辨识或系统性能指标的度量,以便得到系统当前状态的改变情况;2)按照⼀定Lyapunov 提出了运动稳定性的⼀般理论,即Lyapunov 第⼀法和的规律确定当前的控制策略;3)在线修改控制器的参数或可调系统的输Lyapunov 第⼆法。
前者通过求解系统微分⽅程,然后根据解的性质判断系⼊信号。
现在应⽤⽐较⼴泛的⾃适应控制系统主要有两类:模型参考⾃适统的稳定性;后者不需要求解系统⽅程,⽽是通过具有⼴义能量属性的应控制和⾃校正调节器控制。
本⽂围绕模型参考⾃适应控制进⾏研究,并Lyapunov 函数的标量函数直接判定系统的稳定性。
应⽤Lyapunov 稳定性理利⽤MATLAB 仿真分析其性能。
论设计的控制系统既能求出参数调节的⾃适应规律,⼜确保了系统的稳定1 模型参考⾃适应控制性[4]。
假设被控对象的状态变量可以直接得到。
控制对象的状态⽅程为模型参考⾃适应控制是⼀类重要的⾃适应控制,它的主要特点是实现容易,⾃适应速度快,并在航空、汽车、机器⼈、医疗器械等领域得到了⼴泛应⽤。
模型参考⾃适应控制通过迫使被控对象跟踪特性理想的参考模型,来获得要求的闭环系统性能。
模型参考⾃适应控制系统主要由4部分组成[2],即参考模型、被控对象、⾃适应机构(调整控制器参数)和反馈控制器,如图1所⽰。
图1 模式参考⾃适应控制系统从图1可以看出,这类控制系统包含两个环路:内环和外环。
内环是由调节器、被控过程和反馈控制器组成的普通反馈回路,⽽外环包括参考模型和⾃适应机构等,控制器参数由⾃适应机构调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于李雅普诺夫方法设计的模型参考自适应系统Matlab 仿真
一、未加入控制器的系统
其中,上半部分为参考模型,下半部分为控制系统,分别使用阶跃信号和方波信号输入,便可得到相应的输出。
1. 阶跃信号下的输出
2. 方波信号下的输出
仿真时间(s )
幅值
阶跃输入
仿真时间(s )
幅值
广义状态误差
仿真时间(s )
幅值控制对象状态变量
二、加入了自适应控制器的系统
其中,上半部分为参考模型,下半部分为控制系统,仍然使用和先前相同的阶跃信号和方波信号输入,便可得到相应的输出。
仿真时间(s )
幅值
广义状态误差
仿真时间(s )
幅值
控制对象状态变量
仿真时间(s )
幅值
方波输入
1. 阶跃信号下的输出
2. 方波信号下的输出
使用李雅普诺夫方法设计自适应控制器后,可以看到系统的误差明显减小了,同时系统的稳定性也得到了提升。
仿真时间(s )
幅值
广义状态误差
仿真时间(s )
幅值
广义状态误差
仿真时间(s )
幅值
控制对象状态变量
仿真时间(s )
幅值
控制对象状态变量。
