幂的乘方PPT课件
合集下载
《2.1.2 幂的乘方 》(共17张PPT)

4 3 3
m 4
=a .
15
动手试一试吧!
1. 填空: (1)(104)3=
1012 a9 -x15 x8
;
(2)(a3)3=
(3)-(x3)5= (4)(x2)3 · x2=
;
; .
2. 下面的计算对不对?如果不对, 应怎样改正?
(1)(a4)3=a7;不对,应是a4×3=a12. (2)(a3)2=a9. 不对,应是a3×2=a6.
结论
(am)n=amn(m,n都是正整数).
于是,我们得到幂的乘方法则:
幂的乘方,底数不变,指数相乘 .
例4 计算:
(1)(10 ) ;
5 2
( 2) - ( a ) .
3 4
(1) (105)2 解 (105)2 = 105×2
= 1010. ( 2) 解 -(a3)4 = -a3×4 -(a3)4
法则的逆用: amn =(am)n= (an)m (m,n都是正整数).
(am)2 =am+m =a2m
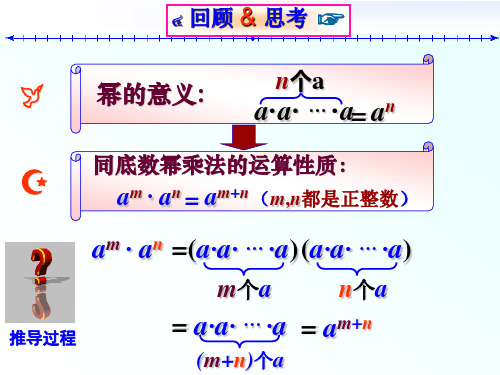
通过观察,你发现上述式子的 指数和底数是怎样变化的?
底数不变,指数相乘.
我思,我进步
同样,我们把上述运算过程推广到一般情况,即
n
个 am
(幂的意义)
(am)n =am· am·… · am n 个 m =am+m+ … +m
(同底数幂的乘法性质) (乘法的意义)
=amn
2
4
做一做
(62)4 = 62· 62· 6 2· 62 =68 2×4 ; 2+2+2+2 =6 =6
(a2)3 = a2· a 2· a2 =a2+2+2 =a6 =a2×3 ;
m 4
=a .
15
动手试一试吧!
1. 填空: (1)(104)3=
1012 a9 -x15 x8
;
(2)(a3)3=
(3)-(x3)5= (4)(x2)3 · x2=
;
; .
2. 下面的计算对不对?如果不对, 应怎样改正?
(1)(a4)3=a7;不对,应是a4×3=a12. (2)(a3)2=a9. 不对,应是a3×2=a6.
结论
(am)n=amn(m,n都是正整数).
于是,我们得到幂的乘方法则:
幂的乘方,底数不变,指数相乘 .
例4 计算:
(1)(10 ) ;
5 2
( 2) - ( a ) .
3 4
(1) (105)2 解 (105)2 = 105×2
= 1010. ( 2) 解 -(a3)4 = -a3×4 -(a3)4
法则的逆用: amn =(am)n= (an)m (m,n都是正整数).
(am)2 =am+m =a2m
通过观察,你发现上述式子的 指数和底数是怎样变化的?
底数不变,指数相乘.
我思,我进步
同样,我们把上述运算过程推广到一般情况,即
n
个 am
(幂的意义)
(am)n =am· am·… · am n 个 m =am+m+ … +m
(同底数幂的乘法性质) (乘法的意义)
=amn
2
4
做一做
(62)4 = 62· 62· 6 2· 62 =68 2×4 ; 2+2+2+2 =6 =6
(a2)3 = a2· a 2· a2 =a2+2+2 =a6 =a2×3 ;
课件114幂的乘方与积的乘方.ppt
证 明
=am+m+ … +m (同底数幂的乘法性质)
=amn (乘法的意义)
幂 的 乘 方 法则
(am)n=amn (m,n都是正整数)
幂的乘方,底数 不变 , 指数 相乘.
阅读 体验 ☞例题解析
【例1】计算:
(1) (102)3 ;
(2) (b5)5 ;
(4) -(x2)m ; (5) (y2)3 ·y ;
V球
4 3
R3
甲球的半径是乙球的10倍,则 甲球的体积V甲= 36000 cm3 .
V甲 是 V乙 的 1000 倍
即 103 倍
如果甲球的半径是乙球的n 倍,那么甲球体积是乙球体积的 n3倍。
地球、木星、太阳可以近似地看作球体 。木星、太阳
的半径分别约是地球的10倍和102倍,它们的体积分别约
是地球的 103 倍和 106 倍. (102)3=106,为什么?
底数 不变 , 指数 相加 .
作作业业
(6) 2(a2)6 – (a3)4 =2a2×6 - a3×4 =2a12-a12 =a12.
随随堂堂练练习习
1、计算: (1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 ·x2 ; (4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 ·x3 .
解:(1) (62)4 = 62·62·62·62=62+2+2+2 =68 =62×4 ;
(2) (a2)3 = a2·a2·a2 =a2+2+2 =a6 =a2×3 ;
(3) (amm)22=am·am =am+m=a2m ;
幂 的乘方(课件)

amn (am )n (an )m
幂的乘方的逆运算:
(1)x20=( x4 )5=(x5)4; (2)a2m =( am)2 =( a2 )m (m为正整数).
(3) 已知3×9n=37,求:n的值.
课堂小结
1.幂的乘方的法则 语言叙述 幂的乘方,底数不变,指数相乘.
符号叙述 (a m )n a mn (m、n都是正整数).
同底数幂相乘,底数不变,指数相加.
想一想:你会计算(a4)3和(x3)4吗?
试一试
计算:(1)(23)2 ; (3)(a3)5 ;
(2)(33)2 ; (4)(am)3.
(1) (23)2=23×23=23+3=2( 2×3 );
(2) (32)3=32×32×32=3( 2+2+2 )=3(2×3 );
乘方
不变
指数 相乘
(a m )n a mn (m、n都是正整数)
公式中的a可表示一 个数、字母、式子等.
来几道吧:
计算 (1)(103)5; (2)(a4)4; (3)(am)2; (4)-(x4)3; (5)(-ym)2; (6)2(a2)6-(a3)4.
1、下列各式对吗?请说出你的观点和理由:
(3) (a3)5=a3×a3×a3×a3×a3=a( 3×5 ) (4) (am)3= am·am·am=a( 3m )
看看计算的结果有什么规律?
猜想 :(a m )n _a_m_n __
(m、n都是正整数)
(am )n amamam (乘方的意义)
n个
n个
a的乘方的运算公式
你能用语言叙述这个 结论吗?
(a m )n a mn (m、n都是正整数)
幂的乘方的逆运算:
(1)x20=( x4 )5=(x5)4; (2)a2m =( am)2 =( a2 )m (m为正整数).
(3) 已知3×9n=37,求:n的值.
课堂小结
1.幂的乘方的法则 语言叙述 幂的乘方,底数不变,指数相乘.
符号叙述 (a m )n a mn (m、n都是正整数).
同底数幂相乘,底数不变,指数相加.
想一想:你会计算(a4)3和(x3)4吗?
试一试
计算:(1)(23)2 ; (3)(a3)5 ;
(2)(33)2 ; (4)(am)3.
(1) (23)2=23×23=23+3=2( 2×3 );
(2) (32)3=32×32×32=3( 2+2+2 )=3(2×3 );
乘方
不变
指数 相乘
(a m )n a mn (m、n都是正整数)
公式中的a可表示一 个数、字母、式子等.
来几道吧:
计算 (1)(103)5; (2)(a4)4; (3)(am)2; (4)-(x4)3; (5)(-ym)2; (6)2(a2)6-(a3)4.
1、下列各式对吗?请说出你的观点和理由:
(3) (a3)5=a3×a3×a3×a3×a3=a( 3×5 ) (4) (am)3= am·am·am=a( 3m )
看看计算的结果有什么规律?
猜想 :(a m )n _a_m_n __
(m、n都是正整数)
(am )n amamam (乘方的意义)
n个
n个
a的乘方的运算公式
你能用语言叙述这个 结论吗?
(a m )n a mn (m、n都是正整数)
幂的乘方(ppt)

木星的半径是地球的10倍,它的体积是地球的103倍! 太阳的半径是地球的102倍,它的体积是地球的(102)3倍! 你知道(102)3等于多少吗?
新知讲解
【做一做】 64表示___4___个____6___相乘. (62)4表示___4____个___6_2___相乘.
a3表示____3_____个___a_____相乘. (a2)3表示___3____个___a_2____相乘. (am)n表示___n___个___a_m___相乘.
新知讲解
【例】已知10m=3,10n=2,求下列各式的值. (1)103m; (2)102n;
【解】(1)103m=(10m)3=33=27; (2)102n=(10n)2=22=4;
课堂练习
1.计算 (1)(a3)4;
(2)(xm-1)2; (3)[(24)3]3; (4)[(m-n)3]4.
猜想:(am)n=_a_m__n_.
新知讲解
验证猜想:一般的,对于任意底数a与任意正整数m,n,
n个am
n个m
(am)n= am·am·…·am = am+m+……+m =amn
即:(am)n= amn (m,n都是正整数) 幂的乘方,底数_不__变___,指数_相__乘___.
新知讲解
【比一比】
解: (2) a2(-a)2(-a2)3+a10 = -a2·a2·a6+a10 = -a10+a10 = 0.
课堂练习
3.已知10x=m,10 y=n,则102x+3y等于( D )
A.2m+3n
B.m2+n3
C.6mn
D.m2n3
拓展提高
4. 比较3500,4400,5300的大小. 解析:这三个幂的底数不同,指数也不相同,不能直接比较大小,通过 观察,发现指数都是100的倍数,故可以考虑逆用幂的乘方法则.
新知讲解
【做一做】 64表示___4___个____6___相乘. (62)4表示___4____个___6_2___相乘.
a3表示____3_____个___a_____相乘. (a2)3表示___3____个___a_2____相乘. (am)n表示___n___个___a_m___相乘.
新知讲解
【例】已知10m=3,10n=2,求下列各式的值. (1)103m; (2)102n;
【解】(1)103m=(10m)3=33=27; (2)102n=(10n)2=22=4;
课堂练习
1.计算 (1)(a3)4;
(2)(xm-1)2; (3)[(24)3]3; (4)[(m-n)3]4.
猜想:(am)n=_a_m__n_.
新知讲解
验证猜想:一般的,对于任意底数a与任意正整数m,n,
n个am
n个m
(am)n= am·am·…·am = am+m+……+m =amn
即:(am)n= amn (m,n都是正整数) 幂的乘方,底数_不__变___,指数_相__乘___.
新知讲解
【比一比】
解: (2) a2(-a)2(-a2)3+a10 = -a2·a2·a6+a10 = -a10+a10 = 0.
课堂练习
3.已知10x=m,10 y=n,则102x+3y等于( D )
A.2m+3n
B.m2+n3
C.6mn
D.m2n3
拓展提高
4. 比较3500,4400,5300的大小. 解析:这三个幂的底数不同,指数也不相同,不能直接比较大小,通过 观察,发现指数都是100的倍数,故可以考虑逆用幂的乘方法则.
《幂的乘方与积的乘方》课件(共26张PPT)【推荐】

2
2
16
(4)(3a4bm)n=3n(a4)n(bm)n=3na4nbmn.
经典例题
题型一 几种幂的综合运算
例1 计算:(1)(-2x2)3+(-3x3)2+(-x)6; (2)x2·x4·x6+(x3)2+[(-x)4]3. 、
题型一 几种幂的综合运算
例1 计算:(1)(-2x2)3+(-3x3)2+(-x)6; (2)x2·x4·x6+(x3)2+[(-x)4]3. 分析 按照先算乘方,再算乘除,最后算加减,若 有小括号先算小括号里的原则进行计算. 、
题型二 幂的运算法则的逆用
例2 计算:(1)已知2×8x×16x=222,求x的值; (2)已知2m=3,2n=4,求22m+n的值.
题型二 幂的运算法则的逆用
例2 计算:(1)已知2×8x×16x=222,求x的值; (2)已知2m=3,2n=4,求22m+n的值.
解析 (1)因为2×8x×16x=222, 所以2×(23)x×(24)x=222, 所以2×23x×24x=222,所以,21+3x+4x=222, 所以1+3x+4x=22,解得x=3. (2)因为2m=3,2n=4, 所以22m+n=(2m)2·2n=9×4=36.
题型一 几种幂的综合运算
例1 计算:(1)(-2x2)3+(-3x3)2+(-x)6; (2)x2·x4·x6+(x3)2+[(-x)4]3. 分析 按照先算乘方,再算乘除,最后算加减,若 有小括号先算小括号里的原则进行计算. 解析(1)原式=-8x6+9x6+x6=2x6. (2)原式=x12+x6+x12=2x12+x6. 、
(3)
1
3
3
1
9
.
3 3
(4)(x4)3-2(x3)4=x12-2x12=-x12.
幂的乘方ppt课件

a33333
a35 a15
7
也就是:
(a4)3a43a12
(a3)5a35a15
8
想一想:幂的乘方,底数变不变? 指数应怎样计算?
9
(a4)3a43a12
(a3)5a35a15
10
幂的乘方,底数不变, 指数相乘。
11
试计算:
(am)n ?
其中m , n都是正整数
12
幂的乘方法则:
(am )n amn
其中m , n都是正整数
13
这就是说, 幂的乘方,底数不变,
指数相乘。
14
例1 计算:
(1)1( 07)2;(2)(b3)3;(3)(a2m)4; (4)(y3)2;(5)[(2)2]3
15
解:
(1)1( 07)210721014
(4)(y3)2
16
[(y3)]2 ( y 3 ) 2
y23 y6
27
解:
[x (y)2]4(xy)24
(x y)8
28
想一想:同底数幂的乘法法则与幂的乘方法 则有什么相同点和不同点?
29
幂的乘方法则:
(am )n amn
同底数幂的乘法法则:
am • an amn
其中m , n都是正整数
30
同底数幂相乘
am • an amn
指数相加Biblioteka 底数不变指数相乘其中m , n都是正整数
1
回忆:
同底数幂的乘法法则:
am • an amn
其中m , n都是正整数
2
练习
am • am a3 •a3 •a3
3
思考:怎样计算
(a ) , (a )
a35 a15
7
也就是:
(a4)3a43a12
(a3)5a35a15
8
想一想:幂的乘方,底数变不变? 指数应怎样计算?
9
(a4)3a43a12
(a3)5a35a15
10
幂的乘方,底数不变, 指数相乘。
11
试计算:
(am)n ?
其中m , n都是正整数
12
幂的乘方法则:
(am )n amn
其中m , n都是正整数
13
这就是说, 幂的乘方,底数不变,
指数相乘。
14
例1 计算:
(1)1( 07)2;(2)(b3)3;(3)(a2m)4; (4)(y3)2;(5)[(2)2]3
15
解:
(1)1( 07)210721014
(4)(y3)2
16
[(y3)]2 ( y 3 ) 2
y23 y6
27
解:
[x (y)2]4(xy)24
(x y)8
28
想一想:同底数幂的乘法法则与幂的乘方法 则有什么相同点和不同点?
29
幂的乘方法则:
(am )n amn
同底数幂的乘法法则:
am • an amn
其中m , n都是正整数
30
同底数幂相乘
am • an amn
指数相加Biblioteka 底数不变指数相乘其中m , n都是正整数
1
回忆:
同底数幂的乘法法则:
am • an amn
其中m , n都是正整数
2
练习
am • am a3 •a3 •a3
3
思考:怎样计算
(a ) , (a )
幂的乘方课件ppt(共19张PPT)

优生必做! 应用提高、拓展创新 问题 如果甲球的半径是乙球的n倍,那 么甲球的体积是乙球的n 3 倍.地球、木星、太 阳可以近似地看做是球体.木星、太阳的半径 分别约是地球的10倍和10 2 倍,它们的体积分 别约是地球的多少倍?
)m (m为正整数).
2.填空:
(1) a6y3=( )3;
(2)81x4y10=( )2 ;
(3)若(a3ym)2=any8, 则m=
, n=
;
;
1 2004 (4) ) = 3 (5) 28×55= .
32004×(-
拓展延伸
(1)0.125
a b
2005
(8)
2006
(2)若10 2,10 3, 求10
a
mn
(a ) (a )
m n
n m
幂的乘方法则顺口溜:
幂乘方,要牢记, 底不变,指数积。
作业
拓展训练
幂的乘方法则的逆用 mn m n
a
(a ) (a )
n m
1、幂的乘方的逆运算:
(1)x13·7=x(2 )=( x4 )5=( x5 )4=( x2 )10; x
0
(2)a2m =( am )2 =( a2
幂的乘方的运算公式
你能用语言叙述这个 结论吗?
(a ) a
m n
mn
(m、n都是正整数)
幂的乘方,底数不变,指数相乘.
在幂的乘方运算中,指数运算降了一级,也就是 多重乘方也具有这一性质.如 m n p mn p 将幂的乘方运算转化为指数的乘法运算,使问题简 [( a ) ] a (其中 m、n、p都是正整数).
14.1.2 幂的乘方
反馈一:
幂的乘方人教八年级上完整PPT课件

点拨:102a+103b=(10a)2+(10b)3=52+63=241.
【规律总结】对于幂的乘方与同底数幂的乘法的混合运算, 先算乘方,再算同底数幂的乘法;幂的乘方与加减混合运算时, 先乘方,后加减,注意合并同类项.
幂的乘方法则的逆用 amn=(am)n=(an)m,即 x6=(x2)3=(x3)2. 例 2:已知 ax=3,ay=2,试求 a2x+3y 的值. 解:a2x+3y=a2x·a3y=(ax)2·(ay)3=32·23=9×8=72.
例 1:计算:
幂的乘方法则(重点)
(1)(x2)3;
(2)-(x9)8;
(3)(a3)2-(a2)3;
(4)(a2)3·a5.
思路导引:运用幂的乘方法则,运算时要先确定符号.
解:(1)(x2)3=x2×3=x6. (2)-(x9)8=-x9×8=-x72. (3)(a3)2-(a2)3=a6-a6=0. (4)(a2)3·a5=a2×3·a5=a6+5=a11.
第2课时 幂的乘方
幂的乘方 探究:1.64表示__4____个__6____相乘; (62)4表示____8__个____6__相乘. 2.a3表示___3___个___a___相乘; (a2)3表示____6__个____a__相乘. 归纳:幂的乘方,底数__不__变__,指数__相__乘__.用字母表示 为“(am)n=___a_m_n___(m、n 为正整数)”.
1.(m2)3·m4等于( B )
A.m9
B.m10
C.m12
D.m14
Байду номын сангаас
2.计算: (1)[(x+y)2]6=____(_x_+__y)_1_2__; (2)a8+(a2)4=_____2_a_8_____.
