冶金物理化学电子教案
冶金物理化学教案03
第五节 可逆过程与膨胀功一、可逆过程体系作功与过程的途径有关。
当体系从某一个初态变到某一个末态时，如果途径不同，则所作的功也不同。
现以理想气体恒温膨胀为例来加以说明。
设有一个气缸，内有n 摩尔理想气体。
假定此气缸的活塞没有重量，活塞移动时和气缸内壁没有摩擦。
将整个气缸放在温度为T 的恒温器中，使体系进行的过程为恒温过程。
设气体初态时的压力为3大气压，体积为1升，末态时的压力为1大气压，体积为3升。
从初态到末态可经过下列三种不同途径：Ⅰ途径：使活塞外的压力P外一次减小到1大气压。
在整个膨胀过程中气体反抗的外压均为1大气压。
体系作功：W 1＝l ×（3－1）＝2atm ·l ＝202.65 J (l atm ·l ＝101.325J )即图中矩形abcB 的面积。
图1-2理想气体恒温膨胀 图1-3理想气体恒温膨胀功Ⅱ途径：先使P 外减小到2大气压，气体反抗2大气压的外压膨胀到体积为1.5升，然后再使外压减小到1大气压，使气体反抗1大气压的外压膨胀到体积为3升。
体系作功：W 2＝2×(1.5－1）＋l ×（3－1.5)＝2.5atm ·1＝253.3125 J 。
即图1-3gbdf 和edcB 二矩形面积之和。
Ⅲ途径：在整个膨胀过程中不断改变外压，始终维持P 外比气体的压力P 小一无限小量dP ， 即维持P 外＝P －dP 。
体系作功： dV dP P dV P W V V V V ⎰⎰-==2121)(â3，略去二级无穷小后，得：=⨯=====⎰⎰13ln 13ln ln 12111232121V V V P V V nRT dV V nRT dV P W V V V V 3.296atm ·1=333.9672J 这个功等于图1-3中曲线AfB 以下的面积AbcBfA 。
比较这三种不同的恒温膨胀过程，可知途径Ⅲ所作的功最大。
冶金物理化学教案11
第三节△G —T 图一、自由焓变化与温度的关系自由焓变化是温度的函数，在不同温度下，其数值是不同的。
设某反应在某温度T 下初态物质（原始物）的自由焓为G 1，末态物质（产物）的自由焓为G 2、则自由焓变化为ΔG=G 2-G 1。
物质的自由焓（G 1和G 2)在一定的压力下随温度的变化为：11)(S T G P -=∂∂ 22)(S T G P -=∂∂S 为熵。
因此在恒压下，反应自由焓变化与温度的关系为：P P PP T G T G T G G T G )()()()(1212∂∂-∂∂=⎥⎦⎤⎢⎣⎡∂-∂=⎥⎦⎤⎢⎣⎡∂∆∂＝一S 2＋S 1＝一ΔS 在温度T 下，因为△G ＝△H 一T △S 将此式代入上式，可得：T H G T G P ∆-∆=⎥⎦⎤⎢⎣⎡∂∆∂)( （3-15）上式称为吉布斯一亥姆霍茨（Gibbs-Helmholtz)公式，表示在恒压下ΔG 随温度的变化。
吉布斯-亥姆霍茨公式还可以变成另一形式，以便于积分。
将式（3-15)移项，得：H G T G T P ∆=∆+⎥⎦⎤⎢⎣⎡∂∆∂)(，两边用T 2除： 22)(T H TG T G T P∆=∆+⎥⎦⎤⎢⎣⎡∂∆∂ 利用微分公式（在微分公式2)(v dx dvudx du v dx vu d -=中，令v ＝T 、u ＝－ΔG 、x ＝T ），可把此式变为： 2)(T H T T G P∆=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∆-∂ （3-16） 这也是吉布斯一亥姆霍茨公式的一种形式。
对于自由能变化与温度的关系，也可以用同样的方法推出相应的公式：式(3-16)可以在恒压下积分，得到ΔG -T 的关系式。
通常计算的是标准自由焓变化，因此：I dT T H T G+∆=∆-⎰︒︒2 I 为积分常数。
当近似把︒∆H 当作常数时可得：︒∆G ＝︒∆H －IT （3-17）式中的积分常数I 可利用已知一个温度的︒∆G （例如︒∆298G ）代入公式而求得，其它常数可由C P 与T 的关系式以及其中一个温度的热效应而求得。
冶金物理化学教案14
第四节实际溶液、活度和活度系数一、实际落液对理想落液的偏差前面已经指出，理想溶液各组元布任何浓度下都服从拉乌尔定律。
但这种溶液是很少的，实际溶液大多数都对拉乌尔定律呈现或大或小的偏差。
也就是说，蒸气压往往大于拉乌尔定律的计算值或小于拉乌尔定律的计算值。
前者称为正偏差，后者称为负偏差。
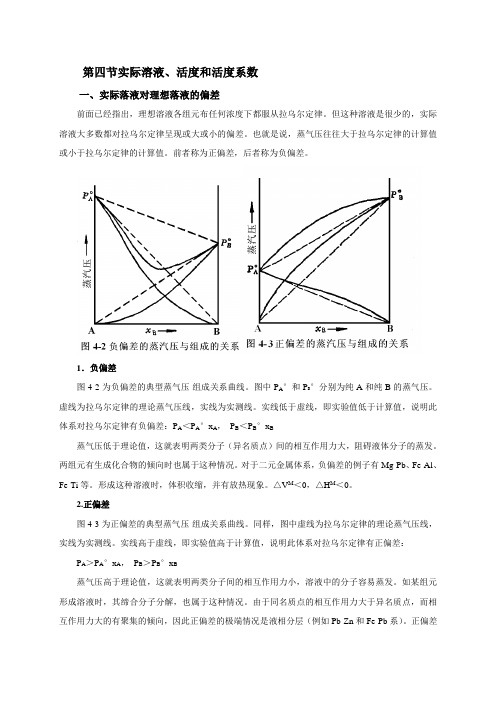
1．负偏差图4-2为负偏差的典型蒸气压-组成关系曲线。
图中P A°和P B°分别为纯A和纯B的蒸气压。
虚线为拉乌尔定律的理论蒸气压线，实线为实测线。
实线低于虚线，即实验值低于计算值，说明此体系对拉乌尔定律有负偏差：P A＜P A°x A，P B＜P B°x B蒸气压低于理论值，这就表明两类分子（异名质点）间的相互作用力大，阻碍液体分子的蒸发。
两组元有生成化合物的倾向时也属于这种情况。
对于二元金属体系，负偏差的例子有Mg-Pb、Fe-Al、Fe-Ti等。
形成这种溶液时，体积收缩，并有放热现象。
△V M＜0，△H M＜0。
2.正偏差图4-3为正偏差的典型蒸气压-组成关系曲线。
同样，图中虚线为拉乌尔定律的理论蒸气压线，实线为实测线。
实线高于虚线，即实验值高于计算值，说明此体系对拉乌尔定律有正偏差：P A＞P A°x A，P B＞P B°x B蒸气压高于理论值，这就表明两类分子间的相互作用力小，溶液中的分子容易蒸发。
如某组元形成溶液时，其缔合分子分解，也属于这种情况。
由于同名质点的相互作用力大于异名质点，而相互作用力大的有聚集的倾向，因此正偏差的极端情况是液相分层（例如Pb-Zn和Fe-Pb系）。
正偏差金属二元系的例子还有A1-Zn 、Al-Sn 等。
形成这种溶液时，体积增大，并有吸热现象。
△V M ＞0，△H M ＞0。
二、活度从上面对实际溶液的讨论可以看到，实际溶液对拉乌尔定律往往有正偏差或负偏差。
另外，实验还指出，对于稀溶液的溶质，当溶液不是足够稀时，实测的蒸气压也往往与亨利定律有偏差。
电子行业冶金物理化学电子教案
电子行业冶金物理化学电子教案一、教学目标1.了解电子行业冶金物理化学的基本概念和理论知识。
2.掌握电子行业冶金物理化学的实验操作技能。
3.培养学生的实验观察和数据分析能力。
4.培养学生的团队合作和沟通能力。
二、教学内容1.冶金物理化学概述–冶金物理化学的定义和作用–冶金物理化学的发展历程–冶金物理化学所涉及的主要内容2.金属的结构和性质–金属的晶体结构和晶格参数–金属的晶体缺陷与缺陷扩散–金属的力学性能和热处理技术3.非金属材料的结构和性质–非金属材料的晶体结构和晶格参数–非金属材料的晶体缺陷和相变–非金属材料的力学性能和热处理技术4.电子行业冶金物理化学实验–冶金物理化学实验室的基本设备与安全操作规范–金属结构和性能的实验方法与数据处理–非金属材料结构和性能的实验方法与数据处理三、教学方法1.讲授法：通过教师的讲解，向学生介绍冶金物理化学的基本概念和理论知识。
2.实验操作：组织学生进行冶金物理化学实验，培养学生的实验操作技能。
3.讨论与分析：在实验后，让学生进行实验数据的讨论和分析，培养学生的实验观察和数据分析能力。
4.团队合作：鼓励学生进行小组合作，共同完成实验任务，培养学生的团队合作和沟通能力。
四、教学过程1.课前准备–教师准备好教学所需的实验设备和实验材料。
–学生预习相关教材，了解基本概念和理论知识。
2.讲授冶金物理化学概述–通过教师的讲解，向学生介绍冶金物理化学的基本概念和作用。
–通过案例分析，让学生了解冶金物理化学的实际应用。
3.金属的结构和性质–通过教师的讲解，向学生介绍金属的晶体结构和晶格参数的概念。
–进行实验观察和数据记录，让学生了解金属的晶体缺陷与缺陷扩散的现象。
–进行实验操作和数据处理，让学生掌握金属的力学性能和热处理技术。
4.非金属材料的结构和性质–通过教师的讲解，向学生介绍非金属材料的晶体结构和晶格参数的概念。
–进行实验观察和数据记录，让学生了解非金属材料的晶体缺陷和相变的现象。
冶金物理化学教案06
第二章热力学第二定律第一节自发过程的方向与限度自然界发生的一切过程都遵守热力学第一定律，但是，许多过程虽然不违背热力学第一定律，却不能实现。
例如，室内放一杯水，温度和室温相等。
水自动从环境吸热而使水温上升，环境温度下降，这是不可想象的事，是不可能发生的。
然而，这个过程如果发生也不违背热力学第一定律，因为体系吸收的热等于环境放出的热，能量仍然守恒。
可见，单有热力学第一定律还不能解决过程能否自动发生的问题。
这个问题要由热力学第二定律来解决。
在指定的温度、压力和浓度等条件下，在所讨论的体系中，过程能否自动发生，最后达到什么限度，这是热力学第二定律要解决的中心问题。
通过下面几个例子，可以看到自发过程的方向以及它们达到的限度。
两块温度不同的铁块相接触，热必自动地从高温铁块流向低温铁块，直至两铁块的温度相等为止。
将装有某种气体的两容器联通，气体必自动地从压力较大的容器向压力较小的容器扩散，直至两容器的压力相等为止。
在1173K，1大气压下，若使CO2气体与固体碳接触，则必自动发生化学反应：C+CO2＝2CO。
如果碳量足够多，则反应能进行到气体中CO含量为97%，CO2还剩下3%为止。
以上各例都是在指定条件下能够自动发生的过程。
自发过程（能自动发生的过程的简称）就是指无需外力帮助，任其自然就能发生的过程。
自发过程不但不需外功，而且在适当的安排下，过程进行时还能对外作功。
例如，可以利用热自动从高温物体流向低温物体这个自发过程造成热机来作功；可以利用自发的化学反应装成电池来产生电能。
也就是说，自发过程都有对外作功的能力。
从类似上述的大量事实可以看出，在一定条件下，自发过程都有一定的方向和限度。
温度相等是热传导的限度。
压力相等是气体流动的限度。
在1173 K，I大气压的条件下，当气体中含CO 97%，CO23%时，化学反应C+CO2＝2CO就达到了限度。
过程达到限度，也就是体系达到了平衡状态。
平衡状态是指在一定条件下，从宏观来看，浓度、压力等性质都不随时间而改变的热力学状态。
物理化学(冶金上册)第一章
联系p、 、 之间关系的方程称为状态方程 之间关系的方程称为状态方程。 联系 、V、T之间关系的方程称为状态方程。
§1.1 理想气体状态方程
1.理想气体状态方程 1.理想气体状态方程 三个低压气体定律( 三个低压气体定律(p<1MPa) 低压气体定律 ) 玻义尔定律 盖-吕萨克定律 一定） pV = 常数 （n、T一定） 一定） （ 一定 V / T = 常数 n、p一定）
3 −1 −1
R = 8.314510Pa im imol iK R = 8.314510J imol iK
−1 −1
2.理想气体模型 2.理想气体模型
(1)分子间作用力 (1)分子间作用力
E = E吸 引 + E排 斥
A B = − 6 + 12 r r
E
E - 分子间相互作用势能 A - 吸引系数 B - 排斥系数
−1
−1
p / MPa
R是对各种气体适用 是对各种气体适用 的常数。 的常数。
§1.2 理想气体混合物
1.混合物的组成 1.混合物的组成 (1)摩尔分数x或y (1)摩尔分数x 摩尔分数 气体混合物的摩 尔分数用y表示。 尔分数用y表示。 液体混合物的摩 尔分数用x表示。 尔分数用x表示。
x（或yB ) = nB / ∑ nA B
8.314 × 273.15 3 −1 Vm = 3 = 22.4dm i mol 101.325 × 10
×
物理量的表示及运算
T = 273 K p = 100 kPa V = 1 cm 3 o = 1000 dm t =0 C = 0.1MPa 运算： 运算： p2 = 2 p1 ( p1 = 100 kPa)
物理化学的内容
冶金物理化学教案16
§5-2电极电位一、电动势的产生在两个相互接触的不同导体之间，常常有一定的电位差存在。
在原电池中包含着好多个两两相互接触的导体，因而在原电池中存在着一系列电位差。
金属晶格是由按一定规律排列着的金属阳离子，以及在其间流动着的电子（称为电子气），组成的。
在一般情况下，例如在真空中或在气相中，金属离子所具有的动能不足以克服金属晶格对它的引力而脱离金属表面。
但与水接触时，由于水分子的极性很大，它的负端对金属阳离子有强烈的吸引力，致使金属阳离子进入溶液中的趋势大为增加。
当金属阳离子进入溶液以后，溶液与金属的电中性就被破坏，金属缺少了正电荷而带负电，溶液增加了阳离子而带正电。
由于正负电荷的相互吸引，所以在金属与溶液界面上形成了双电层，如图5-3所示。
双电层的电位差阻止了金属离子进一步溶入溶液，同时又促进了溶液中的阳离子返回到金属上去，最后达到了平衡。
此时，金属离子自金属转入溶液的速度与溶液中金属离子返回到金属表面的速度相等。
在此平衡条件下，双电层建立了一定的电位差，这就是ZnΦZn2+或CuΦCu2+。
由于金属的化学性质不同，故开始时溶液中的某种金属离子沉积在金属电极上的速度也可能大于金属离子进入溶液的速度。
如果这样，达到平衡时金属表面就带正电，溶液带负电，也形成有一定电位差的双电层。
至于双电层结构，近代研究结果认为，溶液中与金属电极符号相反的离子，并不都被紧紧地吸引在电极表面附近。
这种离子的排列受到两种作用的影响，一方面离子受到金属电极上异号电荷的吸引，趋向于紧密地排列在金属表面附近；另一方面，离子热运动所产生的扩散作用，则力图使离子均匀地分散到溶液中。
这两方面作用的结果，使双电层中溶液一侧只有一部分离子紧靠金属表面排列着，其余的离子则分散到离开电极表面稍远的地方（图5-3)。
前一部分称为紧密层，后一部分称为扩散层。
电极与溶液间的电位差包括这两部分在内，其大小与双电层的结构无关。
对极稀的溶液来说，可以认为在外电场的作用下，整个扩散层均能相对于电极表面运动，所以扩散层的电位差也称为动电电位ζ，它在界面化学中占有重要地位。
冶金物理化学电子教案
冶金物理化学电子教案一、教学目标：1.了解冶金物理化学的基本概念和原理；2.研究冶金物理化学电子方面的基本理论；3.掌握冶金物理化学电子的应用。
二、教学内容：1.冶金物理化学的基本概念和原理2.冶金物理化学电子方面的基本理论3.冶金物理化学电子的应用三、教学方法：1.讲授与实践相结合的方法。
在讲解冶金物理化学电子的基本理论时，适当引入实例来具体说明，加深学生对知识的理解；2.探究式学习方法。
通过实验和讨论，引导学生积极思考和探索，培养学生的观察能力和创新意识；3.合作学习方法。
通过小组合作学习和讨论，促进学生之间的交流和合作，提高学生的团队意识和合作能力。
四、教学过程：1.导入：介绍冶金物理化学的基本概念和原理，引导学生对冶金物理化学的认识。
2.理论讲解：讲解冶金物理化学电子的基本理论，包括金属的电子结构、导电性能、磁性等内容。
3.实验：设计一个小型实验，通过测量金属导电性能的实验，让学生亲自操作仪器，感受冶金物理化学电子的应用。
4.讨论与总结：让学生以小组为单位，讨论实验结果，并总结实验中遇到的问题和解决方法。
5.展示和评价：让学生将实验结果展示给全班，通过展示和讨论，评价学生的实验表现和理解情况。
6.拓展：引导学生进一步思考和应用冶金物理化学电子的其他领域，如材料的改性和金属材料的表面处理等。
五、教学评估：1.实验报告的评估；2.学生小组的讨论和总结评估；3.学生对拓展教学内容的答题评估。
六、教学资源：1.教学PPT；2.实验器材和材料；3.实验报告模板。
七、教学反思：通过本教案的设计，能够帮助学生全面了解冶金物理化学电子的基本原理和应用，培养学生的观察能力和创新意识，培养学生的合作能力和团队意识。
同时，通过实验的设计和讨论，能够提高学生的动手能力和实践操作能力，加深学生对知识的理解和掌握程度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.1 二元系中组元的活度
2. 联系： ●当溶液是理想溶液时，拉乌尔定律的斜率和亨利定律的斜率相等，它们重合 ●拉乌尔定律与亨利定律都有共同的形式：
Pi ki Xi
-------拉乌尔定律或亨利定律第一种表达式（实验式）
当0Xi X'i 时，ki kH ,i ，i服从亨利定律;
当 X"i Xi 1时，k i
i
与标准态
在溶液中，对任一组元，其化学势为
i iRTlnai
或 Gi GiRTlnai
在冶金物理化学中，事实上， i Gi,iGi （分别是i组元在溶液中的摩
尔自由能和标准摩尔自由能），从化学势的关系式可以看出，
i
是组元的活度
时的化学势，称为标准化学势。当组元i所选取的标准态不同时，组元的活度是
当服从亨利定律时（选择质量百分浓度 % i），%i 1(i的质量
百分数为1），ki k%,(i i的质量百分数为1时的假想蒸气压)，k
示假想i的质量百分数为1时的标准态；
i
表
3.2 活度标准态与参考态
3.2.1 活度的引出
对组元i的浓度在 X'i Xi Xi" 区间，组元既不服从拉乌尔
定律，也不服从亨利定律，用这二定律线性关系的形式描述溶
即：当组元以假想的质量百分浓度 % i为1做标准态，
对 % i 进行修正：
pi k%,i
%i
fi
a%,i
a
%
—亨利活度或假想质量百分浓度等于1为标准态的活度,
,i
f
%
－亨利活度系数
,i
3.2 活度标准态与参考态
3.2.3 活度标准态与参考态
3.2.3.1活度选取标准态的必要性
1）溶液中组元i的标准化学势
不同的，既活度的大小，与其标准态的选择有关，所以
i
是不同的，而与组元
i所对选于取组的元标的准浓态度无，关。对应不同标准态的活度aR,i，aH,i，a%,i 在数值上各不相同
在 Xi 1 时,在定义域 X"i Xi 1 成立； ● 线性关系的斜率是纯溶剂i的蒸气压； ● 组元i的浓度必须用摩尔分数。
3.1 二元系中组元的活度
● 是描述溶质组元i在液相中浓度与其在气相中的蒸气压的线性 关系；
在 Xi 0或 %i 0 时,在定义域 0Xi X'i或 0%i%i'
成立； ● 线性关系的斜率是从服从亨利定律的线性关系延长到 X i 1 的 蒸气压（当浓度用摩尔分数，实际上是假想纯溶质i的蒸气压）或 从服从亨利定律的线性关系延长到 %i 1 的蒸气压（当浓度用质 量百分浓度，实际上是假想%i的蒸气压） ● 组元i的浓度可以用摩尔分数，也可以用质量百分浓度。
k
H
,i
,
k
---组元i的浓度等于1或1%时，服从亨利定理的蒸气压；
% ,i
X i , % i ---组元i在液相中的摩尔分数或质量百分浓度；
0 X i X '-i --组元i服从亨利定律的定义域。
3.1 二元系中组元的活度
3.1.2 两者的区别与联系： 1. 区别： 拉乌尔定律： ● 是描述溶剂组元i在液相中浓度与其在气相中的蒸气压的线性 关系；
液中组元i的浓度与其在气相中的蒸气压的关系，对拉乌尔定律
和亨利定律的浓度项进行修正。
拉乌尔定律修正为： P iP ix ii P ia R ,i
亨利定律修正为： P ikH ,i fH ,ixi kH ,iaH ,i
或
或者，
P i k % ,if% ,i% i k % ,ia % ,i
k i 是以下三个特殊状态的值，如图1-3-1，代表着三个标准态：
3.1 二元系中组元的活度
当i服从拉乌尔定律时，X
i
（1 i为纯物质），k i
p
i
(纯物质蒸气
压)，k i 表示纯物质标准态；
当服从亨利定律时（选择摩尔分数 X i），X i 1（i为纯物质）
，ki kH ,i(假想纯物质蒸气压)，k i 表示假想纯物质标准态；
X i ----组元i在液相中的摩尔分数；
X
" i
X
i
1
----组元i服从拉乌尔定律的定义域。
3.1 二元系中组元的活度
2.亨利定律：
定义：在等温等压下，对溶液中的组元i，当其组元
的浓度时，该组元在气相中的蒸气压与其在溶液中的
浓度成线性关系。
数学描述为或：Pi kH,i Xi 0Xi X'i
P i ---组元i在气相Pi中的k蒸%,气i % 压i; 0%i%i'
2.在H基础上( X
i )将之推广到全浓度范围，0≤ X
≤1，
i
即：当组元以假想纯物质为标准态，对 X
pi kH,i
Xi
f
' i
aH,i
进行修正：
i
aH
, i －亨利活度或假想纯物质标准态的活度；f
H
－亨利活度系数
,i
3.2 活度标准态与参考态
3.在H基础上(% i )将之推广到全浓度范围，0≤% i ≤100
Pi Pi Xi
3.1 二元系中组元的活度
3.1.1 拉乌尔定律和亨利定律：
1.拉乌尔定律：
定义：在等温等压下，对溶液中组元i，当其组元的浓
度时，该组元在气相中的蒸气压与其在溶液中的浓度成
线性关系。数学描述为：Pi Pi Xi X"i Xi 1
其中 P i ----组元i在气相中的蒸气压； P i ----纯组元i的蒸气压；
p
i
，i服从拉乌尔定律。
事实上，组元i由液态中的组元变为气态，是一个物理过程
i i g
当过程达平衡且服从拉乌尔定律或亨利定律时，有
ki
pi Xi
-----拉乌尔定律或亨利定律第二种表达式（平衡式）
3.1 二元系中组元的活度
另外，其共同的形式还可以表达为：
Xi
pi ki
-----拉乌尔定律或亨利定律第三种表达式（标准态式）
冶金物理化学电子教案
第三章 真实溶液
第三章 真实溶液
3.1 二元系中组元的活度 3.2 活度标准态与参考态 3.3 不同标准态活度之间的关系 3.4 标准溶解吉布斯自由能 3.5 多元系溶液中活度系数---Wagner模型 3.6 正规溶液 3.7 冶金炉渣溶液 3.8二元系组元活度系数的实验测定与计算
由拉乌尔定律及亨利定律的第三种表达式
Xi
pi ki
3.2 活度标准态与参考态
3.2.2 活度的三种定义
1.以R为基础，将之推广到全浓度范围，0≤ X i ≤1，
即：当组元以纯物质为标准态，对
X
进行修正：
i
a R , i －拉乌尔活度pp或ii纯物X质i标i准系数；