【大学物理】稳恒磁场
合集下载
大学物理Ⅱ第10章 稳恒磁场
r
B
17
2.运动电荷的磁场
q
B
0 4
q r0
r2
r
P B
六、毕奥－萨伐尔定律的应用
r
P
B
1. 载流直导线的磁场
求距离载流直导线为a处 一点P 的磁感应强度 B
解
dB
0
4
Idl sin r2
B
dB
0
4
Idl sin r2
I
Idl
a
r
B
P
根据几何关系
r a csc
l acot acot
萨法尔定律 二、 两定理：磁高斯定理和安培环路定理
三、 两种力：安培力(做功)、洛仑兹力(不做功)
四、 磁介质：磁介质中的环路定理
§10.1 电流 电动势
一、电流、电流密度
大量电荷的定向运动形成电流。 方向规定：正电荷运动方向
1.电流强度： I dq
dt
2.电流密度:
描述导体内各点的电流分布情况
a
da边: F1 I da B
F1 Bl1I sin
bc边: F1/ Ibc B
F2
F1/ Bl1I sin( )
b
F1 d
F2/
pm
c
F1/
ab边: cd边:
F2 I ab B F2/ I cd B
F2 Bl2I F2/ Bl2I
41
•线圈在均匀磁场受合力 F F1 F1/ F2 F2/ 0
B
13
I I
直电流磁感线
圆电流磁感线
I
螺线管 磁感线
(1)磁感应线都是环绕电流的闭合曲线，磁场是 涡旋场。
(2) 任意两条磁感应线在空间不相交。 (3)磁感应线方向与电流方向遵守右螺旋法则。
大学物理,稳恒磁场10-4安培环路定理概述.
0I B
2πR
R
oR r
12
10.4 安培环路定理
第10章 稳恒磁场
例：求无限长载流圆柱面的磁场分布。
L1
r
IR
L2 r
0I B
2π R
oR r
解 0 r R, B d l 0 l r R, l B d l 0I
B0 B 0I
2π r 13
LB dl μ0 I
B d l
L
μ0 ( I1
I1
I1
I2)
μ（0 I1
I
）
2
I1
I2 I3
I1
L
I1
思考：
1） B 是否与回路 L 外的电流有关？
2）若 B d l 0 ，是否回路 L 上各处 B 0 ？ L
是否回路 L 内无电流穿过？
2πR
当 2R d 时，
螺绕环内可视为均匀场。
令：n N
2R
B μ0nI
第10章 稳恒磁场
d
R
10
10.4 安培环路定理
第10章 稳恒磁场
例：无限长载流圆柱体的磁场。
I
解：1）对称性分析
2）选取回路
r R :
Bdl
l
μ0 I
RR
L
r
B
2 π rB 0I,
B μ0 I 2πr
电流共同产生的。
3）环路定理适用于闭合稳恒电流的磁场。而有限电 流（如一段不闭合的载流导线）不适用环路定理。
4）安培环路定理说明磁场性质 —— 磁场是非保守场，是涡旋场。
大学物理 稳恒磁场
第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比.§11－1 基本磁现象磁性，磁力，磁现象;磁极，磁极指向性,N极，S极，同极相斥，异极相吸。
磁极不可分与磁单极。
一、电流的磁效应1819年，丹麦科学家奥斯特发现电流的磁效应;1820年，法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷，磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”，至今科学家一直在努力寻找其存在的证据。
§11－2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B 的定义：（1）规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。
若正电荷沿此方向运动,其所受磁力为零。
（2）正运动电荷沿与磁感强度B 垂直的方向运动时,其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值，规定为磁场中某点磁感强度的大小。
即：qvF B max=磁感强度B 是描写磁场性质的基本物理量。
若空间各点B 的大小和方向均相等,则该磁场为均匀磁场．．．．；若空间各点B 的大小和方向均不随时间改变，称该磁场为稳恒磁场．．．．。
磁感强度B 的单位:特斯拉(T)。
§11－3 毕奥－萨伐尔定律 一、毕－萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。
式中μ0:真空磁导率, μ0＝4π×10－7NA 2 dB 的大小： 20sin 4rIdl dB θπμ=d B 的方向： d B 总是垂直于Id l 与r 组成的平面，并服从右手定则.一段有限长电流的磁场： ⎰⎰⨯==l l r r l Id B d B 304πμ二、应用1。
一段载流直导线的磁场 )cos (cos 42100θθπμ-=r IB 说明:(1)导线“无限长"：002r I B πμ=（2）半“无限长”： 00004221r I r IB πμπμ==2.圆电流轴线上的磁场 磁偶极矩232220)(2x R R IB +=μ讨论：（1）圆心处的磁场：x = 0 RIB 20μ=；（2）半圆圆心处的磁场： RIR I B 422100μμ==（3）远场:x >>R ,引进新概念 磁偶极矩0n IS m =则: m xB 3012πμ=3.载流螺线管轴线上的磁场)cos (cos 2120ββμ-=nIB讨论：（1)“无限长”螺线管：nI B 0μ=（2）半“无限长”螺线管：nI B 021μ=例：求圆心处的B .§11－4 磁通量 磁场的高斯定理 一、磁感线作法类似电场线。
《大学物理课件》稳恒磁场
B 0I 2 r
0rR
B dl L
0
r2 R2
I
2 rB
0r 2
R2
I
B
0 Ir 2 R2
I
RR
r B
I . dB
dI B
B 的方向与 I 成右螺旋
0 r R,
r R,
B
0 Ir 2 R2
B 0I 2 r
I
R
0I B
2 R
oR r
第三节 磁场对电流和运动电荷的作用
一、安培力（载流导线在磁场中所受的宏观力）
2R
三．运动电荷的磁场。
电流激发的磁场可以视为所有运动电荷所激发的磁 场叠加,取载流导线上电流元 Idl ，其截面积为S ，
单度位为体v积,每内个作电定荷向带运电动为的q电。荷数为 n ，定向运动速
Idl
I
r
p
S
q
v
I
I dl
代入
dB 0 4
Idl r r3
0 4
nqsvdl r r3
在个运电动流电元荷中(有q， 电荷v)数在为rd处N的磁n感dV应，强则度一
r
r0
sin
r0 csc
r0
x 1
dB p y
所以
B 0
4
Ir0 csc2 d sin r02 csc2
0I 2 sin d
4 r0 1
Idz
z 2
dB
0 I 4 r0
(cos1
cos2 )
oz x 1
p
y
1， 2 分别是直电流
始点与终点处电流流向与
r
的夹角
讨论（1）若直导线视为“无限长”，
大学物理稳恒磁场小结
4R
O
R
0 I 3 B (1 ) 6R R 2
0 I
O
R
I
R
O
I
O
I
R
B
0 I B 2 4R 4 R
0 I
μ0 I
8R
2、安培定律 大小：
dF Idl B
dF
dF IdlB sin θ 方向：从 Idl 右旋到 B ，
大拇指的指向。
稳恒磁场小结
一.基本概念
1. 磁感强度大小
Fmax B qv
方向：小磁针N极在此所 指方向
pm
2. 载流线圈磁矩 P ISn m
3. 载流线圈的磁力矩 M Pm B
4.磁通量
n
I
m B dS BdS cos
二.基本实验定律
（1）首先选定回路L的绕行方向. （2）按照右手螺旋关系确定出回路的正法线方向. （3）确定通过回路的磁通量的正负. （4）确定磁通量的时间变化率的正负. （5）最后确定感应电动势的正负.
dΦ ε dt
n
L
ε 0 与回路 L绕向相反； ε 0 与回路 L绕向相同。
②感应电流 ③若为N匝
注意： 计算一段有限长载流导线在磁 场中受到的安培力时，应先将其 分割成无限多电流元，将所有电 流元受到的安培力矢量求和—矢 量积分。
B
Idl
Idl
B
L
F dF L Idl B
L
三.稳恒磁场的基本性质： 1.磁场的高斯定理：
m B dS 0
d dq d D D dS I dt dt dt
O
R
0 I 3 B (1 ) 6R R 2
0 I
O
R
I
R
O
I
O
I
R
B
0 I B 2 4R 4 R
0 I
μ0 I
8R
2、安培定律 大小：
dF Idl B
dF
dF IdlB sin θ 方向：从 Idl 右旋到 B ，
大拇指的指向。
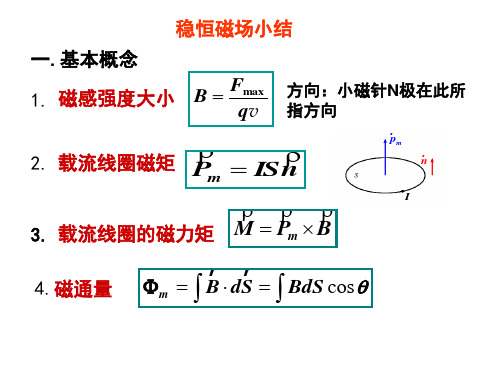
稳恒磁场小结
一.基本概念
1. 磁感强度大小
Fmax B qv
方向：小磁针N极在此所 指方向
pm
2. 载流线圈磁矩 P ISn m
3. 载流线圈的磁力矩 M Pm B
4.磁通量
n
I
m B dS BdS cos
二.基本实验定律
（1）首先选定回路L的绕行方向. （2）按照右手螺旋关系确定出回路的正法线方向. （3）确定通过回路的磁通量的正负. （4）确定磁通量的时间变化率的正负. （5）最后确定感应电动势的正负.
dΦ ε dt
n
L
ε 0 与回路 L绕向相反； ε 0 与回路 L绕向相同。
②感应电流 ③若为N匝
注意： 计算一段有限长载流导线在磁 场中受到的安培力时，应先将其 分割成无限多电流元，将所有电 流元受到的安培力矢量求和—矢 量积分。
B
Idl
Idl
B
L
F dF L Idl B
L
三.稳恒磁场的基本性质： 1.磁场的高斯定理：
m B dS 0
d dq d D D dS I dt dt dt
大学物理稳恒磁场
B2
0
r
r2 R2
I
rR
I
0I rR p r
B20R I2r rR
rp
B 0I rR 2r
B
无限长圆柱导体电流外面的磁场与电流
都集中在轴上的直线电流的磁场相同
.
R
r
无限长通电柱面
B2r 0 rR
0I rR p r I
B0 rR
rp
B 0I rR 2r
B
思考：有人说：“环路不环绕
电流时，环路上磁场必处处为
o
( D ) 20I R
B
( E ) 20I 8R
.
[A]
5.如图所示，电流由长直导线 1 经 a 点流 入电阻均匀分布的正方形线框，再由 b 点 流出，经长直导线 2 返回电源（导线 1、2 的延长线均通过 o 点）。设载流导线 1、2 和正方形线框在框中心o 点产生的磁感应 强度分别用 B1、B2、B3 表示，则 o 点的感 应强度大小
单位长度的电流）到处均匀。大小为 j
解：视为无限多平行
长直电流的场。 B
p
分析场点p的对称性
B
因为电流平面是无限大，故与电流平面等距离的 各点B的大小相等。在该平面两侧的磁场方向相反。
.
作一安培回路如图： bc和 da两边被电流平 面等分。ab和cd 与电 流平面平行,则有
L B d lB 2 lojl
(A )BR2B r. (B)BRBr. (C )2BRB r. (D )BR4Br.
.
[B]
4.两半径为R的相同导体细圆环,互相垂直放 置,且两接触点A、B连线为环的直径,现有 电流1沿AB连线方向由A端流入,再由 B端流 出,则环中心处的磁感应强度大小为:
1.大学物理-稳恒磁场概念
思路: 思路: 实验
理论
应用
磁现象
1)磁体间有相互作用力 1)磁体间有相互作用力 同性相斥, 同性相斥,异性相吸 磁极不能单独存在 2)奥斯特: 奥斯特: 奥斯特 电流 3)安培: 磁体 3)安培: 安培 磁体 4) 洛仑兹: 洛仑兹: 5) 载流导线 磁体 电流 运动电荷 载流导线 –
S S N S N
磁感应强度
一. 磁感应强度概念
r r Fe r →B= 参照:电场强度: 参照:电场强度: E = q0
磁感应强度: 磁感应强度: 运动点电荷: 运动点电荷: 电流元: 电流元:
1. 定义: 定义:
r r Fe = q0 E
r r Fm r Fm r r , B= q0v0 I 0dl0
?
r r r dFm = ( I 0 dl 0 ) × B
3. 画 B x曲线 r 0 IR 2 r B= 3 i 2 2 2( R + x ) 2 练习: 练习:
B
o
x
Bo = ?
I
R
o
R o
I
B0 =
0 I
8R
30 I 0 I B0 = + 8R 4πR
亥姆霍兹圈: 例4.亥姆霍兹圈:实验室用近似均匀磁场 亥姆霍兹圈 两个完全相同的N匝共轴密绕短线圈 匝共轴密绕短线圈, 两个完全相同的 匝共轴密绕短线圈,其中心间距 与线圈半径R相等 相等, 与线圈半径 相等,通同向平行等大电流 I. . 求轴线上 o1 .
磁场 如何作用—通过磁场 1.磁场概念: 磁力如何作用 通过磁场: 1.磁场概念: 磁力如何作用 通过磁场: 磁场概念 电流或运动电荷周围,除了电场, 电流或运动电荷周围,除了电场,还有磁场
大学物理下-- 稳恒磁场
2
2C Nhomakorabea dl
2
2
2B
A
BR sind
d
v
p vB
i
AC
v B dl
2
BR
0
sind
2 BR
2
讨论 本题可用补偿法求解
在AC间加一假想直导线，则 构成半圆形闭合回路，其感应 电动势为零（为什么），即
注意体积元 dV 的选取
4、位移电流的定义：
D d D I d d ds ds S S t dt
通过电场中某截面的电流等于通过该截 面的电位移通量对时间的变化率
5、反映电磁场基本性质和规律的麦克 斯韦方程组的积分形式
D ds
bc
bc 2a
v B dl
所以，线框的感应电动势为
i bc ad 4a B sin t
2
方向：顺时针
讨论：直接由电磁感应定律
d d i BS cos t dt dt 2 BS sin t 4a B sin t
r
N N B dS R2 R2 NI 0 N Bhdr N hdr R1 R1 2r 2 0 N hI R2 ln 2 R1
5. 描述稳恒磁场的两条基 本定律 （1）磁场的高斯定理
s
磁场是无源场（涡旋场） B d s 0
（2）安培环路定理 n
L i 1
L
I1
B d l I 0 i
I2
I3
用安培环路定理计算磁场的条件和方法 I i 正负的确定：规定回路环形方向，由 右手螺旋法则定出
2C Nhomakorabea dl
2
2
2B
A
BR sind
d
v
p vB
i
AC
v B dl
2
BR
0
sind
2 BR
2
讨论 本题可用补偿法求解
在AC间加一假想直导线，则 构成半圆形闭合回路，其感应 电动势为零（为什么），即
注意体积元 dV 的选取
4、位移电流的定义：
D d D I d d ds ds S S t dt
通过电场中某截面的电流等于通过该截 面的电位移通量对时间的变化率
5、反映电磁场基本性质和规律的麦克 斯韦方程组的积分形式
D ds
bc
bc 2a
v B dl
所以，线框的感应电动势为
i bc ad 4a B sin t
2
方向：顺时针
讨论：直接由电磁感应定律
d d i BS cos t dt dt 2 BS sin t 4a B sin t
r
N N B dS R2 R2 NI 0 N Bhdr N hdr R1 R1 2r 2 0 N hI R2 ln 2 R1
5. 描述稳恒磁场的两条基 本定律 （1）磁场的高斯定理
s
磁场是无源场（涡旋场） B d s 0
（2）安培环路定理 n
L i 1
L
I1
B d l I 0 i
I2
I3
用安培环路定理计算磁场的条件和方法 I i 正负的确定：规定回路环形方向，由 右手螺旋法则定出
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0 4
nqvS dl sin
r2
I
dl
dB
0 4
nqvS dl sin
r2
0 4
qv sin
r2
nSdl
dl
dN nSdl
dB 0 4
qv sin
r2 dN
BdN
则电流元中每个点电荷产生的磁场为
B
0 4
q sin
r2
B
0 4
q r
r2
B
0 4
q r
r2
E
q
4 0 r 2
rˆ
B E c2
磁性—能吸引铁钴镍等物质的性质。 人们发现磁铁有以下性质：
（1）两端有两个强磁区，称为磁极
SN
（2）自由悬挂的磁铁转向地的南北方向
（3）两磁铁之间有相互作用，同极相斥，异极相吸
（4）N，S共存
2、电流与磁铁之间的相互作用
奥斯特实验
奥斯特
• 19世纪20年代前，磁 和电是独立发展的
• 奥斯特,丹麦物理学家 Hans Christian Oersted深受康德哲学 关于“自然力”统一观 点的影响，试图找出电、 磁之间的关系
四、磁场的描述 磁感应强度矢量
如何描述磁场？可以用试探的运动电荷检验。 实验结果：
S
N
F
N
q以 v 通过 P 点，受磁力作用。 M
Pq v
F (v, MN)平面，F为横侧向力， 0, F 0
它不改变v大小。
MN —零力线
F q sin
F 恒量
q sin
F 恒量
q sin
SN
定义：在磁场中一点存在一矢量
本章将从基本磁现象出发，研究磁场性质及其描述、 磁场的有关计算以及磁场对电流的作用。
3-1 基本磁现象 磁场及其描述
一、基本磁现象 1、磁铁 天然磁现象 磁铁即 Fe3O4 ，早在春秋战国就有磁现象的记载。
古代写作“慈石”，意即“石铁之母也，以有慈石， 故能引其子”（《吕氏春秋》）。东汉发明“司南 勺”，北宋沈括创制指南针并发现地磁偏角，对世界 文明做出了贡献。
称为磁感应强度 B M
FB N
Pq v
大小：
B F Fmax
qv sin qv
0, F 0 MN —零力线
方向：零力线方向（小磁针N方向）
2
,
F
Fmax
F、v、B满足右手螺旋关系（F qv B)
SN
B 单位：1T 104G, 1T 1 N
cm / s
空间矢量点函数
B=B(x, y, z）
Idl q
v dl , dt
I q dt
B
vr
q
B 0 q r 4 r2
B
0 4
q sin
r2
B (, r )平面
证：
I jS nqvS , dN nSdl (dN个运动电荷）
dN个电荷 即 Idl 产生的磁场（毕-萨-拉定律）
dB
0 4
Idl sin
r2
I nqvS
dB
3、电流与电流之间的相互作用
电流流向相同， 吸引；电流流向 相反，排斥
二、磁性的起源 上述实验现象，启发人们去探索磁现象的本质。
人们总结认为，磁现象起源于运动电荷或电流。
磁铁的磁性：来源于“分子电流”（安培提出）
“分子电流”——分子内电荷运动的总效果相当
于环形电流（小磁针）。
“分子电流”排列杂乱，无磁性
注：
（1）在 r sin 为半径的圆环
上， dB 相等，方向沿切向，
Idl 延线上 dB （ 0 0）。
时，dB最大。
2
dB =0
dB
Idl r dB 最大
（2）比较
1
dE
dq
4 0 r 2
rˆ
同：
r2
dE
异：
dq r
dB
0 4
Idl rˆ r2
dB
r
Idl
dE // r , dB r
r sin dB
r
Idl
dB
r
Idl
dB
0 4
Idl rˆ r2
0 4
Idl r r3
大小：
dB
0 4
Idl sin
r2
方向：
dB
r sin
r dB
Idl
dB (r , dl )平面（右手法则）
r sin dB
r
Idl
dB
r
Idl
dB 0 Idl rˆ 4 r2
dB 0 Idl sin 4 r2
第三章 稳恒磁场
学习思路： 基本磁现象、磁场及其描述 磁相互作用与电相互作用有何异同？ 计算磁感应强度的基本方法 反映磁场性质的基本数学定理 磁场对电流作用的规律 带电粒子在磁场中的运动规律 磁场与介质相互作用
人类对磁现象的认识始于磁铁之间的作用。人们 曾认为，磁铁两极有磁荷（类似于电荷产生电场，磁 荷也产生磁场）。1819年，奥斯特发现电流有磁效应， 从而揭示了电与磁之间的联系。后来，法拉第发现磁 能生电，经麦克斯韦总结，形成了经典电磁学理论。
SN
“分子电流”排列整齐，显磁性
三、磁场 磁相互作用归结于运动电荷或电流之间的相互作
用，这种相互作用是通过什么物质传递的呢？
理论上证明：磁相互作用是通过磁场来传递的 （类似于电场传递电相互作用）
运动电荷
磁场
运动电荷
磁场是一种特殊物质，它存在于运动电荷周围且 只给运动电荷以作用力。
实际上，磁场与电场在本质上有联系，磁场是电 场的相对论效应。磁场和电场是统一的，统称为电 磁场，电磁场的基本粒子是光子。
c2 1
00
c—光速
所以，磁场与电场有本质上的联系（属于同一 本源）。或者说，磁场是电场的相对论效应。通过相 对论可以证明一般情况下，上式成立。
B E c2
v 0，相对观察者静止，B 0, E 0
q
v 0，相对观察者运动，B 0, E 0
实验上可以用铁粉显示。
3-2 毕奥-萨伐尔-拉普拉斯定律
如何计算电流产生的磁场？19世纪20年代，法国 的毕奥三人由大量的实验资料总结分析出了稳恒电流 产生磁场的规律（电磁学基本实验定律之一）。
一、毕-萨-拉定律
dB 0 Idl rˆ 0 Idl r 4 r2 4 r3
0 4 107TmA1 (SI )
dE
与r 方向无关,
dB
与r 方向有关(
)
B
dB
0 4
Idl r r2
稳恒电流磁场是各电 流元产生的磁场叠加。
B Bi
多个电流的磁场是各个电流产 生的磁场叠加。
B B1 B2 B3
r sin dB
r
Idl
dB
r
Idl
二、运动电荷的磁场
类似电流元磁场：
dB
0 4
Idl rˆ r2
M
FB N
Pq v
五、磁力线（磁感应线）
B
用一组曲线可以形象地描述 B 分布。
v
（与电力线描述电场一样）
绘制 方法
B // 切向
B N （磁力线密度） S
dS
dN
常见磁力线举例：
I
I
I
I
性质：（1）闭合或伸向无穷远 （2）不相交 （3）与电流右手法则套合 （4）疏密反映磁感应强度大小
地球磁力线，磁极与南北极偏离 一个角度。