1长方体和正方体的综合
长方体和正方体综合复习

请说说长方体和正方体的表面积、 体积、棱长和公式
棱长和=(长+宽+高)×4 表面积=(长×宽+长×高+宽×高) ×2 S =(ab+ah+bh)×2
体 积=长×宽×高
棱长和V ==棱ab长h×12 表面积=棱长×棱长×6
S=6a2 体 积=棱长×棱长×棱长
V=a3
6厘米
8厘米
的正方形,长2m,50根这样的方木一共是 多少立方米?合多少立方分米? (6)王叔叔要粉刷一个长7.5m,7m,高3.6m 的教室的墙壁(天花板不刷),已知门窗 面积为5.5m2 ,求应粉刷的面积。
白云居课件
7、要把8盒果汁装一箱,果汁盒的长是8cm, 宽是5cm,高是20cm。请你设计 一个包装箱。怎样包装所用的包装纸最少?
)。
白云居课件
5、我能填得对
(1)6.2dm 3=( )cm 3 560cm =3( )dm 3
(2)3.9L=( )ML 0.6m=( )dm
(3)4cm=( )m
2.5dm2 =( 2)cm2
(4)960dm2 =( )m2 1.2m3 =( )dm3
白云居课件
6、解决问题
(1)将一个苹果放进一个长20cm、宽15cm 的长方体容器中,在向容器中注水,使苹 果完全浸没,然后把它取出,这时水面下 降了5cm。这个苹果的体积是多少?
锯成棱长1dm的小正方体,可以锯( )个。 ①18 ②180 ③90
(4)一个长方体的棱长的和是36cm,它的长、宽、 高的和是( )cm。 ①12 ②9 ③6
(5)至少需要( )个同样的小正方体,才可以 一个稍大的正方体。 ①1 ②4 ③8
(6)将一个正方体钢块锻造成长方体,正方体和长 方体( )。①体积相等,表面积不相等
六年级数学上册 第一单元 长方体和正方体综合测试三

第一单元长方体和正方体学校:___________姓名:___________班级:___________考号:___________一、选择题1.用一根52厘米长的铅丝,正好可以焊成长6厘米,宽4厘米,高()厘米的长方体教具.A. 2 B. 3 C. 4 D. 52.从一个体积是30立方厘米的长方体木块中,挖掉一小块后(如图),它的表面积()。
A.和原来同样大 B.比原来小 C.比原来大 D.无法判断3.长方体和正方体都有()个面.A.6B.4C.34.如图是一个正方体的展开图,在原正方体中,两个相对的面上两数之和最大是()A.45B.48C.50D.585.至少()个完全一样的小正方体可以拼成一个稍大的正方体.A.4B.8C.96.用下图中的一张硬纸板粘成的盒子是()A. B. C. D.7.一个长方体,长9分米,宽8分米,高6分米,放在地面上,占地面积最小是()平方分米.A.48B.54C.72D.3488.一个棱长之和是72厘米的长方体,长、宽、高的和是()厘米.A.18B.12C.6二、填空题9.把若干个边长2厘米的正方体重叠起来堆成如图所示的立体图形,这个立体图形的表面积是平方厘米.10.右图是一张带有折痕的纸板(单位:cm ).将这张纸板按折痕折成一个长方体,口向上,这个长方体的底面积是cm2,高是cm.11.正方体的棱长扩大3倍,棱长总和扩大倍,表面积扩大倍,体积扩大倍。
12.3.21平方米=()升=()毫升7.2升=()立方厘米=()立方米,13.一种分别涂红、黄、蓝、黑、白、绿六种颜色的正方体,如图拼成一个长方体.请问:每个小正方体红色面对的是色,黄色面对的是色.14.如果长方体的长和宽相等,那么它一定是正方体..(判断对错)15.正方体的6个面都是正方形.(判断对错)16.正方体是特殊的,正方体的每个面的面积都.三、计算题17.计算下面长方体或正方体的体积。
(1)a=7.5dm;b=4dm;h=3dm(2)a=0.5m。
长方体和正方体的综合练习

1、一个长方体的棱长总和是96cm,长是9cm,宽是8cm,那么高是多少?2、用一根80厘米长的铁丝正好可以焊成一个长8厘米,高4厘米,宽为多少的长方体呢?3、一个玻璃柜台长2米,宽50厘米,高60厘米,现要在柜台各边安上角铁,一共需要多少米?4、一个正方体的棱长总和是60厘米,它的棱长是多少厘米?5、用一根84厘米长的铁丝焊成一个正方体框架,它的棱长是多少厘米?6、一个正方体的棱长之和是42分米,它的表面积是多少平方分米?7、一个粉笔盒长8厘米,宽7厘米,高5厘米,做这个粉笔盒至少要用多少平方厘米的硬纸?8、一个正方体的食品盒,棱长15厘米,在它的四周贴了一圈商标纸(上下面不贴)。
贴商标纸的面积至少有多少平方厘米?9、一个长方体的长是8分米,宽是5分米,高是1.5分米,它的表面积是多少平方分米?10、一个正方体的底面积是20平方厘米,它的表面积是多少?11、一个长方体游泳池长100米,宽80米,深2米,要在池的四壁和底面涂上水泥,每平方米用水泥4千克,共需水泥多少千克?12、一节长方体通风管长4米,横截面是边长为6分米的正方形,做200节这样的通风管,至少需要铁皮多少平方分米?13、一个长方体玻璃缸,长5分米,宽4.5分米,高6分米。
缸中水深4分米,求缸中水的体积是多少?14、一个长方体长是5分米,宽2分米,高3分米,它的体积是?15、一个正方体的棱长总和是48厘米,它的体积是多少?16、把一根工12分米的长方体木料平均锯成3段,它的表面积增加了4.8平方分米,求这根木料的体积?17、一种长方体木料,长4米,宽和高都是4分米,它的体积是多少?18、一个长方体,底面积是24平方米,高是6分米,它的体积是?19、一个长方体,底面是边长8厘米的正方形,高是1分米,它的体积是多少?20、一根长方体的木料长1.6米,如果把它锯短3分米,它的体积就减少45立方分米,求原来这根木料的体积?21、将一个棱长8分米的正方体锻造成一个底面积是16平方分米的长方体,这个长方体的高是多少分米?21、一根木料长3米,横截面是一个边长8分米的正方形,80根这样的木料的体积是多少立方分米?合多少立方米?22、一种汽车上的油箱,从里面量长8分米,宽4分米,高2.5分米,这个油箱可以装多少升的汽油?23、一块长方体铁板长30厘米,宽25厘米,分别切掉四个边长为5厘米的正方形,然后做成无盖的盒子,这个无盖的盒子的容积是多少?24、一个正方体的表面积是24平方米,如果棱长增加1米,体积就增加多少立方米?25、把长9分米,宽3分米,高12厘米的长方体木块切成棱长为3厘米的正方体木块,可以切成多少块?26、一根长方体木料,长4米,宽0.2米,高2分米,把它锯成3段,表面积最少增加多少平方分米。
苏教版六年级上册数学优质课件:长方体与正方体的表面积和体积综合复习微课

戴窑中心小学 韩明存
一、课堂导学 精心整理
1、王明为自己工厂的产品定做一种长5分米、 宽4分米、高20厘米的包装盒,包装盒用钢 丝做框架,外面钉上纸板。
你能提出哪些可以解决的实际问题。
棱
底
侧
表
体
容
全
一、课堂导学 精心整理
1、王明为自己工厂的产品定做一种长5分米、 宽4分米、高20厘米的包装盒,包装盒用钢 丝做框架,外面钉上纸板。
20厘米=2分米 做一个包装盒至少需要多少平方分米的纸板? (5×4+5×2+4×2)×2
5×4×2+5×2×2+4×2×2
一、课堂导学 精心整理
1、王明为自己工厂的产品定做一种长5分米、 宽4分米、高20厘米的包装盒,包装盒用钢 丝做框架,外面钉上纸板。 20厘米=2分米 这个包装盒所占空间有多大?
(9×5+9×4+5×4)×2 =(45+36+20)×2 =101×2 =202(平方分米)
答:做这个油箱至少需要202平 方分米的铁皮。
9×5×4=180(立方分米) 180立方分米=180升 180×850=153000(克) 153000克=153千克
答:这个油箱最多能装153千克柴油。
精心整理
二、基本练习
一个无盖的长方体玻璃鱼缸,长5分米, 宽4分米,高3分米。在鱼缸里注入40升 水,水深大约多少分米?(玻璃厚度忽 略不计)
鱼缸底面积×水深=水的体积
40 ÷ (5×4)
=40 ÷ 20
=2(分米)
答:水深大约2分米。
三、提高练习 精心整理
有一块长12厘米,宽8厘米的长方形铁皮,要从它的四个 角各剪去一个边长是整厘米数的正方形,然后做成一个容积 最大的无盖长方体铁盒。先在下面的方格中画一画,再求出 这个铁盒的容积最大是多少毫升。(铁皮的厚度忽略不计)
六年级上册数学习题课件-1 第一单元综合训练|苏教版(共12张PPT)
二、判断题。(对的画“√”,错的画“ ”)
1.长方体的每个面一定都是长方形。( ) 2.一个长方体木箱的体积是30立方分米,它的容积也是30立方分米。 () 3.棱长为1分米的正方体,它的体积是1立方分米,表面积是1平方分米。 () 4.如果两个长方体的表面积相等,它们的体积也一定相等。( )
三、选择题。
数学 六年级 上册 SJ
一 长方体和正方体
第一单元综合训练
知识导图
优化精练 一、填一填。 1.长方体和正方体都有( 6 )个面,( 12 )条棱,( 8 )个顶点。 2.一个长方体的长是8厘米,宽是6厘米,高是4厘米。它的棱长总和是 ( 72 )厘米,表面积是( 208 )平方厘米,体积是( 192 )立方厘米。 3.一个正方体,它的棱长总和是24分米,它的每条棱长是( 2 )分米, 底面积是( 4 )平方分米,表面积是( 24 )平方分米,体积是( 8 )立方 分米。 4.把20升的水装入容积是125毫升的瓶里,最多能装(160 )瓶。
35×2+20×2+8×4+20=162(厘米) 答:一共需要彩绳162厘米。
六、一个长方体的铁皮饼干盒,它的长是30厘米,宽是20厘米,高是10厘 米。 1.这个饼干盒的占地面积是多少平方厘米?
30×20=600(平方厘米) 答:这个饼干盒的占地面积是600平方厘米。
2.这个饼干盒的容积是多少升?(铁皮的厚度忽略不计) 30×20×10=6000(立方厘米) 6000立方厘米=6升 答:这个饼干盒的容积是6升。 3.如果在饼干盒的侧面贴上一圈商标纸,至少要多少平方厘米的商标纸? (30×10+20×10)×2=1000(平方厘米) 答:至少要1000平方厘米的商标纸。
1.右图是正方体的表面积展开图,与4相对的数字是( C )。
长方体、正方体的体积综合训练(含解析)印刷版

长方体、正方体的体积综合训练一.选择题(共7小题)1.将一个正方体钢坯锻造成长方体,正方体和长方体()A.体积相等,表面积不相等B.体积和表面积都不相等C.表面积相等,体积不相等D.体积和表面积都相等2.量筒里原有180毫升的水,现在将15个棱长都是1厘米的正方体铁块放入量筒内(正方体全部浸没在水中),水面上升到()毫升的位置.A.180B.185C.195D.2053.在一个长4dm、宽3dm、高2dm的长方体容器中注满水,然后把长3dm、宽2dm、高5dm的长方体石条立着放入容器中,求溢出水的体积的算式是()A.4×3×2B.3×2×5C.3×2×2D.3×2×(5﹣2)4.一个长方体的长、宽、高分别是a米、b米和h米,如果高增高1米,体积增加()立方米. A.ab B.abh C.ab(h+1)D.bh5.将一个长6厘米,宽5.2厘米,高4厘米的长方体裁成一个体积最大的正方体,这个正方体体积是()A.64立方厘米B.64平方厘米C.216立方分米D.216立方厘米6.三个同学分别用8个1cm3的立方体测量了3个盒子的容积,容积最小的盒子是()A.B.C.7.贝贝身高1m,在儿童乐园中有一个正方体大型玩具屋,请你试着估一估该大型玩具屋的体积是()A.8m3B.16m3C.4m3二.填空题(共10小题)8.在横线里填上适当的数5.6立方分米=升8600平方厘米=平方分米980立方分米=立方米9.4立方米=立方分米2.7升=毫升=立方厘米75立方厘米=立方分米=升.9.一个长方体,如果锯下5cm长的一段就变成一个正方体,表面积减少了240cm2,原来长方体的体积是cm3。
10.一个长方体,如果高增加2厘米就成了正方体,而且表面积增加了56平方厘米,原来这个长方体的体积是立方厘米.11.如图是两块同样的长方体木块.其中一个长方体的体积是立方厘米;如果把它们拼成表面积最小的长方体,则拼成后的长方体的表面积是平方厘米.12.在一个长20厘米、宽8厘米、高11厘米的长方体中截取一个最大的正方体,这个正方体的棱长是厘米,最多可以截出个这样的正方体.13.如图,从边长是10的立方体中挖去1个小长方体,则剩余部分的体积是,表面积是.14.在一个边长为3cm的正方体木块的每面中心打一个相通的洞.洞口是边长为1cm的正方形.每个面与正方体相对的面平行(如图).挖洞后正方体木块的体积是cm3.15.如图,在水深5dm,棱长10dm的正方体水箱中,把一块长5dm、宽4dm、高5dm的长方体铁块完全浸没水中后,水深为dm。
五年级数学下册长方体和正方体综合练习

长方体和正方体综合练习一1、学校运来7.6m3的沙子,铺在一个长5m、宽38dm的沙坑里,可以铺多厚?2、一个正方体钢坯棱长6分米,把它锻造成一根宽6分米,高4分米的长方体钢材,钢材长多少分米?3、有一个正方体水箱,棱长是4分米,把这个水箱装满水,再倒入一个长8分米,宽2.5分米的长方体水箱中。
这时它的水深是多少?4、一个封闭的长方体容器,如图1放置时水面高6厘米,那么如图2放置时水面高多少厘米?5、珊瑚石的体积是多少?6、爸爸在一个底面积为51dm2的长方体鱼缸里放了一个假山石,水面上升了3cm。
这个假山石的体积有多大?7、在一个长8m、宽5m、高2m的水池中注满水,然后把两条长3m、宽2m、高4m的石柱立着放入池中,水池溢出的水的体积是多少?8、用一根长()的铁丝正好可以做一个长6厘米,宽5厘米,高3厘米的长方体框架。
9、有一块正方形铁皮,从四个角分别剪下一个边长2分米的正方形后,所剩部分正好焊接成一个无盖的正方体铁皮盒。
原来正方形铁皮的面积是多少平方分米?10、一个长方体的无盖铁皮水桶,长和宽都是3分米,深5分米。
做一对这样的水桶,至少需要多少平方分米铁皮?长方体和正方体综合练习二1、一个长方体中相交于一个顶点的三条棱的长度和是15分米,这个长方体的棱长总和是多少分米?2、把一根长12分米的铁丝剪短后做成一个正方体框架,在框架的外面糊上彩纸,做成一个正方体模型。
这个正方体模型的棱长是()分米,表面积是()平方分米,体积是()立方分米3、一个礼物的包装盒,长、宽、高分别是15cm、15 cm、8 cm。
用彩带把这个包装盒捆上,接头处长18 cm ,一共需要多少厘米彩带?4、有两个棱长是6厘米的正方体铁块,要把它们熔铸成一个长方体铁块(假设没有损耗),这个长方体铁块的长是8厘米,高是9厘米,宽是多少厘米?5、一个棱长是3分米的正方体鱼缸里放满了水,然后把水全部倒进一个长40厘米,宽15厘米的长方体鱼缸内,这个长方体鱼缸中的水深多少厘米?6、一节2米长的长方体通风管,横截面为边长2分米的正方形,制作10节这种通风管至少需要铁皮多少?7.一个长18cm、宽12cm、容积是4.32dm3的长方体包装盒,妈妈想用它装长15cm,宽10cm、高22cm的玻璃器皿,能否装得下?为什么?8、一个无盖的立方体盒子,棱长4分米,它的表面积是多少平方分米?9、有一个正方体水箱,从里面量每边长5dm,如果一满箱水倒入一个长8dm、宽25cm的长方体水池内,水深多少分米?10、一块长方体钢板,长1.2m,横截面的面积是2.5dm2。
长方体稍难综合练习题(精选)
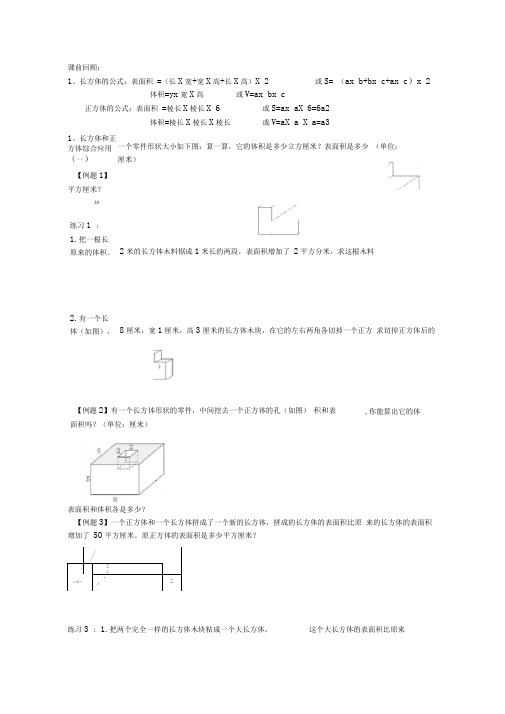
课前回顾:1、长方体的公式:表面积 =(长X 宽+宽X 高+长X 高)X 2或S= (ax b+bx c+ax c )x 2 体积=yx 宽X 高或V=ax bx c 正方体的公式:表面积 =棱长X 棱长X 6或S=ax aX 6=6a2 体积=棱长X 棱长X 棱长 或V=aX a X a=a31、长方体和正方体综合应用(一)【例题1】平方厘米?102米的长方体木料锯成1米长的两段,表面积增加了 2平方分米,求这根木料8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方 求切掉正方体后的表面积和体积各是多少?【例题3】一个正方体和一个长方体拼成了一个新的长方体,拼成的长方体的表面积比原 来的长方体的表面积增加了 50平方厘米。
原正方体的表面积是多少平方厘米?/■■1■■ XJ- jr 1 /1- F Z练习3 : 1.把两个完全一样的长方体木块粘成一个大长方体, 这个大长方体的表面积比原来一个零件形状大小如下图:算一算,它的体积是多少立方厘米?表面积是多少 (单位:厘米) 练习1 :1.把一根长 原来的体积。
2.有一个长体(如图), 【例题2】有一个长方体形状的零件,中间挖去一个正方体的孔(如图) 积和表面积吗?(单位:厘米) ,你能算出它的体两个长方体的表面积的和减少了 46平方厘米,而长是原来长方体的 2倍。
如果拼成的长方体的长是24厘米,那么它的体积是多少立方厘米?2. 一根长80厘米,宽和高都是12厘米的长方体钢材,从钢材的一端锯下一个最大的正方 体后,它的表面积减少了多少平方厘米?3. 把4块棱长都是2分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方分 米?【例题41把11块相同的长方体砖拼成一个大长方体。
已知每块砖的体积是288立方厘米,求大长方体的表面积。
练习4: 1. 一块小正方体的表面积是 6平方厘米,那么,由1000个这样的小正方体所组成 的大正方体的表面积是多少平方厘米?2. 一个长方体的体积是 385立方厘米,且长、宽、高都是质数,求这个长方体的表面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体和正方体的综合
姓名:日期:
【热身训练】
1.长方体和正方体的相同点是都有()个面,()条棱,()个顶点。
不同点是长方体的六个面是(),也可能有两对面是()的。
正方体的六个面都是(),面积都是();长方体相对四条棱(),正方体的12条棱都()。
2.长方体的表面积公式是(),体积公式是()。
3.正方体的表面积公式是(),体积公式是()。
4.一个长方体,长是9厘米,宽是6厘米,高是3厘米,它的棱长
之和是()厘米,表面积是()平方厘米,体积是()立方厘米。
5.一个正方体的棱长为10厘米,则它的棱长之和是()厘米,表面积是()平方厘米,体积是()立方厘米。
若
正方体的棱长增加1倍,则其棱长和增加()倍,表面积增加()倍,体积增加()倍。
【典型例题】
例1.把两个棱长为5厘米的正方体拼成一个长方体,问长方体的体积和表面积各有什么变化?
例2.把一根长5米的长方体木料切了3刀,表面积增加60平方分米,求原体积。
例3.求下图的表面积和体积(单位:厘米)
5
5
课堂小测
姓名:成绩:
1.把一根长1米的长方体木料平均分成5段,表面积增加80平方厘米,求原体积。
2.把三个棱长为10分米的正方体拼成一个长方体,问长方体的体积和表面积各有什么变化?
3.求下图的表面积和体积。
(单位:分米)
12
12
课后作业
姓名:家长签字:
1.把一根长10米的长方体切3刀后,表面积增加120平方分米,求该长方体体积。
2.把两个棱长为6米的正方体拼成一个大长方体,问长方体的体积和表面积各有什么变化?
3.计算它的表面积和体积。
(单位米)。
