由2008年江西高考理科数学最后一题说起
由2008年江西高考理科数学最后一题说起

由2008年江西高考理科数学最后一题说起周湖平年年岁岁卷相似,岁岁年年题不同。
2008年是江西省高考数学自主命题的第四年,今年全省理科平均分为69.37 比去年了降了19.87,特别是理科压轴题的难度系数为0.11,属于超难题。
2007年考生满面笑容,2008年考生叫苦连天。
2008年的理科压轴题是一道函数与不等式的综合题,一改前两年以数列与不等式的综合题为压轴题局面,避免了老师和学生猜题压宝,具有良好的导向作用。
压轴题基于公平的原则体现了试题选拔功能,其设计之新颖,立意之深隧,技巧之高难,把选拔功能体现得酣畅淋漓。
本文以08年江西省高考数学理科压轴题为例谈谈自己的看法。
1考查能力好载体题目 函数()f x =x +11+a +11+8+ax ax ,x ∈(0,+∞). (1)当8a =时,求()f x 的单调区间;(2)对任意正数a ,证明:()12f x <<.解 (1)略(2)对任意给定的0>a ,0>x ,因为ax a x x f 8111111)(+++++=,若令axb 8=,则8=abx ① ba x x f +++++=111111)( ② (一)先证1)(>x f :因为x x +>+1111,a a +>+1111,bb +>+1111 又由x b a +++2≥8244=abx ,∴x b a ++≥6所以(2).再证2)(<x f :由①、②中关于x ,a ,b 的对称性,不妨设x ≥a ≥b ,则0<b ≤2, (Ⅰ).当a+b ≥7,则a ≥5,∴x ≥a ≥5111<+b ,16261611111<=+≤+++a x1)1)(1)(1()()(1)1)(1)(1()()(9)1)(1)(1()(23111111111111)(=++++++++++=+++++++++≥+++++++++=+++++>+++++=b a x abx ax bx ab x b a b a x ax bx ab x b a b a x ax bx ab x b a b a x b a x x f∴2111111)(<+++++=b a x x f(Ⅱ)若a+b<7,由①得ab x 8=,∴811+=+ab ab x ③ 因为222))1(21()(41111b b b a b b b b +-=+++-<+ ∴)1(2111b b b +-<+ ④ 同理得)1(2111a a a +-<+ ⑤,于是 )8211(212)(+-+++-<ab ab b b a a x f ⑥ 今证明8211+>+++ab ab b b a a ⑦ 因为)1)(1(211b a ab b b a a ++>+++,则只要)1)(1(2b a ab ++82+>ab ab 只要ab b a +<++8)1)(1(,即证ab ab b a +<+++81,即a+b<7,而这显然成立。
2008年高考真题精品解析2008年普通高等学校招生全国统一考试(江西卷)(理科)

2008年高考真题精品解析2008年普通高等学校招生全国统一考试(江西卷)(理科) 测试题 2019.91,已知函数(1)求函数的单调区间;(2)若函数的图像与直线恰有两个交点,求的取值范围.2,已知抛物线和三个点,过点的一条直线交抛物线于、两点,的延长线分别交曲线于.(1)证明三点共线;(2)如果、、、四点共线,问:是否存在,使以线段为直径的圆与抛物线有异于、的交点?如果存在,求出的取值范围,并求出该交点到直线的距离;若不存在,请说明理由.3,不等式的解集为 .4,已知双曲线的两条渐近线方程为,若顶点到渐近线的距离为1,则双曲线方程为 .5,连结球面上两点的线段称为球的弦.半径为4的球的两条弦的长度分别等于、之间距离的最大值为 .6,如图,正六边形中,有下列四个命题:4322411()(0)43f x x ax a x a a =+-+>()y f x =()y f x =1y =a 2y x =00000(,)(0,)(,)M x y P y N x y -、、2000(,0)y x y ≠>M A B AP BP 、C E F 、E F N 、、A B M N 0y AB A B 0y AB 224122xx +-≤22221(0,0)x y a b a b -=>>y x =AB CD 、ABCDEFA .B .C .D .其中真命题的代号是 (写出所有真命题的代号). 7,在复平面内,复数对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限8,定义集合运算:设,,则集合的所有元素之和为A .0B .2C .3D .69,若函数的值域是,则函数的值域是 A . B . C . D .10,A .B .C .D .不存在测试题答案1, 解:(1)因为 令得由时,在根的左右的符号如下表所示2AC AF BC +=22AD AB AF =+AC ADAD AB ⋅=⋅()()AD AF EF AD AF EF ⋅=⋅sin 2cos2z i =+{},,.A B z z xy x A y B *==∈∈{}1,2A ={}0,2B =A B *()y f x =1[,3]21()()()F x f x f x =+1[,3]210[2,]3510[,]2310[3,]3x →=12012-322()2(2)()f x x ax a x x x a x a '=+-=+-()0f x '=1232,0,x a x x a =-==0a >()f x '()0f x '=所以的递增区间为的递减区间为 (2)由(1)得到,要使的图像与直线恰有两个交点,只要或,即.2, (1)证明:设,则直线的方程:即:因在上,所以①又直线方程:由得:所以同理,所以直线的方程:令得()f x (2,0)(,)a a -+∞与()f x (2)(0)a a -∞-,与,45()(2)3f x f a a =-=-极小值47()()12f x f a a ==极小值4()(0)f x f a ==极大值()f x 1y =44571312a a -<<41a <a >01a ≤<221122(,)(,)A x xB x x 、(,)(,)E E F F E x y B x y 、AB ()222121112x x y x x x x x -=-+-1212()y x x x x x =+-00(,)M x y AB 012012()y x x x x x =+-AP 21001x y y x y x -=+210012x y y x y x x y⎧-=+⎪⎨⎪=⎩2210010x y x x y x ---=22100012111,E E E x y y y x x x y x x x -+=⇒=-=200222,F F y y x y x x =-=EF 201201212()y x x y y x x x x x +=--0x x =-0120012[()]yy x x x y x x =+-将①代入上式得,即点在直线上 所以三点共线(2)解:由已知共线,所以以为直径的圆的方程:由得所以(舍去),要使圆与抛物线有异于的交点,则所以存在,使以为直径的圆与抛物线有异于的交点 则,所以交点到的距离为3, 依题意4,5, 易求得、到球心的距离分别为3、2,类比平面内圆的情形可知当、与球心共线时,取最大值5。
2008年高考真题精品解析2008年普通高等学校招生全国统一考试(江西卷)(理科)2450

2008年高考真题精品解析2008年普通高等学校招生全国统一考试(江西卷)(理科) 测试题 2019.91,在数列中,, ,则A .B .C .D .2,函数在区间内的图象是3,已知、是椭圆的两个焦点,满足的点总在椭圆内部,则椭圆离心率的取值范围是A .B .C .D .4,展开式中的常数项为 A .1 B .46 C .4245 D .42465,若,则下列代数式中值最大的是A .B .C .D .6,连结球面上两点的线段称为球的弦。
半径为4的球的两条弦、的长度分别等于、、分别为、的中点,每条弦的两端都在球面上运动,有下列四个命题:①弦、可能相交于点 ②弦、可能相交于点 ③的最大值为5 ④的最小值为1 其中真命题的个数为A .1个B .2个C .3个D .4个{}n a 12a =11ln(1)n n a a n +=++n a =2ln n +2(1)ln n n +-2ln n n +1ln n n ++tan sin tan sin y x x x x=+--3(,)22ππ1F 2F 120MF MF ⋅=M (0,1)1(0,]2(0,22610(1(1+121212120,01a a b b a a b b <<<<+=+=,且1122a b a b +1212a a b b +1221a b a b +12AB CD M N AB CD AB CD M AB CD N MN MN7,电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为A .B .C .D .8,已知函数,,若对于任一实数,与至少有一个为正数,则实数的取值范围是A .B .C .D . 9,在中,角所对应的边分别为,,,求及 10,某柑桔基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需分两年实施;若实施方案一,预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二,预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5; 第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案,第二年与第一年相互独立。
2008年普通高等学校招生全国统一考试江西数学理科试卷及答案

2008年普通高等学校招生全国统一考试(江西卷)理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分。
第Ⅰ卷考生注意:1. 答题前,考生务必将自己的准考证号、姓名填写在答题卡上,考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
2. 第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
第Ⅱ卷用黑色墨水签字笔在答题卡上作答。
若在试题卷上作答,答案无效。
3. 考试结束,监考员将试题卷、答题卡一并收回。
参考公式如果事件,A B 互斥,那么 球的表面积公式()()()P A B P A P B +=+ 24S R π=如果事件,A B ,相互独立,那么 其中R 表示球的半径 ()()()P A B P A P B ⋅=⋅ 球的体积公式 如果事件A 在一次试验中发生的概率是p ,那么 343V R π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径()(1)kkn kn n P k C p p -=-一.选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在复平面内,复数sin 2cos 2z i =+对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限2.定义集合运算:{},,.A B z z xy x A y B *==∈∈设{}1,2A =,{}0,2B =,则集合A B *的所有元素之和为A .0B .2C .3D .63.若函数()y f x =的值域是1[,3]2,则函数1()()()F x f x f x =+的值域是A .1[,3]2B .10[2,]3C .510[,]23 D .10[3,]34.1limx →=A .12B .0C .12- D .不存在5.在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a =A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++6.函数tan sin tan sin y x x x x =+--在区间3(,)22ππ内的图象是7.已知1F 、2F 是椭圆的两个焦点,满足120M F M F ⋅=的点M 总在椭圆内部,则椭圆离心率的取值范围是A .(0,1)B .1(0,]2 C.(0,2D.28.6101(1(1++展开式中的常数项为A .1B .46C .4245D .42469若121212120,01a a b b a a b b <<<<+=+=,且,则下列代数式中值最大的是 A .1122a b a b + B .1212a a b b + C .1221a b a b + D .1210.连结球面上两点的线段称为球的弦。
2008年高考数学江西卷(理)全解全析

绝密★启用前2008年普通高等学校招生全国统一考试江西卷数学试题(理科)全解全析本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷l 至2页,第Ⅱ卷3至4页,共150分.第Ⅰ卷考生注意:1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第Ⅱ卷用黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.3.考试结束,监考员将试题卷、答题卡一并收回.参考公式:如果事件A 、B 互斥,那么 球的表面积公式P (A +B)=P (A)+P (B) S =4πR 2如果事件A 、B 相互独立,那么 其中R 表示球的半径 P (A·B)=P (A)·P (B) 球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 V =34πR 3n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径P n (k )=C kn P k (1一P )k n -一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.在复平面内,复数z =sin2+i cos 2对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限 【标准答案】D【试题解析】易知sin2>0 ,cos 2<0。
根据复数的几何意义可知z 所对应的点位于第四象限。
【高考考点】三角函数的定义和复数的几何意义 【易错提醒】实数值与三角函数角的大小的对应。
【学科网备考提示】注意复数的几何意义。
2.定义集合运算:A *B ={z |z =xy ,x ∈A ,y ∈B }.设A ={1,2},B ={0,2},则集合A *B 的所有元素之和为 A .0 B .2 C .3 D .6 【标准答案】D【试题解析】A ,B 两个集合中的元素的乘积:1⨯0=0,1⨯2=2,2⨯0=0,2⨯2=4.故集合A *B 有三个元素0,2,4,它们的和为6。
08年高考数学江西卷(理)最后一题研究

ab 8
1 a 1 b (1 a)(1 b)
只要证
ab
ab ,即 ab 8 (1 a)(1 b) ,即 a b 7 ,据③,此为显然.
(1 a)(1 b) ab 8
因此⑦得证.故由⑥得 f ( x) 2 .综上所述,对任何正数 a, x ,皆有 1 f x 2 .
说句实在话, 该题命题人陶平生教授所给出的证明是最好的。 问题只是这道好题在不恰当的时 间出现在不恰当的地方。
平心而论,不等式做到这个分上,可以说达到了一个佳境。
精心整理
精心整理 2008-07-1221:03scpajmb 的发言: 确实,陶平生教授是不等式高手,所命那道 2005 年全国联赛加试第二题,大家还记忆犹新。
当然,宋老师也是不等式高手。我的这个证明不是最简单的,发到这里供参考。
精心整理
1
ab 1 x
ab , ab 8
因为 1 1 b 1b 1b
b2 4(1 b) 2
[1
b ]2 所以 1
2(1 b)
1b
1
b …④
2(1 b)
同理得 1 1
a
…⑤,于是 f x
1 2
a
b 2 ab …⑥
1a
2(1 a)
2 1 a 1 b ab 8
今证明 a
b 2 ab …⑦ , 因为 a
b2
ab
,
1a 1b
ax
求证 :
上式不等式 (1) 与 2004 年西部奥林匹克 最后一题:
设 a,b,c 是正数,求证: 1
a a2 b2
b b2 c2
c
32
c2 a2
2
类似,且证明比这道西部奥林匹克题还难。 而这道西部奥林匹克题当年参赛选手无一人完全证 出。
08年高考数学江西卷(理)最后一题研究

精心整理08年高考数学江西卷(理)最后一题有点难22.(本小题满分14分)已知函数f (x )=x +11+a +11+8+ax ax ,x ∈(0,+∞). (1)当a =8时,求f (x )的单调区间;(2)对任意正数a ,证明:l <f (x )<2. 令axc x b 8,==,则第(2)等价于:若a,b,c>0,abc=8求证:上式不等式(1)与2004年西部奥林匹克设a,b,c 是正数,求证:12222+++<c b b b a a类似,且证明比这道西部奥林匹克题还难。
出。
另外,2003年中国数学奥林匹克第三题:给定正数n,求最小正数λ,)(22212πθ=n ,就有n θθθcos ...cos cos 21∙∙答案:当当n=33222tan ,tan θθ=c 即得(1)右边的等式。
2小题无人挨边;14分的题全省9分一人,8分二人。
由此可知,(2)右边的不等式,江西的考生无人证出,基本上属于废题。
所以第(2)小题不宜作高考题。
此题也引起了张景中院士的兴趣,在“张景中院士解江西高考压轴题”一贴中2003年中国数学奥林匹克第三题黄玉民教授解答。
22.解:()1、当8a =时,()13f x =+,求得()f x '=, 于是当(0,1]x ∈时,()0f x '≥;而当[1,)x ∈+∞时,()0f x '≤.即()f x 在(0,1]中单调递增,而在[1,)+∞中单调递减.(2).对任意给定的0a >,0x >,由()f x =, 若令8b ax =,则8abx =…①,而()f x =+…② (一)、先证()1f x >11x >+11a >+11b >+,又由28a b x +++≥≥=,得6a b x ++≥.所以2 只要证(1)(1)8ab ab a b ab >+++,即8(1)(1)ab a b +>++,即7a b +<,据③,此为显然. 因此⑦得证.故由⑥得()2f x <.综上所述,对任何正数a,x ,皆有()12f x <<.说句实在话,该题命题人陶平生教授所给出的证明是最好的。
理科2008年高考数学试题(江西卷)
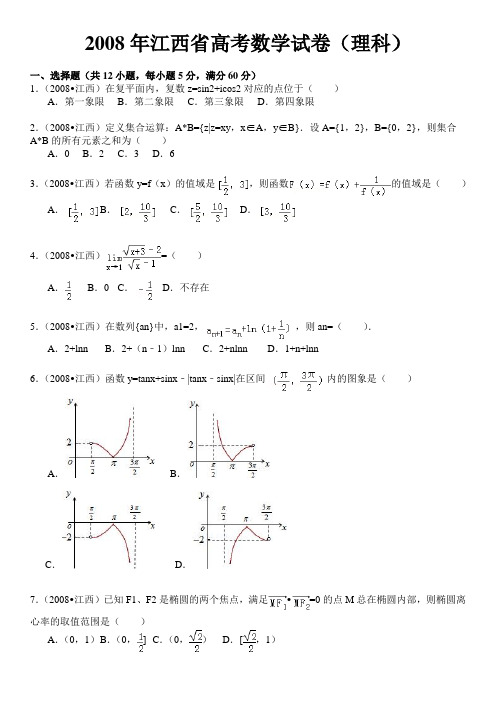
2008年江西省高考数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.(2008•江西)在复平面内,复数z=sin2+icos2对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.(2008•江西)定义集合运算:A*B={z|z=xy,x∈A,y∈B}.设A={1,2},B={0,2},则集合A*B的所有元素之和为()A.0 B.2 C.3 D.63.(2008•江西)若函数y=f(x)的值域是,则函数的值域是()A. B.C.D.4.(2008•江西)=()A.B.0 C.D.不存在5.(2008•江西)在数列{an}中,a1=2,,则an=().A.2+lnn B.2+(n﹣1)lnn C.2+nlnn D.1+n+lnn6.(2008•江西)函数y=tanx+sinx﹣|tanx﹣sinx|在区间内的图象是()A.B.C.D.7.(2008•江西)已知F1、F2是椭圆的两个焦点,满足•=0的点M总在椭圆内部,则椭圆离心率的取值范围是()A.(0,1)B.(0,] C.(0,)D.[,1)8.(2008•江西)展开式中的常数项为()A.1 B.46 C.4245 D.42469.(2008•江西)若0<a1<a2,0<b1<b2,且a1+a2=b1+b2=1,则下列代数式中值最大的是()A.a1b1+a2b2 B.a1a2+b1b2 C.a1b2+a2b1 D.10.(2008•江西)连接球面上两点的线段称为球的弦.半径为4的球的两条弦AB、CD的长度分别等于、,M、N分别为AB、CD的中点,每条弦的两端都在球面上运动,有下列四个命题:①弦AB、CD可能相交于点M;②弦AB、CD可能相交于点N;③MN的最大值为5;④MN的最小值为1其中真命题的个数为()A.1个B.2个C.3个D.4个11.(2008•江西)电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为23的概率为()A.B.C.D.12.(2008•江西)已知函数f(x)=2mx2﹣2(4﹣m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是()A.(0,2) B.(0,8)C.(2,8)D.(﹣∞,0)二、填空题(共4小题,每小题4分,满分16分)13.(2008•江西)直角坐标平面上三点A(1,2)、B(3,﹣2)、C(9,7),若E、F为线段BC的三等分点,则=_________.14.(2008•江西)不等式的解集为_________.15.(2008•江西)过抛物线x2=2py(p>0)的焦点F作倾斜角为30°的直线,与抛物线分别交于A、B两点(点A在y轴左侧),则=_________.16.(2008•江西)如图(1),一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图(2))有下列四个命题:A.正四棱锥的高等于正四棱柱高的一半B.将容器侧面水平放置时,水面也恰好过点PC.任意摆放该容器,当水面静止时,水面都恰好经过点PD.若往容器内再注入a升水,则容器恰好能装满.其中真命题的代号是:_________(写出所有真命题的代号).三、解答题(共6小题,满分74分)17.(2008•江西)在△ABC中,角A,B,C所对应的边分别为a,b,c,,,2sinBcosC=sinA,求A,B及b,c18.(2008•江西)某柑桔基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需分两年实施;若实施方案一,预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案,第二年与第一年相互独立.令ξi(i=1,2)表示方案实施两年后柑桔产量达到灾前产量的倍数.(1).写出ξ1、ξ2的分布列;(2).实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?(3).不管哪种方案,如果实施两年后柑桔产量达不到灾前产量,预计可带来效益10万元;两年后柑桔产量恰好达到灾前产量,预计可带来效益15万元;柑桔产量超过灾前产量,预计可带来效益20万元;问实施哪种方案所带来的平均效益更大?19.(2008•江西)数列{an}为等差数列,an为正整数,其前n项和为Sn,数列{bn}为等比数列,且a1=3,b1=1,数列是公比为64的等比数列,b2S2=64.(1)求an,bn;(2)求证.20.(2008•江西)如图,正三棱锥O﹣ABC的三条侧棱OA、OB、OC两两垂直,且长度均为2.E、F分别是AB、AC的中点,H是EF的中点,过EF作平面与侧棱OA、OB、OC或其延长线分别相交于A1、B1、C1,已知.(1)求证:B1C1⊥平面OAH;(2)求二面角O﹣A1B1﹣C1的大小.21.(2008•江西)设点P(x0,y0)在直线x=m(y≠±m,0<m<1)上,过点P作双曲线x2﹣y2=1的两条切线PA、PB,切点为A、B,定点.(1)求证:三点A、M、B共线.(2)过点A作直线x﹣y=0的垂线,垂足为N,试求△AMN的重心G所在曲线方程.22.(2008•江西)已知函数,x∈(0,+∞).(1)当a=8时,求f(x)的单调区间;(2)对任意正数a,证明:1<f(x)<2.参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(2008•江西)在复平面内,复数z=sin2+icos2对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限考点:复数的代数表示法及其几何意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由2008年江西高考理科数学最后一题说起
周湖平
年年岁岁卷相似,岁岁年年题不同。
2008年是江西省高考数学自主命题的第四年,今年全省理科平均分为69.37 比去年了降了19.87,特别是理科压轴题的难度系数为0.11,属于超难题。
2007年考生满面笑容,2008年考生叫苦连天。
2008年的理科压轴题是一道函数与不等式的综合题,一改前两年以数列与不等式的综合题为压轴题局面,避免了老师和学生猜题压宝,具有良好的导向作用。
压轴题基于公平的原则体现了试题选拔功能,其设计之新颖,立意之深隧,技巧之高难,把选拔功能体现得酣畅淋漓。
本文以08年江西省高考数学理科压轴题为例谈谈自己的看法。
1考查能力好载体
题目 函数()f x =x +11+a +11+8
+ax ax ,x ∈(0,+∞). (1)当8a =时,求()f x 的单调区间;
(2)对任意正数a ,证明:()12f x <<.
解 (1)略
(2)对任意给定的0>a ,0>x ,因为
ax a x x f 8111111)(+
++++=,若令ax b 8=,则8=abx ① b
a x x f +++++=11
1111)( ② (一)先证1)(>x f :因为x x +>+1111,a a +>+1111,b
b +>+1111 又由x b a +++2≥8244=abx ,∴x b a ++≥6
所以
(2).再证2)(<x f :由①、②中关于x ,a ,b 的对称性,不妨设x ≥a ≥b ,则0<b ≤2, (Ⅰ).当a+b ≥7,则a ≥5,∴x ≥a ≥5
111
<+b ,162
61
61
11
11
<=+≤+++a x
1)1)(1)(1()()(1)1)(1)(1()()(9)1)(1)(1()(2311111111
1111)(=++++++++++=+++++++++≥+++++++++=+++++>+++++=b a x abx ax bx ab x b a b a x ax bx ab x b a b a x ax bx ab x b a b a x b a x x f
∴211
11
11
)(<+++++=b a x x f
(Ⅱ)若a+b<7,由①得ab x 8=,∴811+=+ab ab x
③ 因为222))
1(21()(41111b b b a b b b b +-=+++-<+ ∴)1(2111
b b b +-
<+ ④ 同理得)1(2111a a a +-
<+ ⑤,于是 )8
211(212)(+-+++-<ab ab b b a a x f ⑥ 今证明8
211+>+++ab ab b b a a ⑦ 因为)1)(1(211b a ab b b a a ++>+++,则只要)
1)(1(2b a ab ++82+>ab ab 只要ab b a +<++8)1)(1(,即证ab ab b a +<+++81,即a+b<7,而这显然成立。
综上,对任意正数a ,()12f x <<.
此题虽然难,但其第(1)问的入口较宽,只要正确求出函数的导数,便可得到答案;这样变难题的整体把关为难题的分支把关,充分考查学生的个性品质。
数学压轴题已从“一题把关”转为“多题把关”,设置了层次分明的台阶,入口宽,上手易,但是深入难,解到底更难。
第2小题无人挨边;14分的题全省9分一人,8分二人。
第(2)问的构造思想和放缩法等的应用要有很高的技巧,以下引用不等式研究专家宋庆老师的发言:说句实在话,该题命题人陶平生教授[1]所给出的证明是最好的。
问题只是这道好题在不恰当的时间出现在不恰当的地方。
平心而论,不等式做到这个分上,可以说达到了一个佳境。
2似曾相识燕归来
08年江西理科最后一题第(2)小题与2004年西部奥林匹克最后一题类似,且证明比这道西部奥林匹克题还难。
而这道西部奥林匹克题当年参赛选手无一人完全证出。
2004西部数学奥林匹克第八题求证:对任意正实数a、b、c都
有
1
2
<≤(王建伟供题)
提示:令
222
222
,,
b c a
x y z
a b c
===,则,,
x y z R
+
∈,1
xyz=,于是,只须证
明
1
2
<≤,不妨设x y z
≤≤。
《中学数学研究》(南昌)2006年第2期“一道西部数学奥林匹克赛题的溯源与推广”(四川省篷安中学蒋明斌老师著);对那道西部奥林匹克题给出了推广。
福建龙岩学院吴善和老师2004年7月,在《中学数学研究》(南昌)“关于IMO42一个不等式的逆向”一文给出了右边不等式的一种证明。
从历届竞赛题中找借鉴已成为高考命题的一种趋势,2008年有几道高考试题具有竞赛背景,譬如,天津市数学高考理科第22题第(3)小题,需要按4的剩余类讨论,广东省数学高考理科第21题和重庆数学高考理科第22题均涉及求二阶线性递归数列的通项公式。
参加过数学竞赛训练的同学得益明显,试题背景有失公平,引发争议。
3华山不止一条道
著名数学家张景中院士认为此题难度较大,适宜竞赛而不适合高考。
命题者提供的参考答案看似推理自然,但实际上做题者难以想到。
下面提供另一种解法,以供叁考。
=
8
b=x,c=
ax
,问题转化为在三个正数a、b、c且8
abc=
的条件下求(,,)
F a b c=的上下界。
不妨设a b c
≤≤,记
8
,,
t a k ab c
k
===,把(,,)
F a b c看成t的函
数()(,,)
f t F a b c
==
,注意变量和参数范围为02
t
<≤≤,计算导数
33
233
22
2
1
'()((1)(1))((1)())(,)
2
k k
f t t k t t t k Q t k
t t
--
=-+++=+-+,这里(,)
Q t k是某个正值代数式,于是可根据233
()((1)())
g t k t t t k
=+-+
的正负来判断的增减。
注意到0
g=,容易作因式分解:22
()()((3))
g t k t t k k t k
=---+,由第二个因式形成的二次方程2(3)0
t k k t k
--+=的判别式22
(3)4
k k k
=--
V,当4
k<时有0
<
V。
于是
2(3)
t k k t k --+
在上递增,从而()
f t
在t=处最大。
容易检验
有
2
f=<和()1
f t>。
