理论力学振动试验(2015)
第四章理论力学实验
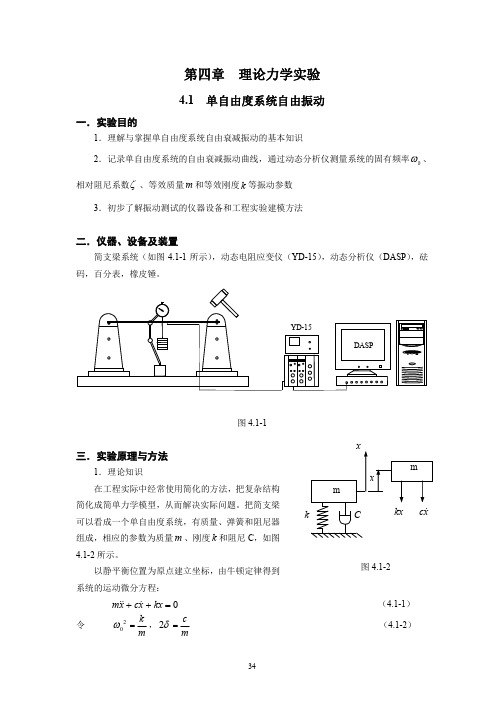
YD-15
DASP
图 4.1-1
三.实验原理与方法
1.理论知识 在工程实际中经常使用简化的方法,把复杂结构
x
m
x
m
简化成简单力学模型,从而解决实际问题。把简支梁
k
可以看成一个单自由度系统,有质量、弹簧和阻尼器
0
2 1 2
1 fd
35
(4.1-8) (4.1-9)
d
2fd
2 Td
0
d 1 2
2fd 1 2 Td
2 1 2
ቤተ መጻሕፍቲ ባይዱ
对数减缩系数 :
ln
ln
Ai Ai1
Td
2 1 2
其中对数减缩系数 进行多次平均,得到
1 ln Ai K Aik
由式(4.1-12)得到
2 1 2
(4.1-10) (4.1-11) (4.1-12) (4.1-13) (4.1-14)
C
kx cx
组成,相应的参数为质量 m 、刚度 k 和阻尼 C,如图
4.1-2 所示。 以静平衡位置为原点建立坐标,由牛顿定律得到
图 4.1-2
系统的运动微分方程:
mx cx kx 0
令
02
k m
, 2
c m
(4.1-1) (4.1-2)
34
其中 称为阻尼系数,单位为 1/s;0 是相应的无阻尼的固有频率,式(4.1-1)可以写成
值,在表 4.1-1 中记录下数据,并计算出等效刚度 k 。
2.自由衰减曲线记录与系统固有频率和阻尼比等参数分析 1)启动动态分析仪 打开计算机电源,进入 WindowsXP 系统,点击分析桌面图标 Coinv Dasp 2005 标准版, 选择虚拟仪器库,点击单通道,分析仪进入采集与分析状态。 2)进入分析仪主窗口 进入分析仪主窗口后,选择波谱双显,分析窗口同时显示时域波形和频谱图。 3)屏幕参数设置
《理论力学》实验指导书

实验一求振动系统的刚度系数和固有频率一、实验目的:1、了解并掌握一维振动系统的刚度系数的测定;2、求取振动系统的固有频率;3、了解考虑弹簧质量时,对振动周期的影响并进行等效质量的计算。
二、实验设备和仪器1、TME—1理论力学多功能实验装置;2、100g砝码1个,200g砝码2个;3、砝码托盘一个;三、实验原理弹簧质量组成的振动系统,在弹簧的线性变形范围内,系统的变形和所受到的外力的大小成线性关系。
据此,施加不同的力,得到不同的变形,可以得到系统的刚度系数。
四、实验方法和步骤1、将砝码托盘钩挂在“弹簧质量系统”的塑料质量模型上2、记录此时塑料质量模型上指针所在的初始位置;3、将100g的砝码放置于砝码托盘上,读取指针的位置并做记录;4、按100g的增量变换砝码,直到砝码重量达500g,并记录相应的指针位置;5、在坐标上画出系统变形与砝码重量之间的关系曲线;6、计算振动系统的刚度系数和固有频率。
五、数据记录与处理12、系统固有频率的计算六、注意事项1、实验前,应通过调节弹簧固定端的调节螺栓使系统的模型保持水平;2、读数时眼睛应平视,以尽量减小读数误差;七、思考题1、在考虑弹簧质量的情况下,系统的等效质量是否等于塑料模型的质量加四根弹簧的质量?2、试分析系统的误差。
实验二、测定“空中输电线”模型的振幅与风速关系曲线一、实验目的1、了解风激励对空中输电线产生的振动响应,认识共振的危害性;2、了解模型的抽象结果;3、测取“空中输电线”模型的振动幅值与风激励速度之间的关系曲线二、实验仪器和设备1、TME—1理论力学多功能实验装置;2、“空中输电线”模型;3、调压器1只;4、风速仪1台;5、光电转速表1只。
三、实验原理“空中输电线”可以抽象为由弹簧和质量块组成的系统模型。
在风激励下,该系统将产生振动。
激励频率与风速有关,而系统振幅又与激励频率有关。
在不同的风速下,系统的振动频率是不同的。
当激励频率接近系统的固有频率时,系统将产生共振。
理论力学第二次实验

实验二 单自由度振动系统固有频率及阻尼的测定一、实验目的1、掌握测定单自由度系统固有频率、阻尼比的几种常用方法2、掌握常用振动仪器的正确使用方法二、实验内容1、记录水平振动台的自由衰减振动波形2、测定水平振动台在简谐激励下的幅频特性3、 测定水平振动台在简谐激励下的相频特性4、 根据上面测得的数据,计算出水平振动台的固有频率、阻尼比三、实验原理具有粘滞阻尼的单自由度振动系统,自由振动微分方程的标准形式为022=++q p q n q&&&,式中q 为广义坐标,n 为阻尼系数,eq eq m C n /2=,eq C 为广义阻力系数,eq m 为等效质量;p 为固有的圆频率,eq eq m K p /2=,eq K 为等效刚度。
在阻尼比1/<=p n ζ的小阻尼情况下,运动规律为)sin(22α+−=−t n p Ae q nt ,式中A ,α由运动的起始条件决定,d f n p π222=−。
具有粘滞阻尼的单自由度振动系统,在广义简谐激振力t H t s ωsin )(=作用下,系统强迫振动微分方程的标准形式为t h p q n qωsin 22=++&&&,式中eq m H h /=。
系统稳态强迫振动的运动规律)sin(ϕω−=t B q ,式中 振幅22220222224)1(4)(λζλωω+−=+−=B n p hB 相位差22212arctg 2arctg λζλωωϕ−=−=p n 其中eq k H ph B ==20,p ωλ=。
由台面、支撑弹簧片及电磁阻尼器组成的水平振动台(见图四),可视为单自由度系统,它在瞬时或持续的干扰力作用下,台面可沿水平方向振动。
1、 衰减振动:用一点电脉冲沿水平方向冲击振动台,系统获得一初始速度而作自由振动,因存在阻尼,系统的自由振动为振幅逐渐减小的衰减振动。
阻尼越大,振幅衰减越快。
为了便于观察和分析运动规律,采用电动式相对速度拾振器将机械振动信号变换为与速度成比例的电压信号,该电压信号经过计算机A/D 和积分处理,得到与运动位移成比例的数字量,并显示运动位移随时间变化的波形。
理论力学振动试验(2015)

实验二:简谐振动幅值测量一、实验目的1.了解振动信号位移、速度、加速度之间的关系。
2.学会用速度传感器测量简谐振动的位移、速度、加速度幅值。
二、实验装置框图实验装置与仪器框图见图1。
图1 实验装置框图三、实验原理在振动测量中,有时往往不需要测量振动信号的时间历程曲线,而只需要测量振动信号的幅值。
振动信号的幅值可根据位移、速度、加速度的关系,用位移传感器或速度传感器、加速度传感器来测量。
设振动位移、速度、加速度分别为x 、、a ,其幅值分别为X 、V 、A : sin()x B t ωϕ=-cos()dy B t dtυωωϕ==-(1)222sin()d ya B t dtωωϕ==--式中:B ——位移振幅 ——振动角频率 ——初相位X =B故: 2V B fB ωπ== (2) B f B A 22)2(πω==振动信号的幅值可根据式(4-2)中位移、速度、加速度的关系,分别用位移传感器、速度传感器或加速度传感器来测量。
也可利用虚拟式信号分析仪和测振仪中的微分、积分功能来测量。
四、实验方法1.激振信号源输出端接电动式激振器,用电动式激振器对简支梁激振。
2.用速度传感器拾振,速度传感器的输出端接测振仪。
3.开启激振信号源的电源开关,对系统施加交变的正弦激振力,使系统产生简谐振动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过载。
4.分别用测振仪的位移X、速度V、加速度A各档进行测量和读数。
五、实验结果与分析1位移X (mm)23.根据速度V,按公式(2)计算位移X、加速度A。
4.根据加速度A,按公式(2)计算位移X、速度V。
5.位移、速度、加速度幅值的实测值与计算值有无差别?若有差别原因是什么?实验三:机械振动系统固有频率的测量一、实验目的1.了解共振前后李萨如图形的变化规律和特点。
2.学会用“共振相位判别法”测量机械振动系统的固有频率。
二、实验装置框图图1 实验装置框图 三、实验原理用简谐力激振,造成系统共振,以寻找系统的固有频率,是一种常用的方法。
理论力学 振动

k1
k2
k1 F1
F2
st
m
st
mg
F2
mg
k2
keq称为等效弹簧刚性系数
并联系统的固有频率为
n
keq m
k1 k2 m
当两个弹簧并联时,其等效弹簧刚度等于两个弹簧刚度的和。
这一结论也可以推广到多个弹簧并联的情形。
(2)弹簧串联
两个刚性系数分别为k1、k2弹簧串联系统。每个弹簧受的力都等于物块的重 量,因此两个弹簧的静伸长分别为:
这个原理可以求出其它类型机械振动系统的固有频率。
实际问题中由机械能守恒,对保守系统,由: d (T V ) 0
dt
可列出系统的运动微分方程,可容易得到系统的固有频率
4)物块沿x轴的运动微分方程为
m
d2x dt 2
mg
sin
k( 0
x)
0
mg
sin k
m d 2 x kx dt 2
0 A
x
h
表明斜面角β与物块运动微分方程无关。
O
固有频率
F
mg
FN
n
k m
0.81000 40rad / s 0.5
x
此系统的通解为 x Asin(nt ) 固有频率与斜面倾角β无关。
单自由度系统; 多自由度系统; 连续体系统。
这里只研究单自由度振动。
§10-1 单自由度系统的自由振动
1. 自由振动微分方程 工程中许多振动可简化为一个质量和一个弹簧的弹簧质量系统,系统在
重力作用下沿铅垂方向振动的,具有一个自由度,简化为图示模型。 下面来分析其运动规律,先列出其运动微分方程。
设弹簧原长为l0,刚性系数为k。
理论力学 第14章 振动

(2)运动分析,选择坐标系。根据系统的运动特性,选出
相应的广义坐标。一般选取系统的静平衡位置为广义坐标的原 点,坐标轴沿振动的方向。 (3)受力分析。为计算方便,最好把系统置于广义坐标为 正值的任意位置,然后画受力图。这时,弹性恢复力与粘滞阻
力应指向坐标的负方向。
Theoretical Mechanics
振幅 周期
2 0 x 2 A x0 2 pn
x A sin( pnt )
pn x0 tan 0 x
f 1 pn T 2π
初相位 频率
2π T pn
系统的固有频率和周期仅与系统的质量与刚度有关,与运 动初始条件无关。振幅和初位相则由运动初始条件决定。
Theoretical Mechanics
pn
――频率比
H b0 ――激振力之最大值引起的弹簧静伸长 k
n ――阻尼比 pn
受迫振动的频率等于激振力频率。
Theoretical Mechanics
返回首页
第14章 振动
振动微分方程的全解为
2 x Ae nt sin( pn 2 t ) B sin(t )
衰减振动
强迫振动
第14章 振动
14.1 主要内容
(5)减振与隔振的概念 为了尽量减小振动,避免在共振区内工作。许多引发振动 的因素防不胜防,或难以避免,这时,可以采用减振或隔振的 措施。 减振:在振体上安装各种减振器,使振体的振动减弱。例 如,利用各种阻尼减振器消耗能量达到减振目的。 隔振:将需要隔离的仪器、设备安装在适当的隔振器(弹 性装置)上,使大部分振动被隔振器所吸收。
2运动方程振幅初相位周期频率sincostheoreticalmechanics返回首页141主要内容振动计算固有频率用能量法的理论基础是机械能守恒定律动能具有最大值tmax速度为零时t0势能具有最大值umax1412计算固有频率的能量法eqeqeqeq33等效的概念等效的概念eq等效刚度eq等效质量自由振动微分方程等效为广义坐标的形式自由振动微分方程等效为广义坐标的形式并联弹簧串联弹簧maxmaxtu常量其中theoreticalmechanics返回首页141主要内容振动1413单自由度系统的衰减振动1振动微分方程标准形式阻尼对周期影响不大而对振幅有显著影响使其按指数曲线衰减
3理论力学振动实验二 共12页

振动实验
被动隔振、动力吸振、连续弹性梁特性测定实验
(综合性实验)
重庆大学力学实验教学中心
振动实验
一、实验目的
1、学会测量和计算被动隔振系数η、隔振效率E,并绘
出隔振效率图( E)。
2、用共振法测量悬臂梁一阶、二阶、三阶固有频率 f1、f2、 ,f3观察并绘出一至三阶主振型图。 3、了解单式动力吸振器的吸振原理、观察吸振现象并
3、主、被动隔振对比
振源
研究对象
测试参数
实测公式
主动隔振 机器(旋转机械等)
地基
力
被动隔振
地基
仪器(旋转机械等) 位移
a
FT F0
力的幅值
p
B 位移的幅值 H
三、实验原理
1、被动隔振实验
振动实验
隔振器 地基
Bsint
精密仪器
Hsint
被测对象
Fk(xx1) Rc(xx1)
m
振动实验
隔振系数 隔振效率
B H
仪器隔振后的振幅 振源振幅
E(1)10% 0
频率比
f
激振力的频率 隔振系统的固有频率
观察与思考
1)当频 0< < 率2时 比, > 1,即仪 B> 器地 振基 H 幅 ;振幅
隔振器不起隔振作用
2)当频率 1时 比,即 f,系统出现共振被 ,隔 共振
绘出幅频特性曲线( B )。 (选作)
二、实验仪器
1、质量块(视为精密仪器和设备)、简支梁(视为地基)
2、ZG-1型传感器2只、隔振器、吸振器;
3、SJF-3型激振信号源、 JZ-1型激振器; 4、SCZ2-3型测振仪、虚拟测试仪; 5、非接触式激振器、连续弹性梁。
理论力学实验报告指导答案

理论力学实验报告指导答案实验一振动测试系统组成及基本仪器使用方法1—底座; 2—支座; 3—二(三)自由度系统; 4—薄壁圆板支承螺杆;5—固定铰;6—非接触式激振器;7—薄壁圆板;8—电动式激振器;9—电机压板;10—偏心电机;11—加速度传感器;12—简支梁;13—活动铰;14—悬臂梁;15—圆支柱;16—质量;17—调压器; 18—电动式激振器支座; 19—ZK-4JCZ型激振测振仪;20—信号源; 21—计算机及虚拟仪器库; 22—打印机图1 实验装置与结构框图传感器1输入传感器2输入一道振动幅值二道振动幅值频率/功率显示值频率,周期,灵敏度调节一道,二道增益及测试方式状态设置选择及参数选择旋扫频选择方式选择灵敏度选择显示选择功率输出选择功率幅度调节信号源调节功率输出B 道功率输出A 道信号源波形输出ZK —4JCZ 型激振测振仪功能分布图ZK-4JCZ 型激振测振仪是一种多功能测量仪器。
它包括信号源、功率放大器及两个配接加速度计的测量通道,可对振动的加速度、加速度或位移进行测量。
实验二简谐振动幅值测量一、实验目的1. 了解振动信号位移、速度、加速度的关系。
2. 学会用压电式加速度传感器测量简谐振动的位移、速度、加速度幅度。
二、实验装置与仪器框图实验装置与仪器框图见图(1)图(1)实验装置与仪器框图四、实验方法1. 激振信号源输出端接电动式激振器,用电动式激振器对简支梁激振。
2. 用加速度传感器拾振,加速度传感器的输出接测振仪。
3. 开启激振信号源的电源开关,对系统施加交变正弦激振力,使系统产生振动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过载。
4. 分别用测振仪的位移X、速度V、加速度A各档进行测量和读数。
五、实验报告1. 实验数据表12. 根据位移X,按公式(2)计算速度V、加速度A。
3. 根据速度V,按公式(2)计算位移X、加速度A。
4. 根据加速度A,按公式(2)计算位移X、速度V。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二:简谐振动幅值测量、实验目的1. 了解振动信号位移、速度、加速度之间的关系。
2•学会用速度传感器测量简谐振动的位移、速度、加速度幅值。
、实验装置框图 实验装置与仪器框图见图1。
图1实验装置框图三、实验原理在振动测量中,有时往往不需要测量振动信号的时间历程曲线,而只需要测量振动信 号的幅值。
振动信号的幅值可根据位移、速度、加速度的关系,用位移传感器或速度传感 器、加速度传感器来测量。
设振动位移、速度、加速度分别为 x 、u 、a ,其幅值分别为X 、V 、A :x= Bsi A® )■-二矽二 Bco s (t -:)dtd 2ya = ― - - 2Bs i n (t _ :)dt 2式中:B ——位移振幅 ----------- 振动角频率:——初相位X=B 故:V = • B = 2 二 fBA =2B =(2 二 f)2B振动信号的幅值可根据式(4-2)中位移、速度、加速度的关系,分别用位移传感器、 度传感器或加速度传感器来测量。
也可利用虚拟式信号分析仪和测振仪中的微分、积分功 能来测量。
四、实验方法1. 激振信号源输出端接电动式激振器,用电动式激振器对简支梁激振。
2. 用速度传感器拾振,速度传感器的输出端接测振仪。
3. 开启激振信号源的电源开关,对系统施加交变的正弦激振力,使系统产生简谐振 动,调整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不 要过载。
(1)4•分别用测振仪的位移X、速度V、加速度A各档进行测量和读数五、实验结果与分析1 •实验数据表2- 12•根据位移X,按公式⑵计算速度V、加速度A。
3•根据速度V,按公式⑵计算位移X、加速度A o4•根据加速度A,按公式(2)计算位移X、速度V o5•位移、速度、加速度幅值的实测值与计算值有无差别?若有差别原因是什么?实验三:机械振动系统固有频率的测量、实验目的1•了解共振前后李萨如图形的变化规律和特点。
2•学会用“共振相位判别法”测量机械振动系统的固有频率 、实验装置框图三、实验原理用简谐力激振,造成系统共振,以寻找系统的固有频率,是一种常用的方法。
这种方 法可以根据振动量的幅值共振来判定共振频率。
但在阻尼较大的情况下,用不同的幅值共 振方法测得的共振频率略有差别,而且用幅值变化来判定共振频率有时不够敏感。
相位判别法是根据共振时的特殊相位值以及共振前后的相位变化规律所提出来的一 种共振判别法。
在简谐力激振的情况下,用相位法来判定共振是一种较为敏感的方法,而 且共振时的频率就是系统的无阻尼固有频率,可以排除阻尼因素的影响。
以下对这两种方法分别加以说明:1 •位移判别共振设激振信号为F ,振动体位移、速度、加速度信号为Y 、dy、dtF 二 FoSin td 乙v—/ m 2Bsin (t -) dt 2测量位移拾振时,测振仪一上所反映的是振动体的位移信号。
将位移信号输入虚拟 式示波的“ 丫通道,激振信号输入“ X ”通道,此时两信号分别为:丫 = y =Bsin( t -)将示波揣置于“ X-Y ”显示档位上,以上两信号在屏幕上显示出一个椭圆图像。
共振 时,「二二「二二2即X 轴信号与丫轴信号的相位差为二2 ,根据李萨如图形原理知,11 ---------------------h辟 1图1实验装置框图d 2y dt 2虐抓仪黔打印机激霍h 訐:源幕上的图像将是一个正椭圆。
当••略大于•・n 或略小于5时,图像都将由正椭圆变为斜椭圆 其变化过程哪图2所示。
由图2见,图像由斜椭圆变为正椭圆时的频率就是振动体的固有 频率。
;.「;.-;:n •=・n >'"'n欠共振共振 过共振图2用位移判别共振的李萨如图形2 •速度判别共振测量速度时,测振仪所反映的是振动体的速度信号。
将速度信号输入示波器 丫轴,激振信号输入示波器X 轴,此时,示波器的X 轴与丫轴的信号分别为:X = F = F 0sin •,t丫 二包二 Bcos(t -:「)= Bsin(t )⑵dt2上述信号使示波器的屏幕上显示一椭圆图像。
共振时,—-n ^二.2,因此,X 轴信号与丫轴信号的信号相位差为0。
根据李萨如图形原理知,屏幕上的图像应是一条直线。
当」略大于•・n 或略小于• F 时,图像都将由直线变为椭圆。
其变化过程如图 3所示。
因此, 图像由椭圆变为直线时的频率就是振动体的固有频率图3用速度判别共振的李萨如图形3 •加速度判别共振测量加速度时,测振仪上所反映的是振动体的加速度信号。
将振动加速度信号输入 示波器丫轴,激振信号输入示波器x 轴,此时,示波器的X 轴与丫轴的信号分别为:X ― F — F o sin •. .•t2Y 二雪--2Bsin (t -)- 2Bsin (t ■- ) (3)dt上述信号使示波器的屏幕上显示一椭圆图像。
共振时,2, X 轴信号与丫轴信号的信号相位差为二2,。
根据李萨如图形原理,屏幕上的图像将是一个正椭圆。
当 「略大于或略小于行时,图像都将由正椭圆变为斜椭圆,并且其轴所在象限也将发生变化- J.-:n欠共振共振过共振其变化过程如图4所示。
因此图像变为正椭圆时的频率就是振动体的固有频率用加速度判别共振的李萨如图形四、 实验方法1激振信号源输出端接电动式激振器,用激振器对简支梁激振。
2•将激振信号源输出端接入虚拟式示波器的 X 轴,速度传感器输出的信号经测振仪 接入示波器的丫轴。
3•开启激振信号源的电源开关,对系统施加交变正弦激振力,使系统产生振动,调 整信号源的输出调节开关便可改变振幅大小。
调整信号源的输出调节开关时注意不要过 载。
4•激振频率由低到高逐渐增加,同时,用测振仪的 X 、V 、A 档测振,观察示波器屏 幕上的图像,根据“共振相位判别法”的原理,分别用位移、速度、加速度、判别共振, 确定共振频率。
五、 实验结果与分析1将用X 、V 、A 档判别共振的结果图分别绘出来。
2 •分析实验结果与理论原理是否相符合。
;.■? - :;F.n-=-n门,门n共振 过共振(3)图1实验装置框图三、实验原理单自由度系统的力学模型如图2所示。
在正弦激振力的作用下系统作简谐强迫振动, 设激振力F 的幅值B 、圆频率■ 0 (频率f = • 2二),系统的运动微分方程式为:d 2xdx害Kx =F dt 2dtd 2x dt 2dx 2 2n2x 二 F Mdt与2空,F Mdt 2 dt式中:——系统固有圆频率•2 = K Mn ――阻尼系数 ――阻尼比 2n =C. MF ――激振力方程(1)的特解,即强迫振动为:x = Asi n (° - J = As i n2「:f - JF = Bsi n pt = Bs i n^~ft)⑵式中:A ——强迫振动振幅;:——初相位B M-~2 r~2 ~2~2 (■ -■ °) 4n °实验四:单自由度系统强迫振动的幅频特性、固有频率和阻尼的测量.实验目的1. 学会测量单自由度系统强迫振动的幅频特性曲线。
2. 学会根据幅频特性曲线确定系统的固有频率 f °和阻尼比。
.实验装置框图式⑶叫做系统的幅频特性。
将式 ⑶所表示的振动幅值与激振频率的关系用图形表示, 称为幅频特性曲线(如图3所示):图3中,A max 为系统共振时的振幅;f 。
为系统固有频率,f l , f 2为半功率点频率当阻尼较小时,f a :、f 。
故以固有频率f 0作为共振频率f a 。
在小阻尼情况下可得=⑸ 2f of l , f 2的确定如图3所示:四、实验方法1 •将速度传感器置于简支梁上,其输出端接测振仪,用以测量简支梁的振动幅值。
2•将电动式激振器接入激振信号源输出端,开启缴振信号源的电源开关,对简支梁 系统施加交变正弦激振力,使系统产生正弦振动。
3. 调整激振信号源输出信号的频率,并从测振仪上读出各频率及其对应的幅值,填 入表4— 1。
4. 利用虚拟式示波器找出 A max 值,然后用虚拟式FFT 分析仪作该幅值信号的频谱, 求出共振频率f a ,这里f a = f o 从而求出系统固有频率。
5. 求出幅值0.707A max ,然后FFT 分析仪的频谱中作出A=0.707A max ,找到与频谱图相 交的两个点的频率f l 和f 2,从而可用式 ⑸求出阻尼比量。
五、实验结果分析1.实验数据 表1频率(HZ )1 202326293235384144475053振幅(Mm )2.根据表1中的实验数据绘制系统强迫振动的幅频特性曲线。
3. 确定系统固有频率f o (幅频特性曲线共振峰的亡最高点对应的频率近似等于系统固 有频率)。
4. 确定阻尼比•。
按图3所示计算0.707A max ,然后在幅值特性曲线上确定f 1, f 2,利 用式(5)计算出阻尼比。
图2单自由度系统力学模型图3单自由度系统振动的幅频特性曲线振幅为A max 时的频率叫共振频率 f a 。
在有阻尼的情况下,共振频率为:。
