RSA和DES加密算法详解
基于DES和RSA的混合加密体制的分析
密文 C 发送
密文 C
M= C d mod n
明文 M 接受方乙
其中，e 和 n 是接收方 B 的公钥，但 d 是接收方 B 的私钥
2.2 RSA 算法的优缺点分析 [ 4 ]
RSA 算法相对于 DES 加密算法有许多有点，通信双方不需事先交换密钥，保 密性好， 在密钥管理及分配上有自己的优越性； 另外公钥密码可以实现数字签名， 保证传输信息的不可否认性。但是，RSA 是建立在大素数分解困难的基础上的。 因子分解越困难，密码就难以破译，解密强度就越高。所以，RSA 算法是基于数 学难题的，加、解密运算时，在计算上的开销相对于 DES 对称加密算法来说是非 常巨大的。
综上所述，DES和RSA混合加密体制兼有加密、解密速度快的常规密码体制的 优点， 以及不需要进行密钥分配且保密管理的密钥量也较少的公开密码体制的优 点，从而构成了相对比较理想的加密体制。
3.4
关于混合加密算法改进的几点想法 [ 3]
在参考了大量文献资料下，我们在此可以对 DES 和 RSA 的混合加密算法进行 以下改进。 （1） 传统的 DES 算法的安全性能已大大降低， 目前也很少有人使用该算法。 因此， 使用基于混沌序列的 DES 算法，也可以使用混沌系统使 DES 加密密钥按要 求处于变化之中， 即可实现一次一密的要求，这样即使攻击者在信道中获得一组 密钥也难以推算出其他密钥而破获整个加密系统， 同时只要加密端和解密端得混 沌初值相同，加密和解密端的密钥便可同步，明显提高了安全性能。 （2）RSA 算法是基于大数因子分解的问题，实现容易，但其安全强度相对 较低。 目前， 用国际上公认的对于 RSA 算法最有效的攻击算法是一般数域筛 （NFS） 方法去破译和攻击，其破译和求解难度是亚指数级的，其复杂度
实训3-2：加密算法DES和RSA的实现
2. MixedCS软件实现RSA加密
➢ （7）单击 解密 按钮开始进行解密，解密完成后显示“解
密成功！”消息框，并产生文件“1.txt”，用词本打开 该文件，其内容仍然是“12345678”。
3. C语言实现RSA算法
3. C语言实现RSA算法
➢ （1）运行Turbo C2.0开发工具，输入RSA的源程序，进
实训设备
设备
服务器 （安装windows2000/2003操作系统） MixedCS.exe软件
Turbo C 2.0开发工具
数量
1台
1套 1套
实训步骤
➢1. MixedCS软件实现DES加密 ➢2. MixedCS软件实现RSA加密 ➢3. C语言实现RSA算法
1. MixedCS软件实现DES加密
第3章 网络加密与认证技术 实训3-2：加密算法DES和RSA的实现
实训目的
➢通过软件对实际数据进行加密和解密来了解DES
的运行原理
➢复习C语言的开发过程 ➢通过RSA的C语言源程序了解RSA的加密、解密
过程，掌握其工作原理；
➢通过实训进一步弄清对称加密DES和非对称加密
RSA的区别。
实训背景
数据加密技术是数据安全的核心技术。尤其是在 当今的电子商务、数字货币、网络银行等各种网 络业务的快速的兴起时代。使得如何保护数据安 全使之不被窃取、不被篡改或破坏等问题越来越 受到人们的重视。解决这些问题的关键就是数据 加密技术。
时该软件将自动采用3DES算法进行加密，加密的时间显 著增加，如所示。
1. MixedCS软件实现DES加密
➢ （6）在主窗口的“输入自动产生解密文件名 ，输入DES密钥，便可进行解密，如所示。
简述des算法和rsa算法的工作原理
DES算法和RSA算法都是密码学中常用的加密算法，它们分别采用了对称加密和非对称加密的方式来实现数据的加密和解密。
下面将分别从DES算法和RSA算法的工作原理，密钥管理以及应用方面对它们进行简述。
一、DES算法的工作原理DES算法是一种对称加密算法，它使用相同的密钥对数据进行加密和解密。
DES算法的工作原理主要包括初始置换、16轮迭代加密和最终置换三个步骤：1. 初始置换（Initial Permutation）：将输入的64位数据按照预定规则进行置换，形成初始置换后的数据。
2. 16轮迭代加密（16 Rounds of Iterative Encryption）：将初始置换后的数据分成左右两部分，分别进行16轮的迭代加密操作。
每一轮的加密操作包括将右半部分数据进行扩展、与本轮的轮密钥进行异或运算、通过S盒进行替换和P盒进行置换等步骤。
3. 最终置换（Final Permutation）：经过16轮迭代加密后，将左右两部分数据进行置换，得到最终的加密结果。
DES算法的解密过程与加密过程相反，即首先进行初始置换，然后进行16轮的迭代解密操作，最后进行最终置换得到解密结果。
二、RSA算法的工作原理RSA算法是一种非对称加密算法，它使用公钥和私钥对数据进行加密和解密。
RSA算法的工作原理主要包括密钥生成、加密和解密三个步骤：1. 密钥生成（Key Generation）：选择两个大素数p和q，计算它们的乘积n，再选择一个与(n)互质的数e作为公钥，计算满足(ed ≡ 1 mod φ(n))的d作为私钥，其中e和φ(n)互质且φ(n) = (p-1)(q-1)。
2. 加密（Encryption）：将明文M通过公钥进行加密运算，得到密文C，具体的加密过程为C ≡ M^e mod n。
3. 解密（Decryption）：将密文C通过私钥进行解密运算，得到明文M，具体的解密过程为M ≡ C^d mod n。
RSA算法的安全性基于大素数分解问题，即很难从n和e的值推导出d的值，但可以用d轻松求出e，所以加密用的是e，解密用的是d。
DES,RSA算法
30
浙江大学计算机学院 陈刚
31
浙江大学计算机学院 陈刚
28
DES与RSA性能比较
浙江大学计算机学院 陈刚
29
混合加密系统
将常规加密算法的数据处理速度和公开密钥算法对密 钥的保密功能相结合 利用常规加密算法加密传输数据 利用公开密钥算法交换密码 适用于需要交流大批量数据的场合 安全套接层（SSL）采用了这种解决方案
浙江大学计算机学院 陈刚
浙江大学计算机学院 陈刚
20
Diffie-Hellman算法的中间人攻击
浙江大学计算机学院 陈刚
21
Diffie－Hellman算法攻击步骤
1. 双方选择素数p以及p的一个原根a(假定O知道)
2. A选择Xa<p,计算Ya=aXa mod p, A→B: Ya
3. O截获Ya,选Xo,计算Yo=aXo mod p,冒充A → B:Yo
计算机安全技术基础
陈刚 浙江大学计算机学院
13906502791 cg@
浙江大学计算机学院 陈刚
1
计算机安全
密码学
浙江大学计算机学院 陈刚
2
教学内容安排
1 常规加密技术 2 公开密钥加密技术 3 鉴别 4 数字签名
5 信息隐藏与数字水印
浙江大学计算机学院 陈刚
3
Review
O永远必须实时截获并冒充转发,否则会被发现
浙江大学由MIT的Rivest, Shamir和Adleman 三人
提出
是一个分组加密方法
目前被最广泛地采用
采用的单向函数是大素数相乘，相乘很容易，但因 子分解很困难
基于数论中的欧拉定理实现
浙江大学计算机学院 陈刚
23
DES与RSA的分析报告
DES与RSA的分析报告DES简介数据加密算法（Data Encryption Algorithm，DEA）是一种对称加密算法，很可能是使用最广泛的密钥系统，特别是在保护金融数据的安全中，最初开发的DEA是嵌入硬件中的。
通常，自动取款机（Automated Teller Machine，ATM）都使用DEA。
它出自IBM的研究工作，IBM也曾对它拥有几年的专利权，但是在1983年已到期后，处于公有范围中，允许在特定条件下可以免除专利使用费而使用。
1977年被美国政府正式采纳。
加密原理DES 使用一个 56 位的密钥以及附加的 8 位奇偶校验位，产生最大64 位的分组大小。
这是一个迭代的分组密码，使用称为 Feistel 的技术，其中将加密的文本块分成两半。
使用子密钥对其中一半应用循环功能，然后将输出与另一半进行“异或”运算；接着交换这两半，这一过程会继续下去，但最后一个循环不交换。
DES 使用 16 个循环，使用异或，置换，代换，移位操作四种基本运算。
RSA简介RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。
RSA是被研究得最广泛的公钥算法，从提出到现在已近二十年，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。
RSA的安全性依赖于大数的因子分解，但并没有从理论上证明破译RSA的难度与大数分解难度等价。
即RSA的重大缺陷是无法从理论上把握它的保密性能如何，而且密码学界多数人士倾向于因子分解不是NPC问题一、RSA 的安全性RSA的安全性依赖于大数分解，但是否等同于大数分解一直未能得到理论上的证明，因为没有证明破解RSA就一定需要作大数分解。
假设存在一种无须分解大数的算法，那它肯定可以修改成为大数分解算法。
目前，RSA 的一些变种算法已被证明等价于大数分解。
不管怎样，分解n是最显然的攻击方法。
现在，人们已能分解多个十进制位的大素数。
因此，模数n 必须选大一些，因具体适用情况而定。
RSA和DES加密算法详解
RSA算法可以用于生成数字签名，验证数据的完整性和来源，确保数据在传输过程中未 被篡改或伪造。
密钥管理
RSA算法可以用于密钥分发和交换，确保通信双方能够安全地共享密钥，进行加密通信。
DES的应用场景
保护金融交易
DES加密算法曾广泛应用于金融交易中，如 信用卡交易和银行转账，保护敏感信息不被 非法获取。
加密过程
将明文转换为数字后，使用公钥(e,n)进行加密，得到密文。解密过程则使用私钥(d,n)进行解密，还原出明文。
RSA算法的安全性
安全性基于大数因子分解
RSA算法的安全性主要基于大数因子分解的困难性。即使攻击者知道了公钥和密文，也很难通过计算 得到原始的明文。
密钥长度决定安全性
RSA算法的安全性取决于密钥长度。一般来说，密钥长度越长，RSA算法的安全性就越高。目前常用 的RSA密钥长度为2048位，被认为是足够安全的。
缺点
01
计算开销大
RSA加密算法相对于DES加密算法需要更多的计算资源和时间，因此在
处理大量数据时可能效率较低。
02
密钥长度较长
为了达到足够的安全强度，RSA加密算法通常需要较长的密钥长度（例
如2048位），这会增加实现和存储密钥的难度和成本。
03
可能遭受侧信道攻击
虽然RSA加密算法本身不容易遭受侧信道攻击，但在某些实现中可能会
暴露密钥信息，从而遭受攻击。
05
DES加密算法的优缺点
优点
安全性高
DES加密算法使用56位密钥，在256次试验中密和解密过程中速度较 快。
易实现
DES算法易于理解和实现，因此在许多编程语言中都 有现成的库可供使用。
缺点
密钥长度短
RSA和DES加密算法详解
RSA和DES加密算法详解RSA加密算法：RSA是一种非对称加密算法，它的安全性基于大数的因数分解难题。
RSA算法的原理如下：1.选择两个不同的质数p和q，并计算它们的乘积n=p*q。
n被称为RSA算法的模数。
2.计算n的欧拉函数φ(n)=(p-1)*(q-1)。
3.选择一个整数e，使得1<e<φ(n)，且e和φ(n)互质。
e被称为RSA算法的公钥指数。
4. 计算整数d，使得d*e ≡ 1 (mod φ(n))。
d被称为RSA算法的私钥指数。
5.公钥为(n,e)，私钥为(n,d)。
6. 加密消息m时，将m的整数表示x，计算密文c ≡ x^e (mod n)。
7. 解密密文c时，计算明文m ≡ c^d (mod n)。
RSA算法的优点是加密速度较快，且在典型情况下很难被破解。
其主要应用领域包括数据传输中的身份认证、数字签名、数字证书等。
DES加密算法：DES（Data Encryption Standard）是一种对称加密算法，它采用64位的分组长度和56位的密钥长度。
DES算法的原理如下：1.初始置换（IP）：将输入的64位明文分为左右两个32位部分。
2.迭代运算：通过16次的迭代运算，先对右半部分进行扩展和异或运算，然后经过S盒置换和P盒置换，最后与左半部分进行异或运算。
3.逆初始置换（IP-1）：将得到的64位结果进行逆初始置换得到密文。
4.这里的迭代运算中，用到了轮密钥生成算法。
DES算法的密钥扩展过程中，通过对56位密钥进行位移、选择和置换操作生成各轮所使用的子密钥。
DES算法的缺点是安全性较低，主要是由于其算法密钥长度较短，易受到穷举攻击。
因此在实际应用中，通常采用3DES算法，即对DES算法进行三次加密。
1.对称加密算法DES的加密速度较快，而非对称加密算法RSA的加密速度较慢。
这是因为RSA算法涉及大数的运算，而DES算法仅涉及位运算。
2.DES算法的密钥长度较短，容易受到穷举攻击，安全性较低。
DES_3DES_AES_IDES_RSA密码算法比较
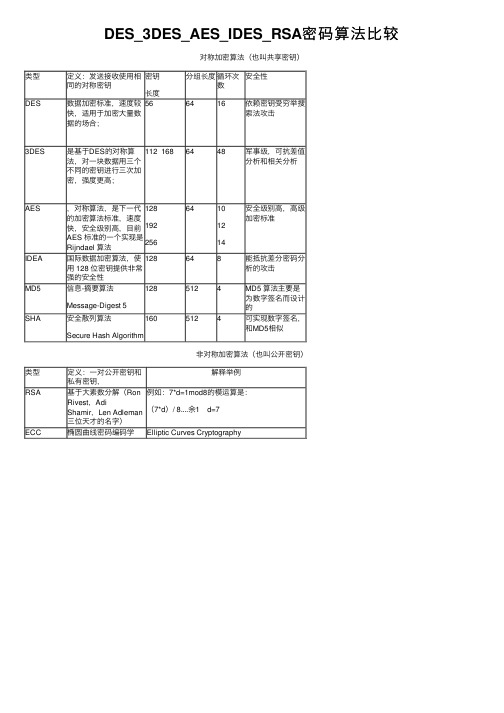
DES_3DES_AES_IDES_RSA密码算法⽐较
对称加密算法（也叫共享密钥）
类型定义：发送接收使⽤相
同的对称密钥
密钥
长度分组长度循环次
数
安全性
DES数据加密标准，速度较
快，适⽤于加密⼤量数
据的场合；566416依赖密钥受穷举搜
索法攻击
3DES是基于DES的对称算
法，对⼀块数据⽤三个
不同的密钥进⾏三次加
密，强度更⾼；112 1686448军事级，可抗差值
分析和相关分析
AES，对称算法，是下⼀代
的加密算法标准，速度
快，安全级别⾼，⽬前
AES 标准的⼀个实现是
Rijndael 算法128
192
256
6410
12
14
安全级别⾼，⾼级
加密标准
IDEA国际数据加密算法，使
⽤ 128 位密钥提供⾮常
强的安全性128648能抵抗差分密码分
析的攻击
MD5信息-摘要算法
Message-Digest 51285124MD5 算法主要是
为数字签名⽽设计
的
SHA安全散列算法
Secure Hash Algorithm 1605124可实现数字签名，
和MD5相似
⾮对称加密算法（也叫公开密钥）
类型定义：⼀对公开密钥和
私有密钥，
解释举例
RSA基于⼤素数分解（Ron
Rivest，Adi
Shamir，Len Adleman
三位天才的名字）例如：7*d=1mod8的模运算是：（7*d）/ 8....余1 d=7
ECC椭圆曲线密码编码学Elliptic Curves Cryptography。
DES和RSA两种加密算法
DES和RSA两种加密算法DES（Data Encryption Standard）和RSA（Rivest, Shamir, 和Adleman）是两种广泛使用的加密算法，被用于保护敏感信息的安全性。
它们具有不同的加密和解密过程，并在不同应用场景中发挥作用。
DES是一种对称加密算法，它使用相同的密钥进行加密和解密操作。
它采用了经典的分组密码结构，将明文分成固定大小的块，并进行相同数量的加密和解密轮。
DES密钥的长度为56位，被分为64位进行轮次加密。
由于密钥长度较短，使得DES对于现代密码分析算法的攻击比较脆弱。
因此，DES已经被更安全和更可靠的加密算法所替代。
RSA是一种非对称加密算法，它使用两个密钥，一个公钥和一个私钥。
公钥用于加密数据，而私钥用于解密数据。
RSA的安全性基于质因数分解问题的困难性，即将大质数做乘法分解的困难性。
RSA密钥的长度可变，通常在1024位到4096位之间。
RSA算法广泛应用于数字签名、密钥交换和安全通信等领域。
尽管DES和RSA都是加密算法，但它们适用的场景和特点有所不同。
首先，DES是一种对称加密算法，而RSA是一种非对称加密算法。
这意味着在使用DES时，相同的密钥用于加密和解密，而在使用RSA时，不同的密钥用于加密和解密。
这使得RSA在密钥管理和分发方面更加便捷，但加解密的性能开销更大。
其次，DES的密钥长度较短，使得它更易受到暴力破解和密码分析的攻击。
相比之下，RSA的安全性基于质因数分解问题，要求较长的密钥长度，增加了攻击者找到合适的密钥的难度。
此外，DES和RSA在加密速度上也存在差异。
由于DES是对称加密算法，它的加密和解密速度通常较快。
相比之下，由于RSA是非对称加密算法，它的加密速度较慢。
这使得DES通常适用于要求高速加密的场景，而RSA适用于安全性要求较高的场景。
最后，DES和RSA在应用领域上有所不同。
由于DES已经被认为不再安全，它主要应用于旧系统或需要与遗留系统兼容的场景。
4种加密，解密算法介绍（MD5,DES,RSA,SSL）
4种加密，解密算法介绍（MD5,DES,RSA,SSL）4种加密，解密算法：
1.MD5 不可逆加密：MD5Encrypt.Encrypt,长度32，2的128次⽅，MD5两次，MD5加盐
MD5 公开的算法，任何语⾔都可以⽤
相同原⽂加密结果式⼀样的；不同内容长度加密后是32位；
不可逆加密
1 防⽌被篡改
2 防⽌明⽂存储
3 防⽌抵赖，数字签名
⽤途：1.防⽌篡改；发个⽂档，事先给别⼈⼀个MD5,是⽂档的摘要
源代码管理器SVN
2.极速妙传：扫描⽂件的MD5和已有的⽂件的MD5对⽐--吻合表⽰⽂件在不⽤上传；
3.密码保存，防⽌看到明⽂，密⽂可见，所以要求密码复杂，加盐（123456+caj);
4.防⽌抵赖，数字签名
2.Des 对称可逆加密：加密，解密是⼀个Key，数据传输；在先打印；
DES AES Blowfish
对称加密算法的优点是速度快，
缺点是密钥管理不⽅便，要求共享密钥。
可逆对称加密密钥长度8
3.RSA ⾮对称可逆加密：加密，解密是⼀对，保证⽂件来⾃某⼈（私有key)
公开加密Key,保证数据安全，速度快
公开解密Key,保证⽂件来⾃某⼈，不可抵赖
4.数字证书SSL加密
百度--》 CA机构⽣成证书签名：--⽤户、
浏览器内置机构证书，⽆条件信任
申请证书；
5点基本知识--MD5加密，在CA⾃⼰加密
单边验证
双边验收
阿⾥云免费申请证书。
DES和RSA两种加密算法
对DES和RSA的总结
数据加密标准（DES）
01
优点：算法成熟，加密速度快 ，适用于大量数据的加密。
02
缺点：密钥长度较短，安全性
可能受到威胁，已被认为不够
安全。
ห้องสมุดไป่ตู้
03
RSA算法
04
优点：密钥长度较长，安全性
较高，适用于加密大量数据和
数字签名。
05
缺点：加密速度较慢，相对于
DES算法来说，RSA算法更加
RSA的安全性还基于离散 对数问题的难度。
已知p和q，求n很容易， 但已知n，求p和q非常困 难。
已知gcd(a,n)=1，求a^x mod n=y容易，但已知y 和n，求x非常困难。
RSA的应用场景
RSA主要用于非对称加密和数字签名 。
在电子商务、电子银行等领域广泛应 用。
04 DES与RSA的比较
安全性比较
安全性
由于DES算法的密钥长度较短，且存在一定的弱点，目前已被认为不够安全，已被更安全的加密算法 所取代。而RSA算法的安全性较高，是目前广泛使用的非对称加密算法之一。
破解难度
对于现代计算机和密码分析技术，破解DES算法相对容易。而RSA算法由于其数学原理和密钥长度的 优势，破解难度相对较大。
3
促进电子商务和电子政务发展
随着电子商务和电子政务的普及，加密算法对于 保障交易安全和政务信息的安全性至关重要。
DES和RSA的简介
DES
DES是一种对称加密算法，使用相同的密钥进行加密和解密操作。它采用56位密 钥和64位明文块进行加密，生成64位密文块。DES算法具有较高的安全性，但随 着计算机性能的提升，其密钥长度相对较短，存在一定的安全隐患。
混合加密算法（RSA和DES）
混合加密算法（RSA和DES）⼀、混合加密的理由 a、前⾯提及了和这两种加解密算法，由于随着计算机系统能⼒的不断发展，DES的安全性⽐它刚出现时会弱得多，追溯历史破解DES 的案例层出不穷，⼀台实际的机器可以在数天内破解DES是让某些⼈相信他们不能依赖DES的安全性的唯⼀⽅法。
⽽相对于DES，RSA的安全性则相对⾼些，虽然破解RSA的案例也有，但其所付出的代价是相对⼤的(相对DES)，如今RSA的密钥也在升级，这说明破解RSA的难度也在增⼤。
b、在中提及到RSA加密明⽂会受密钥的长度限制，这就说明⽤RSA加密的话明⽂长度是有限制的，⽽在实际情况我们要进⾏加密的明⽂长度或许会⼤于密钥长度，这样⼀来我们就不得不舍去RSA加密了。
对此，DES加密则没有此限制。
鉴于以上两点(个⼈观点)，单独的使⽤DES或RSA加密可能没有办法满⾜实际需求，所以就采⽤了RSA和DES加密⽅法相结合的⽅式来实现数据的加密。
其实现⽅式即： 1、信息(明⽂)采⽤DES密钥加密。
2、使⽤RSA加密前⾯的DES密钥信息。
最终将混合信息进⾏传递。
⽽接收⽅接收到信息后： 1、⽤RSA解密DES密钥信息。
2、再⽤RSA解密获取到的密钥信息解密密⽂信息。
最终就可以得到我们要的信息(明⽂)。
⼆、实现例⼦:结合前⾯RSA和DES加密：/// <summary>/// RSA和DES混合加密/// </summary>/// <param name="data">待加密数据</param>/// <param name="publicKey">RSA公钥</param>/// <returns></returns>public Param Encrypt(string data, string publicKey){//加密数据DESSecurity DES = new DESSecurity();string DESKey = DES.GenerateKey();string encryptData = DES.Encrypt(data, DESKey);//加密DESkeyRSASecurity RSA = new RSASecurity();string encryptDESKey = RSA.Encrypt(DESKey, publicKey);Param mixParam = new Param();mixParam.DESKey = encryptDESKey;mixParam.Data = encryptData;return mixParam;}/// <summary>/// RSA和DES混合解密/// </summary>/// <param name="data">待解密数据</param>/// <param name="key">带解密的DESKey</param>/// <param name="privateKey">RSA私钥</param>/// <returns></returns>public string Decrypt(string data, string key, string privateKey){//解密DESKeyRSASecurity RSA = new RSASecurity();string DESKey = RSA.Decrypt(key, privateKey);//解密数据DESSecurity DES = new DESSecurity();return DES.Decrypt(data, DESKey);}Demo下载:。
DES、AES、RSA等常用加密算法介绍与比较
DES、AES、RSA等常用加密算法介绍与比较文本先简单介绍常用的加密算法，后面将逐步推送每个加密算法的加密原理与应用及 java 实现方式。
加密算法分对称加密和非对称算法，其中对称加密算法的加密与解密密钥相同，非对称加密算法的加密密钥与解密密钥不同，此外，还有一类不需要密钥的散列算法。
常见的对称加密算法主要有 DES、3DES、AES 等，常见的非对称算法主要有 RSA、DSA 等，散列算法主要有 SHA-1、MD5 等。
对称算法又可分为两类。
一次只对明文中的单个位（有时对字节）运算的算法称为序列算法或序列密码。
另一类算法是对明文的一组位进行运算（即运算之前将明文分为若干组，然后分别对每一组进行运算，这些位组称为分组），相应的算法称为分组算法或分组密码。
DES 加密算法DES 加密算法是一种分组密码，以 64 位为分组对数据加密，它的密钥长度是 56 位，加密解密用同一算法。
DES 加密算法是对密钥进行保密，而公开算法，包括加密和解密算法。
这样，只有掌握了和发送方相同密钥的人才能解读由 DES 加密算法加密的密文数据。
因此，破译 DES 加密算法实际上就是搜索密钥的编码。
对于 56 位长度的密钥来说，如果用穷举法来进行搜索的话，其运算次数为 2 的 56 次方。
3DES（Triple DES）是基于 DES 的对称算法，对一块数据用三个不同的密钥进行三次加密，强度更高；AES 加密算法AES 加密算法是密码学中的高级加密标准，该加密算法采用对称分组密码体制，密钥长度的最少支持为 128、192、256，分组长度 128 位，算法应易于各种硬件和软件实现。
这种加密算法是美国联邦政府采用的区块加密标准，AES 标准用来替代原先的 DES，已经被多方分析且广为全世界所使用。
RSA 加密算法RSA 加密算法是目前最有影响力的公钥加密算法，并且被普遍认为是目前最优秀的公钥方案之一。
RSA 是第一个能同时用于加密和数宇签名的算法，它能够抵抗到目前为止已知的所有密码攻击，已被 ISO 推荐为公钥数据加密标准。
C语言加密与解密算法详解
C语言加密与解密算法详解1. 引言在信息时代，数据的保密性至关重要。
加密与解密算法是一种重要的保护数据安全性的技术手段。
本文将详细介绍C语言中的加密与解密算法，包括常用的对称加密算法和非对称加密算法。
2. 对称加密算法2.1 Caesar密码Caesar密码是一种简单的替换密码算法，通过将每个字母向后移动固定的位数来加密消息。
解密操作是将每个字母向前移动相同的位数。
2.2 DES算法数据加密标准（DES）是一种对称加密算法，使用56位的密钥对64位的数据进行加密。
DES算法通过多轮迭代和复杂的置换与代换操作来实现高强度的加密。
3. 非对称加密算法3.1 RSA算法RSA算法是一种常用的非对称加密算法。
它通过使用两个密钥：一个公钥和一个私钥，来实现加密和解密操作。
发送方使用接收方的公钥进行加密，而接收方使用自己的私钥进行解密。
3.2 椭圆曲线加密算法椭圆曲线加密算法（ECC）是一种基于椭圆曲线数学原理的非对称加密算法。
它具有较小的密钥长度和高安全性的特点，适用于资源受限的设备。
4. 加密与解密实例4.1 使用Caesar密码加密与解密字符串下面是使用C语言实现Caesar密码算法的示例代码： ```// Caesar密码加密函数void caesarEncrypt(char* text, int key) {int i = 0;while (text[i] != '\0') {if (isalpha(text[i])) {if (islower(text[i])) {text[i] = (text[i] - 'a' + key) % 26 + 'a';} else {text[i] = (text[i] - 'A' + key) % 26 + 'A';}}i++;}}// Caesar密码解密函数void caesarDecrypt(char* text, int key) {caesarEncrypt(text, 26 - key);}```4.2 使用RSA算法加密与解密数据下面是使用C语言中的openssl库实现RSA算法的示例代码：```// RSA加密函数int rsaEncrypt(unsigned char* plainText, int plainTextLen, unsigned char* encryptedText) {// 使用公钥进行加密操作// ...}// RSA解密函数int rsaDecrypt(unsigned char* encryptedText, int encryptedTextLen, unsigned char* decryptedText) {// 使用私钥进行解密操作// ...}```5. 总结加密与解密算法在数据保密性方面发挥着重要的作用。
常用简易数据加密算法
常用简易数据加密算法【最新版】目录1.概述2.常用简易数据加密算法2.1 RSA 加密算法2.2 AES 加密算法2.3 DES 加密算法2.4 3DES 加密算法2.5 Blowfish 加密算法2.6 MD5 加密算法2.7 SHA-1 加密算法3.总结正文一、概述数据加密是指将数据按照一定的规则进行编码，使得未经授权的人无法理解其含义。
在计算机领域，数据加密技术被广泛应用于保护信息的安全。
简易数据加密算法是一种相对简单且易于实现的加密方法，适用于各种场景。
本文将为您介绍几种常用的简易数据加密算法。
二、常用简易数据加密算法1.RSA 加密算法RSA 加密算法是一种非对称加密算法，其安全性高、应用广泛。
RSA 算法中，公钥和私钥是不同的，通过数学上的难题实现加密和解密。
RSA 算法适用于网络通信等场景。
2.AES 加密算法AES 加密算法是一种对称加密算法，其加密和解密使用相同的密钥。
AES 算法支持 128 位、192 位和 256 位密钥长度，安全性较高。
AES 算法广泛应用于各种数据存储和传输场景。
3.DES 加密算法DES 加密算法是一种对称加密算法，其密钥长度为 56 位。
由于密钥长度较短，DES 算法相对容易被暴力破解，但仍然适用于一些对安全性要求不高的场景。
4.3DES 加密算法3DES 加密算法是一种基于 DES 的改进算法，其通过对数据进行三次DES 加密和解密，提高了安全性。
3DES 算法适用于对数据安全性要求较高的场景。
5.Blowfish 加密算法Blowfish 加密算法是一种对称加密算法，由 Bruce Schneier 提出。
Blowfish 算法的特点是加密速度快、安全性高。
其密钥长度最多可达 448 位，适用于各种数据加密场景。
6.MD5 加密算法MD5 加密算法是一种哈希算法，其作用是将任意长度的数据映射成固定长度的摘要。
MD5 算法广泛应用于数据完整性校验、密码安全存储等场景。
DES与RSA算法的分析与研究
是保 障信息安全 的重要手段之 一 。 文就现代 密码学 本 的两 种基 于密钥 的加 密算法 ：对 称加 密算 法 Ｄ Ｓ和 Ｅ 公开 密钥算 法 Ｒ Ａ为代 表展 开分析 研究 ．提 出了 当 Ｓ 前解 决网络上信 息传 输安全性 的方法 。
将密 文 ６ ６发送给接 收方 ， 收者 收到后 ， 接 使用 私
钥恢复 出明文 ：
Ｓ Ｃ ｏ ｎ＝ ６ ７ｍ ｄ（１） １ ＝ ｄｍ ｄ（）６ ７ ｏ １９＝ ９ 上 例 中 Ｐ ｑ并不 大 。 Ｐ ｑ计算 出 ｎ的过程也 十 、 从 、 分 简单 ， 但从 ｎ ｌ９找出 ｐ ７ ｑ ｌ ＝１ ＝ 、＝ ７不是 很容易 。 而在 实 际应用 中 。 Ｐ和 ｑ将是 上百 位 的十进制 素数 ，这样
钥 难 于保 管 的 难 题 ， ＲＳ 算 法 公 钥 算 法 比 较 复 杂 ， 密 速 度 慢 的 缺 点也 客 观 存 在 。 但 Ａ 解 将 二 者 结 合 起 来 ， ＤＥ 用 Ｓ算 法 加 密 数 据 ， 用 ＲＳ 算 法 来 加 密 对 ＤＥ 使 Ａ Ｓ算 法 的 密 钥 ， 在
结 果 后 再 经 Ｓ盒 压 缩 为 ３ ２位 。 将 这 ３ 位 数 据 经 置 再 ２ 换后 与输人数 据的左半 部分 的 ３ ２位 数 据 异 或 。得 到
新一 轮迭代 的右半部分 ， 同时将 该轮迭代输 人数据 的 右 半部 分作 为这一 轮迭 代输 出数据 的左半部 分 。如 此， 就完成 了一轮迭代 。通过 １ ６轮这 样 的迭代 后 ． 产 生 了一 个新 的 ６ ４位数 据 。注 意 ： 最后 一次迭代 后 ， 所
／
过如下计 算得 到密文 ：
DES和RSA两种加密算法
对称加解密算法
通信双方通信前共同拟定一个密钥，不 对第三方公开。
消息发送前都通过该密钥加密，到达后 也通过该密钥解密。
不具有个体原子性，一个密钥被共享， 泄露机率加大。
对称加解密过程
1. 通信双方甲、乙共同拟定一个密钥，共 享。
多层 DES 加解密过程
以Triple DES为例说明。
加密过程： 1. 以 K1 加密 2. 以 K2 解密 3. 以 K3 加密
解密过程 (密钥顺序及应用方向与加密过程相 反)： 1. 以 K3 解密 2. 以 K2 加密 3. 以 K1 解密
多层 DES 衍生
如果令K1=K3，则实际进行了双密钥加 解密，即Triple DES加解密。
多层 DES
DES 算法可能是运用最广的对称加解密算法， 但由于密钥长度较短，导致安全性不高。
故在安全性占首要地位的应用场合如金融业等， 采用多个不同密钥(K1, K2, K3)的多层DES加解 密。
这些多层DES系统被广泛应用，由此衍生出 Triple DES, G-DES, DES-X, LOKI89和ICE等对 称加解密系统。
RSA 则是公钥/私钥系统。该系统比 DES 系统更原子化，具有普遍应用意义。
DES 加解密算法
DES (Data Encryption Standard)，是 IBM在上个世纪70年代开发的单密钥对称 加解密算法。
该算法利用一个56+8奇偶校验位(第8, 16, 24, 32, 40, 48, 56, 64位)=64位的密 钥对以64位为单位的块数据进行加解密。
DES与RSA
DES对称加密技术
DES(Data Encryption Standard)算法，于1977年得到 美国政府的正式许可，是一种用56位密钥来加密64位 数据的方法。
美国国家标准局1973年开始研究除国防部外的 其它部门的计算机系统的数据加密标准，于 1973年5月15日和1974年8月27日先后两次向 公众发出了征求加密算法的公告。
逆置换表IP-1
40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31
38 6
46 14 54 22 62 30 37 5
45 13 53 21 61 29
36 4
44 12 52 20 60 28 35 3
43 11 51 19 59 27
34 2
42 10 50 18 58 26 33 1
32
1
2
3
4
5
4
5
6
7
8
9
8
9
10
11
12
13
12
13
14
15
16
17
16
17
18
19
20
21
20
21
22
23
24
25
24
25
26
27
28
29
28
29
30
31
32
1
Ki是由密钥产生的48位比特串，具体的算法下面介绍。将E的 选位结果与Ki作异或操作，得到一个48位输出。分成8组，每 组6位，作为8个S盒的输入。 每个S盒输出4位，共32位，S盒的工作原理将在第第四步介绍。 S盒的输出作为P变换的输入，P的功能是对输入进行置换。
java后台加密解密方法
java后台加密解密方法Java后台加密解密方法在当今互联网安全领域中具有重要意义。
为了保护数据的安全，各种加密算法应运而生。
本文将介绍几种常见的Java后台加密解密方法，包括RSA、AES、DES和SM2。
1.RSA加密解密原理及实现RSA是一种非对称加密算法，其公钥和私钥是成对存在的。
使用公钥加密后的数据只能通过私钥进行解密。
在Java中，我们可以使用KeyPairGenerator生成一对公私钥，然后使用RSAPrivateKey对数据进行解密。
2.AES加密解密原理及实现AES是一种对称加密算法，加密和解密过程使用相同的密钥。
在Java中，我们可以使用Java的加密库如Java Cryptography Extension (JCE)实现AES 加密解密。
3.DES加密解密原理及实现DES是一种对称加密算法，其加密过程和解密过程使用不同的密钥。
在Java中，我们可以使用Java Cryptography Extension (JCE)实现DES加密解密。
4.SM2加密解密原理及实现SM2是一种国密算法，具有非对称加密和对称加密的特点。
在前端，我们可以使用SM2加密请求参数，然后在后台使用对应的私钥进行解密。
在Java 中，我们可以使用Hutool库实现SM2加密解密。
5.总结：选择合适的加密解密方法及注意事项在实际应用中，选择合适的加密解密方法至关重要。
需要考虑数据安全性、算法复杂度、性能和兼容性等因素。
此外，还需注意以下几点：- 加密解密算法应根据实际需求进行选择，如对称加密算法适用于加密大量数据，非对称加密算法适用于加密少量数据；- 加密密钥和解密密钥应妥善保管，避免泄露；- 在传输加密数据时，应注意防范中间人攻击，可以使用SSL/TLS等安全协议进行保护；- 定期更新和升级加密算法，以应对潜在的安全威胁。
本文介绍了Java后台加密解密方法，包括RSA、AES、DES和SM2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Part 2 RSA 算法描述
1．随机选择两个秘密的质数p、q 2．计算公开的模数，n=p*q 3．计算秘密的φ(n)=(p-1)*(q-1) 4．选择一个与φ(n)互质的量e 5．求K的乘法逆元素，用扩展欧几里得算法，模为φ(n) 6．明文X的值应在0至n-1之间，计算Xe (mod n)产生密 文Y，完成加密操作 7．计算Yd（mod n）产生明文X，完成解密操作
7.计算Yd（mod n）产生 明文X，完成解密操作
void decrypt() {
if(flag == 0) {
cout<<setkey first:<<endl; produce_key(); } 潣瑵? 请输入密文:; cin>>c; m = modular_multiplication(c,pr.d,pr.n); 潣瑵? 明文 is:<<m<<endl;
? 密钥长度为64位。然而只有其中的56位被实际用于算法，其余8 位可以被用于奇偶校验，并在算法中被丢弃。因此，DES的有效 密钥长度为56位，因为密钥太短，现已被攻破。改为使用三重 DES算法，即3DES。
? 经过16轮迭代和置换，得到密文长度为64位。
Part 2 DES 算法原理
明文64 bits
a[i] = b[i]; b[i] = t[i];
{
return b[2] = gcd(m, bin);
}
Part 3 RSA 编程实现（ C 语言）
6．明文X的值应在 0至n-1之间，计算 Xe (mod n)产生密 文Y，完成加密操 作
void encrypt() {
if(flag == 0) {
潣瑵? 请输入下一步操作 ; }
DES算法原理及其编程实现
Part 1 DES 算法简介
? DES = Data Encryption Standard = 数据加密标准
? DES是一种典型的块密码，即一种将固定长度的明文通过一系列 复杂的操作变成同样长度的密文的算法
? 明文长度为64位。同时，DES使用密钥来自定义变换过程，因此 算法认为只有持有加密所用的密钥的用户才能解密密文。
RSA算法原理及其编程实现
Part 1 RSA 算法的产生
Ron Rives Adi
t Shamir
Leonard Adleman
RSA公钥加密算法
? RSA是目前最有影响力的公钥加密算法，它能够抵抗到目前为止 已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。
? RSA算法基于一个十分简单的数论事实：将两个大素数相乘十分 容易，但是想要对其乘积进行因式分解却极其困难，因此可以 将乘积公开作为加密密钥。
}
b[0] = 0, b[1] = 1, b[2] = bin;
int q = ห้องสมุดไป่ตู้[2] / b[
if (b[2] == 0)
for(int i=0; i<3; i++)
{
{
return a[2] = bg[i]c; d(m, bin); t[i] = a[i] - q *
}
if (b[2] ==1)
密钥64 bits
子密钥48 bits
密文64 bits
F函数32 bits
Part 2 DES 算法原理 — — 初 始 置 换 和 逆 置 换
DES算法中所有的置换表都是给定的
Part 3 DES 编程实现 — — 初 始 置 换 和 逆 置 换
Part 2 DES 算法原理 — — 第 一 轮 迭 代
cout<<setkey first:<<endl; produce_key(); } 潣瑵? 请输入明文 :; cin>>m; c = modular_multiplication(m,pu.e,pu.n) 潣瑵? 密文 is:<<c<<endl; 潣瑵? 请输入下一步操作 ; }
Part 3 RSA 编程实现（ C 语言）
Part 3 RSA 编程实现（ C 语言）
1、随机选择两个秘密的质 数p，q （89 ，97） 2．计算公开的模数n＝p*q （8633） 3．计算秘密的欧拉函数 φ(n)=(p-1)*(q-1) （8448）
/* 判定一个数是否为素数 */ bool test_prime(Elemtype m) {
Part 2 DES 算法原理 — — F 函 数 生 成
左边32bitsE盒 置换得到48bits
异或 得到48bits
Part 3 DES 编程实现 — — E 置 换 表
17
Part 2 DES 算法原理 — — F 函 数 生 成
左边32bitsE盒 置换得到48bits
bool pd; int i; for(i = 2;i < m;i++)
if(m % i ==0) break;
if(m == i) pd = 1;
else pd = 0;
return pd;
Part 3 RSA 编程实现（ C 语言）
4、选择一个与φ(n)互质的量 e
/* 求最大公约数 */
{
Elemtype gcd(Elemtype a, Elemtype b)
Elemtype extend_euclid(Elemtype m,
while(true)
Elemtype bin)
{
{
if (b[2] ==1)
order(m,bin);
{
return b[1];
Elemtype a[3],b[3],t[3];
break;
a[0] = 1, a[1] = 0, a[2] = m;
? 64bits明文进行IP置换 ? 64bits明文分为左右两部分，分
别为32bits ? 右边32bits直接放入下一轮的左
边32bits ? 左边32bits与F函数异或之后放入
下一轮的右边32bits
Part 2 DES 算法原理 — — 子 密 钥 生 成
56bits密钥分成左右两边，经过置换、左移、选位得到48bits的子密钥
order(a,b);
int r;
if(b == 0)
{
return a;
}
else
}
while(true) { r = a % b; a = b; b = r; if (b == 0)
{ return a; break;
}
Part 3 RSA 编程实现（ C 语言）
5．用扩展欧几里得算法求 K的乘法逆元素d，模为φ(n)