边坡的稳定性计算方法
岩质边坡稳定性分析计算

岩质边坡稳定性分析计算引言:岩质边坡是指由岩石构成的边坡体,它的稳定性分析是地质工程中的一项重要内容。
本文将围绕岩质边坡的稳定性分析进行详细讨论,包括边坡的力学特性、稳定性分析的方法和计算步骤。
一、岩质边坡力学特性:岩质边坡的力学特性主要包括边坡坡度、岩性、结构构造、地质构造、坡面覆盖物、地下水等。
这些因素对边坡的稳定性有着重要影响。
1.边坡坡度:边坡坡度是指地面或水平面与边坡倾斜线的夹角,是影响边坡稳定性的重要因素。
坡度越大,边坡的稳定性越差。
2.岩性:岩石的强度、粘聚力、内摩擦角等岩性参数对边坡稳定性有着重要影响。
一般来说,岩性较强的边坡稳定性较好。
3.结构构造:边坡中的断层、节理、褶皱等结构构造对边坡的稳定性有着重要影响。
结构面的发育程度和倾角越大,边坡的稳定性越差。
4.地质构造:地质构造包括岩层倾角、层面、节理等,对边坡的稳定性具有重要影响。
地质构造的研究可以帮助我们了解边坡的受力特点和变形规律。
5.坡面覆盖物:坡面覆盖物通常包括土壤、草地、水层等,这些覆盖物的分布情况和特性对边坡的稳定性有着显著影响。
6.地下水:地下水的存在对边坡的稳定性具有重要影响。
当地下水位上升时,边坡会受到水的浸润,导致边坡强度降低,从而增加边坡失稳的可能性。
二、岩质边坡稳定性分析方法:岩质边坡的稳定性分析方法主要有极限平衡法和有限元法两种,下面将对这两种方法进行介绍。
1.极限平衡法:极限平衡法是一种经典的岩质边坡稳定性分析方法,它基于边坡体在其稳定状态下的力学平衡原理进行计算。
这种方法通常将边坡分割为无限小的切割体,并假设切割体沿着内摩擦边界面滑动,从而得到边坡的稳定状态。
2.有限元法:有限元法是一种基于有限元理论进行边坡稳定性分析的方法。
这种方法将边坡体离散为有限数量的单元,通过求解单元之间的位移和应力,得到边坡的稳定状态。
有限元法能够模拟较为复杂的边坡几何形状和边界条件,但计算复杂度较大。
三、岩质边坡稳定性计算步骤:进行岩质边坡稳定性分析计算时,通常需要进行以下步骤:1.边坡参数确定:根据实地调查和实验数据,确定边坡的坡度、坡高、岩石强度参数、结构面参数等。
(整理)边坡稳定性计算方法

一、边坡稳定性计算方法在边坡稳定计算方法中,通常采用整体的极限平衡方法来进行分析。
根据边坡不同破裂面形状而有不同的分析模式。
边坡失稳的破裂面形状按土质和成因不同而不同,粗粒土或砂性土的破裂面多呈直线形;细粒土或粘性土的破裂面多为圆弧形;滑坡的滑动面为不规则的折线或圆弧状。
这里将主要介绍边坡稳定性分析的基本原理以及在某些边界条件下边坡稳定的计算理论和方法。
(一)直线破裂面法化计算这类边坡稳定性分析采用直线破裂面法。
能形成直线破裂面的土类包括:均质砂性土坡;透水的砂、砾、碎石土;主要由内摩擦角控制强度的填土。
图 9 - 1 为一砂性边坡示意图,坡高 H ,坡角β,土的容重为γ,抗剪度指标为c、φ。
如果倾角α的平面AC面为土坡破坏时的滑动面,则可分析该滑动体的稳定性。
沿边坡长度方向截取一个单位长度作为平面问题分析。
图9-1 砂性边坡受力示意图已知滑体ABC重 W,滑面的倾角为α,显然,滑面 AC上由滑体的重量W= γ(ΔABC)产生的下滑力T和由土的抗剪强度产生的抗滑力Tˊ分别为:T=W · sina和则此时边坡的稳定程度或安全系数可用抗滑力与下滑力来表示,即为了保证土坡的稳定性,安全系数F s 值一般不小于 1.25 ,特殊情况下可允许减小到 1.15 。
对于C=0 的砂性土坡或是指边坡,其安全系数表达式则变为从上式可以看出,当α =β时,F s 值最小,说明边坡表面一层土最容易滑动,这时当 F s =1时,β=φ,表明边坡处于极限平衡状态。
此时β角称为休止角,也称安息角。
此外,山区顺层滑坡或坡积层沿着基岩面滑动现象一般也属于平面滑动类型。
这类滑坡滑动面的深度与长度之比往往很小。
当深长比小于 0.1时,可以把它当作一个无限边坡进行分析。
图 9-2表示一无限边坡示意图,滑动面位置在坡面下H深度处。
取一单位长度的滑动土条进行分析,作用在滑动面上的剪应力为,在极限平衡状态时,破坏面上的剪应力等于土的抗剪强度,即得式中N s =c/ γ H 称为稳定系数。
第三讲边坡稳定性计算全过程

第三讲边坡稳定性计算全过程边坡是指地面或岩石的斜坡,由于地质、工程结构或人为因素等原因,边坡可能会发生滑坡、坍塌等不稳定现象,因此边坡稳定性计算是工程设计中的重要环节。
本文将介绍边坡稳定性计算的全过程。
边坡稳定性计算过程主要包括选取边坡几何参数、确定边坡承载力和应力状态、计算安全系数和稳定性分析。
首先,需要选取合适的边坡几何参数,包括边坡的高度、坡度、坡面角等。
这些参数对边坡的稳定性有着重要的影响,需要根据具体情况进行选取。
接下来,需要确定边坡的承载力和应力状态。
边坡的承载力是指边坡能够承受的最大荷载,其取决于边坡材料的强度特性。
根据土壤或岩石的强度参数,可以计算边坡的承载力。
应力状态是指边坡内部的应力分布情况,可以通过有限元分析或理论计算进行确定。
然后,需要进行边坡的安全系数计算。
安全系数是评价边坡稳定性的重要指标,是边坡承载力与作用在边坡上的力的比值。
通常,安全系数大于1时,表示边坡稳定;安全系数小于1时,表示边坡不稳定。
安全系数的计算可以使用理论方法、有限元分析或实测数据等多种方法。
最后,进行边坡稳定性分析。
边坡稳定性分析是根据边坡参数、承载力和应力状态,通过计算安全系数来评估边坡的稳定性。
在分析过程中,通常需要考虑边坡的剪切强度、抗滑稳定性、土体的重力等因素,并进行相应的计算。
边坡稳定性分析可以通过手算、计算软件或有限元分析等方法进行。
总结起来,边坡稳定性计算的全过程包括选取边坡几何参数、确定边坡承载力和应力状态、计算安全系数和稳定性分析。
在实际工程中,为了确保边坡的稳定性,需要进行细致的计算过程,并根据计算结果进行相应的工程设计和措施的采取。
边坡稳定性设计计算

边坡稳定性计算一、基本资料土力学指标:天然容重(KN/m3)塑限(%)液限(%)含水量(%)粘聚力(kPa)内摩擦角(。
)tanφ18 14 27 19 19 28 0.53171二、稳定性验算公路按一级公路标准,双向四车道,设计车速为80km/h,路基宽度为24.5m,荷载为车辆重力标准值550KN,中间带取2m,车道宽度3.75m,硬路肩2.5m,土路肩0.75m,进行最不利布载时对左右各布3辆车。
路堤横断面图如下:1)将标准车重转换成土柱高度,按下列公式计算:ℎ0= NQ BLγ公式中:L按《公路丁程技术标准》(JTG BOl)规定对千标准车辆荷载取 12. 8m。
B为荷载横向分布宽度 (m)表示如下:B=Nb+(N-1)m+d其中:N为车辆数,取6;m为相邻两车的轮距,取1.3m ;d为轮胎着地宽度,取0.6m。
即:B = 6×1.8+(6-1)×1.3+0.6 = 17.9m因此ℎ0=NQBLγ=6×55017.9×12.8×18=0.8m2)计算高度HH = h0+H1+H2 =0.8+7+8 =15.8m3)计算平均坡度I已知上部坡度为1:1.25,下部坡度为1:1.5,台阶宽为2m,由已知数据可得平均坡度I为:I =(0.8+7+8):(8.75+2+12)=1:1.44 =1:1.5查规范得β1=26°、β2=35°三、按4.5H法确定滑动圆心辅助线,并绘制不同位置的滑动曲线1)滑动曲线过路基左边缘3/4处,将圆弧范围土体分成8块,如下:(从右往左分为5100×7+5450×1,8块)为4375×8,8块)右往左分为3600×7+3675×1,8块)4)滑动曲线过路基左边缘3/16处,将圆弧范围土体分成8块,如下:(从右往左分为3400×7+3543×1,8块)5)滑动曲线过路基左边缘1/8处,将圆弧范围土体分成8块,如下:(从右往左分为3300×7+2712×1,8块)6)由此可得出5个滑动面的K值,并作图如下:各个滑动面K值数据由上表可见K3曲线为极限的滑动面。
用理正岩土计算边坡稳定性

用理正岩土计算边坡稳定性边坡稳定性是岩土工程领域中非常重要的一个问题。
在土石方工程、地质工程、水利工程、交通工程等领域中,边坡稳定性问题的解决是确保工程安全和可靠性的关键。
边坡稳定性的计算常用的方法之一是理正岩土法。
理正岩土法是一种基于土力学力学和岩石力学理论的计算方法,可以用来评估边坡的稳定性。
边坡稳定性计算的基本思路是通过计算边坡的稳定性系数,判断其是否达到稳定状态。
稳定性系数是指边坡在其中一种条件下的抗滑能力与产力之间的比值。
边坡稳定性系数越大,边坡的稳定性越好。
理正岩土法主要包括以下几个步骤:1.确定边坡的几何形状和边坡材料的力学参数。
边坡的几何形状可以通过实测或者地质调查获得,包括边坡的坡度、高度和倾角等参数。
边坡材料的力学参数需要通过室内试验或者现场试验获得,包括土的内摩擦角、压缩模量、黏聚力等。
2.划分边坡的水平面和垂直面,计算边坡的产力和水平力。
产力是指作用在边坡上的重力力量,可以通过边坡材料的体积和密度来计算。
水平力是指作用在边坡上的水平方向的力量,可以通过产力与边坡的倾角来计算。
3.根据边坡的几何形状和材料的力学参数,计算边坡的抗滑力和抗滑力矩。
抗滑力是指边坡阻止滑动的力量,可以通过产力和材料的摩擦力来计算。
抗滑力矩是指抵抗滑动力矩的力矩,可以通过抗滑力和边坡的几何形状来计算。
4.计算边坡的稳定性系数。
稳定性系数是指抗滑力和抗滑力矩与产力和水平力之间的比值。
稳定性系数越大,边坡的稳定性越好。
通过计算稳定性系数,可以判断边坡是否达到稳定状态。
需要注意的是,理正岩土法是基于一定的假设和条件进行计算的,计算结果具有一定的不确定性。
为了提高计算结果的可靠性,需要进行室内试验和现场试验来获取准确的力学参数,并且要结合实际情况进行综合分析。
总之,理正岩土法是一种常用的边坡稳定性计算方法,通过计算边坡的稳定性系数,可以评估边坡的稳定性。
在实际工程中,要根据具体情况选择合适的计算方法,并结合实际情况进行综合分析,以确保边坡的稳定性和工程的安全可靠性。
边坡岩体稳定性分析的计算方法

边坡岩体稳定性分析的计算方法边坡岩体稳定性分析是地质工程设计工作中十分重要的一部分,是评价和研究边坡岩体稳定性的重要方法之一。
随着地质工程的发展,计算机技术的发展和应用,计算边坡岩体稳定性的方法也在不断发展和完善。
本文介绍了边坡岩体稳定性分析的计算方法,以及计算边坡岩体稳定性的重要步骤和要素。
二、边坡岩体稳定性的计算方法1.计算要求计算边坡岩体稳定性的要求是首先进行岩体的力学性质分析,确定岩体的抗剪强度和抗压强度,以及岩体的尺寸、形状、排列结构和构造;随后确定边坡的几何形状参数和水文地质因素,以及重力作用体系的参数;最后,按照边坡分析方法进行计算,确定边坡岩体的稳定系数。
2.计算过程(1)岩体力学性质分析。
首先分析岩体的抗剪强度和抗压强度,其次施加水平和垂直运动,确定岩体的变形特性;(2)边坡几何形状分析。
确定边坡的几何形状参数,包括坡度、坡面宽度、坡面长度等,同时确定水文地质因素,如雨水、渗水、地下水等;(3)重力作用体系分析。
确定边坡岩体的重力作用体系,包括自重、滑移压力、地下水压力、渗水压力等;(4)运用边坡分析方法计算边坡岩体的稳定性。
可以采用等效滑动面法、艾里克斯准则、薛定谔方程等方法,计算边坡岩体的稳定性。
三、边坡岩体稳定性分析的要素1.岩体力学特性岩体的抗剪强度和抗压强度是影响边坡岩体稳定性的主要因素之一。
岩体的抗剪强度可以通过抗拉强度、抗折强度等相关试验来测定,而抗压强度可以通过抗压强度试验、岩石试验等来确定。
2.边坡几何参数边坡几何参数是指边坡的坡度、坡面宽度、坡面长度等参数,这些参数是影响边坡岩体稳定性的重要因素。
一般来说,边坡坡度越陡,边坡稳定性越低;坡面宽度、坡面长度越小,边坡稳定性越低。
3.水文地质条件水文地质条件是指边坡周围的雨水、渗水、地下水等情况,这些条件也是影响边坡岩体稳定性的重要因素。
一般来说,边坡周围有大量雨水、地下水时,边坡稳定性就会变差。
4.重力作用体系重力作用体系是指边坡岩体受到的重力、滑移压力、地下水压力、渗水压力等因素的综合作用,这也是影响边坡岩体稳定性的重要因素。
平面、折线滑动法边坡稳定性计算书
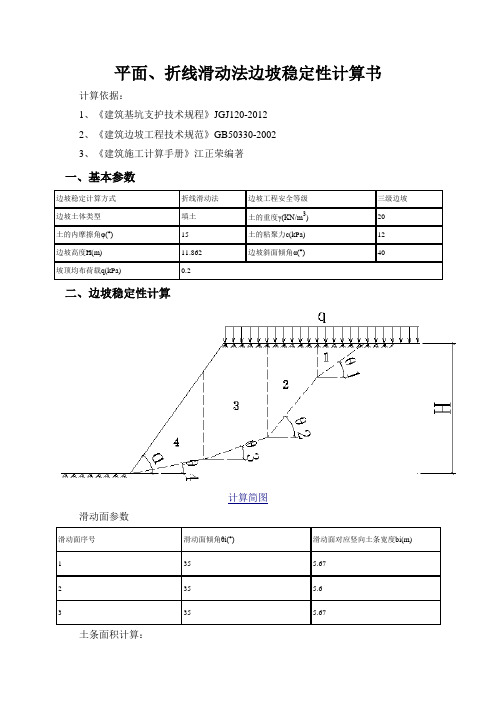
平面、折线滑动法边坡稳定性计算书计算依据:1、《建筑基坑支护技术规程》JGJ120-20122、《建筑边坡工程技术规范》GB50330-20023、《建筑施工计算手册》江正荣编著一、基本参数边坡稳定计算方式折线滑动法边坡工程安全等级三级边坡边坡土体类型填土土的重度γ(KN/m3) 20土的内摩擦角φ(°)15 土的粘聚力c(kPa) 12边坡高度H(m) 11.862 边坡斜面倾角α(°)40坡顶均布荷载q(kPa) 0.2二、边坡稳定性计算计算简图滑动面参数滑动面序号滑动面倾角θi(°)滑动面对应竖向土条宽度bi(m)1 35 5.672 35 5.63 35 5.67土条面积计算:R1=(G1+qb1)cosθ1×tanφ+c×l1=(156.213+0.2×2.803)×cos(35°)×tg(15°)+12×6.922=117.474 kN/mT1=(G1+ qb1)sinθ1 =(156.213+0.2×2.803)×sin(35°)=89.922 kN/mR2=(G2+qb2)cosθ2×tanφ+c×l2=(131.759+0.2×0)×cos(35°)×tg(15°)+12×6.836=110.952 kN/mT2=(G2+ qb2)sinθ2 =(131.759+0.2×0)×sin(35°)=75.574 kN/mR3=(G3+qb3)cosθ3×tanφ+c×l3=(44.652+0.2×0)×cos(35°)×tg(15°)+12×6.922=92.865kN/mT3=(G3+ qb3)sinθ3 =(44.652+0.2×0)×sin(35°)=25.611 kN/mK s=(∑R iψiψi+1...ψn-1+R n)/(∑T iψiψi+1...ψn-1+T n),(i=1,2,3,...,n-1)第i块计算条块剩余下滑推力向第i+1计算条块的传递系数为:ψi=cos(θi-θi+1)-sin(θi-θi+1)×tanφiK s=(∑R iψiψi+1...ψn-1+R n)/(∑T iψiψi+1...ψn-1+T n)=(117.474×1×1+110.952×1+92.865)/(89.922×1×1+75.574×1+25.611)=1.681≥1.25满足要求!。
边坡稳定性分析方法

第二节边坡稳定性分析方法力学验算法和工程地质法是路基边坡稳定性分析和验算方法常用的两种方法。
1.力学验算法(1)数解法假定几个不同的滑动面,按力学平衡原理对每个滑动面进行验算,从中找出最危险滑动面,按此最危险滑动面的稳定程度来判断边坡的稳定性。
此方法计算较精确,但计算繁琐。
(2)图解或表解法在图解和计算的基础上,经过分析研究,制定图表,供边坡稳定性验算时采用。
以简化计算工作。
2.工程地质法根据稳定的自然山坡或已有的人工边坡进行土类及其状态的分析研究,通过工程地质条件相对比,拟定出与路基边坡条件相类似的稳定值的参考数据,作为确定路基边坡值的依据。
一般土质边坡的设计常用力学验算法进行验算,用工程地质法进行校核;岩石或碎石土类边坡则主要采用工程地质法进行设计。
3.力学验算法的基本假定滑动土楔体是均质各向同性、滑动面通过坡脚、不考虑滑动土体内部的应力分布及各土条(指条分法)之间相互作用力的影响。
一、直线滑动面法松散的砂类土路基边坡,渗水性强,粘性差,边坡稳定主要靠其内摩擦力。
失稳土体的滑动面近似直线状态,故直线滑动面法适用于砂类土:如图2-2-4所示,验算时,先通过坡脚或变坡点假设一直线滑动面,将路提斜上方分割出下滑土楔体ABD,沿假设的滑动面AD滑动,其稳定系数K按下式计算(按边坡纵向单位长度计):验算的边坡是否稳定,取决于最小稳定系数Kmin的值。
当Kmin=1.0时,边坡处于极限平衡状态。
由于计算的假定,计算参数(r,Ψ,c)的取值都与实际情况存在一定的差异,为了保证边坡有足够的稳定性,通常以最小稳定系数Kmin≥1.25来判别边坡的稳定性。
但Kmin过大,则设计偏于保守,在工程上不经济。
当路堤填料为纯净的粗砂、中砂、砾石、碎石时,其粘聚力很小,可忽略不计,则式(2-2-3)变为:式(2-2-3)也适用于均质砂类土路堑边坡的稳定性验算。
二、圆弧滑动面法用粘性土填筑的路堤,边坡滑坍时的破裂面形状为一曲面,为简化计算,通常近似地假设为一圆弧状滑动面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
边坡稳定性计算方法
目前的边坡的侧压力理论,得出的计算结果,显然与实际情形不符。
边坡稳定性计算,有直线法和圆弧法,当然也有抛物线计算方法,这些不同的计算方法,都做了不同的假设条件。
当然这些先辈拿出这些计算方法之前,也曾经困惑,不做假设简化,基本无法计算。
而根据各种假设条件,是会得出理论上的结果,但与实际情况又不符。
倒是有些后人不管这些假设条件,直接应用其计算结果,把这些和实际不符的公式应用到现有的规范和理论中。
瑞典条分法,其中的一个假设条件破裂面为圆弧,另一个条件为假设的条间土之间,没有相互作用力,这样的话,对每一个土条在滑裂面上进行力学分解,然后求和叠加,最后选取系数最小的滑裂面。
从而得出判断结果。
其实,那两个假设条件对吗?都不对!
第一、土体的实际滑动破裂面,不是圆弧。
第二、假设的条状土之间,会存在粘聚力与摩擦力。
边坡的问题看似比较简单,只有少数的几个参数,但是,这几个参数之间,并不是线性相关。
对于实际的边坡来讲,虽然用内摩擦角Ф和粘聚力C来表示,但对于不同的破裂面,破裂面上的作用力,摩擦力和粘聚力,都是破裂面的函数,并不能用线性的方法分别求解叠加,如果是那样,计算就简单多了。
边坡的破裂面不能用简单函数表达,但是,如果不对破裂面作假设,那又无从计算,直线和圆弧,是最简单的曲线,所以基于这两种曲线的假设,是计算的第一步,但由于这种假设与实际不符,结果肯
定与实际相差甚远。
条分法的计算,是来源于微积分的数值计算方法,如果条间土之间,存在相互作用力,那对条状土的力学分解,又无法进行下去。
所以才有了圆弧破裂面的假设与忽略条间土的相互作用的假设。
其实先辈拿出这样与实际不符的理论,内心是充满着矛盾的。
实际看到的边坡的滑裂,大多是上部几乎是直线,下部是曲线形状,不能用简单函数表示,所以说,要放弃求解函数表达式的想法。
计算还是可以用条分法,但要考虑到条间土的相互作用。
用微分迭代的方法求解,能够得出近似破裂面,如果每次迭代,都趋于收敛,那收敛的曲线,就是最终的破裂面。
h1
图3
参照图3,下面将介绍这种方法的求解步骤。
对于单一的土体,其重度γ,粘聚力为C,内摩擦角为Ф,求垂直边坡的自然破裂面。
如果粘聚力为0,那土体的破裂角就是内摩擦角,这样的土体,只是沙漠地带,以及实验室中水洗烘干的砂土,粘聚力是0。
但是其高度h不唯一,这个稳定解是角度为内摩擦角,相互平行于的一族直线。
粘聚力不为0的情况单位长度土体的平衡条件。
第一步,对三角形土体ABC,进行力学分解,列出满足斜面AB 的力学平衡方程,这时,一个方程中会出现两个变量(h,θ),这当然也是一族解。
对于这一族解,只有条件最先满足的那种情况,才最可能发生。
这时可以有2种方法继续,一是把θ看成是h的变量,用函数求极值的方法,求出最小的边坡高度h,二是先假设θ值,然后直接用计算程序搜索计算,比较得出最小的高度h。
对于单一土层,第一种方法比较合适,但对于多层土,困难就比较大了,直接用计算程序搜索,得到最小的高度(h,θ),以此为基础,进一步计算。
第二步,再对三角形BDE、梯形ACDE进行力学分解,求极限平衡,由于DE小于h,如果DE面上没有摩擦力和粘聚力,那三角形BDE上的抗滑力大于下滑力,梯形ACDE上的抗滑力小于下滑力。
考虑到DE面上的应力,由于三角形BDE、梯形ACDE有相互分离的趋势,只考虑DE面上的粘聚力,DE面上的最大应力粘聚力C乘
以DE的面积,对于三角形土体BDE,沿BE进行力学分解,根据极限平衡的条件,求得DE。
第三步,再对CD进行n等分,已知DE面上的应力为C×h1,AC面上的粘聚力为0,再假设条间土的相互作用力,为线性分布,即DE面上的应力到AC面上的应力,为线性递减(这一点也许和实际不符)。
从CD开始建立各个梯形条状土的的平衡条件,求出各梯形条状土下端的角度,将这些线段连接起来,就近似得到边坡土体的破裂面。
经过这三步的计算,这个破裂面已经和实际情况很接近。
如果想进一步去求解,可以根据上面的计算结果,再次迭代。
AC面到DE面上的条件土的应力,可以有不同的函数假设,只要级数足够多,最小的破裂面,可以无限接近真实的破裂面,这样的求解方法,在理论上是完备的。
一般情况下,对函数级数的假设,过多的话,计算量会很大,根据实际情况通常取到一级或二级,只是在完备性分析的时候,才会假设的无穷级数。
斜边坡的自然稳定性计算
图4
自然坡角为β的边坡,如图4所示,仍然可以按照垂直边坡的计算步骤,但比垂直边坡更复杂一些。
第一步,建立三角型土体ABC的静力平衡关系,根据静力平衡条件,求解出最小的稳定边坡高度h。
第二步,根据三角型BDE的静力平衡关系,求解DE面以及DE 面上的应力,这个步骤与前面垂直边坡的求解方法形同。
第三步,根据梯形CDEF的静力平衡关系,求解CF面上的应力,由于梯形土体CDEF和下部三角型土体ACF是相互挤压的关系,其实际应力是根据平衡条件所计算确定。
第四步部,对CD和AC之间的土体,进一步细化求解,从D点开始,根据细化的土体条块体的稳定性,确定下部的破裂角。
其中DE面到CF面之间的条状土之间的应力,以及CF面到下边A点的条状土之间的应力,可以假定按照线性分布去计算。
多层土体边坡稳定性计算
对于多层土体,由于各层土体的土力学参数不一样,情况会更为复杂。
对于垂直边坡,对于图3的情况,先从上到下根据三角型BDE 的稳定性,求解DE的高度,求解出最小的DE面。
然后根据梯形ACDE 的静精力平衡条件,求解出满足精力平衡条件的最小高度h,再细化条状土,根据细化的条状土平衡条件求解。
对于有坡度的边坡,如图4,仍然采取上述的步骤,先求解DE 面,然后根据静力平衡条件,求解不规则土体ACDE,然后再进行下一步的计算。
至此,自然边坡的稳定性计算(及边坡面无外力约束的条件),可以得到精确的数值解。
