锐角三角函数—正切优秀课件
合集下载
《锐角三角函数》PPT教学课件(第1课时)

BC AC
= 12 =
AC
34,所以AC=9.故填9.
随堂训练
AB 6.如图,在Rt△ABC中,∠C=90°,BC
17 15
,则tan
15 A=_8__.
由正切定义可知tan A=BACC , 因为 AB 17 , 可设BC=15a,AB=17a,从而可
BC 15
用勾股定理表示出第三边AC=8a,再用正切的定义求解得 tan A= BC 15 .
由勾股定理可得 AB= BC2 AC2 122 162 =20.
∴AB的长为20.
课堂小结
1.正切的定义: 如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻
边的比便随之确定,这个比叫做 ∠A的正切,记作tan A, 即tan A= A的对边
A的邻边
2.tanA的值越大,梯子(坡)越陡
图①
图②
新课导入
问题引入
如图所示,轮船在A处时,灯塔B位于它 的北偏东35°的方向上.轮船向东航行5 km 到达C处时,轮船位于灯塔的正南方,此时轮 船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知 ∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
C,C'.
BC AC
与BACC
具有怎样的关系?
在两个直角三角形中,当一对锐角相等
时,这两个直角三角形相似,从而两条对应直
角边的比相等,即当∠A(小于90°)确定时,以 ∠A为锐角的Rt△ABC的两条直角边的比 BC
AC
是确定的.
知识讲解
1.正切的定义
如图所示,在Rt△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫
24.1锐角的三角函数(正切定义)PPT课件

乘以“A”. (0°<A<90°) 2,它表示∠A的正切,记号里习惯省去角的 符号“∠” . 如果用三个字母表示角,则角的 符号不能省略
▪3,tanA没有单位,在Rt△中,它表示一个比值
表示锐角A的对边和邻边的比。并且tanA随A
的增大而增大。
2021/3/12
7
i=
形式)
(坡度通常写作h:l 的
8080
8080
则第一个坡 。面较陡
x 20 80 100
我们只要 30比 与2较 0的大小就.可以了 80 100
2021/3/12
3
• 如图所示:
B B1 B2
A
C C 1 C2
在锐角A一边上任取一点B,自点B向另一边作垂线,
垂足为C,得到RtABC; 再任取一点B1,自点B1向
另一边作垂线,垂足为C1,得到另一个RtAB1C1
坡面与h水平面的夹角叫做坡角,记 作α,于l 是有
i= =
h
l
tan
显然,坡度越大,坡角越大,坡面就越陡。
2021/3/12
8
如图,在Rt△ABC中, ∠C=90°,AC=4,BC=3,求tanA和tanB.
B 解:
A
tanA= BC = AC
3 4
C
tanB= AC BC
=
4 3
2021/3/12
9
练一练
1.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,tanA的值(C )
A.扩大100倍
B.缩小
C.不变
D.不能确定
2021/3/12
10
• 2.在Rt⊿ABC中,∠C=90°,BC=12
㎝,AB=20㎝,求tanA和tanB的值?
▪3,tanA没有单位,在Rt△中,它表示一个比值
表示锐角A的对边和邻边的比。并且tanA随A
的增大而增大。
2021/3/12
7
i=
形式)
(坡度通常写作h:l 的
8080
8080
则第一个坡 。面较陡
x 20 80 100
我们只要 30比 与2较 0的大小就.可以了 80 100
2021/3/12
3
• 如图所示:
B B1 B2
A
C C 1 C2
在锐角A一边上任取一点B,自点B向另一边作垂线,
垂足为C,得到RtABC; 再任取一点B1,自点B1向
另一边作垂线,垂足为C1,得到另一个RtAB1C1
坡面与h水平面的夹角叫做坡角,记 作α,于l 是有
i= =
h
l
tan
显然,坡度越大,坡角越大,坡面就越陡。
2021/3/12
8
如图,在Rt△ABC中, ∠C=90°,AC=4,BC=3,求tanA和tanB.
B 解:
A
tanA= BC = AC
3 4
C
tanB= AC BC
=
4 3
2021/3/12
9
练一练
1.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,tanA的值(C )
A.扩大100倍
B.缩小
C.不变
D.不能确定
2021/3/12
10
• 2.在Rt⊿ABC中,∠C=90°,BC=12
㎝,AB=20㎝,求tanA和tanB的值?
锐角三角函数--余弦、正切(黄美萍)PPT课件
B
B
13
3
5
A
4
C
C
A
(1)
(2)
-
10
例题示范
例1 如图,在Rt△ABC中,∠C=90°,BC
=6,sinA= ,3
B
5
求cosA、tanB的值.
6
A
C
-
11
例3、在△ABC中,AB=AC=4,BC=6,求∠B的 三角函数值。
例4、已知∠A为锐角,sinA= 15 ,求cosA、tanA的
值。
斜边c
B 对边a
A
邻边b
C
-
6
【探究】
观察图中的Rt△ABC和Rt△A/B/C/中,它们之间有 什么关系? 此时 AC , BC 又分别等于哪两条线段的比?
AB AC B/
BLeabharlann ┏AC-C/
7
一般地,在Rt△ABC中,∠C=90°,
我们把∠A的邻边与斜边的比叫做∠A的余弦
B
(cosine),记作cosA,即
斜边
a c
cosA=
A的 邻 边 斜边
=
b c
tanA=
1、锐角三角函数的概念。
A的 对 边 A的 邻 边
=
a b
sinA、 cosA 、tanA的大小只与∠A的大小有关,
而与直角三角形的边长无关。
2、利用定义进行计算。
如上图:sinA=cosB
3、直角三角形两个锐角的 -
三角函数之间的关系:
cosA=sinB
如图,在矩形ABCD中,AB=10,BC=8,E为 AD上的一点,沿CE将△CDE对折,点D正好落在 AB边的F上。求tan∠AFE的值。
锐角三角函数正切优质课一等奖课件

请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
实践出真知
请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
实践出真知
请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
实践出真知
B
请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
A
C
实验结论应用
如图,比较梯子AB和EF哪个更陡?
闯关题:第三级
如图所示,Rt△ABC是一防洪堤背水坡的横截面图, 高度AC的长为12 m,它的坡角为45°,为了提高该堤的防 洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,
求增加的宽度BD的长?
驶向胜利 的彼岸
12 m
三角函数的由来
∠A的对边
a
tanA=
=
∠A的邻边
b
c
a
b
16世纪,德国数学家雷提库斯把锐角三角函 数定义为直角三角形的边长之比,并采用了六个 函数(正切、正弦、余弦、余切、正割、余割)。 三角函数在建筑,航海及天文等方面测量、计算 中有着重要的作用.
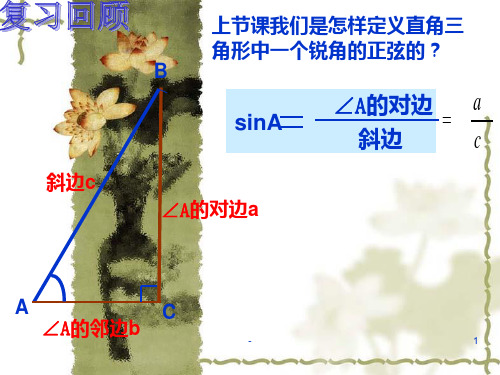
复习回顾
勾股定理
直 角 三 角 形
第一章 解直角三角形
锐角三角函数
第1课时 B
A
C
1.通过生活中梯子倾斜的引例,经历探索直角三 角形中边角关系的过程.理解正切的意义,并会用正 切值来判断梯子或斜坡的陡与缓.
2.会用正切表示直角三角形中两直角边的比,并 能进行简单的计算.
B
A
C
数学实验室
实验工具:课本、两把直尺(一长一短)
AC AC1 AC2
证明:∵∠A=∠A ∠ACB = ∠AC1B1=∠AC2B2 ∴ Rt△ACB ∽ Rt△AC1B1∽Rt△AC2B2
实践出真知
请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
实践出真知
请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
实践出真知
B
请思考: 梯子在上升变“陡” 的过程中,哪些量发生了变化?
A
C
实验结论应用
如图,比较梯子AB和EF哪个更陡?
闯关题:第三级
如图所示,Rt△ABC是一防洪堤背水坡的横截面图, 高度AC的长为12 m,它的坡角为45°,为了提高该堤的防 洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,
求增加的宽度BD的长?
驶向胜利 的彼岸
12 m
三角函数的由来
∠A的对边
a
tanA=
=
∠A的邻边
b
c
a
b
16世纪,德国数学家雷提库斯把锐角三角函 数定义为直角三角形的边长之比,并采用了六个 函数(正切、正弦、余弦、余切、正割、余割)。 三角函数在建筑,航海及天文等方面测量、计算 中有着重要的作用.
复习回顾
勾股定理
直 角 三 角 形
第一章 解直角三角形
锐角三角函数
第1课时 B
A
C
1.通过生活中梯子倾斜的引例,经历探索直角三 角形中边角关系的过程.理解正切的意义,并会用正 切值来判断梯子或斜坡的陡与缓.
2.会用正切表示直角三角形中两直角边的比,并 能进行简单的计算.
B
A
C
数学实验室
实验工具:课本、两把直尺(一长一短)
AC AC1 AC2
证明:∵∠A=∠A ∠ACB = ∠AC1B1=∠AC2B2 ∴ Rt△ACB ∽ Rt△AC1B1∽Rt△AC2B2
28.1锐角三角函数--余弦、正切ppt

AB 5
BC 3
例2 如图,在Rt△ABC中,∠C=90°,BC=2,
AB=3,求∠A,∠B的正弦、余弦、正切值. B
解:在RtABC中,
3
2
AC AB2 BC2 32 22 5,
A
C
sin A BC 2,cos A AC 5 ,tan A BC 2 2 5 .
AB 3
AB 3
∴ AB = 19.608 080 89≈19.61m 即旗杆的高度是19.61m.
练习:
使用计算器求下列锐角的三角函数值.(精确到 0.01)
(1)sin20°,cos70°; sin35°,cos55°; sin15°32′,cos74°28′;
(2)tan3°8′,tan80°25′43″;
新知探索:60°角的三角函数值
B
2
3
60.0
A
C
1
sin60°= A的对边 3
斜边
2
cos60°= A的邻边 1 斜边 2
tan60°= A的对边 3 A的邻边
30°、45°、60°角的正弦值、余弦值和正切 值如下表:
锐角a 三角函数
30°
45°
60°
sin a
1
2
3
2
2
2
cos a
3
2
1
28.1锐角三角函数(2)
——正弦 正切
复习与探究:
在 RtABC中, C 90
B 1.锐角正弦的定义
c
A
b
a
∠A的正弦:
s
inA
A的对边 斜边
BC AB
a c
C
2、当锐角A确定时,∠A的对边与斜边的比就随之 确定。此时,其他边之间的比是否也随之确定?为 什么?
《锐角三角函数》课件

锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
锐角的三角函数-正切.ppt

tanA= ∠A的对边 BC a
∠A的邻边 AC b
说明:
1. tanA是一个完整的符 号,不表示tan乘以∠A。
∠B的正切 怎么表示?
2.它表示∠A的正切,记 号里习惯省去角的符号 ∠A的对边a ∠。
∠A的邻边b
3. tanA没有单位,它表 示一个比值。
4.初中阶段仅研究直角 三角形中锐角的正切。
来自身边的数学
怎样描述山坡陡的程度呢?
看一看 说一说
有两个直角三角形,直角边AC与DF表示水平长度, BC与EF表示铅直高度,AB与DE表示两个不同的坡面, 坡面AB与DE哪个更陡?你是怎么判断的?
20 100
30 (1)
100
30 80
30 (2)
100
30 80
40 (3) 100
感性到理性
3. 如图,在Rt∆ABC中,∠C=90°,CD 为斜边上的个高,
BC=3,AC=4, ∠BCD= ,则tan
的值是( A )
A. 3 B. 4 C. 3 D. 4
4
3
5
5
4.在Rt∆ABC中,∠C=90°,AB=15,tan A 3 , 4
求BC的长。
5. 如图,某一大坝的横截面是四边形ABCD,其 中,AB//CD,坝顶宽CD=3m,坝高6m,迎水坡BC 的坡度i1=1:2, 背水坡AD的坡度i2=1:1,求斜坡 AD 的坡角和坝底宽AB.
DC
A
B
谈谈你的收获
谢 谢 !
132 52 12
乙梯中,tan 6 3 .
84
∵tanβ>tanα,∴乙梯更陡.
试试身手
1、如图,在Rt∆ABC中,∠C=90°, AC=4,BC=3,求tanA和tanB.
《锐角三角函数----正切》课件

九年级数学(下)第一章
直角三角形的边角关系
我们从梯子的倾斜程度来进入
锐角三角函数之正切
温馨寄语:
• 锐角三角函数是描述直角三角形中边与 角的关系,它是一个变量之间重要的函 数关系。它既新奇,又富有魅力,同学 们可要与它建立好感情哟!
有的放矢 1
看看谁的本领大
大家请看这幢高楼:
直挂云帆 济沧海
你猜一猜:这幢高楼有多高?
3.tanA是一个比值(直角边之比.注意比的顺序, 且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角 形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等, 则这两个锐角相等.
独立
P6 习题1.1 1,2,3题 作业
1. 在Rt△ABC中,∠C=90°,AC=5,AB=13,求tanA和tanB.
(
)(
)(
.
)
A
┌ DB
7.在上图中,若BD=6,CD=12.求tanB的值.
老师提示: 模型“双垂直三角形”的有关性质你可曾记得?
小结 拓展
回味无穷
定义中应该注意的几个问题:
驶向胜利 的彼岸
1.tanA是在直角三角形中定义的,∠A是一个锐角 (注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯 省去“∠”号;
源于生活的数学:
我们从梯子的倾斜程度 来说起吧!
梯子是我们日常生活中常 见的物体
那你能比较下这两个梯子 哪个更陡吗?你有何办法?
直挂云帆 济沧海
想一想 4
生活问题数学化
直挂云帆 济沧海
梯子AB和EF哪个 更陡?你是怎样判
直角三角形的边角关系
我们从梯子的倾斜程度来进入
锐角三角函数之正切
温馨寄语:
• 锐角三角函数是描述直角三角形中边与 角的关系,它是一个变量之间重要的函 数关系。它既新奇,又富有魅力,同学 们可要与它建立好感情哟!
有的放矢 1
看看谁的本领大
大家请看这幢高楼:
直挂云帆 济沧海
你猜一猜:这幢高楼有多高?
3.tanA是一个比值(直角边之比.注意比的顺序, 且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角 形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等, 则这两个锐角相等.
独立
P6 习题1.1 1,2,3题 作业
1. 在Rt△ABC中,∠C=90°,AC=5,AB=13,求tanA和tanB.
(
)(
)(
.
)
A
┌ DB
7.在上图中,若BD=6,CD=12.求tanB的值.
老师提示: 模型“双垂直三角形”的有关性质你可曾记得?
小结 拓展
回味无穷
定义中应该注意的几个问题:
驶向胜利 的彼岸
1.tanA是在直角三角形中定义的,∠A是一个锐角 (注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯 省去“∠”号;
源于生活的数学:
我们从梯子的倾斜程度 来说起吧!
梯子是我们日常生活中常 见的物体
那你能比较下这两个梯子 哪个更陡吗?你有何办法?
直挂云帆 济沧海
想一想 4
生活问题数学化
直挂云帆 济沧海
梯子AB和EF哪个 更陡?你是怎样判
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:1、tanA tanα tan∠BAC tan∠1 tan45° 2、tanA的值只与∠A的大小有关,0°< ∠A <90 °
时∠A越大tanA
坡度(坡比)就是坡角的正切
比眼力,观察哪个梯子更陡
牛刀小试
1、在Rt△ABC中∠C=90°, 求tanA·tanB
2、如图△ABC中 AB=BC=5,AC=6求tanA
锐角三角函数—正切
比眼力,观察哪个梯子更陡
比眼力,观察哪个梯子更陡
比眼力,观察哪个梯子更陡
探索与思考:
1、Rt△ABC中B2 是AB边 上的动点,B2C2 ⊥AC Rt△AB2C2与Rt△ABC是什 么关系?
2、 、 什么关系?
当∠A大小变化时它们怎 么变? Nhomakorabea正切的定义:
• 在Rt△ABC中锐角A确定,那么∠A的对边与 邻边之比也随之确定。这个比叫∠A的正切, 记作tanA 即tanA=
牛刀小试
3、如图,在Rt△ABC中, AC=8, tanA= 求AB
4、如图,在Rt△ABC中, ∠ACB=90°,CD⊥AB,BC=1 ,AC=2 求tan∠BCD
用数学的眼光观察世界 用数学的思维分析世界
时∠A越大tanA
坡度(坡比)就是坡角的正切
比眼力,观察哪个梯子更陡
牛刀小试
1、在Rt△ABC中∠C=90°, 求tanA·tanB
2、如图△ABC中 AB=BC=5,AC=6求tanA
锐角三角函数—正切
比眼力,观察哪个梯子更陡
比眼力,观察哪个梯子更陡
比眼力,观察哪个梯子更陡
探索与思考:
1、Rt△ABC中B2 是AB边 上的动点,B2C2 ⊥AC Rt△AB2C2与Rt△ABC是什 么关系?
2、 、 什么关系?
当∠A大小变化时它们怎 么变? Nhomakorabea正切的定义:
• 在Rt△ABC中锐角A确定,那么∠A的对边与 邻边之比也随之确定。这个比叫∠A的正切, 记作tanA 即tanA=
牛刀小试
3、如图,在Rt△ABC中, AC=8, tanA= 求AB
4、如图,在Rt△ABC中, ∠ACB=90°,CD⊥AB,BC=1 ,AC=2 求tan∠BCD
用数学的眼光观察世界 用数学的思维分析世界
