FFT离散傅氏变换的快速算法
[理学]离散傅里叶变换及其快速算法
![[理学]离散傅里叶变换及其快速算法](https://img.taocdn.com/s3/m/a4bbbd1b0912a21615792901.png)
非周期序列的离散时间傅里叶变换 (DTFT) /序列的傅里叶变换
• 定义序列x(n)的离散时间傅里叶变换(DTFT)为:
X (e ) DTFT{x(n)}
j n jn x ( n )e
• 序列x(n)的离散时间傅里叶逆变换(IDTFT)为:
x(n) IDTFT{X (e j )} 1 2
按时间抽取的FFT算法
• 设N=2M,M为正整数,如取N=23=8,即离散时间信号为
x(n) {x(0), x(1), x(2), x(3), x(4), x(5), x(6), x(7)}
• 按照规则①将序列x(n)分为奇偶两组,一组序号为偶数, 另一组序号为奇数,即
{x(0), x(2), x(4), x(6) | x(1), x(3), x(5), x(7)}
X (e j )e jn d
傅里叶变换对小结
• 傅里叶级数(FS)(时域:连续周期;频域:非周期离散)
1 Xk T
T 2
T 2
x(t )e jk1t dt
x(t )
k
X k e jk1t
k 0, 1, 2,
• 傅里叶变换(FT)(时域:连续非周期;频域:非周期连续)
第三章-离散傅里叶变换(DFT)及其快速算法(FFT)

• 序列x(n)的N点DFT是 x(n)的Z变换在单位圆上的N点等 间隔采样;
• X(k)为x(n)的傅立叶变换 X (e j ) 在区间 [0, 2 ]上的N
点等间隔采样。这就是DFT的物理意义。
j ImZ
2 3
4
5 6
1 2
N
k=0 ReZ
7 (N-1)
DFT与z变换
X(ejω)
)
N M
xN (n) x((n))N X (k ) X ((k ))N
有限长序列x(n)的DFT变换X(k),就是x(n)的周期延拓序列 ~x(n) 的DFS系数 X~(k ) 的主值序列
返回
回到本节
DFS与FT之间的关系:
M 1
X (k) DFS[xN (n)] x(n)WNkn n0
x(n)
IDFT[ X (k)]N
1 N
N 1
X (k)WNk n ,
k 0
n 0, 1,
, N 1
长度为 N的离 散序列
返回回Biblioteka 本节例3.1: x(n) R8(n),分别计算x(n)的8点、16点DFT。 解: x(n)的8点DFT为
X (k)
7 n0
R8 (n)W8k n
k 0,1, , N 1
n0
返回
回到本节
比较前面三式,得到
X (k) X (z) j2k ,k=0, 1, 2, …, N-1 ze N
X (k) X (ej ) 2k ,k=0, 1, 2, …, N-1 N
结论: (1)序列的N点DFT是序列傅里叶变换在频率区间[0,2] 上的N点等间隔采样,采样间隔为2 /N。 (2)序列的N点DFT是序列的Z变换在单位圆上的N点等间隔 采样,频率采样间隔为2 /N。
FFT-快速傅里叶变换

p=6.283185306/n;
pr[1]=cos(p);
pi[1]=-sin(p);
if (l)
pi[1]=-pi[1];
for(i=2;i<=n-1;i++){
p=pr[i-1]*pr[1];
q=pi[i-1]*pi[1];
s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);
注:亲测,这个版本无法运行,作者删改了重要内容[1] 请参考源码(2)
//快速傅立叶变换
// 入口参数:
// l: l=0, 傅立叶变换;l=1, 逆傅立叶变换
// il: il=0,不计算傅立叶变换或逆变换模和幅角;il=1,计算模和幅角
// n: 输入的点数,为偶数,一般为32,64,128,...,1024等
wi = wi*wpr + wtemp*wpi + wi;
}
mmax = istep;
}
}
在C++环境下的源码
bool FFT(complex<double> * TD, complex<double> * FD, int r)
{
//一维快速Fourier变换。
//complex<double> * TD ——指向时域数组的指针; complex<double> * FD ——指向频域数组的指针; r ——2的幂数,即迭代次数
// fr[]: l=0, 返回傅立叶变换的实部
// l=1, 返回逆傅立叶变换的实部
// fi[]: l=0, 返回傅立叶变换的虚部
离散傅里叶变换及其快速算法
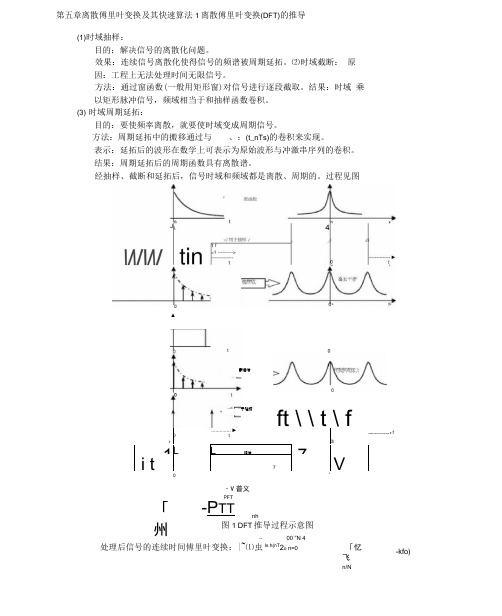
第五章离散傅里叶变换及其快速算法1离散傅里叶变换(DFT)的推导(1)时域抽样:目的:解决信号的离散化问题。
效果:连续信号离散化使得信号的频谱被周期延拓。
⑵时域截断: 原因:工程上无法处理时间无限信号。
方法:通过窗函数(一般用矩形窗)对信号进行逐段截取。
结果:时域 乘以矩形脉冲信号,频域相当于和抽样函数卷积。
(3) 时域周期延拓:目的:要使频率离散,就要使时域变成周期信号。
方法:周期延拓中的搬移通过与 、:(t_nTs)的卷积来实现。
表示:延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。
结果:周期延拓后的周期函数具有离散谱。
经抽样、截断和延拓后,信号时域和频域都是离散、周期的。
过程见图▲t載曲后ft \ \ t \ f.............. ►t---------------- r fi0/1LL紹后-7ii t7V亍延拓・V 普义PFT「州-P TTnh图1 DFT 推导过程示意图〜00 ”N 4处理后信号的连续时间傅里叶变换:|~⑴虫ls h(nT 2o n=0「忆飞n/N-kfo)(i)l~(f)是离散函数,仅在离散频率点f 二kf 。
k —处存在冲激,强度为a k ,其To NTs余各点为0。
〜 N N 1(ii) H(f)是周期函数,周期为Nfo == I ,每个周期内有N 个不同的幅值。
To NTs Ts(iii)时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。
2 DFT 及IDFT 的定义(1) DFT 定义:设hnTs 是连续函数h(t)的N 个抽样值J ,这N 个点的宽度为N 的 DFT 为:DFT N h(nTs)]=A h(nTs)ej 2ffi /N =H ——J (k =0,1,..., N_1)7l NT s 丿IDFT 定义:设H 上是连续频率函数吧的N 个抽样值k 亠,…• N J ,这N 个点(NTs 丿 的宽度为N的IDFT 为:DFTN 1Hk_L7HLe 「2「伙/N 厶 门Ts,(k=0,1,…,N —1)|L NsN k 卫 NTs“Rk/N 称为N 点DFT 的变换核函数,龊讪称为N 点IDFT 的变换核函数。
第三章离散傅里叶变换及其快速计算方法(DFT、FFT)

X (e jw )
(2)Z 变换 -- 提供任意序列的 z 域表示。
n
x( n)e jnw
X (z)
n
x ( n) z n
这两种变换有两个共同特征:
(1)变换适合于无限长序列 (2)它们是连续变量 ω 或 z 的函数
华北电力大学自动化系
3
3.1 问题的提出:可计算性
X (z)
而对于
n
x ( n) z n
n
x ( n) z n
找不到衰减因子使它绝对可和(收敛)。为此,定义新函 数,其 Z 变换:
华北电力大学自动化系
15
DFS 定义:正变换
X ( z)
n
x ( n) z n ~ ( n ) z n x
华北电力大学自动化系
6
3.1 问题的提出:傅里叶变换的四种形式 (3)
2. 周期连续时间信号:傅里叶级数 FS
~ (t ) x X (n 0 )
t T
时域周期频域离散
0
2 T
x(t)
~
n -
X(n 0 )e jn0t
时域连续函数造成频域是非周期的谱。 频域的离散对应时域是周期函数。
X (e jT )
T T
X (e jT )e jnT d
取样定理
n
x(nT )e jnT
1 X ( 0 ) T n
时域的离散化造成频域的周期延拓 时域的非周期对应于频域的连续
华北电力大学自动化系
8
第2章 离散傅里叶变换(DFT)及其快速算法(FFT)

电信系信息技术教研室
2.1.1 离散傅里叶级数DFS
信号特性的时频域对应关系 连续 离散 周期
非周期 周期 离散
电信系信息技术教研室
2.1.1 离散傅里叶级数DFS
?如何对周期为N的周期序列进行频域分析……
如: ~(n) ~(n kN ) x x 周期序列不能进行Z变换,因为其在 n=-到+ 都 周而复始永不衰减,即 z 平面上没有收敛域,所以 其DTFT亦不存在。但是,如同连续时间周期信号可用 傅氏级数表达,周期序列也可用离散的傅氏级数来表 示。
2 1 2 1
X (2) 0 X (6) 0
X (3) 1 j X (7 ) 1 j
2 1 2 1
电信系信息技术教研室
解法二:公式解
N 1 j 2 N 7 j 2 8 kn
X
k
DFS x n
mk
ki mk ~ ~ x (i ) wN wN X ( k ) i 0
N 1
电信系信息技术教研室
3)共轭对称性
x 对于复序列 ~n ,其共轭序列为
~* ~* DFS x n X k
* *
~* x n
,则:
~ ~ DFSx n X k
解:上述序列的基本周期为 N=4,因而
W4 = e-j2π /4 = -j,
~ X (k )
~ X (0) ~ X (1 ) ~ X (2) ~ X (3)
n0
3
nk ~ x ( n )W 4
3
n0
3
~ ( n )W x 4
FFT是离散傅立叶变换的快速算法

FFT是离散傅立叶变换的快速算法离散傅立叶变换(Discrete Fourier Transform, DFT)是一种将离散信号变换到频域的方法,它在数字信号处理中有着广泛的应用。
然而,传统的DFT算法的计算复杂度为O(N^2),对于大规模的信号序列而言,计算时间会很长。
为了解决这个问题,FFt算法应运而生。
快速傅立叶变换(Fast Fourier Transform, FFT)是一种通过分治思想将DFT算法转化成更高效的计算方式。
FFT算法的核心思想是将一个长度为N的信号分解成N个长度为1的信号,然后逐步合并计算每个信号的频域表示,最终得到整个信号的频域表示。
FFT算法的时间复杂度为O(NlogN),大大提高了计算效率。
FFT算法的基本思想是基于蝶形运算和旋转因子的运用。
蝶形运算是指将两个频域采样值进行乘法和加法操作,然后得到两个新的频域采样值。
旋转因子是指用来调整频域采样的运算公式,可以通过旋转因子将频域采样值分解成两个较小规模的频域采样值。
通过不断地重复蝶形运算和旋转因子的运算,最终可以得到整个信号的频域表示。
在FFT算法中,需要注意的是将信号序列长度N转化为2的幂次方,这是因为FFT算法要求信号序列的长度必须是2的幂次方。
如果信号序列的长度不是2的幂次方,需要进行长度的补齐或者截断操作。
通过对信号序列进行补齐或者截断,可以避免频谱泄漏的问题,并且可以确保FFT算法的正确性。
FFT算法的具体实现通常采用递归或者迭代的方式。
递归实现的FFT算法主要是通过将整个信号序列分解成较小规模的子序列,然后对每个子序列进行FFT计算,最终得到整个信号的频域表示。
迭代实现的FFT算法则是通过依次计算每个蝶形运算的结果,从而得到整个信号的频域表示。
FFT算法在数字信号处理领域有着广泛的应用。
例如,它可以用于信号的滤波和去噪、信号的频谱分析和频率成分提取、图像处理中的边缘检测和特征提取等。
由于FFT算法具有高效的计算速度,尤其适合处理大规模信号序列,因此在实际应用中被广泛采用。
离散傅里叶变换及快速算法

(5-5)
W e N
j
2 N
的性质:
正交性,周期性,
共轭对称性(偶序列),可约性。
§5.离散傅里叶变换及快速算法
1.离散傅里叶级数
1.2离散傅里叶级的计算
例5-1 求出下面周期序列的DFS
x(n) 0 ,1,2,3, 0 ,1,2,3, 0,1,2,3
n0
为改进嵌套循环计算的效率,将循环结构改为矩阵形式计算
§5.离散傅里叶变换及快速算法
0.概述
离散时间傅里叶变换(DTFT)是通过周期频谱 来描述一个离散信号序列,即DTFT是连续变 量w的连续函数。离散傅里叶变换(DFT)则是 针对有限长序列,是对DTFT采样后得到的离 散序列。 此种表示方法非常有利于数值计算以及数字信 号处理算法的DSP硬件实现。 本章将研究离散傅里叶级数,离散傅里叶变换 (DFT),及离散傅里叶变换的快速算法FFT。
(5-3)
n0
称之为离散傅里叶级数DFS的系数。是一个基波周期为N的 周期序列。
X (k) X (k N)
§5.离散傅里叶变换及快速算法
W e 在DFS变换中引入复数 N
j
2 N
将DFS正反变换描述为
N 1
X (k) x(n)WNnk
n0
x (n)
1 N
N 1
X (k )WNnk
k 0
n0
x(n)
1 N
N 1
X (k )WNnk
k 0
x
1 N
WN* X
WN WNkn 0
k,n
N
1
1 1
1
WN1
1
W ( N 1) N
1
W ( N 1) N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int n, mmax, m, j, istep, i; double wtemp, wr, wpr, wpi, wi, theta; double tempr, tempi; n = nn << 1; j = 1; for (i = 1; i < n; i += 2) { if (j > i) { tempr = data[j]; data[j] = data[i]; data[i] = tempr; tempr = data[j+1]; data[j+1] = data[i+1]; data[i+1] = tempr; } m = n >> 1; while (m >= 2 && j > m) { j -= m; m >>= 1; } j += m; } mmax = 2; while (n > mmax) { istep = 2*mmax; theta = TWOPI/(isign*mmax); wtemp = sin*theta); wpr = *wtemp*wtemp; wpi = sin(theta); wr = ; wi = ; for (m = 1; m < mmax; m += 2) { for (i = m; i <= n; i += istep) { j =i + mmax; tempr = wr*data[j] - wi*data[j+1]; tempi = wr*data[j+1] + wi*data[j];
相关文档:
• • • • • • • • • •
更多相关文档请访问:
} // 将时域点写入 X1 memcpy(X1, TD, sizeof(complex) * count); // 采用蝶形算法进行快速 Fourier 变换 for(k = 0; k < r; k++) { for(j = 0; j < 1 << k; j++) { bfsize = 1 << (r-k); for(i = 0; i < bfsize / 2; i++) { p = j * bfsize; X2[i + p] = X1[i + p] + X1[i + p + bfsize / 2] * W[i * (1<
FFT(离散傅氏变换的快速算法)
FFT(离散傅氏变换的快速算法) 目录 1 算法简介 2DFT 算法 3 源码表示 4MATLAB 中 FFT 的使用方法 1 算法简介编辑 FFT(Fast Fourier Transformation),即为快速傅氏变换,是离散傅氏变换的快 速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法 进行改进获得的。它对傅氏变换的理论并没有新的 FFT 算法图(Bufferfly 算法) 发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是 进了一大步。 设 x(n)为 N 项的复数序列,由 DFT 变换,任一 X(m)的计算都需要 N 次复数乘 法和 N-1 次复数加法,而一次复数乘法等于四次实数乘法和两次实数加法,一次复数 加法等于两次实数加法,即使把一次复数乘法和一次复数加法定义成一次“运 算”(四次实数乘法和四次实数加法),那么求出 N 项复数序列的 X (m),即 N 点 DFT 变换大约就需要 N^2 次运算。当 N=1024 点甚至更多的时候,需要 N2=1048576 次运算,在 FFT 中,利用 WN 的周期性和对称性,把一个 N 项序列(设 N=2k,k 为正整 数),分为两个 N/2 项的子序列,每个 N/2 点 DFT 变换需要(N/2)2 次运算,再用 N 次 运算把两个 N/2 点的 DFT 变换组合成一个 N 点的 DFT 变换。这样变换以后,总的 运算次数就变成 N+2*(N/2)^2=N+(N^2)/2。继续上面的例子, N=1024 时,总的 运算次数就变成了 525312 次,节省了大约 50%的运算量。而如果我们将这种“一 分为二” 的思想不断进行下去,直到分成两两一组的 DFT 运算单元,那么 N 点的 DFT 变 换就只需要 Nlog2N 次的运算,N 在 1024 点时,运算量仅有 10240 次,是先前的直 接算法的 1%,点数越多,运算量的节约就越大,这就是 FFT 的优越性。 2DFT 算法编辑 For length N input vector x, the DFT is a length N vector X, with elements
data[j] = data[i] - tempr; data[j+1] = data[i+1] - tempi; data[i] += tempr; data[i+1] += tempi; } wr = (wtemp = wr)*wpr - wi*wpi + wr; wi = wi*wpr + wtemp*wpi + wi; } mmax = istep; } } 在 C++环境下的源码 bool FFT(complex * TD, complex * FD, int r) { //一维快速 Fourier 变换。 //complex * TD ——指向时域数组的指针; complex * FD ——指向频域数 组的指针; r ——2 的幂数,即迭代次数 LONG count; // Fourier 变换点数 int i,j,k; // 循环变量 int bfsize,p; // 中间变量 double angle; // 角度 complex *W,*X1,*X2,*X; count = 1 << r; // 计算 Fourier 变换点数为 1 左移 r 位 W = new complex[count / 2]; X1 = new complex[count]; X2 = new complex[count]; // 分配运算所需存储器 // 计算加权系数(旋转因子 w 的 i 次幂表) for(i = 0; i < count / 2; i++) { angle = -i * PI * 2 / count; W[ i ] = complex (cos(angle), sin(angle));
N X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N. n=1 The inverse DFT (computed by IFFT) is given by N x(n) = (1/N) sum X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N. k=1 3 源码表示编辑 在 C 环境下的源码 源码(1): 注:亲测,这个版本无法运行,作者删改了重要内容[1]请参考源码(2) (see pages 507-508 of Numerical Recipes in C) Inputs: data[] : array of complex* data points of size 2*NFFT+1. data[0] is unused, * the n'th complex number x(n), for 0 <= n <= length(x)-1, is stored as: data[2*n+1] = real(x(n)) data[2*n+2] = imag(x(n)) if length(Nx) < NFFT, the remainder of the array must be padded with zeros nn : FFT order NFFT. Thisห้องสมุดไป่ตู้MUST be a power of 2 and >= length(x). isign: if set to 1, computes the forward FFT if set to -1, computes Inverse FFT - in this case the output values have to be manually normalized by multiplying with 1/NFFT. Outputs: data[] : The FFT or IFFT results are stored in data, overwriting the input. */ void four1(double data[], int nn, int isign) {
